Abstract
Bird strikes are a common, serious, and devastating event in aviation accidents, and multi-bird strikes are also frequently reported. A numerical multi-bird-strike simulation was performed to investigate the effect of flocking birds striking on engine blades. The smooth particle hydrodynamics (SPH) method was adopted in the hemispherical-ended bird substitute model, and the finite element method (FEM) with EOS state equation was adopted for the fan model as well. Impact analyses have been presented using different flocking birds and impact location distributions. A “0-2-1” supported rotor system dynamic model was established to study the effect of the multi-bird-strike impact forces on the rotor system. The results show that bird-strike severity is related to the impact location distribution, with blade-root impacts being the most dangerous. The small flocking bird strikes had little effect on the fan compared to the cases of medium flocking birds and the large single bird. The dynamic response of the fan to the small flocking birds was the same as without a bird strike, while the other cases changed the motion period and excited the rotor first-order vibration.
1. Introduction
Bird strike is a sudden and frequent accident, posing a serious threat to aviation flight safety. Structural bird-strike resistance should be evaluated during the design stages of aircraft components such as fan blades and rotor systems. Numerous studies on bird strikes have been carried out [1]. Previous studies focused on single bird strikes on engines, whereas in practice aircraft were often struck by flocks of birds. In 2009, both engines of United States (US) Airways Flight 1549 lost thrust after encountering a flock of birds and ditched on the Hudson River [2]. According to Federal Aviation Administration (FAA, Washington, DC, USA) statistics, there were 141,067 bird strikes between 1990 and 2020, with strikes by multiple birds 19,484 times, accounting for 13.8% of the total [3]. To confirm bird numbers and weights in future certification testing requirements, a relationship between bird flock density and a biometric factor has been described [4]. To evaluate the bird-strike airworthiness requirement, the bird-strike impact energy distribution under the environment of bird flocks was studied [5]. Studies show that it is important to study bird strikes with multiple birds.
In the early days, limited by computational techniques, experimental methods were mainly used to study bird-strike processes [1]. With advances in technology, numerical methods for bird-strike simulations have become diverse. Due to the large deformation in the high-speed bird-strike process, the mesh is prone to distortion during the calculation, leading to calculation errors [6]. The SPH method is a meshless method that has been widely used in simulations.
In both experimental and simulation studies, bird modeling has always been a key question. To improve the accuracy of bird substitute models, the International Bird-strike Research Group (IBRG, Amsterdam, The Netherlands) studied the biometric data of different bird species and proposed a relationship between bird mass and the substitute model’s geometric parameters [7]. There are currently four mainstream models used to replace real birds in experiments and simulations: namely the sphere, ellipsoid, straight-ended cylinder, and hemispherical-ended cylinder models. Much research had been conducted on these substitute models. Hedayati et al. compared four traditional models, and the results showed that the hemispherical-ended cylinder was closer to the bird model in the experimental test [8]. I. Smojver et al. [9] and Chandra, C. et al. [10] both used hemispherical-ended cylinders to carry out bird-strike simulations and obtained acceptable results. Whereas traditional models were merely a simplification of the real bird body, in recent years three-dimensional (3D) scanning technology has been used to build a real-bird model, allowing the effect of body parts (head, tail, wings, etc.) on bird strikes to be studied [11,12]. However, this model can only be used for specific birds, cannot change their volume and mass, is difficult to modify, and is not well-suited to multi-bird strikes. Therefore, the hemispherical-ended substitute model was used in this paper.
For impact targets, which evolved from flat plates in the beginning to the current rotating blades, blades differ in terms of configuration and material. Single straight blades were first used [13,14], but this model did not reflect the bird-strike process well, as birds tended to contact with multiple blades. While straight blades were simple, the twist of the blades also influenced bird-strike results [15]. Hence, multi-blades with twisting angles were closer to the actual situation. To better observe the stress distribution, an entire fan was also introduced into the bird strike model [16,17]. The fan materials were mainly rigid at the beginning, and the blades could not be deformed during impact, which was not in line with reality [18]. Based on the characteristics of the blade material, materials that could reflect the blade’s elasticity were used in simulations [12]. The Johnson-Cook material model, which can consider blade yield deformation and even fracture, is now widely applied [19,20,21]. According to the above study, a rotating fan using the Johnson-Cook material model was selected as the impact target in this paper.
Rotor systems are susceptible to sudden loads that can occur after a bird strike on an engine [22]. The transient impact can change the engine’s operation, causing it damage. The engine is very sensitive to these changes, whether the transient loads are triggered by the bird strike, rub impact or airflow excitation [23,24,25]. To study the effect of different bird flocks striking on the engine rotor system and obtain the most dangerous scenario, this paper calculated the effect of multi-bird impact forces on the rotor system.
In conclusion, it was observed that although multi-bird strikes on engines are common, there is still less research on flocking bird strikes on fans and fewer studies involving rotor system response to bird-strike forces. The multi-bird strike differs from that of a single bird in that the impact mass is larger and more blades are in contact. To study the hazards of flocking birds striking a fan, the hemispherical-ended model was applied in this paper with easily modifiable dimensions to simulate different birds and meet the requirements for multi-bird-strike simulations. An entire stage fan was considered to obtain the blade stress distribution and impact forces. As transient impacts from bird strikes have a significant effect on the rotor system, the bird-strike forces in hazardous working conditions were extracted and the rotor system response at the fan was calculated for different bird flock strikes. The study in this paper contributes to a preliminary understanding of flocking bird impact effects and provides a reference for the development and modification of requirements for bird-strike airworthiness in aero engines.
2. Bird-Strike and Rotor Dynamics System Modeling
2.1. Bird SPH Model and Validation
As previously mentioned, a hemispherical-ended cylinder bird model is frequently used as the best substitute model. It was chosen as the bird model in this paper. The bird geometric model is shown in Figure 1a. The length-to-diameter ratio is the key parameter in this model. Many studies have been performed on suitable geometric models, and a hemispherical-ended cylinder with the length-to-diameter ratio of 2 was proposed [8,26], i.e., , where and are the length and diameter of the hemispherical-ended model. To determine the and for each model, we introduce the equation for calculating hemispherical-ended volume:
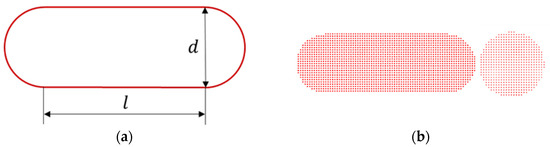
Figure 1.
The hemispherical-ended cylinder model: (a) Geometric model; (b) SPH model.
is the hemispherical-ended volume, combined with the mass calculation equation:
is the bird mass, is the bird density. The diameter of the bird substitute model can be calculated by:
According to airworthiness standards [3], bird ingestion requirements have been defined for a large single bird and small and medium flocking birds. As the applied engine inlet throat area is , suitable bird parameters were selected for the simulation experiments, as shown in Table 1 (The data in the table refer to each bird).

Table 1.
Bird categories and parameters.
The SPH method was used to discretize the bird model (see Figure 1b). The large bird model consisted of 36,755 SPH particles, with each particle weight 0.075 g. The larger medium bird SPH particles totaled 15,215 and weighed 0.0756 g each. The smaller medium bird SPH particles totaled 47,020 and weighed 0.0744 g each. The small flocking birds were discretized with 17,776 SPH particles, each weighing 0.0765 g.
The bird material model is a null material model. The bird density is . When the null material model is used with SPH elements, an equation-of-state (EOS) is necessary [27]. For this, the Gruneisen EOS was adopted. For compressed materials, the Gruneisen EOS defines the pressure as:
For the expanded material, the pressure is defined as:
where is the vs − vp curve’s intercept; S1, S2, and S3 are the vs − vp curve’s slope coefficients; is the Gruneisen constant; a is the Gruneisen gamma’s first-order correction; and where is the material’s density and is the reference density. E is the elastic modulus of the material. For the bird substitute model, , and ; all other parameters were set to 0.
Wilbeck performed many bird-strike tests and provided many test results [28]. In previous studies [12,22], the hemispherical-ended bird model has been proven to be accurate.
2.2. Fan Modeling
An aero-engine fan consisting of 24 equidistant narrow chord blades and a rigid hub was meshed as the impact target in the simulation. Each blade measured 603.2 mm in length with a torsion angle of 61.3°. Ignoring the connection between the blade and the hub, the fan model was discretized with 1,520,208 solid elements using the FEM. To consider the bearing’s effect rather than ignore it in the bird-strike simulation, the rolling type bearing is regarded as a stiffness-damping system. Two nodes fixed to the center of rotation connected by two discrete elements were used to model the bearing in the simulation. These two discrete elements could define the stiffness and damping of the bearing. The FE fan model is shown in Figure 2.
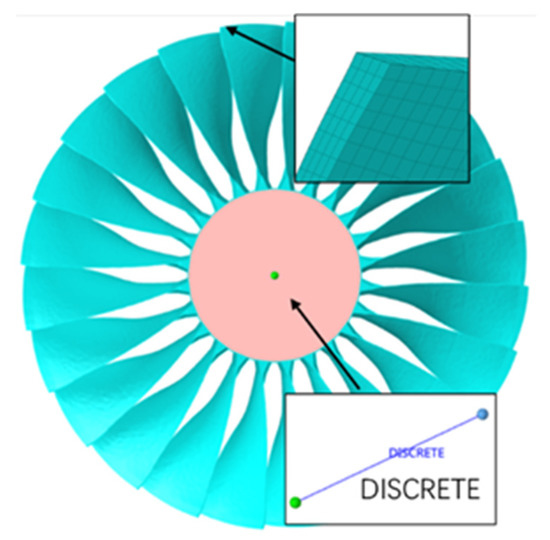
Figure 2.
The FE fan model with bearing used in numerical simulation.
The Johnson-Cook material model has often been chosen as the material model to simulate blade behaviors [9,29]. The blades were made of titanium alloy Ti-6Al-4V; the material parameters are given in Table 2.

Table 2.
Johnson-Cook material parameters for Ti-6Al-4V.
As with the bird modeling, when using the Johnson-Cook material model in LS-DYNA, it is requisite to define an EOS for the material model. The Gruneisen EOS was adopted again. For the Ti-6Al-4V Gruneisen EOS [14], parameters m/s, , and were set, and other parameters were zero.
2.3. Bird-Strike Settings
To investigate the difference between a single bird and bird flocks striking the aero engine, a single large bird striking the fan and small and medium flocking birds striking the fan were simulated in this paper. The bird-flock-strike setting required in the airworthiness manual [3] stated that the birds must be targeted to the first exposed locations and evenly distributed over the engine face area. Combining the selected engine structure with the research objectives, nine calculation cases were set up in this paper (see Figure 3a–c). The root, middle, and tip represented 1/6, 3/6, and 5/6 of the blade height, respectively.
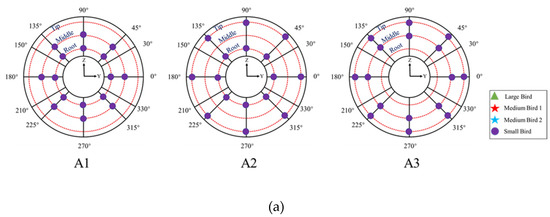
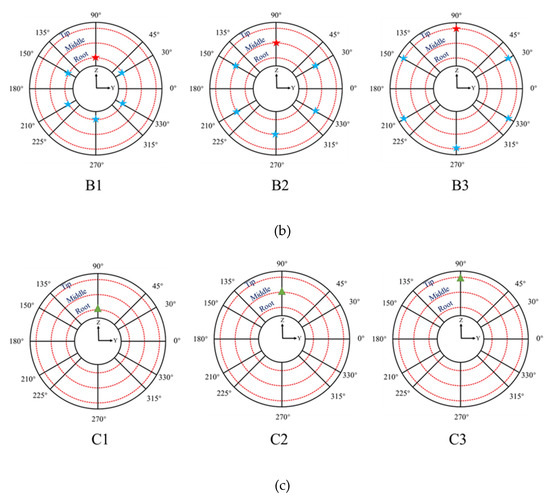
Figure 3.
The different bird-strike cases: (a) small flocking birds, (b) medium flocking birds, (c) single large bird.
To model the interaction between a single bird or bird flocks and the engine fan, a suitable contact algorithm was adopted to model the bird-strike event in the simulation. The contact between bird SPH particles and the fan FE elements was nodes-to-surface, which is one of the main approaches for contact treatment [14]. The bird-strike boundary conditions were the same, except for the different bird weights, quantities, and locations. The termination time for all nine cases was set to 6 ms to ensure the impact process ended. For each case, outputs were divided into 100 steps, i.e., 0.06 ms per time step. Each bird’s initial velocity was 253 m/s, while the fan was given angular velocity of . The bearing stiffness and the damping values were set to N/m and 500 N·s/m, respectively.
2.4. Prestress Analysis
The large rotating radius of the fan blades made preloading the blades necessary. Several studies had investigated the influence of blade prestressing and found that the blade deformation was affected by prestressing [13,30]. To obtain more accurate bird-strike simulation results, a prestress analysis was performed before bird-strike analysis. Fan rotational speed was 395 rad/s, which was the take-off speed of the engine. In LS-DYNA, dynamic relaxation was applied to obtain the prestress Von Mises stress distribution. Results are shown in Figure 4. The maximum stress on a fan with prestressing loaded was 578 MPa. The Von Mises stress was higher at the blade root.
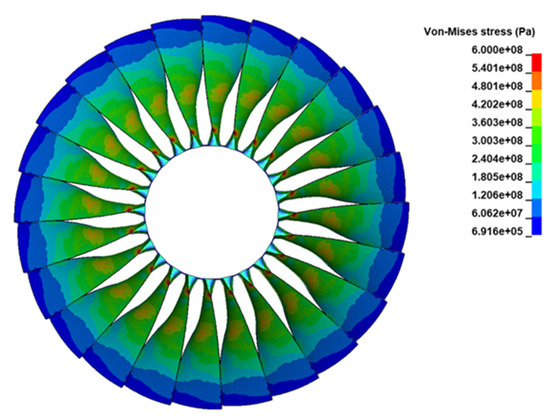
Figure 4.
The prestress Von Mises stress distribution of fan.
2.5. Aero-Engine Rotor System and Validation
Bird strikes have a strong influence on aircraft engine function [31]. To investigate the aero-engine rotor system dynamic response to different bird-strike events, a rotor dynamics system was established from a real aero engine. Combining the impact forces from the bird-strike simulation above, the rotor dynamic response was obtained under a large bird strike and small and medium flocking bird strikes.
An accurate rotor dynamics model is essential in dynamic calculations. A low-pressure rotor system was selected for study with a “0-2-1” bearing supporting mode. It consisted of a four-stage low-pressure turbine, a fan and three rolling bearings. The low-pressure rotor system comprised three coordinates scanned by BESTSCAN 751 (HOLON 3D, Shenzhen, China) three-dimensional (3D) scanner (see Figure 5). The point cloud data of each component were obtained and entered in the software HL-Scan, then a 3D model was constructed in the software CATIA. According to the material and geometry of the rotor system, the 3D model was used to establish the rotor system dynamics model by the lumped-mass method, as shown in Figure 6.

Figure 5.
The 3D scanning of the aero-engine low-pressure rotor system.
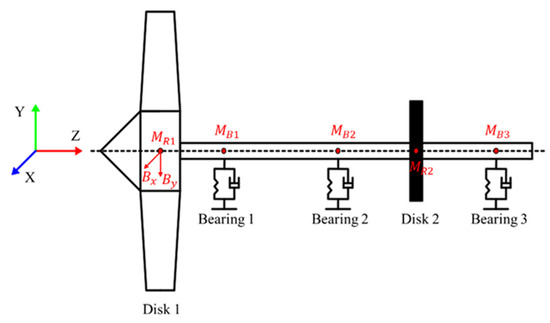
Figure 6.
The rotor system dynamics model.
This study examined the radial vibration in the x-y plane due to birds impacting the fan. Vibrations in other directions were not considered. The torsional vibration was also neglected, and the following assumptions were given:
- Consider the fan hub and blades as a disk, and add the bird impact force to this disk;
- The eccentricity of the rotor system existed only on the two simplified rotor disks;
- The connection between blades and disk was ignored, and the shaft and disks were considered to be rigidly connected;
- Gyroscopic effects of the rotor system were not considered due to the low speed of 3772 r/min.
According to the vibration differential equation, the equation for the rotor system could be written as:
and () are the bearing forces in the x and y directions. The rolling bearings could be simplified as an elastic system, and the stiffness of each bearing was set to constant (). The forces could be written as and . The other parameters are shown in Table 3.

Table 3.
The definitions and values of rotor system parameters.
We established a similar rotor system in our previous research [32]. The ”0-2-1” supported rotor test rig was also built by the 3D scan method and scaled down by the kinetic similarity principle. The vibration response at 1500 r/min was measured experimentally. Comparison with the numerical calculation results showed that the dynamical system vibration response was consistent with the vibration response of the experimental setup [22]. Therefore, the rotor dynamic model established in this paper was reliable.
2.6. Dynamic Calculation Settings
As described earlier, the bird-strike forces are crucial in rotor dynamics calculations. In this study, the worst conditions on the engine needed to be considered, so among the nine impact scenarios that were proposed, the one with the highest bird impact force in the x and y directions (the coordinates in Figure 6) was selected for the dynamic calculations. According to the existing simulation conclusion, the maximum impact force of a bird occurred when it hit the blade root. Meanwhile, to study the influence of the large bird’s and small and medium-sized flocks’ impact on the rotor system, these three situations were calculated separately. Therefore, cases A1, B1 and C1 were chosen for dynamic calculations.
Equation (6) was programmed and solved using the Newmark-β method. A total of 400 calculation cycles were carried out in the dynamic response calculation, and the iteration’s initial step size was set to s. To exclude fluctuating disturbances, the bird impact force was added after the calculation stabilized (chosen at s). The method to substitute the impact force data into the dynamic equation was a linear interpolation. These data could be obtained in the bird strike simulations. To observe the difference before and after a bird strike, the data selected for analysis were taken from s. For the dynamic vibration response under bird strike faults, the time domain figure, the orbit map, and the spectrogram were plotted to analyze the vibration characteristics.
Due to the complexity of the system model and the long response time required to solve the model, the system equations were dimensionless to improve the calculation speed. The rolling bearing clearance was introduced for non-dimensional disposal and . The parameters for the non-dimensional calculations were the displacement, speed, and acceleration, where and ,
and ,
and .
3. Results and Discussion
3.1. Bird Strike Simulation
The impact of a single bird on a fan has been studied by many scholars, focusing on the stress distribution on the blades, the kinetic energy loss, and the impact force on the fan, which determine how the engine is affected by bird strikes. In this paper, the results mentioned above were also been obtained for the cases involving a large single bird and small and medium flocking bird strikes. The effects of these cases on the fan blades were investigated. The damage to the fan caused by birds of different mass and different distributions of bird impact locations was also analyzed.
The distribution of Von Mises stress under nine impact cases is shown in Figure 7. In Figure 7a, when the small flocking birds impacted the fan blades using three different impact location distributions, the Von Mises stress distributions were similar. The higher stress areas were concentrated at the leading edge in direct contact with the bird body. However, the difference in the maximum of Von Mises stress was pronounced. In the case of A1 (striking on the middle and root of blades), the value for maximum stress was 1084 MPa, whereas the value in A2 (striking on the tip and root of blades) was 945 MPa. For A3 (striking on the tip and middle of blades), the maximum was only 858 MPa. The yield stress of the blade was 1098 MPa; there was no permanent deformation of the blades, so the small flocking birds impacting on the blades would increase the Von Mises stress on the fan but with less damage to blades. Additionally, we noticed that when small flocking birds struck the fan, the maximum stress was generated by simultaneous impacts on the blade middle and root. Therefore, case A1 could be considered as the bird distribution with the most significant effect on blade stress of the three.
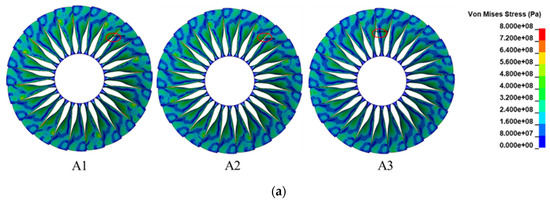
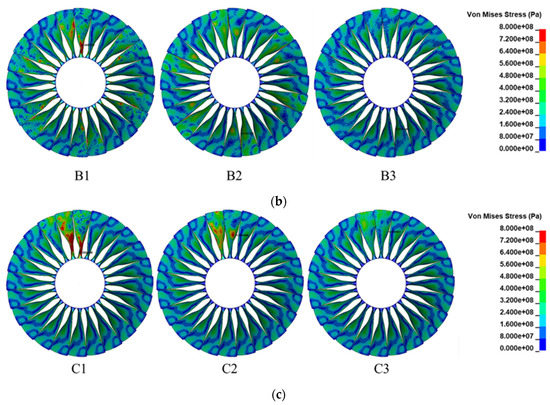
Figure 7.
Distribution of Von Mises stress after impact by: (a) small flocking birds; (b) medium flocking birds; (c) large single bird.
In Figure 7b, the stress maximums of medium flocking birds impacting the fan were 1236, 1117 and 900.2 MPa in case of B1 (medium flocking birds striking on the blade root), B2 (medium flocking birds striking on the blade middle), B3 (medium flocking birds striking on the blade tip), respectively. The stress maximums in cases B1 and B2 were both beyond the material yield stress; blades would be permanently deformed in these cases, causing damage to the engine. This damage would be much less in the case of B3. The stress distribution showed that the stresses at the bird–blade contact location were significantly higher than in other areas. There was no such phenomenon when the bird impacted the blade tip. Comparing the large-medium bird with the small-medium bird, the greater the mass, the greater the stress generated.
The situation with the single large bird Impact was similar to that in previous studies; the maximum Von Mises stress developed by impacting the blade root reached 1269 MPa. The values for the other cases, C2 (large single bird striking on the blade middle) and C3 (large single bird striking on the blade tip), were 1198.7 and 949 MPa, respectively. In Figure 7c, the areas of high stress were concentrated on the blades in contact with the bird. The case of C1 (large single bird striking on the blade root) was the most dangerous scenario.
The contact force and the bearing force under nine impact conditions are shown in Figure 8. From Figure 8a, the maximum bird impact force was generated for the case of A1 (148 kN), followed by the cases of A2 (82 kN) and A3 (71.3 kN). The magnitude ordering of the bearing forces was the same as that of the impact forces in Figure 8d. The maximum values, in descending order of magnitude, were A1 (174 kN), A2 (159 kN) and A3 (80.3 kN), and the trend in force over time was the same. As could be seen from the bird impact forces and the bearing forces, there was little difference in impact during the small flocking bird impact, with the maximum values occurring when the birds impacted the root and middle of the blades. In Figure 8b, the maximum impact force occurred in the case of B2 (419 kN), while the maximum bearing force was generated in case B1 (650 kN) in Figure 8e. We thought that the situation where there was a greater impact force in hitting blade middle than in hitting the root was because the axial impact force had increased due to the larger bird size, leading to an increase in the resultant force, while the radial force was still greater in B1 (83.5 kN) than in B2 (41.1 kN). Maximums of the contact forces in cases C1, C2, and C3 were 818, 298 and 45.4 kN, respectively (Figure 8c), and maximums of the bearing forces were 639, 214 and 69.2 kN, respectively (Figure 8f). A lower impact location in the case of a large bird results in a higher magnitude of the contact force and bearing force.
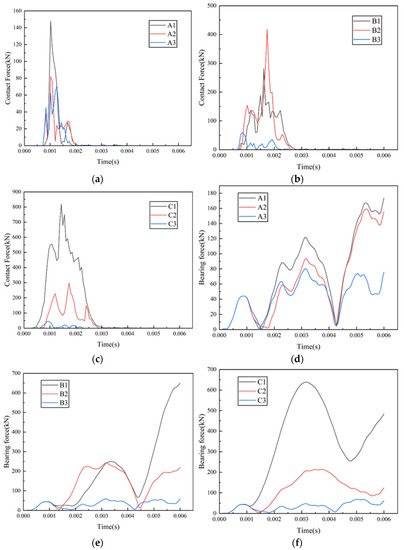
Figure 8.
Contact force vs. time: (a) small flocking birds; (b) medium flocking birds; (c) large single bird. The bearing force vs. time: (d) small flocking birds; (e) medium flocking birds; (f) large single bird.
As for the changes in bird kinetic energy in Figure 9a, it can be seen that the kinetic energy increased when small flocking birds impacted the fan; the growth values were 43, 27.3 and 12 kJ, respectively. In cases of B1, B2, C1 and C2, the kinetic energy had increased to 186, 97, 111.3 and 41.3 kJ, respectively (Figure 9b,c). When the large and medium birds hit the blade tip, there was a tiny kinetic-energy loss for the birds, of 0.52 and 3 kJ, respectively. Combined with the previous data on the stress, it could be assumed that this was due to the absence of plastic deformation and, therefore, the low energy loss of the fan.
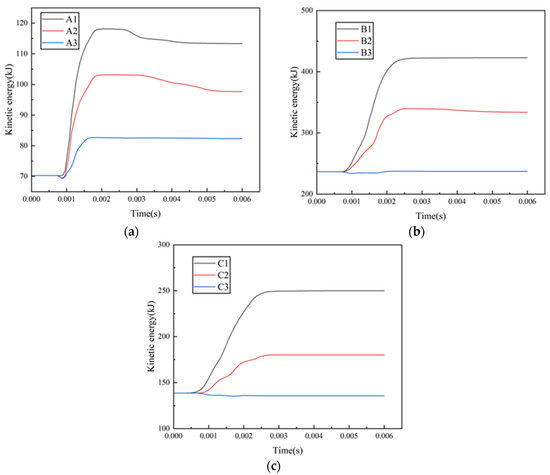
Figure 9.
Kinetic energy vs. time: (a) small flocking birds; (b) medium flocking birds; (c) large single bird.
Comparing the above nine cases, small flocking birds impacted the fan with minimal effect. The impact of medium flocking birds on the blades was similar to that of large single birds. Bird distribution in a flock had a significant effect on the flocking bird strike due to the effect of the impact location. The most dangerous impact scenario often occurred when the bird impacted the blade root; here, the maximum radial force was generated on the fan. Therefore, to investigate the effect of different bird impacts on the rotor system, cases A1, B1 and C1 were chosen as the preconditions required for the dynamics calculations.
3.2. Rotor System Dynamics Calculation
Combining the simulation results with the dynamics equations, the response of the rotor dynamics system before and after bird impact can be obtained. The rotor displacement in the x direction vs. time is shown in Figure 10a, when no bird impacts the blades. The x-direction displacement at Disk1 is stable over time with a maximum amplitude of 0.88. It also can be seen in Figure 10e that the axis orbit is a regular and closed circle spanning −0.88 to 0.88 in the x direction and −3 to −1.7 in the y direction. The system has a single periodic motion before bird strike. When bird-strike forces are added at s, the displacement vs. time and axial orbit change.
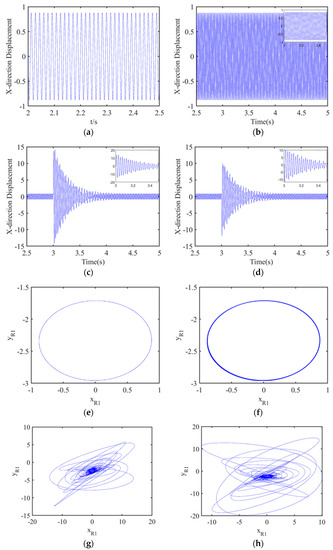
Figure 10.
The dynamic response of the fan before and after bird strike: displacement vs. time in the X direction (a) before bird strike; (b) after small flocking bird strike; (c) after medium flocking bird strike; (d) after large single bird strike; axis orbit: (e) before bird strike; (f) after small flocking bird strike; (g) after medium flocking bird strike; (h) after large single bird strike.
In Figure 10b, f, there is no discernible difference between bird strikes and no bird strikes. The x-direction displacement curves remain largely unchanged at , and the axial orbit remains within the original range and is a closed circle. Therefore, it can be assumed that small flocking bird impacts have almost no effect on the rotor system, and the same conclusion can be drawn in conjunction with the previous Von Mises stress distribution results.
When the medium flocking birds impact the fan, the displacement curve has obvious change, as shown in Figure 10c. The maximum displacement is 14.7 in the x direction, and it gradually decreases with the damping, eventually returning to normal. The impact was caused by the bird strike. The axial orbit becomes disordered, and the motion amplitude increases compared to before the bird strike. In the x direction, the amplitude changes from −14.2 to 13.8, and in the y direction, it changes from −12.4 to 5.8 in Figure 10g, with the amplitude becoming at most 16 times larger. In the middle of the graph, there is a stable circular area, corresponding to the final stage of stabilization with the rotor system, where the whole process changes from a stable, single periodic motion to a complex irregular quasi-periodic motion, and then to a single periodic motion under the effect of damping when the bird impact force disappears.
The impact of the large single bird has an effect similar to that of the medium flocking birds, differing in magnitude first in the time history diagram (Figure 10d), where the curves of change take the same form, both starting to vary dramatically after bird impact. The range of variation in x-direction amplitude variation is −11.9 to 10.1, which is smaller than that of the medium flocking birds, due to the smaller component of force in the x direction when the large bird impacts the fan. The axial orbit line (Figure 10h) shows that the variation of displacement in the y direction ranges from −19.7 to 14.9; the range of variation becomes more extensive.
The time history of displacement and the axis orbit show that the large single bird and medium flocking birds have a more pronounced effect on the rotor system, while the small bird flocks have no effect. Therefore, for practical testing, it is recommended to use the medium flocking birds to test the engine impact characteristics in the event of a flock impact.
Figure 11a shows the frequency spectrum of a small flock of birds, before and after the bird strike; there is only a fundamental frequency of 62.9 Hz, which is the same as the rotation frequency. In Figure 11d, e, the time-frequency graph displays the same results, namely, that small flocking birds’ impacts have little effect on the frequency of the rotor system.
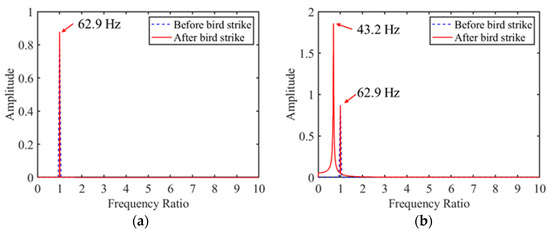
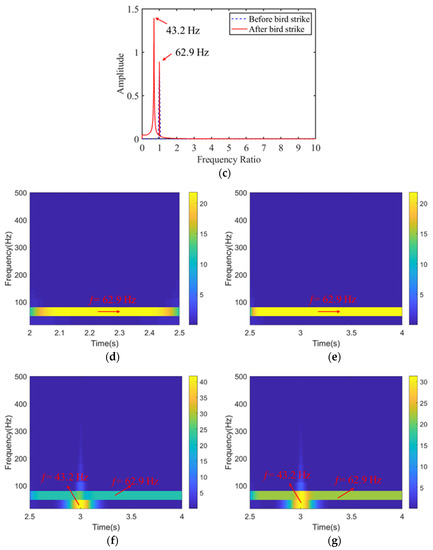
Figure 11.
The dynamic response of the fan before and after bird strike: frequency spectrum of (a) small flocking bird strike; (b) medium flocking bird strike; (c) large single bird strike; time-frequency graph of (d) no bird strike; (e) small flocking bird strike; (f) medium flocking bird strike; (g) large single bird strike.
As for the medium flocking bird strike, besides the fundamental frequency of 69.2 Hz, a frequency of 43.2 Hz appears after the bird strike and has a much higher amplitude in Figure 11b. This additional generation frequency can also be found in Figure 11c. This frequency is close to the first-order frequency of the rotor system. The rotor system first-order response was excited by the bird-strike impact force coming from the medium flocking bird and large single bird strikes.
In Figure 11f,g, the frequency 43.2 Hz also appears after bird strike with a high-frequency peak. Therefore, compared with the impact of small flocking birds, the large bird and medium flocking bird strikes on the fan are more obvious and can excite the natural frequency of the system, which is more meaningful to study in bird strikes.
4. Conclusions
This paper analyzed the scenarios of medium flocking birds, small flocking birds, and a single large bird striking blades according to the airworthiness regulations. The distribution of bird impact locations was ranked to find the most dangerous scenario, and then the bird impact forces were combined with the established rotor model to obtain the dynamic response of the engine fan under bird impact. The following conclusions were drawn:
(1) The distribution of impact locations affects the magnitude of the stresses on the blades; the maximums of stress were 1084, 1236 and 1269 MPa. The maximum values of impact forces were 174, 650, 639 kN, and maximum bearing forces were 148, 419 and 818 kN in the three bird-strike cases, basically occurring when birds impacted the blades’ root. As the height of impact decreases, the risk of bird strike becomes more severe.
(2) The total bird mass has a significant effect on the bird-strike process. The small flocking bird strike had little effect on the fan, with maximum stress of 1084 MPa (impact on the blade root), whereas medium flocking birds had an effect similar to that of a single large bird, with maximum stresses of 1236 and 1269 MPa, respectively, both exceeding the yield strength and causing damage to the fan blades.
(3) With small flocking bird impacts, the rotor dynamic response changed little. With medium flocking bird or single large bird strikes, the bird-strike forces excited the fundamental frequency of the rotor system (43.2 Hz). The motion changed to a complex irregular motion at the moment of the bird strike and finally returned to a single-periodic motion under the damping effect.
(4) Combined with the above results, the use of a larger mass of birds and a lower blade impact location in impact tests would allow for more severe test conditions to be obtained to verify the bird impact resistance of the engine blades. As variations in airfoil structure can affect the bird-strike results and the conclusions may not apply to all engine types, this paper sought to provide a research idea to guide the design of multi-bird-strike experiments.
Author Contributions
Conceptualization, B.W. and J.Z.; methodology, B.W., A.X. and J.L.; software, B.W. and G.Z.; validation, B.W., J.Z. and H.D.; resources, H.D. and J.L.; data curation, H.D.; writing—original draft preparation, B.W.; writing—review and editing, H.D. and N.W.; supervision, A.X.; project administration, J.Z.; and funding acquisition, G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by joint funds of the National Science Foundation of China and the Civil Aviation Administration Foundation of China (U1833108).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this paper are available on request from the corresponding author.
Acknowledgments
The authors wish to especially acknowledge the contributions of Z. L. of Midea Group.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Nomenclature | |
| Abbreviation | Definition |
| 3D | Three-Dimensional |
| CT | Computed Tomography |
| EOS | Equation Of State |
| FAA | Federal Aviation Administration |
| FE | Finite Element |
| FEM | Finite Element Method |
| IBRG | International Bird-strike Research Group |
| SPH | Smoothed Particle Hydrodynamics |
| US | United States |
| List of symbols | |
| Symbol | Definition |
| Yield stress | |
| a | First-order volume correction to γ0 |
| Strain hardening modulus | |
| Bird impact forces in the x and y directions | |
| C | The intercept of the velocity curve |
| Damping coefficients of ball bearings | |
| Damping coefficients of the disk | |
| Strain rate dependence coefficient | |
| D | Damage parameter |
| Failure parameters | |
| E | Elastic modulus of material |
| The eccentricity of Disk 1 | |
| The eccentricity of Disk 2 | |
| Rate-of-deformation tensor | |
| Shear modulus | |
| Gravitational acceleration | |
| Stiffness of the shaft | |
| Mass of Disk 1 | |
| Mass of Disk 2 | |
| Mass of Bearing 1 | |
| Mass of Bearing 2 | |
| Mass of Bearing 3 | |
| Softening exponent | |
| Strain hardening exponent | |
| p | Pressure |
| S1, S2, S3 | Slope coefficients of the velocity curve |
| Current temperature | |
| The melt temperature of the material | |
| Room temperature | |
| Homologous temperature | |
| Displacement in the x and y directions | |
| Velocity in the x and y directions | |
| , | Acceleration in the x and y directions |
| Dynamic viscosity coefficient | |
| Gruneisen constant | |
| Clearance of the ball bearing | |
| The density of the material | |
| Reference density | |
| Rotational speed | |
| List of Markings | |
| Symbol | Definition |
| A1 | Small flocking bird strike on the root and middle of blades |
| A2 | Small flocking bird strike on the root and tip of blades |
| A3 | Small flocking bird strike on the middle and tip of blades |
| B1 | Medium flocking bird strike on the root of blades |
| B2 | Medium flocking bird strike on the middle of blades |
| B3 | Medium flocking bird strike on the tip of blades |
| C1 | Large single bird strikes on the root of blades |
| C2 | Large single bird strikes on the middle of blades |
| C3 | Large single bird strikes on the tip of blades |
References
- Heimbs, S. Computational methods for bird strike simulations: A review. Comput. Struct. 2011, 89, 2093–2112. [Google Scholar] [CrossRef]
- Atkins, E. Emergency Landing Automation Aids: An Evaluation Inspired by US Airways Flight 1549. In Proceedings of the AIAA Infotech@Aerospace, Atlanta, GA, USA, 20–22 April 2010. [Google Scholar]
- Regulation, F.A. Part 33, Airworthiness Standards: Aircraft Engines. Federal Avia 2011, 332–371. Available online: https://www.law.cornell.edu/cfr/text/14/part-33.
- Budgey, R. Three dimensional bird flock structure and its implications for birdstrike tolerence in aircraft. Proc. Int. Bird Strike Comm. 1999, 24, 307–320. Available online: https://canadianbirdstrike.ca/wp-content/uploads/2018/02/Budgey_1998.pdf.
- Cai, J.; Bao, H.; Zuo, H.; Huang, Y. Safety evaluation of airworthiness requirement of bird-strike on aeroplane. Eng. Fail. Anal. 2019, 102, 407–416. [Google Scholar] [CrossRef]
- El-Sayed, A.F. Bird strike in Aviation: Statistics, Analysis and Management; John Wiley & Sons: New York, NY, USA, 2019. [Google Scholar]
- Budgey, R. The development of a substitute artificial bird by the international Bird strike Research Group for use in aircraft component testing. International Bird Strike Committee ISBC25/WP-IE3, Amsterdam. In Proceedings of the International Bird Strike Committee, Amsterdam, The Netherlands, 17–21 April 2000. [Google Scholar]
- Hedayati, R.; Ziaei-Rad, S. Effect of bird geometry and orientation on bird-target impact analysis using SPH method. Int. J. Crashworthiness 2012, 17, 445–459. [Google Scholar] [CrossRef]
- Smojver, I.; Ivančević, D. Numerical simulation of bird strike damage prediction in airplane flap structure. Compos. Struct. 2010, 92, 2016–2026. [Google Scholar] [CrossRef]
- Chandra, C.; Wong, T.Y.; Bayandor, J. Crashworthiness assessment in aircraft ditching incidents. In Proceedings of the 27th international congress of the aeronautical sciences, Nice, France, 19–24 September 2010. [Google Scholar]
- Zhang, D.; Fei, Q. Effect of bird geometry and impact orientation in bird striking on a rotary jet-engine fan analysis using SPH method. Aerosp Sci Technol 2016, 54, 320–329. [Google Scholar] [CrossRef]
- Hedayati, R.; Sadighi, M. Bird Strike: An Experimental, Theoretical and Numerical Investigation; Woodhead Publishing: Sawston, UK, 2015. [Google Scholar]
- Puneeth, M.; JayaPrakash, D. Influence of bird mass and impact height on the fan-blade of an aero-engine. Mater. Today Proc. 2021, 44, 1028–1038. [Google Scholar] [CrossRef]
- Vignjevic, R.; Orłowski, M.; De Vuyst, T.; Campbell, J.C. A parametric study of bird strike on engine blades. Int. J. Impact Eng. 2013, 60, 44–57. [Google Scholar] [CrossRef]
- Husainie, S.N. Bird Strike and Novel Design of Fan Blades. In Proceedings of the 2017 Science in the Age of Experience, Chicago, IL, USA, 15–18 May 2017. [Google Scholar]
- Sun, Y.; Zhang, Y.; Zhou, Y.; Zhang, H.; Yang, K. Evaluating Impact Damage of Flat Composite Plate for Surrogate Bird-Strike Testing of Aeroengine Fan Blade. J. Compos. Sci. 2021, 5, 171. [Google Scholar] [CrossRef]
- Sinha, S.K. 5th International LS-DYNA Users Conference Transient Dynamics of Slicing-Impact Loading on Jet Engine Fan Blades during a Bird-strike Event. In Proceedings of the LSDYNA International Conference, Detroit, MI, USA, 10–12 June 2018. [Google Scholar]
- Allaeys, F.; Luyckx, G.; Paepegem, W.V.; Degrieck, J. Characterization of real and substitute birds through experimental and numerical analysis of momentum, average impact force and residual energy in bird strike on three rigid targets: A flat plate, a wedge and a splitter. Int. J. Impact Eng. 2017, 99, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Shahimi, S.S.; Abdullah, N.A.; Hrairi, M.; Ahmad, M.I.B.M. Numerical Investigation on the Damage of Whirling Engine Blades Subjected to Bird Strike Impact *. J. Aeronaut. Astronaut. Aviat. Ser. A 2021, 53, 193–199. [Google Scholar]
- Ritt, S.A.; Johnson, A.F.; Voggenreiter, H. Analysis of Bird Strike under Blunt and Splitting Impact. In Proceedings of the Aerospace Structural Impact Dynamics International Conference (ASIDIC), Wichita, KS, USA, 17–19 October 2017. [Google Scholar]
- Fu, L.; Zhang, J.; Hu, Z.; Zhang, M.; Guo, Y. Numerical Analysis of Bird Impact on an Aluminum Alloy Plate. In Proceedings of the Postdoctoral Symposium of China on Materials Science & Engineering-advanced Materials for Sustainable Development, Shanghai, China, 19 October 2012. [Google Scholar]
- Wu, B.; Lin, J.; Hedayati, R.; Zhang, G.; Zhang, J.; Zhang, L. Dynamic responses of the aero-engine rotor system to bird strike on fan blades at different rotational speeds. Appl. Sci. 2021, 11, 8883. [Google Scholar] [CrossRef]
- Wu, T.; Wang, L.; Wu, L.; Su, S. Transient Response of Flexible Supported Rotor under Airflow Excitation. At. Energy Sci. Technol. 2019, 53, 563–568. [Google Scholar]
- Gao, P.; Hou, L.; Yang, R.; Chen, Y. Local defect modelling and nonlinear dynamic analysis for the inter-shaft bearing in a dual-rotor system. Appl. Math. Model. 2019, 68, 29–47. [Google Scholar] [CrossRef]
- Ma, H.; Yin, F.; Wu, Z.; Tai, X.; Wen, B. Nonlinear vibration response analysis of a rotor-blade system with blade-tip rubbing. Nonlinear Dyn. 2016, 84, 1225–1258. [Google Scholar] [CrossRef]
- Zhu, S.H.; Tong, M.B.; Peng, G.; Kun, X.U. Experimental Study of a Full-Scale Aircraft Windshield Subjected to Bird Impact. J. Exp. Mech. 2009, 24, 61–66. [Google Scholar]
- Manual, L.-D.K.U.s. Volume II. US Army Engineer Waterways Experiment Station, Coastal and Hydraulics Laboratory; Coastal and Hydraulics Laboratory (U.S. Army Engineer Waterways Experiment Station): Vicksburg, MS, USA, 1998. [Google Scholar]
- Wilbeck, J.S. Impact Behavior of Low Strength Projectiles; Texas A&M University: College Station, TX, USA, 1977. [Google Scholar]
- Moakhar, S.; Hentati, H.; Barkallah, M.; Louati, J.; Haddar, M. Parametric study of aluminum bar shearing using Johnson-Cook material modeling. Proc. Inst. Mech. Eng. Part B: J. Eng. Manuf. 2021, 235, 1399–1411. [Google Scholar] [CrossRef]
- Eren, Z.; Tataroglu, S.; Balkan, D.; Mecitoglu, Z. Modeling of Bird Strike on a Composite Helicopter Rotor Blade. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Duckitt, S.; Bisagni, C.; Shahpar, S. Parametric bird strike study of A transonic rotor using isogeometric analysis. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference & Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Ding, K.; Wang, Z.; Lu, X.; Zhang, J.; Ma, L. Vibration investigation of rotor system with unbalance and blade-casing rubbing coupling faults. J. Vibroengineering 2020, 22, 353–365. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).