Modeling Aircraft Departure at a Runway Using a Time-Varying Fluid Queue
Abstract
:1. Introduction
2. Data Analysis of the Departure Traffic
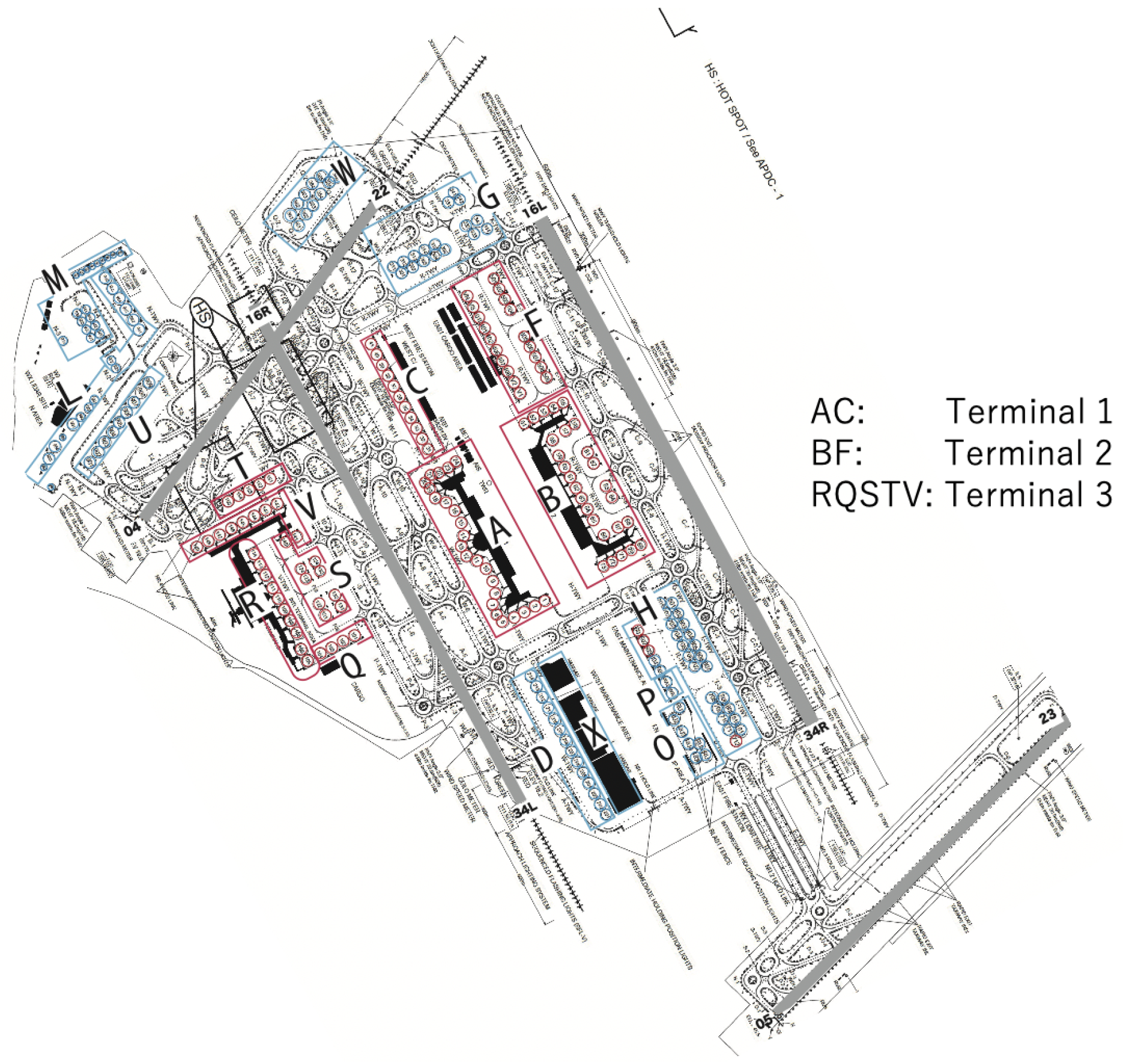
2.1. Airport Operation at Tokyo International Airport (RJTT)
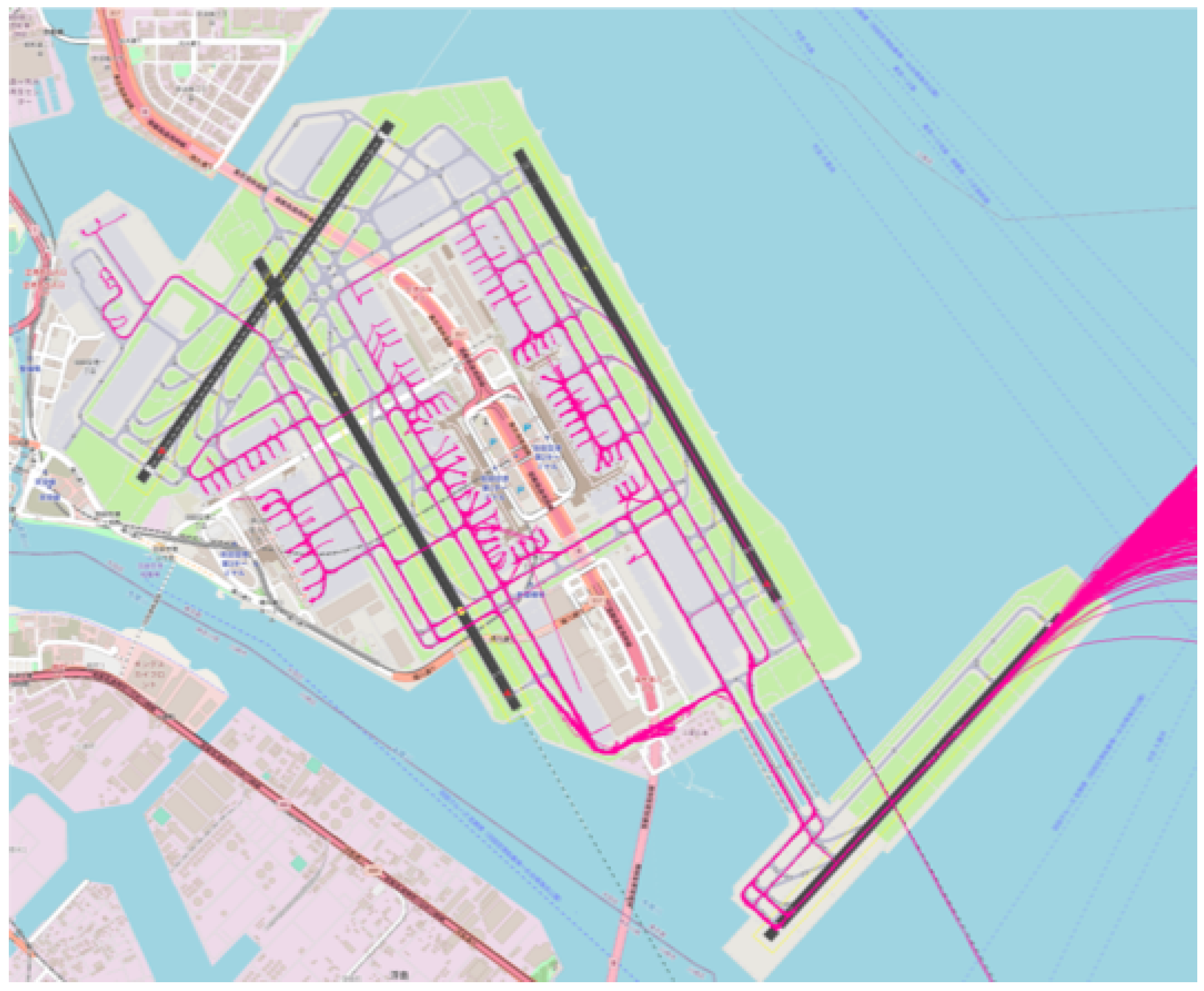
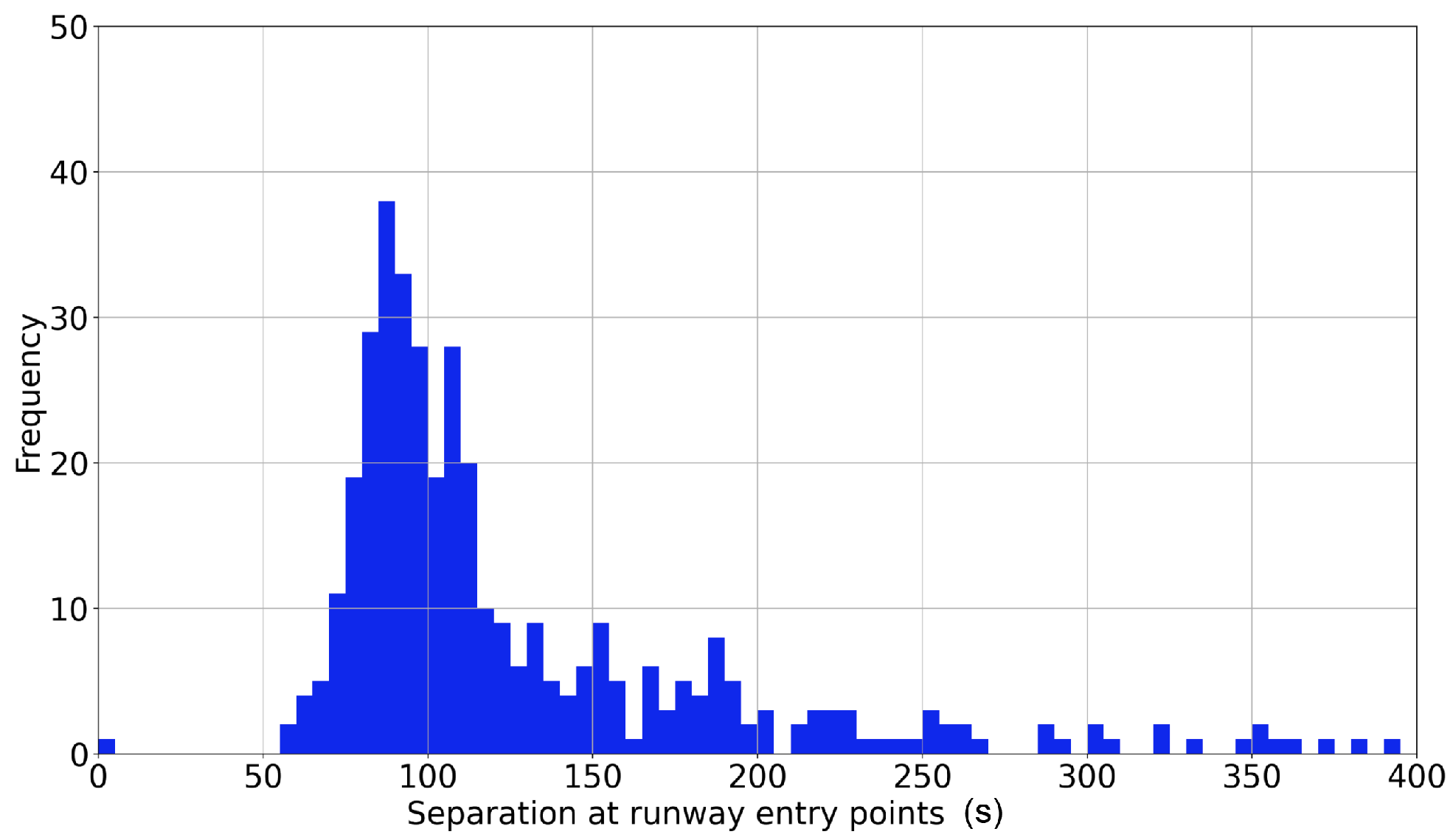
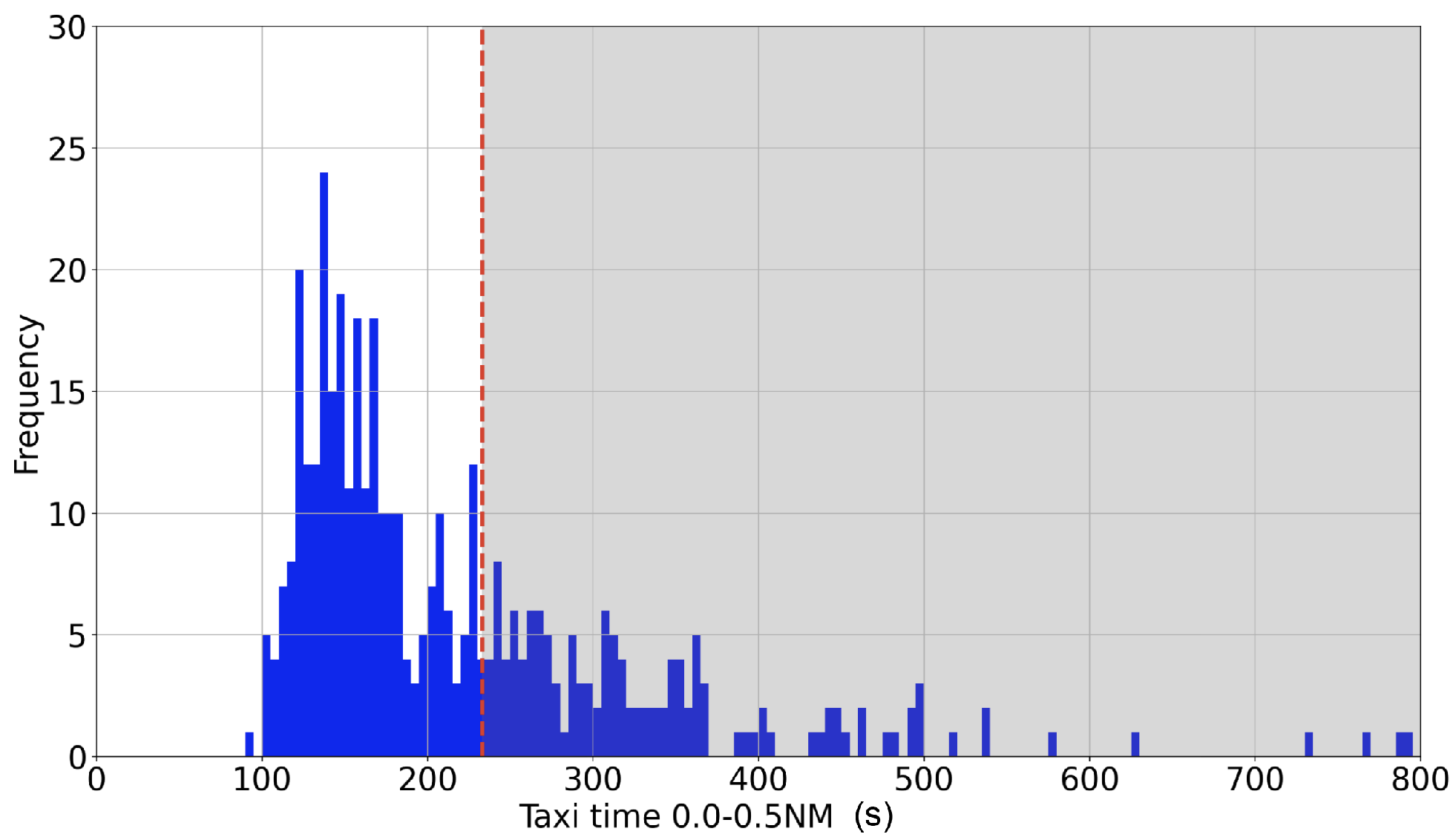
2.2. Departure Traffic Queue at Runway 05
3. Model Description and Formulation
3.1. Modeling Departure Queue at a Single Runway
3.2. Time-Varying Fluid Queue
3.3. Conditions of Flow in System
3.3.1. UL Condition
3.3.2. OL Condition
3.4. Aircraft Departure Waiting Time
4. Estimating Departure Queues
4.1. Stochastic Features in the Queuing Model
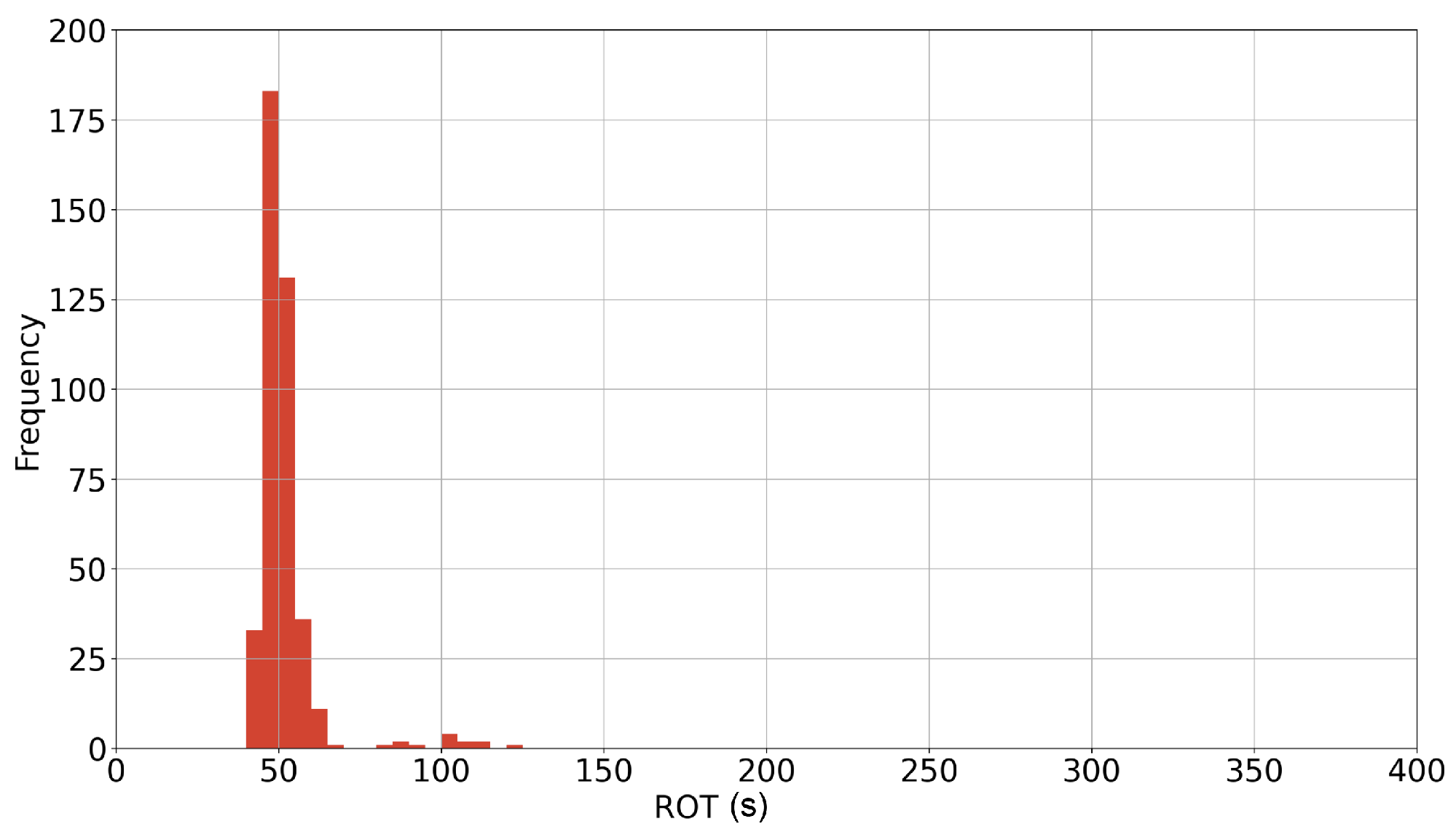
4.1.1. Arrival Rate
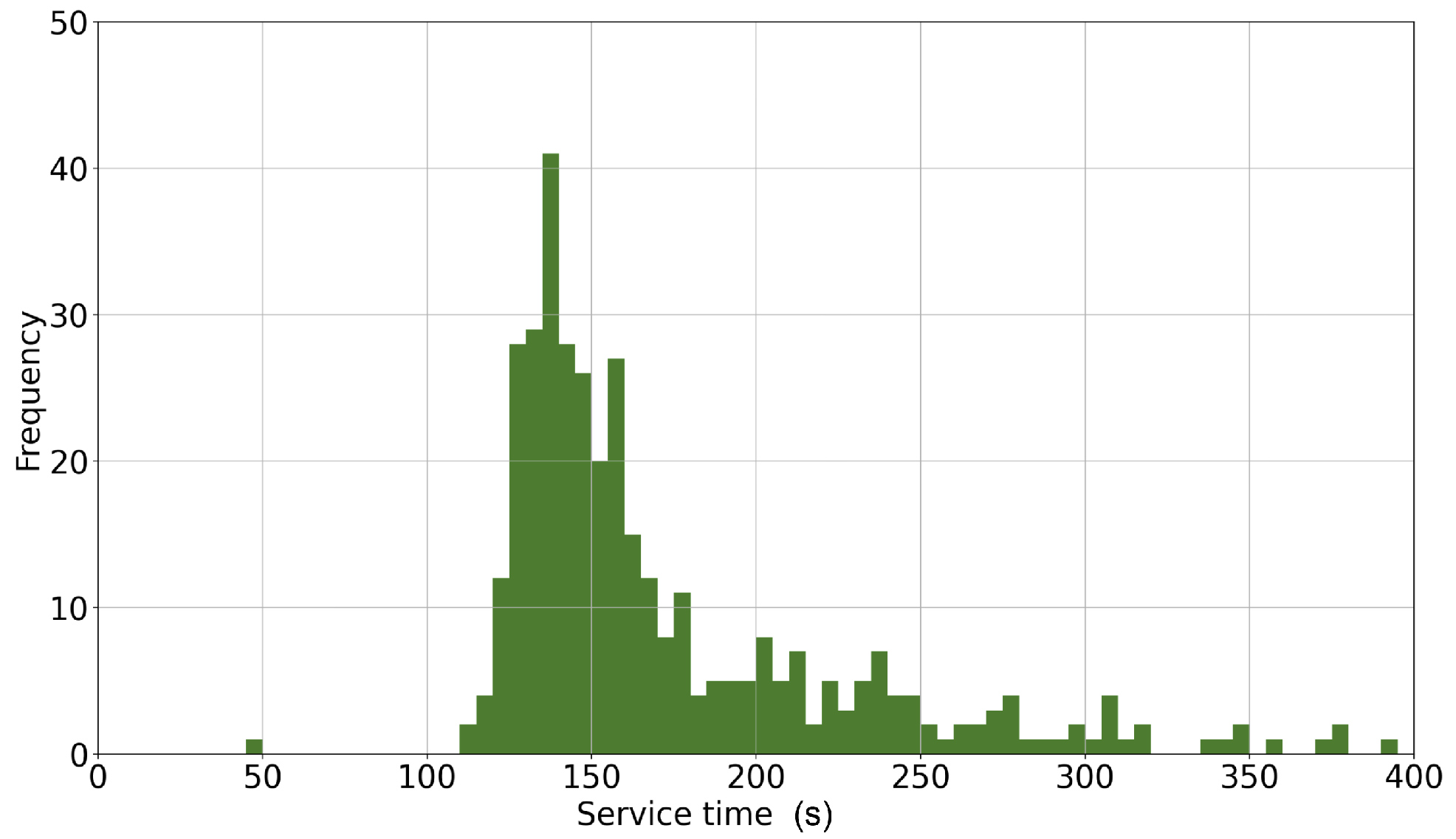
4.1.2. Service Time
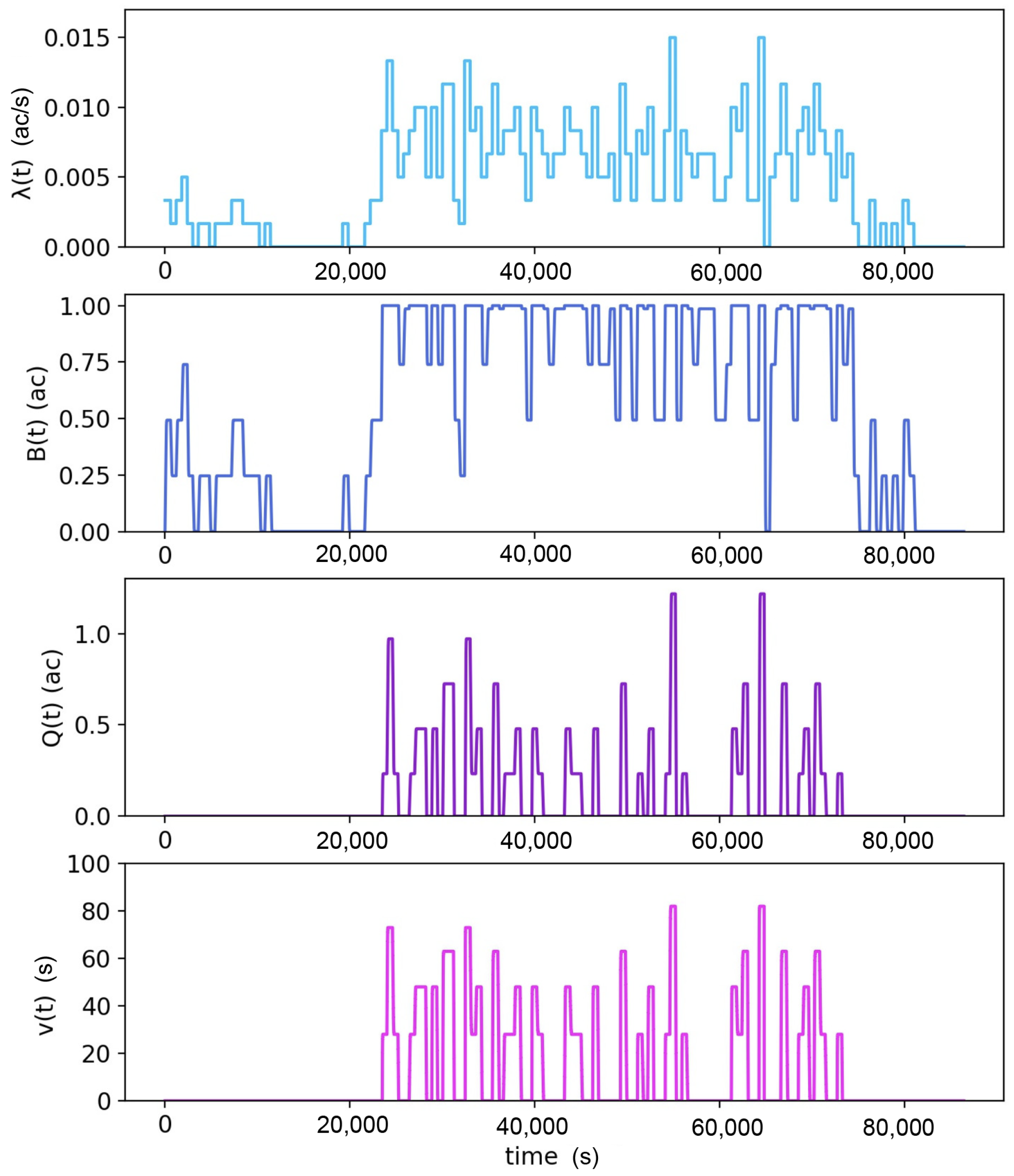
4.2. Time-Varying States in the Departure Queue
4.3. Departure Waiting Time in the Queue
4.4. Model Validation
5. Estimating Ecological and Economical Impacts Due to Departure Queue
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IATA. COVID-19 Outlook for Air Travel in the Next 5 Years; IATA: Montreal, QC, Canada, 2020. [Google Scholar]
- FAA Surface CDM Team. US Airport Surface Collaborative Decision Making (CDM) Concept of Operations (ConOps) in the Near-Term: Applications of Surface CDM at United States Airports; FAA Surface CDM Team: Washington, DC, USA, 2012. [Google Scholar]
- EUROCONTROL Airport CDM Team. Airport CDM Implementation-The Manual; EUROCONTROL Airport CDM Team: Brussels, Belgium, 2018. [Google Scholar]
- Badrinath, S.; Balakrishnan, H.; Joback, E.; Reynolds, T. Impact of Off-Block Time Uncertainty on the Control of Airport Surface Operations. Transp. Sci. 2020, 54, 855–1152. [Google Scholar] [CrossRef]
- Ball, M.; Vossen, T.; Hoffman, R. Analysis of demand uncertainty effects in ground delay programs. In Proceedings of the 4th USA/Europe Air Traffic Management R & D Seminar, Santa Fe, NM, USA, 4–7 December 2001. [Google Scholar]
- McFarlanee, P.; Balakrishnan, H. Optimal control of airport pushbacks in the presence of uncertainties. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016. [Google Scholar]
- Liu, Y.; Hansen, M.; Gupta, G.; Malik, W.; Jung, Y. Predictability impacts of airport surface automation. Transp. Res. Part C Emerg. Technol. 2014, 44, 128–145. [Google Scholar] [CrossRef]
- Simaiakis, I.; Balakrishnan, H. A queuing model of the airport departure process. Transp. Sci. 2015, 50, 94–109. [Google Scholar] [CrossRef]
- Badrinath, S.; Li, M.; Balakrishnan, H. Integrated surface—Airspace model of airport departures. J. Guid. Control. Dyn. 2018, 42, 1049–1063. [Google Scholar] [CrossRef]
- Liu, Y.; Whitt, W. The Gt/GI/st+GI many-server fluid queue. Queuing Syst. 2012, 71, 405–444. [Google Scholar] [CrossRef] [Green Version]
- Whitt, W. Time-Varying Queues. Oueueing Model. Serv. Manag. 2018, 1, 79–164. [Google Scholar]
- Bäuerle, N.; Engelhardt-Funke, O.; Kolonko, M. On the waiting time of arriving aircrafts and the capacity of airports with one or two runways. Eur. J. Oper. Res. 2007, 177, 1180–1196. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Johnson, J.; Gaier, E.M.; Kostiuk, P.F. Modeling Air Traffic Management Technologies with a Queuing Network Model of the National Airspace System; NASA Langley Technical Report Server: Washington, DC, USA, 1999. [Google Scholar]
- Rue, R.C.; Rosenshine, M. The application of semi-Markov decision processes to queuing of aircraft for landing at an airport. Transp. Sci. 1985, 19, 154–172. [Google Scholar] [CrossRef]
- Bolender, M.; Slater, G. Evaluation of scheduling methods for multiple runways. J. Aircr. 2000, 37, 410–416. [Google Scholar] [CrossRef] [Green Version]
- Itoh, E.; Mitici, M. Queue-based Modeling of the Aircraft Arrival Process at a Single Airport. Aerospace 2019, 6, 103. [Google Scholar] [CrossRef] [Green Version]
- Itoh, E.; Mitici, M. Analyzing Tactical Control Strategies for Aircraft Arrivals at an Airport Using a queuing Model. J. Air Transp. Manag. 2020, 89, 101938. [Google Scholar] [CrossRef]
- Itoh, E.; Mitici, M. Evaluating the Impact of New Aircraft Separation Minima on Available Airspace Capacity and Arrival Time Delay. Aeronaut. J. 2020, 124, 447–471. [Google Scholar] [CrossRef] [Green Version]
- Airports Council International (ACI). Passenger Traffic 2017 FINAL (Annual). In Passenger Summary; Airports Council International: Montreal, QC, Canada, 2019. [Google Scholar]
- Ministry of Land, Infrastructure, Transport and Tourism. AIS Japan—Japan Aeronautical Information Service Center. 2021. Available online: https://aisjapan.mlit.go.jp (accessed on 27 January 2022).
- ICAO. ICAO Engine Emissions Databank. 2018. Available online: https://www.easa.europa.eu/easa-and-you/environment/icao-aircraft-engine-emissions-databank (accessed on 31 July 2021).

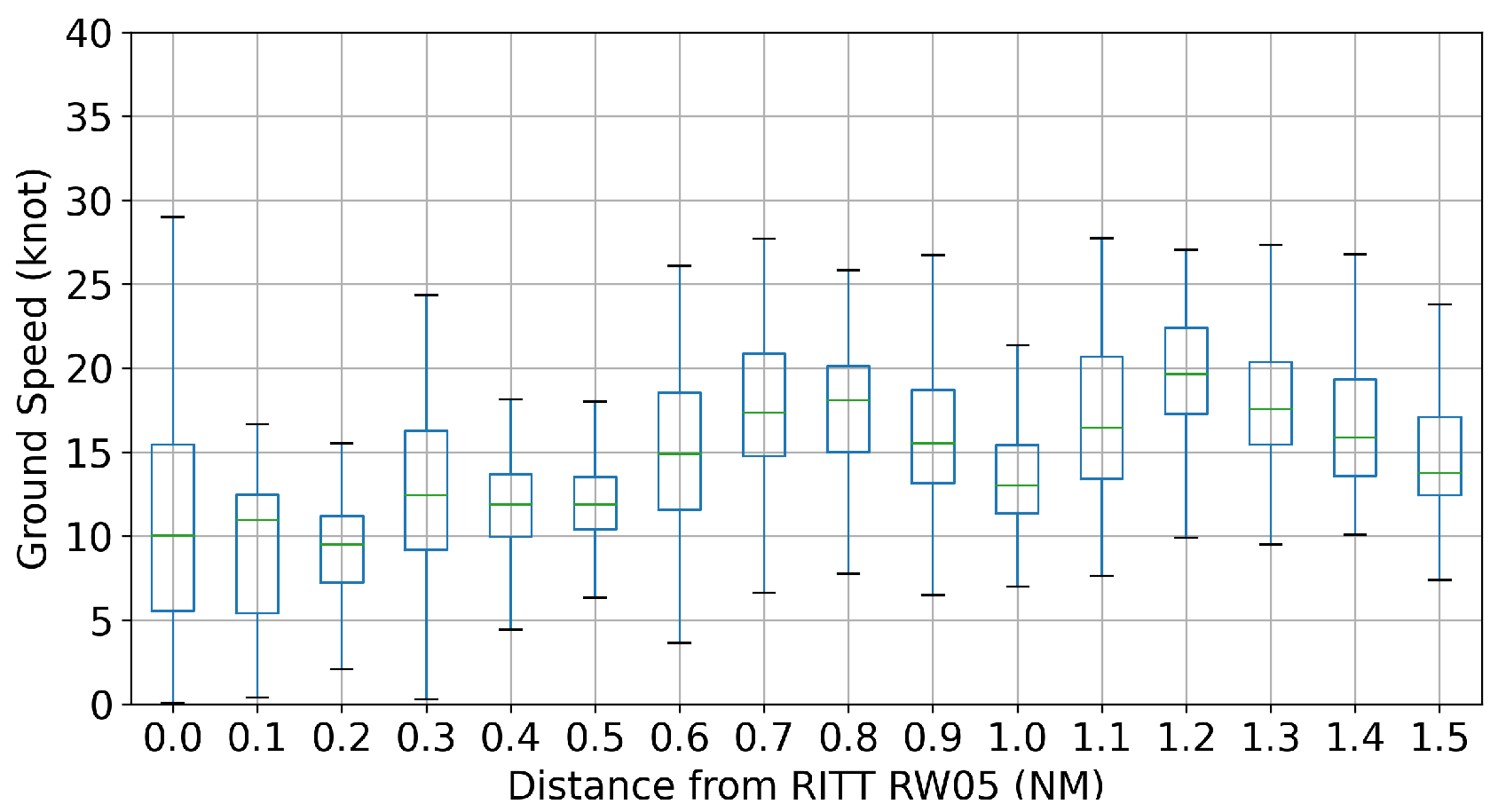
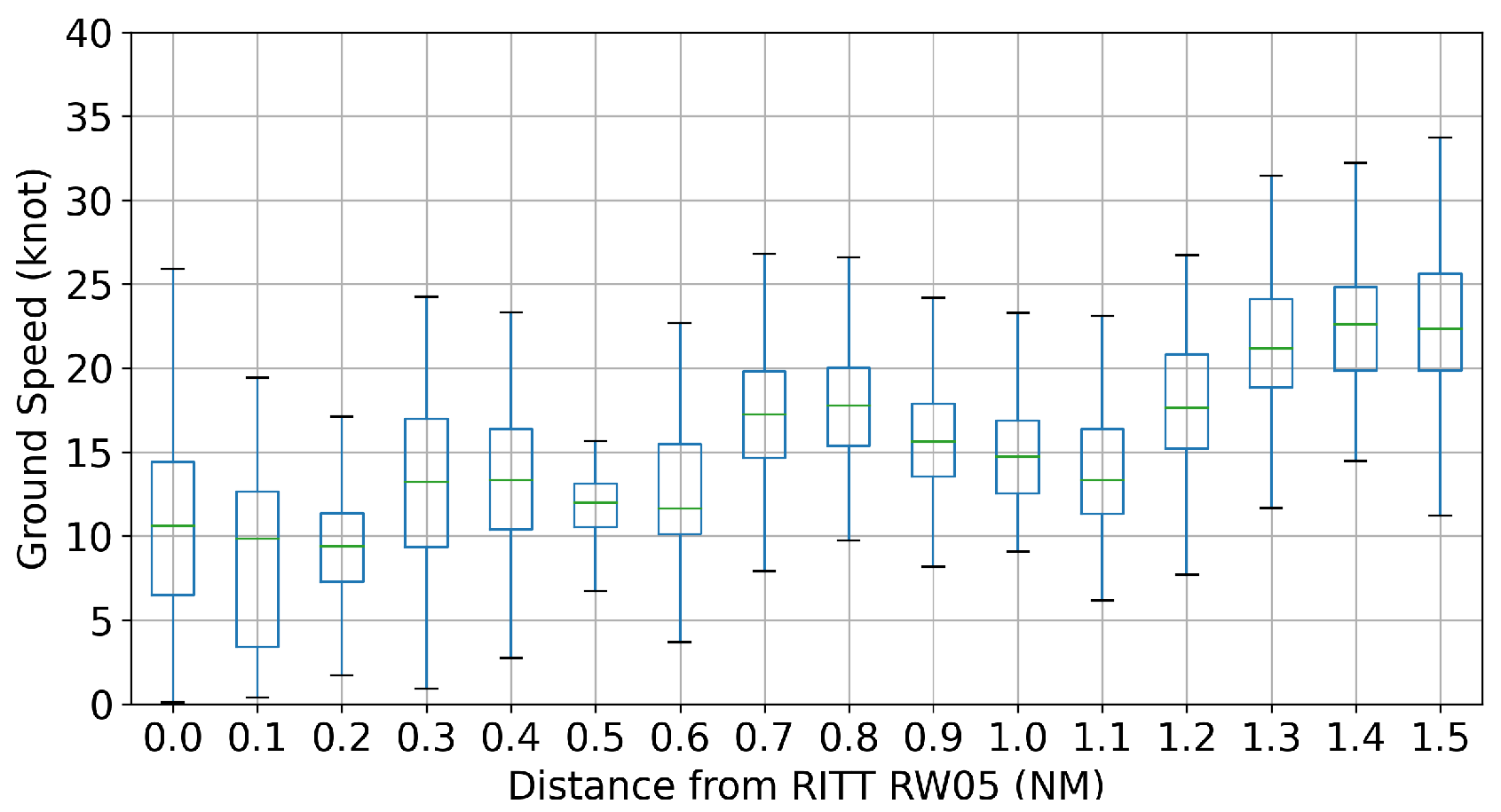
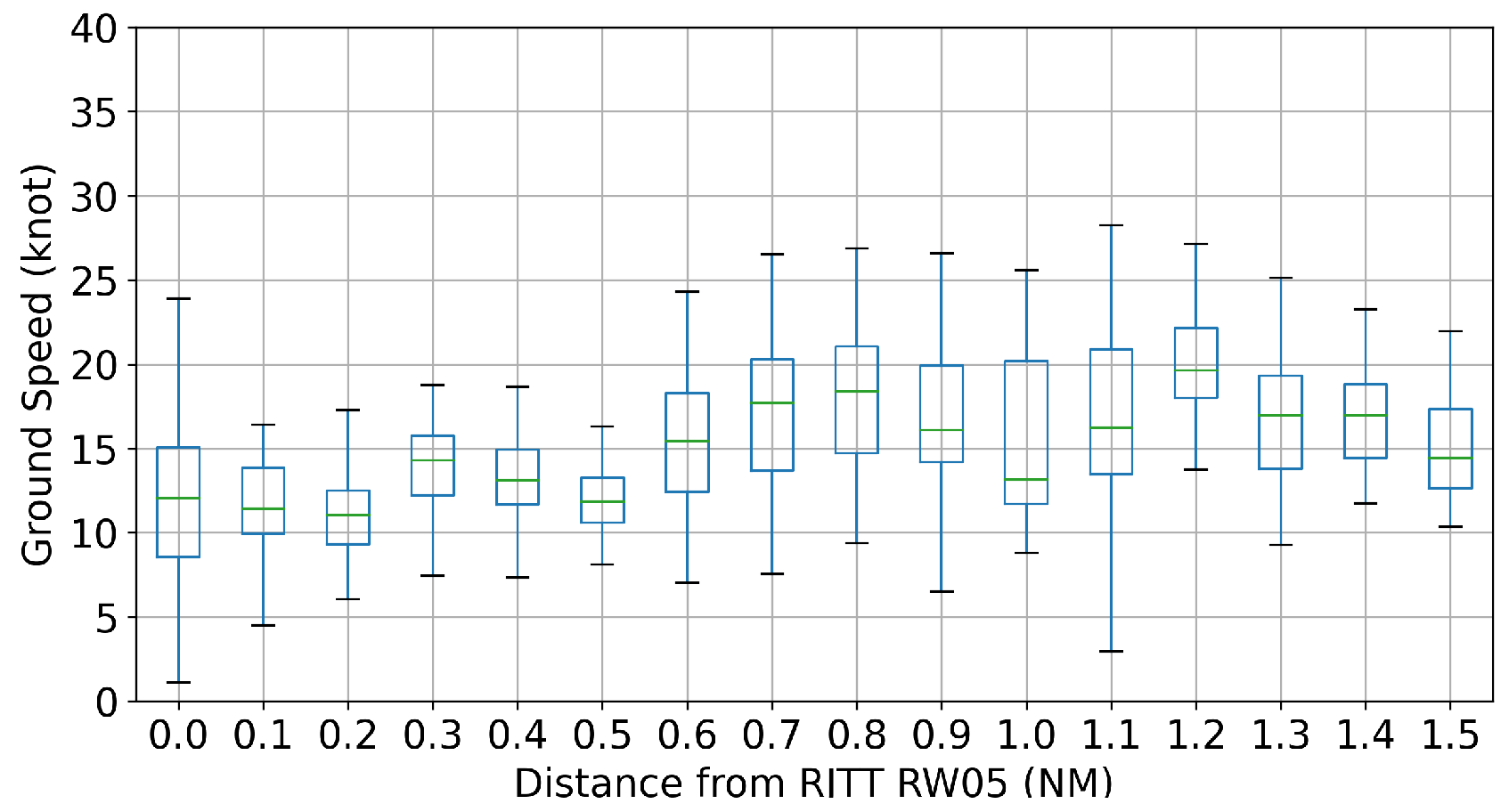
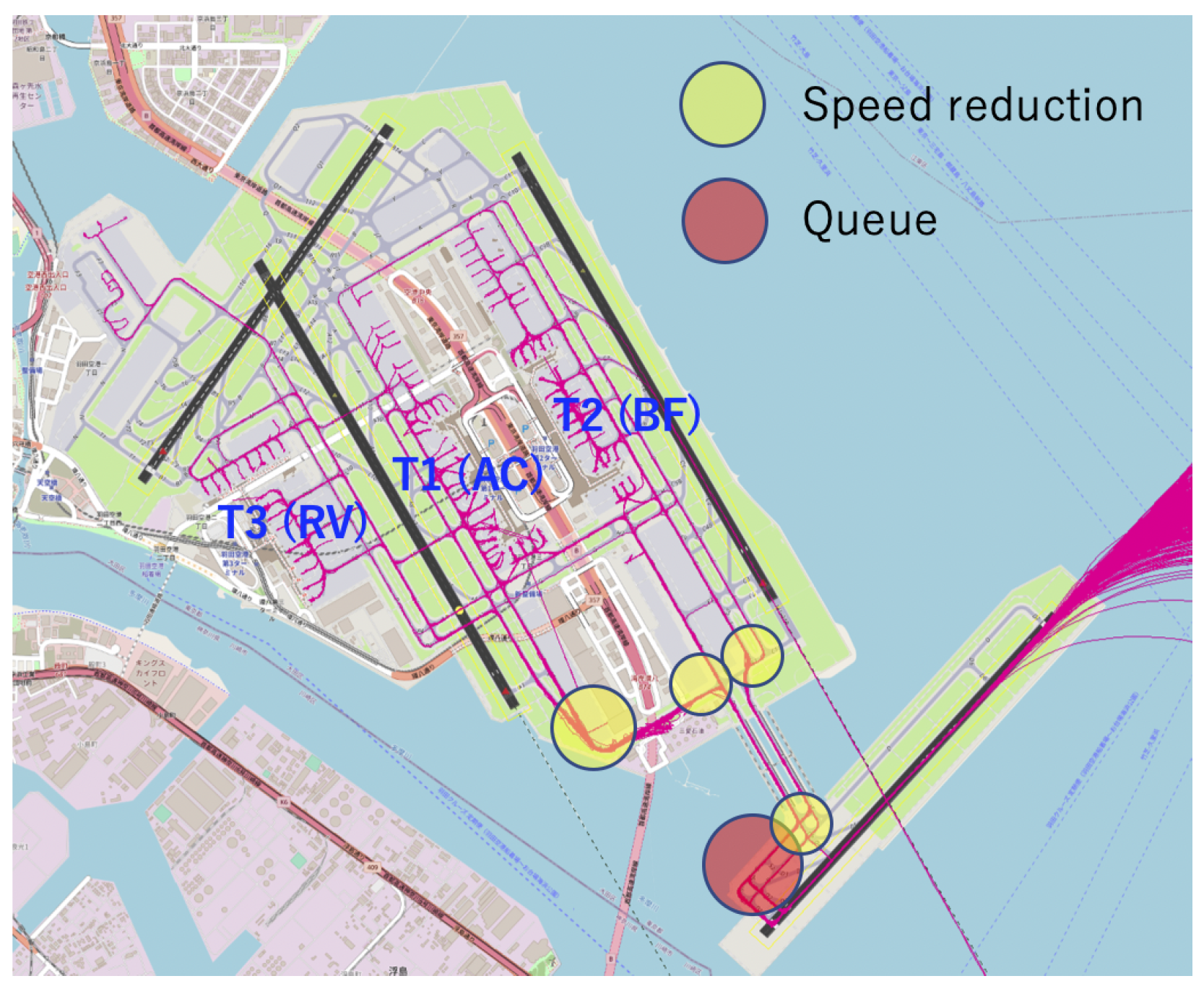
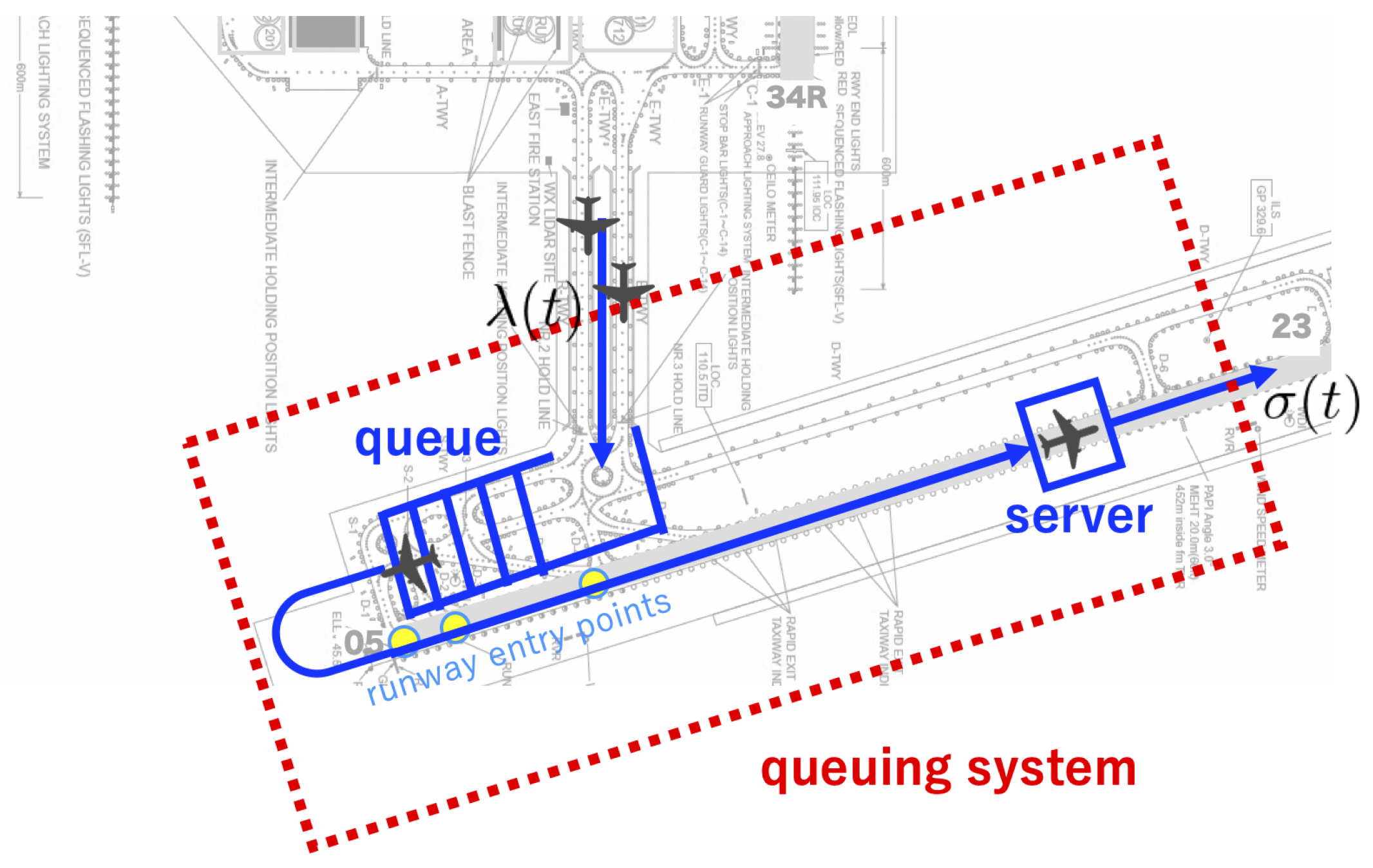
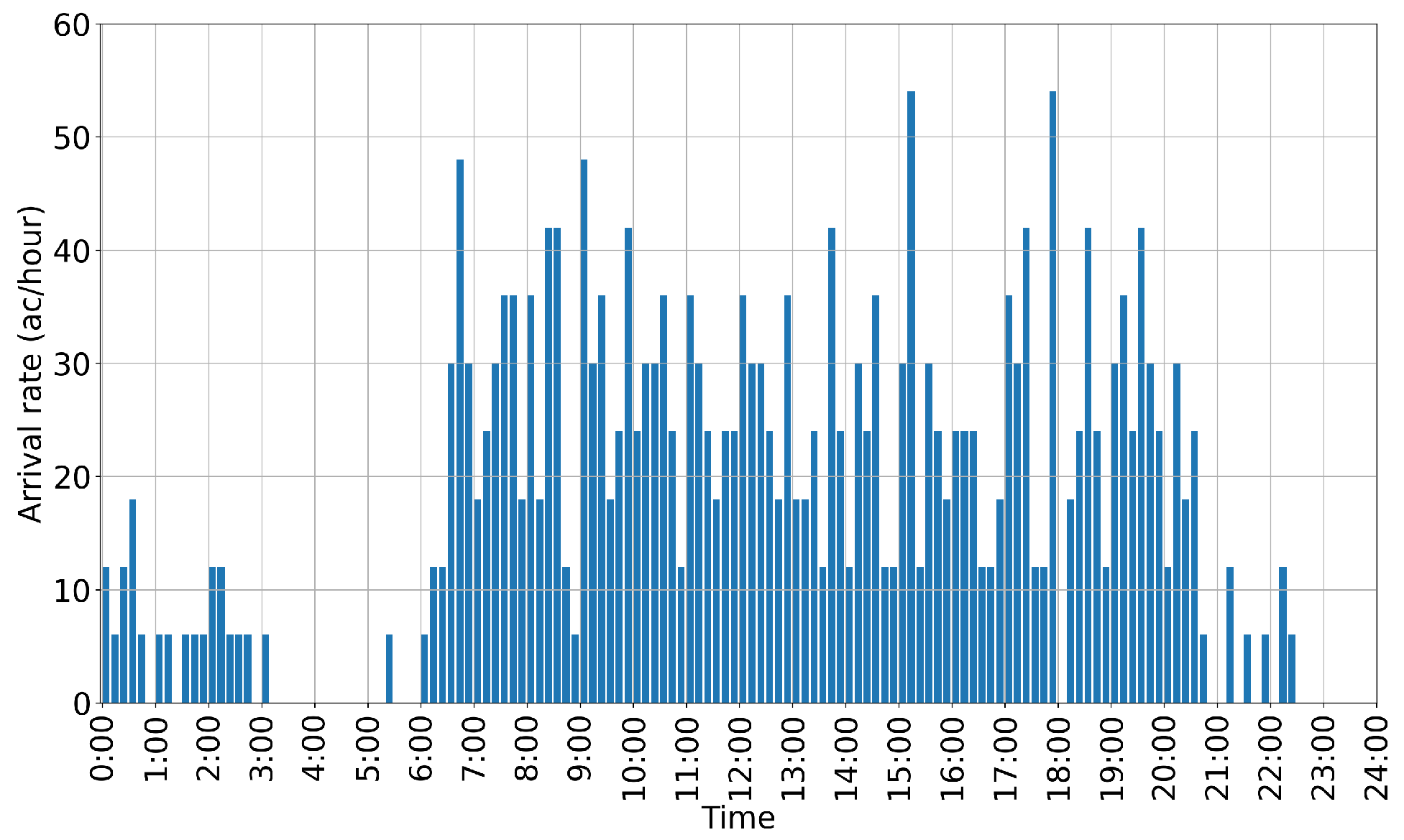

| Distance (NM) | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| Total (%) | 26 | 10 | 9.9 | 5.0 | 2.6 | 1.4 | 0.75 | 0.35 | 0.15 |
| T1 (%) | 27 | 11 | 10 | 5.4 | 2.8 | 1.4 | 0.71 | 0.30 | 0.24 |
| T2 (%) | 29 | 11 | 10 | 5.6 | 3.0 | 1.5 | 0.83 | 0.35 | 0.043 |
| T3 (%) | 16 | 6.6 | 10 | 2.4 | 1.2 | 0.95 | 0.68 | 0.47 | 0.14 |
| Parameter | Description |
|---|---|
| B | Quantity of flow in service |
| b | Density of flow in service |
| Q | Quantity of flow waiting in the queue |
| q | Density of flow waiting in the queue |
| X | Total quantity of the flow in the system |
| Total of arrival flow (departure traffic flow) into the system | |
| Arrival rate at the system | |
| G | Cumulative distribution function of service time |
| g | Probability density function of service time |
| Parameter defined in Equation (5) | |
| Parameter defined in Equation (6) | |
| Over Load (OL) terminate time | |
| OL start time | |
| Under Load (UL) terminate time | |
| UL start time | |
| Quantity of flow which completes service | |
| v | Waiting time |
| E | Quantity of flow entering service |
| i | (s) | (s) | (s) | (Aircraft) | (s) |
|---|---|---|---|---|---|
| 1 | 25,270 | 1768 | 73 | 17 | 734 |
| 2 | 28,296 | 1887 | 48 | 16 | 627 |
| 3 | 29,496 | 643 | 48 | 5 | 213 |
| 4 | 31,288 | 1248 | 63 | 13 | 774 |
| 5 | 34,296 | 1831 | 73 | 18 | 869 |
| 6 | 36,166 | 763 | 63 | 8 | 415 |
| 7 | 38,559 | 1950 | 48 | 14 | 454 |
| 8 | 40,947 | 1270 | 48 | 10 | 351 |
| 9 | 45,147 | 1942 | 48 | 17 | 553 |
| 10 | 46,896 | 643 | 48 | 7 | 298 |
| 11 | 49,966 | 705 | 63 | 6 | 321 |
| 12 | 51,747 | 645 | 28 | 5 | 121 |
| 13 | 52,872 | 667 | 48 | 6 | 252 |
| 14 | 55,305 | 1203 | 82 | 10 | 542 |
| 15 | 56,547 | 645 | 28 | 6 | 145 |
| 16 | 63,088 | 1835 | 63 | 16 | 716 |
| 17 | 64,882 | 638 | 82 | 6 | 418 |
| 18 | 67,366 | 763 | 63 | 5 | 259 |
| 19 | 69,759 | 1257 | 48 | 9 | 322 |
| 20 | 71,547 | 1344 | 63 | 13 | 541 |
| 21 | 73,270 | 568 | 28 | 4 | 103 |
| k | Aircraft Type | Rate (%) | Fuel Flow (kg/s) |
|---|---|---|---|
| 1 | B738 | 34 | 0.097 |
| 2 | B763 | 18 | 0.20 |
| 3 | B772 | 14 | 0.21 |
| 4 | A320 | 10 | 0.10 |
| 5 | B788 | 6 | 0.21 |
| 6 | B773 | 3 | 0.34 |
| 7 | B77W | 3 | 0.30 |
| 8 | B789 | 2 | 0.23 |
| 9 | A321 | 2 | 0.11 |
| 10 | B737 | 2 | 0.12 |
| 11 | A333 | 2 | 0.26 |
| 12 | E170 | 1 | 0.060 |
| 13 | A332 | 0.6 | 0.259 |
| 14 | B744 | 0.5 | 0.228 |
| 15 | B734 | 0.4 | 0.124 |
| 16 | Others | 0.8 | 0.089 |
| Case Study Day | (h) | Fuel Consumption (ton) |
|---|---|---|
| Day 1 | 2.51 | 2.89 |
| Day 2 | 2.64 | 3.04 |
| Day 3 | 1.77 | 2.04 |
| Day 4 | 2.62 | 3.02 |
| Day 5 | 2.60 | 3.00 |
| Day 6 | 2.12 | 2.44 |
| Day 7 | 2.15 | 2.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Itoh, E.; Mitici, M.; Schultz, M. Modeling Aircraft Departure at a Runway Using a Time-Varying Fluid Queue. Aerospace 2022, 9, 119. https://doi.org/10.3390/aerospace9030119
Itoh E, Mitici M, Schultz M. Modeling Aircraft Departure at a Runway Using a Time-Varying Fluid Queue. Aerospace. 2022; 9(3):119. https://doi.org/10.3390/aerospace9030119
Chicago/Turabian StyleItoh, Eri, Mihaela Mitici, and Michael Schultz. 2022. "Modeling Aircraft Departure at a Runway Using a Time-Varying Fluid Queue" Aerospace 9, no. 3: 119. https://doi.org/10.3390/aerospace9030119
APA StyleItoh, E., Mitici, M., & Schultz, M. (2022). Modeling Aircraft Departure at a Runway Using a Time-Varying Fluid Queue. Aerospace, 9(3), 119. https://doi.org/10.3390/aerospace9030119








