Characterization of Low-Energy Quasiperiodic Orbits in the Elliptic Restricted 4-Body Problem with Orbital Resonance
Abstract
:1. Introduction
2. The Elliptic Restricted 4-Body Problem
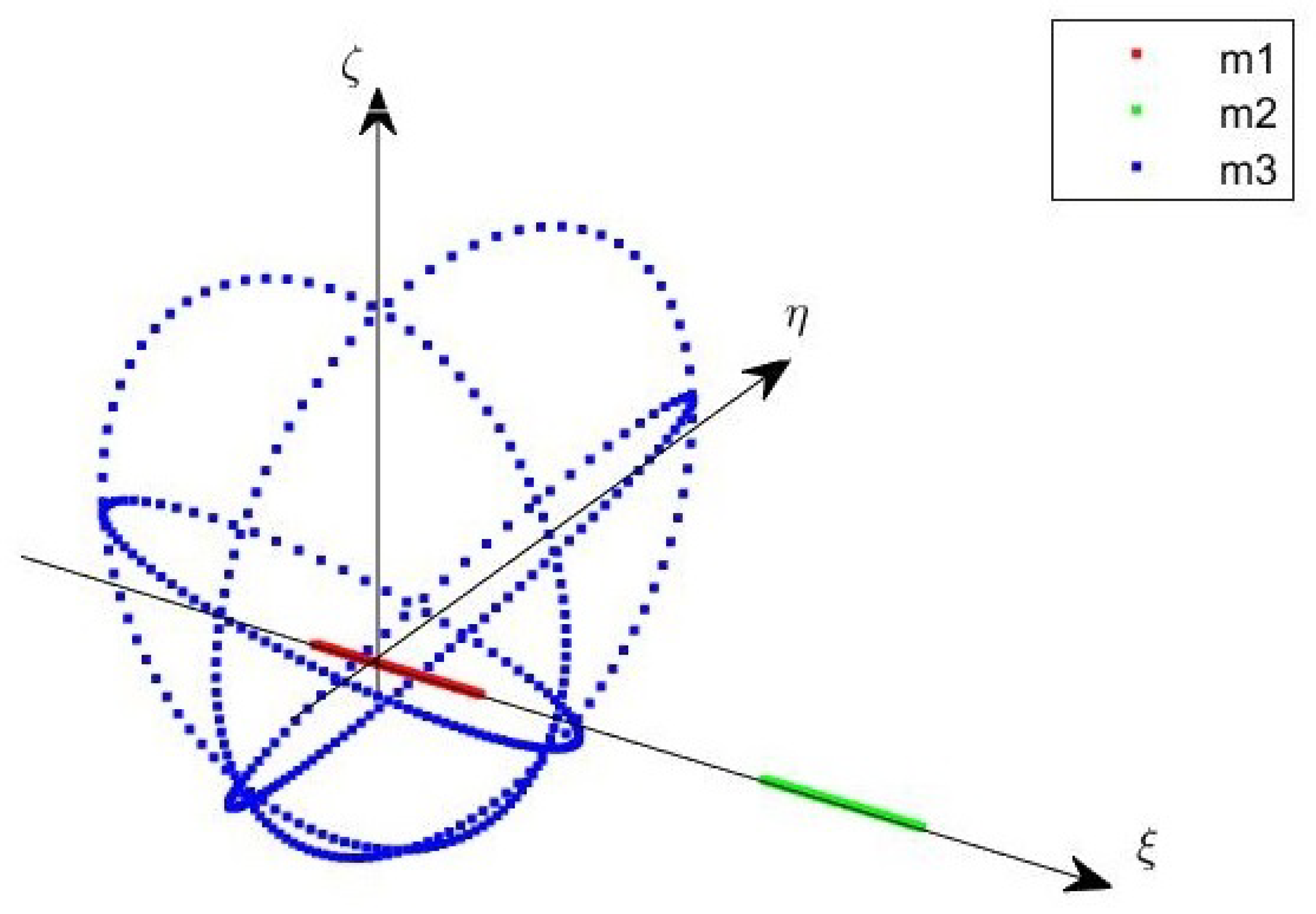
2.1. Dynamical Model
- The center of mass of the system is indicated as O;
- The relative motion of with respect to describes a Keplerian orbit onto the plane with semimajor axis a and eccentricity e;
- The relative motion of with respect to describes a Keplerian orbit onto the plane with semimajor axis and eccentricity ;
- The orbital plane is tilted of an angle with respect to ;
2.2. Hamiltonian Formalism
3. Classification of Low-Energy Trajectories in the Elliptic Restricted 4-Body Problem
3.1. Persistence of the Topological Properties
3.2. Normal Forms for the Elliptic Restricted 4-Body Problem
3.3. Topological Characterization of Low-Energy Trajectories
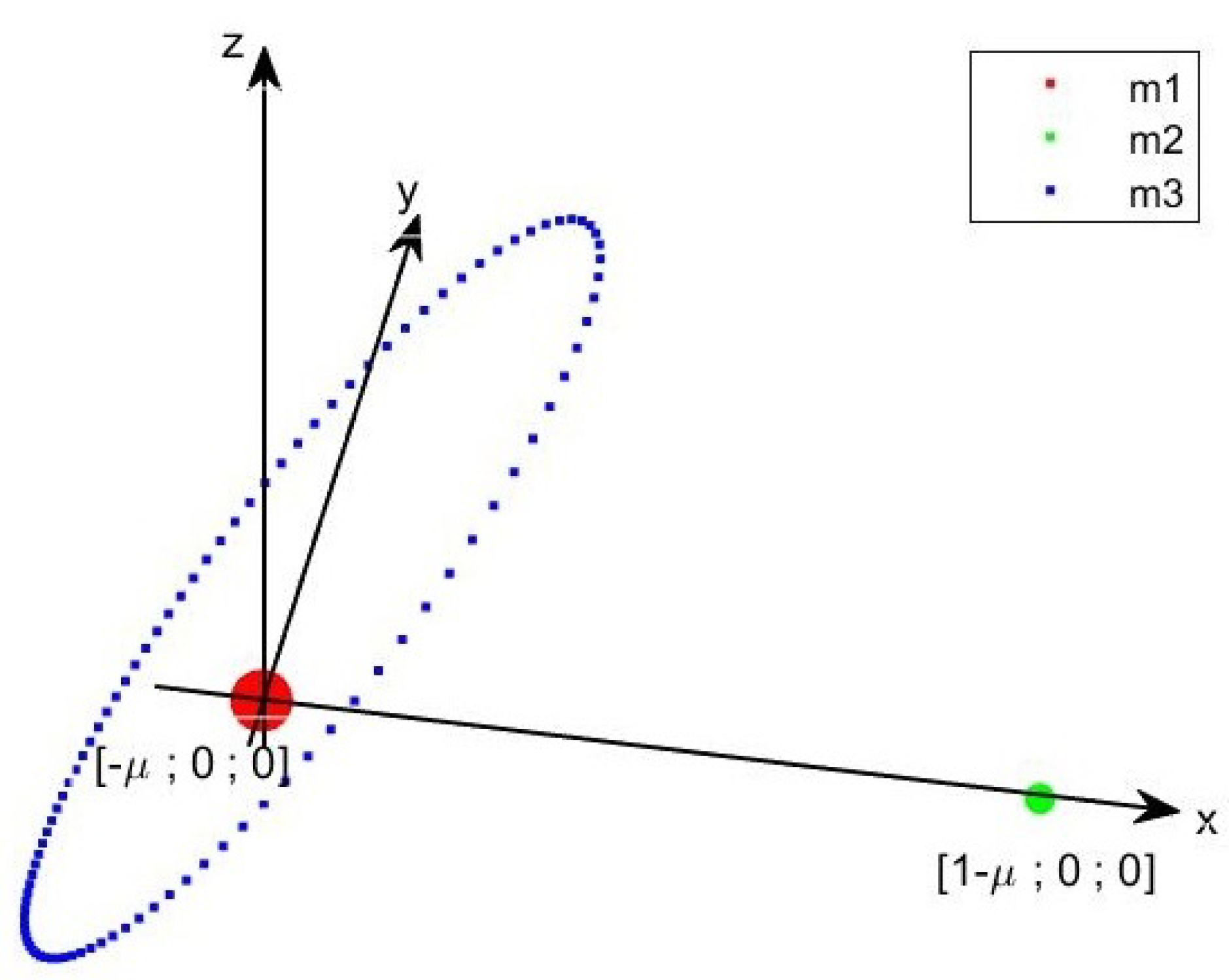
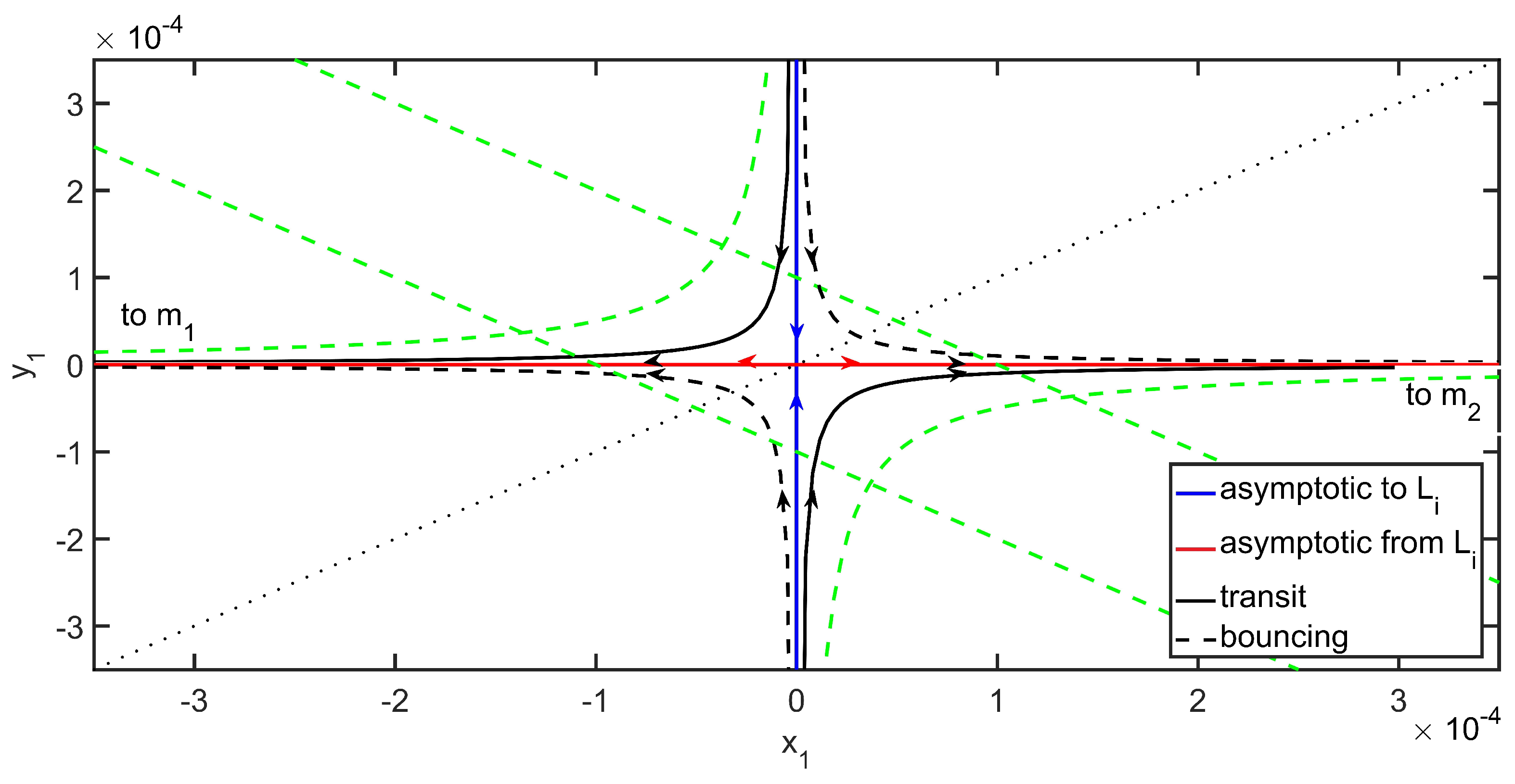
- Lissajous quasiperiodic orbits, characterized by , which evolve inside the equilibrium region;
- Transit trajectories, corresponding to the hyperbolic segments , which cross the equilibrium region twice, once towards and once towards , in a finite interval of time;
- Bouncing trajectories, corresponding to the hyperbolic segments , which never cross the equilibrium region;
- Long-term ballistic captures, characterized by either or , which cross the equilibrium region twice, over an indefinitely long interval of time.
4. Resonant Terms and Quasiperiodic Solutions
4.1. Identification of Resonant Terms
4.2. Determination of Stationary Points
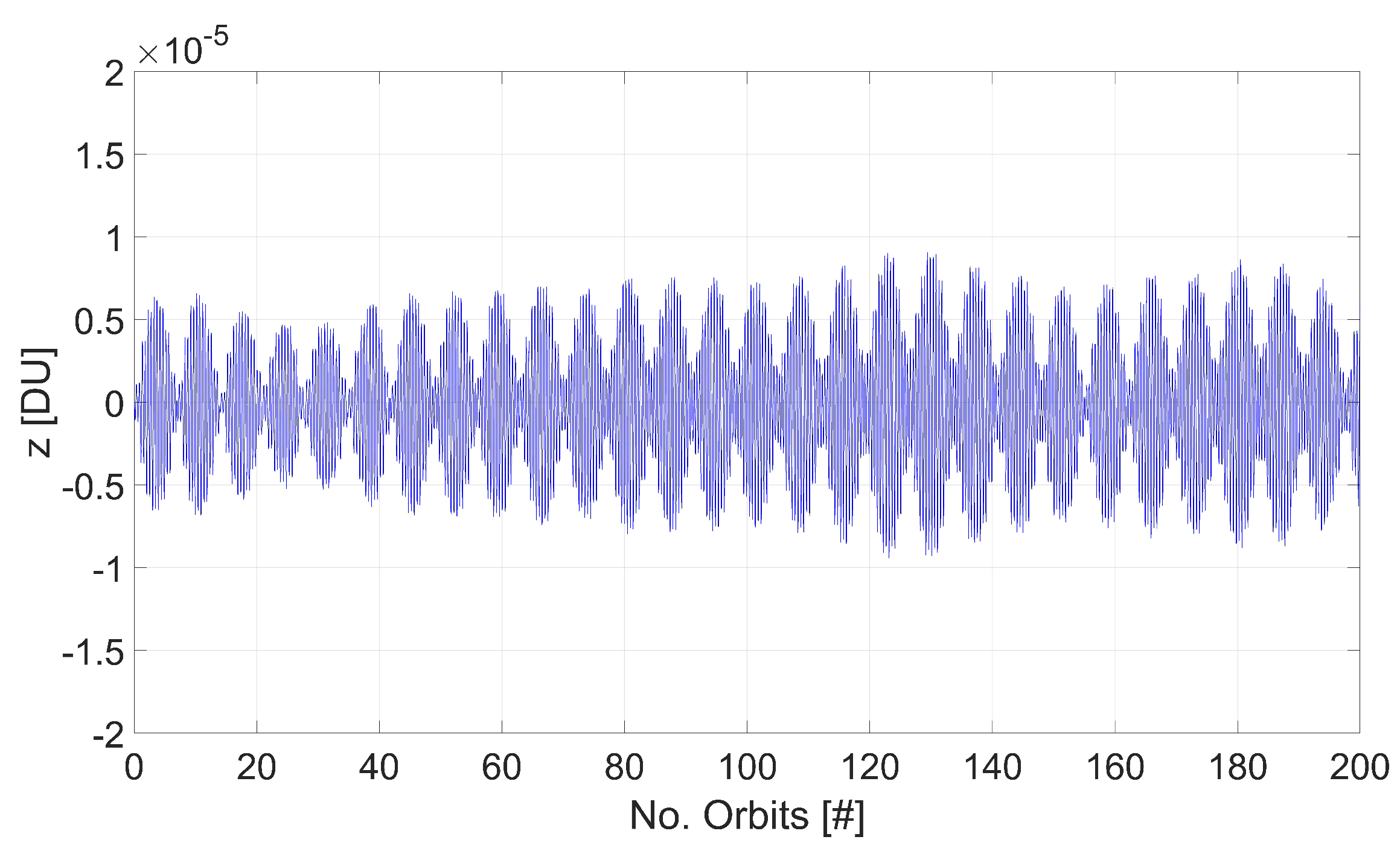
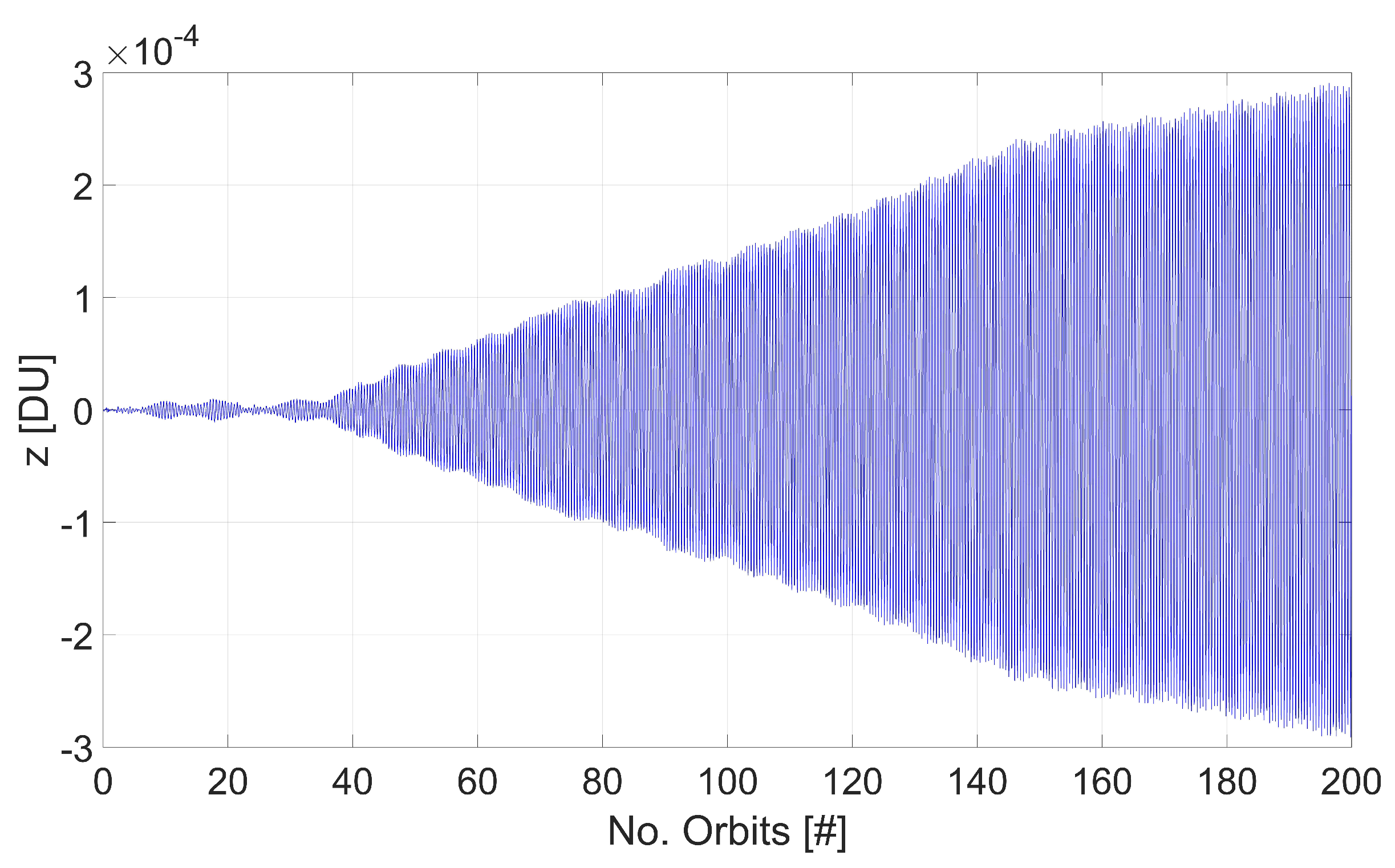
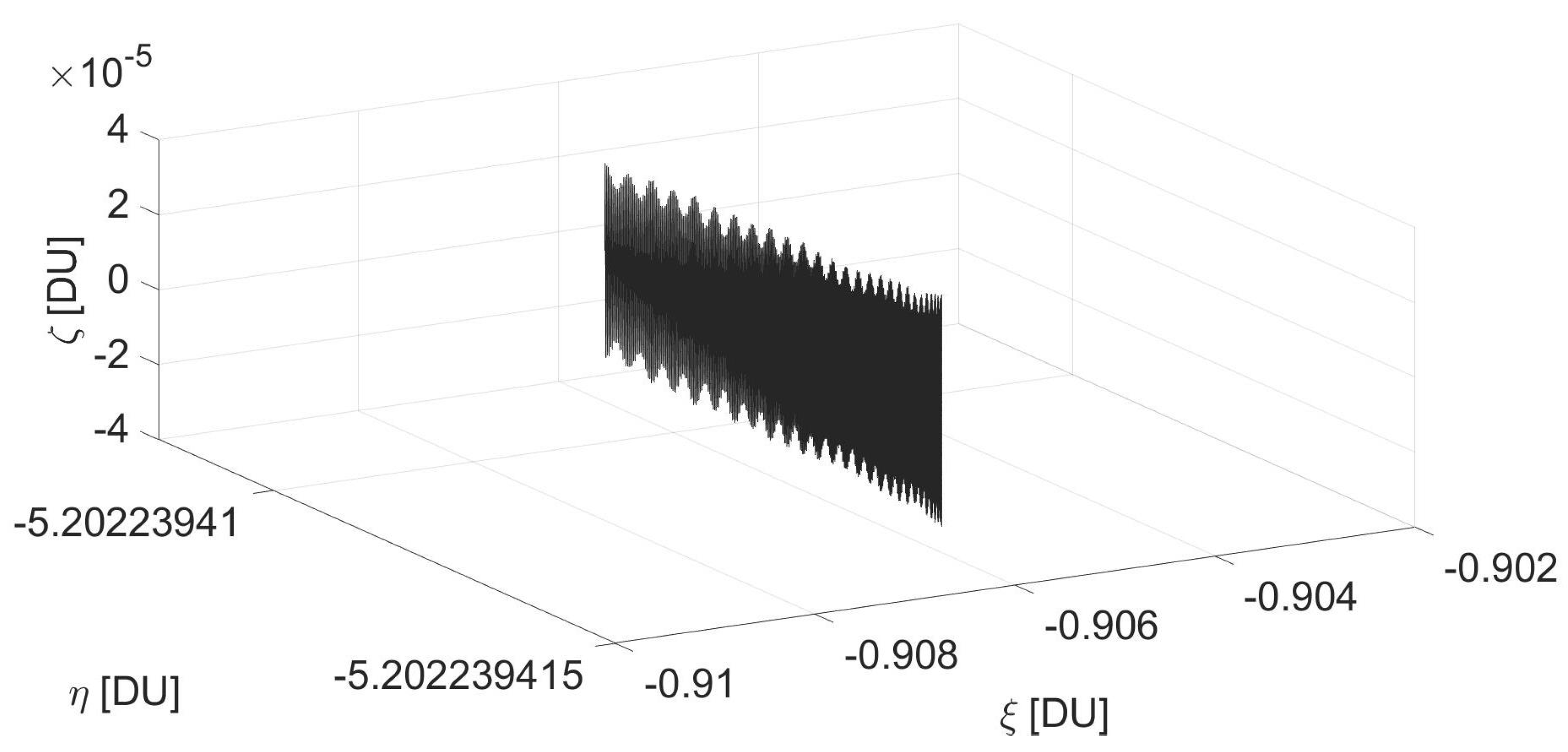
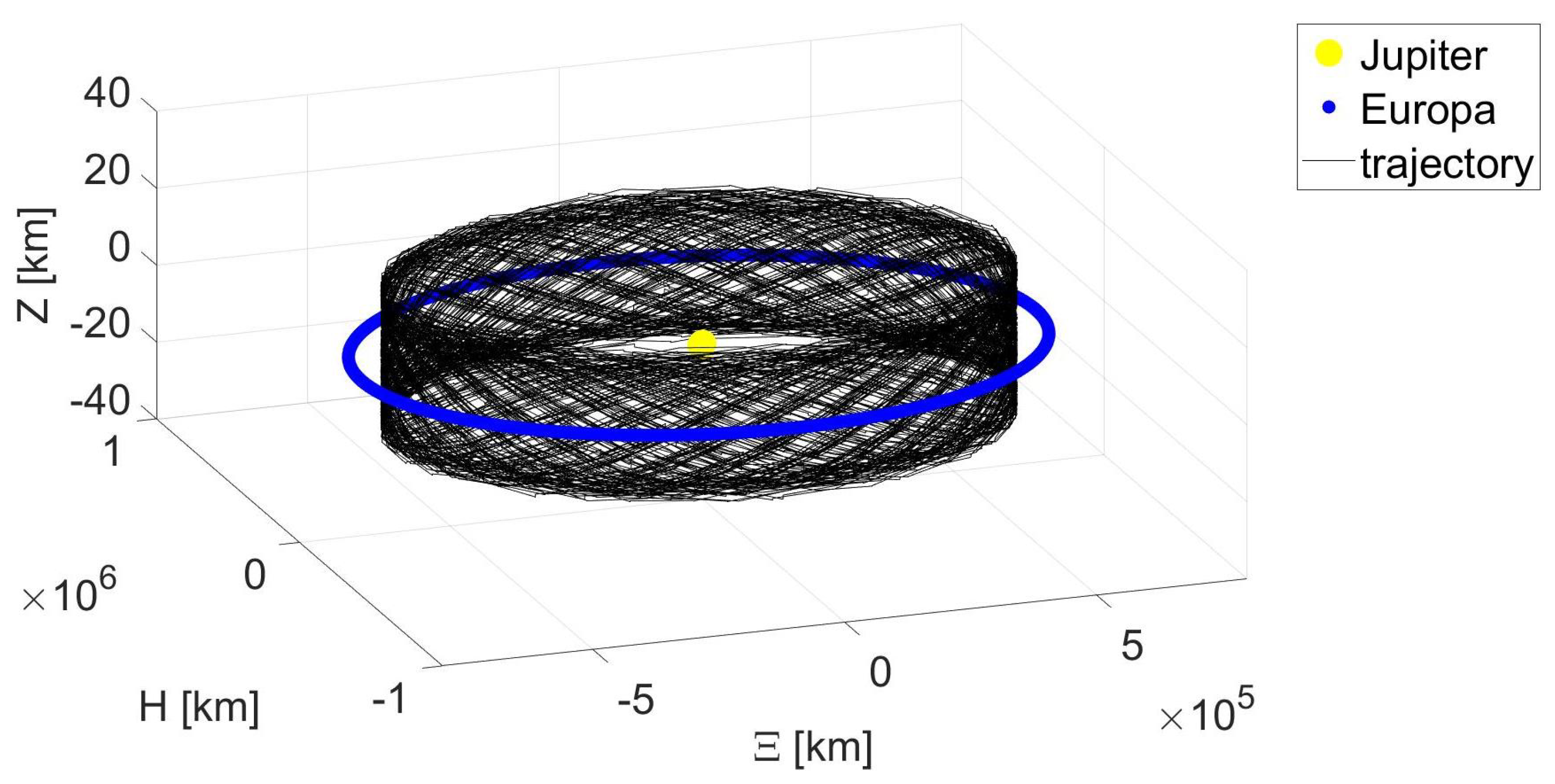
5. Numerical Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Terms of the Power Series Expansion
Appendix B. Canonical Transformations
Appendix B.1. Second Order
Appendix B.2. Third Order
References
- Rathsman, P.; Kugelberg, P.; Bodin, P.; Racca, D.G.; Foing, B.; Stagnaro, L. SMART-1: Development and Lessons Learnt. Acta Astronaut. 2005, 56, 455–468. [Google Scholar] [CrossRef]
- Lo, M.W.; Williams, B.G.; Bollman, W.E.; Han, D.S.; Hahn, Y.S.; Bell, J.L.; Hirst, E.; Corwin, R.; Hong, R.; Howell, K.; et al. Genesis mission design. J. Astronaut. Sci. 2011, 49, 169–184. [Google Scholar] [CrossRef]
- Folta, D.C.; Woodard, M.; Howell, K.; Patterson, C.; Schlei, W. Applications of multi-body dynamical environments the ARTEMIS transfer trajectory design. Acta Astronaut. 2012, 73, 237–249. [Google Scholar] [CrossRef] [Green Version]
- Roncoli, R.B.; Fujii, K.K. Mission design overview for the gravity recovery and interior laboratory GRAIL mission. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Farquhar, R.W. The Flight of ISEE-3/ICE Origins, Mission History, and a Legacy. J. Astronaut. Sci. 2001, 49, 23–73. [Google Scholar] [CrossRef]
- Dunham, D.W.; Jen, S.J.; Roberts, C.E.; Seacord, A.W., II; Sharer, P.J.; Folta, D.C.; Muhonen, D.P. Transfer trajectory design for the SOHO libration-point mission. In Proceedings of the 43rd International Astronautical Congress, Washington, DC, USA, 28 August–5 September 1992. [Google Scholar]
- Sharer, P.; Harrington, T. Trajectory Optimization for the ACE Halo Orbit Mission. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, USA, 29–31 July 1996. AIAA paper 96-3601-CP. [Google Scholar]
- Franz, H.; Sharer, P.; Ogilvie, K.; Desch, M. WIND Nominal Mission Performance and Extended Mission Design. J. Astronaut. Sci. 2001, 49, 145–167. [Google Scholar] [CrossRef]
- Uesugi, K.; Matuso, H.; Kawaguchi, J.; Hayashi, T. Japanese first double Lunar swingby mission HITEN. Acta Astronaut. 1991, 25, 347–355. [Google Scholar] [CrossRef]
- Belbruno, E.; Miller, J. Sun-perturbed Earth-to-Moon transits with balistic capture. J. Guid. Control Dyn. 1993, 16, 770–775. [Google Scholar] [CrossRef]
- Szebehely, V. Theory of Orbit the Restricted Problem of Three Bodies; Academic Press: London, UK, 1967. [Google Scholar]
- Goḿez, G.; Masdemont, J. Some zero cost transfers between libration points orbits. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Clearwater, FL, USA, 23–26 January 2000. Paper AAS 00-177. [Google Scholar]
- Breakwell, J.V.; Brown, J.V. The halo family of 3-dimensional periodic orbits in the Earth–Moon restricted 3-body problem. Celest. Mech. Dyn. Astron. 1979, 20, 389–404. [Google Scholar] [CrossRef]
- McCarthy, B.P.; Howell, K.C. Leveraging quasi-periodic orbits for trajectory design in cislunar space. Astrodynamics 2021, 5, 139–165. [Google Scholar] [CrossRef]
- Farquhar, R.W.; Kamel, A.A. Quasi-periodic orbits about the translunar libration point. Celest. Mech. Dyn. Astron. 1973, 7, 458–473. [Google Scholar] [CrossRef]
- Moeckel, R. A variational proof of existence of transit orbits in the restricted three-body problem. Dyn. Syst. Int. J. 2005, 20, 45–58. [Google Scholar] [CrossRef] [Green Version]
- Anderson, R.L.; Easton, R.W.; Lo, M.W. Isolating blocks as computational tools in the circular restricted three-body problem. Physica D 2017, 343, 38–50. [Google Scholar] [CrossRef]
- Giancotti, M.; Pontani, M.; Teofilatto, P. Lunar capture trajectories and homoclinic connections through isomorphic mapping. Celest. Mech. Dyn. Astron. 2012, 114, 55–76. [Google Scholar] [CrossRef]
- Conley, C.C. Low energy transit orbits in the restricted three-body problem. J. Appl. Math. 1968, 16, 732–746. [Google Scholar] [CrossRef]
- Conley, C.C. On the Ultimate Behavior of Orbits with Respect to an Unstable Critical Point l. Oscillating, Asymptotic, and Capture Orbits. J. Differ. Equ. 1969, 5, 136–158. [Google Scholar] [CrossRef] [Green Version]
- Koon, W.S.; Lo, M.W.; Marsden, J.E.; Ross, S.D. Low Energy transit to the Moon. Celest. Mech. Dyn. Astron. 2001, 81, 63–73. [Google Scholar] [CrossRef]
- Giancotti, M.; Pontani, M.; Teofilatto, P. Cylindrical isomorphic mapping applied to invariant manifold dynamics for Earth-Moon Missions. Celest. Mech. Dyn. Astron. 2014, 120, 249–268. [Google Scholar] [CrossRef]
- Anderson, R.L.; Lo, M.W. Spatial approaches to moons from resonance relative to invariant manifolds. Acta Astronaut. 2014, 105, 335–372. [Google Scholar] [CrossRef]
- Khaja Fayaz, H.; Khaja Faisal, H.; Carletta, S.; Teofilatto, P. Deployment of a microsatellite constellation around the Moon using chaotic multi body dynamics. In Proceedings of the 71st International Astronautical Congress, Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Carletta, S.; Pontani, M.; Teofilatto, P. Earth-Mars microsatellite missions using ballistic capture and low-thrust propulsion. In Proceedings of the 71st International Astronautical Congress, Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Szebehely, V.; Giacaglia, G.E.O. On the elliptic restricted problem of three bodies. Astronaut. J. 1964, 69, 230–235. [Google Scholar] [CrossRef]
- Michalodimitrakis, M. The circular restricted four-body problem. Astrophys. Space Sci. 1981, 75, 289–305. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Station-keeping about sun-mars three-dimensional quasi-periodic collinear libration point trajectories. Adv. Astronaut. Sci. 2020, 173, 299–311. [Google Scholar]
- Carletta, S.; Pontani, M.; Teofilatto, P. Long-term capture orbits for low-energy space missions. Celest. Mech. Dyn. Astron. 2018, 130, 46. [Google Scholar] [CrossRef] [Green Version]
- Conley, C.; Easton, R. Isolated invariant sets and isolating blocks. Trans. Am. Math. Soc. 1971, 158, 35–61. [Google Scholar] [CrossRef]
- Graziani, F.; Sparvieri, N.; Carletta, S. A low-cost Earth-Moon-Mars Mission Using a Microsatellite Platform. In Proceedings of the 71st International Astronautical Congress, Online Event, 12–14 October 2020. [Google Scholar]
- Carletta, S. Design of fuel-saving lunar captures using finite thrust and gravity-braking. Acta Astronaut. 2021, 181, 190–200. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Dynamics of three-dimensional capture orbits from libration region analysis. Acta Astronaut. 2019, 165, 331–343. [Google Scholar] [CrossRef]
- Arnold, V.I. Small denominators and problems of stability of motion in classical and celestial mechanics. In Collected Works; Vladimir I. Arnold—Collected Works; Givental, A.B., Khesin, B.A., Marsden, J.E., Varchenko, A.N., Vassiliev, V.A., Viro, O.Y., Zakalyukin, V.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 1. [Google Scholar]
- Blanc, M.; Alibert, Y.; André, N.; Atreya, S.; Beebe, R.; Benz, W.; Bolton, S.J.; Coradini, A.; Coustenis, A.; Dehant, V.; et al. LAPLACE: A mission to Europa and the Jupiter System for ESA’s Cosmic Vision Programme. Exp. Astron. 2009, 23, 849–892. [Google Scholar] [CrossRef] [Green Version]
- Phillips, C.B.; Pappalardo, R.T. Europa Clipper Mission Concept: Exploring Jupiter’s Ocean Moon. EOS 2014, 95, 165–167. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Design of low-energy capture trajectories in the elliptic restricted four-body problem. In Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Liu, C.; Gong, S. Hill stability of the satellite in the elliptic restricted four-body problem. Astrophys. Space Sci. 2018, 363, 162. [Google Scholar] [CrossRef]
- Llibre, J.; Piñol, C. On the elliptic restricted three-body problem. Celest. Mech. Dyn. Astron. 1990, 48, 319–345. [Google Scholar] [CrossRef]
- Meyer, K.R.; Hall, G.R.; Offin, D. Introduction to Hamiltonian Dynamical Systems and the N-Body Problem. In Applied Mathematical Sciences; Springer Science+Business Media: New York, NY, USA, 2009. [Google Scholar]
- Siegel, C.L.; Moser, J.K. Lectures on Celestial Mechanics Reprint of the 1971 Edition; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Koon, W.S.; Lo, M.W.; Marsden, J.E.; Ross, S.D. Dynamical Systems, the Three-Body Problem and Space Mission Design; Marsden Books, 2011; Available online: https://www.researchgate.net/publication/328913173_Dynamical_Systems_the_Three-Body_Problem_and_Space_Mission_Design (accessed on 20 February 2022).
- Moser, J. On the generalization of a theorem of A. Liapounoff. Commun. Pure Appl. Math. 1958, 11, 257–271. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Dynamics of capture orbits from libration region analysis. In Proceedings of the 69th International Astronautical Congress, Bremen, Germany, 1–5 October 2018. [Google Scholar]
| Variable | Symbol | Value |
|---|---|---|
| Mass of Jupiter | 1.899 × 10 kg | |
| Mass of Europa | 4.799 × 10 kg | |
| Mass of Io | 8.932 × 10 kg | |
| Jupiter–Europa semimajor axis | a | 6.711 × 10 km |
| Jupiter–Io semimajor axis | 4.218 × 10 km | |
| Jupiter–Europa eccentricity | e | 0.0094 |
| Jupiter–Io eccentricity | 0.0041 | |
| Inclination between the orbital planes | 0.430 deg | |
| Coordinate of the libration point | 6.081 × 10 km | |
| Resonant Hamiltonian terms | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carletta, S.; Pontani, M.; Teofilatto, P. Characterization of Low-Energy Quasiperiodic Orbits in the Elliptic Restricted 4-Body Problem with Orbital Resonance. Aerospace 2022, 9, 175. https://doi.org/10.3390/aerospace9040175
Carletta S, Pontani M, Teofilatto P. Characterization of Low-Energy Quasiperiodic Orbits in the Elliptic Restricted 4-Body Problem with Orbital Resonance. Aerospace. 2022; 9(4):175. https://doi.org/10.3390/aerospace9040175
Chicago/Turabian StyleCarletta, Stefano, Mauro Pontani, and Paolo Teofilatto. 2022. "Characterization of Low-Energy Quasiperiodic Orbits in the Elliptic Restricted 4-Body Problem with Orbital Resonance" Aerospace 9, no. 4: 175. https://doi.org/10.3390/aerospace9040175
APA StyleCarletta, S., Pontani, M., & Teofilatto, P. (2022). Characterization of Low-Energy Quasiperiodic Orbits in the Elliptic Restricted 4-Body Problem with Orbital Resonance. Aerospace, 9(4), 175. https://doi.org/10.3390/aerospace9040175






