A Real-Time Reentry Guidance Method for Hypersonic Vehicles Based on a Time2vec and Transformer Network
Abstract
:1. Introduction
2. Problem Statement
2.1. Reentry Dynamics Model
2.2. Flight Constraints
2.2.1. Process Constraints
2.2.2. Quasi-Equilibrium Glide Condition
2.2.3. Terminal Constraints
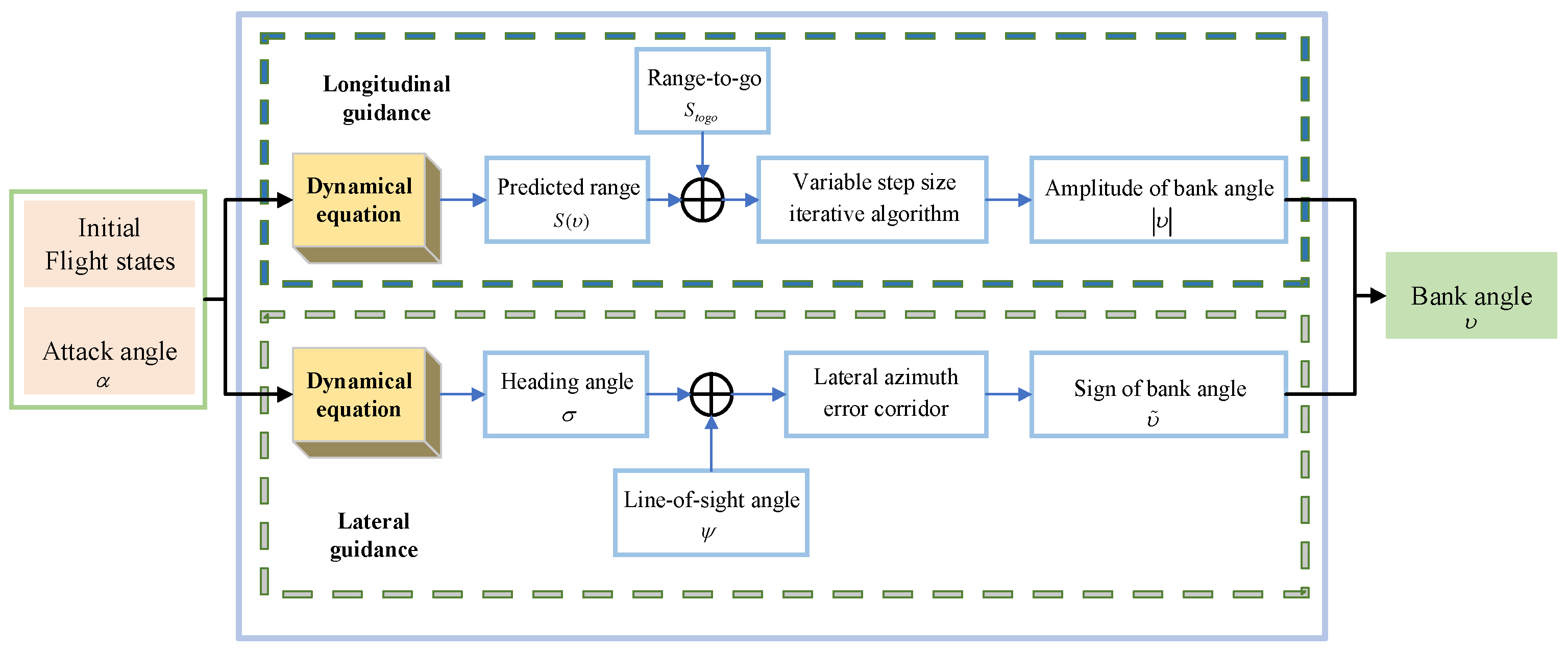
3. Predictor-Corrector Guidance Method
3.1. Design of Attack Angle
3.2. Design of Bank Angle
3.2.1. Amplitude Design of Bank Angle
| Algorithm 1 Variable step-size iterative |
| 1: Initialization 2: Set , 3: While ), do 4: bring into formula (5) and get 5: if , do 6: 7: end while 8: elseif , do 9: 10: elseif , do 11: 12: 13: end 14: Get H |
3.2.2. Sign Design of Bank Angle
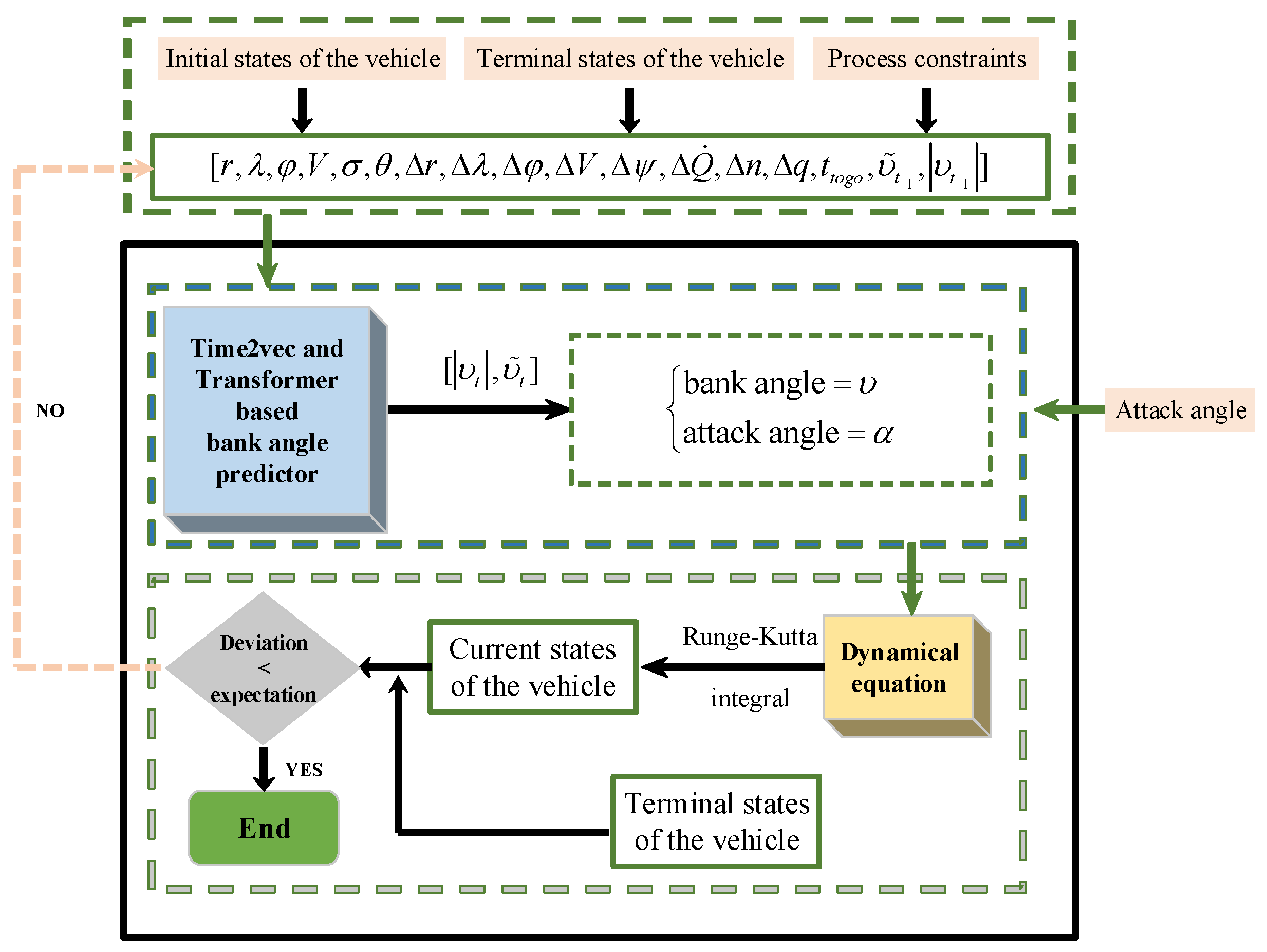
4. Predictive Reentry Guidance Based on Time2vec and Transformer Network
4.1. Inputs and Outputs of Network
- The terminal speed out of bounds;
- The process constraints out of bounds;
- The prediction lag of the bank angle inversion.
4.2. Bank Angle Predictor
5. Simulations and Analysis
5.1. Bank Angle Predictor Training
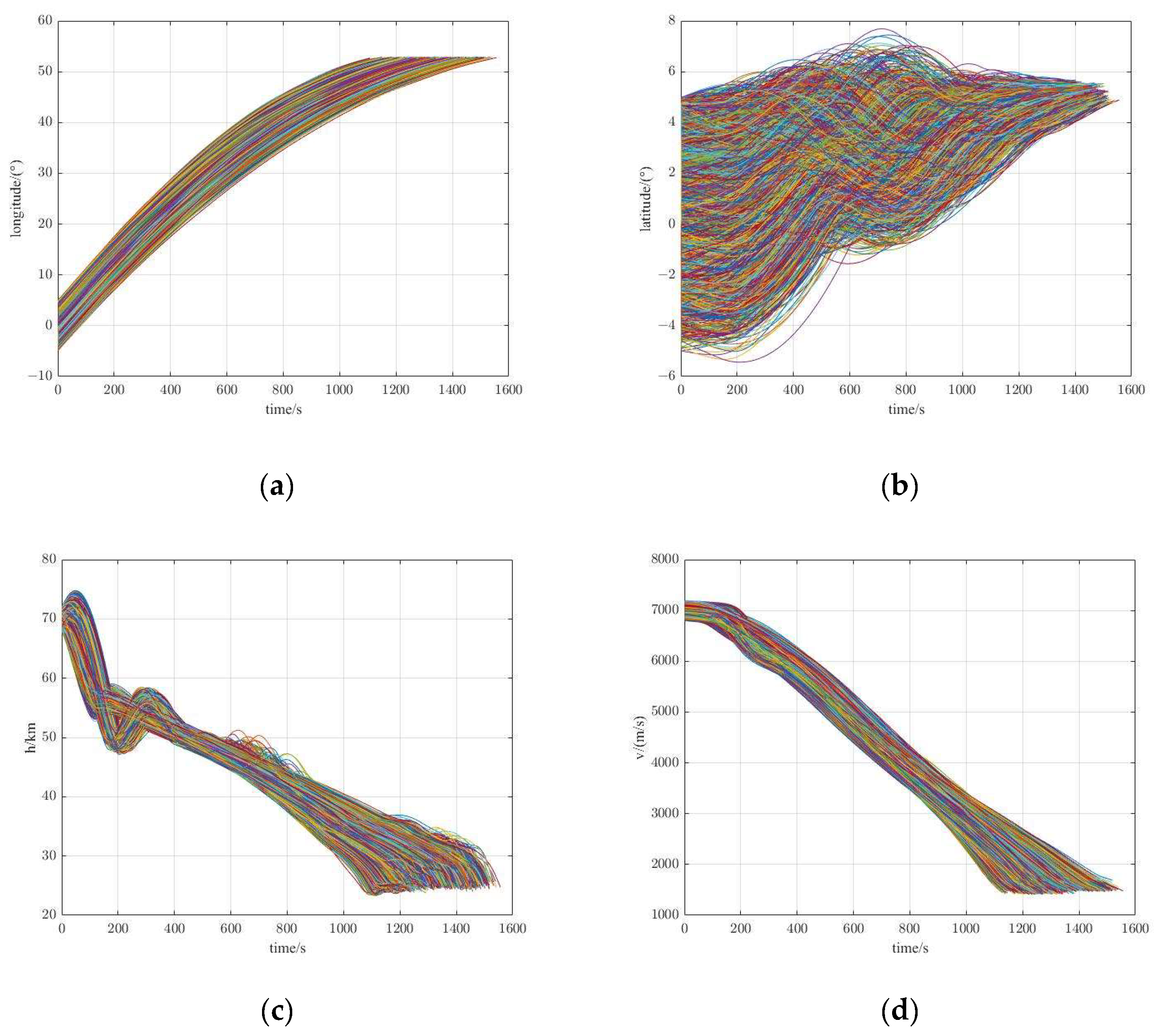
5.1.1. Generation of Training Datasets
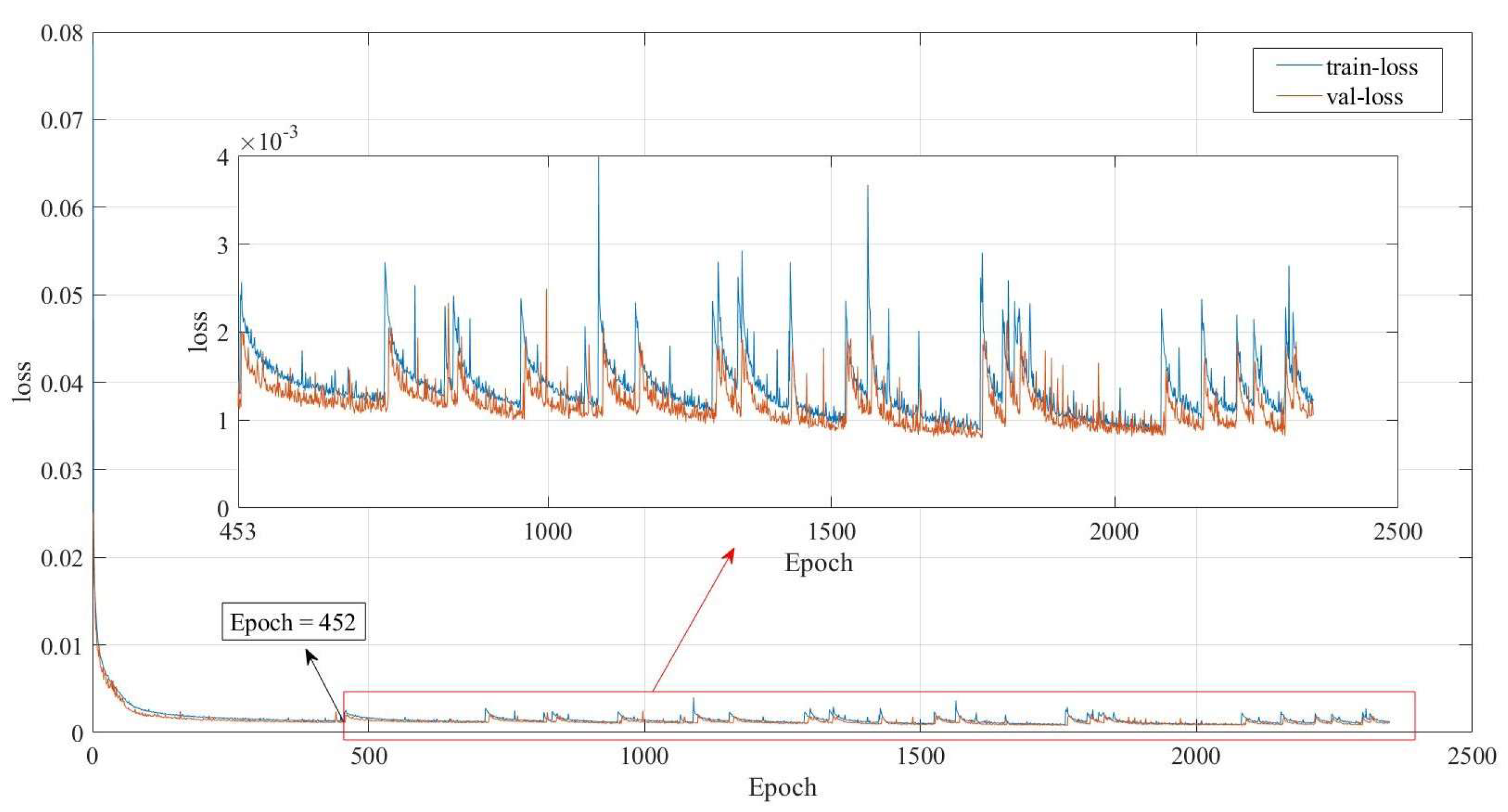
5.1.2. Predictor Training
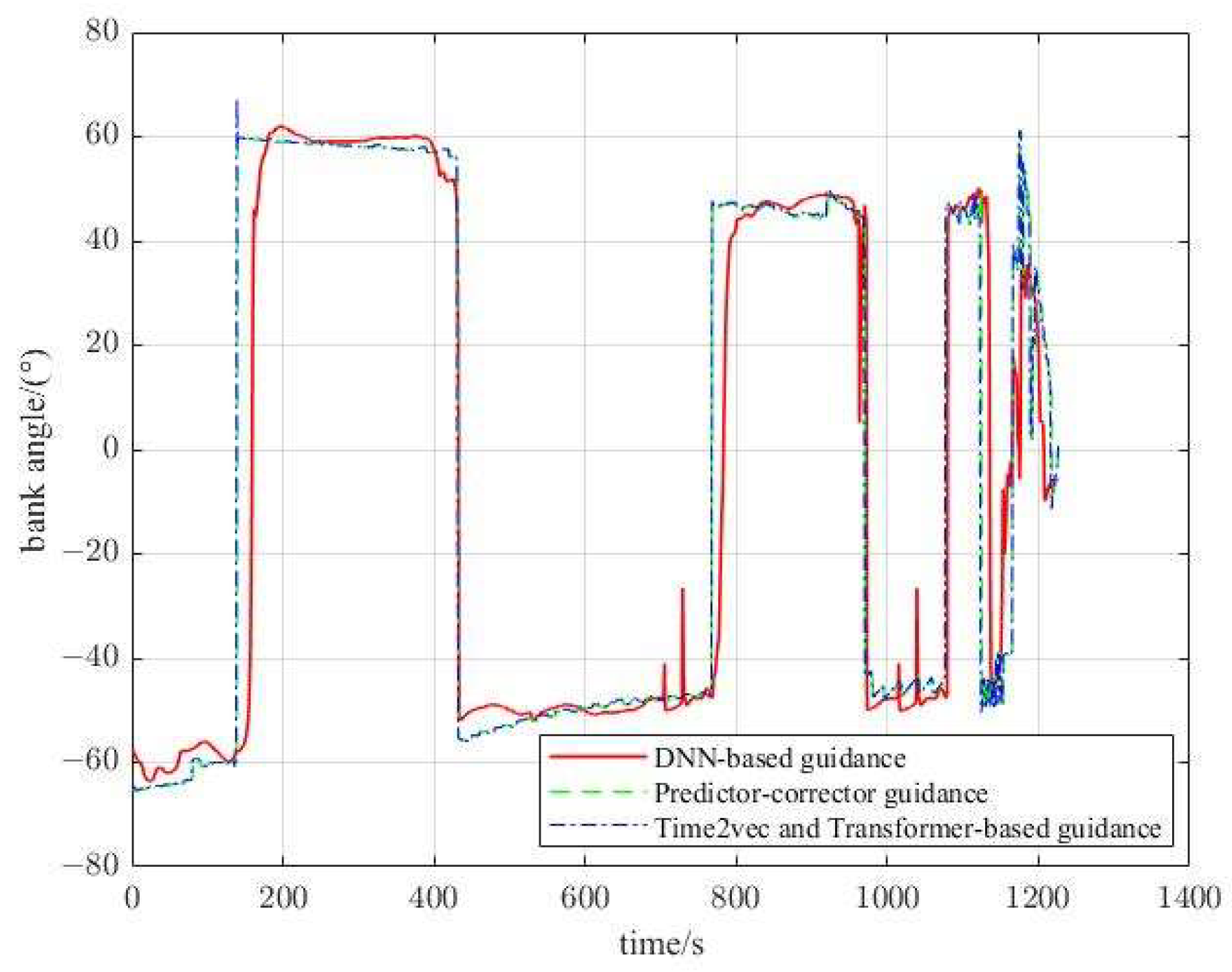
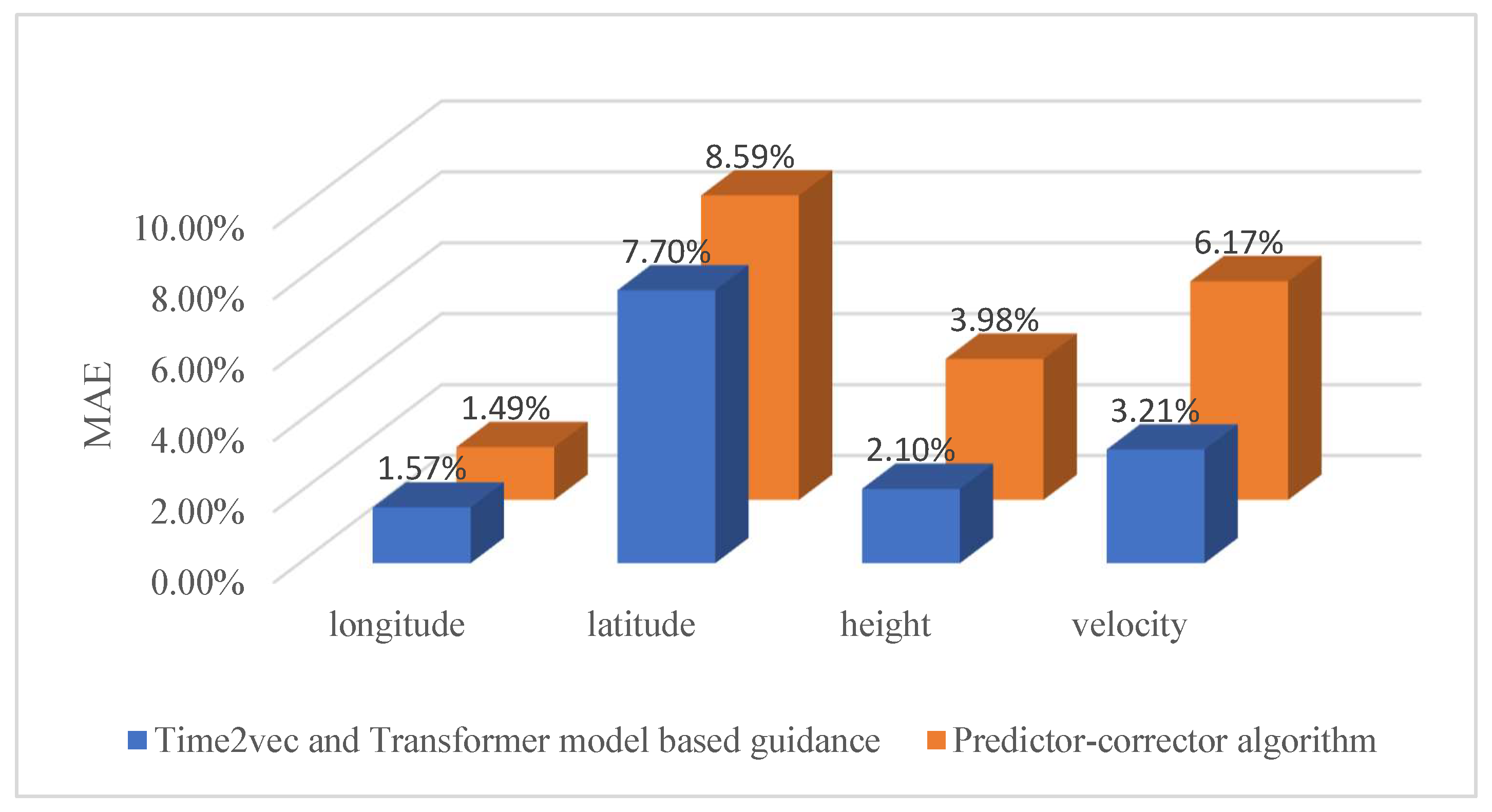
5.2. Evaluations on Guidance Precision
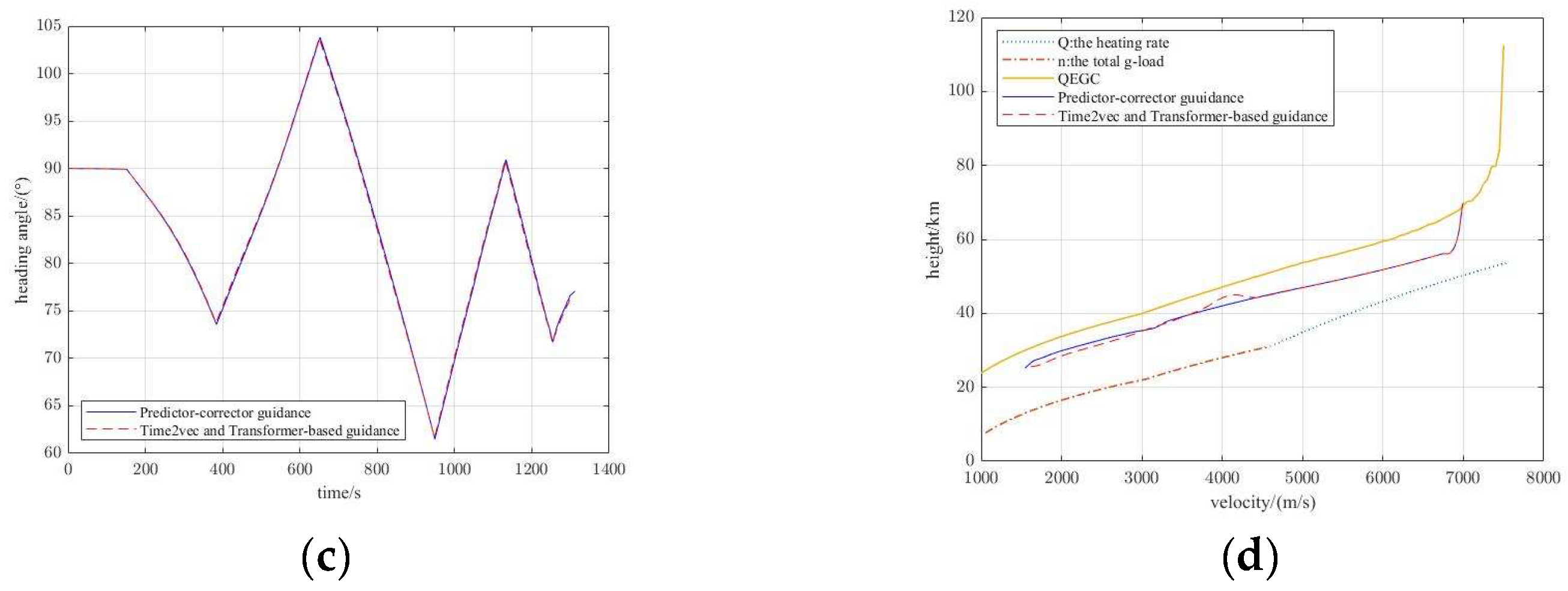
5.3. Evaluations on Bank Angle Prediction
5.4. Evaluations on Monte Carlo Simulations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, P. Entry guidance: A unified method. J. Guid. Control. Dyn. 2014, 37, 713–728. [Google Scholar] [CrossRef]
- Guo, Y.; Li, X.; Zhang, H.; Wang, L.; Cai, M. Entry guidance with terminal time control based on quasi-equilibrium glide condition. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 887–896. [Google Scholar] [CrossRef]
- Xue, S.; Lu, P. Constrained predictor-corrector entry guidance. J. Guid. Control. Dyn. 2010, 33, 1273–1281. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, H.; Zeng, L.; Tang, G. A robust predictor–corrector entry guidance. Aerosp. Sci. Technol. 2017, 66, 103–111. [Google Scholar] [CrossRef]
- Cheng, L.; Jiang, F.; Wang, Z.; Li, J. Multiconstrained real-time entry guidance using deep neural networks. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 325–340. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, L.; Wang, Y. On-line reentry guidance algorithm with both path and no-fly zone constraints. Acta Astronaut. 2015, 117, 243–253. [Google Scholar] [CrossRef]
- Wang, X.; Guo, J.; Tang, S.; Qi, S.; Wang, Z. Entry trajectory planning with terminal full states constraints and multiple geographic constraints. Aerosp. Sci. Technol. 2019, 84, 620–631. [Google Scholar] [CrossRef]
- Xu, J.; Qiao, J.; Guo, L.; Chen, W. Enhanced predictor–corrector Mars entry guidance approach with atmospheric uncertainties. IET Control. Theory Appl. 2019, 13, 1612–1618. [Google Scholar]
- Lu, P.; Forbes, S.; Baldwin, M. Gliding Guidance of High L/D Hypersonic Vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; Available online: https://arc.aiaa.org/doi/10.2514/6.2013-4648 (accessed on 6 July 2022).
- Sivan, K.; Savithri, A.S.; Ashok, J. An Adaptive Reentry Guidance; Indian Institute of Technology Bornbay: Mumbai, India, 2004. [Google Scholar]
- Li, Z.; Sun, X.; Hu, C.; Liu, G.; He, B. Neural network based online predictive guidance for high lifting vehicles. Aerosp. Sci. Technol. 2018, 82–83, 149–160. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, O.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, M.; Li, S. The rapid data-driven prediction method of coupled fluid-thermal-structure for hypersonic vehicles. Aerospace 2021, 8, 265. [Google Scholar] [CrossRef]
- Strijhak, S.; Ryazanov, D.; Koshelev, K.; Ivanov, A. neural network prediction for ice shapes on airfoils using icefoam simulations. Aerospace 2022, 9, 96. [Google Scholar] [CrossRef]
- Wang, N.; Er, M.J. Self-constructing adaptive robust fuzzy neural tracking control of surface vehicles with uncertainties and unknown disturbances. IEEE Trans. Control. Syst. Technol. 2014, 23, 991–1002. [Google Scholar]
- Hu, R.; Zhang, Y. Fast path planning for long-range planetary roving based on a hierarchical framework and deep reinforcement learning. Aerospace 2022, 9, 101. [Google Scholar] [CrossRef]
- Du, X.; Chen, J.; Zhang, H.; Wang, J. Fault detection of aero-engine sensor based on inception-CNN. Aerospace 2022, 9, 236. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Liu, M.; Yang, M.; Liang, H. A real-time trajectory optimization method for hypersonic vehicles based on a deep neural network. Aerospace 2022, 9, 188. [Google Scholar] [CrossRef]
- Horn, J.F.; Schmidt, E.M.; Geiger, B.R.; DeAngelo, M.P. Neural network-based trajectory optimization for un-manned aerial vehicles. J. Guid. Control. Dyn. 2012, 35, 548–562. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Z. A Deep Learning-Based Approach to Real-Time Trajectory Optimization for Hypersonic Vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Orlando, FL, USA, 6–10 January 2020; Available online: https://arc.aiaa.org/doi/10.2514/6.2020-0023 (accessed on 6 July 2022).
- Xu, M.; Chen, K.; Liu, L.; Tang, G. Quasi-equilibrium glide adaptive guidance for hypersonic vehicles. Sci. China Technol. Sci. 2012, 55, 856–866. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 6000–6010. [Google Scholar]
- Cheng, J.; Dong, L.; Lapata, M. Long Short-Term Memory-Networks for Machine Reading. 2016. Available online: https://arxiv.org/abs/1601.06733 (accessed on 6 July 2022).
- Malibari, N.; Katib, I.; Mehmood, R. Predicting stock closing prices in emerging markets with transformer neural networks: The saudi stock exchange case. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 878–886. [Google Scholar] [CrossRef]
- Paulus, R.; Xiong, C.; Socher, R. A Deep Reinforced Model for Abstractive Summarization. 2017. Available online: https://doi.org/10.48550/arXiv.1705.04304 (accessed on 6 July 2022).
- Kazemi, S.M.; Goel, R.; Eghbali, S.; Ramanan, J.; Sahota, J.; Thakur, S.; Wu, S.; Smyth, C.; Poupart, P.; Brubaker, M. Time2vec: Learning a Vector Representation of Time. 2019. Available online: https://doi.org/10.48550/arXiv.1907.05321 (accessed on 6 July 2022).




| Parameters | Value |
|---|---|
| batch size | 128 |
| timestep | 100 |
| feature number | 17 |
| output number | 2 |
| attention heads number | 12 |
| learning rate | 0.0001 |
| dropout rate | 0.1 |
| Parameters | Distributions |
|---|---|
| Parameters | Settings |
|---|---|
| 1.225 | |
| 7200 | |
| 6378 | |
| 5.188 × 10−8 | |
| 2000 | |
| 10 | |
| 500 | |
| 25 | |
| 10 | |
| 3000 | |
| 5000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Tong, X.; Xu, X.; Zhao, K. A Real-Time Reentry Guidance Method for Hypersonic Vehicles Based on a Time2vec and Transformer Network. Aerospace 2022, 9, 427. https://doi.org/10.3390/aerospace9080427
Song J, Tong X, Xu X, Zhao K. A Real-Time Reentry Guidance Method for Hypersonic Vehicles Based on a Time2vec and Transformer Network. Aerospace. 2022; 9(8):427. https://doi.org/10.3390/aerospace9080427
Chicago/Turabian StyleSong, Jia, Xindi Tong, Xiaowei Xu, and Kai Zhao. 2022. "A Real-Time Reentry Guidance Method for Hypersonic Vehicles Based on a Time2vec and Transformer Network" Aerospace 9, no. 8: 427. https://doi.org/10.3390/aerospace9080427
APA StyleSong, J., Tong, X., Xu, X., & Zhao, K. (2022). A Real-Time Reentry Guidance Method for Hypersonic Vehicles Based on a Time2vec and Transformer Network. Aerospace, 9(8), 427. https://doi.org/10.3390/aerospace9080427







