Anisotropic Turbulent Kinetic Energy Budgets in Compressible Rectangular Jets
Abstract
:1. Introduction
1.1. Budget Analysis of Incompressible and Compressible Flow in Open Literature
1.2. TKE Budget Equation
1.3. LES Solvers—Subgrid-Scale Turbulence and Applications
2. Methodology
2.1. Nozzle Geometry
2.2. Governing Equations and Numerical Methods
2.3. Computational Domain and Boundary Conditions
2.4. Averaging of Flow Variables
3. Results
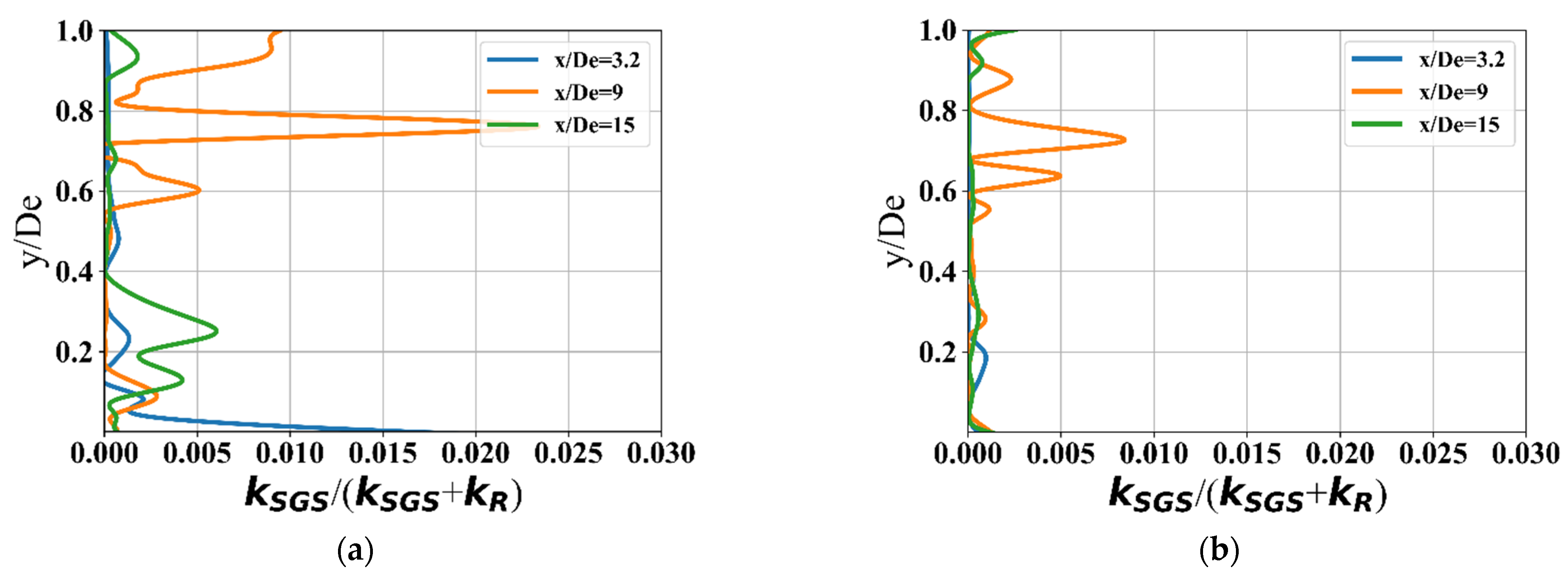
3.1. Resolution of TKE
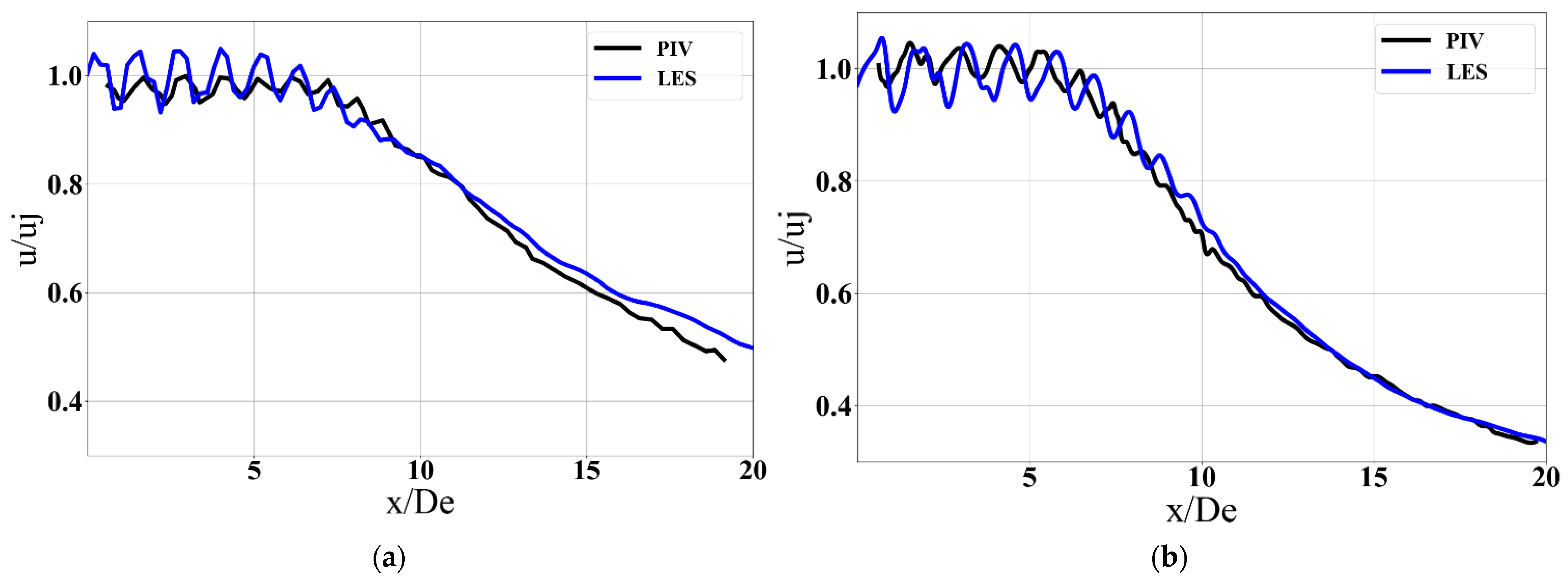
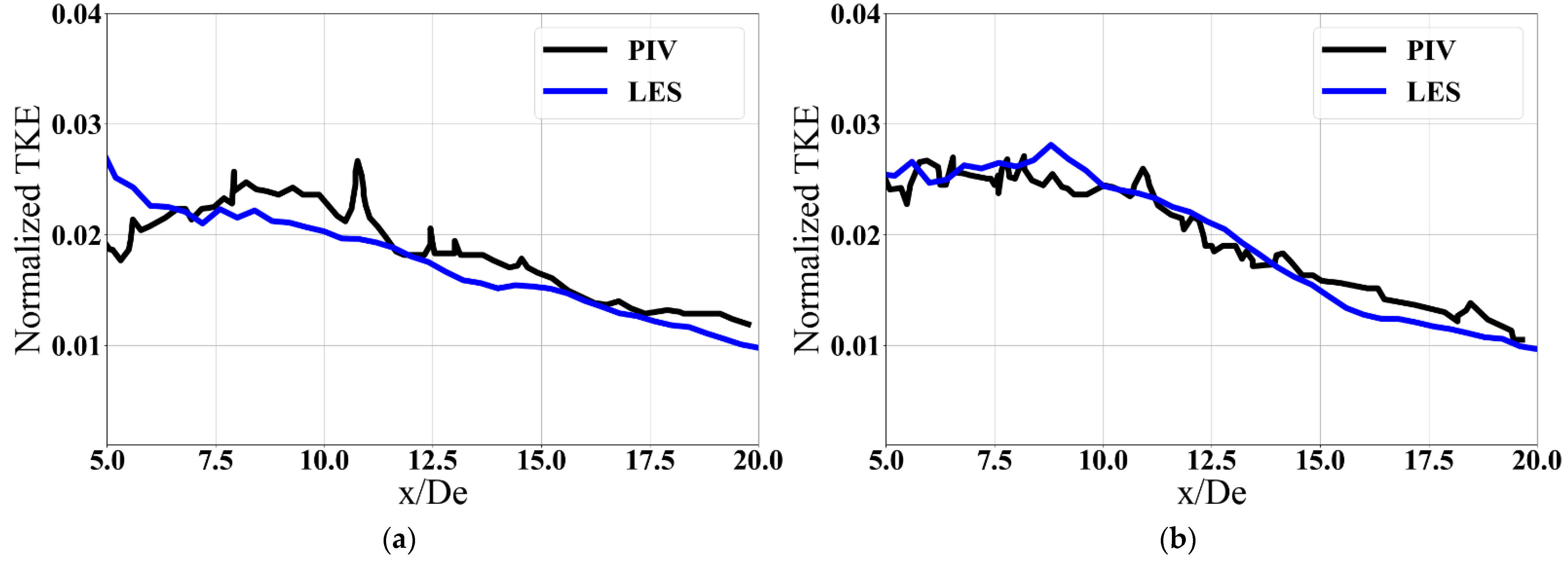
3.2. Validation with PIV Experimental Data
3.3. Instantaneous Flowfield Visualization
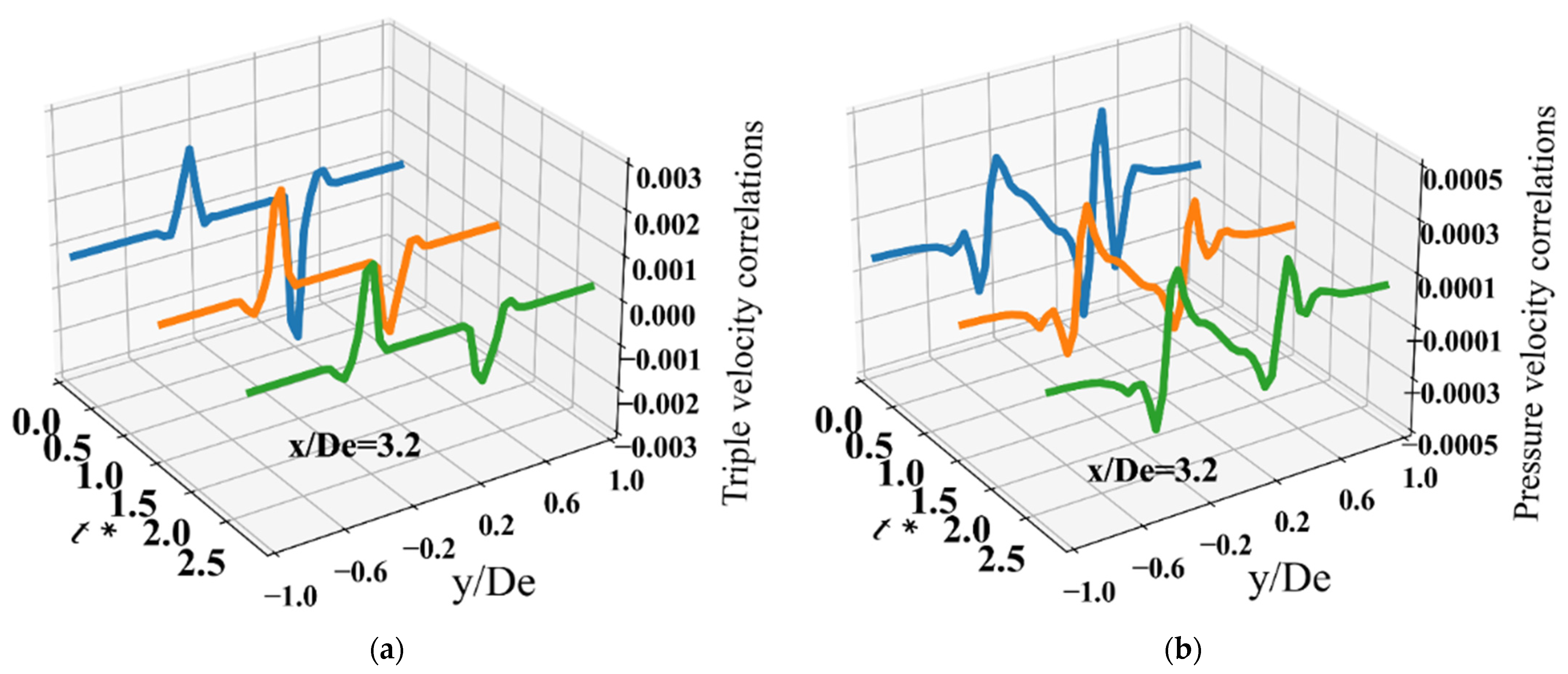
3.4. Temporal Convergence of Higher-Order Statistics
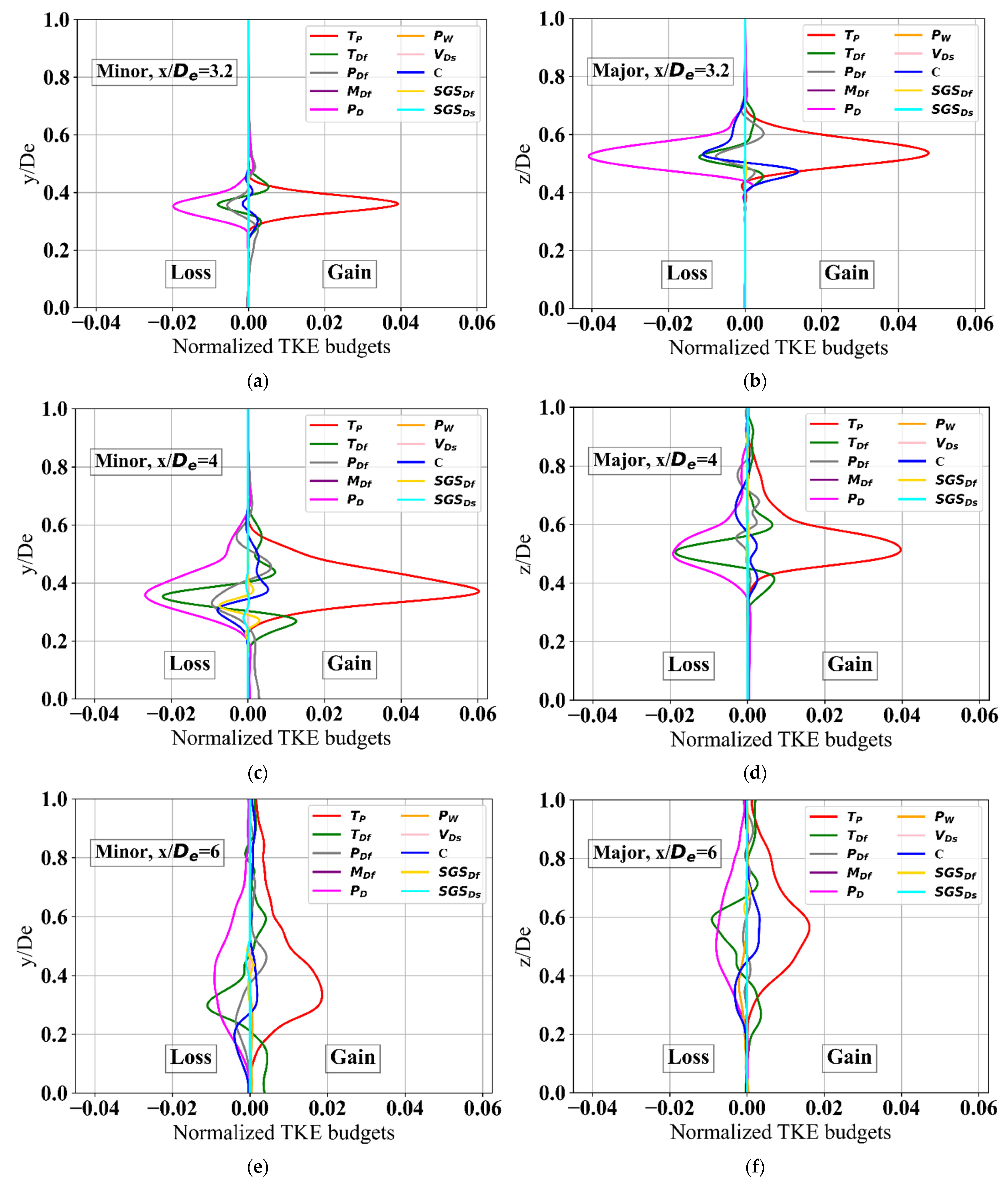
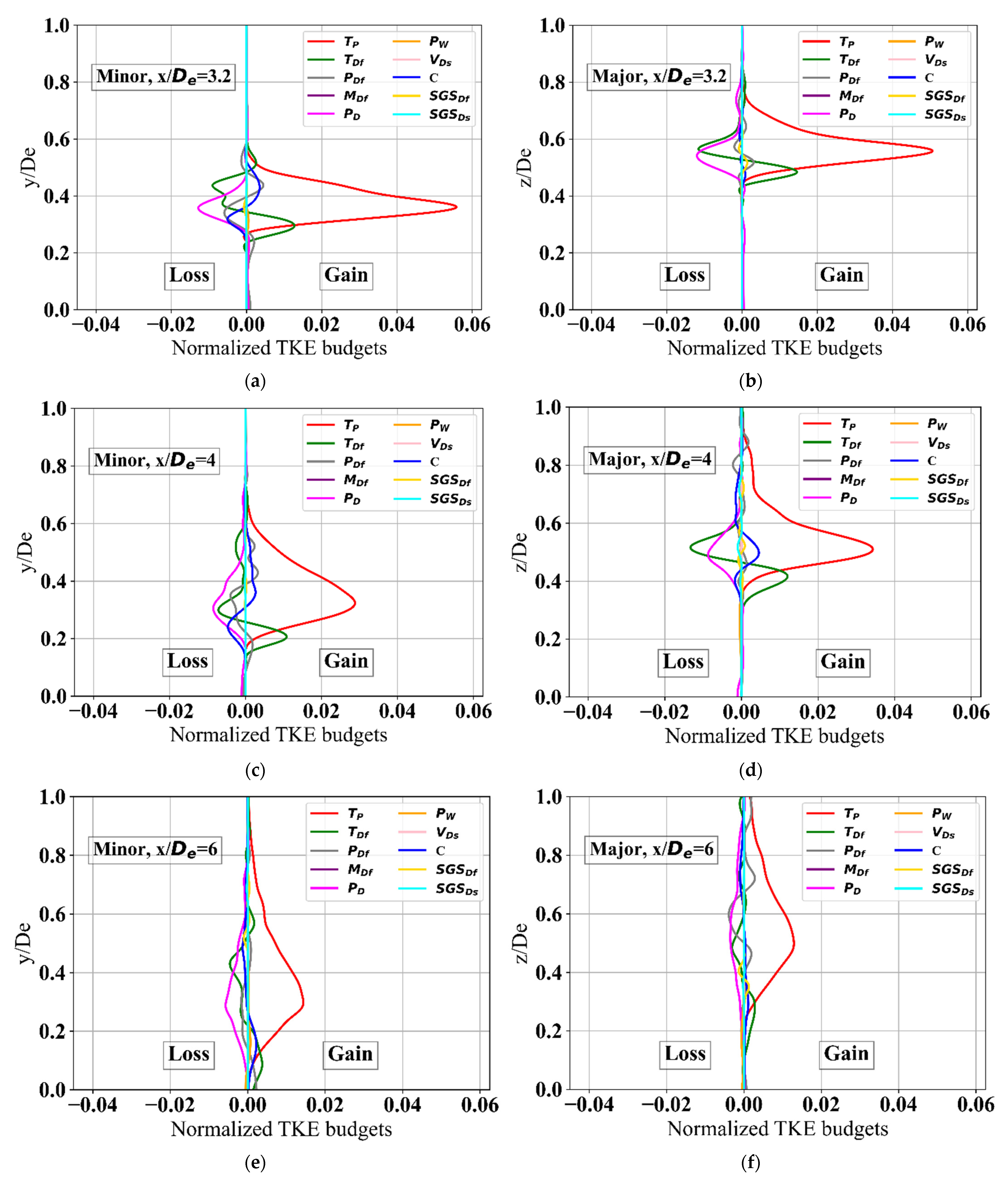
3.5. TKE Budgets—Before The End of Potential Core
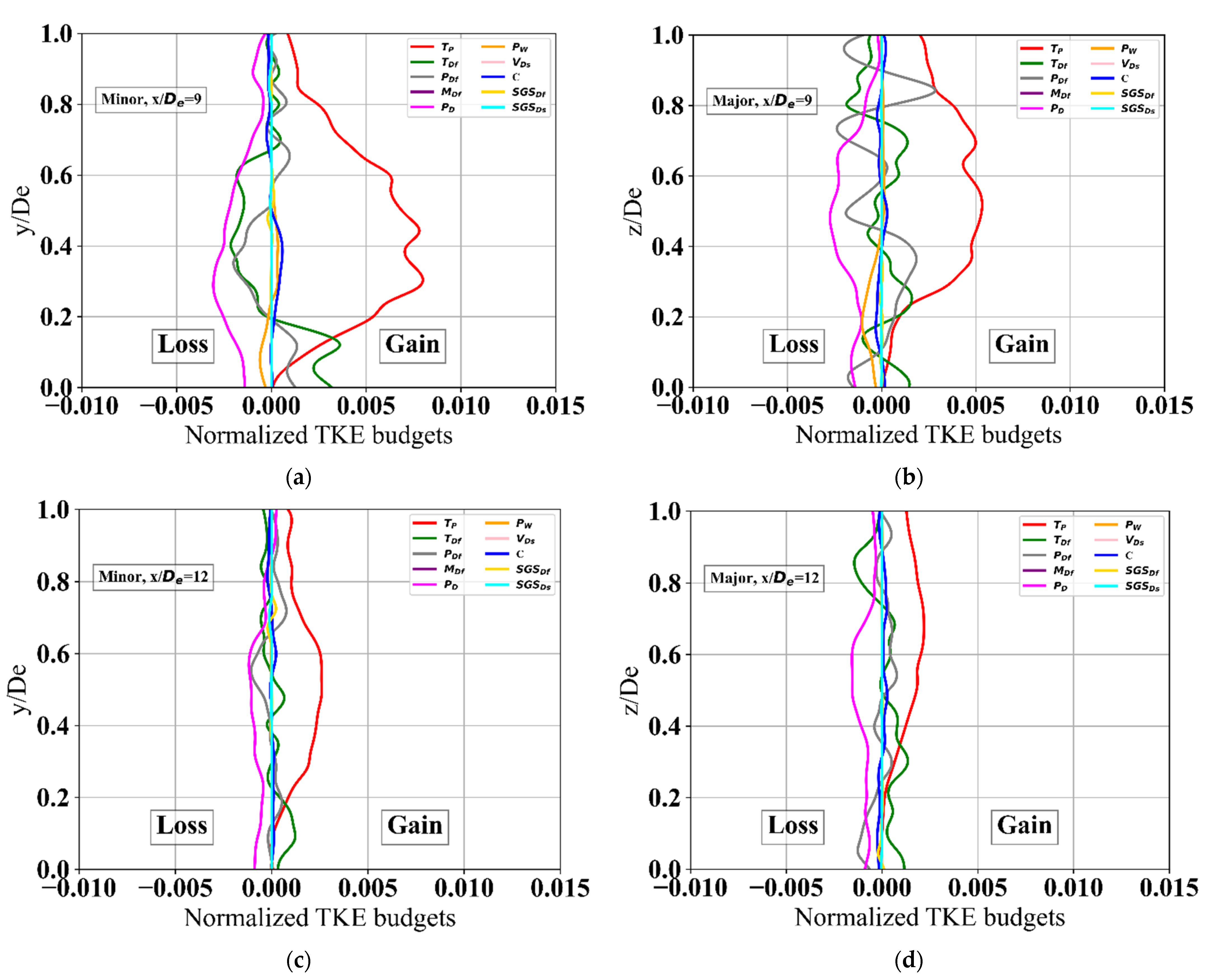
3.6. TKE Budgets—After the End of Potential Core
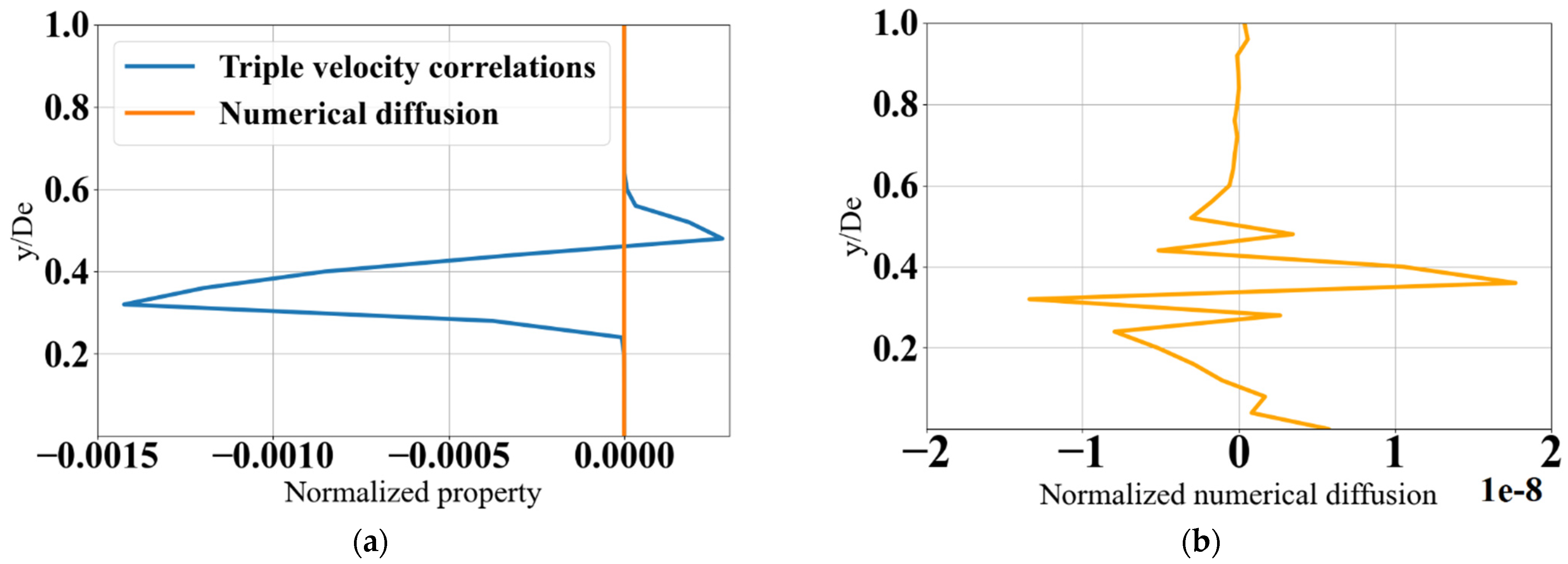
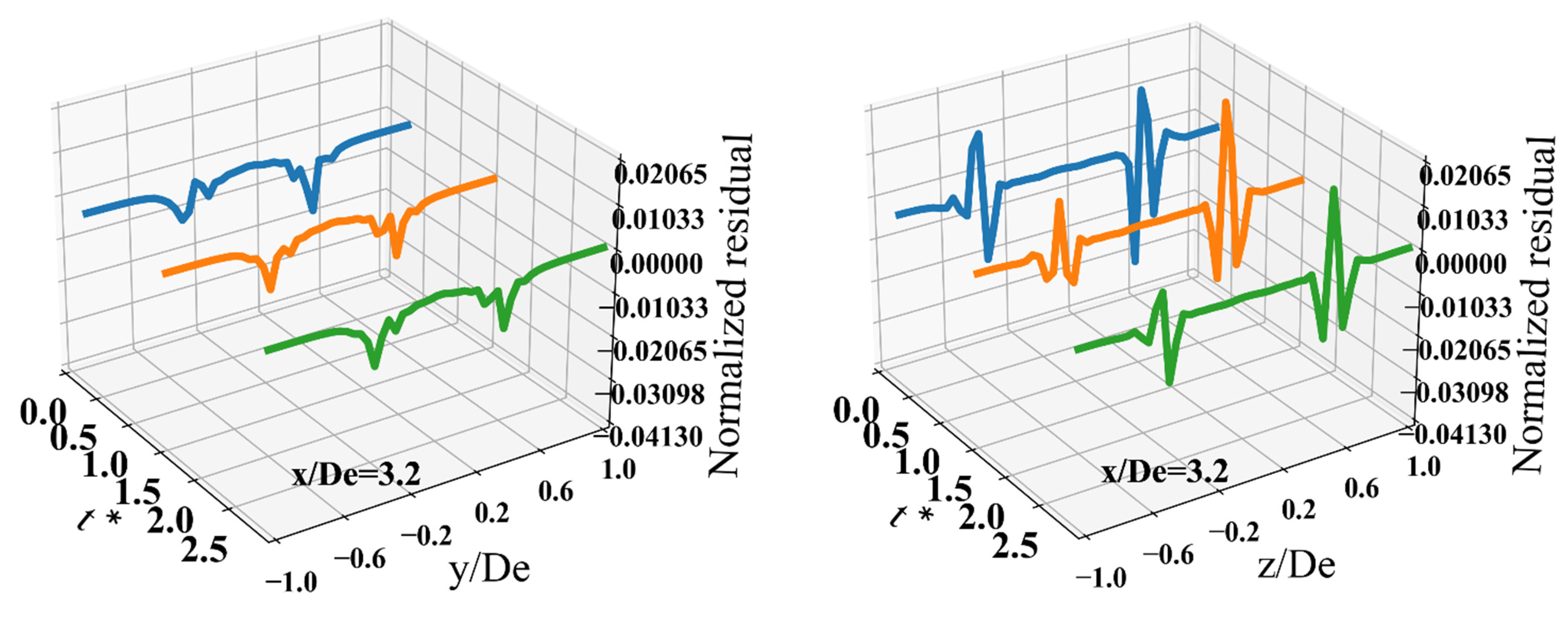
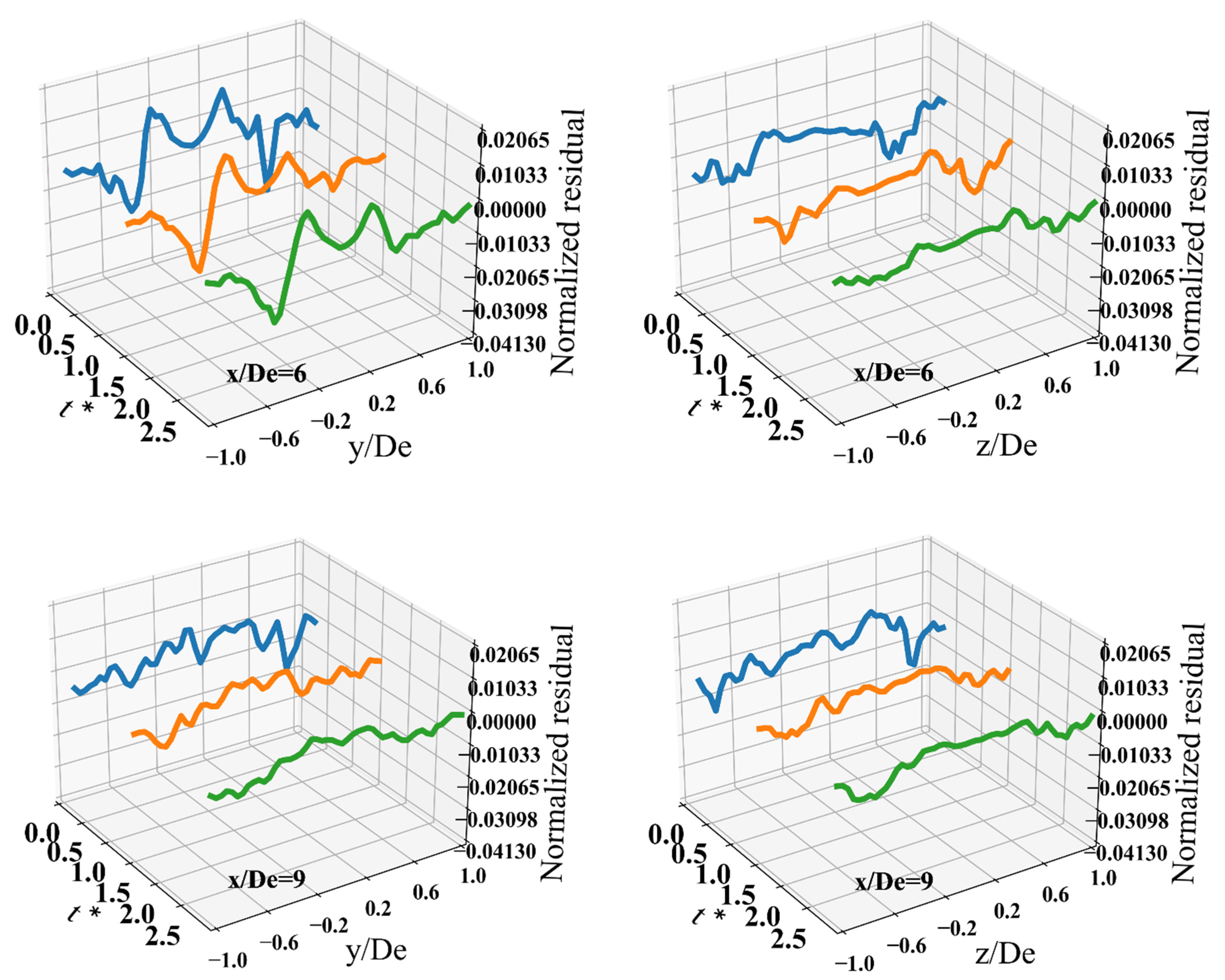
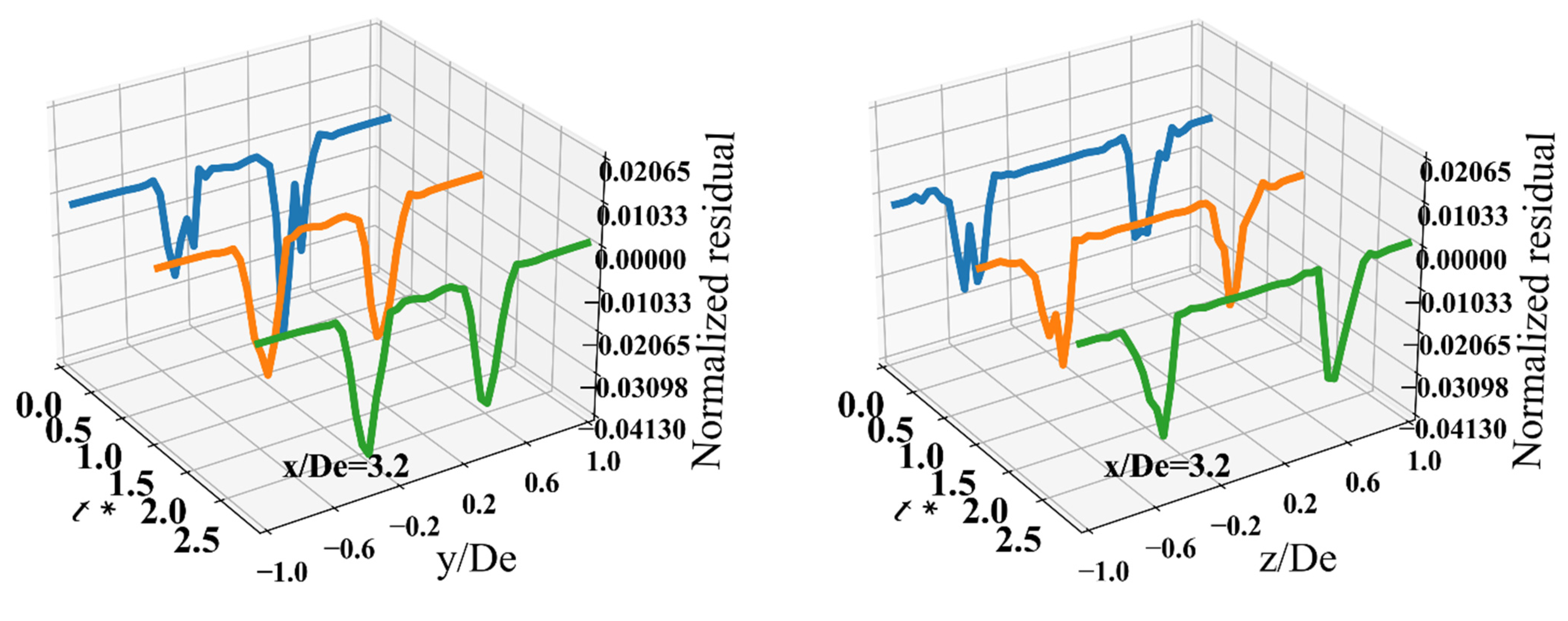
3.7. Temporal Evolution of Budget Residuals
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AR | Aspect ratio |
| CFD | Computational fluid dynamics |
| CPU | Central processing unit |
| DNS | Direct numerical simulation |
| ESFR | Energy stable flux reconstruction |
| FD | Finite difference |
| FV | Finite volume |
| HPC | High performance computing |
| LES | Large Eddy Simulation |
| PIV | Particle image velocimetry |
| TKE | Turbulent Kinetic Energy |
| RANS | Reynolds Averaged Navier Stokes |
| MUSCL | Monotone upstream-centered schemes |
| NPR | Nozzle pressure ratio |
| SST | Shear Stress Transport |
| WALE | Wall-adapting local eddy viscosity |
| De | Nozzle-exit equivalent diameter |
| u | Axial component of velocity |
| uj | Jet velocity at nozzle exit |
| Jet density at nozzle exit | |
| C | Convection |
| TKE production | |
| Turbulence diffusion | |
| Molecular diffusion | |
| Mj | Jet Mach number at nozzle exit |
| Pressure diffusion | |
| Pressure dilatation | |
| Pressure work | |
| Viscous dissipation | |
| Subgrid-scale diffusion | |
| Subgrid-scale dissipation | |
| R | Residual |
| Rej | Jet Reynolds number |
| Subgrid-scale TKE | |
| Resolved TKE | |
| SGS | Subgrid scale |
| Fluctuation in Reynolds averaged quantity | |
| Fluctuation in Favre averaged quantity | |
| Favre-averaged quantity | |
| Reynolds averaged quantity |
References
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1998; Volume 2. [Google Scholar]
- Gutmark, E.; Wygnanski, I. The planar turbulent jet. J. Fluid Mech. 1976, 73, 465–495. [Google Scholar] [CrossRef]
- Nishino, K.; Samada, M.; Kasuya, K.; Torii, K. Turbulence statistics in the stagnation region of an axisymmetric impinging jet flow. Int. J. Heat Fluid Flow 1996, 17, 193–201. [Google Scholar] [CrossRef]
- Cavo, A.; Lemonis, G.; Panidis, T. Experimental investigation of the energy budget and enstrophy in the near field of a rectangular turbulent jet. In Turbulence Heat and Mass Transfer 6. Proceedings of the Sixth International Symposium on Turbulence Heat and Mass Transfer; Begel House Inc.: Rome, Italy, 2009. [Google Scholar]
- Liu, X.; Thomas, F.O. Measurement of the turbulent kinetic energy budget of a planar wake flow in pressure gradients. Exp. Fluids 2004, 37, 469–482. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Turbulence and energy budget in a self-preserving round jet: Direct evaluation using large eddy simulation. J. Fluid Mech. 2009, 627, 129–160. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Large eddy simulations of transitional round jets: Influence of the Reynolds number on flow development and energy dissipation. Phys. Fluids 2006, 18, 065101. [Google Scholar] [CrossRef]
- Bonelli, F.; Viggiano, A.; Magi, V. High-speed turbulent gas jets: An LES investigation of Mach and Reynolds number effects on the velocity decay and spreading rate. Flow Turbul. Combust. 2021, 107, 519–550. [Google Scholar] [CrossRef]
- Vyas Manan, A.; Waindim, M.; Gaitonde, D.V. Budget of Turbulent Kinetic Energy in a Shock Wave/Boundary-layer Interaction. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 3187. [Google Scholar]
- Kokkinakis, I.W.; Drikakis, D.; Ritos, K.; Spottswood, S.M. Direct numerical simulation of supersonic flow and acoustics over a compression ramp. Phys. Fluids 2020, 32, 066107. [Google Scholar] [CrossRef]
- Orlandi, P.; Pirozzoli, S. Secondary Flow in Smooth and Rough Turbulent Circular Pipes: Turbulence Kinetic Energy Budgets. Fluids 2021, 6, 448. [Google Scholar] [CrossRef]
- Tian, G.; Conan, B.; Calmet, I. Turbulence-Kinetic-Energy Budget in the Urban-Like Boundary Layer Using Large-Eddy Simulation. Boundary-Layer Meteorol. 2020, 178, 201–223. [Google Scholar] [CrossRef]
- Watanabe, T.; Sakai, Y.; Nagata, K.; Ito, Y. Large eddy simulation study of turbulent kinetic energy and scalar variance budgets and turbulent/non-turbulent interface in planar jets. Fluid Dyn. Res. 2016, 48, 021407. [Google Scholar] [CrossRef]
- Lai, C.C.K.; Socolofsky, S.A. Budgets of turbulent kinetic energy, Reynolds stresses, and dissipation in a turbulent round jet discharged into a stagnant ambient. Environ. Fluid Mech. 2018, 19, 349–377. [Google Scholar] [CrossRef]
- Zhang, J.A.; Drennan, W.; Black, P.G.; French, J.R. Turbulence Structure of the Hurricane Boundary Layer between the Outer Rainbands. J. Atmos. Sci. 2009, 66, 2455–2467. [Google Scholar] [CrossRef]
- Wu, Y.; Porté-Agel, F. Atmospheric turbulence effects on wind-turbine wakes: An LES study. Energies 2012, 5, 5340–5362. [Google Scholar] [CrossRef]
- Zippel, S.F.; Farrar, J.T.; Zappa, C.J.; Plueddemann, A.J. Parsing the Kinetic Energy Budget of the Ocean Surface Mixed Layer. Geophys. Res. Lett. 2022, 49, e2021GL095920. [Google Scholar] [CrossRef] [PubMed]
- Balakumar, P.; Rubinstein, R.; Rumsey, C.L. DNS, Enstrophy Balance, and the Dissipation Rate Equation in a Separated Turbulent Channel Flow. In Proceedings of the 21st AIAA Computational Fluid Dynamics Conference, San Diego, CA, USA, 24–27 June 2013; p. 2723. [Google Scholar]
- Siddappaji, K.; Turner, M. Improved Prediction of Aerodynamic Loss Propagation as Entropy Rise in Wind Turbines Using Multifidelity Analysis. Energies 2022, 15, 3935. [Google Scholar] [CrossRef]
- Siddappaji, K.; Turner, M. Multifidelity Analysis of a Solo Propeller: Entropy Rise Using Vorticity Dynamics and Kinetic Energy Dissipation. Fluids 2022, 7, 177. [Google Scholar] [CrossRef]
- Siddappaji, K. On the Entropy Rise in General Unducted Rotors using Momentum, Vorticity and Energy Transport. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2018. [Google Scholar]
- Siddappaji, K.; Turner, M.G. Versatile Tool for Parametric Smooth Turbomachinery Blades. Aerospace 2022, accepted. [Google Scholar]
- Gao, F. Advanced Numerical Simulation of Corner Separation in a Linear Compressor Cascade. Ph.D. Thesis, Ecole Centrale de Lyon, Lyon, France, 2014. [Google Scholar]
- Monier, J.-F.; Boudet, J.; Caro, J.; Shao, L. Budget Analysis of Turbulent Kinetic Energy in a Tip-Leakage Flow of a Single Blade: RANS Vs Zonal LES. In Proceedings of the 12th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Stockholm, Sweden, 3–7 April 2017. [Google Scholar]
- Chen, H.; Turner, M.G.; Siddappaji, K.; Mahmood, S.M.H. Flow Diagnosis and Optimization Based on Vorticity Dynamics for Transonic Compressor/Fan Rotor. Open J. Fluid Dyn. 2017, 7, 40. [Google Scholar] [CrossRef]
- Bhide, K.; Siddappaji, K.; Abdallah, S.; Roberts, K. Improved Supersonic Turbulent Flow Characteristics Using Non-Linear Eddy Viscosity Relation in RANS and HPC-Enabled LES. Aerospace 2021, 8, 352. [Google Scholar] [CrossRef]
- Bhide, K.R.; Abdallah, S. Turbulence statistics of supersonic rectangular jets using Reynolds Stress Model in RANS and WALE LES. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, Virtual, 27 June–1 July 2022; p. 3344. [Google Scholar]
- Morkovin, M. Effects of compressibility on turbulent flow. In The Mechanics of Turbulence; Favre, A., Ed.; Gordon and Breach: Philadelphia, PA, USA, 1962; pp. 367–380. [Google Scholar]
- Bradshaw, P. Compressible Turbulent Shear Layers. Annu. Rev. Fluid Mech. 1977, 9, 33–52. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Computation of a high Reynolds number jet and its radiated noise using large eddy simulation based on explicit filtering. Comput. Fluids 2005, 35, 1344–1358. [Google Scholar] [CrossRef]
- Brès, G.; Ham, F.E.; Nichols, J.W.; Lele, S.K. Unstructured Large-Eddy Simulations of Supersonic Jets. AIAA J. 2017, 55, 1164–1184. [Google Scholar] [CrossRef]
- Karami, S.; Stegeman, P.; Ooi, A.; Soria, J. High-order accurate large-eddy simulations of compressible viscous flow in cylindrical coordinates. Comput. Fluids 2019, 191, 104241. [Google Scholar]
- Eliasson, P. EDGE: A Navier-Stokes Solver for Unstructured Grids. FOI-Swedish Defence Research Agency, Division of Aeronautics; FOI: Stockholm, Sweden, 2001. [Google Scholar]
- Zhang, H.; Li, Y.; Xiao, J.; Jordan, T. Large eddy simulations of the all-speed turbulent jet flow using 3-D CFD code GASFLOW-MPI. Nucl. Eng. Des. 2018, 328, 134–144. [Google Scholar] [CrossRef]
- López, M.R.; Sheshadri, A.; Bull, J.R.; Economon, T.D.; Romero, J.; Watkins, J.E.; Williams, D.M.; Palacios, F.; Jameson, A.; Manosalvas, D.E. Verification and Validation of HiFiLES: A High-Order LES unstructured solver on multi-GPU platforms. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 3168. [Google Scholar]
- Kailasanath, K.; Corrigan, A.T.; Liu, J.; Ramamurti, R. Efficient supersonic jet noise simulations using JENRE. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014; p. 3740. [Google Scholar]
- Kiris, C.C.; Housman, J.A.; Barad, M.F.; Brehm, C.; Sozer, E.; Moini-Yekta, S. Computational framework for Launch, Ascent, and Vehicle Aerodynamics (LAVA). Aerosp. Sci. Technol. 2016, 55, 189–219. [Google Scholar] [CrossRef]
- Stich, G.D.; Ghate, A.S.; Housman, J.A.; Kiris, C.C. Wall Modeled Large Eddy Simulations for NASA’s jet noise consensus database of single-stream, round, convergent jets. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0684. [Google Scholar]
- Aprovitola, A.; Denaro, F.M. Using symbolic computation software packages in production of multidimensional finite volume-based large eddy simulation codes. Int. J. Numer. Methods Fluids 2012, 71, 562–583. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- DeBonis, J. A high-resolution capability for large-eddy simulation of jet flows. In Proceedings of the 40th Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, 28 June–1 July 2010; p. 5023. [Google Scholar]
- Bhide, K.; Siddappaji, K.; Abdallah, S. Aspect Ratio Driven Relationship between Nozzle Internal Flow and Supersonic Jet Mixing. Aerospace 2021, 8, 78. [Google Scholar]
- Bhide, K.; Siddappaji, K.; Abdallah, S. Influence of fluid–thermal–structural interaction on boundary layer flow in rectangular supersonic nozzles. Aerospace 2018, 5, 33. [Google Scholar] [CrossRef]
- Bhide, K. Supersonic retro propulsion: Aero-thermal-structural analysis. In Proceedings of the 7th International Conference on Jets, Wakes and Separated Flows, Tokyo, Japan, 15–17 March 2022. [Google Scholar]
- Baier, F.; Mora, P.; Gutmark, E.; Kailasanath, K. Flow measurements from a supersonic rectangular nozzle exhausting over a flat surface. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0932. [Google Scholar]
- Star-CCM+ User Guide. Available online: https://support.sw.siemens.com/en-US/ (accessed on 16 July 2022).
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Cuppoletti, D.R. Supersonic Jet Noise Reduction with Novel Fluidic Injection Techniques. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2013. [Google Scholar]
- Heeb, N.S. Azimuthally Varying Noise Reduction Techniques Applied to Supersonic Jets. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2015. [Google Scholar]
- Wilson, B.M.; Smith, B.L. Uncertainty on PIV mean and fluctuating velocity due to bias and random errors. Meas. Sci. Technol. 2013, 24, 035302. [Google Scholar]
- Lazar, E.; DeBlauw, B.; Glumac, N.; Dutton, C.; Elliott, G. A practical approach to PIV uncertainty analysis. In Proceedings of the 27th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Chicago, IL, USA, 28 June–1 July 2010; p. 4355. [Google Scholar]




| Name | Reference | Subgrid Turbulence | Application | Convective Flux Discretization | Filtering |
|---|---|---|---|---|---|
| ALESIA | Bogey et al. [30] | Explicit filtering | External | Thirteen-point stencil FD | Explicit |
| CharLES | Bres et al. [31] | Vreman | External | Second order accurate blend of central and upwind | Spatial |
| ECNSS | Karami et al. [32] | Modified Germano method | External | Sixth-order central FD | Spatial |
| EDGE | Eliasson et al. [33] | Implicit LES | External | Second-order accurate node centered FV | - |
| FLEDS | Bonelli et al. [8] | Smagorinsky, Artificial-Fluid LES model | External | Sixth-order compact scheme, derived from Pade schemes | Spatial |
| GASFLOW-MPI | Zhang et al. [34] | Smagorinsky | External | Second-order accurate van Leer MUSCL | Cube-root of cell volume |
| HiFiLES | Lopez et al. [35] | WSM | Wall-bounded, external | ESFR high-order | Cube-root of cell volume |
| JENRE | Kailasnath et al. [36] | MILES | External | Flux-Corrected Transport | - |
| LAVA | Kiris et al. [37], Stich et al. [38] | Implicit, Vreman | Wall-bounded, external | Mid-point central differencing operator | - |
| Maple | Aprovitola et al. [39] | Smagorinsky | Incompressible | Third-order accurate FV upwind | Cube-root of cell volume |
| OpenFOAM | Weller [40] | Smagorisnky, one equation eddy viscosity | Wall-bounded, external | Second-order semi discrete non-staggered KNP | Cube-root of cell volume |
| WRLES | Debonis [41] | Implicit LES, Smagorinsky | External | Central difference | Solution filtering based on low-pass filter |
| Star-CCM+ | Present work | WALE | Wall-bounded, external | Second-order accurate bounded-central difference | Cube-root of cell volume |
| Case Name | Jet-Exit Condition | NPR | Heated Conditions | Mj | Rej |
|---|---|---|---|---|---|
| LEScold | Ideally expanded | 3.67 | Cold flow | 1.5 | ~850,000 |
| LEShot | Under-expanded | 4 | Hot flow, TR = 2.6 | 1.57 | ~350,000 |
| Number of Cells (Million) | Zone I | Zone II | Zone III |
|---|---|---|---|
| 73 | De/51 | De/82 | De/51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhide, K.; Abdallah, S. Anisotropic Turbulent Kinetic Energy Budgets in Compressible Rectangular Jets. Aerospace 2022, 9, 484. https://doi.org/10.3390/aerospace9090484
Bhide K, Abdallah S. Anisotropic Turbulent Kinetic Energy Budgets in Compressible Rectangular Jets. Aerospace. 2022; 9(9):484. https://doi.org/10.3390/aerospace9090484
Chicago/Turabian StyleBhide, Kalyani, and Shaaban Abdallah. 2022. "Anisotropic Turbulent Kinetic Energy Budgets in Compressible Rectangular Jets" Aerospace 9, no. 9: 484. https://doi.org/10.3390/aerospace9090484
APA StyleBhide, K., & Abdallah, S. (2022). Anisotropic Turbulent Kinetic Energy Budgets in Compressible Rectangular Jets. Aerospace, 9(9), 484. https://doi.org/10.3390/aerospace9090484





