Regional and Seasonal Dependence of the Potential Contrail Cover and the Potential Contrail Cirrus Cover over Europe
Abstract
:1. Introduction
2. Data and Methods
2.1. Schmidt–Appleman Threshold Temperature
2.2. Meteorological Data
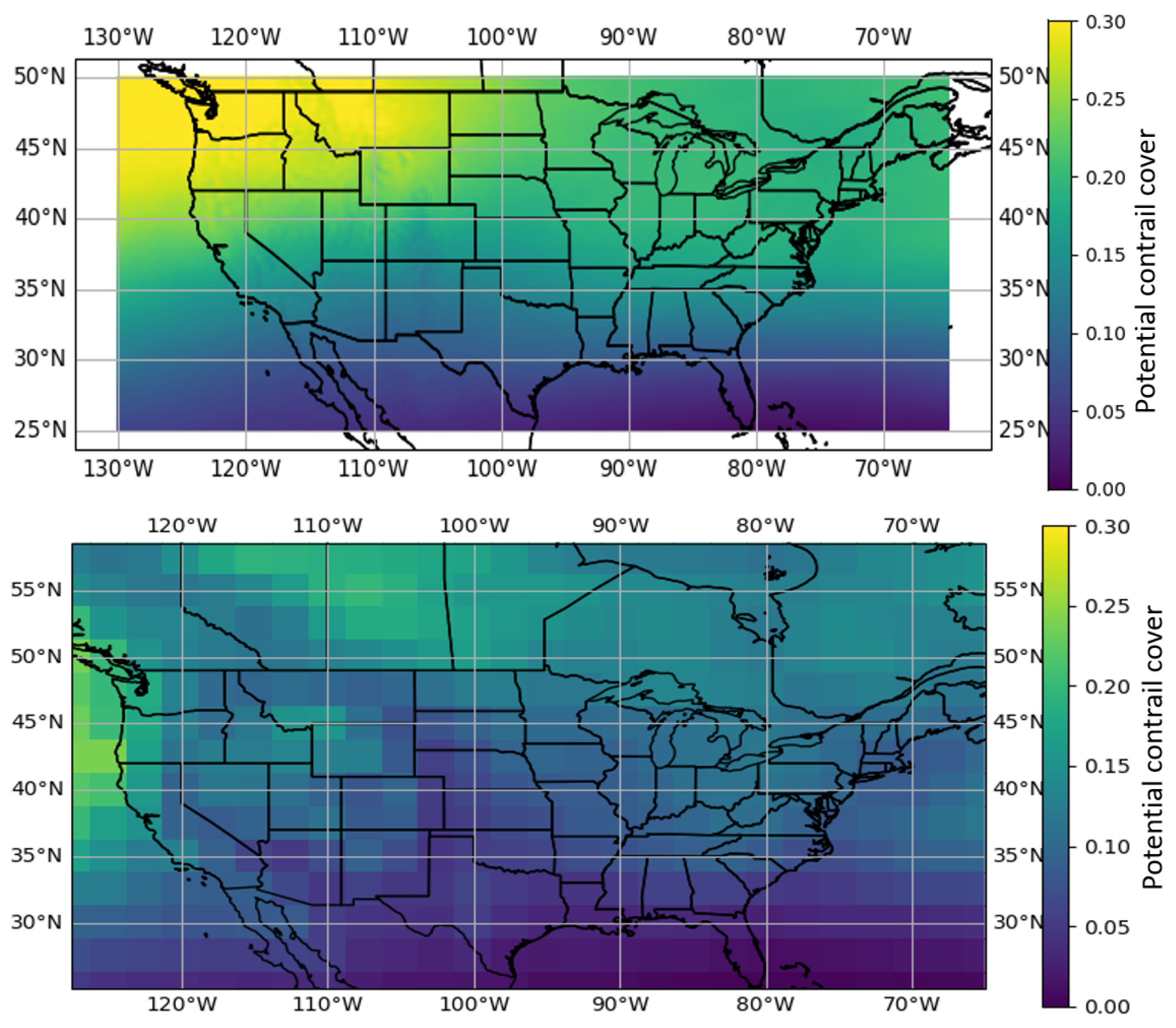
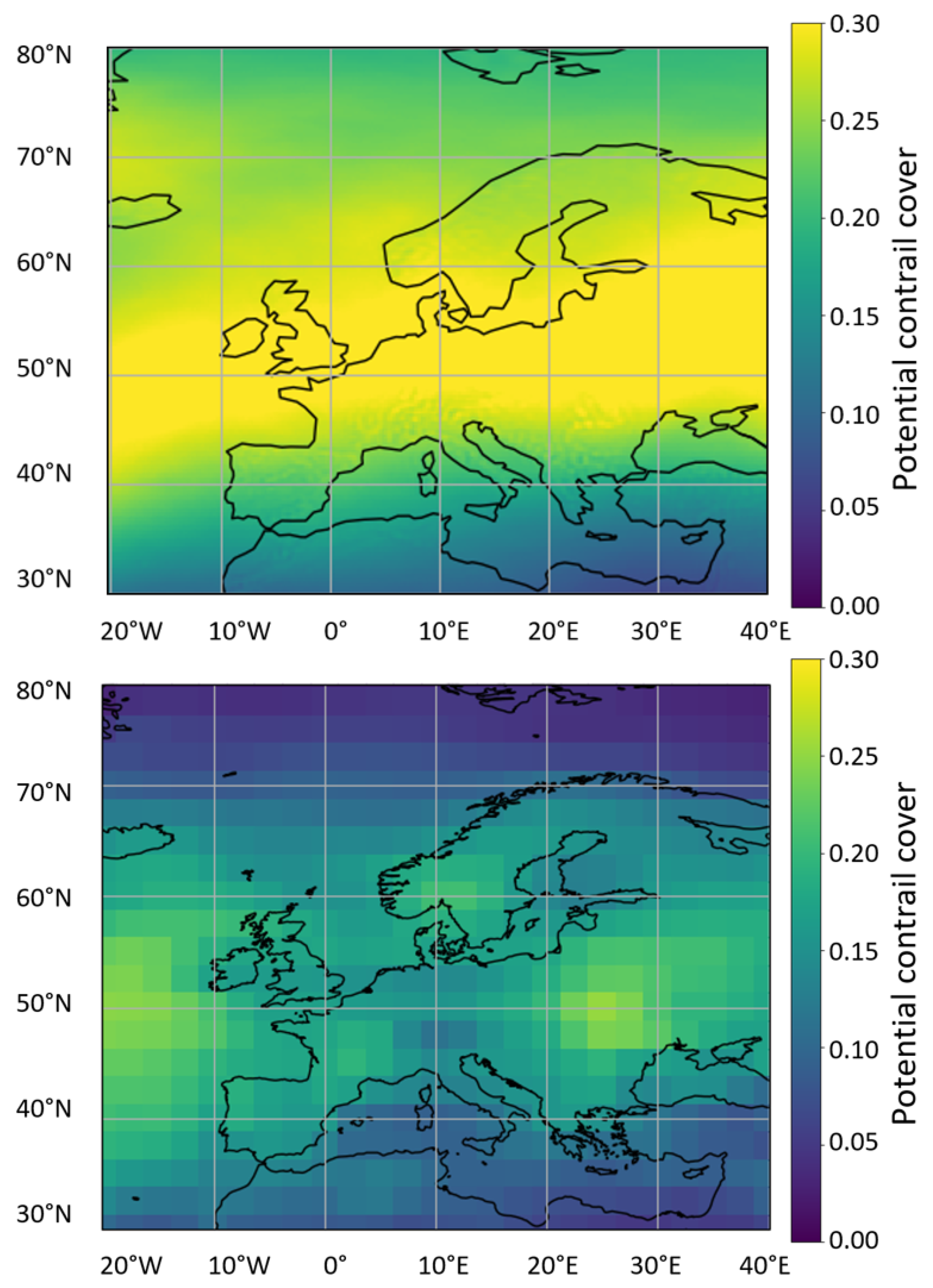
2.3. Comparison of ECMWF and NCEP Data
3. Results
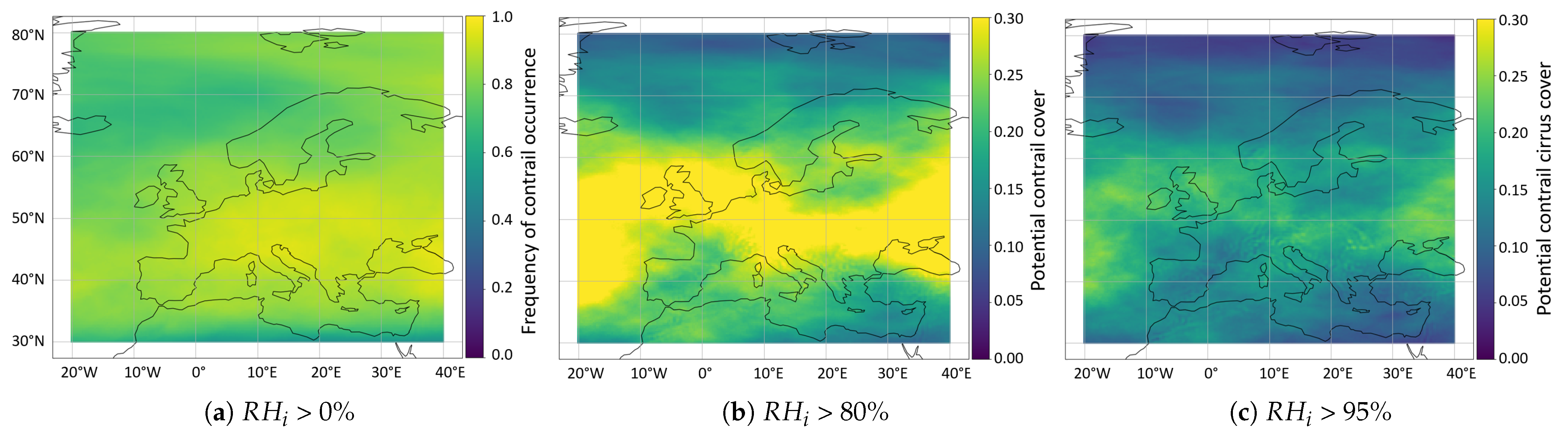
3.1. Influence of the Threshold for Relative Humidity on the Potential Contrail Cover
3.2. Variation in Potential Contrail Cover over Altitude
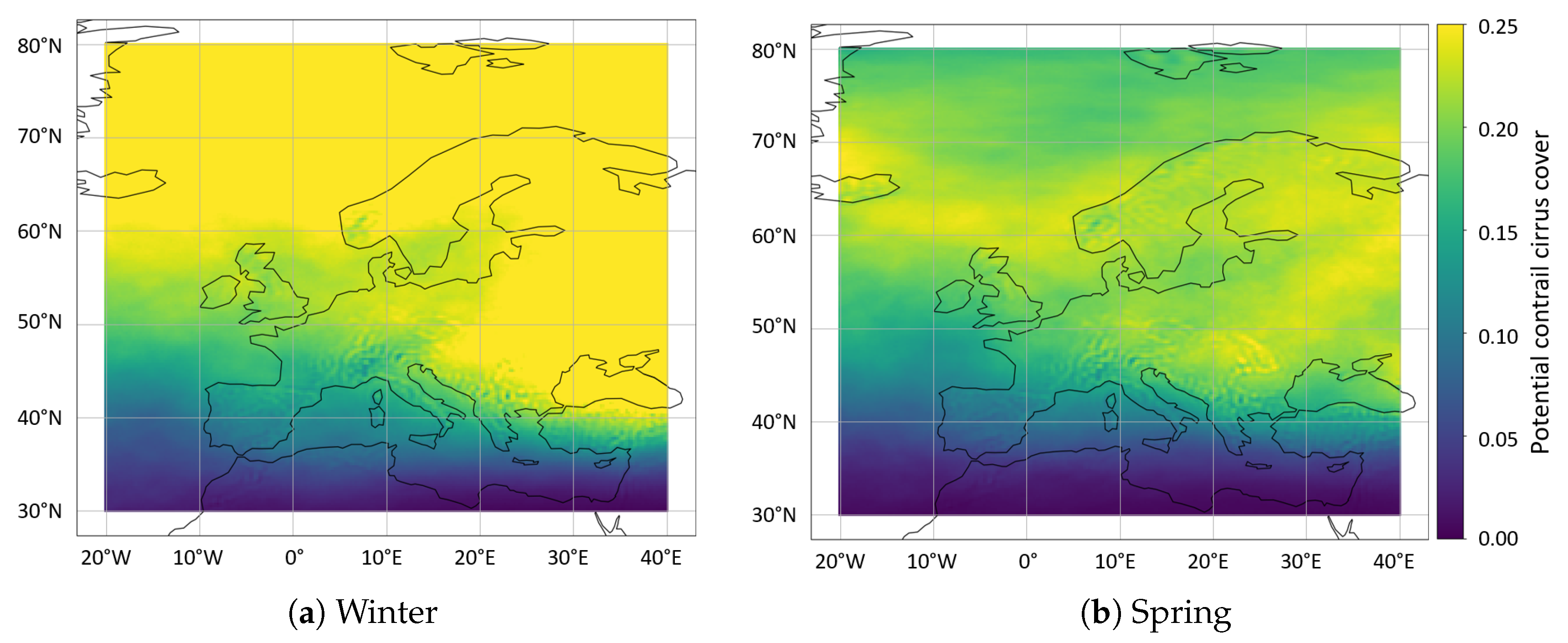
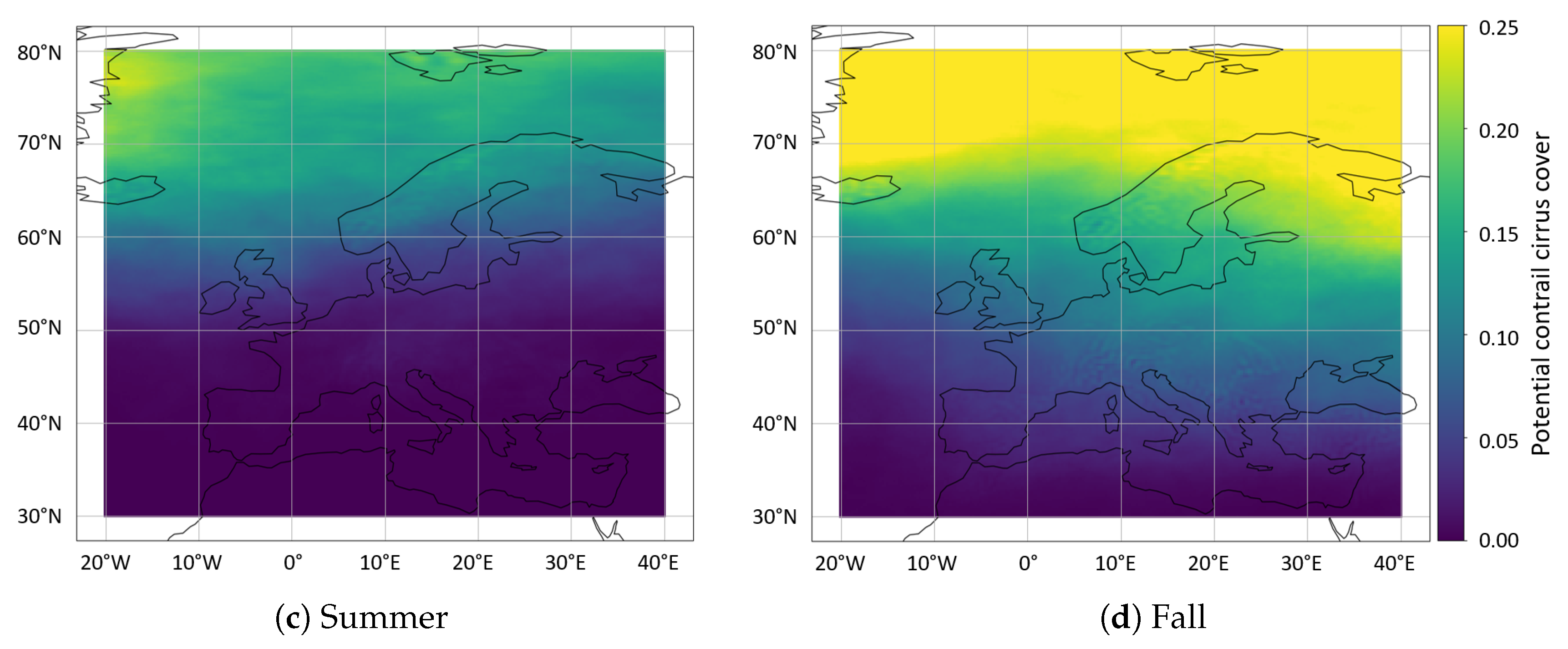
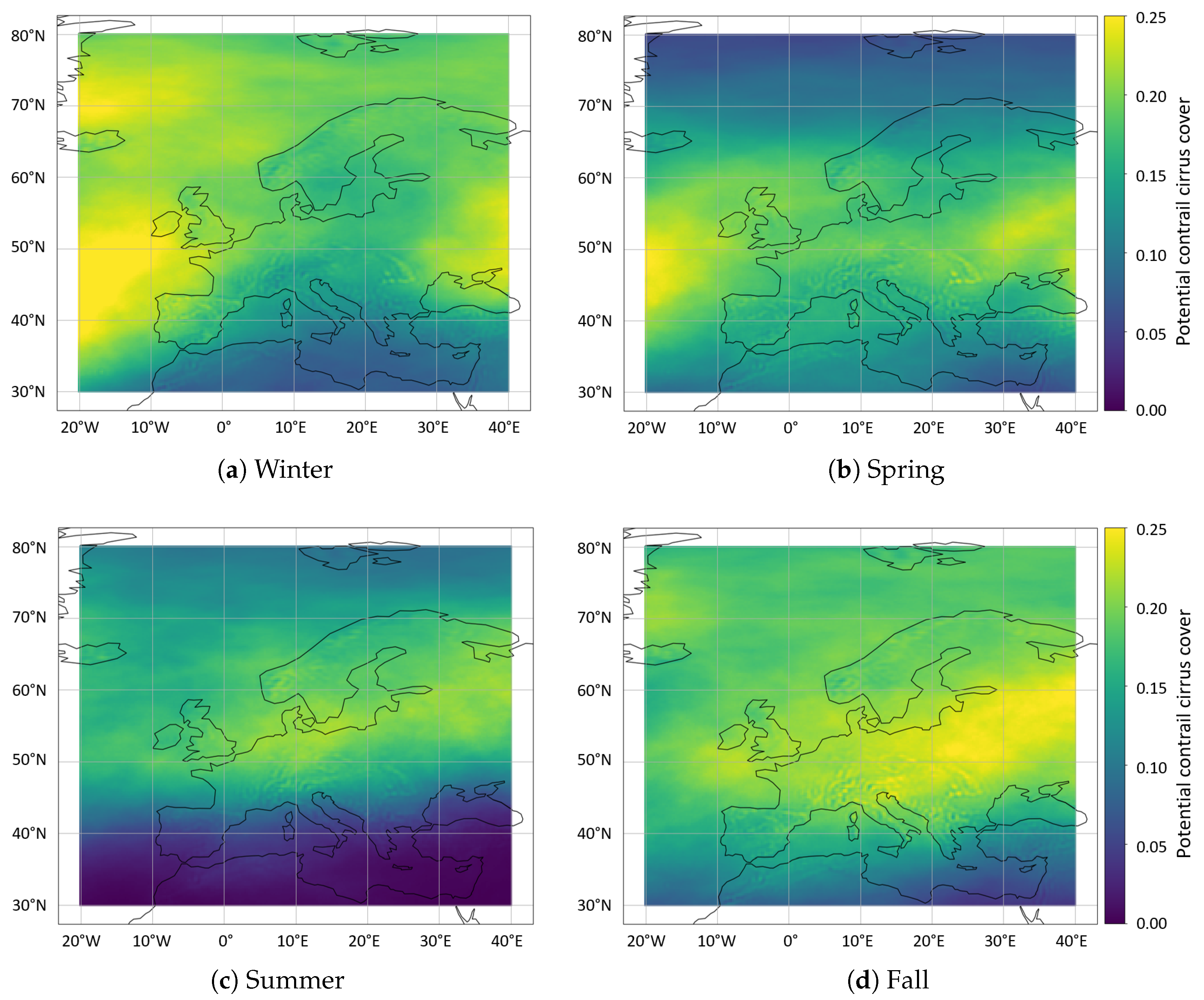
3.3. Seasonal Variation of the Potential Contrail Cirrus Cover
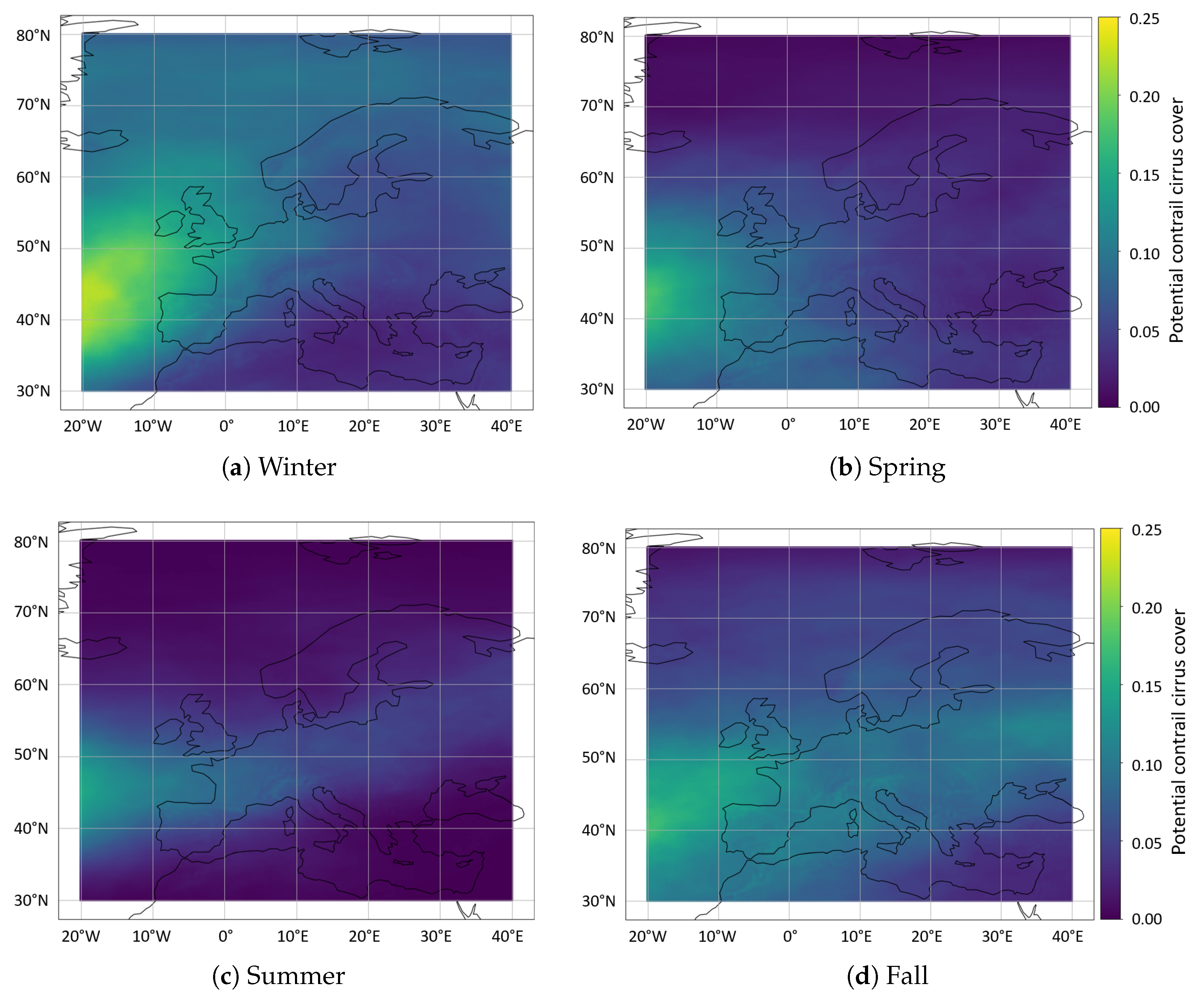
3.4. Temporal and Seasonal Evolution of the Potential Contrail Cirrus Cover
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lee, D.; Fahey, D.; Skowron, A.; Allen, M.; Burkhardt, U.; Chen, Q.; Doherty, S.; Freeman, S.; Forster, P.; Fuglestvedt, J.; et al. The contribution of global aviation to anthropogenic climate forcing for 2000 to 2018. Atmos. Environ. 2021, 244, 117834. [Google Scholar] [CrossRef]
- Schumann, U. Über Bedingungen zur Bildung von Kondensstreifen aus Flugzeugabgasen. Meteorol. Z. 1996, 5, 4–23. [Google Scholar] [CrossRef]
- Appleman, H. The Formation of Exhaust Condensation Trails by Jet Aircraft. Bull. Am. Meteorol. Soc. 1953, 34, 14–20. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on pressure levels from 1979 to present. Copernic. Clim. Chang. Serv. (C3S) Clim. Data Store (CDS) 2018. [Google Scholar] [CrossRef]
- Kleine, J.; Voigt, C.; Sauer, D.; Schlager, H.; Scheibe, M.; Jurkat-Witschas, T.; Kaufmann, S.; Kärcher, B.; Anderson, B.E. In Situ Observations of Ice Particle Losses in a Young Persistent Contrail. Geophys. Res. Lett. 2018, 45, 13553–13561. [Google Scholar] [CrossRef]
- Voigt, C.; Kleine, J.; Sauer, D.; Moore, R.; Bräuer, T.; Le Clercq, P.; Kaufmann, S.; Scheibe, M.; Jurkat-Witschas, T.; Aigner, M.; et al. Cleaner burning aviation fuels can reduce contrail cloudiness. Commun. Earth Environ. 2021, 2, 114. [Google Scholar] [CrossRef]
- Bräuer, T.; Voigt, C.; Sauer, D.; Kaufmann, S.; Hahn, V.; Scheibe, M.; Schlager, H.; Diskin, G.S.; Nowak, J.B.; DiGangi, J.P.; et al. Airborne Measurements of Contrail Ice Properties—Dependence on Temperature and Humidity. Geophys. Res. Lett. 2021, 48, e2020GL092166. [Google Scholar] [CrossRef]
- Vázquez-Navarro, M.; Mannstein, H.; Kox, S. Contrail life cycle and properties from 1 year of MSG/SEVIRI rapid-scan images. Atmos. Chem. Phys. 2015, 15, 8739–8749. [Google Scholar] [CrossRef]
- Schumann, U.; Busen, R.; Plohr, M. Experimental Test of the Influence of Propulsion Efficiency on Contrail Formation. J. Aircr. 2000, 37, 1083–1087. [Google Scholar] [CrossRef]
- Teoh, R.; Schumann, U.; Gryspeerdt, E.; Shapiro, M.; Molloy, J.; Koudis, G.; Voigt, C.; Stettler, M. Aviation contrail climate effects in the North Atlantic from 2016–2021. Atmos. Chem. Phys. Discuss. 2022, 2022, 1–27. [Google Scholar] [CrossRef]
- Murphy, D.M.; Koop, T. Review of the vapour pressures of ice and supercooled water for atmospheric applications. Q. J. R. Meteorol. Soc. 2005, 131, 1539–1565. [Google Scholar] [CrossRef]
- Schumann, U. (Ed.) Atmospheric Physics: Background, Methods, Trends; Research topics in aerospace; Springer: Heidelberg, Germany; New York, NY, USA, 2012; OCLC: Ocn793690099. [Google Scholar]
- Weger, M.; Heinold, B.; Engler, C.; Schumann, U.; Seifert, A.; Fößig, R.; Voigt, C.; Baars, H.; Blahak, U.; Borrmann, S.; et al. The impact of mineral dust on cloud formation during the Saharan dust event in April 2014 over Europe. Atmos. Chem. Phys. 2018, 18, 17545–17572. [Google Scholar] [CrossRef]
- Kunz, A.; Spelten, N.; Konopka, P.; Müller, R.; Forbes, R.M.; Wernli, H. Comparison of Fast In situ Stratospheric Hygrometer (FISH) measurements of water vapor in the upper troposphere and lower stratosphere (UTLS) with ECMWF (re)analysis data. Atmos. Chem. Phys. 2014, 14, 10803–10822. [Google Scholar] [CrossRef]
- Gierens, K.; Matthes, S.; Rohs, S. How Well Can Persistent Contrails Be Predicted? Aerospace 2020, 7, 169. [Google Scholar] [CrossRef]
- Schumann, U.; Baumann, R.; Baumgardner, D.; Bedka, S.T.; Duda, D.P.; Freudenthaler, V.; Gayet, J.F.; Heymsfield, A.J.; Minnis, P.; Quante, M.; et al. Properties of individual contrails: A compilation of observations and some comparisons. Atmos. Chem. Phys. 2017, 17, 403–438. [Google Scholar] [CrossRef]
- Kaufmann, S.; Voigt, C.; Jeßberger, P.; Jurkat, T.; Schlager, H.; Schwarzenboeck, A.; Klingebiel, M.; Thornberry, T. In situ measurements of ice saturation in young contrails. Geophys. Res. Lett. 2014, 41, 702–709. [Google Scholar] [CrossRef]
- Kübbeler, M.; Hildebrandt, M.; Meyer, J.; Schiller, C.; Hamburger, T.; Jurkat, T.; Minikin, A.; Petzold, A.; Rautenhaus, M.; Schlager, H.; et al. Thin and subvisible cirrus and contrails in a subsaturated environment. Atmos. Chem. Phys. 2011, 11, 5853–5865. [Google Scholar] [CrossRef]
- Vay, S.A.; Anderson, B.E.; Sachse, G.W.; Collins, J.E.; Podolske, J.R.; Twohy, C.H.; Gandrud, B.; Chan, K.R.; Baughcum, S.L.; Wallio, H.A. DC-8-based observations of aircraft CO, CH4, N2O, and H2O emission indices during SUCCESS. Geophys. Res. Lett. 1998, 25, 1717–1720. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Amer. Meteor. Soc. 1996, 77, 437–470. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts. ERA-Interim. Available online: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim (accessed on 24 August 2021).
- Paltridge, G.; Arking, A.; Pook, M. Trends in middle- and upper-level tropospheric humidity from NCEP reanalysis data. Theor. Appl. Climatol. 2009, 98, 351–359. [Google Scholar] [CrossRef]
- Kaufmann, S.; Voigt, C.; Heller, R.; Brown, T.R.; Krämer, M.; Rolf, C.; Zöger, M.; Giez, A.; Buchholz, B.; Ebert, V.; et al. Intercomparison of midlatitude tropospheric and lower-stratospheric water vapor measurements and comparison to ECMWF humidity data. Atmos. Chem. Phys. 2018, 18, 16729–16745. [Google Scholar] [CrossRef]
- Lührs, B.; Linke, F.; Matthes, S.; Grewe, V.; Yin, F. Climate Impact Mitigation Potential of European Air Traffic in a Weather Situation with Strong Contrail Formation. Aerospace 2021, 8, 50. [Google Scholar] [CrossRef]
- Matthes, S.; Lührs, B.; Dahlmann, K.; Grewe, V.; Linke, F.; Yin, F.; Klingaman, E.; Shine, K.P. Climate-Optimized Trajectories and Robust Mitigation Potential: Flying ATM4E. Aerospace 2020, 7, 156. [Google Scholar] [CrossRef]
- Bräuer, T.; Voigt, C.; Sauer, D.; Kaufmann, S.; Hahn, V.; Scheibe, M.; Schlager, H.; Huber, F.; Le Clercq, P.; Moore, R.H.; et al. Reduced ice number concentrations in contrails from low-aromatic biofuel blends. Atmos. Chem. Phys. 2021, 21, 16817–16826. [Google Scholar] [CrossRef]
- Schripp, T.; Anderson, B.E.; Bauder, U.; Rauch, B.; Corbin, J.; Smallwood, G.; Lobo, P.; Crosbie, E.; Shook, M.A.; Miake-Lye, R.C.; et al. Aircraft Engine Particulate Matter and Gaseous Emissions from Sustainable Aviation Fuels: Results from Ground-Based Measurements During the Nasa/Dlr Campaign Eclif2/Nd-Max. Preprint. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Vazquez-Navarro, M.; Mannstein, H.; Mayer, B. An automatic contrail tracking algorithm. Atmos. Meas. Tech. 2010, 3, 1089–1101. [Google Scholar] [CrossRef]
- Duda, D.P.; Bedka, S.T.; Minnis, P.; Spangenberg, D.; Khlopenkov, K.; Chee, T.; Smith Jr., W.L. Northern Hemisphere contrail properties derived from Terra and Aqua MODIS data for 2006 and 2012. Atmos. Chem. Phys. 2019, 19, 5313–5330. [Google Scholar] [CrossRef]
- Tan, Z.; Ma, S.; Zhao, X.; Yan, W.; Lu, E. Evaluation of Cloud Top Height Retrievals from China’s Next-Generation Geostationary Meteorological Satellite FY-4A. J. Meteorol. Res. 2019, 33, 553–562. [Google Scholar] [CrossRef]
- Agarwal, A.; Meijer, V.R.; Eastham, S.D.; Speth, R.L.; Barrett, S.R.H. Reanalysis-driven simulations may overestimate persistent contrail formation by 100%–250%. Environ. Res. Lett. 2022, 17, 014045. [Google Scholar] [CrossRef]
- Wilhelm, L.; Gierens, K.; Rohs, S. Meteorological Conditions That Promote Persistent Contrails. Appl. Sci. 2022, 12, 4450. [Google Scholar] [CrossRef]
- Edwards, J.T. Reference Jet Fuels for Combustion Testing. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; American Institute of Aeronautics and Astronautics: Grapevine, TX, USA, 2017. [Google Scholar] [CrossRef]
- Gierens, K. Theory of Contrail Formation for Fuel Cells. Aerospace 2021, 8, 164. [Google Scholar] [CrossRef]
- Schumann, U. A contrail cirrus prediction model. Geosci. Model Dev. 2012, 5, 543–580. [Google Scholar] [CrossRef]
- Teoh, R.; Schumann, U.; Stettler, M.E.J. Beyond Contrail Avoidance: Efficacy of Flight Altitude Changes to Minimise Contrail Climate Forcing. Aerospace 2020, 7, 121. [Google Scholar] [CrossRef]



| Parameter | Value | Source |
|---|---|---|
| Air temperature, T | variable | ECMWF ERA-5 |
| Rel. humidity (ice), | variable | ECMWF ERA-5 |
| Air pressure, p | variable | ECMWF ERA-5 |
| Specific heat capacity (air), | 1004 J kg K | [2] |
| Molar mass ratio HO/air, | 0.622 | [2] |
| Emission index of water vapor, | 1.23 kg kg | [19] |
| Combustion heat, Q | 43.2 MJ kg | [9] |
| Propulsion efficiency, | 0.33 | [9,10] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dischl, R.; Kaufmann, S.; Voigt, C. Regional and Seasonal Dependence of the Potential Contrail Cover and the Potential Contrail Cirrus Cover over Europe. Aerospace 2022, 9, 485. https://doi.org/10.3390/aerospace9090485
Dischl R, Kaufmann S, Voigt C. Regional and Seasonal Dependence of the Potential Contrail Cover and the Potential Contrail Cirrus Cover over Europe. Aerospace. 2022; 9(9):485. https://doi.org/10.3390/aerospace9090485
Chicago/Turabian StyleDischl, Rebecca, Stefan Kaufmann, and Christiane Voigt. 2022. "Regional and Seasonal Dependence of the Potential Contrail Cover and the Potential Contrail Cirrus Cover over Europe" Aerospace 9, no. 9: 485. https://doi.org/10.3390/aerospace9090485





