Abstract
We propose and justify a numerical method for computing the double integral with variable upper limits that leads to the variableness of the region of integration. Imposition of simple variables as functions for upper limits provides the form of triangles of integration region and variable in the external limit of integral leads to a continuous set of similar triangles. A variable grid is overlaid on the integration region. We consider three cases of changes of the grid for the division of the integration region into elementary volumes. The first is only the size of the imposed grid changes with the change of variable of the external upper limit. The second case is the number of division elements changes with the change of the external upper limit variable. In the third case, the grid size and the number of division elements change after fixing their multiplication. In these cases, the formulas for computing double integrals are obtained based on the application of cubatures in the internal region of integration and performing triangulation division along the variable boundary. The error of the method is determined by expanding the double integral into the Taylor series using Barrow’s theorem. Test of efficiency and reliability of the obtained formulas of the numerical method for three cases of ways of the division of integration region is carried out on examples of the double integration of sufficiently simple functions. Analysis of the obtained results shows that the smallest absolute and relative errors are obtained in the case of an increase of the number of division elements changes when the increase of variable of the external upper limit and the grid size is fixed.
1. Introduction
When solving various engineering and scientific problems, we fail to deal with the necessity to calculate double integrals with variable integration limits. Thus, the analytical solution for the problem of migration of contaminants with a solving in multilayered water filters can be obtained only in integral form. Then, the resulting solution must be integrated once again to determine the concentration of particles absorbed on the filter skeleton over a certain time interval. In this case, the time variable which is in the upper limit of the external integral should not be considered as a parameter, because to establish the optimal regimes of operation of industrial filters still need to solve numerically the functional equation containing this double integral over a time interval of unknown length [,,,].
Similar problems arise for
- determining the amount of radioactive contamination that gets groundwater during radiation pollution of the soil,
- the quantity of heat that a multiphase porous body can lose or get,
- determining the loss of alloying doping impurities of reinforced material during intensive exploitation of the object in conditions of the aggressive external environment, etc. [,,].
Therefore, it is necessary to develop numerical methods for integrating double integrals with variable limits and an intricate integrand.
In the literature (for example, [,,]) methods of double integration have been developed, but within definite limits.
The first method explicitly devised for multiple integrals was published in 1877 in a paper by James Clerk Maxwell [] proposed the formulas for the rectangle and the rectangular parallelopipedon []. After the 1950s, several new methods were devised, which have begun to make the numerical evaluation of multiple integrals available as a working tool for scientists and engineers []. Krylov, V. I. and I. P. Mysovskikh made a significant contribution to the theory of approximate calculation of integrals [,]. General overviews to the problems of numerical approximation of multiple integrals are contained in [,]. Encyclopedic work on multiple numerical integrations was published by Arthur H. Stroud []. Cubature formulas have been developed for different regions of integration, namely cubature formulas for the cube [,], for triangle [,], for the sphere [], for the space with weight function [,], for the space with weight function [,] and for the simplex [,]. In addition, we can mention the class of Monte Carlo methods, which has been extended by S. M. Ulam and John von Neumann [,]. Monte Carlo methods are constructed on a fundamentally different basis. They use random sampling to obtain numerical results, but an aleatory generation of points makes the problem more dependent on luck, increasing the chance of obtaining uncertainties in the results [,,].
As concerns double and multiple integrals, numerical integration methods are developed to calculate the definite integrals and the integrals with definite limits in the external integration [] and solve Volterra’s integral equations [], i.e., the regions of integration are constant or fixed. In the work [], it collects together theoretical results in the area of numerical cubature over triangles. The theory relating to regular integrands and the corresponding theory of singular integrands are considered here. The existence of cubature formulas for planar regions was shown by A. H. Stroud, which used m2 points with polynomial precision 2 m−1 [,]. Thus, in [], sufficient conditions are formulated for the existence of cubature formulas using fewer than m2 of points with the same polynomial accuracy.
As a rule, only elements that are fully within the scope of the integration region are taken into account, while others are rejected. As a result, the problem of assurance of the accuracy of the calculations, because to increase the accuracy it is proposed increasing the number of elements of the division, i.e., compressing the grid, and in turn for complex and intricate integrands, this leads to a significant accumulation of computational error.
Approximations of the double integral are obtained under the assumption that the partial derivatives of the integrand belong to the Lebesgue space for certain []. In this case, it is not enough to satisfy the condition that integrand is a simple integrated function. So it is necessary to impose additional restrictions: if the integrand is real in the domain then the formulas for numerical integration of the double integral exist under the assumption that the mixed partial derivative belongs to one of the Lebesgue spaces for some (if , then is a continuously differentiable function of both variables). Thus, it is assumed that the norm is limited. Moreover, the integration error can be estimated in the terms of the norm [].
In the case of double integral with variable limits, it is not possible to estimate the calculation error by classical methods. Moreover, the variable limits of the integral
are functions of independent variables τ, that leads to variableness of the integration region.
We suppose that integral (1), functions f(τ′, τ″, τ), and satisfy necessary restrictions (in particular, functions , are continuous functions of their arguments). Without loss of generality, we can accept that and , because, if the inverse functions and exist, then using change of variables and the integral (1) can be reduced to the form
Note that zero values of the lower limits of integration can be obtained using the additive property of an integral.
2. Construction of Formula for Computing Double Integrals with Variable Upper Limits
A method of numerical integration of double integrals with variable upper limits, which we propose, may be divided into such steps:
- determination of integration region;
- overlaying square or rectangular grid on the integration region;
- decomposing of integration region into subregions, which consist of square (rectangular) and triangular elements;
- application of cubatures in the subdomain consisting of square elements;
- realization of triangulation division along the variable boundary τ″ = τ′;
- calculating the volumes of elementary elements based on triangles;
- calculation of the original integral;
- determination of calculation error.
2.1. Determination of Integration Region
The region of integration of the integrand (1) in the space has the form of an inclined triangle (Figure 1). Taking into account that τ is a variable, i.e., it changes continuously in or in the interval (for example, if τ is time) or in any closed interval, then with the change of τ the region of integration in space remains a triangle. The change of variable τ leads to a change in the maximum values of τ′ and τ″.
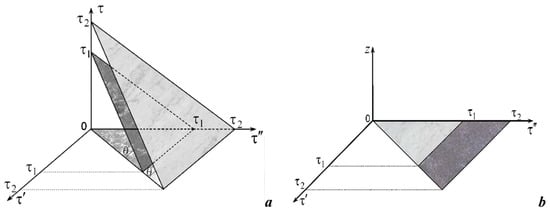
Figure 1.
Region of integration in the space Oττ′τ″ (a) and schematic representation of the set of integration regions in the space Oτ′τ″z (b).
For τ = τ1 we have max τ′ = max τ″= τ1, and for τ = τ2 we have max τ′ = max τ″ = τ2 (Figure 1a). These regions are similar triangles that are in parallel planes, i.e., they are at the same angle θ to the plane Oτ′τ″ (Figure 1a). However, an area of the surface of integration changes. For τ = 0 the integration, the region is the point (0, 0, 0).
Let us make a projection of the surface of integration on the plane Oτ′τ″ (Figure 1b). Then we obtain the set of regions of integration in the space Oτ′τ″z.
As a result, we obtain a family of integrands parameterized by the variable τ (Figure 2).
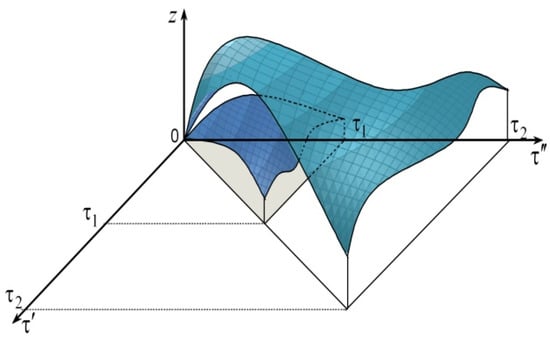
Figure 2.
Schematic representation of the set of integrands in the space Oτ′τ″z.
2.2. Overlaying a Grid for the Variable Region of Integration
Let us overlay a square grid on the projection of the integration region (Figure 3a). Then we take into account the variableness of the integration region. Note, that with changes of value of τ either the number of division elements or the width of the grid (step) h can change, i.e., , and .
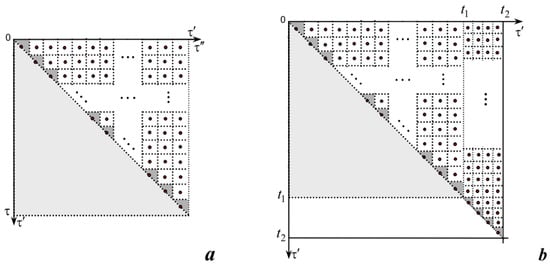
Figure 3.
Decomposition of the integration region for fixed τ (a) and of the integration region for increasing τ from t1 to t2 (b).
If we consider that the integration region S is a triangle, then with increasing τ from t1 to t2 the integration region remains a triangle, increases, and the area of the additional region increases by (Figure 3b). Then, if the grid for (, ) is fixed, then at the same step h the number of division elements increases by elements. If we fix the number of division elements , then with the changing τ from t1 to t2 there is a change in the width of the grid . Note that the number of elements and the width of the grid can change together, and the relation is always fulfilled.
At the same time, if necessary, the additional region can be divided with a different grid from the grid of the region S with the width .
Analogous reasoning can be made for the rectangular grid, but we restrict ourselves to the case of the square grid.
2.3. Formula for Finding a Double Integral with Variable Upper Limits
We break up the integration region into small subregions. Then we apply the cubature formula with the weight function . Depending on the number of division elements changes or the grid width changes when changing the variable τ we get the following cases.
- (A)
- With the change of τ, only the size of the imposed grid h(τ) changes
- (B)
- With the change of τ, only the number of division elements Nel(τ) changes
- (C)
- With the change of τ, both the size of the grid and the number of division elements changewhere Vel is the volume of the individual element of division of the integration region.
As a result of the division of the integration region, we obtained square (Figure 4a) and triangular (Figure 4b) elements. Here the summation is carried out over all elements .
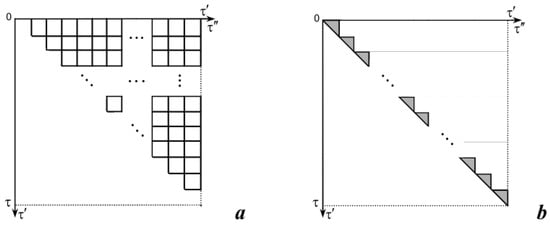
Figure 4.
Subregions consisting of square (a) and triangular (b) elements at the fixed τ.
We separate square and triangular elements:
Let us select the elements Vel, which are squares (Figure 4a). Here we apply numerical integration in cubatures. So, we have
, , is the number of square elements in the longest line, h(τ) is the grid width depending on τ.
, n(τ) changes with changing τ.
n(τ) and h(τ) change with changing τ.
Note that h(τ) = τ/n(τ).
Consider the subregion consisting of triangles only (Figure 4b). The sum of the volumes of the elements with a triangular base takes the form
where n is the number of triangular elements; ; and are the values of τ′ and τ″ in the ith node (the i-th triangular elements).
Note that the number of triangular elements is 1 more than the square elements in the longest line.
By Formulas (6)–(8), we sum the relations (9)–(11) and (12)–(14) respectively. Then we obtain the formulas of numerical integration for a double integral with variable upper limits:
where ; .
Schematically, such a method of numerical integration for a double integral with variable upper limits at a fixed value of τ is presented in Figure 5.
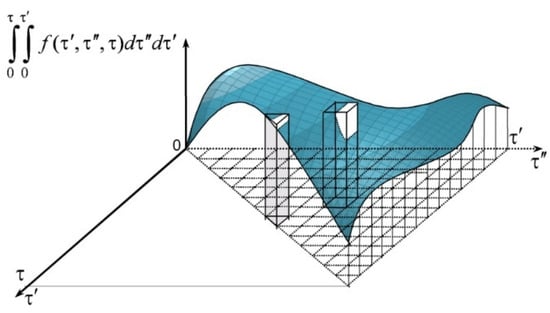
Figure 5.
Scheme of numerical double integration with variable upper limits for the fixed τ.
3. Error of Numerical Integration
We find the error of numerical integration by the Taylor formula [,].
The main term of the error is [,].
where is the area of the region of integration, is the central point of the region of integration.
We choose the central point of the integration region in the vicinity of which we expand the function
into the Taylor series
Note that the function F(τ, τ′, τ″) can be expanded into a Taylor series if in some vicinity of the point its continuous partial derivatives exist up to order [].
Let f(τ, τ′, τ″) be continuous in the domain . Then it is integrated into this domain, as well as integrated into any subdomain of []. Then F(τ, τ′, τ″) is continuous in the domain . If f(τ, τ′, τ″) is continuous in the domain then F(τ, τ′, τ″) is differentiable in the domain [].
Taking into consideration that F(τ, τ′, τ″) is the double integral with variable upper limits, we obtain (by the analogy of double integration in cubatures)
Here we have used Barrow’s theorem []
Note that as distinct from double integrating within the definite limits, the first derivatives do not disappear and must be taken into account. We include them in error.
We will write down separately the errors for triangular and square elements. The integration error (18) for each triangular element takes the form
The error of integration (18) for each square element is
Here and are areas of the ith triangular element and the ijth square element accordingly.
Summing the expressions (19) and (20) for the region in which the integral is defined, we obtain the error of our method
or
Since higher degrees of h(τ) are rejected in the estimates (19) and (20), the relation for the error (21) is asymptotic, and it is satisfied at h(τ)→0 with an accuracy to the terms of a higher order of smallness than h(τ).
If we impose the definite limits of integration, the obtained Formula (21) is reduced to the classical formula for the error by the expansion of an integrand into the Taylor series and estimation of the error of the method takes the form .
4. Examples of Numerical Integration for the Double Integral with Variable Upper Limits
To test the efficiency and reliability of the obtained formulas of the numerical method, we apply it to the integration of sufficiently simple functions for which the integration expression can be found analytically.
I. Let such an integrand be given f(τ′, τ″) = τ′τ″. The surface formed by the function f(τ′, τ″) over the integration region is shown in Figure 6.
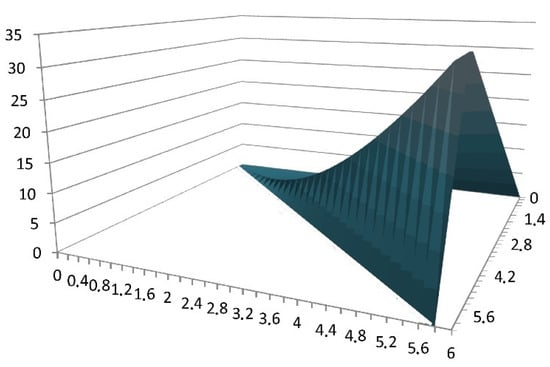
Figure 6.
The surface generated by the function f(τ′, τ″) = τ′τ″.
Then we calculate the integral by Formulas (15)–(17) depending on the number of division elements changes and the grid width and analytically, namely .
The results of calculations are shown in Table 1, Table 2, Table 3 and Table 4 for different numbers of triangular elements n(τ) and grid width h(τ). It is given the values of the total volumes of square and triangular elements, the difference between the analytical and numerical calculation |Ianalyt − Inum|, as well as the relative error E(τ)= |Ianalyt − Inum/Ianalyt| [,]. We choose such basic values of parameters n(1) = 104, h(1) = 10−4.

Table 1.
Calculation of integral for the case of A.

Table 2.
Calculation of integral for the case B.

Table 3.
Calculation of integral for the case C for increasing function .

Table 4.
Calculation of integral for the case C for decreasing function .
Table 1 shows the corresponding values for the case when only the size of the imposed grid h(τ) changes with the change of τ, (A). The calculated values for the case when only the number of division elements changes. With the change of τ, (B) are presented in Table 2. In Table 3 and Table 4 it is shown the corresponding values of integration parameters for the case when with the change of τ, both the size of the grid and the number of division elements change (C). The change in the number of nodes in Table 3 is described by the increasing function , then . The change in the number of nodes in Table 4 is described by the decreasing function , and then .
Figure 7 demonstrates comparative graphs of absolute and relative errors in numerical integration by Formula (15) of the case of A, (16) of the case of B, (17) of the cases of C1 for increasing function n(τ) and C2 for decreasing n(τ).
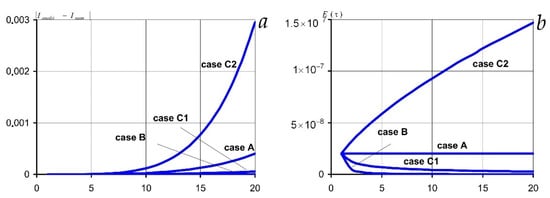
Figure 7.
Graphs of absolute (a) and relative (b) errors for four considered cases, A, B, C1, and C2, of the relation between the number of nodes and grid width for the integrand f(τ′, τ″) = τ′τ″.
Note that the values closest to the analytical values of the integral are obtained in the case of the constant width of the grid and of increase in the number of partition elements together with an increase in the integration (Figure 7a,b). The results calculated by the Formula (17) at the imposition of the increasing function of nodes quantity n(τ) (case C1, Figure 7) show that the values of absolute and relative errors are quite acceptable. However, in this case, the number of operations is smaller than in the case of B. Note that only one case C2, i.e., imposition of the decreasing function of the number of nodes n(τ), leads to a sharp increase in absolute and relative errors with increasing τ and can go beyond a given accuracy of calculations (Figure 7, Table 4). In the cases of A, B, and C1 the difference between the analytical and numerical calculations of |Ianalyt − Inum| is within the acceptable deviation.
In this case, at a denser grid overlaid on the variable region of integration both absolute and relative errors decrease. In particular, the difference |Ianalyt − Inum| decreases by two orders of magnitude when n increases by an order (Table 1, Table 2, Table 3 and Table 4).
II. Consider next integrand f(τ′, τ″) = eτ′τ″ for the same values of τ. The surface formed by the function f(τ′, τ″) over the integration region is shown in Figure 8.
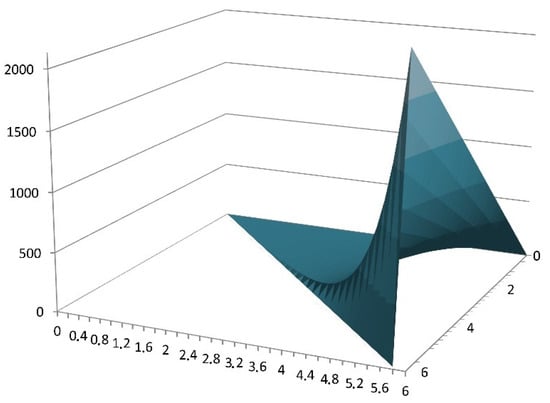
Figure 8.
The surface generated by the function f(τ′, τ″) = eτ′τ″.
We also calculate the integral by Formulas (15)–(17). The analytical expression has been found in the form .
The results of calculations are presented in Table 5, Table 6, Table 7 and Table 8 for different numbers of triangular elements n(τ) and grid width h(τ).

Table 5.
Calculation of integral for the case of A.

Table 6.
Calculation of integral for the case of B.

Table 7.
Calculation of integral for the case of C for increasing function .

Table 8.
Calculation of integral for the case of C for decreasing function .
Table 5 shows the corresponding values for the case when only the size of the imposed grid h(τ) changes with the change of τ, (A). The calculated values for the case when only the number of division elements changes with the change of τ, (B) are presented in Table 6. In Table 7 and Table 8 it is shown the values of integration parameters for the case when with the change of τ, both the size of the grid and the number of division elements change (C), namely for , and , correspondingly.
Figure 9 demonstrates comparative graphs of absolute (Figure 9a) and relative (Figure 9b) errors in numerical integration by Formula (15) of the case of A, (16) of the case of B, (17) of the cases of C1 for increasing function n(τ) and C2 for decreasing n(τ).
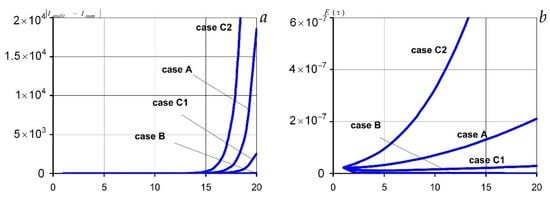
Figure 9.
Graphs of absolute (a) and relative (b) errors for four considered cases of A, B, C1, and C2 of the relation between the number of nodes and grid width for the integrand f(τ′, τ″) = exp(τ′)τ″.
When the integrand contains an exponential function, the sharp increase in the integrand has almost no effect on the value of both absolute and relative errors for numerical calculation of the integral by Formulas (16) and (17) under the increasing function of the number of nodes, i.e., case C1 (Figure 9, Table 6 and Table 7).
For this integral, the difference between the analytical and numerical calculation |Ianalyt − Inum| is also within the acceptable deviation for the cases of A, B, and C1. However, as distinct from the previous case I, the magnitude of this difference is an order larger. So, for the case of B and , , but (Table 2 and Table 6). Herewith, when increasing n by an order of magnitude, the relative error decreases by two orders.
III. Now we consider the integrand f(τ′, τ″) = sin(τ′)sin(τ″) for the same values of τ. The surface formed by the function f(τ′, τ″) over the integration region is shown in Figure 10.
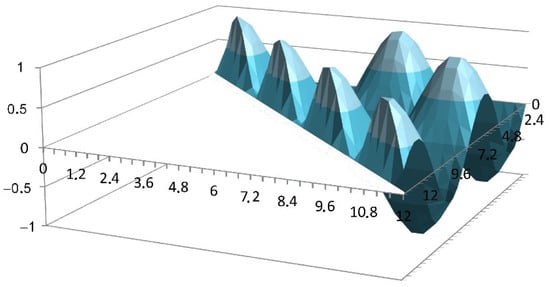
Figure 10.
The surface generated by the function f(τ′, τ″) = sin(τ′)sin(τ″).
The integral is also calculated by Formulas (15)–(17). The analytical expression has been found in the form .
The results of calculations are presented in Table 9, Table 10, Table 11 and Table 12 for different numbers of triangular elements n(τ) and grid width h(τ).

Table 9.
Calculation of integral for the case of A.

Table 10.
Calculation of integral for the case B.

Table 11.
Calculation of integral for the case of C for increasing function .

Table 12.
Calculation of integral for the case of C for decreasing function .
Table 9 shows the corresponding values for the case when only the size of the imposed grid h(τ) changes with the change of τ, (A). The calculated values for the case when only the number of division elements changes with the change of τ, (B) are presented in Table 10. In Table 11 and Table 12 it is shown the values of integration parameters for the case when with the change of τ, both the size of the grid and the number of division elements change (C), namely for , and , correspondingly.
Figure 11 demonstrates comparative graphs of absolute (Figure 11a) and relative (Figure 11b) errors in numerical integration by Formula (15) of the case of A, (16) of the case of B, (17) of the cases of C1 for increasing function n(τ) and C2 for decreasing n(τ).
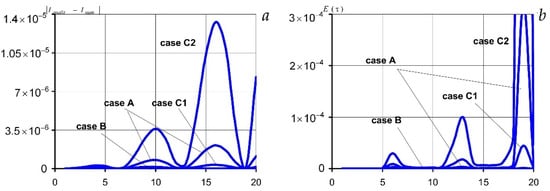
Figure 11.
Graphs of absolute (a) and relative (b) errors for four considered cases of A, B, C1, and C2 of the relation between the number of nodes and grid width for the integrand f(τ′, τ″) = sin(τ′)sin(τ″).
Note that for the periodic integrand, the closest to the analytical value of the integral is obtained in the case of the constant width of the grid and in the case of an increase in the number of partition elements together with an increase in the integration region (Figure 11a,b). Here the results for the absolute and relative error calculated by the Formula (17) for the imposition of the increasing function of the number of nodes n(τ), case C1 (Figure 11) are quite acceptable. For this integrand, the integration results obtained by Formulas (15)–(17) with increasing τ remain within the given accuracy of calculations (Figure 11, Table 9, Table 10, Table 11 and Table 12).
In this case, the difference between the analytical and numerical calculation |Ianalit − Inum| is of the same order as for the integrand . When increasing n by an order of magnitude, the value of E(τ) also decreases by two orders of magnitude.
Note that for all three considered integrands, no significant accumulation of machine error was observed.
If we apply the proposed method to calculate the double integral with a given external limit of integration, the result is the same (within accuracy) as the value of the same integral, calculated by Maple. For example, according to the calculations in the Maple integral , in our case (the fifth line from the top in Table 1); integral , in our case (the fifth line from the top in Table 5); integral , in our case (the fifth line from the top in Table 9) under .
The CPU time of the program module was calculated by the algorithm in []. It was determined that the times of program execution for calculation of integral were from 2.2189994808 s at and to 215.3279999737 s at ; of integral were from 4.7030001646 s at and to 463.6879999191 s at ; of integral were from 6.4680001466 s at and to 635.4220004054 s at .
5. Application of the Method to Calculating the Double Integral with Variable Upper Limits Depending on One External Variable
We use the proposed method to calculate double integrals with variable upper limits, which are functions of the external variable τ but do not depend on the integration variables. This kind of integrals is in some sense a partial case of the above integrals with due regard that there is no variable limit in the region of integration (Figure 3). At the same time, the integration region in is variable.
Taking into account that in all considered examples of the application of the method in chapter 4, the lowest values of absolute and relative errors are achieved in the case of increasing the number of variable elements of division and fixing the grid cell size, i.e., Case B, here we consider only this case of constructing a variable grid.
Divide the integration region into cells by a rectangular grid that contains elements of the same length along the axis and elements of the same length along the axis . Then in the case of B, the cubature formula with weight function (16) is modified into the form
where ; .
We obtain the estimation of the error of the method for this case from Formula (21) taking into account the rectangular grid of division of the integration region and the notation introduced here. So, in the general case, we have
or
If the lengths of the sides of rectangular cells are constant (fixed), then we obtain the estimation of the method error in the classical form of the error of the cells method [].
Consider the typical cases of the kind of function g(τ).
- (1)
- g(τ) = τ.
In this case, the integration region is a square that enlarges equally along both coordinate axes in proportion to the growth τ (Figure 12).

Figure 12.
Schematic representation of the set of integration regions in the points τ = τ1, τ = τ2, τ = τ3 for g(τ) = τ.
Here we accept , that is we impose a square grid. Then Formula (22) is simplified to the form
The application of this formula is implemented for the simple integrand . The results of the calculations are shown in Table 13.

Table 13.
Calculation of integral .
- (2)
- g(τ) = ατ.
In this case, the integration region is a rectangle that enlarges with growth τ. If α > 1 then the side length of this rectangle along the axis Oτ″ is always α times greater than the side length along the axis Oτ′. Then with increasing τ, the region of integration increases in two coordinates, but with a greater rate along the axis Oτ″ (Figure 13).

Figure 13.
Schematic representation of set of integration regions in the points τ = τ1, τ = τ2, τ = τ3 for g(τ) = ατ, α > 1.
If α < 1 then the side length of this rectangle along the axis Oτ″ is always α times less than the side length along the axis Oτ′. Then with increasing τ, the region of integration increases in two coordinates, but with a greater rate along the axis Oτ′ (Figure 14).

Figure 14.
Schematic representation of set of integration regions in the points τ = τ1, τ = τ2, τ = τ3 for g(τ) = ατ, α < 1.
When applying this method here and hereafter, under constructing a grid, it is not necessary to take into account the type of function g(τ), i.e., a rectangular grid can be overlayed in different combinations. We will abide by the structure of the function g(τ) when constructing the grid.
Let n(τ) = αm(τ). Then Formula (22) is modified to the form
The application of this formula is implemented to calculate the integral . The results of the calculations are shown in Table 14 for α > 1 and in Table 15 for α < 1.

Table 14.
Calculation of integral for α > 1.

Table 15.
Calculation of integral for α < 1.
- (3)
- g(τ) = τ2.
In this case, the integration region is also a rectangle that increases with growth τ. Moreover, the growth rate for this region along the axis Oτ″ is much greater than along the axis Oτ′ and the difference between them increases with the increase of τ (Figure 15).

Figure 15.
Schematic representation of set of integration regions in the points τ = τ1, τ = τ2, τ = τ3 for g(τ) = τ2.
Let n(τ) = (m(τ))2 under constructing the variable grid. Then the Formula (22) takes the form
The application of this formula is implemented to the calculation of the integral (Table 16).

Table 16.
Calculation of integral .
- (4)
- g(τ) = , .
In this case, the integration region is also a rectangle that changes with growth τ. The integration region increases proportionally along the axis Oτ′ and decreases along the axis Oτ″ (Figure 16).

Figure 16.
Schematic representation of set of integration regions in the points τ = τ1, τ = τ2, τ = τ3 (τ1 < τ2 < τ3) for g(τ) = .
If at constructing the grid we choose a variable number of elements according to the type of function g(τ), i.e., for this case n(τ) = τm(τ), then with increasing τ the number of elements increases along the axis Oτ′, and decreases along the axis Oτ″ according to the change of the integration region. Then at each step, an additional check of the condition m(τ) ≥ 1 (or n(τ)/τ ≥ 1) is required, as there must be at least one grid element along the axis Oτ″.
For this case, we carry out the calculation of integrals by the formula
Its application was realized for the calculation of the integral (Table 17).

Table 17.
Calculation of integral .
In our opinion, for this case of the type of function g(τ) it is advisable to choose the construction of the grid in the case C1 with the correct (appropriate) choice of function m(τ) and step hm(τ).
If the function g(τ) is periodic (for example g(τ) = sin(τ)), then the region of integration is variable and rectangular. At the intervals of this function increasing, the integration region increases along the axis Oτ″, and at the intervals of decrease, it decreases along the axis Oτ″, respectively. That is, the increasing and decreasing of the integration region have cyclical (periodic) nature. Then the variable integration grid must be chosen by the case C1 with the choice of suitable periodic functions as m(τ) and hm(τ).
6. Conclusions and Perspectives
All obtained results are new. The numerical method for calculating doubles integrals with variable upper limits was developed. It can be divided into several stages as determining the variable region of integration; overlaying the square or rectangular grid on the integration region; separating the integration subregions consisting of square and triangular elements; applying the cubatures in the subregion with square elements; triangulation partition along variable boundary; calculating the volumes of elementary elements with triangular basis, calculating the reference integral and establishing the calculation error.
The variable region of integration leads to the necessity to change the grid of its division into elementary volumes. The variable of the upper limit of the external integral has a significant effect. Here we consider three cases of a possible change of the grid, namely when this variable changes, we change only the size of the imposed grid and fix the number of partition elements; only the number of division elements changes, and the grid size is fixed, as well as both the number of division elements and the grid size change under fixing their multiplication. In the latter case, we considered an assignment of increasing and decreasing functions describing the change in the number of integration nodes on specific examples. In all considered examples of the application of the proposed method the smallest values of absolute and relative errors are reached for the case of an increase of the number of division elements changes and the grid size is fixed. At the same time, the question remains whether the choice of the function of the number of integration nodes, which increases much more sharply, will give rise to descent the error of the method. Additionally, note that the imposition of a variable grid on the integration region, if necessary, can be applied to definite double integrals.
When finding the estimate of the error of the method, we expanded the integral itself into a Taylor series using Barrow’s theorem. If we impose the definite limits of integration, the obtained formula will be reduced to the classical formula for expanding an integrand into the Taylor series. It is also necessary to carry out an individual investigation on the influence of setting variables of the number of elements of the division of the integration region and the size of the grid on the error estimate.
In this paper, we have considered the case when a double integral with variable limits can be reduced to an integral with simple variables in the upper limits of integration and zero lower limits. However, the proposed changes of variables are not always appropriate. Therefore, further research is needed on numerical integration, which limits functions, including the establishment of conditions and constraints on these functions, the integrand, and the variable region of integration that will be formed.
Author Contributions
Conceptualization, O.C. and Y.B.; methodology, O.C. and N.S.; software, Y.B. and N.S.; validation, O.C., Y.B., N.S. and R.K.; formal analysis, O.C. and Y.B.; investigation, O.C. and Y.B.; resources, R.K.; data curation, N.S.; writing—original draft preparation, O.C. and Y.B.; writing—review and editing, R.K.; visualization, Y.B.; project administration, R.K.; funding acquisition, R.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ahmedov, A.A.; bin Abd Sathar, M.H. Numerical integration of the integrals based on Haar wavelets. J. Phys. Conf. Ser. 2013, 435, 012042. [Google Scholar] [CrossRef]
- Bomba, A.; Safonyk, A. Modelling of processes of liquids cleaning from multicomponent impurities in sorption filters. Phys. Math. Model Inf. Technol. 2012, 16, 32–41. [Google Scholar]
- Chernukha, O.; Bilushchak, Y.; Pakholok, B. System approach to mathematical description of transport processes with chemical reaction in multiphase multicomponent body. In Proceedings of the 2020 IEEE 2nd International Conference on System Analysis & Intelligent Computing (SAIC), Kyiv, Ukraine, 5–9 September 2020; pp. 144–149. [Google Scholar] [CrossRef]
- Chernukha, O.; Bilushchak, Y. Interpolation of Boundary Condition at Time-Interval of Unknown Lenghth for the Problem of Convective Diffusion in a Three-Layered Water Filter. In Modeling, Control and Information Technologies, Proceedings of III International Scientific and Practical Conference, Kyiv, Ukraine, 14–16 November 2019; National University of Water and Environmental Engineering: Kyiv, Ukraine, 2019; pp. 25–28. [Google Scholar]
- Klasson, K.T.; Taylor, P.A. Remediation of Groundwater Contaminated with Radioactive Compounds. Environ. Ecol. Chem. 2006, 3, 26–44. [Google Scholar]
- Lekatoua, A.; Karantzalisa, A.E.; Evangeloua, A.; Gousiaa, V.; Kaptayb, G.; Gacsib, Z.; Baumlib, P.; Simonb, A. Aluminium reinforced by WC and TiC nanoparticles (ex-situ) and aluminide particles (in-situ): Microstructure, wear and corrosion behaviour. Mater. Des. 2015, 65, 1121–1135. [Google Scholar] [CrossRef]
- Ma, R.; Zheng, C.; Liu, C. Groundwater Impacts of Radioactive Wastes and Associated Environmental Modeling Assessment. In Encyclopedia of Sustainability Science and Technology; Springer: New York, NY, USA, 2012; pp. 4774–4784. [Google Scholar]
- Panteleev, A.V.; Kudryavtseva, I.A. Chislennye metody. Praktikum. In Numerical Methods: Practical Work; Infra-M: Moscow, Russia, 2017; p. 416. [Google Scholar]
- Ueberhuber, C.W. Numerical Computation, Vol. II; Springer: Berlin, Germany, 1997. [Google Scholar]
- Zadachin, V.M.; Konyushenko, I.G. Numerical Methods; Publishing Kharkiv National Economic University: Kharkiv, Ukraine, 2014; p. 180. [Google Scholar]
- Maxwell, J.C. On approximate multiple integration between limits of summation. Cambridge Phil. Soc. Proc. 1880, 3, 39–47. [Google Scholar]
- Preston, C.; Hammer, A.W. Wymore Numerical Evaluation of Multiple Integrals I. Math. Tables Other Aids Comput. 1957, 11, 59–67. [Google Scholar]
- Haber, S. Numerical evaluation of multiple integrals. SIAM Rev. 1970, 12, 481–526. [Google Scholar] [CrossRef]
- Krylov, V.I. Approximate Calculation of Integrals; Nauka: Moscow, Ukraine, 1967. [Google Scholar]
- Mysovskikh, I.P. Interpolatory Cubature Formulas; Izdat. Nauka: Moscow, Russia, 1981. [Google Scholar]
- Cools, R. An encyclopaedia of cubature formulas. J. Complex. 2003, 19, 445–453. [Google Scholar] [CrossRef]
- Solodusha, S.; Bulatov, M. Integral Equations Related to Volterra Series and Inverse Problems: Elements of Theory and Applications in Heat Power Engineering. Mathematics 2021, 9, 1905. [Google Scholar] [CrossRef]
- Sobolev, S.L.; Vaskevich, V. The Theory of Cubature Formulas; Springer: New York, NY, USA, 1997; p. 438. [Google Scholar] [CrossRef]
- Lyness, J.N.; Cools, R. A survey of numerical cubature over triangles. In Preprint MCS-P410-0194, Mathematics and Computer Science Division; Argonne National Laboratory: Argonne, IL, USA, 1994. [Google Scholar] [CrossRef] [Green Version]
- Dai, F.; Xu, Y. Approximation Theory and Harmonic Analysis on Spheres and Balls; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Glaubitz, J. Stable high order quadrature rules for scattered data and general weight functions. SIAM J. Numer. Anal. 2020, 58, 2144–2164. [Google Scholar] [CrossRef]
- Glaubitz, J. Construction and Application of Provable Positive and Exact Cubature Formulas. arXiv 2021, arXiv:2108.02848. [Google Scholar]
- Costabile, F.A.; Guzzardi, L. On a class of embedded cubature formulae on the simplex. Av. Cienc. Ing. 2014, 6, A19–A25. [Google Scholar]
- Keast, P. Cubature formulas for the sphere and the simplex (Technical report). J. Comput. Appl. Math. 1987, 17, 151–172. [Google Scholar] [CrossRef] [Green Version]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Neumann, J. Various techniques used in connection with random digits. National bureau of standards symposium. Appl. Math. Ser. 1951, 12, 36–38. [Google Scholar]
- Caflisch, R.E. Monte carlo and quasi-monte carlo methods. Acta Numer. 1998, 7, 1–49. [Google Scholar] [CrossRef] [Green Version]
- Filho, A.C.B.B. A computational algorithm for the numerical integration of a function of one or more variables. Int. J. Sci. Res. 2018, 7, 923–928. [Google Scholar] [CrossRef]
- Robert, C.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Stroud, A.H.; Secrest, D. Gaussian Quadrature Formulas; Prentice-Hall, Inc.: London, UK, 1966; 374p. [Google Scholar]
- Cools, R.; Rabinowitz, P. Monomial cubature rules since ‘‘Stroud’’: A compilation. J. Comput. Appl. Math. 1993, 48, 309–326. [Google Scholar] [CrossRef]
- Franke, R. Obtaining Cubatures for Rectangles and Other Planar Regions by Using Orthogonal Polynomials. Math. Comput. 1971, 25, 803–817. [Google Scholar] [CrossRef]
- Poole, D. Linear Algebra: A Modern Introduction, 2nd ed.; Thomson Brooks/Cole: Toronto, ON, Canada, 2006; 736p. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; 9th Printing; US Government Printing Office: Washington, DC, USA, 1972; p. 880.
- Whittaker, E.T.; Watson, G.N. Forms of the Remainder in Taylor’s Series: A Course in Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1990; pp. 95–96. [Google Scholar]
- Laurie, D.P. Practical error estimation in numerical integration. J. Comput. Appl. Math. 1985, 12–13, 425–431. [Google Scholar] [CrossRef] [Green Version]
- Gavrilyuk, I.P.; Makarov, V.L. Methods of Calculation. Part 1; Publishing Vyshcha Shkola: Kyiv, Ukraine, 1995; p. 367. [Google Scholar]
- Dorogovtsev, A.Y. Mathematical Analysis. A Short Course in a Modern Presentation, 2nd ed.; Publishing Fakt: Kyiv, Ukraine, 2004; p. 560. [Google Scholar]
- Robert, S. Woodward Mathematical Monographs, No 7. Probability and Theory of Errors; Trieste Publishing Pty Limited: Victoria, Australia, 2017; p. 82. [Google Scholar]
- Topping, J. Theory of Errors. In Errors of Observation and Their Treatment; Chapman and Hall: London, UK, 1972; p. 120. [Google Scholar] [CrossRef]
- Elsayed, B.; Sultan, A.; Abdallah, G. A Comparative Study among New Hybrid Root Finding Algorithms and Traditional Methods. Mathematics 2021, 9, 1306. [Google Scholar] [CrossRef]
- Verzhbitsky, V.M. Numerical Methods. Linear Algebra and Nonlinear Equations: Textbook; Publishing House Higher School: Moscow, Russia, 2000. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).