Conservative Finite-Difference Scheme for 1D Ginzburg–Landau Equation
Abstract
:1. Introduction
2. Problem Statement
3. Invariant of the Problem
3.1. Linear Problem:
3.2. Nonlinear Problem without the Terms Describing the Linear Absorption (Amplification) of the Optical Energy and Homogeneous Phase Shift of the Optical Pulse:
3.3. Nonlinear Problem with the Linear Absorption (Amplification) of the Optical Energy and Homogeneous Shift of the Optical Pulse’s Phase:
4. Finite-Difference Scheme and Iterative Method for Its Realization
5. Conservativeness of the Finite-Difference Scheme
5.1. Linear Problem without Homogeneous Phase Shift and Absorption:
5.2. Linear Problem with Homogeneous Phase Shift and Absorption:
5.3. Nonlinear Problem with and without the Homogeneous Phase Shift and Absorption:
5.4. Nonlinear Problem with Homogeneous Phase Shift and Linear Absorption:
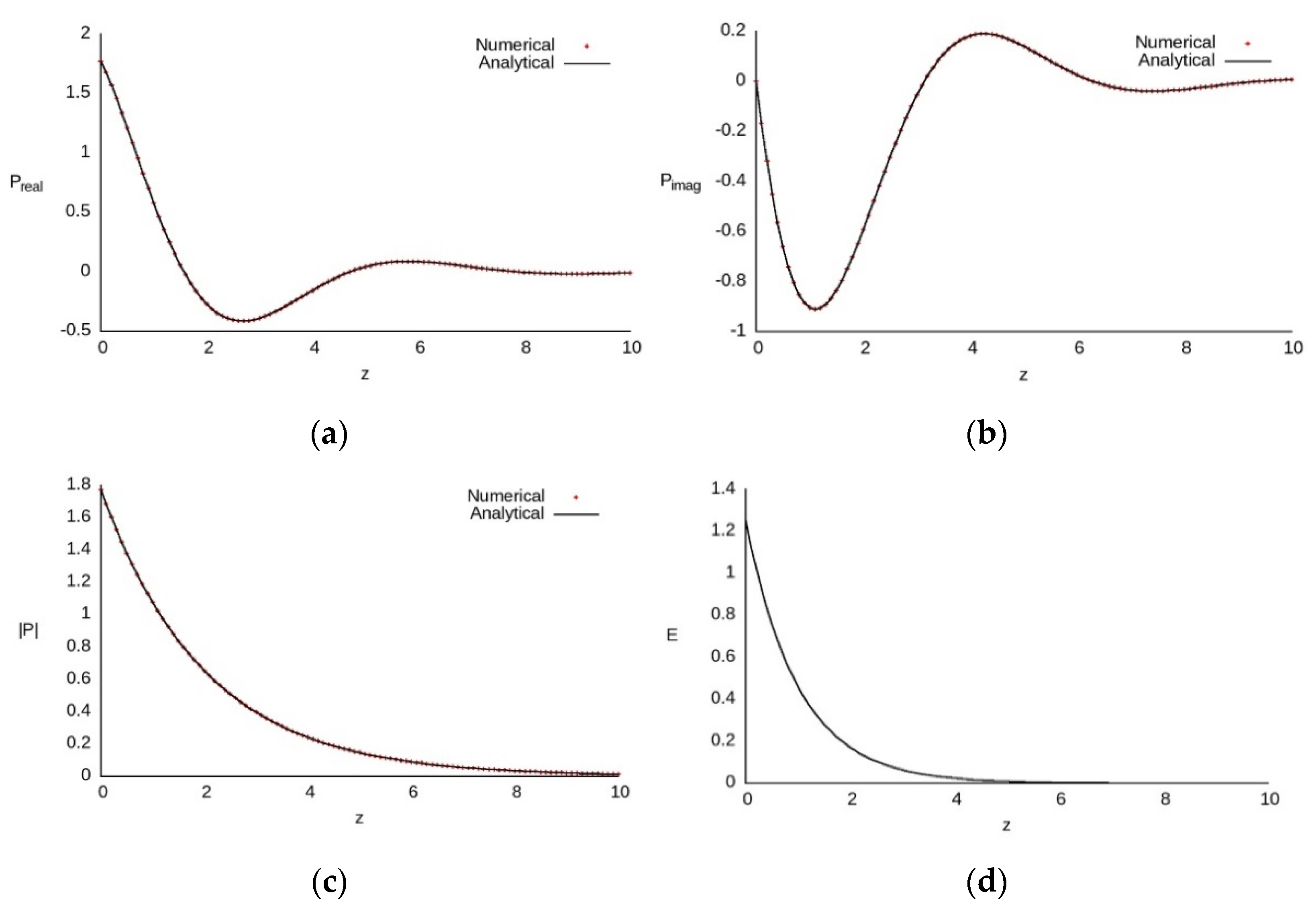
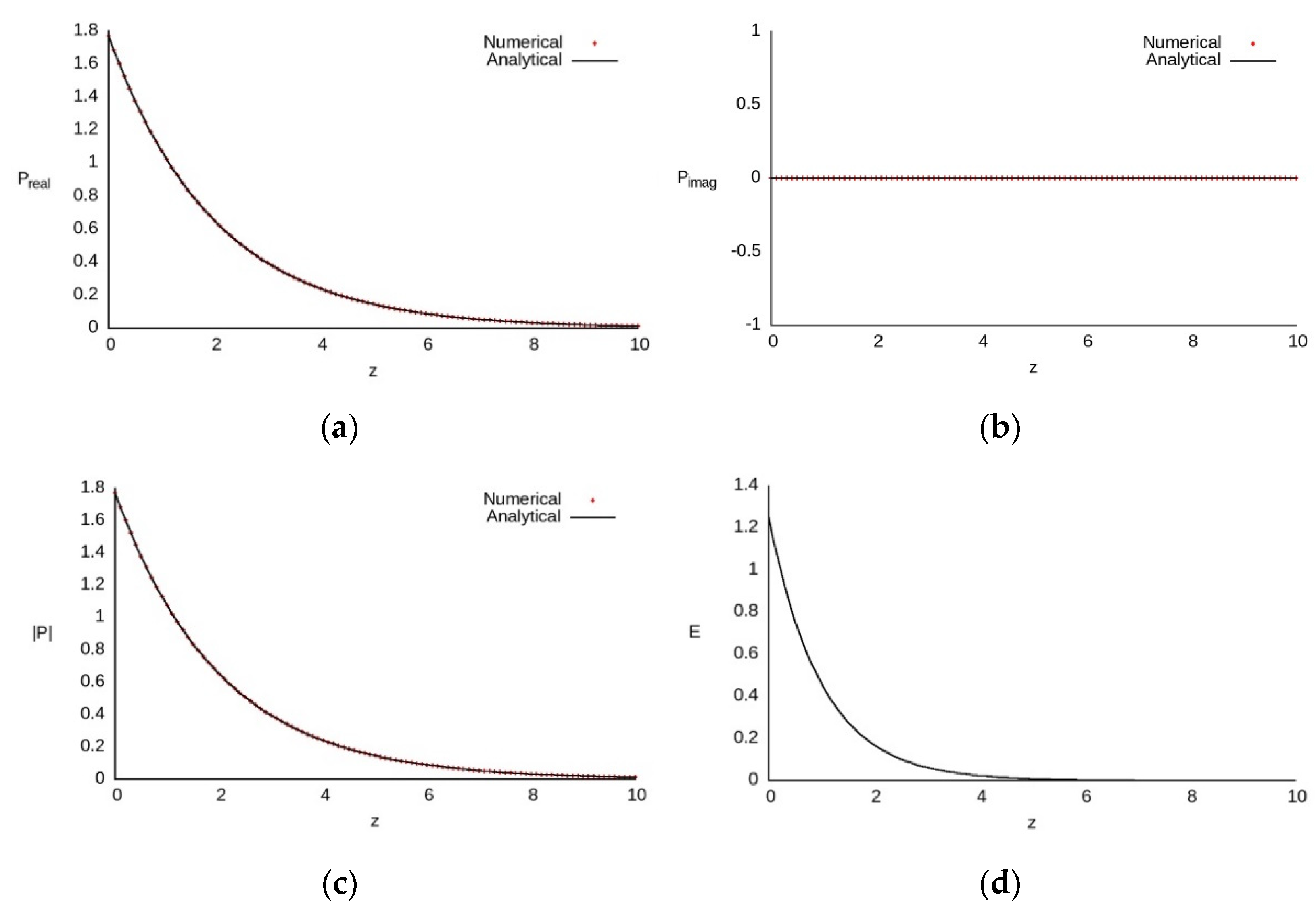
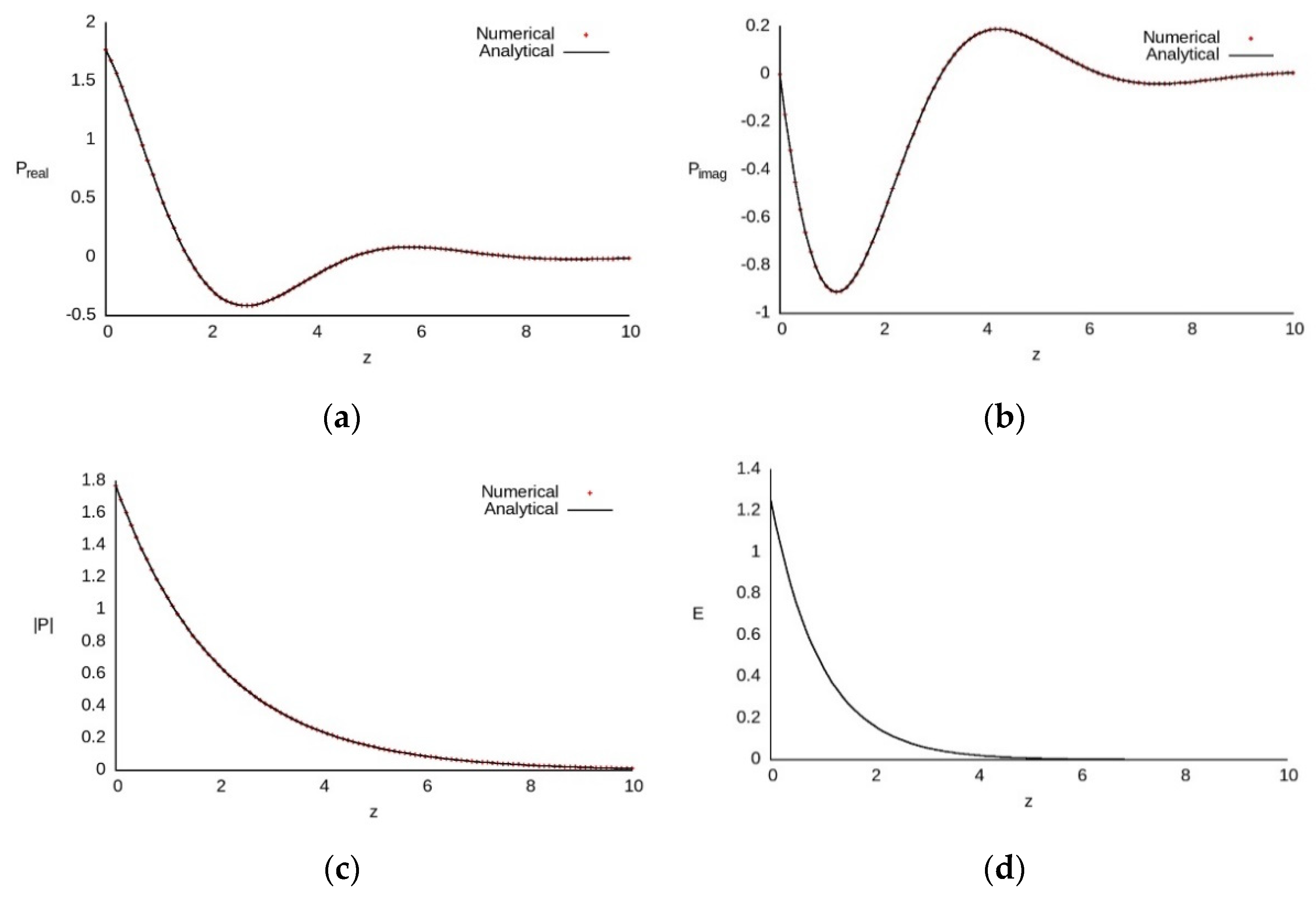
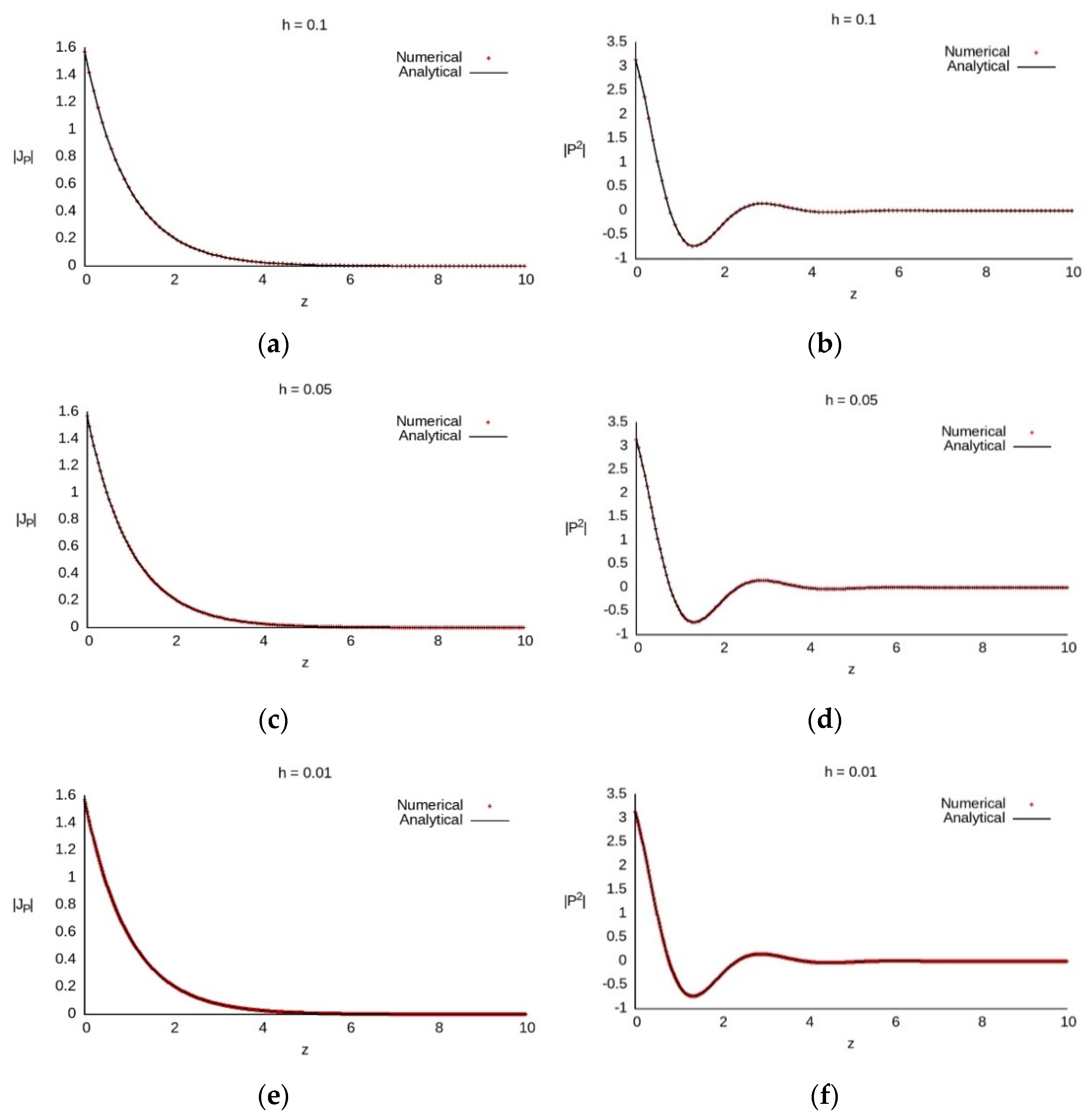
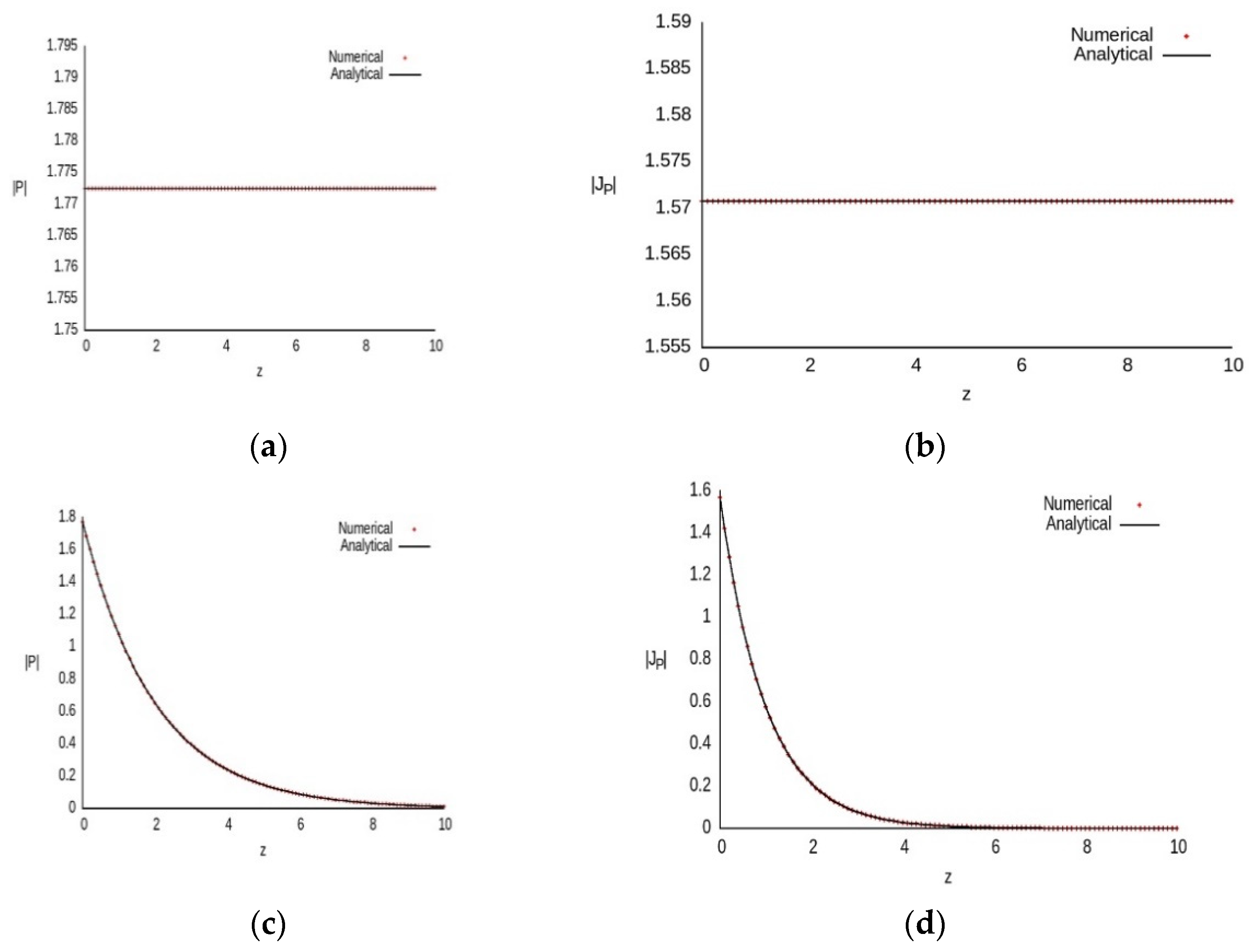
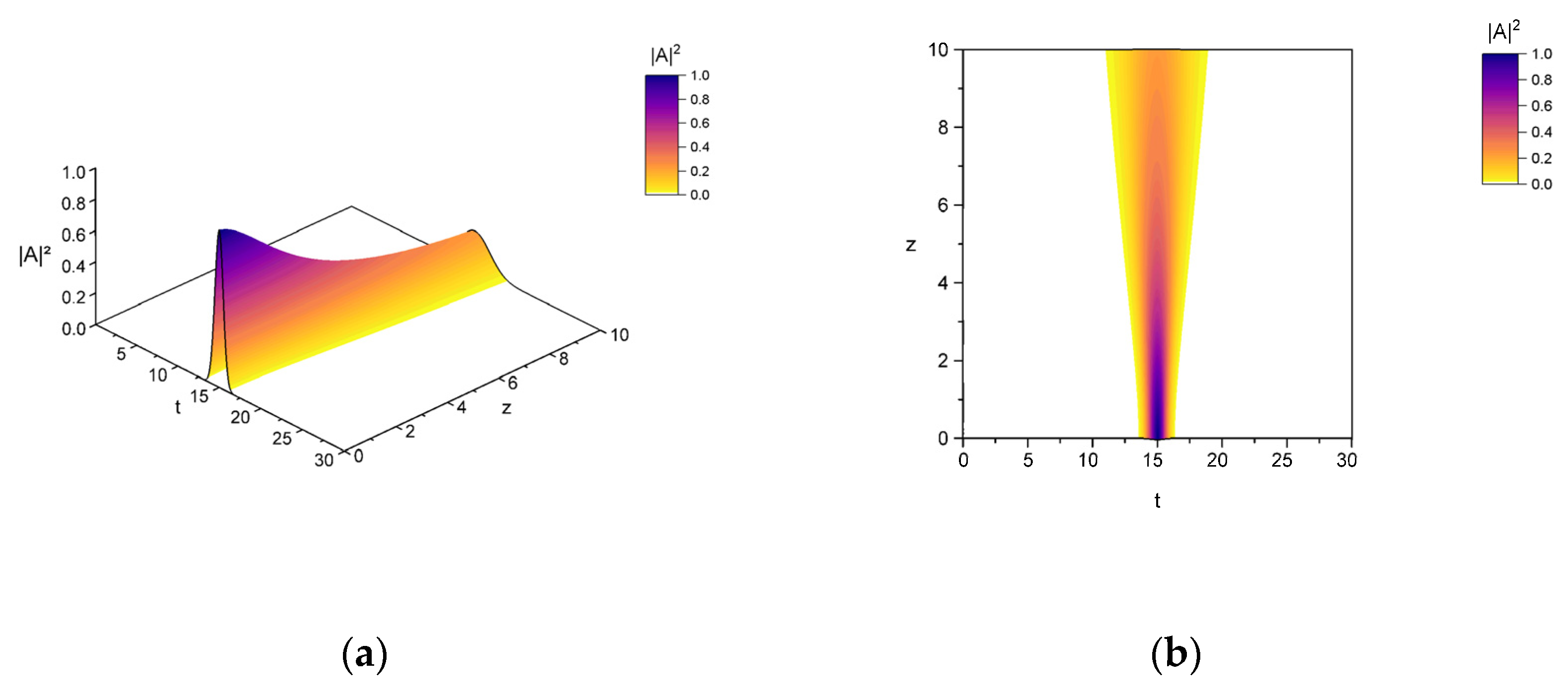
6. Computer Simulation Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductivity. In On Superconductivity and Superfluidity; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ginzburg, V.L. Superconductivity and superfluidity (what is done and what is not done). Phys.-Uspekh 1997, 40, 407–432. [Google Scholar] [CrossRef]
- Das, M.P.; Wilson, B.J. Novel superconductivity: From bulk to nano systems. Adv. Nat. Sci.-Nanosci. Nanotechnol. 2015, 6, 013001. [Google Scholar] [CrossRef] [Green Version]
- Kamenev, A.; Levchenko, A. Keldysh technique and non-linear sigma-model: Basic principles and applications. Adv. Phys. 2009, 58, 197–319. [Google Scholar] [CrossRef]
- Stoof, H.T.C. Time-dependent Ginzburg-Landau theory for a weak-coupling superconductor. Phys. Rev. B 1993, 47, 7979–7985. [Google Scholar] [CrossRef] [Green Version]
- Aguirre, C.A.; Martins, Q.S.; Barba-Ortega, J. Superconducting 3D Multi-layer Sample Simulated Via Nonuniform Ginzburg–Landau Parameter. J. Low Temp. Phys. 2021, 202, 360–371. [Google Scholar] [CrossRef]
- Megne, L.T.; Tabi, C.B.; Kofane, T.C. Modulation instability in nonlinear metamaterials modeled by a cubic-quintic complex Ginzburg-Landau equation beyond the slowly varying envelope approximation. Phys. Rev. E 2020, 102, 042207. [Google Scholar] [CrossRef] [PubMed]
- Gavish, N.; Kenneth, O.; Keren, A. Ginzburg–Landau model of a Stiffnessometer—A 3D Multi-layer stiffness meter device. Phys. D Nonlinear Phenom. 2021, 415, 132767. [Google Scholar] [CrossRef]
- Kong, L.; Luo, Y.; Wang, L.; Chen, M.; Zhao, Z. HOC–ADI schemes for two-dimensional Ginzburg–Landau equation in superconductivity. Math. Comput. Simul. 2021, 190, 494–507. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Extended Ginzburg-Landau equations and Abrikrosov vortex and geometric transition from square to rectangular lattice in a magnetic field. Phys. C Supercond. Its Appl. 2021, 581, 1353808. [Google Scholar] [CrossRef]
- Sadaf, M.; Akram, G.; Dawood, M. An investigation of fractional complex Ginzburg–Landau equation with Kerr law nonlinearity in the sense of conformable, beta and M-truncated derivatives. Opt. Quantum Electron. 2022, 54, 248. [Google Scholar] [CrossRef]
- Bu, C. The Ginzburg-Landau equation with nonzero Neumann boundary data. Nonlinear Anal. Theory Methods Appl. 1994, 23, 399–404. [Google Scholar] [CrossRef]
- Chen, X.Y.; Jimbo, S.; Morita, Y. Stabilization of vortices in the Ginzburg-Landau equation with a variable diffusion coefficient. Siam J. Math. Anal. 1998, 29, 903–912. [Google Scholar] [CrossRef]
- Rajantie, A. Vortices and the Ginzburg-Landau phase transition. Phys. B Condens. Matter 1998, 255, 108–115. [Google Scholar] [CrossRef] [Green Version]
- Ivey, T.; Lafortune, S. Spectral stability analysis for periodic traveling wave solutions of NLS and CGL perturbations. Phys. D Nonlinear Phenom. 2008, 237, 1750–1772. [Google Scholar] [CrossRef]
- Liu, C.S. Exact traveling wave solutions for a kind of generalized Ginzburg-Landau equation. Commun. Theor. Phys. 2005, 43, 787–790. [Google Scholar]
- Mohamadou, A.; Jiotsa, A.K.; Kofane, T.C. Effects of competing first- and second-neighbour couplings on the propagation of unstable patterns in the discrete complex cubic Ginzburg-Landau equation. Phys. Scr. 2005, 72, 281–289. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. Explicit and implicit solutions for the one-dimensional cubic and quintic complex Ginzburg-Landau equations. Appl. Math. Lett. 2006, 19, 1007–1012. [Google Scholar] [CrossRef] [Green Version]
- Facao, M.; Carvalho, M.I.; Latas, S.C.; Ferreira, M.F. Control of complex Ginzburg-Landau equation eruptions using intrapulse Raman scattering and corresponding traveling solutions. Phys. Lett. A 2010, 374, 4844–4847. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, M.I.; Facao, M. Dissipative solitons for generalizations of the cubic complex Ginzburg-Landau equation. Phys. Rev. E 2019, 100, 032222. [Google Scholar] [CrossRef]
- Balla, P.; Agrawal, G.P. Nonlinear interaction of vector solitons inside birefringent optical fibers. Phys. Rev. A 2018, 98, 023822. [Google Scholar] [CrossRef] [Green Version]
- Biswas, P.; Gandhi, H.K.; Mishra, V.; Ghosh, S. Propagation and asymmetric behavior of optical pulses through time-dynamic loss-gain-assisted media. Appl. Opt. 2018, 57, 7167–7171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tafo, J.B.G.; Nana, L.; Kofane, T.C. Effects of nonlinear gradient terms on the defect turbulence regime in weakly dissipative systems. Phys. Rev. E 2017, 96, 022205. [Google Scholar] [CrossRef] [PubMed]
- Bouzida, A.; Triki, H.; Ullah, M.Z.; Zhou, Q.; Biswas, A.; Belic, M. Chirped optical solitons in nano optical fibers with dual-power law nonlinearity. Optik 2017, 142, 77–81. [Google Scholar] [CrossRef]
- Li, H.; Yuan, X. Quasi-periodic solution for the complex Ginzburg-Landau equation with continuous spectrum. J. Math. Phys. 2018, 59, 112701. [Google Scholar] [CrossRef]
- Li, X.; Liu, B. Finite time blow-up and global existence for the nonlocal complex Ginzburg-Landau equation. J. Math. Anal. Appl. 2018, 466, 961–985. [Google Scholar] [CrossRef]
- Aleksic, B.N.; Uvarova, L.A.; Aleksic, N.B.; Belic, M.R. Cubic quintic Ginzburg Landau equation as a model for resonant interaction of EM field with nonlinear media. Opt. Quantum Electron. 2020, 52, 175. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.J.; Duan, J.Q. On the initial-value problem for the generalized two-dimensional Ginzburg-Landau equation. J. Math. Anal. Appl. 1997, 216, 536–548. [Google Scholar] [CrossRef]
- Lu, K.N.; Pan, X.B. Eigenvalue problems of Ginzburg-Landau operator in bounded domains. J. Math. Phys. 1999, 40, 2647–2670. [Google Scholar] [CrossRef] [Green Version]
- Podivilov, E.; Kalashnikov, V.L. Heavily-chirped solitary pulses in the normal dispersion region: New solutions of the cubic-quintic complex Ginzburg-Landau equation. J. Exp. Theor. Phys. Lett. 2005, 82, 467–471. [Google Scholar] [CrossRef]
- Shtyrina, O.V.; Yarutkina, I.A.; Skidin, A.S.; Podivilov, E.V.; Fedorukt, M.P. Theoretical analysis of solutions of cubic-quintic Ginzburg-Landau equation with gain saturation. Opt. Express 2019, 27, 6711–6718. [Google Scholar] [CrossRef]
- Aranson, I.S.; Kramer, L. The world of the complex Ginzburg-Landau equation. Rev. Mod. Phys. 2002, 74, 99–143. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Morales, V.; Krischer, K. The complex Ginzburg-Landau equation: An introduction. Contemp. Phys. 2012, 53, 79–95. [Google Scholar] [CrossRef]
- Elcoot, A.E.K. Nonlinear stability of an axial electric field: Effect of interfacial charge relaxation. Appl. Math. Model. 2010, 34, 1965–1983. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, G.P. Optical pulse propagation in doped fiber amplifiers. Phys. Rev. A 1991, 44, 7493–7501. [Google Scholar] [CrossRef]
- Agrawal, G.P. Applications of Nonlinear Fiber Optics, 2nd ed.; Academic Press: Rochester, NY, USA, 2008. [Google Scholar] [CrossRef]
- Arteaga-Sierra, F.R.; Antikainen, A.; Agrawal, G.P. Dynamics of soliton cascades in fiber amplifiers. Opt. Lett. 2016, 41, 5198–5201. [Google Scholar] [CrossRef]
- van Tartwijk, G.H.M.; Agrawal, G.P. Maxwell-Bloch dynamics and modulation instabilities in fiber lasers and amplifiers. J. Opt. Soc. Am. B Opt. Phys. 1997, 14, 2618–2627. [Google Scholar] [CrossRef]
- Lugiato, L.A. Transverse nonlinear optics—introduction and review. Chaos Solitons Fractals 1994, 4, 1251–1258. [Google Scholar] [CrossRef]
- Otsuka, K. Complex dynamics in coupled nonlinear element systems. Int. J. Mod. Phys. B 1991, 5, 1179–1214. [Google Scholar] [CrossRef]
- Malomed, B.A. Optical Solitons and Vortices in Fractional Media: A Mini-Review of Recent Results. Photonics 2021, 8, 353. [Google Scholar] [CrossRef]
- Antoine, X.; Bao, W.; Besse, C. Computational methods for the dynamics of the nonlinear Schrödinger/Gross–Pitaevskii equations. Comput. Phys. Commun. 2013, 184, 2621–2633. [Google Scholar] [CrossRef] [Green Version]
- Sanz-Serna, J.M. Methods for the numerical solution of the nonlinear Schrödinger equation. Math. Comput. 1984, 43, 21–27. [Google Scholar] [CrossRef]
- Delfour, M.; Fortin, M.; Payr, G. Finite-difference solutions of a non-linear Schrödinger equation. J. Comput. Phys. 1981, 44, 277–288. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, X.Q.; Shao, Z.Y.; Gao, J.Q.; Yang, X.F. Multi-symplectic integrator of the generalized KdV-type equation based on the variational principle. Sci. Rep. 2019, 9, 15883. [Google Scholar] [CrossRef]
- Zhou, M.X.; Kanth, A.S.V.; Aruna, K.; Raghavendar, K.; Rezazadeh, H.; Inc, M.; Aly, A.A. Numerical solutions of time fractional Zakharov-Kuznetsov equation via natural transform decomposition method with nonsingular kernel derivatives. J. Funct. Spaces 2021, 2021, 9884027. [Google Scholar] [CrossRef]
- Tala-Tebue, E.; Korkmaz, A.; Rezazadeh, H.; Raza, N. New auxiliary equation approach to derive solutions of fractional resonant Schrödinger equation. Anal. Math. Phys. 2021, 11, 167. [Google Scholar] [CrossRef]
- Samarskii, A.A. The Theory of Difference Schemes, 1st ed.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar] [CrossRef]
- Zhang, F.; Peréz-Ggarcía, V.M.; Vázquez, L. Numerical simulation of nonlinear Schrödinger equation system: A new conservative scheme. Appl. Math. Comput. 1995, 71, 165–177. [Google Scholar] [CrossRef]
- Li, S.; Vu-Quoc, L. Finite difference calculus invariant structure of a class of algorithms for the nonlinear Klein–Gordon equation. SIAM J. Numer. Anal. 1995, 32, 1839–1875. [Google Scholar] [CrossRef]
- Gauckler, L. Numerical long-time energy conservation for the nonlinear Schrödinger equation. IMA J. Numer. Anal. 2017, 37, 2067–2090. [Google Scholar] [CrossRef] [Green Version]
- Ismail, M.S.; Taha, T.R. A linearly implicit conservative scheme for the coupled nonlinear Schrödinger equation. Math. Comput. Simul. 2007, 74, 302–311. [Google Scholar] [CrossRef]
- Hu, H.; Hu, H. Maximum norm error estimates of fourth-order compact difference scheme for the nonlinear Schrödinger equation involving a quintic term. J. Inequalities Appl. 2018, 1, 180. [Google Scholar] [CrossRef]
- Wang, T.; Guo, B. Unconditional convergence of two conservative compact difference schemes for non-linear Schrödinger equation in one dimension. Sci. Sin. Math. 2011, 41, 207–233. [Google Scholar] [CrossRef]
- Trofimov, V.A.; Peskov, N.V. Comparison of finite-difference schemes for the Gross-Pitaevskii equation. Math. Model. Anal. 2009, 14, 109–126. [Google Scholar] [CrossRef]
- Wang, T.; Jiang, J.; Wang, H.; Xu, W. An efficient and conservative compact finite difference scheme for the coupled Gross–Pitaevskii equations describing spin-1 Bose-Einstein condensate. Appl. Math. Comput. 2018, 323, 164–181. [Google Scholar] [CrossRef]
- Barletti, L.; Brugnano, L.; Caccia, G.F.; Iavernaro, F. Energy-conserving methods for the nonlinear Schrödinger equation. Appl. Math. Comput. 2018, 318, 3–18. [Google Scholar] [CrossRef]
- Feng, X.; Liu, H.; Ma, S. Mass- and Energy-Conserved Numerical Schemes for Nonlinear Schrödinger Equations. Commun. Comput. Phys. 2019, 26, 1365–1396. [Google Scholar] [CrossRef] [Green Version]
- Amiranashvili, S.; Čiegis, R.; Radziunas, M. Numerical methods for a class of generalized nonlinear Schrödinger equations. Kinet. Relat. Models 2015, 8, 215. [Google Scholar] [CrossRef]
- Trofimov, V.A.; Stepanenko, S.; Razgulin, A. Conservation laws of femtosecond pulse propagation described by generalized nonlinear Schrödinger equation with cubic nonlinearity. Math. Comput. Simul. 2021, 182, 366–396. [Google Scholar] [CrossRef]
- Varentsova, S.A.; Volkov, A.G.; Trofimov, V.A. The conservative difference scheme for the problem of femtosecond laser pulse propagation through a medium with a cubic nonlinearity. Comput. Math. Math. Phys. 2003, 43, 1644–1656. [Google Scholar]
- Trofimov, V.; Loginova, M. Conservative Finite-Difference Schemes for Two Nonlinear Schrödinger Equations Describing Frequency Tripling in a Medium with Cubic Nonlinearity: Competition of Invariants. Mathematics 2021, 9, 2716. [Google Scholar] [CrossRef]
- Paasonen, V.I.; Fedoruk, M.P. Three-level non-iterative high accuracy scheme for Ginzburg—Landau equation. Comput. Technol. 2015, 20, 46–57. [Google Scholar]
- Du, Q.; Wu, X.N. Numerical solution of the three-dimensional Ginzburg-Landau models using artificial boundary. Siam J. Numer. Anal. 1999, 36, 1482–1506. [Google Scholar] [CrossRef] [Green Version]
- Borzi, A.; Grossauer, H.; Scherzer, O. Analysis of iterative methods for solving a Ginzburg-Landau equation. Int. J. Comput. Vis. 2005, 64, 203–219. [Google Scholar] [CrossRef] [Green Version]
- Salete, E.; Vargas, A.M.; García, Á.; Negreanu, M.; Benito, J.J.; Ureña, F. Complex Ginzburg–Landau equation with generalized finite differences. Mathematics 2020, 8, 2248. [Google Scholar] [CrossRef]
- Takac, P. Invariant 2-tori in the time-dependent Ginzburg-Landau equation. Nonlinearity 1992, 5, 289–321. [Google Scholar] [CrossRef]
- Du, Q. Discrete gauge invariant approximations of a time dependent Ginzburg-Landau model of superconductivity. Math. Comput. 1998, 67, 965–986. [Google Scholar] [CrossRef] [Green Version]
- Koma, Y.; Toki, H. Weyl invariant formulation of the flux-tube solution in the dual Ginzburg-Landau theory. Phys. Rev. D 2000, 62, 054027. [Google Scholar] [CrossRef] [Green Version]
- Lopez, V. Numerical continuation of invariant solutions of the complex Ginzburg-Landau equation. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 248–270. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Ju, L.; Xie, W. A Stabilized Semi-Implicit Euler Gauge-Invariant Method for the Time-Dependent Ginzburg-Landau Equations. J. Sci. Comput. 2019, 80, 1083–1115. [Google Scholar] [CrossRef]
- Kulikov, A.; Kulikov, D. Invariant varieties of the periodic boundary value problem of the nonlocal Ginzburg-Landau equation. Math. Methods Appl. Sci. 2021, 44, 11985–11997. [Google Scholar] [CrossRef]
- Moroz, L.I.; Maslovskaya, A.G. Computer simulation of hysteresis phenomena for ferroelectric switching devices. In Proceedings of the 2020 International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 6–9 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, G.F. Fast iterative solvers for the two-dimensional spatial fractional Ginzburg–Landau equations. Appl. Math. Lett. 2021, 121, 107350. [Google Scholar] [CrossRef]
- Ding, H.; Yi, Q. The construction of higher-order numerical approximation formula for Riesz derivative and its application to nonlinear fractional differential equations (I). Commun. Nonlinear Sci. Numer. Simul. 2022, 110, 106394. [Google Scholar] [CrossRef]
- Du, R.; Wang, Y.; Hao, Z. High-dimensional nonlinear Ginzburg–Landau equation with fractional Laplacian: Discretization and simulations. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105920. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Ostermann, A.; Gu, X.M. A low-rank Lie-Trotter splitting approach for nonlinear fractional complex Ginzburg-Landau equations. J. Comput. Phys. 2021, 446, 110652. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trofimov, V.; Loginova, M.; Fedotov, M.; Tikhvinskii, D.; Yang, Y.; Zheng, B. Conservative Finite-Difference Scheme for 1D Ginzburg–Landau Equation. Mathematics 2022, 10, 1912. https://doi.org/10.3390/math10111912
Trofimov V, Loginova M, Fedotov M, Tikhvinskii D, Yang Y, Zheng B. Conservative Finite-Difference Scheme for 1D Ginzburg–Landau Equation. Mathematics. 2022; 10(11):1912. https://doi.org/10.3390/math10111912
Chicago/Turabian StyleTrofimov, Vyacheslav, Maria Loginova, Mikhail Fedotov, Daniil Tikhvinskii, Yongqiang Yang, and Boyuan Zheng. 2022. "Conservative Finite-Difference Scheme for 1D Ginzburg–Landau Equation" Mathematics 10, no. 11: 1912. https://doi.org/10.3390/math10111912





