Abstract
Analysis of black hole spacetimes requires study of the motion of particles and light in these spacetimes. Here exact solutions of the geodesic equations are the means of choice. Numerous interesting black hole spacetimes have been analyzed in terms of elliptic functions. However, the presence of a cosmological constant, higher dimensions or alternative gravity theories often necessitate an analysis in terms of hyperelliptic functions. Here we review the method and current status for solving the geodesic equations for the general hyperelliptic case, illustrating it with a set of examples of genus : higher dimensional Schwarzschild black holes, rotating dyonic black holes, and black rings.
MSC:
83C57; 83C10; 83C15
1. Introduction
More than one hundred years ago, Einstein proposed his theory of general relativity, based on the revolutionary idea, that gravity is encoded in the geometric properties of space and time. General relativity is very well supported by experiments and has many applications such as the global positioning system GPS [1,2]. One of the predictions of general relativity is the existence of black holes and their formation in the collapse of very massive stars after exhaustion of their nuclear fuel [3,4,5,6]. Black holes possess an event horizon, and thus a boundary beyond which no communication with the exterior is possible. By now there is strong observational evidence not only for stellar black holes, but also for supermassive black holes at the core of galaxies [7,8,9,10,11,12,13,14,15].
A powerful tool to study black holes is the analysis of their geodesics. The motion of particles and light around a black hole provides valuable information about the spacetime. In particular, analytic solutions of the geodesic equations can be used to calculate observables with high accuracy, to be compared with observations in order to test theories and models.
For many well-known spacetimes like Schwarzschild and Kerr the equations of motion are of elliptic type (see, e.g., [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40] and references therein). These can easily be solved analytically in terms of the elliptic and therefore doubly-periodic Weierstraß ℘-function. However, when additional parameters (like the cosmological constant), higher dimensions or alternative theories of gravity are considered, the equations of motion become often more complicated and one encounters hyperelliptic integrals [41,42,43,44].
Inspired by the work on the double pendulum by Enolski et al. [45], exact solutions of the hyperelliptic equations of motion of genus two () arising in Schwarzschild-(anti-) de Sitter spacetime were obtained by Hackmann and Lämmerzahl [46,47]. Subsequently exact solutions of the geodesic equations were obtained for spherically and axially symmetric black holes in four and higher dimensions [48,49,50]. The inversion of hyperelliptic integrals was then generalized by Enolski et al. [51] to obtain solutions of the geodesic equations also for higher genus, . First applications included a nine-dimensional spacetime with cosmological constant and charge [51] and special cases of a Hořava–Lifshitz spacetime [52].
2. Geodesic Motion around Black Holes
Black holes represent some of the most intriguing objects of the universe, making their study both observationally and mathematically highly interesting. When the black hole spacetime is obtained as a solution of the gravitational field equations, the exploration of the properties of this spacetime relies to a large extent on the analysis of the motion of particles and light in this spacetime. For neutral point particles this motion is described by the geodesic equation
where are the coordinates, is an affine parameter along the orbit, and the symbol denotes the connection coefficients (and the Einstein summation convention is employed). Given a spacetime described by the invariant square of the infinitesimal line element
with metric coefficients , the connection coefficients are known functions of the coordinates. The geodesic Equation (1) forms a set of coupled differential equations, whose solution describes the sought after orbital motion in the spacetime. However, it is often of advantage to apply the Hamilton–Jacobi formalism to obtain an equivalent set of equations, starting from the Hamilton–Jacobi equation
with Hamilton’s principal function S, and to exploit the symmetries of the spacetime to obtain a separation of variables.
Black holes in four dimensions, i.e., one time and three spatial dimensions, are certainly of highest interest from an astrophysical point of view. In this case separability requires four constants of motion. The first constant of motion is associated with the square of the particle momentum, . Setting the particle mass to yields , whereas for light . The simplest black hole solutions of General Relativity are the static spherically symmetric Schwarzschild black hole and the stationary axially symmetric (rotating) Kerr black hole. Clearly, the symmetries of these spacetimes correspond to the existence of Killing vectors associated with two constants of motion. In particular, stationarity leads to conservation of energy E and axial symmetry to conservation of angular momentum L. However, the separability of the equations of motion of the Kerr spacetime involves still another constant of motion, the so called Carter constant [17], that derives from the existence of a Killing tensor [53]. In Boyer–Lindquist coordinates the geodesic equations can then be solved after employing the separation ansatz
leading to elliptic integrals, just as for the case of the static Schwarzschild black hole.
From a theoretical point of view it is very interesting to consider General Relativity also in higher dimensions, since additional dimensions are present in various theories like Kaluza–Klein theory or string theory. Moreover, it allows to discern genuine properties of black holes in General Relativity and properties only present in four dimensions. Higher dimensional generalizations of the static spherically symmetric Schwarzschild black hole were obtained by Tangherlini [54]. The high symmetry of these solutions implies separability of the equations of motion, but depending on the spacetime dimension D hyperelliptic integrals arise, starting with [48]. The generalizations of the rotating Kerr black hole to higher dimensions was accomplished by Myers and Perry [55]. Myers–Perry black holes in D dimensions are characterized by independent angular momenta, associated with rotation in N independent planes. Thus 5-dimensional Myers–Perry black holes possess two conserved angular momenta, showing the need for another conserved quantity for separability. Analogous to the Kerr case separability is guaranteed based on the presence of a Killing tensor [56,57]. Analysis of the geodesic equations leads again to elliptic integrals [26,32]. Proof of separability of the geodesic equations in still higher dimensions is based on the existence of Killing-Yano tensors [58,59]. In these spacetimes hyperelliptic integrals arise unless substitutions can be made to reduce the order of the polynomial in the geodesic equations. As discussed in more detail below, hyperelliptic integrals arise also in numerous further black hole spacetimes, for instance, when a cosmological constant, electromagnetic fields, etc. are present.
3. Hyperelliptic Integrals
When the equations of motion are of hyperelliptic type they take the form
with the initial values and , and have to be solved for a function . is a polynomial of order . The number n can take the values where .
Equation (5) leads to a hyperelliptic integral of the first kind
which has to be inverted to find . The solution has been discussed in [46,47,48,51,52]. The inversion of the integral should not depend on the integration path and thus for a closed integration path with the integral the following must apply: . Therefore is periodic. For each y the square root in the integrand can take two different signs. It is therefore not clearly defined in the complex plane. To resolve this issue, a Riemann surface can be constructed, where is a single valued function. The two signs of correspond to two copies of the Riemann sphere. Both spheres are cut between pairs of the zeros with of the polynomial . Here the zeros are called branch points. The branch cuts between the branch points should not be right next to each other, i.e., there should not be two cuts starting at the same branch point. If d is odd, the branch point is placed at infinity. At the branch points is the same at both spheres and therefore they can be identified here. Along the branch cuts the two spheres can be put together to get the Riemann surface, which now has holes. The number of holes is described by the genus . For example in the case , the Riemann surface is a double torus with two holes.
Let be the polynomial with one branch point at infinity. For the problems considered in this review, the polynomial is often considered in the canonical form, which is defined by setting the first coefficient . The factor 4 is chosen so that the canonical form looks like the Weierstraß form of the polynomial in the corresponding elliptic problem [51].
Then a basis of holomorphic differentials of the first kind and meromorphic differentials of the second kind with is defined as
A differential is holomorphic if . However, if a pole at infinity occurs and the differential is therefore meromorphic.
A homology basis of closed integration paths can be introduced to calculate the period matrices and of the solution of the inversion problem (6)
The period matrices satisfy the Legendre relation, see [47] or [52]. If the periods are calculated numerically for a specific problem, the Legendre relation can be used to check the calculations.
In the case it is possible to find a solution for a given . Each component of the solution vector is determined by the equation [47]
and can be extracted using the theorem of Vieta. However, it should be noted that the order of the components is not defined. The generalized Weierstraß function is defined as the second logarithmic derivative of the Kleinian -function
The Kleinian -function is defined as [47]
with . The constant C is given in [52]. The -function is
is the vector of Riemann constants [47,52].
The solution of Equation (6) can be obtained in a limiting process which restricts the Jacobi inversion problem to the -divisor, the set of zeros of the -function. Let us demonstrate the limiting process in the case of genus 2 (see [47,48]). For the Jacobi inversion problem is
If , the Jacobi inversion problem has a solution in the form of Equation (10). Therefore we rewrite the Equation (14)
with
The solution of Equation (15) can by expressed as
by applying the theorem of Vieta to Equation (10).
Now we take the limit . In this limit one can write as
Inserting Equation (17) yields
where is the ith derivative of the Kleinian -function and . It can be shown [47] that is an element of the -divisor, which is the set of zeros of the -function. That means and therefore . Then we have
In the end we want to find the inversion of the integral (6). For this we have to consider
In a nutshell, for a genus 2 curve the inversion of the integral (6) with the initial value is
The vector depends on the considered holomorphic integral:
and
where and . The components and are determined by the condition .
In higher genera the inversion is given by [51,52]
where
is the Jacobian of the Riemannian surface , where is the lattice spanned by the periods and . The solution formula (27) is a conjecture based on the properties of the Schur-Weierstraß functions. A relation similar to Equation (27) holds for the Schur-Weierstraß polynomials and in [51,52] it was conjectured that this formula can also be used for the -function. An analogue of this formula was considered in [60]. In the case genus Equation (27) also holds, as shown in [61].
However, some geodesic equations yield hyperelliptic integrals of the third kind
where p is a pole and a polynomial of order d. A formula to solve these integrals, which can be proven with the help of the Riemann vanishing theorem [62], was found in [52]
and are the vectors of the holomorphic differentials of the first kind and the meromorphic differentials of the second kind respectively (Equation (7)). The basepoint is a zero of the polynomial . is the vector of Riemann constants. The integral can be rewritten in terms of the -function
and the characteristic
of a branch point [52]. In [52] the characteristics are explicitly calculated for in section (V.A.) and for in section (VI.A.). The vectors and have the entries or 0. Then the integral is
where and are the half period matrices (see Equation (8)), and the gth component of the vector is and for we have
The are elementary symmetric functions of order k built on branch points : , , etc [52].
4. Examples for Geodesic Motion
4.1. Higher Dimensional Schwarzschild Black Holes
Schwarzschild black hole spacetimes in D dimensions are given by [54]
with Schwarzschild radius and standard metric on the -sphere . Since energy E and angular momentum L are conserved, and the motion is confined to an equatorial plane
the remaining equation of motion is the radial equation
respectively, the orbital equation
yielding the particle orbit in the black hole spacetime. Introducing dimensionless quantities
the right hand side of Equation (39) can be expressed as , where is a polynomial of order n. Moreover, a substitution is possible in odd dimensions, , to reduce the order of the polynomial by a factor of 2. Thus a case is obtained in , 9 and 11 dimensions (while and 7 are still elliptic) [48]. In 9 and 11 dimensions, the orbital equations read
respectively, leading to the solutions
where in the latter 11 dimensional case a substitution was performed, with a root of , transforming the orbital equation to [48]. The are defined as
with and .
Further analysis of the possible particle motion reveals, that these higher dimensional Schwarzschild black hole spacetimes do not allow for periodic bound orbits. Only escape orbits away from the black hole to spatial infinity are allowed and orbits terminating at the central black hole singularity.
4.2. Rotating Dyonic Black Holes
The problem of dark matter and dark energy is still an unsolved problem of physics, which could possibly be solved by introducing scalar fields like the dilaton and the axion. An interesting spacetime containing these fields is the rotating dyonic black hole with four electromagnetic charges of the gauged supergravity found by Chow and Compère [63]. The exact solutions of the equations of motion in the rotating dyonic black hole spacetime were found in [64]. The metric is given by
with
Here M describes the mass of the black hole, a is the rotation parameter, e and v correspond to the charges, is the Newman-Unti-Tamburino (NUT) parameter and g is the gauge coupling constant. The Boyer-Lindquist like coordinates transform to Cartesian coordinates as
Using the Hamilton-Jacobi formalism as described in Section 2 one finds four differential equations which describe the motion of particles and light in the above spacetime.
with the functions
Here dimensionless quantities were used
The definition of with simplifies the equation by absorbing the r and dependent prefactor .
The equations of motion are of hyperelliptic type and can be solved in terms of the Kleinian -function. The r-Equation (50) yields a hyperelliptic integral of the first kind. In general the right hand side of (50) is a polynomial of order six . The substitution , where is a zero of X, transforms X into a polynomial of order five and the r-equation becomes
A separation of variables yields the hyperelliptic integral
As described in Section 3, see Equations (24) and (26), the solution of the above equation is
where is the ith derivative of the Kleinian -function and
is determined by the condition . A resubstitution yields the full solution of (50)
The -Equation (51) can be solved similarly by substituting , where is a zero of Y, so that
The solution is
with
where is determined by the condition .
The -Equation (52) involves hyperelliptic integrals of the third kind. Here we use the Equations (50) and (51) to rewrite the -Equation (52) as
and can be solved separately. Both integrals can be decomposed into several integrals of the form
where Z is a pole and is a polynomial of the fifth order. The solution is (see Equation (30) in Section 3)
is a zero of the polynomial with the coefficients and the holomorphic and meromorphic differentials are
Analogously, the solution of the -Equation (53) can be found.
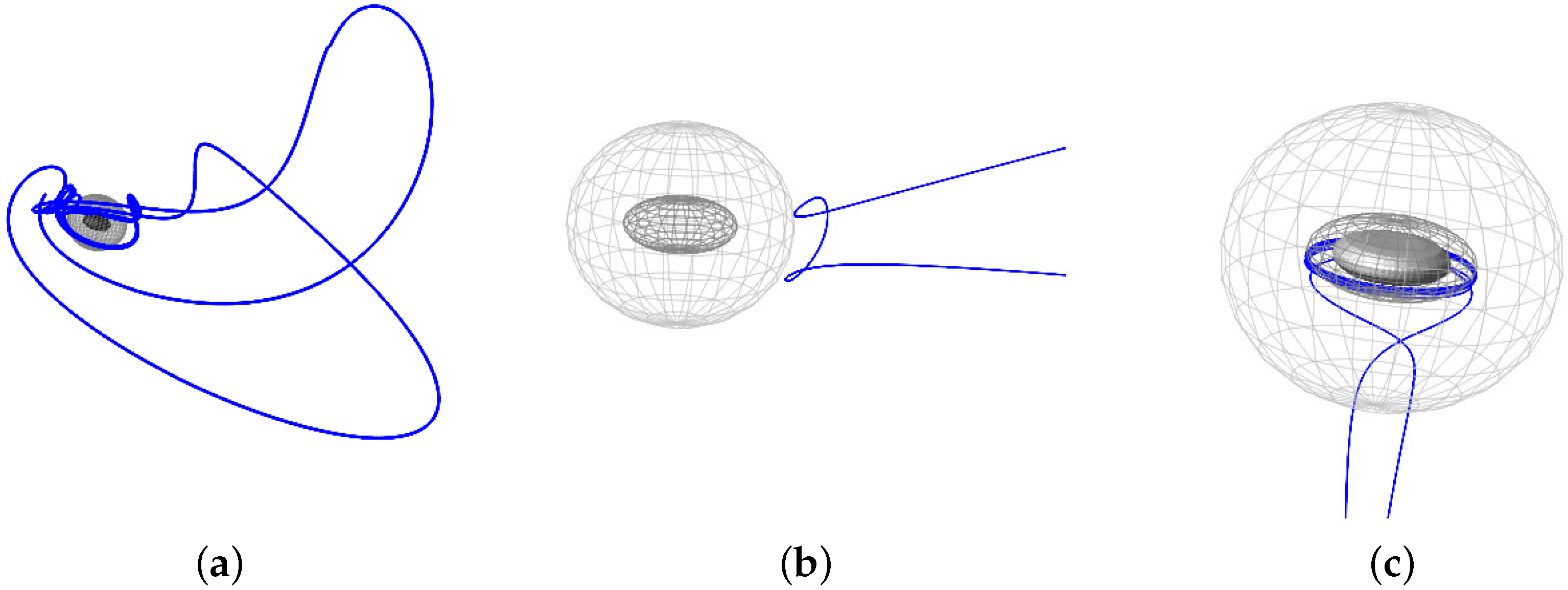
With the full set of analytical solutions we can visualize the orbits in this spacetime, see Figure 1.
Figure 1.
Orbits of particles (blue curves) around the rotating dyonic black hole. The horizons are represented by grey ellipsoids and the dark grey structure is the singularity of the black hole. (a) Bound orbit; (b) Escape orbit; (c) Two-world escape orbit crossing both horizons twice and emerging into another universe.
For the calculation of a specific orbit, first the periods have to be computed according to Equation (8). The integration path depends on the location of the zeros of the polynomial in the complex plane. The zeros are singularities of the integrand and therefore the integral has to be split into several parts, integrating from one zero to the next. When complex zeros occur, real and imaginary parts are integrated separately. One has to keep in mind that the sign of the square root is different for each part of the integration, see [47] for further details and pictures of the integration paths.
As the starting point in Equation (57) we choose one of the turning points of the orbit we want to plot, i.e., a zero of the polynomial. This has the advantage, that in Equation (59) can be expressed in terms of the periods (if we choose ). The solution of the radial equation is computed pointwise. For each gamma in , we have to compute a according to the condition . Here we use the Newton-Raphson method to determine . With the resulting vector , we can compute the solution (Equation (60)). All our calculations are performed with the help of the software MAPLE, including the numerical calculation of the - and -function and their derivatives.
Possible types of motion are bound orbits and escape orbits, which can also cross the horizons. The maximal analytic extension of the spacetime gives rise to an infinite set of universes or worlds, i.e., asymptotically flat regions, that are connected by intermediate regions delimited by horizons and by regions containing a singularity. Thus a particle can pass from one asymptotically flat region via an outer horizon into an intermediate region, from there via an inner horizon into a region with a singularity, leave again this region via an inner horizon, pass through another intermediate region, and then leave across an outer horizon into another asymptotically flat region. Such a two-world escape orbit is illustrated in Figure 1c. Here the first outer horizon represents a black hole horizon for the particle, whereas the second outer horizon is experienced by the particle as a white hole horizon, allowing it to leave the black hole it had entered. The Figure 1c does not distinguish between the universes, though, and identifies their spatial coordinates. Furthermore, the shape of the singularity (which varies from ring-like to three dimensional structures) allows some geodesics to pass the singularity and reach negative , that can be interpreted as reaching a universe with anti-gravity. The types of orbits around the rotating dyonic black hole are similar those in the Kerr-Newman-AdS spacetime.
4.3. Black Rings
In four dimensions the event horizon of a black hole is spherical, however, in higher dimension new topologies arise. In 2001 Emparan and Reall [65] presented a black hole solution with a topology of : the rotating black ring. A doubly spinning black ring with two independent angular momenta was found by Pomeransky and Sen’kov [66]. Elvang constructed a charged singly spinning black ring in 2003 [67] and soon after, Hoskisson presented a doubly spinning version of the charged black ring [68]. Exact solutions of the equations of motion were found in the singly spinning black ring spacetime [69] and the charged doubly spinning black ring spacetime [70].
The metric of a doubly spinning charged black ring can be written as
The metric functions read
The shape, mass and angular momenta of the black ring are represented by the parameters R, and , where and . The metric reduces to a singly spinning black ring for . The doubly spinning black ring possesses two independent angular momenta and thus the rotation is given by
with
The charge is described by the parameters
For and one obtaines an uncharged black ring.
The black ring metric is given in toroidal coordinates with , and . and are -periodic. The toroidal coordinates can be seen as two pairs of polar coordinates
with
, , , are four-dimensional Cartesian-like coordinates.
A ring-like curvature singularity is located at , light and particles cannot return from this area. At the metric has a coordinate singularity resulting in two horizons
If the angle is constant, the black ring horizon has a donut-like topology . On the other hand if is constant the horizon will look like two spheres.
To obtain the equations of motion for light and test particles in the five-dimensional spacetime of a charged doubly spinning black ring, we use the Hamilton-Jacobi formalism, see Section 2. The metric of the black ring and the Hamiltonian do not depend on the coordinates t, and and therefore three conserved momenta with the associated killing vector fields , and exist
The dot denotes a derivative with respect to the affine parameter .
In the Hamilton-Jacobi equation we need the non-vanishing components of the inverse metric
E is the energy of the particle and its angular momenta in - and -direction are and . In the x- and y-direction the conjugate momenta are:
It is useful to split the polynomials and into x- and y-parts
with
Having the three constants of motion E, and one can think of an ansatz to solve the Hamilton-Jacobi equation
Inserting everything into the Hamilton-Jacobi equation yields
In general Equation (87) does not seem to be separable. However, it can be separated in three cases:
- 1.
- : This special case describes zero energy null geodesics, which are realistic inside the ergoregion only.
- 2.
- : This case describes geodesics in the equatorial plane of the black ring, which is also the “axis” of rotation in -direction. The equatorial plane can be divided into two parts: The plane enclosed by the black ring and the plane around the black ring
- 3.
- : Here geodesics on the “axis” of rotation in -direction are considered. The case describes a plane between two spheres which represent the horizon of the black ring.
In the first case the Hamilton-Jacobi formalism yields five equations of motion, which are of elliptic type and can be solved in terms of the Weierstraß ℘-, - and -function. In the second and third case, the motion takes place in a plane and we get three equations of motion, which are of hyperelliptic type. Since the solution in the two planes of rotation is similar we will focus here on the case .
On the “axis” of -rotation, we have , and . Then the Hamilton-Jacobi equation depends on the coordinate x only
From this we get the derivative of the action S
and the ansatz for the action S in the Hamilton-Jacobi equation (see Section 2) becomes
Following the Hamilton-Jacobi formalism we set the partial derivatives of S with respect to the constants , E and to zero, which gives us three differential equations of motion
with
and
We also defined to simplify the equations of motion.
It is possible to solve the equations of motion (91)–(93) if is a polynomial, which happens in two cases
- 1.
- (which implies and ): This case represents the motion of photons or particles around an uncharged doubly spinning black ring.
- 2.
- : In this case the motion of photons around a charged doubly spinning black ring is described.
In both cases the equations of motion are of hyperelliptic type (genus ), since the polynomial is of 6th order.
The substitution , where is a zero of X, transforms X into a polynomial of order five and the x-Equation (91) becomes
A separation of variables yields the hyperelliptic integral
A resubstitution yields the full solution of (91)
where is the ith derivative of the -function and
with . is determined by the condition .
Next we will solve the -Equation (92) of the black ring. Using Equation (91) the -equation can be written as
The substitution and a partial fraction decomposition yields
The constants and the poles depend on the parameters of the black ring and the test particle.
The hyperelliptic integrals of the first kind are known from the solution of the x-Equation (91) and thus
and
where can be calculated in terms of the periods if is chosen to be a zero of .
The hyperelliptic integral of the third kind
can be solved with the solution Equation (30) in Section 3.
The complete solution of the -Equation (92) is
Analogously, the solution of the t-Equation (93) can be found.
Using the analytical solutions we can plot orbits in the black ring spacetime. Figure 2a shows an escape orbit in the equatorial plane () of the black ring. In Figure 2b a many-world bound orbit for light in the case is depicted. As discussed above for Figure 1c, also for this ring spacetime the maximal analytic extension consists of an infinite set of worlds, intermediate regions and regions with a singularity. A bound orbit of a particle that crosses both outer and inner horizons twice then emerges into another world, only to enter the black ring again, and repeat this whole process periodically. A bound orbit is shown in Figure 2c. In the black ring spacetime bound orbits only exist in the plane of -rotation (). Interestingly, in higher dimensional spherical black hole spacetimes, such as the higher dimensional Schwarzschild and Myers-Perry black holes, stable bound orbits are not possible. In the Myers-Perry spacetime stable bound orbits can only be found hidden behind the horizons. Therefore, the bound orbit in Figure 2c seems to be a particular feature of the black ring. We note, that Figure 2 illustrates orbits in the black ring spacetime by making use of different projections. Figure 2a,b suppress one spatial coordinate of the and retain the , whereas Figure 2c suppresses the while retaining the . Therefore the horizons look connected and ringlike in (a) and (b), whereas in (c) the horizon appears as two separate spheres.
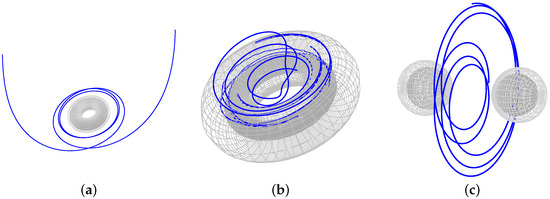
Figure 2.
Orbits of particles (blue curves) around the black ring. The horizons are depicted as grey tori or spheres. (a) Escape orbit in the equatorial plane (); (b) Many-world bound orbit in the case ; (c) Bound orbit in the plane of -rotation ().
5. Conclusions
Geodesic motion in black hole spacetimes is of utmost relevance for fundamental physics and astrophysics, as well as for technological applications. Since exact solutions of the differential equations provide arbitrary accuracy, they are the means of choice. Numerous black hole spacetimes allow for exact solutions, based on elliptic and hyperelliptic integrals. Whereas the elliptic case has been widely studied, hyperelliptic geodesic equations have received much less attention [43,47,48,49,50,51,52,64,71,72,73,74,75,76,77,78].
Here we have reviewed the general method for constructing solutions of hyperelliptic geodesic equations [51], and we have illustrated the method for the case with several examples: 9- and 11-dimensional Schwarzschild black holes, 4-dimensional supergravity black holes, and 5-dimensional black rings. Whereas numerous interesting spacetimes with hyperelliptic geodesic equations are still awaiting analysis, this is even more so for spacetimes with hyperelliptic equations [51,52].
However, in alternative theories of gravity also geodesic equations can arise, that are characterized by polynomials of the more general type
with polynomials of order m in x. For instance, in Hořava–Lifshitz black hole spacetimes [79,80,81] as well as Gauß–Bonnet black hole [82] spacetimes quartic equations of the form
arise. While in special cases such curves can be reduced to lower genera and the above methods become applicable [52], for the general set of geodesic equations so far only numerical analysis has been performed [83]. The extension of the above methods to obtain exact solutions also in such general cases remains a challenge to be tackled.
Author Contributions
S.G. has contributed the major part of the text and all of the figures, J.K. has contributed the remaining part of the text. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the DFG Research Training Group 1620.
Data Availability Statement
Data is available by request from the authors.
Acknowledgments
We are deeply grateful to our numerous collaborators on this subject over the years and, in particular, to the late Victor Enolski, to Valeria Diemer (née Kagramanova), Eva Hackmann, and Claus Lämmerzahl, who introduced us to this interesting topic.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ashby, N. Relativity in the Global Positioning System. Living Rev. Relativ. 2003, 6, 1–42. [Google Scholar] [CrossRef] [PubMed]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Oppenheimer, J.R.; Snyder, H. On Continued gravitational contraction. Phys. Rev. 1939, 56, 455–459. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett. 1965, 14, 57–59. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse: The role of general relativity. Riv. Nuovo Cim. 1969, 1, 252–276. [Google Scholar]
- Penrose, R. "Golden Oldie": Gravitational collapse: The role of general relativity. Gen. Rel. Grav. 2002, 34, 1141–1165. [Google Scholar] [CrossRef]
- Webster, B.L.; Murdin, P. Cygnus X-1-a Spectroscopic Binary with a Heavy Companion? Nature 1972, 235, 37–38. [Google Scholar] [CrossRef]
- Bolton, C.T. Dimensions of the Binary System HDE 226868 = Cygnus X-1. Nat. Phys. Sci. 1972, 240, 124–127. [Google Scholar] [CrossRef]
- Kormendy, J.; Richstone, D. Inward bound: The Search for supermassive black holes in galactic nuclei. Ann. Rev. Astron. Astrophys. 1995, 33, 581. [Google Scholar] [CrossRef]
- Eckart, A.; Genzel, R. Observations of stellar proper motions near the Galactic Centre. Nature 1996, 383, 415–417. [Google Scholar] [CrossRef]
- Ghez, A.M.; Klein, B.L.; Morris, M.; Becklin, E.E. High proper motion stars in the vicinity of Sgr A*: Evidence for a supermassive black hole at the center of our galaxy. Astrophys. J. 1998, 509, 678–686. [Google Scholar] [CrossRef]
- Celotti, A.; Miller, J.C.; Sciama, D.W. Astrophysical evidence for the existence of black holes: Topical review. Class. Quant. Grav. 1999, 16, A3. [Google Scholar] [CrossRef]
- Ferrarese, L.; Ford, H. Supermassive black holes in galactic nuclei: Past, present and future research. Space Sci. Rev. 2005, 116, 523–624. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Hagihara, Y. Theory of the Relativistic Trajectories in a Gravitational Field of Schwarzschild. Jpn. J. Astron. Geophys. 1931, 8, 67. [Google Scholar]
- Carter, B. Global structure of the Kerr family of gravitational fields. Phys. Rev. 1968, 174, 1559–1571. [Google Scholar] [CrossRef]
- Bardeen, J. Timelike and null geodesics in the Kerr metric. In Black Holes; DeWitt, C., DeWitt, B., Eds.; Gordon and Breach: New York, NY, USA, 1973; p. 215. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon Press: Oxford, UK, 1985. [Google Scholar]
- Perlick, V. Gravitational lensing from a spacetime perspective. Living Rev. Rel. 2004, 7, 9. [Google Scholar]
- Kraniotis, G.V. Periapsis and gravitomagnetic precessions of stellar orbits in Kerr and Kerr-de Sitter black hole spacetimes. Class. Quant. Grav. 2007, 24, 1775–1808. [Google Scholar] [CrossRef]
- Kagramanova, V.; Kunz, J.; Hackmann, E.; Lämmerzahl, C. Analytic treatment of complete and incomplete geodesics in Taub-NUT space-times. Phys. Rev. D 2010, 81, 124044. [Google Scholar] [CrossRef]
- Grunau, S.; Kagramanova, V. Geodesics of electrically and magnetically charged test particles in the Reissner-Nordström space-time: Analytical solutions. Phys. Rev. D 2011, 83, 044009. [Google Scholar] [CrossRef]
- Hackmann, E.; Hartmann, B.; Lämmerzahl, C.; Sirimachan, P. Test particle motion in the space-time of a Kerr black hole pierced by a cosmic string. Phys. Rev. D 2010, 82, 044024. [Google Scholar] [CrossRef]
- Kraniotis, G.V. Precise analytic treatment of Kerr and Kerr-(anti) de Sitter black holes as gravitational lenses. Class. Quant. Grav. 2011, 28, 085021. [Google Scholar] [CrossRef]
- Kagramanova, V.; Reimers, S. Analytic treatment of geodesics in five-dimensional Myers-Perry space–times. Phys. Rev. D 2012, 86, 084029. [Google Scholar] [CrossRef]
- Hackmann, E.; Xu, H. Charged particle motion in Kerr-Newmann space-times. Phys. Rev. D 2013, 87, 124030. [Google Scholar] [CrossRef]
- Diemer, V.; Smolarek, E. Dynamics of test particles in thin-shell wormhole spacetimes. Class. Quant. Grav. 2013, 30, 175014. [Google Scholar] [CrossRef]
- Diemer, V.; Kunz, J. Supersymmetric rotating black hole spacetime tested by geodesics. Phys. Rev. D 2014, 89, 084001. [Google Scholar] [CrossRef]
- Grunau, S.; Khamesra, B. Geodesic motion in the (rotating) black string spacetime. Phys. Rev. D 2013, 87, 124019. [Google Scholar] [CrossRef]
- Grenzebach, A.; Perlick, V.; Lämmerzahl, C. Photon Regions and Shadows of Kerr-Newman-NUT Black Holes with a Cosmological Constant. Phys. Rev. D 2014, 89, 124004. [Google Scholar] [CrossRef]
- Diemer, V.; Kunz, J.; Lämmerzahl, C.; Reimers, S. Dynamics of test particles in the general five-dimensional Myers-Perry spacetime. Phys. Rev. D 2014, 89, 124026. [Google Scholar] [CrossRef]
- Flathmann, K.; Grunau, S. Analytic solutions of the geodesic equation for Einstein-Maxwell-dilaton-axion black holes. Phys. Rev. D 2015, 92, 104027. [Google Scholar] [CrossRef]
- Kraniotis, G.V. Gravitational lensing and frame dragging of light in the Kerr-Newman and the Kerr-Newman-(anti) de Sitter black hole spacetimes. Gen. Rel. Grav. 2014, 46, 1818. [Google Scholar] [CrossRef]
- Kraniotis, G. Gravitational lensing and frame dragging of light in the Kerr-Newman and the Kerr-Newman-(anti) de Sitter black hole spacetimes. Proc. Sci. 2015, PLANCK2015, 073. [Google Scholar] [CrossRef]
- Paranjape, S.; Reimers, S. Dynamics of test particles in the five-dimensional, charged, rotating Einstein-Maxwell-Chern-Simons spacetime. Phys. Rev. D 2016, 94, 124003. [Google Scholar] [CrossRef]
- Grunau, S.; Neumann, H.; Reimers, S. Geodesic motion in the five-dimensional Myers-Perry-AdS spacetime. Phys. Rev. D 2018, 97, 044011. [Google Scholar] [CrossRef]
- Eickhoff, K.; Reimers, S. Dynamics of test particles in the five-dimensional Gödel spacetime. Phys. Rev. D 2018, 98, 044050. [Google Scholar] [CrossRef]
- Willenborg, F.; Grunau, S.; Kleihaus, B.; Kunz, J. Geodesic motion around traversable wormholes supported by a massless conformally-coupled scalar field. Phys. Rev. D 2018, 97, 124002. [Google Scholar] [CrossRef]
- Drawer, J.C.; Grunau, S. Geodesic motion around a supersymmetric AdS5 black hole. Eur. Phys. J. C 2020, 80, 536. [Google Scholar] [CrossRef]
- Baker, H.M. Abelian Functions: Abel’s Theorem and the Allied Theory of Theta Functions; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Kraniotis, G.V.; Whitehouse, S.B. Exact calculation of the perihelion precession of mercury in general relativity, the cosmological constant and jacobi’s inversion problem. Class. Quant. Grav. 2003, 20, 4817–4835. [Google Scholar] [CrossRef]
- Kraniotis, G.V. Precise relativistic orbits in Kerr and Kerr–(anti) de Sitter spacetimes. Class. Quant. Grav. 2004, 21, 4743–4769. [Google Scholar] [CrossRef]
- Kraniotis, G.V. Frame-dragging and bending of light in Kerr and Kerr-(anti) de Sitter spacetimes. Class. Quant. Grav. 2005, 22, 4391–4424. [Google Scholar] [CrossRef]
- Enolski, V.; Pronine, M.; Richter, P.H. Double Pendulum and θ-Divisor. J. Nonlinear Sci. 2003, 13, 157–174. [Google Scholar] [CrossRef]
- Hackmann, E.; Lämmerzahl, C. Complete Analytic Solution of the Geodesic Equation in Schwarzschild- (Anti-) de Sitter Spacetimes. Phys. Rev. Lett. 2008, 100, 171101. [Google Scholar] [CrossRef]
- Hackmann, E.; Lämmerzahl, C. Geodesic equation in Schwarzschild- (anti-) de Sitter space-times: Analytical solutions and applications. Phys. Rev. D 2008, 78, 024035. [Google Scholar] [CrossRef]
- Hackmann, E.; Kagramanova, V.; Kunz, J.; Lämmerzahl, C. Analytic solutions of the geodesic equation in higher dimensional static spherically symmetric space-times. Phys. Rev. D 2008, 78, 124018. [Google Scholar] [CrossRef]
- Hackmann, E.; Kagramanova, V.; Kunz, J.; Lämmerzahl, C. Analytic solutions of the geodesic equation in axially symmetric space-times. EPL 2009, 88, 30008. [Google Scholar] [CrossRef]
- Hackmann, E.; Lämmerzahl, C.; Kagramanova, V.; Kunz, J. Analytical solution of the geodesic equation in Kerr-(anti) de Sitter space-times. Phys. Rev. D 2010, 81, 044020. [Google Scholar] [CrossRef]
- Enolski, V.; Hackmann, E.; Kagramanova, V.; Kunz, J.; Lämmerzahl, C. Inversion of hyperelliptic integrals of arbitrary genus with application to particle motion in General Relativity. J. Geom. Phys. 2011, 61, 899–921. [Google Scholar] [CrossRef]
- Enolski, V.; Hartmann, B.; Kagramanova, V.; Kunz, J.; Lämmerzahl, C.; Sirimachan, P. Inversion of a general hyperelliptic integral and particle motion in Hořava–Lifshitz black hole space-times. J. Math. Phys. 2012, 53, 012504. [Google Scholar] [CrossRef]
- Walker, M.; Penrose, R. On quadratic first integrals of the geodesic equations for type [22] spacetimes. Commun. Math. Phys. 1970, 18, 265–274. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Schwarzschild field in n dimensions and the dimensionality of space problem. Nuovo Cim. 1963, 27, 636–651. [Google Scholar] [CrossRef]
- Myers, R.C.; Perry, M.J. Black Holes in Higher Dimensional Space-Times. Ann. Phys. 1986, 172, 304. [Google Scholar] [CrossRef]
- Frolov, V.P.; Stojkovic, D. Quantum radiation from a five-dimensional rotating black hole. Phys. Rev. D 2003, 67, 084004. [Google Scholar] [CrossRef]
- Frolov, V.P.; Stojkovic, D. Particle and light motion in a space-time of a five-dimensional rotating black hole. Phys. Rev. D 2003, 68, 064011. [Google Scholar] [CrossRef]
- Page, D.N.; Kubiznak, D.; Vasudevan, M.; Krtous, P. Complete integrability of geodesic motion in general Kerr-NUT-AdS spacetimes. Phys. Rev. Lett. 2007, 98, 061102. [Google Scholar] [CrossRef] [PubMed]
- Kubiznak, D.; Frolov, V.P. Hidden Symmetry of Higher Dimensional Kerr-NUT-AdS Spacetimes. Class. Quant. Grav. 2007, 24, F1–F6. [Google Scholar] [CrossRef]
- Matsutani, S.; Previato, E. Jacobi inversion on strata of the Jacobian of the Crs curve yr = f(x). J. Math. Soc. Jpn. 2008, 60, 1009–1044. [Google Scholar] [CrossRef]
- Ônishi, Y. Complex Multiplication Formulae for Hyperelliptic Curves of Genus Three. Tokyo J. Math. 1998, 21, 381–431. [Google Scholar] [CrossRef]
- Mumford, D. Tata Lectures on Theta, Vol. I and II; Birkhäuser: Boston, MA, USA, 1983. [Google Scholar]
- Chow, D.D.K.; Compère, G. Dyonic AdS black holes in maximal gauged supergravity. Phys. Rev. D 2014, 89, 065003. [Google Scholar] [CrossRef]
- Flathmann, K.; Grunau, S. Analytic solutions of the geodesic equation for U(1)2 dyonic rotating black holes. Phys. Rev. D 2016, 94, 124013. [Google Scholar] [CrossRef]
- Emparan, R.; Reall, H.S. A Rotating black ring solution in five-dimensions. Phys. Rev. Lett. 2002, 88, 101101. [Google Scholar] [CrossRef]
- Pomeransky, A.A.; Sen’kov, R.A. Black ring with two angular momenta. arXiv 2006, arXiv:hep-th/0612005. [Google Scholar]
- Elvang, H. A Charged rotating black ring. Phys. Rev. D 2003, 68, 124016. [Google Scholar] [CrossRef]
- Hoskisson, J. A Charged Doubly Spinning Black Ring. Phys. Rev. D 2009, 79, 104022. [Google Scholar] [CrossRef]
- Grunau, S.; Kagramanova, V.; Kunz, J.; Lämmerzahl, C. Geodesic Motion in the Singly Spinning Black Ring Spacetime. Phys. Rev. D 2012, 86, 104002. [Google Scholar] [CrossRef]
- Grunau, S.; Kagramanova, V.; Kunz, J. Geodesic Motion in the (Charged) Doubly Spinning Black Ring Spacetime. Phys. Rev. D 2013, 87, 044054. [Google Scholar] [CrossRef]
- García, A.; Hackmann, E.; Kunz, J.; Lämmerzahl, C.; Macías, A. Motion of test particles in a regular black hole space–time. J. Math. Phys. 2015, 56, 032501. [Google Scholar] [CrossRef]
- Hackmann, E.; Lämmerzahl, C.; Obukhov, Y.N.; Puetzfeld, D.; Schaffer, I. Motion of spinning test bodies in Kerr spacetime. Phys. Rev. D 2014, 90, 064035. [Google Scholar] [CrossRef]
- Hendi, S.H.; Tavakkoli, A.M.; Panahiyan, S.; Eslam Panah, B.; Hackmann, E. Simulation of geodesic trajectory of charged BTZ black holes in massive gravity. Eur. Phys. J. C 2020, 80, 524. [Google Scholar] [CrossRef]
- Grunau, S.; Kruse, M. Motion of charged particles around a scalarized black hole in Kaluza-Klein theory. Phys. Rev. D 2020, 101, 024051. [Google Scholar] [CrossRef]
- Soroushfar, S.; Saffari, R.; Kazempour, S.; Grunau, S.; Kunz, J. Detailed study of geodesics in the Kerr-Newman-(A)dS spacetime and the rotating charged black hole spacetime in f(R) gravity. Phys. Rev. D 2016, 94, 024052. [Google Scholar] [CrossRef]
- Hoseini, B.; Saffari, R.; Soroushfar, S.; Kunz, J.; Grunau, S. Analytic treatment of complete geodesics in a static cylindrically symmetric conformal spacetime. Phys. Rev. D 2016, 94, 044021. [Google Scholar] [CrossRef]
- Flathmann, K.; Wassermann, N. Geodesic equations for particles and light in the black spindle spacetime. J. Math. Phys. 2020, 61, 122504. [Google Scholar] [CrossRef]
- Chatterjee, A.K.; Flathmann, K.; Nandan, H.; Rudra, A. Analytic solutions of the geodesic equation for Reissner-Nordström–(anti–)de Sitter black holes surrounded by different kinds of regular and exotic matter fields. Phys. Rev. D 2019, 100, 024044. [Google Scholar] [CrossRef]
- Kehagias, A.; Sfetsos, K. The Black hole and FRW geometries of non-relativistic gravity. Phys. Lett. B 2009, 678, 123–126. [Google Scholar] [CrossRef]
- Lü, H.; Mei, J.; Pope, C.N. Solutions to Horava Gravity. Phys. Rev. Lett. 2009, 103, 091301. [Google Scholar] [CrossRef]
- Park, M. The Black Hole and Cosmological Solutions in IR modified Horava Gravity. JHEP 2009, 09, 123. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. String Generated Gravity Models. Phys. Rev. Lett. 1985, 55, 2656. [Google Scholar] [CrossRef] [PubMed]
- Enolskii, V.; Hartmann, B.; Kagramanova, V.; Kunz, J.; Lämmerzahl, C.; Sirimachan, P. Particle motion in Horava-Lifshitz black hole space-times. Phys. Rev. D 2011, 84, 084011. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).