Rough Semiring-Valued Fuzzy Sets with Application

Abstract

Many of the new fuzzy structures with complete $MV$-algebras as value sets, such as hesitant, intuitionistic, neutrosophic, or fuzzy soft sets, can be transformed into one type of fuzzy set with values in special complete algebras, called $AMV$-algebras. The category of complete $AMV$-algebras is isomorphic to the category of special pairs $(\mathcal{R},{\mathcal{R}}^{\ast })$ of complete commutative semirings and the corresponding fuzzy sets are called $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets. We use this theory to define $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations, lower and upper approximations of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets by $(\mathcal{R},{\mathcal{R}}^{\ast })$-relations, and rough $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets, and we show that these notions can be universally applied to any fuzzy type structure that is transformable to $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets. As an example, we also show how this general theory can be used to determine the upper and lower approximations of a color segment corresponding to a particular color.

1. Introduction

Rough set theory and fuzzy set theory represent two different approaches to the issue of vague, imprecise, inconsistent, and uncertain knowledge. The basic principle of fuzzy set theory for solving these problems is the possibility that the object has a given property to a certain degree. In contrast, rough set theory provides an opportunity to approximate concepts in the presence of incomplete information. It is therefore understandable that a new theory named fuzzy rough sets emerged very soon, which made it possible to combine both approaches. The foundations of this common theory were first presented in [1,2] and were further extended and applied in many other papers.

Over time, various generalizations and modifications of fuzzy sets have become increasingly common, such as intuitionistic fuzzy sets [3], hesitant fuzzy sets [4], neutrosophic fuzzy sets or fuzzy soft sets [5], Pythagorean fuzzy sets [6], and many others. As expected, soon after the introduction of these fuzzy structures, new variants of rough set theory made it possible to approximate the concepts expressed using these new fuzzy structures. For example, intuitionistic fuzzy rough sets [7,8], soft rough fuzzy sets [9], hesitant fuzzy rough sets [10] or rough neutrosophic sets [11], and many other variants of these hybrid structures. Given the way these hybrid structures were created, it is not surprising that in many cases there are several variants that define these structures. To illustrate it, let us give at least an example of different definitions of soft fuzzy rough sets in [9,12].

Another typical feature of these hybrid structures is that many similar properties of these new hybrid structures are individually proven for each new hybrid system, despite the fact that for many hybrid structures there are common proofs of these properties.

In our previous paper [13], we tried to unify the constructions of certain classes of new fuzzy structures, namely fuzzy structures with the complete $MV$-algebra as a set of values. The key assumption of all these constructions was the fact that they all relate to standard L-fuzzy sets, i.e., mappings $X\to L$. Although many of the new L-fuzzy structures are traditionally called L-fuzzy sets, where L is the lattice of the given type, these structures are, in fact, $M(L)$-fuzzy sets, where M is a functor from the category of lattices L to (sometimes) another category of lattices. For example, if L is the complete $MV$-algebra and if we consider L-fuzzy soft sets in space $(X,K)$, where X is the basic set and K is the set of criteria, a L-fuzzy soft set is a mapping $X\to M(L)$, where $M(L)=\{(E,\psi ):E\subseteq K,\psi \in L^K\}\subseteq L^K$ (see [13]).

The transformation of the new L-fuzzy structure $\mathcal{F}$ into the $M_{\mathcal{F}}(L)$-fuzzy sets presented in [13] was based on the use of pairs $(\mathcal{R},{\mathcal{R}}^{\ast })$ of commutative idempotent semirings with the same underlying set R and with the self-inverse isomorphism $\neg :\mathcal{R}\to {\mathcal{R}}^{\ast }$. The advantage of this construction of the ordered structure $M_{\mathcal{F}}(L)$ is, among other things, that the pair $(\mathcal{R},{\mathcal{R}}^{\ast })$ explicitly defines pairs of some dual constructions, standardly used in the theory of L-fuzzy sets. Examples of such constructions are the upper and lower approximations of L-fuzzy set defined by the L-fuzzy relations, the upper and lower F-transforms of L-fuzzy sets defined by fuzzy partitions, or upper and lower monads defined by power set operators. In these cases, one type of the pair of transformations is defined by semiring $\mathcal{R}$ and the other by semiring ${\mathcal{R}}^{\ast }$. This creates a precondition for a better understanding of the relationship between the values $M_{\mathcal{F}}(L)$ of the new fuzzy structures $\mathcal{F}$ and these constructs.

On the other hand, the ordered structure defined by the pair $(\mathcal{R},{\mathcal{R}}^{\ast })$ of semirings is relatively confusing and difficult to compare with other ordered structures used in fuzzy set theory. Therefore, in the first part of this paper, we will focus on the simplification of the ordered structure defined by the pair $(\mathcal{R},{\mathcal{R}}^{\ast })$ of semirings and on its equivalent definition in the form of a standard algebraic system with axioms. This modified ordered structure will be called the almost $MV$-algebra (or simply, $AMV$-algebra), and we will show that the $AMV$-algebras are equivalently defined by the dual pairs of semirings. The corresponding fuzzy sets will be called $AMV$-fuzzy sets. Therefore, we can say that any $AMV$-fuzzy set is also defined by the dual pair of semirings. This will make it easier to compare this structure with other lattices used in fuzzy set theory. Namely, we present an example showing that this $AMV$-algebra is not, in general, the $MV$-algebra. In the paper, we use both equivalent definitions to work with $AMV$-fuzzy sets.

In the next part of the paper, we focus on another construction that is commonly used in L-fuzzy sets, namely the issue of rough L-fuzzy sets. The main goal of this paper is to show how the theory of $AMV$-fuzzy sets can be used to unify the rough set theory for various L-fuzzy structures, currently used mainly in applications.

The contributions of the paper are the following:

• we present how to use $AMV$-fuzzy sets to define the general notion of a $AMV$-fuzzy relation and how this notion can be transformed to variants of fuzzy relations in new fuzzy structures;
• we define the notion of the upper and lower approximations of $AMV$-fuzzy sets defined by $AMV$-fuzzy relations and we present properties of these approximations;

and that brings the following advantages:

• the notion of rough $AMV$-fuzzy sets can be universally applied to any fuzzy structure that is transformable to $AMV$-fuzzy sets;
• the properties of rough $AMV$-fuzzy sets can be directly transferred to the analogous properties of these new rough fuzzy structures without new proofs;
• using dual semiring structures $(\mathcal{R},{\mathcal{R}}^{\ast })$, new types of $AMV$-fuzzy sets and their rough sets can be introduced. The properties of these new rough structures will copy the properties of the general $AMV$-rough sets.

The structure of this paper is as follows. In Section 2, we recall some basic definitions and properties related to dual pairs of semirings $(\mathcal{R},{\mathcal{R}}^{\ast })$, the definition of the $AMV$-algebra and its basic properties, the notion of the $AMV$-fuzzy set in a set X, and the definitions of basic operations with $AMV$-fuzzy sets. Most of these notions were first published in our previous paper [13] as properties of dual pairs of semirings $(\mathcal{R},{\mathcal{R}}^{\ast })$.

In Section 3, we present several examples of dual pairs of semirings. Although some of these examples were presented in our previous paper [13], we recall the basic definitions of these examples because they will be used later in the paper. We also present some examples of new fuzzy structures that can be transformed into $AMV$-fuzzy sets.

In Section 4, we deal with rough $AMV$-fuzzy sets defined by $AMV$-fuzzy relations. We introduce the notions of lower and upper approximations of $AMV$-fuzzy sets defined by $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations, and we present some basic properties of these constructions. We investigate some relationships between fuzzy relations of some fuzzy structures and $AMV$-fuzzy relation and show how to transform rough sets of some fuzzy structures into rough $AMV$-fuzzy sets. We also present several relationships among dual pairs of semirings associated with existing fuzzy structures and investigate relationships between two types of categories with approximations as objects on the one hand and two types of $AMV$-relations as objects on the other hand. We prove that all these categories are isomorphic, which makes it possible to significantly simplify the research of these approximations in arbitrary fuzzy structures that are transformable into $AMV$-fuzzy sets.

In Section 5, we present two examples of applications of rough $AMV$-fuzzy sets, namely, we show how the variants of rough fuzzy soft sets and rough intuitionistic fuzzy sets defined by rough $AMV$-fuzzy sets can be used to determine the lower and upper approximations of the color segment corresponding to a particular color in a color image.

2. Methods and Basic Structures

In this section, we introduce the basic definitions and properties of a new lattice structure, called $AMV$-algebra and we show that these structures can be equivalently defined by dual pairs of semirings, introduced in [13]. This structure represents the main tool that enables unifying the theory of some of the new fuzzy structures, including intuitionistic, hesitant, neutrosophic, or soft fuzzy sets with values in a complete $MV$-algebra, including their mutual combinations. We also introduce the notion of $AMV$-fuzzy sets and basic operations with these fuzzy sets.

The basic algebraic structure we use in this paper, the complete $AMV$-algebra, is defined by the following definition.

Definition 1.

The complete $AMV$-algebra is the algebra $(R,+,\times ,\neg ,0,1)$ of type $(2,2,1,0,0)$ defined by

1.

$(R,+,0)$ is the complete idempotent commutative monoid, the sum of elements from $S\subseteq R$ is denoted by ${\sum }_{r\in S}r$,

2.

$(R,\times ,1)$ is a commutative monoid,

3.

$\neg :R\to R$ is the involution mapping, $\neg 0=1$,

4.

$(\forall x,y_i\in R,i\in I),x\times {\sum }_i{y}_i={\sum }_i(x\times y_i)$,

5.

$(\forall x\in R),x\times 0=0$,

6.

If for $x,y\in R$, we set $x{+}^{\ast }y:=\neg (\neg x+\neg y),x{\times }^{\ast }y:=\neg (\neg x\times \neg y)$, then for $x,y,z,y_i\in R$,

(a)

$(x{+}^{\ast }y=y)\iff (x+y=x)$,

(b)

$x{\times }^{\ast }{\sum }_i{y}_i={\sum }_i(x{\times }^{\ast }{y}_i)$,

(c)

$x+(y{+}^{\ast }z)=(x+y){+}^{\ast }(x+z)$.

In the following lemma, we present the basic properties of the complete $AMV$-algebra.

Lemma 1.

Let $\mathcal{R}=(R,+,\times ,\neg ,0,1)$ be the complete $AMV$-algebra. Then $\mathcal{R}$ has the following properties.

1.

The relation ≤ defined by

$$x,y\in R,x\le y\iff x+y=y$$

is an order relation on R,

2.

$(R,\le )$ is the complete lattice, where for arbitrary $S\subseteq R$,

$$supS=\bigvee S=\sum _{x\in S}x,infS=\bigwedge S=\sum _{x\in S}^{\ast }x,$$

where ${\sum }_{x\in S}^{\ast }s$ is the sum of elements with respect to ${+}^{\ast }$.

3.

$(R,\le ,\times ,\neg )$ is the complete Girard monoid.

Remark 1.

Whenever we talk about the $AMV$-algebra $(R,+,\times ,\neg ,0,1)$, by the symbols $\le ,\vee ,\wedge$ we will understand the ordering relation and lattice operations defined in the Lemma 1.

Let us consider the following two examples, where in the first example we show that complete $MV$-algebras are $AMV$-algebras, and in the other example we show that the opposite implication is not true, i.e., the $AMV$-algebra is not the $MV$-algebra, in general.

Example 1.

Let $(L,\otimes ,\neg ,1)$ be the complete $MV$-algebra (see, e.g., [14]). Recall that the following operations can be defined in any $MV$-algebra for elements $x,y,z\in L$:

$$\begin{array}{c}x\oplus y:=\neg (\neg x\otimes \neg y),x\vee y:=(x\oplus \neg y)\otimes y,x\wedge y:=(x\otimes \neg y)\oplus y,0:=\neg 1.\end{array}$$

(1)

An $MV$-algebra is called complete if $(L,\vee ,\wedge ,0,1)$ is a complete lattice.

Let the operation + on L be defined by $x+y=x\vee y$. Then $\mathcal{L}=(L,+,\otimes ,\neg ,0,1)$ is the complete $AMV$-algebra.

Example 2.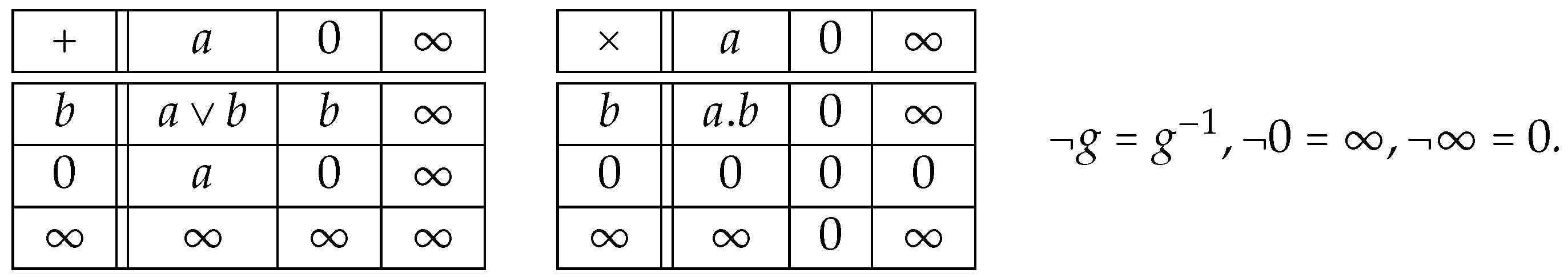

Recall (see, e.g., [15]) that an abelian lattice ordered group (l-group, in short) is a commutative group $(G,.)$ with distributive lattice operations $\vee ,\wedge$ which are compatible with the group multiplication, that is, the following identities hold for elements from G:

$$\begin{array}{c}a·(b\wedge c)=a·b\wedge a·c,a·(b\vee c)=a·b\vee a·c,\\ {(a\vee b)}^{-1}=a^{-1}\wedge b^{-1},{(a\wedge b)}^{-1}=a^{-1}\vee b^{-1},\\ a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c),a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c).\end{array}$$

Let 0 and ∞ be new elements added to G and let the order relation on G be extended to the order relation on $G\cup \{0,\infty \}$ such that $0<g<\infty$, for arbitrary $g\in G$. Let the structure $\mathcal{G}=(G\cup \{0,\infty \},+,\times ,\neg ,0)$ be defined by

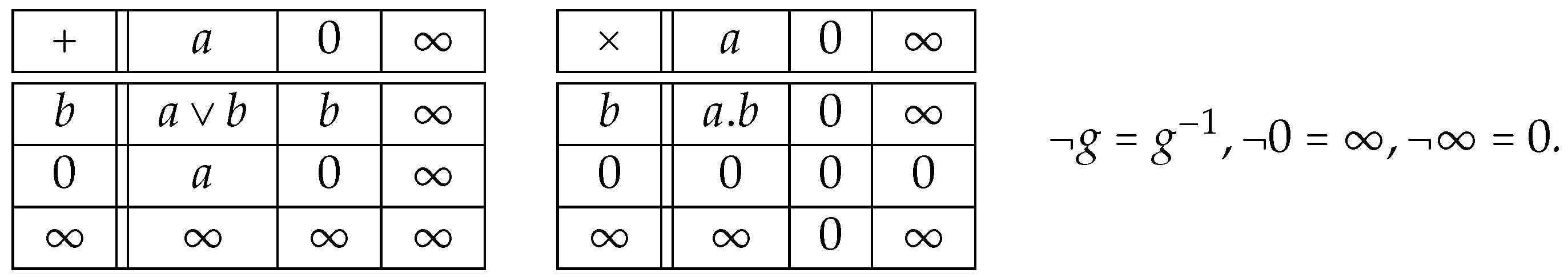
Then $\mathcal{G}=(G\cup \{0,\infty \},+,\times ,\neg ,0)$ is the complete $AMV$-algebra, but $(G\cup \{0,\infty \},\times ,\neg ,1)$ is not the corresponding $MV$-algebra. In fact, according to (1), if $\mathcal{G}$ is the $MV$-algebra, the ordering in $\mathcal{G}$ should be such that $a\vee b=(a\oplus \neg b)\times b$, where $a\oplus b=\neg (\neg a\times \neg b)$. If $a<b$ in ordering in the l-group G, we have $b=a\vee b=(a\oplus \neg b)\otimes b=a$, a contradiction. Therefore, $\mathcal{G}$ is not $MV$-algebra.

The basic structure with which we will work with is the $AMV$-fuzzy set. Although this notion has not yet been used, implicitly it occurs very often, especially in connection with new fuzzy structures, such as intuitionistic, neutrosophic, or fuzzy soft sets, which are currently objects of considerable interest. In our previous paper [13] we proved that these $MV$-valued structures are the so-called $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets. In the next part, we show that $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets are equivalent to $AMV$-fuzzy sets.

Definition 2.

Let $\mathcal{R}=(R,+,\times ,\neg ,0,1)$ be the $AMV$-algebra. Let X be a set.

1.

A mapping $s:X\to R$ is called the $\mathcal{R}$-fuzzy set in X.

2.

Operations with $\mathcal{R}$-fuzzy sets are defined by

(a)

The intersection $s\sqcap t$ is defined by $(s\sqcap t)(x)=s(x)\wedge t(x)$, $x\in X$,

(b)

The union $s\bigsqcup t$ is defined by $(s\bigsqcup t)(x)=s(x)\vee t(x)$, $x\in X$,

(c)

The complement $\neg s$ is defined by $(\neg s)(x)=\neg (s(x))$,

(d)

The external multiplication ⋆ by elements of R is defined by

$(a\star s)(x)=a\times s(x)$,

(e)

The order relation ≤ between $s,t$ is defined by $s\le t\iff (\forall x\in X)s(x)\le t(x)$.

In the following proposition, some basic properties of operations with $AMV$-fuzzy sets are summarized.

Proposition 1.

Let $\mathcal{R}=(R,+,\times ,\neg ,0,1)$ be the $AMV$-algebra. Let X be a set and $s,t,w$ be $\mathcal{R}$-fuzzy sets. Then the following statements are valid.

1.

$s\sqcap s=s,s\bigsqcup s=s$,

2.

$s\sqcap t\le s$, $s\le s\bigsqcup t$,

3.

$s\sqcap t\le s\bigsqcup t$,

4.

$s\sqcap (t\bigsqcup w)=(s\sqcap t)\bigsqcup (s\sqcap w)$,

5.

$s\bigsqcup (t\sqcap w)=(s\bigsqcup t)\sqcap (s\bigsqcup w)$,

6.

$a\star (t\bigsqcup w)=(a\star t)\bigsqcup (a\star w)$,

7.

$a\star (t\sqcap w)=(a\star t)\sqcap (a\star w)$,

8.

$\neg (s\bigsqcup t)=\neg s\sqcap \neg t$, $\neg (s\sqcap t)=\neg s\bigsqcup \neg t$,

9.

$s\le t\Rightarrow s\bigsqcup w\le t\bigsqcup w,s\sqcap w\le t\sqcap w$,

10.

$s⊑(t\sqcap t^{\prime })=(s⊑t){+}^{\ast }(s⊑t^{\prime })$.

Proof. 

The proof is a simple transcription of the properties of $\mathcal{R}$ from Definition 1 and will be omitted. □

As we mentioned in the introduction, the $AMV$-algebra can be equivalently defined using a pair of commutative idempotent semirings, among which there is an involutive isomorphism. As redundant as this definition may seem, it becomes especially useful in situations where each of these semirings defines a different type of operations that are dual in some way. Typical examples of such constructions are, for example, upper and lower approximations of fuzzy sets using fuzzy relations or lower and upper F-transforms. Since the main results of this paper relate to a pair of such transformations, namely rough $AMV$-fuzzy sets, we will use this variant of the definition of the $AMV$-algebra in the following text. In the next part, we recall the definition of the dual pair of semirings $(\mathcal{R},{\mathcal{R}}^{\ast })$ and we show that $AMV$-fuzzy sets and $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets are identical structures, and for both these structures we use the name $AMV$-fuzzy sets only.

To recall the definition of dual pairs of semirings, we repeat the definition of the commutative idempotent semiring.

Definition 3

([16,17]). An idempotent complete commutative semiring $\mathcal{R}=(R,+,\times ,0,1)$ (or, shortly, a semiring) is an algebraic structure with the following properties:

• $(R,+,0)$ is a complete idempotent commutative monoid,
• $(R,\times ,1)$ is a commutative monoid,
• $x\times {\sum }_{i\in I}{y}_i={\sum }_{i\in I}(x\times y_i)$ holds for all $x,y_i\in R$,
• $0\times x=0$ holds for all $x\in R$.

A semiring $\mathcal{R}$ is called ordered semiring, if there exists an order relation ≤ on R such that the following conditions hold for all $a,b,c\in R$:

$$\begin{array}{c}a\ge 0,a\le b\Rightarrow (a+c\le b+c,a\times c\le b\times c).\end{array}$$

The notion of a semiring homomorphism is defined as a standard homomorphism between algebraic structures.

We introduce the simplified version of the dual pair of semirings $(\mathcal{R},{\mathcal{R}}^{\ast })$ which was introduced in [13].

Definition 4.

Let $\mathcal{R}=(R,+,\times ,0,1)$ and ${\mathcal{R}}^{\ast }=(R,{+}^{\ast },{\times }^{\ast },0^{\ast },1^{\ast })$ be complete idempotent commutative semirings with the same underlying set R. The pair $(\mathcal{R},{\mathcal{R}}^{\ast })$ is called the dual pair of semirings if there exists a semiring isomorphism $\neg :\mathcal{R}\to {\mathcal{R}}^{\ast }$ and the following statements hold:

1.

$\neg :\mathcal{R}\to {\mathcal{R}}^{\ast }$ is the involutive isomorphism,

2.

$\forall a\in R,S\subseteq Ra{\times }^{\ast }({\sum }_{b\in S}b)={\sum }_{b\in S}(a{\times }^{\ast }b)$,

3.

$\forall a\in R,S\subseteq Ra+({\sum }_{b\in S}^{\ast }b)={\sum }_{b\in S}^{\ast }(a+b)$, where ${\sum }^{\ast }$ is the addition operation in ${\mathcal{R}}^{\ast }$,

4.

$\forall a,b\in R,a+b=a\iff a{+}^{\ast }b=b.$

Using the isomorphism ¬, it is easy to see that the following dual statements also hold for arbitrary dual pair of semirings $(\mathcal{R},{\mathcal{R}}^{\ast })$:

2’.

$\forall a,\in R,S\subseteq R,a\times {\sum }_{b\in S}^{\ast }b={\sum }_{b\in S}^{\ast }(a\times b)$,

3’.

$\forall a,\in R,S\subseteq R,a{+}^{\ast }{\sum }_{b\in S}b={\sum }_{b\in S}(a{+}^{\ast }b)$.

Remark 2.

Whenever in the next part of the paper we talk about a dual pair of semirings $(\mathcal{R},{\mathcal{R}}^{\ast })$, we always understand the pair of semirings with operations from Definition 4. If necessary, instead of ∑ and ${\sum }^{\ast }$ we use ${\sum }^{\mathcal{R}}$ and ${\sum }^{{\mathcal{R}}^{\ast }}$, respectively.

We prove that a dual pair of semirings $(\mathcal{R},{\mathcal{R}}^{\ast })$ defines the unique $AMV$-algebra and, conversely, any $AMV$-algebra defines the unique dual pair of semirings $(\mathcal{R},{\mathcal{R}}^{\ast })$. To do this, we need to define the category of $AMV$-algebras and the category of dual pairs of semirings.

Definition 5.

The category $\mathbf{APSem}$ of dual pairs of semirings is defined by

1.

Objects $((\mathcal{R},{\mathcal{R}}^{\ast }),{\neg }_{\mathcal{R}})$ are dual pairs $(\mathcal{R},{\mathcal{R}}^{\ast })$ of semirings with involutive isomorphism ${\neg }_{\mathcal{R}}:\mathcal{R}\to {\mathcal{R}}^{\ast }$,

2.

Morphisms $((\mathcal{R},{\mathcal{R}}^{\ast }),{\neg }_{\mathcal{R}})\to ((\mathcal{S},{\mathcal{S}}^{\ast }),{\neg }_{\mathcal{S}})$ are mappings between underlying sets $\phi :R\to S$, such that

(a)

$\phi :\mathcal{R}\to \mathcal{S}$ and $\phi :{\mathcal{R}}^{\ast }\to {\mathcal{S}}^{\ast }$ are homomorphisms of semirings.

(b)

The identity ${\neg }_{\mathcal{S}}.\phi =\phi .{\neg }_{\mathcal{R}}$ holds.

(c)

The compositions of the morphisms are the standard compositions of the mappings.

Definition 6.

The category $\mathbf{RAlg}$ of complete $AMV$-algebras is defined by

1.

Objects are $AMV$-algebras $\mathcal{R}=(R,+,\times ,\neg ,0,1)$,

2.

Morphisms $\psi :(R,+,\times ,\neg ,0,1)\to (S,{+}_1,{\times }_1,{\neg }_1,0_1,1_1)$ are mappings $\psi :R\to S$ such that for all $x,y\in R$,

(a)

$\psi (x+y)=\psi (x){+}_1\psi (y)$,

(b)

$\psi (x\times y)=\psi (x){\times }_1\psi (y)$,

(c)

$\psi (\neg x)={\neg }_1(\psi (x))$,

(d)

$\psi (0)=0_1,\psi (1)=1_1$.

The relationship between $\mathbf{RAlg}$ and $\mathbf{APSem}$ is described in the following theorem.

Theorem 1.

The categories $\mathbf{APSem}$ and $\mathbf{RAlg}$ are isomorphic.

Proof. 

We define the functor $F:\mathbf{RAlg}\to \mathbf{APSem}$. Let $\mathcal{A}=(R,+,\times ,\neg ,0,1)$ be object of $\mathbf{RAlg}$. We set $F(\mathcal{A})=((\mathcal{R},{\mathcal{R}}^{\ast }),\neg )$, where $\mathcal{R}=(R,+,\times ,0,1)$, ${\mathcal{R}}^{\ast }=(R,{+}^{\ast },{\times }^{\ast },1,0)$, and operations ${+}^{\ast },{\times }^{\ast }$ are defined by

$$x{+}^{\ast }y=\neg (\neg x+\neg y),x{\times }^{\ast }y=\neg (\neg x\times \neg y).$$

It is easy to see that $((\mathcal{R},{\mathcal{R}}^{\ast }),\neg )$ is the object of $\mathbf{APSem}$ and if $\psi$ is a morphism of $\mathbf{RAlg}$, then $\psi =F(\psi )$ is also a morphism in $\mathbf{APSem}$. The functor $F^{-1}:\mathbf{APSem}\to \mathbf{RAlg}$ is defined so that for an object $((\mathcal{R},{\mathcal{R}}^{\ast }),\neg )$ we set $F^{-1}((\mathcal{R},{\mathcal{R}}^{\ast }),\neg )=(R,+,\times ,\neg ,0,1)$ and for a morphism $\phi$ in $\mathbf{APSem}$ we set $F^{-1}(\phi )=\phi$. It is easy to see that $F^{-1}$ is the functor and F and $F^{-1}$ are mutually inverse. □

Remark 3.

From Theorem 1 it follows that if $\mathcal{A}$ is a $AMV$-algebra, the $\mathcal{A}$-fuzzy set can be equivalently called the $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy set, where $F(\mathcal{A})=((\mathcal{R},{\mathcal{R}}^{\ast }),\neg )$. We use this terminology of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets in the remainder of the paper. The power set of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets will be denoted by ${(\mathcal{R},{\mathcal{R}}^{\ast })}^X$.

3. Examples of Dual Pairs of Semirings

In this section, we present several examples of dual pairs of semirings. Because we use two of these examples in the application section, we repeat them, although they were published in [13]. All these examples are used to demonstrate the possibility to transform many new $MV$-valued fuzzy structures to $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets, including their basic operations. In addition, we show that by using appropriate $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets, we can also derive another new type of fuzzy structure.

Examples 3–5 (which we recall from [13] and which will be used later) illustrate how the power sets of $MV$-valued intuitionistic, neutrosophic, or fuzzy soft sets in a set X can be isomorphically transformed into power sets of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets, including basic operations with these structures. This makes it possible to create a basis for the unified theory for these types of fuzzy structures, and it is not necessary to define and prove the properties of individual constructions within these new fuzzy structures. In Example 6, using the neutrosophic fuzzy soft sets, introduced in [18], we show how the power sets of hybrid combinations of these new fuzzy structures can also be transformed into power sets of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets in a set X. The last two examples are devoted to new types of fuzzy sets, based on extensional fuzzy sets, or fuzzy sets with values in extensions of abelian lattice-ordered groups.

On the other hand, as we briefly mentioned in the introduction, for some new fuzzy structures, the operations with these structures are defined in several variants, or in a non-standard way in comparison with classical fuzzy sets. An example can be hesitant fuzzy sets, where ∩ and ∪ operations are defined so that the set of hesitant fuzzy sets is not a distributive lattice (see, e.g., [4]). This greatly complicates operations with these structures and also complicates applications. Because the power set ${(\mathcal{R},{\mathcal{R}}^{\ast })}^X$ is a distributive lattice with respect to operations ⊓ and ⊔, the power set of the hesitant fuzzy sets cannot be isomorphically transformed to ${(\mathcal{R},{\mathcal{R}}^{\ast })}^X$ without changing the definition of ∪ and ∩ of the hesitant fuzzy sets.

Example 3

([13]).

1.

The semiring ${\mathcal{R}}_1=(R_1,{+}_1,{\times }_1,0_1,1_1)$ is defined by

(a)

$R_1=\{(\alpha ,\beta )\in L^2:\neg \alpha \ge \beta \}\subseteq L^2$,

(b)

$(\alpha ,\beta ){+}_1({\alpha }_1,{\beta }_1):=(\alpha \vee {\alpha }_1,\beta \wedge {\beta }_1)$,

(c)

$(\alpha ,\beta ){\times }_1({\alpha }_1,{\beta }_1):=(\alpha \otimes {\alpha }_1,\beta \oplus {\beta }_1)$,

(d)

$0_1=(0_L,1_L),1_1=(1_L,0_L)$,

2.

The semiring ${\mathcal{R}}_1^{\ast }=(R,{+}^{\ast },{\times }^{\ast },0^{\ast },1^{\ast })$ is defined by

(a)

$(\alpha ,\beta ){+}_1^{\ast }({\alpha }_1,{\beta }_1):=(\alpha \wedge {\alpha }_1,\beta \vee {\beta }_1)$,

(b)

$(\alpha ,\beta ){\times }_1^{\ast }({\alpha }_1,{\beta }_1):=(\alpha \oplus {\alpha }_1,\beta \otimes {\beta }_1)$,

(c)

$0_1^{\ast }=(1_L,0_L),1_1^{\ast }=(0_L,1_L)$,

Let ${\neg }_1:{\mathcal{R}}_1\to {\mathcal{R}}_1^{\ast }$ be defined by

$$(\alpha ,\beta )\in R_1,{\neg }_1(\alpha ,\beta )=(\beta ,\alpha ).$$

Then $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$ is the dual pair of semirings, ${\neg }_1$ is the self-inverse semiring isomorphism and the algebraic system $(J(X),\cap ,\cup ,\neg ,\le )$ of all intuitionistic L-fuzzy sets is isomorphic to $(R_1^X,\sqcap ,\bigsqcup ,\neg ,\le )$.

Example 4

([13]).

1.

Let K be the fixed set of criteria. The semiring ${\mathcal{R}}_2=(R_2,{+}_2,{\times }_2,0_2,1_2)$ is defined by

(a)

$R_2=\{(E,\psi ):E\subseteq K,\psi \in L^K\}\subseteq L^K$, where $(E,\psi )\in L^K$ is defined by

$$k\in K,(E,\psi )(k)=\left\{\begin{array}{cc}\psi (k),\hfill & k\in E,\hfill \\ 0_L,\hfill & k\notin E\hfill \end{array}\right..$$

(b)

$(E,\phi ),(F,\psi )\in R_2$, $(E,\phi ){+}_2(F,\psi ):=(E\cap F,\phi \vee \psi )$, where $\phi \vee \psi$ is the supremum in $L^K$,

(c)

$(E,\phi ),(F,\psi )\in R_2$, $(E,\phi ){\times }_{2}F,\psi )=(E\cap F,\phi \times \psi )$, where $\phi \times \psi \in L^K$ is defined by $\phi \times \psi (k)=\phi (k)\otimes \psi (k)$,

(d)

$0_2=(K,{\underline{0}}_L)$, $1_2=(K,{\underline{1}}_L)$, where $\underline{\alpha }(k)=\alpha$ for arbitrarily $k\in K$, $\alpha \in L$.

2.

The semiring ${\mathcal{R}}_2^{\ast }=(R_2,{+}_2^{\ast },{\times }_2^{\ast },0_2^{\ast },1_2^{\ast })$ is defined by

(a)

$(E,\phi ),(F,\psi )\in R_2$, $(E,\phi ){+}_2^{\ast }(F,\psi ):=(E\cap F,\phi \wedge \psi )$, where $\phi \wedge \psi$ is the infimum in $L^K$,

(b)

$(E,\phi ),(F,\psi )\in R_2$, $(E,\phi ){\times }_2^{\ast }(F,\psi )=(E\cap F,\phi \oplus \psi )$, where ⊕ in $L^K$ is defined component-wise.

(c)

$0_2^{\ast }=(K,{\underline{1}}_L)$, $1_2^{\ast }=(K,{\underline{0}}_L)$, where $\underline{\alpha }(k)=\alpha$ for arbitrary $k\in K$, $\alpha \in L$.

Let ${\neg }_2:{\mathcal{R}}_2\to {\mathcal{R}}_2^{\ast }$ be defined by

$$(E,\psi )\in R_2,{\neg }_2(E,\psi )=(E,\neg \psi ),$$

where $\neg \psi$ is defined componentwise. Then $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$ is the dual pair of semirings, ${\neg }_2$ is the self-inverse semiring isomorphism and the algebraic system $(S(X),\cap ,\cup ,\neg ,\le )$ of all L-fuzzy soft sets in X is isomorphic to $(R_2^X,\sqcap ,\bigsqcup ,\neg ,\le )$.

Example 5

([13]).

1.

The semiring ${\mathcal{R}}_3=(R_3,{+}_3,{\times }_3,0_3,1_3)$ is defined by

(a)

$R_3=L^3$,

(b)

$(\alpha ,\beta ,\gamma ){+}_3({\alpha }_1,{\beta }_1,{\gamma }_1):=(\alpha \vee {\alpha }_1,\beta \wedge {\beta }_1,\gamma \wedge {\gamma }_1)$,

(c)

$(\alpha ,\beta ,\gamma ){\times }_3({\alpha }_1,{\beta }_1,{\gamma }_1):=(\alpha \otimes {\alpha }_1,\beta \wedge {\beta }_1,\gamma \oplus {\gamma }_1)$,

(d)

$0_3=(0_L,1_L,1_L),1_3=(1_L,1_L,0_L)$.

2.

The semiring ${\mathcal{R}}_3^{\ast }=(R_3,{+}_3^{\ast },{\times }_3^{\ast },0_3^{\ast },1_3^{\ast })$ is defined by

(a)

$(\alpha ,\beta ,\gamma ){+}_3^{\ast }({\alpha }_1,{\beta }_1,{\gamma }_1):=(\alpha \wedge {\alpha }_1,\beta \vee {\beta }_1,\gamma \vee {\gamma }_1)$,

(b)

$(\alpha ,\beta ,\gamma ){\times }_3^{\ast }({\alpha }_1,{\beta }_1,{\gamma }_1):=(\alpha \oplus {\alpha }_1,\beta \vee {\beta }_1,\gamma \otimes {\gamma }_1)$,

(c)

$0_3^{\ast }=(1_L,0_L,0_L),1_3^{\ast }=(0_L,0_L,1_L)$.

Let ${\neg }_3:{\mathcal{R}}_3\to {\mathcal{R}}_3^{\ast }$ be defined by

$$(\alpha ,\beta ,\gamma )\in R_3,{\neg }_3(\alpha ,\beta ,\gamma )=(\gamma ,\neg \beta ,\alpha ).$$

Then $({\mathcal{R}}_3,{\mathcal{R}}_3^{\ast })$ is the dual pair of semirings, ${\neg }_3$ is the self-inverse semiring isomorphism and the algebraic system $(N(X),\cap ,\cup ,\neg ,\le )$ of all neutrosophic L-fuzzy sets in X is isomorphic to $(R_3^X,\sqcap ,\bigsqcup ,\neg ,\le )$.

Example 6.

Recall the definition of the neutrosophic L-fuzzy soft set ([18]). Let K be the fixed set of criteria, and let X be a set. Using the notation of Examples 4 and 5, the neutrosophic L-fuzzy soft set in a set X is a pair $(E,s)$, where $E\subseteq K$ and $s:K\to {\mathcal{R}}_3^X$ is such that $s(k)={\underline{0}}_{{\mathcal{R}}_3}$, if $k\in K\setminus E$, where ${\underline{0}}_{{\mathcal{R}}_3}:X\to {\mathcal{R}}_2$ is a constant function with the value $0_{{\mathcal{R}}_3}$. We set

$$\begin{array}{c}{\mathcal{R}}_4={\mathcal{R}}_3^K,{\mathcal{R}}_4^{\ast }={({\mathcal{R}}_3^{\ast })}^K,\end{array}$$

and let the semiring operations in ${\mathcal{R}}_4$ and ${\mathcal{R}}_4^{\ast }$ be defined point-wise from the operations in ${\mathcal{R}}_3$ and ${\mathcal{R}}_3^{\ast }$, respectively.

Let the mapping ${\neg }_4:{\mathcal{R}}_4\to {\mathcal{R}}_4^{\ast }$ be defined by

$$\begin{array}{c}f\in {\mathcal{R}}_4,k\in K,{\neg }_4(f)(k)={\neg }_3(f(k)).\end{array}$$

It is easy to see that $({\mathcal{R}}_4,{\mathcal{R}}_4^{\ast })$ is the dual pair of semirings and ${\neg }_4$ is the self-inverse isomorphism. We show that there exists an isomorphism between the algebraic structure $(NS(X),\cup ,\cap ,\neg ,\le )$ of all neutrosophic L-fuzzy soft sets in a set X with operations $\cup ,\cap ,\neg$ defined in [19] and algebraic structure $({\mathcal{R}}_4^X,\bigsqcup ,\sqcap ,\neg ,\le )$.

In fact, let us define the map $\Gamma :NS(X)\to {\mathcal{R}}_4^X={({\mathcal{R}}_3^K)}^X$ by

$$\begin{array}{c}(E,s)\in NS(X),x\in X,k\in K,\Gamma (E,s)(x)(k)=\left\{\begin{array}{cc}s(k)(x)\in {\mathcal{R}}_3,\hfill & k\in E,\hfill \\ 0_{{\mathcal{R}}_3},\hfill & k\in K\setminus E.\hfill \end{array}\right.\end{array}$$

Γ is the surjective map. In fact, for $f\in {\mathcal{R}}_4^X$, we set

$$\begin{array}{c}x\in X,E_x=\{k\in K:f(x)(k)\ne 0_{{\mathcal{R}}_3}\},\\ E=\bigcup _{x\in X}{E}_x,s:K\to {\mathcal{R}}_3^X,\\ k\in K,x\in X,s(k)(x)=\left\{\begin{array}{cc}f(x)(k),\hfill & k\in E_x,\hfill \\ 0_{{\mathcal{R}}_3},\hfill & k\in K\setminus E_x.\hfill \end{array}\right.\end{array}$$

It follows that $\Gamma (E,s)=f$ and it is easy to see that Γ is the isomorphism and the algebraic system $(NS(X),\cap ,\cup ,\neg ,\le )$ of all neutrosophic L-fuzzy soft sets in X is isomorphic to $(R_4^X,\sqcap ,\bigsqcup ,\neg ,\le )$.

The following example of dual pair of semirings will be used in the next section to demonstrate examples of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations.

Example 7.

Let L be the complete $MV$-algebra and let Ω be a set with the fuzzy equivalence relation $\delta :\Omega \times \Omega \to L$. An L-fuzzy set $f\in L^{\Omega }$ is called δ-extensional if

$$\forall x,y\in X,f(x)\otimes \delta (x,y)\le f(y).$$

For arbitrary $g\in L^{\Omega }$, the extensional hull $\overline{g}$ of g is defined by $\overline{g}(x)={\bigvee }_{t\in \Omega }g(t)\otimes \delta (t,x)$. Let us consider the following structures.

1.

Let ${\mathcal{R}}_5=(R_5,{+}_5,{\times }_5,0_5,1_5)$ be defined by

(a)

$R_5=\{f\in L^{\Omega }:f$ is δ-extensional},

(b)

$f,g\in R_5,f{+}_{5}g=f\vee g$, where ∨ is the supremum in $L^{\Omega }$,

(c)

$f,g\in R_5,f{\times }_{5}g=\overline{f\otimes g}$, where ⊗ is defined point-wise,

(d)

$0_5(x)=0_L,1_5(x)=1_L$, for arbitrary $x\in \Omega$.

2.

Let ${\mathcal{R}}_5^{\ast }=(R_5,{+}_5^{\ast },{\times }_5^{\ast },0_5^{\ast },1_5^{\ast })$ be defined by

(a)

$f,g\in R_5,f{+}_5^{\ast }g=f\wedge g$,

(b)

$f,g\in R_5,f{\times }_5^{\ast }g=\overline{(f\oplus g)}$, where $f\oplus g$ is defined point-wise,

(c)

$0_5^{\ast }=1_5,1_5^{\ast }=0_5$.

Let ${\neg }_5:{\mathcal{R}}_5\to {\mathcal{R}}_5^{\ast }$ be defined by

$$f\in R_5,{\neg }_5(f)=\neg f, \mathit{defined} \mathit{point}-\mathit{wise}$$

Then, $({\mathcal{R}}_5,{\mathcal{R}}_5^{\ast })$ is the dual pair of semirings and ${\neg }_5$ is the self-inverse isomorphism. It should be observed that this example is correct because the negation $\neg f$ of an extensional L-fuzzy set is also extensional, as follows from the inequality

$$\neg f(y)\to \neg f(x)=f(x)\to f(y)\ge \delta (x,y).$$

Example 8.

Let $\mathcal{G}$ be the $AMV$-algebra of Example 2. Using this example and Theorem 1, we can introduce the dual pair $(\mathcal{G},{\mathcal{G}}^{\ast })$ of semirings. The corresponding $(\mathcal{G},{\mathcal{G}}^{\ast })$-fuzzy sets can be called l-group-valued fuzzy sets. One of the features of these l-group-valued fuzzy sets is that elements from $\{g\in G:g\ge 1_G\}$ are membership degrees describing property "to be in F" and elements from $\{g\in G:g\le 1_G\}$- are membership degrees of the property "not to be in F". In that case, the element $1_G$ is in the special position, which corresponds to the element $0.5$ in $[0,1]$-fuzzy sets. This is in contrast to classical L-fuzzy sets, where the values of L can simultaneously describe the membership degrees of both properties.

The relationship between dual pairs $(\mathcal{R},{\mathcal{R}}^{\ast })$ of semirings and algebraic systems $(R^X,\sqcap ,\bigsqcup ,\neg \le )$ of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets can be described by a functor between the category $\mathbf{APSem}$ defined in Definition 5 and the following category of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets.

Definition 7.

The category $\mathbf{ASSem}$ of algebraic systems of $AMV$-fuzzy sets is defined by

1.

Objects are all algebraic systems ${(\mathcal{R},{\mathcal{R}}^{\ast })}^X=(R^X,\bigsqcup ,\sqcap ,\neg ,\le )$ of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets in a set X.

2.

Morphisms from ${(\mathcal{R},{\mathcal{R}}^{\ast })}^X$ to ${(\mathcal{S},{\mathcal{S}}^{\ast })}^Y$ are mappings $R^X\to S^Y$ which are standard homomorphisms of algebraic systems.

3.

The composition of morphisms is the standard composition of mappings.

The following proposition describes the relationship between dual pairs of semirings and algebraic systems of $AMV$-fuzzy sets.

Proposition 2.

Let ${\mathbf{Set}}^{op}$ be the dual category of the category $\mathbf{Set}$ of sets. There exists the functor

$$F:\mathbf{APSem}\times {\mathbf{Set}}^{op}\to \mathbf{ASSem}.$$

Proof. 

Let $((\mathcal{R},{\mathcal{R}}^{\ast }),\neg ,X)$ be an object of the product category $\mathbf{APSem}\times {\mathbf{Set}}^{op}$. We set $H((\mathcal{R},{\mathcal{R}}^{\ast }),\neg ,X)={(\mathcal{R},{\mathcal{R}}^{\ast })}^X\in \mathbf{ASSem}$ and for a morphism $(\phi ,u):((\mathcal{R},{\mathcal{R}}^{\ast }),{\neg }_R,X)\to ((\mathcal{S},{\mathcal{S}}^{\ast }),{\neg }_S,Y)$ in this product category, we define $H(\phi ,u):{(\mathcal{R},{\mathcal{R}}^{\ast })}^X\to {(\mathcal{S},{\mathcal{S}}^{\ast })}^Y$ by

$$\begin{array}{c}f\in R^X,y\in Y,H(\phi ,u)(f)(y)=\phi .f.u(y).\end{array}$$

Then $H(\phi ,u)$ is the morphism in the category $\mathbf{ASSem}$. In fact, let $f,g\in R^X$ and $y\in Y$. We have

$$\begin{array}{c}H(\phi ,u)(f{\bigsqcup }_{R}g)(y)=\phi ·(f{\bigsqcup }_{R}g)·u(y)=\phi (f·u(y){+}_{R}g·u(y))=\\ \phi ·f·u(y){+}_S\phi ·f·u(y)=\left(H(\phi ,u)(f){\bigsqcup }_{S}H(\phi ,u)(g)\right)(y),\\ H(\phi ,u)(f{\sqcap }_{R}g)(y)=\phi ·(f{\sqcap }_{R}g)·u(y)=\phi (f·u(y){+}_R^{\ast }g·u(y))=\\ \phi ·f·u(y){+}_S^{\ast }\phi ·f·u(y)=\left(H(\phi ,u)(f){\sqcap }_{S}H(\phi ,u)(g)\right)(y),\\ H(\phi ,u)({\neg }_{R}f)(y)=\phi ·({\neg }_{R}f)·u(y)=\phi ({\neg }_R(f·u(y)))={\neg }_S(\phi ·f·u(y))={\neg }_{R}H(\phi ,u)(f)(y).\end{array}$$

□

From Proposition 2, it follows that any morphism $\phi :((\mathcal{R},{\mathcal{R}}^{\ast }),{\neg }_R)\to ((\mathcal{S},{\mathcal{S}}^{\ast }),{\neg }_S)$ between objects of $\mathbf{APSem}$ can be extended to the morphism ${(\mathcal{R},{\mathcal{R}}^{\ast })}^X\to {(\mathcal{S},{\mathcal{S}}^{\ast })}^Y$ between the corresponding algebraic systems of these dual pairs. Examples of morphisms from the category $\mathbf{APSem}$ that are based on examples from this section are presented below.

Example 9.

Let $(L^{\vee },L^{\wedge })=F(\mathcal{L})$, where $\mathcal{L}$ is the $AMV$-algebra of Example 1.

1.

The morphism ${\phi }_1:((L^{\vee },L^{\wedge }),\neg )\to (({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast }),{\neg }_1)$ is defined by

$$\alpha \in L,\phi (\alpha )=(\alpha ,\neg \alpha )\in R_1.$$

2.

The morphism ${\phi }_2:((L^{\vee },L^{\wedge }),\neg )\to (({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast }),{\neg }_2)$ is defined by

$$\alpha \in L,{\phi }_2(\alpha )=(K,\underline{\alpha })\in R_2,$$

where $\underline{\alpha }\in L^K$ is the constant function with the value α.

3.

The morphism ${\phi }_3:(({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast }),{\neg }_1)\to (({\mathcal{R}}_4,{\mathcal{R}}_4^{\ast }),{\neg }_4)$ is defined by

$$(\alpha ,\beta )\in R_1,{\phi }_3(\alpha ,\beta )=(\alpha ,0_L,\beta )\in R_4.$$

In fuzzy set theory, the category $L(X)$ of L-fuzzy sets in a set X is well known, where morphisms $u:f\to g$ between two fuzzy sets $f,g\in L^X$ are defined as mappings $u:X\to X$, such that $g.u(x)\ge f(x)$ for all $x\in X$. Analogically, we can define the category $\$(X)$ of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets in a set X. Therefore, $L^X$ is not only the set of all fuzzy sets in X, it is also a category.

Definition 8.

Let X be a set, and $(\mathcal{R},{\mathcal{R}}^{\ast })$ be an dual pair of semirings. The category ${(\mathcal{R},{\mathcal{R}}^{\ast })}^X$ of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets in a set X is defined by

1.

Objects are $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets in X, i.e., mappings $f:X\to R$.

2.

The morphisms from an object f to the object g are mappings $u:X\to X$, such that

$$f(x)\le g.u(x),$$

where ≤ is the order relation defined in the Lemma 1.

3.

The composition of morphisms is the composition of mappings.

For illustration, we present some examples of functors between categories ${(\mathcal{R},{\mathcal{R}}^{\ast })}^X$ for various dual pairs of semirings.

Example 10.

Let X be a set. The following functors exist among the corresponding categories.

$$\begin{array}{ccccc} & & {({\mathcal{R}}_3, {\mathcal{R}}_3^{\ast })}^X& & {({\mathcal{R}}_2, {\mathcal{R}}_2^{\ast })}^X\\ & & J\downarrow \uparrow M& & P\uparrow \\ {({\mathcal{R}}_2, {\mathcal{R}}_2^{\ast })}^X& \stackrel{F}{\leftarrow }& {(L^{\vee },L^{\wedge })}^X& \underset{N}{\overset{G}{\rightleftarrows }}& {({\mathcal{R}}_1, {\mathcal{R}}_1^{\ast })}^X\end{array}$$

We show how these functors are defined.

(1) Let $f,g:X\to R_3$ be objects of ${({\mathcal{R}}_3,{\mathcal{R}}_3^{\ast })}^X$ and let $u:f\to g$ be a morphism in this category. For $x\in X$, let $f(x)=(f_1,f_2,f_3)$, $g(u(x))=(g_1,g_2,g_3)$. The functor J is defined by

$$x\in X,J(f)(x)=f_1\oplus \neg f_2\oplus \neg f_3.$$

Because for arbitrary $x\in X$, $f(x){\le }_{3}g.u(x)$, we obtain $J(f)(x)=f_1\oplus \neg f_2\oplus \neg f_3\le g_1\oplus \neg g_2\oplus \neg g_3=J(g)(x)$ and it follows that $J(u)=u$ is also the morphism in ${(L^{\vee },L^{\wedge })}^X$. Therefore, J is a functor.

(2) Let $f,g:X\to R_1$ be objects of ${(L^{\vee },L^{\wedge })}^X$ and let $u:f\to g$ be a morphism in this category. The functor M is defined by

$$x\in X,M(f)(x)=(f(x),0_L,\neg f(x)),M(u)=u.$$

Because for arbitrary $x\in X$, $f(x)\le gu(x)$, we obtain $M(f)(x){\le }_{3}M(g)(u(x)$ and it follows that $M(u)=u$ is also the morphism in ${({\mathcal{R}}_3,{\mathcal{R}}_3^{\ast })}^X$. Therefore, M is a functor.

(3) Let $f,g:X\to L$ be objects of ${(L^{\vee },L^{\wedge })}^X$ and let $u:f\to g$ be a morphism in this category. The functor G is defined by

$$x\in X,G(f)(x)=(f(x),\neg f(x))\in R_1,G(u)=u.$$

Because for arbitrary $x\in X$, $f(x){\le }_{L}g.u(x)$, we obtain $(f(x),\neg f(x)){\le }_1(g(u(x)),\neg g(u(x)))$ and it follows that $G(u)=u$ is also the morphism in ${({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })}^X$. Therefore, G is a functor.

(4) Let $f,g:X\to L$ be objects of ${(L^{\vee },L^{\wedge })}^X$ and let $u:f\to g$ be a morphism in this category. The functor F is defined by

$$x\in X,F(f)(x)=(K,\underline{f(x)}),J(u)=u,$$

where $\underline{f(x)}:K\to L$ is the constant function with the value $f(x)$ for all $k\in K$. Because for arbitrary $x\in X$, $f(x){\le }_{L}g.u(x)$, we obtain $(K,\underline{f(x)}){\le }_2(K,\underline{g(u(x))})$ and it follows that $F(u)=u$ is also the morphism in ${({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })}^X$. Therefore, F is a functor.

(5) Let $f,g:X\to R_1$ be objects of ${({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })}^X$ and let $u:f\to g$ be a morphism in this category. For $x\in X$, we set $f(x)=({\alpha }_x,{\beta }_x),g(u(x))=({\alpha }_x^{\prime },{\beta }_x^{\prime })\in R_1$. The functor N is defined by

$$x\in X,N(f)(x)={\alpha }_x\oplus \neg {\beta }_x,H(u)=u.$$

Because for arbitrary $x\in X$, $({\alpha }_x,{\beta }_x){\le }_1({\alpha }_x^{\prime },{\beta }_x^{\prime })$, we obtain ${\alpha }_x\oplus \neg {\beta }_x{\le }_L{\alpha }_x^{\prime }\oplus \neg {\beta }_x^{\prime }$ and it follows that $H(u)=u$ is also the morphism in ${(L^{\vee },L^{\wedge })}^X$. Therefore, N is a functor.

(6) Let $f,g:X\to R_1$ be objects of ${({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })}^X$ and let $u:f\to g$ be a morphism in this category. For $x\in X$, we set $f(x)=({\alpha }_x,{\beta }_x),g(u(x))=({\alpha }_x^{\prime },{\beta }_x^{\prime })\in R_1$. Let $k_1,k_2\in K$ be fixed elements. The functor P is defined by

$$\begin{array}{c}x\in X,P(f)(x)=(E_x,s_x),E_x=\{k_1,k_2\}\subseteq K,s_x:K\to L,\\ s_x(k)=\left\{\begin{array}{cc}{\alpha }_x,\hfill & k=k_1,\hfill \\ \neg {\beta }_x,\hfill & k=k_2,\hfill \\ 0_L,\hfill & k\in K\setminus \{k_1,k_2\}.\hfill \end{array}\right.\end{array}$$

Let $P(g.u)(x)=(E_x^{\prime },s_x^{\prime })$. Because for arbitrary $x\in X$, $({\alpha }_x,{\beta }_x){\le }_1({\alpha }_x^{\prime },{\beta }_x^{\prime })$, we obtain $(E_x,s_s){\le }_3(E_x^{\prime },s_x^{\prime })$ and it follows that $P(u)=u$ is also the morphism in ${({\mathcal{R}}_3,{\mathcal{R}}_3^{\ast })}^X$. Therefore, P is a functor.

4. Rough $(\mathcal{R},{\mathcal{R}}^{\ast })$-Fuzzy Sets

As we mentioned in the introduction, our goal in this paper is to define the theory of rough fuzzy structures, which could be applied to the new $MV$-fuzzy structures in such a way that these applications will respect the existing rough fuzzy sets in these structures. For this goal, we use results from the previous part, namely the fact that important parts of new fuzzy structures can be expressed as the $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets.

In this section, we define the theory of rough $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets and use that theory to unify the theory of rough fuzzy structures of new fuzzy sets which can be expressed as $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets for some dual pairs of semirings. Similar to classical fuzzy rough sets, this rough $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy set theory will be based on the notion of the $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy binary relation.

4.1. $(\mathcal{R},{\mathcal{R}}^{\ast })$-Fuzzy Relations

We start this section with the definition of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations and we present some basic properties of these relations. Recall that we use the notation and operations from Definitions 4 and 2. Recall that by $(\mathcal{R},{\mathcal{R}}^{\ast })$ we understand the semirings $\mathcal{R}=(R,+,\times ,0_R,1_R)$ and ${\mathcal{R}}^{\ast }=(R,{+}^{\ast },{\times }^{\ast },0_R^{\ast },1_R^{\ast })$.

Definition 9.

Let $(\mathcal{R},{\mathcal{R}}^{\ast })$ be the dual pair of semirings with the self-inverse isomorphism ¬ and let X be a set.

1.

By the $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relation in a set X we understand a $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy set $T:X\times X\to R$ in the Cartesian product $X\times X$.

2.

An $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relation T in X is called a

(a)

reflexive, if for arbitrary $x\in X$, $T(x,x)=1_R$,

(b)

symmetric, if for arbitrary $x,y\in X$, $T(x,y)=T(y,x)$,

(c)

transitive, if for arbitrary $x,y,z\in X$, $T(x,y)\times T(y,z)\le T(x,z)$,

(d)

equivalence if it is reflexive, transitive, and symmetric.

Similarly to classical fuzzy relations, we can define operations for the $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations.

Definition 10.

Let $S,T$ be $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations in a set X.

1.

The composition of S and T is the $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relation $T\circ S(x,z)={\sum }_{y\in X}S(x,y)\times T(y,z)$ for arbitrary $x,z\in X$.

2.

The dual composition of S and T is defined by $T{\circ }^{\ast }S(x,z)={\sum }_{y\in X}^{\ast }S(x,y){\times }^{\ast }T(y,z)$.

3.

The negation $\neg T$ of T is defined by $(\neg T)(x,y):=\neg (T(x,y))$.

4.

$S⪯T$ iff $\forall x,y\in X,S(x,y)\le T(x,y)$ and $S{⪯}^{\ast }T$ iff $\forall x,y\in X,S(x,y){\le }^{\ast }T(x,y)$ hold, where ≤ is defined in Lemma 1 and $x{\le }^{\ast }y\iff y\le x$.

Some basic properties of these operations are mentioned in the following lemma.

Lemma 2.

Let $T,\{S_i:i\in I\}$ be $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations in X. The following statements hold.

1.

$T\circ ({⨆}_{i\in I}{S}_i)={⨆}_{i\in I}(T\circ S_i),T{\circ }^{\ast }({\sqcap }_{i\in I}{S}_i)={\sqcap }_{i\in I}(T{\circ }^{\ast }{S}_i)$

2.

$T\circ S=\neg (\neg T{\circ }^{\ast }\neg S),T{\circ }^{\ast }S=\neg (\neg T\circ \neg S)$

3.

$S⪯S^{\prime }\Rightarrow T\circ S⪯T\circ S^{\prime }$, $T{\circ }^{\ast }S⪯T{\circ }^{\ast }{S}^{\prime }$

The proof follows directly from the properties of operations in the dual pair of semirings, and will be omitted.

Because our main goal is to show the possibility of using the theory of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy rough sets in other fuzzy structures, $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations should comprise the existing fuzzy relations in these new fuzzy structures. It should be mentioned that, for some fuzzy structures, there exist several variants of definitions of relations. An example of this situation can be fuzzy soft sets, where there are several variants of the definition of fuzzy soft relations. For example, see Definition 3.1 in [20], where the fuzzy soft relation is defined between two fuzzy soft sets, and Definition 6 in [21], where the fuzzy soft relation is defined between two fuzzy soft spaces $(K,X)$ and $(K,Y)$.

For an illustration of relationships between L-fuzzy relations in new fuzzy structures and $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations, we show that $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy relations in a set X are isomorphic to L-fuzzy soft relations in a soft space $(K,X)$ defined in [21], and $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy relations are identical to intuitionistic L-fuzzy relations with composition defined in [22,23].

Proposition 3.

1.

Let $(\mathcal{S}(X\times X),⊠)$ be the monoid of all L-fuzzy soft relations in a set X with the composition ⊠ of fuzzy soft set relations defined in [21], and let $(R_2^{X\times X},\circ )$ be the monoid of all $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy relations in X with composition ∘. Then these monoids are isomorphic, i.e.,

$$(\mathcal{S}(X\times X),⊠)\cong (R_2^{X\times X},\circ ).$$

2.

Let $(\mathcal{J}(X\times X),⊠)$ be the monoid of all intuitionistic L fuzzy relations in a set X with the composition ⊠ of intuitionistic relations defined in [22], and let $(R_1^{X\times X},\circ )$ be the monoid of all $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy relations in X with the composition ∘. Then we have

$$(\mathcal{J}(X\times X),⊠)=(R_1^{X\times X},\circ ).$$

Proof. 

(1) If $(K,X)$ is a fuzzy soft space, then a fuzzy soft relation in $(K,X)$ (in the variant according to [21]; Definition 6) is a fuzzy soft set $(E,T)$ in a set $X\times X$, that is, $E\subseteq K$, $T:K\to L^{X\times X}$ and $(E,T):X\times X\to L^K$ is defined by

$$k\in K,(x,x^{\prime })\in X\times X,(E,T)(x,x^{\prime })(k)=\left\{\begin{array}{cc}T(k)(x,x^{\prime }),\hfill & k\in E,\hfill \\ 0_L,\hfill & k\in K\setminus E.\hfill \end{array}\right.$$

We define a mapping $\Psi :S(X\times X)\to R_2^{X\times X}$ such that for $(E,T)\in \mathcal{S}(X\times X)$, $\Psi (E,T):=\mathcal{T}$, where $\mathcal{T}:X\times X\to R_2$ is defined by

$$\begin{array}{c}(x,x^{\prime })\in X\times X,\mathcal{T}(x,x^{\prime }):=(E,{\psi }_{x{x}^{\prime }})\in R_2,\end{array}$$

(2)

$$\begin{array}{c}{\psi }_{x{x}^{\prime }}:K\to L,{\psi }_{x{x}^{\prime }}(k):=T(k)(x,x^{\prime }),\end{array}$$

(3)

$$\begin{array}{c}(E,{\psi }_{x{x}^{\prime }})(k)=\left\{\begin{array}{cc}{\psi }_{x{x}^{\prime }}(k),\hfill & k\in E,\hfill \\ 0_L,\hfill & k\in K\setminus E.\hfill \end{array}\right.\end{array}$$

(4)

It follows that $(E,T)(x,x^{\prime })(k)=\Psi (E,T)(x,x^{\prime })(k)$. In contrast, let $\mathcal{T}\in R_2^{X\times X}$ and let $\mathcal{T}(x,x^{\prime })=(E_{x{x}^{\prime }},{\tau }_{x{x}^{\prime }})\in R_2$ for arbitrary $(x,x^{\prime })\in X\times X$. We set $E={\bigcup }_{(x,x^{\prime })\in X\times X}{E}_{x{x}^{\prime }}$ and define the mapping $S:K\to L^{X\times X}$ by

$$\begin{array}{c}k\in K,(x,x^{\prime })\in X\times X,S(k)(x,x^{\prime })=\left\{\begin{array}{cc}{\tau }_{x{x}^{\prime }}(k),\hfill & k\in E_{x{x}^{\prime }}\hfill \\ 0_L,\hfill & k\in K\setminus E_{x{x}^{\prime }}.\hfill \end{array}\right.\end{array}$$

Then $(E,S)\in \mathcal{S}(X\times X)$ and we have $(E,S)(x,x^{\prime })(k)=(E,{\tau }_{x{x}^{\prime }})(k)=\mathcal{T}(x,x^{\prime })(k)$. Therefore, we can put ${\Psi }^{-1}(\mathcal{T})=(E,S)$ and it is clear that $\Psi :\mathcal{S}(X\times X)\to R_2^{X\times X}$ is the bijection. Finally, we show that

$$\Psi ((E,T)⊠(F,S))=\Psi (E,T)\circ \Psi (F,S).$$

Let $\Psi (E,T)=\mathcal{T},\Psi (F,S)=\mathcal{S}$, where, according to the previous part of the proof, $\mathcal{S}(x,x^{\prime })=(E,{\psi }_{x{x}^{\prime }}),\mathcal{T}(y,y^{\prime })=(F,{\tau }_{y{y}^{\prime }})$ satisfies the corresponding conditions (2), (3), and (4), i.e., ${\psi }_{x{x}^{\prime }}=S(k)(x,x^{\prime })$ and ${\tau }_{y{y}^{\prime }}(k)=T(k)(y,y^{\prime })$. The composition ⊠ of L-fuzzy soft relations is defined by $(E,T)⊠(F,S)=(E\cap F,T\diamond S)$, where

$$\begin{array}{c}k\in K,x,z\in X,T\diamond S(k)(x,x^{\prime })=\underset{y\in X}{\bigvee }S(k)(x,y)\otimes T(k)(y,z),\\ (E\cap F,T\diamond S)(x,x^{\prime })(k)=\left\{\begin{array}{cc}T\diamond S(k)(x,x^{\prime }),\hfill & k\in E\cap F,\hfill \\ 0_L,\hfill & k\in K\setminus E\cap F.\hfill \end{array}\right.\end{array}$$

For arbitrarily $x,z\in X,k\in K$, according to Definition 10, we obtain

$$\begin{array}{c}\Psi (E,T)\circ \Psi (F,S)(x,z)(k)=\mathcal{T}\circ \mathcal{S}(x,z)(k)=\\ (\sum _{y\in X}^{{\mathcal{R}}_2}\mathcal{S}(x,y){\times }_2\mathcal{T}(y,z))(k)=(\sum _{y\in X}^{{\mathcal{R}}_2}(E,{\psi }_{xy}{\times }_{2}F,{\tau }_{yz}))(k)=(\sum _{y\in X}^{{\mathcal{R}}_2}(E\cap F,{\psi }_{xy}\otimes {\tau }_{yz}))(k)=\\ (E\cap F,\underset{y\in X}{\bigvee }{\psi }_{xy}\otimes {\tau }_{yz})(k)=\left\{\begin{array}{cc}\underset{y\in X}{\bigvee }{\psi }_{xy}(k)\otimes {\tau }_{yz}(k),\hfill & k\in E\cap F\hfill \\ 0_L,\hfill & k\in K\setminus E\cap F\hfill \end{array}\right.=\\ (E\cap F,{\sigma }_{xz})(k)=\Psi (E\cap F,T\diamond S)(x,z)(k)=\Psi ((E,T)⊠(F,S))(x,z)(k),\end{array}$$

where ${\sigma }_{xz}(k)=T\diamond S(k)(x,z)$. Therefore, $\Psi$ is the isomorphism.

(2) Recall that by the intuitionistic L-fuzzy relation in X we understand the intuitionistic L-fuzzy set in $X\times X$. For $(t,s)\in \mathcal{J}(X\times X)$ and arbitrary $(x,x^{\prime })\in X\times X$ we have $(t,s)(x,x^{\prime })=(t(x,x^{\prime }),s(x,x^{\prime }))$, where $\neg t(x,x^{\prime })\ge s(x,x^{\prime })$ and it follows that $(s,t)(x,x^{\prime })\in R_1$. Therefore, $(s,t)$ can be identified with the $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy set $X\times X\to R_1$. The rest follows directly from Proposition 2. □

As another example, we show a fuzzy relation that can be transformed to the $({\mathcal{R}}_5,{\mathcal{R}}_5^{\ast })$-fuzzy relation.

Example 11.

If we want to specify how two elements $x,y\in X$ correspond to some fuzzy relation Q, that is, to determine the value $Q(x,y)$, under certain conditions, this value depends on the observation points $\alpha \in \Omega$, the points $x,y$ are observed. For the correct determination of the value of $Q(x,y)$, it should be assumed that if the positions of two observation points are similar, the observed values of the relation Q should also be close. Therefore, instead of the fuzzy relation $Q:X\times X\to L$, there is the fuzzy relation $Q^{\prime }:X\times X\times \Omega \to L$, where Ω is the set of observation points. This approach was first discussed by A. Šostak in [24], where he introduced the concept of many-level L-fuzzy relations. We show that these structures can be transformed into $({\mathcal{R}}_5,{\mathcal{R}}_5^{\ast })$-fuzzy relations. To do this, we first specify this notion more precisely.

Definition 11.

Let X be a set, and let $(\Omega ,\rho )$ be a set with the L-fuzzy equivalence relation ρ. The L-fuzzy relation $Q:X\times X\times \Omega \to L$ is called the Ω-level L-fuzzy relation, if the following holds:

$$\begin{array}{c}x,y\in X,\alpha ,\beta \in \Omega ,Q(x,y,\alpha )\leftrightarrow Q(x,y,\beta )\ge \rho (\alpha ,\beta ),\end{array}$$

(5)

where ↔ is the biresiduum operation in the $MV$-algebra L.

We show that there is a bijection between the set of all $\Omega$-level L-fuzzy relations in a set X and the set of $({\mathcal{R}}_5,{\mathcal{R}}_5^{\ast })$-fuzzy relations in a set X. For $Q:X\times X\times \Omega \to L$ and $S:X\times X\to R_5$ we define the map $\Theta :L^{X\times X\times \Omega }\to R_5^{X\times X}$ and the inverse map ${\Theta }^{-1}$ by

$$\Theta (Q)(x,y)(\alpha ):=Q(x,y,\alpha ),{\Theta }^{-1}(S)(x,y,\alpha )=S(x,y)(\alpha ).$$

It is clear that $\Theta (Q)(x,y)\in L^{\Omega }$ is $\rho$-extensional, ${\Theta }^{-1}(S)$ is the $\Omega$-level L-fuzzy relation, and $\Theta$ and ${\Theta }^{-1}$ are mutually inverse mappings. Using this bijection and Example 7, we can define operations for $\Omega$-level L-fuzzy sets. For example, the composition $T\circ S$ of two $\Omega$-level L-fuzzy relations S and T in X can be defined using Definition 10 by

$$\begin{array}{c}(T\circ S)(x,z,\alpha )={\Theta }^{-1}\left(\Theta (T){\circ }_5\Theta (S)\right)(x,z)(\alpha )=\sum _{y\in X}^{{\mathcal{R}}_5}(\Theta (S)(x,y){\times }_5\Theta (T)(y,z))(\alpha )=\\ \sum _{y\in Y}^{{\mathcal{R}}_5}\overline{\Theta (S)(x,y)\otimes \Theta (T)(y,z)}(\alpha )=\underset{y\in X}{\bigvee }\underset{\beta \in \Omega }{\bigvee }\Theta (S)(x,y)(\beta )\otimes \Theta (T)(y,z)(\beta )\otimes \rho (\alpha ,\beta )=\\ \underset{y\in X}{\bigvee }\underset{\beta \in \Omega }{\bigvee }S(x,y)(\beta )\otimes T(y,z)(\beta )\otimes \rho (\alpha ,\beta ).\end{array}$$

4.2. $(\mathcal{R},{\mathcal{R}}^{\ast })$-Approximation Spaces

In the following definition, we introduce the notion of upper and lower approximations of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets defined by the $(\mathcal{R},{\mathcal{R}}^{\ast })$-relations. If T is a $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy equivalence relation in X, the pair $(X,T)$ is called the $(\mathcal{R},{\mathcal{R}}^{\ast })$-approximation space.

Definition 12.

Let $(\mathcal{R},{\mathcal{R}}^{\ast })$ be the dual pair of semirings with the self-inverse isomorphism ¬ and let $T:X\times Y\to R$ be a $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relation.

1.

The upper $(\mathcal{R},{\mathcal{R}}^{\ast })$-approximation defined by T is the mapping $T^{\uparrow }:R^X\to R^Y$ defined by

$$s\in R^X,y\in Y,T^{\uparrow }(s)(y)=\sum _{x\in X}^{\mathcal{R}}s(x)\times T(x,y).$$

2.

The lower $(\mathcal{R},{\mathcal{R}}^{\ast })$-approximation defined by T is the mapping $T^{\downarrow }:R^X\to R^Y$ defined by

$$s\in R^X,y\in Y,T^{\downarrow }(s)(y)=\sum _{x\in X}^{{\mathcal{R}}^{\ast }}s(x){\times }^{\ast }\neg (T(x,y)).$$

3.

If $X=Y$ and T is the $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy equivalence relation, pair $(T^{\downarrow }(s),T^{\uparrow }(s))$ is called the $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy rough set of s with respect to $(X,T)$.

Definition 12 allows us to introduce the concept of rough fuzzy structure for all types of new fuzzy structures that can be transformed into $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets. To illustrate the possible application of Definition 12, we present the upper and lower approximations for two examples of fuzzy structures. Namely, we show that the existing definitions of the rough intuitionistic L-fuzzy set defined by [8] and the rough L-fuzzy soft set in the variant defined by [21] are identical to the rough fuzzy structures according to Definition 12. In the last section, we present applications of these rough $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy structures to the color segmentation of color images.

A simple example of $(\mathcal{R},{\mathcal{R}}^{\ast })$-approximation mappings is given by two variants of Zadeh’s extension principle for $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets.

Example 12.

Let $(\mathcal{R},{\mathcal{R}}^{\ast })$ be the dual pair of semirings and let $f:X\to Y$ be a mapping. Let $\left[f\right]:X\times Y\to R$ be the $(\mathcal{R},{\mathcal{R}}^{\ast })$-relation defined by

$$\left[f\right](x,y)=\left\{\begin{array}{cc}{1}_R,\hfill & f(x)=y,\hfill \\ 0_R,\hfill & f(x)\ne y\hfill \end{array}\right..$$

The lower and upper Zadeh’s extension mappings $R^X\to R^Y$$f^{\Rightarrow }$ and $f^{\to }$, respectively, are defined by

1.

$s\in R^X,y\in Y,f^{\Rightarrow }(s)(y)={\left[f\right]}^{\downarrow }(s)(y)={\sum }_{x\in X,f(x)=y}^{{\mathcal{R}}^{\ast }}s(x)$,

2.

$s\in R^X,y\in Y,f^{\to }(s)(y)={\left[f\right]}^{\uparrow }(s)(y)={\sum }_{x\in X,f(x)=y}^{\mathcal{R}}s(x).$

By mapping f we can also define the $(\mathcal{R},{\mathcal{R}}^{\ast })$-relation $(f):Y\times X\to R$, such that $(f)(y,x)=\left[f\right](x,y)$. In that case, the upper and lower approximations defined by $(f)$ represent (only one) version of the Zadeh’s inverse extension $R^Y\to R^X$, i.e.,

$$t\in R^Y,x\in X,f^{\leftarrow }(t)(y)=:{(f)}^{\uparrow }(t)(x)=t(f(x))={(f)}^{\downarrow }(t)(x).$$

Example 13.

Let S be the intuitionistic L-fuzzy relation in X and let f be an intuitionistic L-fuzzy set in X. According to [8], the upper and lower intuitionistic approximations $\overline{S}(f),\underline{S}(f)$ of f are defined by

$$\begin{array}{c}\overline{S}(f)(x)=\left(\underset{y\in X}{\bigvee }T(S_1(x,y),f_1(y)),\underset{y\in X}{\bigwedge }I(S_2(x,y),f_2(y))\right),\\ \underline{S}(f)(x)=\left(\underset{y\in X}{\bigwedge }I(\neg (S_2(x,y)),f_1(y)),\underset{y\in X}{\bigvee }T(S_1(x,y),f_2(y))\right),\end{array}$$

where for arbitrary $(x,x^{\prime })\in X\times X$, $S(x,x^{\prime })=(S_1(x,x^{\prime }),S_2(x,x^{\prime }))$ and $f(x)=(f_1(x),f_2(x))$, T is a t-norm and I is an implicator (see [8]).

From Proposition 3, it follows that S is also $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-relation, i.e., $S:X\times X\to R_1$ and if for $a,b\in L$ we set

$$T(a,b)=a\otimes b,I(a,b)=\neg a\oplus b,$$

we obtain $S^{\uparrow }(f)(x)=\overline{S}(f)(x)$ and $S^{\downarrow }(f)(x)=\underline{S}(f)(x)$. Therefore, if L is the $MV$-algebra, the intuitionistic L-fuzzy rough sets are $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy rough sets.

In the next example, we will focus on rough fuzzy soft sets. Unlike the well-known and unambiguously defined classical rough L-fuzzy sets, the notion of rough L-fuzzy soft set is not defined in a generally accepted way. In contrast, there are a number of variants, including possible variants of names. For example, in [25] the construction of upper and lower fuzzy soft approximations is defined for approximations of classical fuzzy sets, where instead of fuzzy soft relations, fuzzy soft sets are used. On the other hand, in [26], fuzzy soft relations are explicitly used to define upper and lower soft approximations of fuzzy soft sets, but without the notion of rough fuzzy soft sets.

That brief overview shows that rough fuzzy soft sets or upper and lower soft approximations of fuzzy soft sets defined by fuzzy soft relations have not been systematically introduced so far. In the next example, we show how we can explicitly define this notion. According to Example 4, a fuzzy soft set in X can be identified with the mapping $X\to R_2$ and according to Proposition 3, a fuzzy soft relation in X with the mapping $X\times X\to R_2$. By Definition 12, we obtain:

Example 14.

Let $(K,X)$ be a soft space and let $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$ be the dual pair of semirings from Example 4. For a $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy soft set $f:X\to R_2$ we put $f(x)=(F_x,f_x)\in R_2$, where $F_x\subseteq K$, $f_x:K\to L$ is a mapping, and $(F_x,f_x):K\to L$ is such that

$$(F_x,f_x)(k)=\left\{\begin{array}{cc}{f}_x(k),\hfill & k\in F_x,\hfill \\ 0_L,\hfill & k\in K\setminus F_x.\hfill \end{array}\right.$$

According to Proposition 3, L-fuzzy soft relation in a set X can be identified with the $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy relation $X\times X\to R_2$. For this relation $\mathcal{T}:X\times X\to R_2$, for $(x,x^{\prime })\in X\times X$ we set

$$\begin{array}{c}\mathcal{T}(x,x^{\prime })=(E_{x{x}^{\prime }},{\phi }_{x{x}^{\prime }})\in R_2,\\ k\in K,(E,{\phi }_{x{x}^{\prime }})(k)=\left\{\begin{array}{cc}{\phi }_{x{x}^{\prime }}(k),\hfill & k\in E_{x{x}^{\prime }},\hfill \\ 0_L,\hfill & k\in K\setminus E_{x{x}^{\prime }}.\hfill \end{array}\right.\end{array}$$

It is easy to see that $\mathcal{T}$ is the $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy equivalence relation if and only if T is the L-fuzzy soft equivalence relation. Therefore, according to Definition 12 and Example 4, the rough $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy soft set $({\mathcal{T}}^{\downarrow }(f),{\mathcal{T}}^{\uparrow }(f))$ is defined for $x\in X,k\in K$, by

$$\begin{array}{c}{\mathcal{T}}^{\uparrow }(f)(x)(k)=\left(\sum _{z\in X}^{{\mathcal{R}}_2}\mathcal{T}(x,z){\times }_{2}f(z)\right)(k)=\left(\sum _{z\in X}^{{\mathcal{R}}_2}(E_{xz},{\phi }_{xz}){\times }_2(F_z,f_z)\right)(k)=\\ \left(\sum _{z\in X}^{{\mathcal{R}}_2}(E_{xz}\cap F_z,{\phi }_{xz}\otimes f_z)\right)(k)=\\ \underset{z\in X}{\bigvee }\left\{\begin{array}{cc}{\phi }_{xz}(k)\otimes f_z(k),\hfill & k\in E_{xz}\cap F_z,\hfill \\ 0_L,\hfill & k\in K\setminus E_{xz}\cap F_z,\hfill \end{array}\right.=\underset{\{z\in X:k\in E_{xz}\cap F_z\}}{\bigvee }{\phi }_{xz}(k)\otimes f_z(k),\\ {\mathcal{T}}^{\downarrow }(f)(x)(k)=\left(\sum _{z\in X}^{{\mathcal{R}}_2^{\ast }}\neg (\mathcal{T}(x,z)){\times }_2^{\ast }f(z)\right)(k)=\left(\sum _{z\in X}^{{\mathcal{R}}_2^{\ast }}\neg (E_{xz},{\phi }_{xz}){\times }_2^{\ast }(F_z,f_z)\right)(k)=\\ \left(\sum _{z\in X}^{{\mathcal{R}}_2^{\ast }}(E_{xz}\cap F_z,\neg {\phi }_{xz}\oplus f_z)\right)(k)=\\ \underset{z\in X}{\bigwedge }\left\{\begin{array}{cc}{\neg }_2({\phi }_{xz}(k))\oplus f_z(k),\hfill & k\in E_{xz}\cap F_z,\hfill \\ 0_L,\hfill & k\in K\setminus E_{xz}\cap F_x.\hfill \end{array}\right.=\underset{\{z\in X:k\in E_{xz}\cap F_z\}}{\bigwedge }{\neg }_2({\phi }_{xz}(k)\oplus f_z(k).\end{array}$$

It can be proven that the $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy rough set $({\mathcal{T}}^{\downarrow }(f),{\mathcal{T}}^{\uparrow }(f))$ can be identified with the rough fuzzy soft set defined in [26] or [21].

In the next part of the paper, we concentrate on the basic properties of the upper and lower $(\mathcal{R},{\mathcal{R}}^{\ast })$-approximations of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets. Because some L-fuzzy structures can be transformed into $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets, the lower and upper approximations of these $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets in the $(\mathcal{R},{\mathcal{R}}^{\ast })$-approximation space can be converted to lower and upper approximations of these L-fuzzy structures. The properties of the lower and upper approximations created in this way then copy the properties of rough $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets, and it is not necessary to prove them for individual fuzzy structures.

The basic properties of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy rough sets are presented in the following proposition. For $a\in R$, we denote by $\underline{a}$ the constant $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy set with the only value a. We also use the following $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy set ${\eta }_X(z)\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^X$, where ${\eta }_X(z)(y)=\left\{\begin{array}{cc}{1}_R,\hfill & y=z,\hfill \\ 0_R,\hfill & y\ne z\hfill \end{array}\right.$ and ${\eta }_X^{\ast }(z)=\neg {\eta }_X(z).$ Using this notation we obtain the following simple lemma.

Lemma 3.

For arbitrarily $f\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^X$ we have

$$f=\underset{x\in X}{⨆}(f(x)\star {\eta }_X(x))={\sqcap }_{x\in X}(f(x){\star }^{\ast }{\eta }_X^{\ast }(x)).$$

The Proof is trivial, and it will be omitted.

Proposition 4.

Let $(\mathcal{R},{\mathcal{R}}^{\ast })$ be the dual pair of semirings with the self-inverse isomorphism ¬ and let T be a $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relation in X. Let $a\in R$ and $s,t,s_i\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^X$, $i\in I$.

1.

$T^{\uparrow }({⨆}_{i\in I}{s}_i)={⨆}_{i\in I}{T}^{\uparrow }(s_i)$, $T^{\downarrow }({\sqcap }_{i\in I}{s}_i)={\sqcap }_{i\in I}{T}^{\downarrow }(s_i)$,

2.

$T^{\uparrow }(a\star s)=a\star T^{\uparrow }(s)$, $T^{\downarrow }(a{\star }^{\ast }s)=a{\star }^{\ast }{T}^{\downarrow }(s)$,

3.

$s\le t\Rightarrow T^{\downarrow }(s)\le T^{\downarrow }(t),T^{\uparrow }(s)\le T^{\uparrow }(t)$,

4.

$T^{\downarrow }(s)=\neg (T^{\uparrow }(\neg (s)))$, $T^{\uparrow }(s)=\neg (T^{\downarrow }(\neg (s)))$,

5.

if T is reflexive, $T^{\downarrow }(s)\le s\le T^{\uparrow }(s)$.

6.

The following statements are equivalent for arbitrary $s\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^X$

(a)

T is transitive,

(b)

$T^{\uparrow }(T^{\uparrow }(s))\le T^{\uparrow }(s)$,

(c)

$T^{\downarrow }(T^{\downarrow }(s))\ge T^{\downarrow }(s)$.

Proof. 

To prove 1.–3. is the routine only, and it will be omitted.

4. We have

$$\begin{array}{c}{T}^{\downarrow }(s)(x)=\sum _{z\in X}^{{\mathcal{R}}^{\ast }}\neg T(x,z)){\times }^{\ast }s(z)=(\sum _{z\in X}^{{\mathcal{R}}^{\ast }}\neg (T(x,z)\times \neg s(z))=\\ \neg (\sum _{z\in X}^{\mathcal{R}}(T(x,z))\times \neg (s(z)))=\neg (T^{\uparrow }(\neg s))(x),\end{array}$$

and similarly for the other part.

5. It is easy to see that $T^{\uparrow }(s)\ge s$ for a reflexive T. The rest is derived from the inequality $\neg T^{\downarrow }(s)=T^{\uparrow }(\neg s)\ge \neg s$. 6. The implication (a) ⇒ (b) can be proved simply. Implication (b) ⇒ (c) follows from the inequality.

$$\begin{array}{c}\neg T^{\downarrow }(T^{\downarrow }(s))=T^{\uparrow }(\neg T^{\downarrow }(s))=T^{\uparrow }{T}^{\uparrow }(\neg s)\le T^{\uparrow }(\neg s)=\neg T^{\downarrow }(s),\end{array}$$

and it follows $T^{\downarrow }{T}^{\downarrow }(s)\ge T^{\downarrow }(s)$. To prove $(c)\Rightarrow (a)$, we put $s={\eta }_X^{\ast }(z)$. Since $T^{\downarrow }({\eta }_X^{\ast }(z))(x)=\neg T(x,z)$, we obtain the following.

$$\begin{array}{c}{T}^{\downarrow }(T^{\downarrow }({\eta }_X^{\ast }(z))(x)=\sum _{y\in X}^{{\mathcal{R}}^{\ast }}\neg T(x,y){\times }^{\ast }{T}^{\downarrow }({\eta }_x^{\ast }(z))(y)=\sum _{y\in X}^{{\mathcal{R}}^{\ast }}\neg T(x,y){\times }^{\ast }\neg T(y,z)=\\ \neg (\sum _{y\in X}^{\mathcal{R}}T(x,y)\times T(y,z))\ge \neg T(x,z),\end{array}$$

and we obtain $T(x,y)\times T(y,z)\le {\sum }_{y\in X}^{\mathcal{R}}T(x,t)\times T(t,z)\le T(x,z)$. Therefore, T is the transitive $(\mathcal{R},{\mathcal{R}}^{\ast })$-relation. □

From Proposition 4 and Lemma 3, we immediately obtain the following lemma, which will be used in the next theorem.

Lemma 4.

Let Γ and ${\Gamma }^{\prime }$ be upper and Δ and ${\Delta }^{\prime }$ be lower $(\mathcal{R},{\mathcal{R}}^{\ast })$-approximations $R^X\to R^X$, respectively. Then the following implications hold.

$$\begin{array}{c}\forall s\in R^X,\Gamma (s)={\Gamma }^{\prime }(s)\iff \forall x\in X,\Gamma ({\eta }_X(x))={\Gamma }^{\prime }({\eta }_X(x)),\\ \forall s\in R^X,\Delta (s)={\Delta }^{\prime }(s)\iff \forall x\in X,\Delta ({\eta }_X^{\ast }(x))=\Delta ({\eta }_X^{\ast }(x)).\end{array}$$

In the paper [27], the axiomatic characterization of the lower and upper approximations of the $[0,1]$-fuzzy sets was presented. In the next part, we prove that an analogical axiomatic characterization of $(\mathcal{R},{\mathcal{R}}^{\ast })$-approximations of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets can also be proven. It follows without any proof that this axiomatic characteristic holds for an arbitrary fuzzy structure, which can be transformed into $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets.

Proposition 5.

Let $(\mathcal{R},{\mathcal{R}}^{\ast })$ be the dual pair of semirings, X be a set, and let $\Gamma :R^X\to R^X$ be a mapping. The following statements are equivalent.

1.

There exists a $(\mathcal{R},{\mathcal{R}}^{\ast })$-equivalence relation T in X, such that $\Gamma =T^{\uparrow }$.

2.

For arbitrary $s,s_i\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^X$, $a\in R$, the mapping Γ satisfies the following conditions.

(a)

$\Gamma (s)\ge s$,

(b)

$\Gamma \Gamma (s)=\Gamma (s)$,

(c)

$\Gamma ({⨆}_{i\in I}{s}_i)={⨆}_{i\in I}\Gamma (s_i)$,

(d)

$\Gamma (a\star s)=a\star \Gamma (s)$,

(e)

$\Gamma ({\eta }_X(x))(z)=\Gamma ({\eta }_X(z))(x)$.

Proof. 

The implication $1\Rightarrow 2$ follows from Proposition 4. We prove the implication $2\Rightarrow 1$. Let conditions 2) hold. We define the symmetric and reflexive $(\mathcal{R},{\mathcal{R}}^{\ast })$-relation T by

$$x,y\in X,T(x,y)=\Gamma ({\eta }_X(x))(y)=\Gamma ({\eta }_X(y))(x)=T(y,x),$$

and we show that it is transitive. According to Lemma 3, for arbitrary $s\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^X$, we have the following.

$$\begin{array}{c}\Gamma (s)(x)=\Gamma \left(\underset{t\in X}{⨆}s(t)\star {\eta }_X(t)\right)(x)=\sum _{t\in X}s(t)\times \Gamma ({\eta }_X(t))(x)=\sum _{t\in X}s(t)\times T(x,y)=\\ T^{\uparrow }(s)(x),\end{array}$$

where T is a symmetric and reflexive $(\mathcal{R},{\mathcal{R}}^{\ast })$-relation. According to Proposition 4, T is also transitive. □

An analogous axiomatic characterization can be performed for the lower $(\mathcal{R},{\mathcal{R}}^{\ast })$-approximation.

Proposition 6.

Let $(\mathcal{R},{\mathcal{R}}^{\ast })$ be the dual pair of semirings, X be a set, and let $\Lambda :R^X\to R^X$ be a mapping. The following statements are equivalent.

1.

There exists the $(\mathcal{R},{\mathcal{R}}^{\ast })$-equivalence relation S in X, such that $\Lambda =S^{\downarrow }$.

2.

For arbitrary $s,s_i\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^X$, $a\in R$, the mapping Λ satisfies the following conditions.

(a)

$\Lambda (s)\le s$,

(b)

$\Lambda \Lambda (s)=\Lambda (s)$,

(c)

$\Lambda ({\sqcap }_{i\in I}{s}_i)={\sqcap }_{i\in I}\Lambda (s_i)$,

(d)

$\Lambda (a{\star }^{\ast }s)=a{\star }^{\ast }\Lambda (s)$,

(e)

$\Lambda ({\eta }_X^{\ast }(x))(y)=\Lambda ({\eta }_X^{\ast }(y))(x)$.

Proof. 

The implication $1\Rightarrow 2$ follows from Proposition 4. Now, let Condition 2 hold. We define the symmetric and reflexive $(\mathcal{R},{\mathcal{R}}^{\ast })$-relation S by

$$S(x,y)=\neg (\Lambda ({\eta }_X^{\ast }(x)(y))=\neg (\Lambda ({\eta }_X^{\ast }(y)(x))=S(y,x).$$

According to Lemma 3, for arbitrary $s\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^X$ we have

$$\begin{array}{c}\Lambda (s)(x)=\Lambda \left({\sqcap }_{t\in X}s(t){\star }^{\ast }{\eta }_X^{\ast }(t)\right)(x)=\sum _{t\in X}s(t){\times }^{\ast }\Lambda ({\eta }_X^{\ast }(t))(x)=\\ \sum _{t\in X}s(t){\times }^{\ast }\neg (S(x,t))=S^{\downarrow }(s)(x),\end{array}$$

and S is also transitive, according to Proposition 4. □

Relationships between approximation mappings satisfying conditions (a)–(e) from previous propositions, on the one hand, and $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations, can be more precisely described by category theory. Let us introduce the following three categories.

Definition 13.

Let $(\mathcal{R},{\mathcal{R}}^{\ast })$ be the dual pair of semirings.

1.

The category ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$ of upper approximation mappings between power sets of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets is defined by

(a)

objects are mappings $\Gamma :R^X\to R^X$, satisfying conditions (a)–(e) of Proposition 5,

(b)

morphisms from $\Gamma :R^X\to R^X$ to $\Delta :R^Y\to R^Y$ are mappings $f:X\to Y$, such that in the diagram

$$\begin{array}{ccc}{R}^X& \stackrel{\Gamma }{\to }& R^X\\ f^{\to }\downarrow & \hspace{1em}& \downarrow f^{\to }\\ R^Y& \stackrel{\Delta }{\to }& R^Y\end{array}$$

the inequality $\Delta .f^{\to }\ge f^{\to }.\Gamma$ holds.

2.

The category ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$ of lower approximation mappings between power sets of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets is defined by

(a)

objects are mappings $\Gamma :R^X\to R^X$, satisfying conditions (a)–(e) of Proposition 6,

(b)

morphisms from $\Gamma :R^X\to R^X$ to $\Delta :R^Y\to R^Y$ are mappings $f:X\to Y$, such that in the diagram

$$\begin{array}{ccc}{R}^X& \stackrel{\Gamma }{\to }& R^X\\ f^{\leftarrow }\uparrow & \hspace{1em}& \uparrow f^{\leftarrow }\\ R^Y& \stackrel{\Delta }{\to }& R^Y\end{array}$$

the inequality $f^{\leftarrow }.\Delta {\ge }^{\ast }\Gamma .f^{\leftarrow }$ holds.

3.

The category $Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$ of the upper $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations is defined by

(a)

objects are $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy equivalence relations $Q:X\times X\to R$,

(b)

morphisms from $Q:X\times X\to R$ to $S:Y\times Y\to R$ are mappings $f:X\to Y$, such that for arbitrary $x,x^{\prime }\in X$, the inequality $Q(x,x^{\prime })\le S(f(x),f(x^{\prime }))$ holds.

4.

The category $Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })$ of the lower $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy relations is defined by

(a)

objects are $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy equivalence relations $Q:X\times X\to R$,

(b)

morphisms from $Q:X\times X\to R$ to $S:Y\times Y\to R$ are mappings $f:X\to Y$, such that for arbitrary $x,x^{\prime }\in X$, the inequality $Q(x,x^{\prime }){\le }^{\ast }S(f(x),f(x^{\prime }))$ holds.

The compositions of the morphisms in all these categories are standard compositions of mappings.

The relationship between these three categories describes the following theorem.

Theorem 2.

Let $(\mathcal{R},{\mathcal{R}}^{\ast })$ be the dual pair of semirings with the self-inverse isomorhism ¬. There exist isomorphic functors $E,F,G,H$ such that the following diagram commutes.

$$\begin{array}{ccc}\hfill {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }\hfill & \hfill \stackrel{H}{\to }\hfill & \hfill {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }\hfill \\ \hfill F\downarrow \hfill & \hfill \hspace{1em}\hfill & \hfill G\downarrow \hfill \\ \hfill {\mathit{Rel}}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })\hfill & \hfill \stackrel{E}{\to }\hfill & \hfill {\mathit{Rel}}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })\hfill \end{array}$$

Proof. 

(1) We define the functor $F:{(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }\to Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$. Let $\Gamma :R^X\to R^X$ be an object of ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$. We put

$$F(\Gamma )=\widehat{\Gamma }:X\times X\to R,\mathrm{such}\mathrm{that}\widehat{\Gamma }(x,x^{\prime })=\Gamma ({\eta }_X(x))(x^{\prime }).$$

For a morphism $f:\Gamma \to \Delta$, where $\Delta :R^Y\to R^Y$ is the object of ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$, we set $F(f)=f$. We prove that this definition is correct, that is, f is the morphism in $Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$. We need to prove that $\widehat{\Gamma }(x,x^{\prime })\le \widehat{\Delta }(f(x),f(x^{\prime }))$, for arbitrary $x,x^{\prime }\in X$. Since f is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$, we have $\Delta .f^{\to }\ge f^{\to }.\Gamma$ and obtain

$$\begin{array}{c}\widehat{\Gamma }(x,x^{\prime })=\Gamma ({\eta }_X(x))(x^{\prime })\le \sum _{z\in X,f(z)=f(x^{\prime })}^{\mathcal{R}}\Gamma ({\eta }_X(x))(z)=f^{\to }.\Gamma ({\eta }_X(x))(f(x^{\prime }))\le \\ \Delta ·f^{\to }({\eta }_X(x))(f(x^{\prime }))=\Delta ({\eta }_Y(f(x))(f(x^{\prime }))=\widehat{\Delta }(f(x),f(x^{\prime })).\end{array}$$

Therefore, f is a morphism in $Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$ and it is easy to see that F is a functor.

We define the inverse functor $F^{-1}:Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })\to {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$ by

$$F^{-1}(Q)=Q^{\uparrow },$$

where $Q:X\times X\to R$ is an object of $Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$, and for the morphism $f:Q\to S$ in $Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$, where $S:Y\times Y\to R$, we set $F^{-1}(f)=f$. As follows from Proposition 5, this definition is correct, and we only need to show that $f:Q^{\uparrow }\to S^{\uparrow }$ is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$. For $s\in R^X,y\in Y$, we have

$$\begin{array}{c}{f}^{\to }.Q^{\uparrow }(s)(y)=\sum _{\{x\in X,f(x)=y\}}^{\mathcal{R}}{Q}^{\uparrow }(s)(x)=\sum _{\{x\in X,f(x)=y\}}^{\mathcal{R}}\sum _{x^{\prime }\in X}^{\mathcal{R}}s(x^{\prime })\times Q(x^{\prime },x)\le \\ \sum _{\{x\in X,f(x)=y\}}^{\mathcal{R}}\sum _{x^{\prime }\in X}^{\mathcal{R}}s(x^{\prime })\times S(f(x^{\prime }),f(x))=\sum _{\{x\in X,f(x)=y\}}^{\mathcal{R}}\sum _{x^{\prime }\in X}^{\mathcal{R}}s(x^{\prime })\times S(f(x^{\prime }),y)=\\ \sum _{x^{\prime }\in X}^{\mathcal{R}}s(x^{\prime })\times S(f(x^{\prime }),y)=\sum _{\{(x^{\prime },z)\in X\times Y:f(x^{\prime })=z\}}^{\mathcal{R}}s(x^{\prime })\times S(z,y)\le \sum _{z\in Y}^{\mathcal{R}}{f}^{\to }(s)(z)\times S(z,y)=\\ S^{\uparrow }(f^{\to }(s))(y).\end{array}$$

It follows that f is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$. We show that F and $F^{-1}$ are mutually inverse functors. For $Q:X\times X\to R$ and for $\Gamma :R^X\to R^X$, $s\in R^X,x,x^{\prime }\in X$, according to the Lemma 3 and the properties of $\Gamma$, we have

$$\begin{array}{c}F·F^{-1}(Q)(x,x^{\prime })=F(Q^{\uparrow })(x,x^{\prime })=Q^{\uparrow }({\eta }_X(x))(x^{\prime })=\sum _{t\in X}^{\mathcal{R}}{\eta }_X(x)(t)\times Q(t,x^{\prime })=\\ Q(x,x^{\prime }),\\ F^{-1}·F(\Gamma )(s)(x)=F^{-1}(\widehat{\Gamma })(s)(x)={\widehat{\Gamma }}^{\uparrow }(s)(x)=\sum _{t\in X}^{\mathcal{R}}s(t)\times \widehat{\Gamma }(t,x)=\\ \sum _{t\in X}^{\mathcal{R}}s(t)\times \Gamma ({\eta }_X(t))(x)=\Gamma (\underset{t\in X}{\overset{\mathcal{R}}{⨆}}s(t)\times {\eta }_X(t))(x)=\Gamma (s)(x),\end{array}$$

and $F,F^{-1}$ are mutually inverse functors.

(2) We define the functor $H:{(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }\to {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$. For an object $\Gamma :R^X\to R^X$ from ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$ we set

$$\begin{array}{c}H(\Gamma )={\widehat{\Gamma }}^{\downarrow }\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow },\\ x,x^{\prime }\in X,\widehat{\Gamma }(x,x^{\prime })=\Gamma ({\eta }_X(x))(x^{\prime }).\end{array}$$

Let $\Delta :R^Y\to R^Y$ be another object from ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$ and let $f:\Gamma \to \Delta$ be a morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$. We set $H(f)=f$. According to Proposition 6, we only need to prove that $f:{\widehat{\Gamma }}^{\downarrow }\to {\widehat{\Delta }}^{\downarrow }$ is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$. Since f is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$, for ${\eta }_X(x)\in R^X$, $v\in Y$, we obtain $\Delta .f^{\to }({\eta }_X(x))(v)\ge f^{\to }.\Gamma ({\eta }_X(x))(v)$ and it follows that

$$\begin{array}{c}\widehat{\Delta }(f(x),v)=\Delta ({\eta }_Y(f(x)))(v)=\Delta (f^{\to }({\eta }_X(x)))(v)\ge \\ f^{\to }(\Gamma ({\eta }_X(x)))(v)=\sum _{u\in X,f(u)=v}^{\mathcal{R}}\Gamma ({\eta }_X(x))(u)=\sum _{u,f(u)=v}^{\mathcal{R}}\widehat{\Gamma }(x,u).\end{array}$$

We can prove that $f:{\widehat{\Gamma }}^{\downarrow }\to {\widehat{\Delta }}^{\downarrow }$ is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$, that is, we prove that for arbitrary $t\in R^Y$, $x\in X$, the inequality ${\widehat{\Gamma }}^{\downarrow }.f^{\leftarrow }(t)(x){\le }^{\ast }{f}^{\leftarrow }.{\widehat{\Delta }}^{\downarrow }(t)(x)$ holds. Since $f^{\leftarrow }$ is the lower approximation defined by the relation $(f)$, according to Lemma 3, for arbitrary $t\in R^Y$, we have

$$\begin{array}{c}t=\sum _{v\in Y}^{{\mathcal{R}}^{\ast }}t(v){\times }^{\ast }{\eta }_Y^{\ast }(v),\\ f^{\leftarrow }(t)=f^{\leftarrow }\left(\sum _{v\in Y}^{{\mathcal{R}}^{\ast }}t(v){\times }^{\ast }{\eta }_Y^{\ast }(v)\right)=\sum _{v\in Y}^{{\mathcal{R}}^{\ast }}t(v){\times }^{\ast }{f}^{\leftarrow }({\eta }_Y^{\ast }(v)),\\ {\widehat{\Gamma }}^{\downarrow }(f^{\leftarrow }(t))={\widehat{\Gamma }}^{\downarrow }\left(\sum _{v\in Y}^{{\mathcal{R}}^{\ast }}t(v){\times }^{\ast }{f}^{\leftarrow }({\eta }_Y^{\ast }(v))\right)=\sum _{v\in Y}^{{\mathcal{R}}^{\ast }}t(v){\times }^{\ast }{\widehat{\Gamma }}^{\downarrow }.f^{\leftarrow }({\eta }_Y^{\ast }(v)).\end{array}$$

Therefore, according to the Lemma 4, to prove the inequality, instead of a general function $t\in R^Y$, we can consider only functions $t={\eta }_Y^{\ast }(v)$.

$$\begin{array}{c}{\widehat{\Gamma }}^{\downarrow }·f^{\leftarrow }({\eta }_Y^{\ast }(v))(x^{\prime })=\sum _{t\in X}^{{\mathcal{R}}^{\ast }}{f}^{\leftarrow }({\eta }_Y^{\ast }(v))(t){\times }^{\ast }\neg \left(\widehat{\Gamma }(t,x^{\prime })\right)=\\ \sum _{t\in X}^{{\mathcal{R}}^{\ast }}{\eta }_Y^{\ast }(v)(f(t)){\times }^{\ast }\neg (\widehat{\Gamma }(t,x^{\prime }))=\sum _{t\in X,f(t)=v}^{{\mathcal{R}}^{\ast }}\neg \left(\widehat{\Gamma }(t,x^{\prime })\right)=\\ \neg \left(\sum _{t\in X,f(t)=v}^{\mathcal{R}}\widehat{\Gamma }(t,x^{\prime })\right){\le }^{\ast }\neg \left(\widehat{\Delta }(f(t),f(x^{\prime }))\right)=\neg (\widehat{\Delta }(v,f(x^{\prime })))=\\ \sum _{z\in Y}^{{\mathcal{R}}^{\ast }}{\eta }_Y^{\ast }(v)(z){\times }^{\ast }\neg (\widehat{\Delta }(z,f(x^{\prime })))={\widehat{\Delta }}^{\downarrow }({\eta }_Y^{\ast }(v))(f(x^{\prime }))=\\ f^{\leftarrow }·{\widehat{\Delta }}^{\downarrow }({\eta }_Y^{\ast }(v)(x^{\prime })).\end{array}$$

and it follows that ${\widehat{\Gamma }}^{\downarrow }.f^{\leftarrow }(t)(x){\le }^{\ast }{f}^{\leftarrow }.{\widehat{\Delta }}^{\downarrow }(t)(x)$. Therefore, H is the functor.

We define the inverse functor $H^{-1}$. Let $f:\Gamma \to \Delta$ be a morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$, where $\Gamma :R^X\to R^X$ and $\Delta :R^Y\to R^Y$. We put

$$H^{-1}(\Gamma )={(\neg \tilde{\Gamma })}^{\uparrow }\in {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow },H^{-1}(f)=f,$$

where $\tilde{\Gamma }(x,x^{\prime })=\Gamma ({\eta }_X^{\ast }(x))(x^{\prime })$ for arbitrary $x,x^{\prime }\in X$. We show that $f:{(\neg \tilde{\Gamma })}^{\uparrow }\to {(\neg \tilde{\Delta })}^{\uparrow }$ is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$. In fact, because f is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$, analogously as in the proof of the functor G, we can show that

$$\tilde{\Gamma }(x,x^{\prime }){\le }^{\ast }\tilde{\Delta }(f(x),f(x^{\prime })).$$

We need to prove the inequality $f^{\to }.{(\neg \tilde{\Gamma })}^{\uparrow }(s)(y)\le {(\tilde{\Delta })}^{\uparrow }.f^{\to }(s)(y)$, for arbitrary $s\in R^X$ and $y\in Y$. Analogously as in the proof of the functor H, according to Lemma 4, it suffices to prove this inequality only for $s={\eta }_X(x)$, for arbitrary $x\in X$. We have

$$\begin{array}{c}{f}^{\to }{(\neg \tilde{\Gamma })}^{\uparrow }({\eta }_X(x))(y)=\sum _{t\in X,f(t)=y}^{\mathcal{R}}{(\neg \tilde{\Gamma })}^{\uparrow }({\eta }_X(x))(t)=\\ \sum _{t\in X,f(t)=y}^{\mathcal{R}}\sum _{u\in X}^{\mathcal{R}}{\eta }_X(x)(u)\times \neg (\tilde{\Gamma }(u,t))=\sum _{t\in X,f(t)=y}^{\mathcal{R}}\neg (\tilde{\Gamma }(x,t))\le \sum _{t\in X,f(t)=y}\neg (\tilde{\Delta }(f(x),y))=\\ \sum _{v\in Y}{f}^{\to }({\eta }_X(x))(v)\times \neg (\tilde{\Delta }(v,y))={(\neg \tilde{\Delta })}^{\uparrow }(f^{\to }({\eta }_X(x))(y).\end{array}$$

Therefore, t is the morphism of ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$ and $H^{-1}$ is the functor. We prove that H and $H^{-1}$ are inverse functors. Let $\Gamma \in {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$. We need to prove that $H.H^{-1}(\Gamma )(g)=\Gamma (g)$, for arbitrary $g\in R^X$. According to Lemma 4, we prove it for $g={\eta }_X^{\ast }(x)$, for arbitrary $x\in X$. We have the following.

$$\begin{array}{c}H·H^{-1}(\Gamma )({\eta }_X^{\ast }(x))(x^{\prime })=H({(\neg \tilde{\Gamma })}^{\uparrow })({\eta }_X^{\ast }(x))(x^{\prime })={({\widehat{\neg \tilde{\Gamma }}}^{\uparrow })}^{\downarrow }({\eta }_X^{\ast }(x))(x^{\prime })=\\ \sum _{t\in X}^{{\mathcal{R}}^{\ast }}{\eta }_X^{\ast }(x)(t){\times }^{\ast }\neg ({\widehat{\neg \tilde{\Gamma }}}^{\uparrow })(t,x^{\prime })=\neg ({\widehat{\neg \tilde{\Gamma }}}^{\uparrow })(x,x^{\prime })=\neg ({(\neg \tilde{\Gamma })}^{\uparrow })({\eta }_X(x))(x^{\prime })=\\ \neg \left(\sum _{t\in X}^{\mathcal{R}}{\eta }_X(x)(t)\times \neg (\tilde{\Gamma })(t,x^{\prime })\right)=\neg (\neg (\tilde{\Gamma }))(x,x^{\prime })=\Gamma ({\eta }_X^{\ast }(x))(x^{\prime }).\end{array}$$

Analogously, for $\Delta \in {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\uparrow }$, we obtain the following.

$$\begin{array}{c}{H}^{-1}·H(\Delta )({\eta }_X(x))(x^{\prime })=H^{-1}({\widehat{\Delta }}^{\downarrow })({\eta }_X(x))(x^{\prime })=\neg (\widetilde{{\widehat{\Delta }}^{\downarrow }})({\eta }_X(x))(x^{\prime })=\\ \sum _{t\in X}^{\mathcal{R}}{\eta }_X(x)(t)\times \neg (\widetilde{{\widehat{\Delta }}^{\downarrow }})(t,x^{\prime })=\neg (\widetilde{{\widehat{\Delta }}^{\downarrow }})(x,x^{\prime })=\neg {\widehat{\Delta }}^{\downarrow }({\eta }_X^{\ast }(x))(x^{\prime })=\\ \neg \left(\sum _{t\in X}^{{\mathcal{R}}^{\ast }}{\eta }_X^{\ast }(x)(t){\times }^{\ast }\neg (\widehat{\Delta }(t,x^{\prime }))\right)=\Delta ({\eta }_X(x))(x^{\prime }).\end{array}$$

(3) We define the functor G. Let $f:\Gamma \to \Delta$ be a morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$, where $\Gamma :R^X\to R^X$ and $\Delta :R^Y\to R^Y$ are objects of category ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$. We set

$$\begin{array}{c}G(f)=f,G(\Gamma )=\tilde{\Gamma },\\ \tilde{\Gamma }(x,x^{\prime })=\Gamma ({\eta }_X^{\ast }(x))(x^{\prime }).\end{array}$$

We show that G is a functor, that is, $G(\Gamma )(x,x^{\prime }){\le }^{\ast }G(\Delta )(f(x),f(x^{\prime }))$. Since f is the morphism of ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$, we have $\Gamma .f^{\leftarrow }{\le }^{\ast }{f}^{\leftarrow }.\Delta$. Using the inequality $f^{\leftarrow }({\eta }_Y^{\ast }(f(x)))(x^{\prime }){\ge }^{\ast }{\eta }_X^{\ast }(x)(x^{\prime })$ for an arbitrary $x^{\prime }\in X$, and the fact that $\Gamma$ is the non-decreasing mapping with respect to both relations ≤ and ${\le }^{\ast }$, we obtain

$$\begin{array}{c}\tilde{\Gamma }(x,x^{\prime })=\\ \Gamma ({\eta }_X^{\ast }(x))(x^{\prime }){\le }^{\ast }\Gamma (f^{\leftarrow }({\eta }_Y^{\ast }(f(x)))(x^{\prime }){\le }^{\ast }{f}^{\leftarrow }.\Delta ({\eta }_Y^{\ast }(f(x))(x^{\prime })=\Delta ({\eta }_Y^{\ast }(f(x))(f(x^{\prime }))=\\ \tilde{\Delta }(f(x),f(x^{\prime })).\end{array}$$

Therefore, f is the morphism of $Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })$ and G is the functor.

We define the functor $G^{-1}:Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })\to {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$. Let $f:Q\to S$ be a morphism in $Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })$, where $Q:X\times X\to R$ and $S:Y\times Y\to R$ be objects of $Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })$. We set

$$G^{-1}(f)=f,G^{-1}(Q)=\neg (Q^{\downarrow }).$$

We show that f is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$, that is, for arbitrary $g\in R^Y$, $\neg Q^{\downarrow }.f^{\leftarrow }(g){\le }^{\ast }{f}^{\leftarrow }.\neg S^{\downarrow }(g)$ holds. According to Lemma 3 and the properties of the objects of ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$, it suffices to prove it for $g={\eta }_Y^{\ast }(v)$, for arbitrary $v\in Y$. For arbitrarily $x^{\prime }\in X$, from $Q(x,x^{\prime }){\le }^{\ast }S(f(x),f(x^{\prime }))$, we obtain the following.

$$\begin{array}{c}\neg Q^{\downarrow }·f^{\leftarrow }({\eta }_Y^{\ast }(v))(x^{\prime })=\neg \left(\sum _{t\in X}^{{\mathcal{R}}^{\ast }}{f}^{\leftarrow }({\eta }_Y^{\ast }(v))(t){\times }^{\ast }\neg (Q(t,x^{\prime }))\right)=\\ \sum _{t\in X}^{\mathcal{R}}\neg (f^{\leftarrow }({\eta }_Y^{\ast }(v))(t))\times Q(t,x^{\prime })=\sum _{t\in X}^{\mathcal{R}}{\eta }_Y(v)(f(t))\times Q(t,x^{\prime })=\\ \sum _{t\in X,f(t)=v}^{\mathcal{R}}Q(t,x^{\prime }).\end{array}$$

Since $Q(t,x^{\prime }){\le }^{\ast }S(v,f(x^{\prime }))$ for arbitrary $t\in X,f(t)=v$, we have $Q(t,x^{\prime })\ge S(v,f(x^{\prime }))$ and because the operation + is idempotent, we obtain

$$\sum _{t\in X,f(t)=v}^{\mathcal{R}}Q(t,x^{\prime })\ge \sum _{t,f(t)=v}^{\mathcal{R}}S(v,f(x^{\prime }))=S(v,f(x^{\prime })).$$

It follows that

$$\begin{array}{c}\sum _{t\in X,f(t)=v}^{\mathcal{R}}Q(t,x^{\prime }){\le }^{\ast }S(v,f(x^{\prime }))=\sum _{z\in Y}^{\mathcal{R}}{\eta }_Y(v)(z)\times S(z,f(x^{\prime }))=\\ \neg \left(\sum _{z\in Y}^{{\mathcal{R}}^{\ast }}{\eta }_Y^{\ast }(v)(z){\times }^{\ast }\neg (S(z,f(x^{\prime }))\right)=\neg S^{\downarrow }({\eta }_Y^{\ast }(v))(f(x^{\prime }))=f^{\leftarrow }(\neg S^{\downarrow }({\eta }_Y^{\ast }(v)))(x^{\prime }).\end{array}$$

Therefore, we have $\neg Q^{\downarrow }.f^{\leftarrow }{\le }^{\ast }{f}^{\leftarrow }.\neg S^{\downarrow }$ and it follows that f is the morphism in ${(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$ and $G^{-1}$ is the functor. We prove that G and $G^{-1}$ are mutually inverse functors. Let $Q\in Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })$. We have, for an arbitrarily $x,x^{\prime }\in X$,

$$\begin{array}{c}G·G^{-1}(Q)(x,x^{\prime })=G(\neg Q^{\downarrow })(x,x^{\prime })=\widetilde{\neg Q^{\downarrow }}(x,x^{\prime })=\neg Q^{\downarrow }({\eta }_X^{\ast }(x))(x^{\prime })=\\ \neg \left(\sum _{u\in X}^{{\mathcal{R}}^{\ast }}{\eta }_X^{\ast }(x)(u){\times }^{\ast }\neg (Q(u,x^{\prime }))\right)=Q(x,x^{\prime }).\end{array}$$

On the contrary, let $\Gamma \in {(\mathcal{R},{\mathcal{R}}^{\ast })}^{\downarrow }$. To prove that for arbitrary $s\in R^X$, the identity $G^{-1}.G(\Gamma )(s)=\Gamma (s)$ is valid, according to Lemma 3, we need to prove this identity only for ${\eta }_X^{\ast }(x)$, for arbitrary $x\in X$. We have the following.

$$\begin{array}{c}{G}^{-1}·G(\Gamma )({\eta }_X^{\ast }(x))(x^{\prime })=G^{-1}(\tilde{\Gamma })({\eta }_X^{\ast }(x))(x^{\prime })=\neg {\tilde{\Gamma }}^{\downarrow }({\eta }_X^{\ast }(x))(x^{\prime })=\\ \neg \left(\sum _{t\in X}^{{\mathcal{R}}^{\ast }}{\eta }_X^{\ast }(x)(t){\times }^{\ast }\neg \tilde{\Gamma }(t,x^{\prime })\right)=\sum _{t\in X}^{\mathcal{R}}\neg ({\eta }_X^{\ast }(x)(t))\times \tilde{\Gamma }(t,x^{\prime })=\\ \sum _{t\in X}^{\mathcal{R}}{\eta }_X(x)(t)\times \Gamma ({\eta }_X^{\ast }(t))(x^{\prime })=\Gamma ({\eta }_X^{\ast }(x))(x^{\prime }).\end{array}$$

Therefore, $G^{-1}.G$ is the identity functor.

(4) We define the functor $E:Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })\to Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })$. Let $f:Q\to S$ be a morphism in $Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$, where $Q:X\times X\to R$ and $S:Y\times Y\to R$ be objects of $Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$. We set

$$E(f)=f,E(Q)=\neg Q.$$

It follows that $Q(x,x^{\prime })\le S(f(x),f(x^{\prime }))$, for arbitrary $x,x^{\prime }\in X$, and we obtain $\neg Q(x,x^{\prime }){\le }^{\ast }\neg S(f(x),f(x^{\prime }))$. Therefore, f is the morphism of $Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })$ and E is the functor. Now, let $g:Q\to S$ be a morphism in $Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })$. The inverse functor $E^{-1}:Re{l}^{\downarrow }(\mathcal{R},{\mathcal{R}}^{\ast })\to Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$ is defined by

$$E^{-1}(f)=f,E^{-1}(Q)=\neg Q.$$

It is clear that f is the morphism in $Re{l}^{\uparrow }(\mathcal{R},{\mathcal{R}}^{\ast })$ and $E^{-1}$ is the functor, which is the inverse functor to E. Finally, it is easy to see that the diagram commutes. □

5. Examples of Applications

In this section, we show two examples of possible applications of fuzzy rough structures created using the theory of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy rough sets. For this purpose, we will use the $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy rough set defined for the fuzzy soft set in Example 14 and $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy rough sets defined for intuitionistic fuzzy sets in Example 13. In both cases, we show how these fuzzy rough structures can be used to determine the upper and lower approximations of a color segment corresponding to a particular color k in a color image. Because we use the same default conditions in these examples, it allows us to compare how $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy sets and $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy sets solve this problem.

We suppose that a color image consists of pixels of the set X. We also assume that for each pixel $x\in X$ a value $S(x)$ represents the color in a pixel x. The value $S(x)$, a color code, can be given by numerous color models; we selected the HSV (hue saturation value) color model, which allows us to fix the hue (such as red or yellow) and, taking all combinations of saturation and values, obtain all possible visualizations of the color. In that case, this value is represented as a vector $S(x)=[h_x,s_x,v_x]$, where $h_x$ represents the hue of the color, $s_x$ represents a saturation dimension, and $v_x$ represents the dimension of the value that resembles the mixture of those paints with varying amounts of black or white paint in the pixel x. Let K be the set of all possible colors.

In the next part, we suppose that $L=([0,1],\otimes ,\oplus ,\neg )$ is the Łukasiewicz algebra with the biresiduum ↔ defined by $a\leftrightarrow b=(a\to b)\wedge (b\to a)$.

5.1. $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-Fuzzy Rough Sets

To illustrate the possible applications of rough $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy sets from the soft space $(K,X)$, we present a method for approximations of a colour segment in an image. Unlike Examples 10 and 11 of [28], for these approximations, we use a different $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-relation $\mathcal{T}$.

Let $E=S(X)\subseteq K$ and consider the $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy set $f:X\to R_2^K$ defined by

$$\begin{array}{c}x\in X,f(x)=(E,f_x)\in L^K,\mathrm{where}{f}_x\in L^K,\\ k\in K,f_x(k):=\frac{{\sum }_{z\in X}\rho (x,z).\sigma (S(z),k)}{{\sum }_{z\in X}\rho (x,z)}\in [0,1],\\ k\in K,f(x)(k)=\left\{\begin{array}{cc}{f}_x(k),\hfill & k\in E,\hfill \\ 0_L,\hfill & k\in K\setminus E.\hfill \end{array}\right.\end{array}$$

where $\sigma (k,k^{\prime })\in [0,1]$ represents the degree of similarity of two colors in K and the fuzzy similarity relation $\rho :X\times X\to [0,1]$ expresses the fact that pixels x and z are spatially close to each other. For example, we can set

$$(x,y)\in X\times X,\rho (x,y)=\left\{\begin{array}{cc}\frac{1}{d{(x,y)}^{\omega }},\hfill & d(x,y)\ne 0,\hfill \\ 1,\hfill & d(x,y)=0,\hfill \end{array}\right.$$

where $d:X\times X\to R_{+}$ is the real-valued metric in the set X and $\omega$ is a positive real number. Similarly, the similarity relation $\sigma$ can be defined by

$$k=[h_k,s_k,v_k],m=[h_m,s_m,v_m]\in K,\sigma (k,m):=1-\frac{|h_k-h_m|+|s_k-s_m|+|v_k-v_m|}{3},$$

where $h,s,v\in [0,1]$. In that case, the $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy set f represents the concept that describes the segments that correspond to the colors of the set K. This means that the point $x\in X$ corresponds to the color segment of color $k\in K$ with the truth value $f(x)(k)$.

The lower and upper approximations of the segment f are defined as the $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-rough set $({\mathcal{T}}^{\downarrow }(f),{\mathcal{T}}^{\uparrow }(f))$ of f with respect to the $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-relation $\mathcal{T}:X\times X\to R_2$, defined by

$$\begin{array}{c}(x,x^{\prime })\in X\times X,\mathcal{T}(x,x^{\prime })=(E,{\psi }_{x{x}^{\prime }})\in R_2,\\ k\in K,{\psi }_{x{x}^{\prime }}(k)=\sigma (S(x),k)\leftrightarrow \sigma (S(x^{\prime }),k)\in [0,1].\end{array}$$

According to Example 14, the rough $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy set $({\mathcal{T}}^{\downarrow }(f),{\mathcal{T}}^{\uparrow }(f))$ is defined by

$$\begin{array}{c}{\mathcal{T}}^{\downarrow }(f)(x)(k)=\left\{\begin{array}{cc}\underset{z\in X}{\bigwedge }\neg {\psi }_{xz}(k)\oplus f_z(k),\hfill & k\in E,\hfill \\ 0_L,\hfill & k\in K\setminus E,\hfill \end{array}\right.\\ {\mathcal{T}}^{\uparrow }(f)(x)(k)=\left\{\begin{array}{cc}\underset{z\in X}{\bigvee }{\psi }_{xz}(k)\otimes f_z(k),\hfill & k\in E,\hfill \\ 0_L,\hfill & k\in K\setminus E.\hfill \end{array}\right.\end{array}$$

The upper and lower approximations of the color segment f corresponding to the color $k\in K$ can be approximated by the $\alpha$-cuts, i.e., by subsets.

$$\begin{array}{c}{\mathcal{T}}^{\downarrow }(f){(k)}_{\alpha }=\{x\in X:{\mathcal{T}}^{\downarrow }(f)(x)(k)\ge \alpha \},\\ {\mathcal{T}}^{\uparrow }(f){(k)}_{\alpha }=\{x\in X:{\mathcal{T}}^{\uparrow }(f)(x)(k)\ge \alpha \},\end{array}$$

where $\alpha \in L$. The corresponding visualization of these color segments can be created, for example, so that the color of the pixels $x\in {\mathcal{T}}^{\uparrow }(f){(k)}_{\alpha }$ or $x\in {\mathcal{T}}^{\downarrow }(f){(k)}_{\alpha }$ will be $S(x)$ and the color of the other pixels will be transformed to the color on the black and white scale, that is, set the saturation to zero.

5.2. $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-Fuzzy Rough Sets

We illustrate how the same problem of the color segment approximation can be solved by rough $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy sets. To compare the results of Section 5.1 and Section 5.2, we use the $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy sets that represent the concept that describes a color segment, and we involve the same function $f_x\in L^K$ and transform it into the $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy set $X\to R_1$. For this purpose, we use the so-called intuitionistic fuzzy generators defined in [29].

Definition 14

([29]). A function $\phi :[0,1]\to [0,1]$ is called an intuitionistic fuzzy generator if $\phi (x)\le 1-x$ for all $x\in [0,1]$.

Using the intuitionistic fuzzy generator $\phi$, the $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy set $w_{k,\phi }$ is defined by

$$x\in X,w_{k,\phi }(x)=\left(f_x(k),\frac{1-f_x(k)}{1+\lambda f_x(k)}\right)\in {\mathcal{R}}_1,-1<\lambda <0,$$

which represents the intuitionistic concept describing the segment in the color image corresponding to the color $k\in K$. As in the previous example, using the definition of the relation ${\psi }_{x{x}^{\prime }}$, the approximation of this intuitionistic concept $w_{k,\phi }$ can be defined as the rough $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy set of $w_{k,\phi }$ with respect to the $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy relation ${\mathcal{F}}_k:X\times X\to R_1$, such that

$$(x,x^{\prime })\in X\times X,{\mathcal{F}}_k(x,x^{\prime })=\left({\psi }_{x{x}^{\prime }}(k),\phi ({\psi }_{x{x}^{\prime }}(k))\right)\in R_1,$$

where we use the same intuitionistic fuzzy generator $\phi$. According to Example 13, the upper and lower approximations of the intuitionistic color segment $w_{k,\phi }$ corresponding to color k are defined for $x\in X$ by

$$\begin{array}{c}{\mathcal{F}}_k^{\downarrow }(w_{k,\phi })(x)=\left(\underset{y\in Y}{\bigwedge }\phi ({\psi }_{xy}(k))\oplus w_k(y),\underset{y\in Y}{\bigvee }{\psi }_{xy}\otimes \phi (w_k(y))\right),\\ {\mathcal{F}}_k^{\uparrow }(w_{k,\phi })(x)=\left(\underset{y\in X}{\bigvee }{\psi }_{xy}(k)\otimes w_k(y),\underset{y\in Y}{\bigwedge }\phi ({\psi }_{xy}(k))\oplus \phi (w_k(y))\right).\end{array}$$

To be able to visualize these upper and lower intuitionistic approximations of $w_{k,\phi }$, we must first transform intuitionistic fuzzy sets into classical fuzzy sets. According to the procedure presented in [30], we use the transformation of elements $(\gamma ,\delta )\in R_1$ into the classical L value of a fuzzy set defined by

$$(\gamma ,\delta )\in {\mathcal{R}}_1\mapsto \frac{1}{2}(1+\gamma -\delta )\in L.$$

In that way, from $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy sets ${\mathcal{F}}^{\uparrow }(w_{k,\phi })$ and ${\mathcal{F}}^{\downarrow }(w_{k,\phi })$ we obtain standard L-fuzzy sets ${W_k}^{\uparrow }(w_{k,\phi })$ and ${W_k}^{\downarrow }(w_{k,\phi })$, and, analogously to the previous example, these fuzzy sets can be approximated by $\alpha$-cuts ${W_k}^{\uparrow }{(w_{k,\phi })}_{\alpha }$ and ${W_k}^{\downarrow }{(w_{k,\phi })}_{\alpha }$.

5.3. Visualization

Rough $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$ and $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy sets can be created from arbitrary-dimensional data; here, we will demonstrate visualization using 2D image data. The color of pixels $x\in {\mathcal{T}}^{\uparrow }(f){(k)}_{\alpha }$ or $x\in {\mathcal{T}}^{\downarrow }(f){(k)}_{\alpha }$ for $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy rough sets and ${W_k}^{\uparrow }{(w_{k,\phi })}_{\alpha }$ or ${W_k}^{\downarrow }{(w_{k,\phi })}_{\alpha }$ for $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$- fuzzy rough sets will be $S(x)$ and the color of the other pixels will be transformed to the color on the black and white scale, that is, the saturation of these pixels will be reduced to zero; see Figure 1 and Figure 2. The figures also visually nicely confirm the following:

• $|{\mathcal{T}}^{\downarrow }(f){(k)}_{\alpha }|\le |{\mathcal{T}}^{\uparrow }(f){(k)}_{\alpha }|$ for $({\mathcal{R}}_2,{\mathcal{R}}_2^{\ast })$-fuzzy rough sets,
• $|{W_k}^{\downarrow }{(w_{k,\phi })}_{\alpha }|\le |{W_k}^{\uparrow }{(w_{k,\phi })}_{\alpha }|$ for $({\mathcal{R}}_1,{\mathcal{R}}_1^{\ast })$-fuzzy rough sets,
• $|{\mathcal{T}}^{\downarrow }(f){(k)}_{\alpha }|\le |{W_k}^{\downarrow }{(w_{k,\phi })}_{\alpha }|$,
• $|{\mathcal{T}}^{\uparrow }(f){(k)}_{\alpha }|\le |{W_k}^{\uparrow }{(w_{k,\phi })}_{\alpha }|$.

6. Conclusions

The paper is a continuation of our previous paper [13], where we introduced the notion of semiring-valued fuzzy sets and investigated the F-transforms of these structures. In the actual paper, we focus on another construction that is commonly used in the theory and applications of L-fuzzy sets, namely the issue of rough L-fuzzy sets. The main goal of this paper was to create a tool that could be used to apply this method universally to a large part of new fuzzy structures, currently used mainly in applications, such as intuitionistic, hesitant, neutrosophic, or fuzzy soft sets and their mutual combinations. For the basic structure of this tool, we used the so-called dual pairs of semirings $(\mathcal{R},{\mathcal{R}}^{\ast })$ and fuzzy sets with values in these dual pairs of semirings, so-called $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets, which were presented in modified form in [13]. This structure makes it possible to transform a large part of new fuzzy structures with values in complete $MV$-algebras into suitable $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets, which in turn makes it possible to unify the theory of these new fuzzy structures.

Another possible use of this universal method of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets offers the possibility of creating new types of fuzzy sets, defined using suitable examples of dual pairs of semirings. We also gave examples of this procedure, when we mentioned the possibility of introducing fuzzy sets with values in Abelian l-groups of application of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets in many-level fuzzy sets and relations introduced by Šostak [24]. It can be assumed that further research in this direction will show many other examples of new types of fuzzy sets.

However, it should be noted that the universality of applications of this method for $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets has also limitations. An example of these limitations is the fact that, for example, some new fuzzy structures do not have uniformly established terminology, and use, for example, several types of fuzzy relations or several types of rough fuzzy structures. In that case, the transformation of these fuzzy structures into $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy structures can reflect only one selected variant of these constructions. If we want to transform another variant, it would probably require the use of a completely new dual pair of semirings.

Another type of limitation of using the $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets method to transform new types of fuzzy structures (e.g., intuitionistic, neutrosophic, or fuzzy soft sets) to $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets is that in all existing transformation examples it was necessary to assume that the basic value-set structure used in these types of fuzzy structures is the complete $MV$-algebra. If we want to reduce this assumption to a weaker assumption, it would be necessary to modify the definition of the basic algebraic structure, which we use to construct dual pairs of semirings, that is the $AMV$-algebra.

The great advantage of the presented method of transformation of various new fuzzy structures is the fact that instead of specific power set structures of different types of fuzzy sets and different types of their basic operations we can use one universal type of power set structure of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets with one structure of basic operations. This makes it possible to define for a large part of the new fuzzy structures most of the constructions (such as various approximations and transformations) on their power set structures in a uniform way.

Our further research will focus, among other things, on examples of new dual pairs of semirings, which could become the basis for new types of fuzzy sets which can be used in applications. At the same time, however, we will deal with the extension of theoretical tools applicable in the theory of $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets, such as algebraic or topological structures defined above as $(\mathcal{R},{\mathcal{R}}^{\ast })$-fuzzy sets.