Application of Fuzzy-Based Support Vector Regression to Forecast of International Airport Freight Volumes
Abstract
1. Introduction
2. Methods
2.1. Dataset Description
2.2. Support Vector Regression
2.3. Fuzzy SVR
| Algorithm 1: Fuzzy time series using variations of data | |
| Definition: Universal set U contains the interval between the least and greatest variations in the dataset. Ui = Xi+1 − Xi, i = 1, 2, …, n − 1 U = [Min [39], Max [39]] | |
| Input: Air traffic: passenger, aircraft movements, and freight data set Xi corresponds to time ti, i=1, 2, …, n. | |
| Output: Fuzzy model of air traffic volume time series with the smallest RMSE value. | |
| 1 | , where initial values m = 5, 6, 7, …, 11 |
| 2 | Calculate the C value of each interval t = 0 initial values k = 500, ε = 1 × 106, |
| 3 | if (t = i && i ≥ 1) |
| 4 | |
| 5 | if (a = 0 && b = 1) |
| 6 | |
| 7 | if (a = 0 && b ≠ 1) |
| 8 | |
| 9 | if (a ≠ 0 && b = 1) |
| 10 | |
| 11 | if (a ≠ 0 && b ≠ 1) |
| 12 | |
| 13 | Run IFTS to find |
| 14 | Find |
| 15 | Determine respective values of the set of the fuzzy set with C, |
| 16 | Choose a basis w=12 (1 < w < n), corresponding to the intervals of prior time. |
| 17 | . |
| 18 | Define F(t) the fuzzy forecasting of variations at the moment t |
| 19 | Forecast 7(m(7)×w(1)) fuzzy model data for time series, forecast value, and the result is calculated for the value t = w based on the variations in the result of prior values(t−1, …, t−w) |
| 20 | Each fuzzy model data are compared with real data, using the RMSE for all the fuzzy model data calculated, and we use the RMSE as an evaluation criterion to compare with the listed models. |
- The schedule in winter and summer in accordance with the time zone of each airport;
- The role of each airport in the global air transport network in terms of its unique function due to its geographical location;
- The continuous holidays of countries in each region;
- Demand for tourism in the low and peak seasons or the impact of significant activities, such as the Olympic Games or World Expo.
2.4. Evaluation Criteria
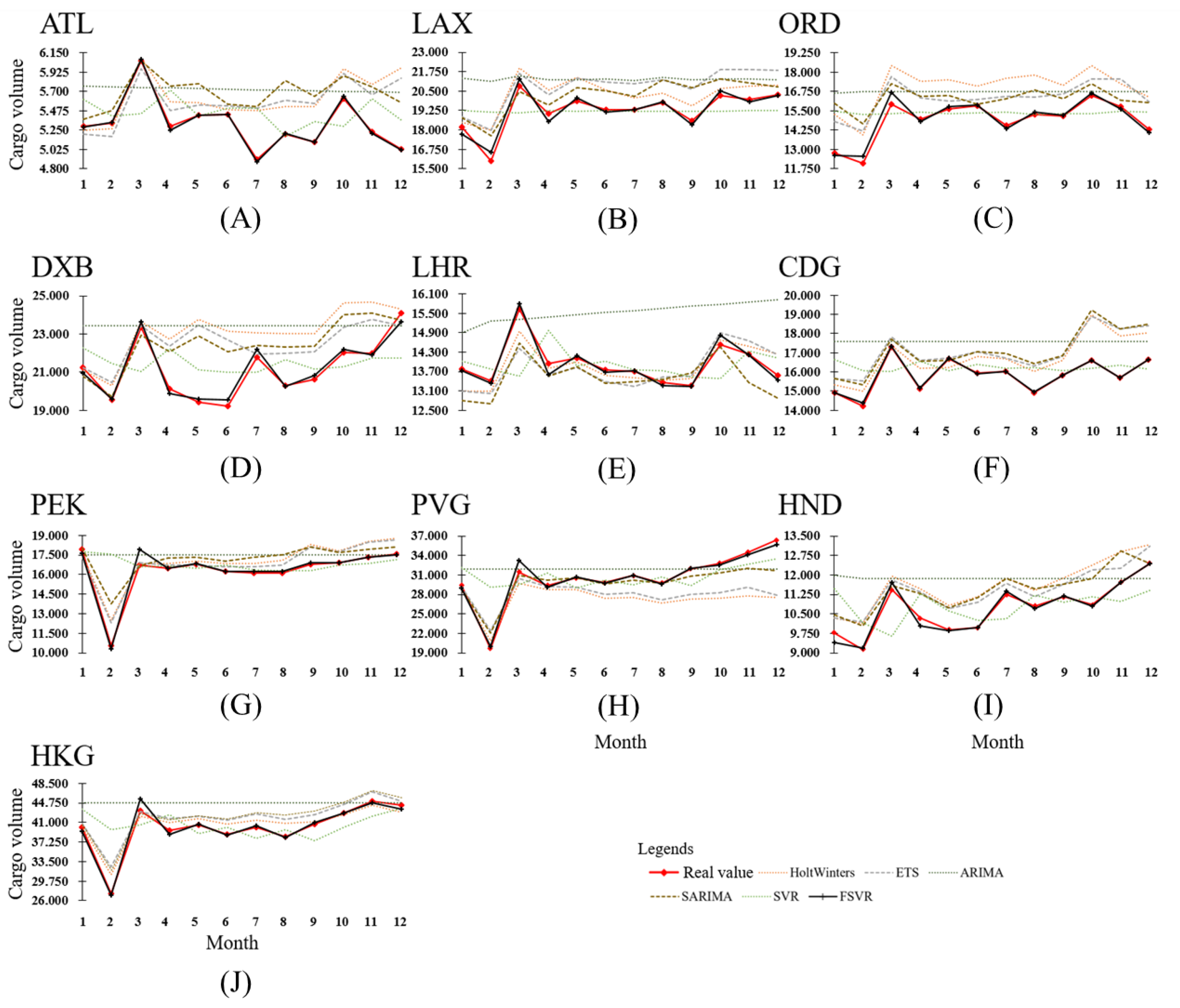
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ritzer, G.; Dean, P. Globalization: The Essentials; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Duarte, R.; Pinilla, V.; Serrano, A. Factors driving embodied carbon in international trade: A multiregional input–Output gravity model. Econ. Syst. Res. 2018, 30, 545–566. [Google Scholar] [CrossRef]
- Hannan, S.A. Revisiting the Determinants of Capital Flows to Emerging Markets—A Survey of the Evolving Literature; International Monetary Fund: Washington, DC, USA, 2018. [Google Scholar]
- Fatehi, K.; Choi, J. International Business Management; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- IATA. 20 Year Passenger Forecast; International Air Transport Association (IATA): Geneva, Switzerland, 2018. [Google Scholar]
- Dube, K.; Nhamo, G. Major Global aircraft manufacturers and emerging responses to the SDGs Agenda. In Scaling Up SDGs Implementation; Springer: Berlin/Heidelberg, Germany, 2020; pp. 99–113. [Google Scholar]
- Gupta, D.; Garg, A. Sustainable development and carbon neutrality: Integrated assessment of transport transitions in India. Transp. Res. Part D Transp. Environ. 2020, 85, 102474. [Google Scholar] [CrossRef]
- Alam, M.; Parveen, R. COVID-19 and Tourism. Int. J. Adv. Res. 2021, 9, 788–804. [Google Scholar] [CrossRef]
- Abate, M.; Christidis, P.; Purwanto, A.J. Government support to airlines in the aftermath of the COVID-19 pandemic. J. Air Transp. Manag. 2020, 89, 101931. [Google Scholar] [CrossRef] [PubMed]
- Bowen, J. Low-Cost Carriers in Emerging Countries; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Dorian, J.P.; Franssen, H.T.; Simbeck, D.R. Global challenges in energy. Energy Policy 2006, 34, 1984–1991. [Google Scholar] [CrossRef]
- Belobaba, P.; Odoni, A.; Barnhart, C. The Global Airline Industry; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wensveen, J.G. Air Transportation: A Management Perspective; Routledge: London, UK, 2018. [Google Scholar]
- Wong, K.K.; Song, H.; Witt, S.F.; Wu, D.C. Tourism forecasting: To combine or not to combine? Tour. Manag. 2007, 28, 1068–1078. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Valipoor, M.; Behbahani, S.M. Comparison of autoregressive static and artificial dynamic neural network for the forecasting of monthly inflow of dez reservoir. J. Environ. Sci. Technol. 2011, 13, 1–14. [Google Scholar]
- Saayman, A.; Saayman, M. Forecasting tourist arrivals in South Africa. Acta Commer. 2010, 10, 281–293. [Google Scholar] [CrossRef][Green Version]
- Hassani, H. Singular spectrum analysis: Methodology and comparison. J. Data Sci. 2007, 5, 239–257. [Google Scholar] [CrossRef]
- De Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting time series with complex seasonal patterns using exponential smoothing. J. Am. Stat. Assoc. 2011, 106, 1513–1527. [Google Scholar] [CrossRef]
- Suryani, E.; Chou, S.-Y.; Chen, C.-H. Dynamic simulation model of air cargo demand forecast and terminal capacity planning. Simul. Model. Pract. Theory 2012, 28, 27–41. [Google Scholar] [CrossRef]
- Alexander, D.; Merkert, R. Applications of gravity models to evaluate and forecast US international air freight markets post-GFC. Transp. Policy 2021, 104, 52–62. [Google Scholar] [CrossRef] [PubMed]
- Hassani, H.; Silva, E.S.; Antonakakis, N.; Filis, G.; Gupta, R. Forecasting accuracy evaluation of tourist arrivals. Ann. Tour. Res. 2017, 63, 112–127. [Google Scholar] [CrossRef]
- Cao, J.; Guan, X.; Zhang, N.; Wang, X.; Wu, H. A hybrid deep learning-based traffic forecasting approach integrating adjacency filtering and frequency decomposition. IEEE Access 2020, 8, 81735–81746. [Google Scholar] [CrossRef]
- Cao, X.; Ma, C.; Jia, Y. ARIMA and SVM Combination Forecast for Holiday Subway Passenger Traffic. In Proceedings of the 2018 World Transport Convention, Beijing, China, 18–21 June 2018. [Google Scholar]
- Bildirici, M.; Ersin, Ö. Asymmetric power and fractionally integrated support vector and neural network GARCH models with an application to forecasting financial returns in ise100 stock index. Econ. Comput. Econ. Cybern. Stud. Res. 2014, 48, 1–22. [Google Scholar]
- Sharifian, S.; Barati, M. An ensemble multiscale wavelet-GARCH hybrid SVR algorithm for mobile cloud computing workload prediction. Int. J. Mach. Learn. Cybern. 2019, 10, 3285–3300. [Google Scholar] [CrossRef]
- Gao, R.; Duru, O. Parsimonious fuzzy time series modelling. Expert Syst. Appl. 2020, 156, 113447. [Google Scholar] [CrossRef]
- Bose, M.; Mali, K. Designing fuzzy time series forecasting models: A survey. Int. J. Approx. Reason. 2019, 111, 78–99. [Google Scholar] [CrossRef]
- Vovan, T. An improved fuzzy time series forecasting model using variations of data. Fuzzy Optim. Decis. Mak. 2019, 18, 151–173. [Google Scholar] [CrossRef]
- Airports Council International. Preliminary World Airport Traffic Rankings Released. ACI World. 2019. Available online: https://aci.aero/2019/03/13/preliminary-world-airport-traffic-rankings-released/ (accessed on 5 July 2022).
- Unal, A.; Hu, Y.; Chang, M.E.; Odman, M.T.; Russell, A.G. Airport related emissions and impacts on air quality: Application to the Atlanta International Airport. Atmos. Environ. 2005, 39, 5787–5798. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Processing Syst. 1996, 9, 155–161. [Google Scholar]
- Müller, K.-R.; Smola, A.J.; Rätsch, G.; Schölkopf, B.; Kohlmorgen, J.; Vapnik, V. Predicting time series with support vector machines. In Proceedings of the International Conference on Artificial Neural Networks, Lausanne, Switzerland, 8–10 October 1997; pp. 999–1004. [Google Scholar]
- Rüping, S. SVM Kernels for Time Series Analysis; Technical Report: Komplexitätsreduktion in Multivariaten Datenstrukturen; Sonderforschungsbereich 475; Universität Dortmund: Dortmund, Germany, 2001. [Google Scholar]
- Rohmah, M.; Putra, I.; Hartati, R.; Ardiantoro, L. Comparison Four Kernels of SVR to Predict Consumer Price Index. J. Phys. Conf. Ser. 2021, 1737, 012018. [Google Scholar] [CrossRef]
- Yang, C.-H.; Moi, S.-H.; Hou, M.-F.; Chuang, L.-Y.; Lin, Y.-D. Applications of deep learning and fuzzy systems to detect cancer mortality in next-generation genomic data. IEEE Trans. Fuzzy Syst. 2020, 29, 3833–3844. [Google Scholar] [CrossRef]
- Yang, C.-H.; Chuang, L.-Y.; Lin, Y.-D. Epistasis analysis using an improved fuzzy C-means-based entropy approach. IEEE Trans. Fuzzy Syst. 2019, 28, 718–730. [Google Scholar] [CrossRef]
- Zeng, G.; Yu, W.; Wang, R.; Lin, A. Research on Mosaic Image Data Enhancement for Overlapping Ship Targets. arXiv 2021, arXiv:2105.05090. [Google Scholar]
- Zhang, Y.; Li, G.; Muskat, B.; Law, R. Tourism demand forecasting: A decomposed deep learning approach. J. Travel Res. 2021, 60, 981–997. [Google Scholar] [CrossRef]
- Parashar, N.; Khan, J.; Aslfattahi, N.; Saidur, R.; Yahya, S.M. Prediction of the Dynamic Viscosity of MXene/palm Oil Nanofluid Using Support Vector Regression. In Recent Trends in Thermal Engineering; Springer: Berlin/Heidelberg, Germany, 2022; pp. 49–55. [Google Scholar]
- Yang, Y.; Che, J.; Deng, C.; Li, L. Sequential grid approach based support vector regression for short-term electric load forecasting. Appl. Energy 2019, 238, 1010–1021. [Google Scholar] [CrossRef]
- Shamsah, S.M.I.; Owolabi, T.O. Modeling the maximum magnetic entropy change of doped manganite using a grid search-based extreme learning machine and hybrid gravitational search-based support vector regression. Crystals 2020, 10, 310. [Google Scholar] [CrossRef]

| Airport | Min | Max | Mean | Q1 | Q3 | IQR | SD | CV |
|---|---|---|---|---|---|---|---|---|
| Atlanta | 4.76 | 6.39 | 5.46 | 5.16 | 5.71 | 0.56 | 0.38 | 6.92 |
| Beijing | 10.371 | 18.87 | 16.49 | 16.10 | 17.52 | 1.43 | 1.74 | 10.54 |
| Dubai | 18.62 | 24.10 | 21.45 | 20.32 | 22.21 | 1.89 | 1.39 | 6.47 |
| Los Angeles | 15.16 | 21.66 | 19.01 | 18.06 | 20.42 | 2.36 | 1.64 | 8.63 |
| Haneda, Tokyo | 8.43 | 13.19 | 10.64 | 9.89 | 11.46 | 1.57 | 1.13 | 10.66 |
| O’Hare | 11.49 | 18.33 | 15.20 | 14.16 | 16.46 | 2.31 | 1.57 | 10.29 |
| Heathrow, London | 12.33 | 16.31 | 14.09 | 13.32 | 14.72 | 1.40 | 0.94 | 6.70 |
| Hongkong | 26.40 | 47.50 | 39.87 | 37.10 | 43.10 | 6.00 | 4.35 | 10.91 |
| Pudong, Shanghai | 19.43 | 36.39 | 29.82 | 27.87 | 32.06 | 4.19 | 3.36 | 11.28 |
| Charles de Gaulle, Paris | 14.01 | 20.10 | 16.24 | 15.32 | 16.91 | 1.59 | 1.19 | 7.30 |
| Total | 141.00 | 222.82 | 188.27 | 177.29 | 200.57 | 23.29 | 17.69 | 89.71 |
| Airport | Freight Volume | |
|---|---|---|
| Seasonal | Trend | |
| Atlanta (ATL) | 0.74 | 0.80 |
| Dubai (PEK) | 0.96 | 0.77 |
| Dubai (DXB) | 0.69 | 0.48 |
| Los Angeles (LAX) | 0.86 | 0.87 |
| Haneda (HND) | 0.92 | 0.87 |
| O’Hare (ORD) | 0.73 | 0.71 |
| Heathrow, London (LHR) | 0.88 | 0.90 |
| Hongkong (HKG) | 0.94 | 0.87 |
| Pudong (PVG) | 0.93 | 0.89 |
| Charles de Gaulle (CDG) | 0.79 | 0.53 |
| Airport | Holt–Winters (ADD) (α, β, γ) | ETS (α, β, γ) | ARIMA (p, d, q) | SARIMA (p, d, q)(P, D, Q)S | SVR (ε, C, σ) | FSVR (ε, C, σ) |
|---|---|---|---|---|---|---|
| ATL | (0.404, 0.000, 0.194) | (0.462, N, 0.001) | (1, 0, 1) with non-zero mean | (2, 0, 2) (1, 0, 0) with non-zero mean | (0.536, 1.000, 0.125) | (0.010, 91.000, 0.125) |
| LAX | (0.731, 0.000, 1.000) | (0.772, 0.001, 0.001) | (4, 1, 1) | (2, 0, 0) (1, 0, 0) with non-zero mean | (0.59, 0.020, 0.04) | (0.010, 0.500, 0.100) |
| ORD | (0.438, 0.026, 1.000) | (0.589, N, 0.001) | (0, 1, 2) | (1, 0, 0) (1, 0, 0) with non-zero mean | (0.616, 0.010, 0.758) | (0.044, 0.794, 0.054) |
| DXB | (0.797, 0.000, 1.000) | (0.718, N, 0.002) | (0, 1, 2) with drift | (0, 1, 0) (0, 1, 0) | (0.435, 1.000, 0.189) | (0.088, 90.510, 0.088) |
| LHR | (0.046, 0.661, 0.432) | (0.001, 0.001, 0.003) φ = 0.973 | (0, 1, 0) | (0, 1, 1)(0, 1, 1) | (0.354, 0.316, 0.074) | (0.010, 5.000, 0.016) |
| CDG | (0.273, 0.000, 0.560) | (0.365, N, 0.001) | (0, 1, 0) | (0, 1, 1) (0, 1, 1) | (0.500, 0.562, 0.063) | (0.100, 256.000, 0.100) |
| PEK | (0.327, 0.006, 0.612) | (0.424, N, 0.001) | (0, 1, 2) | (1, 0, 1) (1, 0, 0) with non-zero mean | (0.650, 8.000, 0.101) | (0.100, 64.000, 1.000) |
| PVG | (0.333, 0.000, 0.479) | (0.373, N, 0.001) | (0, 1, 1) | (0, 0, 2) (1, 0, 1) with non-zero mean | (0.287, 0.251, 0.574) | (0.032, 512.000, 0.001) |
| HND | (0.208, 0.569, 0.724) | (0.188, 0.133, 0.001) | (0, 1, 1) | (0, 1, 2) (0, 1, 1) | (0.100, 1.000, 0.300) | (0.100, 128.000, 0.001) |
| HKG | (0.204, 0.317, 0.749) | (0.515, N, 0.001) | (0, 1, 0) | (1, 1, 0) (0, 1, 1) | (0.650, 1.00, 0.790) | (0.100, 512.000, 0.001) |
| Airport | Criteria | Holt–Winters (ADD) | ETS | ARIMA | SARIMA | SVR | FSVR |
|---|---|---|---|---|---|---|---|
| ATL | MAPE(%) | 6.120 | 6.036 | 8.601 | 6.915 | 5.381 | 0.300 |
| MAE | 0.316 | 0.313 | 0.449 | 0.359 | 0.286 | 0.016 | |
| RMSE | 0.412 | 0.385 | 0.485 | 0.419 | 0.349 | 0.020 | |
| LAX | MAPE(%) | 5.304 | 7.961 | 10.782 | 5.418 | 4.937 | 1.431 |
| MAE | 1.002 | 1.521 | 1.988 | 1.024 | 0.914 | 0.268 | |
| RMSE | 1.115 | 1.577 | 2.304 | 1.139 | 1.223 | 0.321 | |
| ORD | MAPE(%) | 14.430 | 9.957 | 13.146 | 9.957 | 6.835 | 1.590 |
| MAE | 2.125 | 1.441 | 1.830 | 1.406 | 0.933 | 0.232 | |
| RMSE | 2.176 | 1.536 | 2.204 | 1.628 | 1.334 | 0.297 | |
| DXB | MAPE(%) | 9.781 | 7.356 | 11.845 | 7.376 | 6.708 | 1.071 |
| MAE | 1.997 | 1.490 | 2.404 | 1.512 | 1.410 | 0.230 | |
| RMSE | 2.425 | 1.931 | 2.735 | 1.835 | 1.574 | 0.266 | |
| LHR | MAPE(%) | 2.154 | 3.287 | 11.952 | 3.703 | 3.793 | 0.816 |
| MAE | 0.303 | 0.465 | 1.641 | 0.520 | 0.546 | 0.115 | |
| RMSE | 0.374 | 0.535 | 1.740 | 0.610 | 0.778 | 0.154 | |
| CDG | MAPE(%) | 6.454 | 7.916 | 11.585 | 5.697 | 5.753 | 0.176 |
| MAE | 1.019 | 1.243 | 1.779 | 0.900 | 0.887 | 0.026 | |
| RMSE | 1.211 | 1.424 | 1.979 | 1.053 | 1.050 | 0.047 | |
| PEK | MAPE(%) | 5.566 | 4.688 | 9.925 | 6.649 | 7.125 | 1.197 |
| MAE | 0.840 | 0.705 | 1.311 | 0.952 | 0.854 | 0.190 | |
| RMSE | 0.998 | 0.865 | 2.195 | 1.229 | 2.040 | 0.373 | |
| PVG | MAPE(%) | 10.544 | 9.353 | 10.497 | 4.180 | 9.011 | 1.243 |
| MAE | 3.385 | 2.927 | 2.704 | 1.263 | 2.377 | 0.384 | |
| RMSE | 4.190 | 3.713 | 4.114 | 1.827 | 3.264 | 0.598 | |
| HND | MAPE(%) | 8.492 | 6.867 | 12.366 | 6.994 | 7.930 | 1.114 |
| MAE | 0.900 | 0.720 | 1.254 | 0.729 | 0.843 | 0.117 | |
| RMSE | 0.948 | 0.780 | 1.475 | 0.811 | 0.977 | 0.170 | |
| HKG | MAPE(%) | 3.688 | 5.615 | 13.717 | 6.100 | 8.777 | 1.254 |
| MAE | 1.347 | 2.061 | 4.808 | 2.292 | 3.099 | 0.510 | |
| RMSE | 1.648 | 2.431 | 6.454 | 2.578 | 4.220 | 0.797 | |
| Ave. of MAPE(%) | 7.253 | 6.904 | 11.442 | 6.299 | 6.625 | 1.019 | |
| Ave. of MAE | 1.323 | 1.288 | 2.017 | 1.096 | 1.215 | 0.209 | |
| Ave. of RMSE | 1.550 | 1.518 | 2.568 | 1.313 | 1.681 | 0.304 | |
| Order | Freight Volume | ||
|---|---|---|---|
| RMSE | MAPE | No. of Support Vectors | |
| 12 periods behind | 0.586 | 10.555 | 51 |
| 1 period behind | 0.368 | 5.523 | 46 |
| Area | North America | Middle East and Europe | Asia | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Airport | ATL | LAX | ORD | DXB | LHR | CDG | PEK | PVG | HND | HKG |
| Freight volume | 5 | 6 | 7 | 10 | 7 | 6 | 6 | 7 | 9 | 6 |
| Freight Volume | Lag1-RMSE | Fuzzy-RMSE |
|---|---|---|
| ATL | 0.397 | 0.048 |
| LAX | 1.462 | 0.586 |
| ORD | 1.438 | 0.452 |
| LHR | 0.855 | 0.250 |
| CDG | 1.420 | 0.055 |
| DXB | 1.416 | 0.439 |
| PEK | 2.033 | 0.574 |
| PVG | 3.237 | 0.943 |
| HKG | 4.252 | 1.328 |
| HND | 1.122 | 0.300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.-H.; Shao, J.-C.; Liu, Y.-H.; Jou, P.-H.; Lin, Y.-D. Application of Fuzzy-Based Support Vector Regression to Forecast of International Airport Freight Volumes. Mathematics 2022, 10, 2399. https://doi.org/10.3390/math10142399
Yang C-H, Shao J-C, Liu Y-H, Jou P-H, Lin Y-D. Application of Fuzzy-Based Support Vector Regression to Forecast of International Airport Freight Volumes. Mathematics. 2022; 10(14):2399. https://doi.org/10.3390/math10142399
Chicago/Turabian StyleYang, Cheng-Hong, Jen-Chung Shao, Yen-Hsien Liu, Pey-Huah Jou, and Yu-Da Lin. 2022. "Application of Fuzzy-Based Support Vector Regression to Forecast of International Airport Freight Volumes" Mathematics 10, no. 14: 2399. https://doi.org/10.3390/math10142399
APA StyleYang, C.-H., Shao, J.-C., Liu, Y.-H., Jou, P.-H., & Lin, Y.-D. (2022). Application of Fuzzy-Based Support Vector Regression to Forecast of International Airport Freight Volumes. Mathematics, 10(14), 2399. https://doi.org/10.3390/math10142399








