Research on Maximum Likelihood b Value and Confidence Limits Estimation in Doubly Truncated Apparent Frequency–Amplitude Distribution in Rock Acoustic Emission Tests
Abstract
:1. Introduction
2. Derivation of MLE b Value and Confidence Limits Estimation Scheme in DTFAD for Rock AE Tests
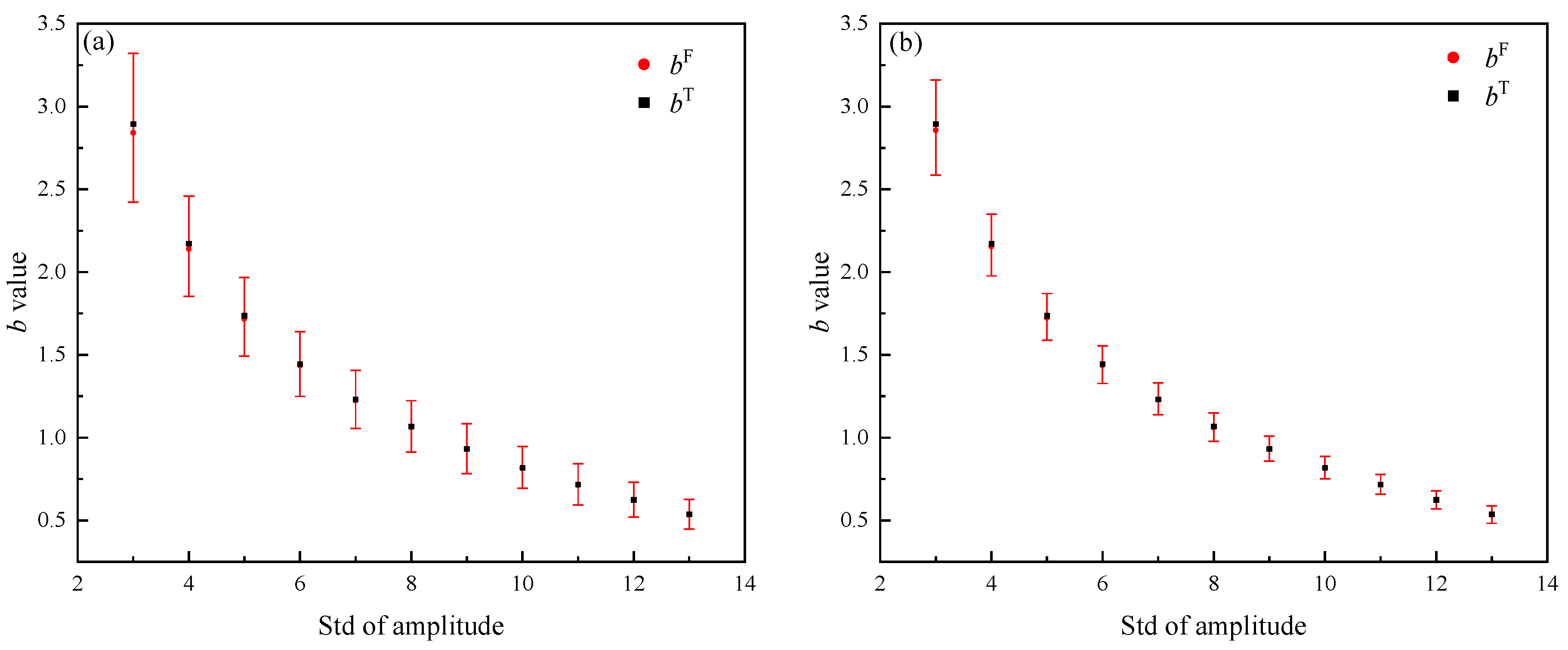
3. Performance Verification of the Derived MLE b Value and Confidence Limits Estimation Scheme in DTFAD Based on Synthetic Data
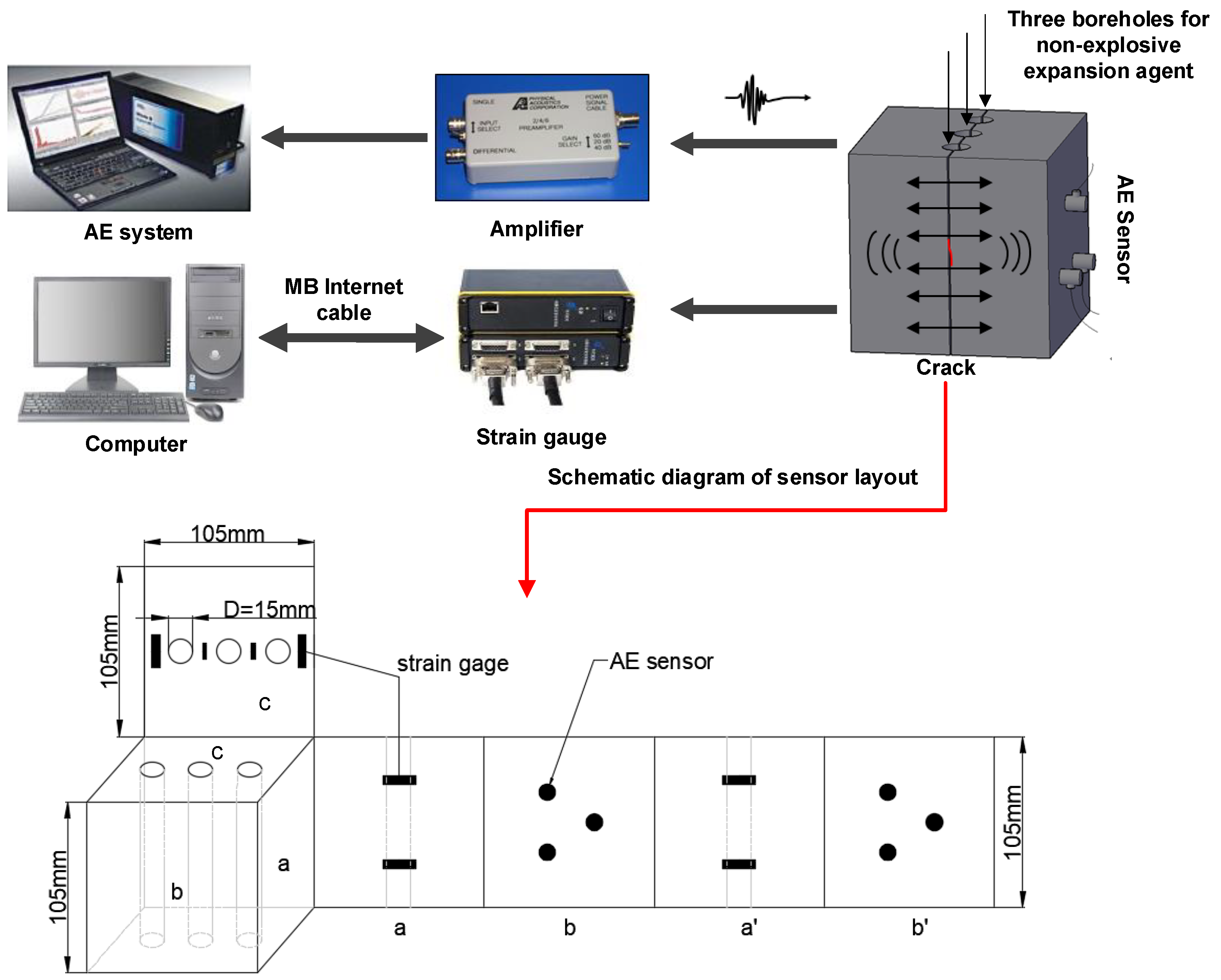
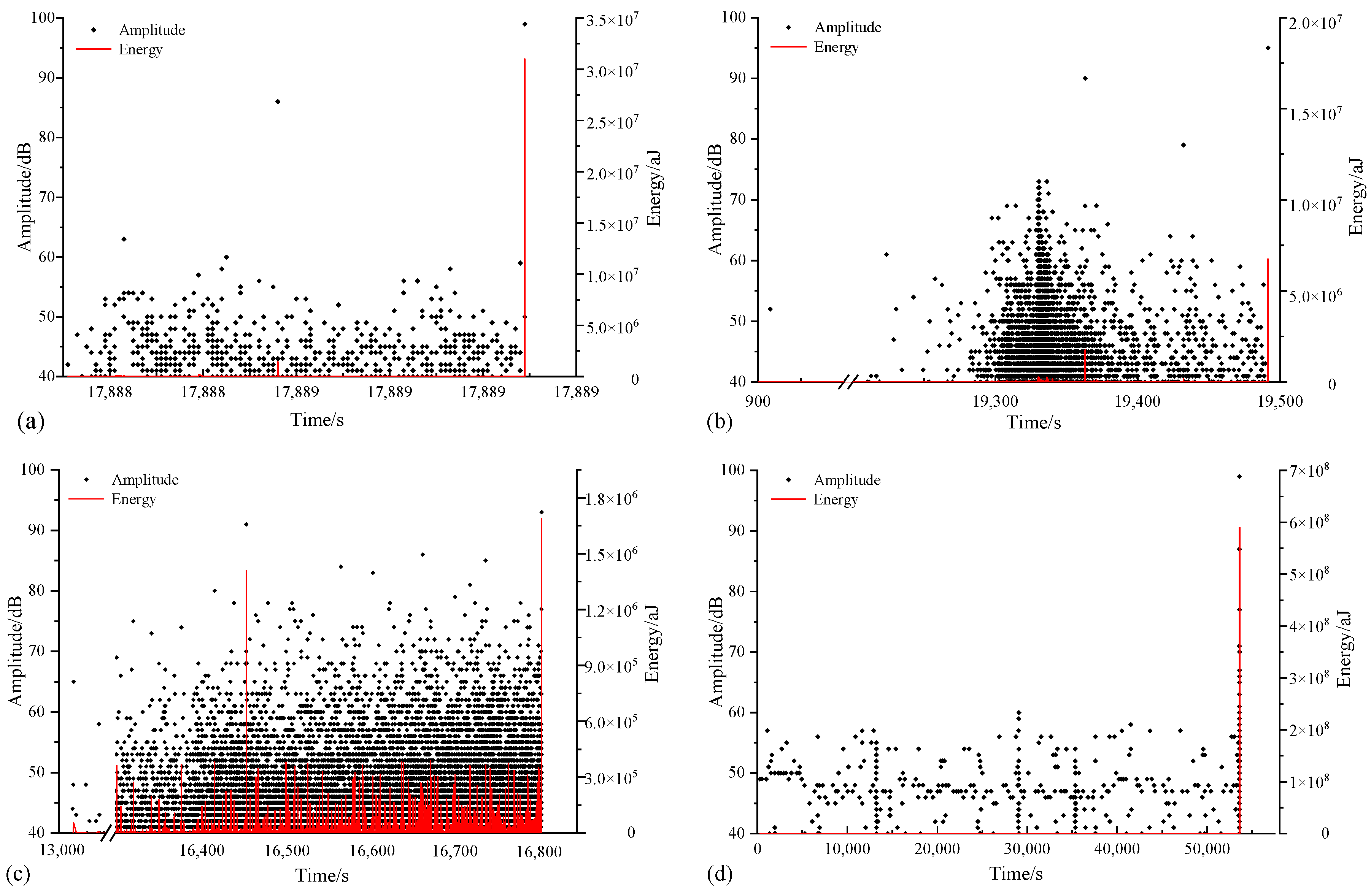
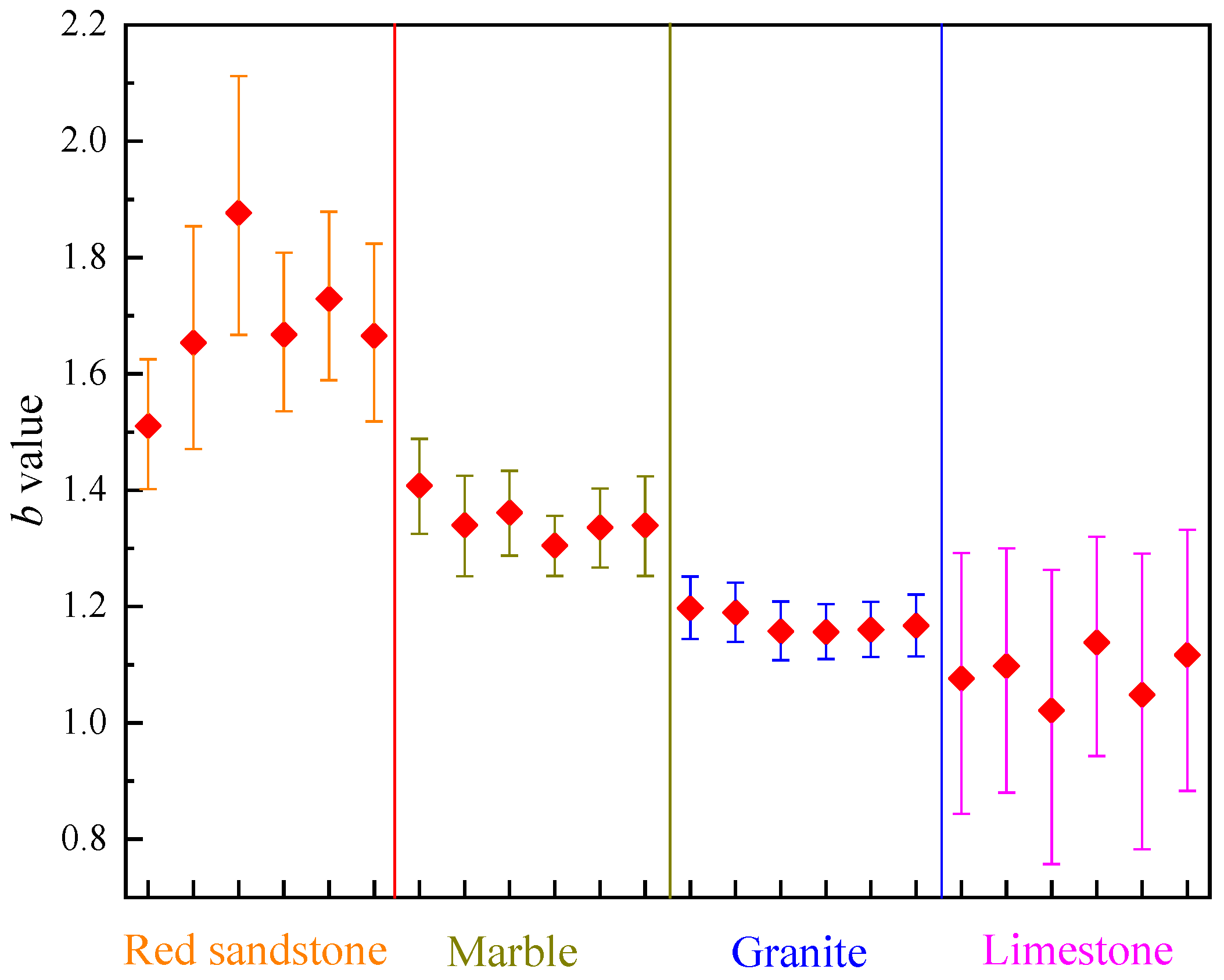
4. Applicability of the MLE b Value and Confidence Limits Estimation Scheme in Specifically Designed Rock Deformation Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Amorese, D. Applying a change-point detection method on frequency-magnitude distributions. Bull. Seismol. Soc. Am. 2007, 97, 1742–1749. [Google Scholar] [CrossRef]
- Shi, Y.; Bolt, B.A. The standard error of the magnitude-frequency b value. Bull. Seismol. Soc. Am. 1982, 72, 1677–1687. [Google Scholar] [CrossRef]
- Page, R. Aftershocks and microaftershocks of the great Alaska earthquake of 1964. Bull. Seismol. Soc. Am. 1968, 58, 1131–1168. [Google Scholar]
- Bender, B. Maximum likelihood estimation of b values for magnitude grouped data. Bull. Seismol. Soc. Am. 1983, 73, 831–851. [Google Scholar] [CrossRef]
- Main, I.G.; Meredith, P.G.; Henderson, J.R.; Sammonds, P.R. Positive and negative feedback in the earthquake cycIe: The role of pore fluids on states of criticality in the crust. Ann. Geophys. 1994, 37, 1461–1479. [Google Scholar]
- Telesca, L. Maximum likelihood estimation of the nonextensive parameters of the earthquake cumulative magnitude distribution. Bull. Seismol. Soc. Am. 2012, 102, 886–891. [Google Scholar] [CrossRef]
- Shiotani, T. Application of the AE Improved b-Value to Quantiative Evaluation of Fracture Process in Concrete-Materials. J. Acoust. Emiss. 2001, 19, 118–133. [Google Scholar]
- Rao, M.; Lakshmi, K.J.P. Analysis of b-value and improved b-value of acoustic emissions accompanying rock fracture. Curr. Sci. 2005, 89, 1577–1582. [Google Scholar]
- Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I.; Stavrakas, I.; Triantis, D. Mechanical response of notched marble beams under bending versus acoustic emissions and electric activity. J. Theor. Appl. Mech. 2018, 56, 523–547. [Google Scholar] [CrossRef]
- Casertano, L. A statistical analysis of upper and lower limits of earthquake magnitude. Pure Appl. Geophys. 1982, 120, 840–849. [Google Scholar] [CrossRef]
- Cooke, P. Statistical inference for bounds of random variables. Biometrika 1979, 66, 367–374. [Google Scholar] [CrossRef]
- Cooke, P. Optimal linear estimation of bounds of random variables. Biometrika 1980, 67, 257–258. [Google Scholar] [CrossRef]
- Kijko, A.; Sellevoll, M.A. Estimation of earthquake hazard parameters from incomplete data files Part I Utilization of extreme and complete catalogs with different threshold magnitudes. Bull. Seismol. Soc. Am. 1989, 79, 645–654. [Google Scholar] [CrossRef]
- Tate, R.F. Unbiased estimation: Functions of location and scale parameters. Ann. Math. Stat. 1959, 30, 341–366. [Google Scholar] [CrossRef]
- Yegulalp, T.M.; Kuo, J.T. Statistical prediction of the occurrence of maximum magnitude earthquakes. Bull. Seismol. Soc. Am. 1974, 64, 393–414. [Google Scholar] [CrossRef]
- Zöller, G.; Holschneider, M.; Hainzl, S. The maximum earthquake magnitude in a time horizon: Theory and case studies. Bull. Seismol. Soc. Am. 2013, 103, 860–875. [Google Scholar] [CrossRef] [Green Version]
- Holschneider, M.; Zöller, G.; Hainzl, S. Estimation of the maximum possible magnitude in the framework of a doubly truncated Gutenberg-Richter model. Bull. Seismol. Soc. Am. 2011, 101, 1649–1659. [Google Scholar] [CrossRef]
- Geller, R.J.; Jackson, D.D.; Kagan, Y.Y.; Mulargia, F. Earthquakes cannot be predicted. Science 1997, 275, 1616. [Google Scholar] [CrossRef] [Green Version]
- Goebel, T.H.W.; Schorlemmer, D.; Becker, T.W.; Dresen, G.; Sammis, C.G. Acoustic emissions document stress changes over many seismic cycles in stick-slip experiments. Geophys. Res. Lett. 2013, 40, 2049–2054. [Google Scholar] [CrossRef] [Green Version]
- Lockner, D. The role of acoustic emission in the study of rock fracture. Int. J. Rock Mech. Min. Sci. 1993, 30, 883–899. [Google Scholar] [CrossRef]
- Lei, X.; Masuda, K.; Nishizawa, O.; Jouniaux, L.; Liu, L.; Ma, W.; Satoh, T.; Kusunose, K. Detailed analysis of acoustic emission activity during catastrophic fracture of faults in rock. J. Struct. Geol. 2004, 26, 247–258. [Google Scholar] [CrossRef]
- Mogi, K. The Influence of Dimensions of Specimens of the Fracture Strength of Rocks-comparison between the Strength of Rock Specimens and that of the Earth’s Crust. Bull. Earthq. Res. Inst. Univ. Tokyo. 1962, 40, 175–185. [Google Scholar]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar] [CrossRef]
- Lei, X.-L.; Kusunose, K.; Nishizawa, O.; Cho, A.; Satoh, T. On the spatio-temporal distribution of acoustic emissions in two granitic rocks under triaxial compression: The role of pre-existing cracks. Geophys. Res. Lett. 2000, 27, 1997–2000. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Qin, X.; Xiling, L.; Xibing, L.; Yu, L.; Daolong, C. Study on the acoustic emission characteristics of different rock types and its fracture mechanism in Brazilian splitting test. Front. Phys. 2021, 9, 192. [Google Scholar]
- Liu, X.; Li, X.; Hong, L.; Yin, T.B.; Rao, M. Acoustic emission characteristics of rock under impact loading. J. Cent. S. Univ. 2015, 22, 3571–3577. [Google Scholar] [CrossRef]
- Thompson, B.D.; Young, R.P.; Lockner, D.A. Fracture in Westerly granite under AE feedback and constant strain rate loading: Nucleation, quasi-static propagation, and the transition to unstable fracture propagation. Pure Appl. Geophys. 2006, 163, 995–1019. [Google Scholar] [CrossRef]
- Zang, A.; Christian Wagner, F.; Stanchits, S.; Dresen, G.; Andresen, R.; Haidekker, M.A. Source analysis of acoustic emissions in Aue granite cores under symmetric and asymmetric compressive loads. Geophys. J. Int. 1998, 135, 1113–1130. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Liu, X.; He, W.; Xia, C.; Gong, F.; Li, X.; Cao, X. Effect of attenuation on amplitude distribution and b value in rock acoustic emission tests. Geophys. J. Int. 2022, 229, 933–947. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Liu, H.; Du, K.; Liu, X. Acoustic Emission b Value Characteristics of Granite under True Triaxial Stress. Mathematics 2022, 10, 451. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Z.; Li, X.; Gong, F.; Du, K. Experimental study on the effect of strain rate on rock acoustic emission characteristics. Int. J. Rock Mech. Min. Sci. 2020, 133, 104420. [Google Scholar] [CrossRef]
- Xie, Q.; Li, S.; Liu, X.; Gong, F.-Q.; Li, X.-B. Effect of loading rate on fracture behaviors of shale under mode I loading. J. Cent. S. Univ. 2020, 27, 3118–3132. [Google Scholar] [CrossRef]
- Cox, S.J.D.; Meredith, P.G. Microcrack formation and material softening in rock measured by monitoring acoustic emissions. Int. J. Rock Mech. Min. Sci. 1993, 30, 11–24. [Google Scholar] [CrossRef]
- Sagar, R.V.; Prasad, B.K.R.; Kumar, S.S. An experimental study on cracking evolution in concrete and cement mortar by the b-value analysis of acoustic emission technique. Cem. Concr. Res. 2012, 42, 1094–1104. [Google Scholar] [CrossRef]
- Weiss, J. The role of attenuation on acoustic emission amplitude distributions and b-values. Bull. Seismol. Soc. Am. 1997, 87, 1362–1367. [Google Scholar]
- Cosentino, P.; Ficarra, V.; Luzio, D. Truncated exponential frequency-magnitude relationship in earthquake statistics. Bull. Seismol. Soc. Am. 1977, 67, 1615–1623. [Google Scholar] [CrossRef]
- Liu, X.; Han, M.; He, W.; Li, X.B.; Chen, D.L. A new b value estimation method in rock acoustic emission testing. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019658. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula log N= a-bM and its confidence limits. Bull. Earthq. Res. Inst. Tokyo Univ. 1965, 43, 237–239. [Google Scholar]
- Utsu, T. A method for determining the value of “b” in a formula log n= a-bm showing the magnitude-frequency relation for earthquakes. Geophys. Bull. Hokkaido Univ. 1965, 13, 99–103. [Google Scholar]
- Marzocchi, W.; Sandri, L. A review and new insights on the estimation of the b-valueand its uncertainty. Ann. Geophys. 2003, 46, 1271–1282. [Google Scholar] [CrossRef]
- Unander, T.E. The effect of attenuation on b-values in acoustic emission measurements—A theoretical investigation. In Proceedings of the 34th U.S. Symposium on Rock Mechanics (USRMS), Madison, WI, USA, 28 June 1993. [Google Scholar]
- Nishikawa, T.; Ide, S. Earthquake size distribution in subduction zones linked to slab buoyancy. Nat. Geosci. 2014, 7, 904–908. [Google Scholar] [CrossRef]
- Wang, K.; Bilek, S.L. Invited review paper: Fault creep caused by subduction of rough seafloor relief. Tectonophysics 2014, 610, 1–24. [Google Scholar] [CrossRef]
- Yang, J.; Chen, J.; Liu, H.; Zheng, J. Comparison of two large earthquakes in China: The 2008 Sichuan Wenchuan Earthquake and the 2013 Sichuan Lushan Earthquake. Nat Haz. 2014, 73, 1127–1136. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ma, J.; Sun, D.; Zhang, L.; Chen, Y. AE characteristics of rockburst tendency for granite influenced by water under uniaxial loading. Front. Earth Sci. 2020, 8, 55. [Google Scholar] [CrossRef] [Green Version]
- Kurkoulis, S.K.; Pasiou, E.D.; Dakanali, I.; Stavrakas, I.; Triantis, D. Notched marble plates under tension: Detecting prefailure indicators and predicting entrance to the “critical stage”. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 776–786. [Google Scholar] [CrossRef]
- Kurkoulis, S.K.; Pasiou, E.D.; Loukidis, A.; Stavrakas, I.; Triantis, D. Comparative Assessment of Criticality Indices Extracted from Acoustic and Electrical Signals Detected in Marble Specimens. Infrastructures 2022, 7, 15. [Google Scholar] [CrossRef]
- Triantis, D.; Pasiou, E.D.; Stavrakas, I.; Kourkoulis, S.K. Hidden Affinities Between Electric and Acoustic Activities in Brittle Materials at Near-Fracture Load Levels. Rock Mech. Rock Eng. 2022, 55, 1325–1342. [Google Scholar] [CrossRef]
- Liu, X.; Cui, J.; Li, X.; Liu, Z. Study on attenuation characteristics of elastic wave in different types of rocks. J. Rock. Mech. Eng. 2018, 37, 3223–3230. [Google Scholar]


| Data Volume | bT | bA | bF | Confidence Limits of bF | Segment Determined by FGS | |||
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | Left Endpoint | Right Endpoint | Span/20 | ||||
| 300 | 2.1715 | 3.2272 | 2.0804 | 0.7956 | 4.0562 | 40.71 | 48.55 | 0.3920 |
| 1.0666 | 2.4161 | 1.0753 | 0.2272 | 2.3090 | 41.96 | 53.46 | 0.5750 | |
| 0.6245 | 1.7274 | 0.5716 | 0.1478 | 1.4862 | 43.92 | 62.64 | 0.9360 | |
| 500 | 2.1715 | 3.2211 | 2.1098 | 1.0917 | 3.5840 | 40.50 | 48.24 | 0.3870 |
| 1.0666 | 2.1184 | 1.0090 | 0.4725 | 1.7834 | 41.61 | 53.22 | 0.5805 | |
| 0.6245 | 1.9165 | 0.6119 | 0.2102 | 1.1016 | 43.68 | 58.36 | 0.7340 | |
| 800 | 2.1715 | 3.0030 | 2.1350 | 1.3169 | 3.2732 | 40.42 | 48.83 | 0.4205 |
| 1.0666 | 2.0981 | 1.0634 | 0.5701 | 1.6672 | 42.15 | 54.49 | 0.6170 | |
| 0.6245 | 1.6907 | 0.5981 | 0.2518 | 1.0192 | 43.03 | 58.34 | 0.7655 | |
| 1000 | 2.1715 | 2.9978 | 2.1307 | 1.3936 | 3.0845 | 40.37 | 48.75 | 0.4190 |
| 1.0666 | 2.0112 | 1.0649 | 0.5634 | 1.6356 | 42.05 | 54.70 | 0.6325 | |
| 0.6245 | 1.4890 | 0.6068 | 0.3329 | 0.9525 | 43.74 | 61.26 | 0.8760 | |
| 2000 | 2.1715 | 2.7451 | 2.1751 | 1.6421 | 2.4591 | 40.22 | 50.31 | 0.5045 |
| 1.0666 | 1.8940 | 1.0618 | 0.7085 | 1.4579 | 41.73 | 54.83 | 0.6550 | |
| 0.6245 | 1.1968 | 0.6191 | 0.4270 | 0.8486 | 44.11 | 66.35 | 1.1120 | |
| 3000 | 2.1715 | 2.6223 | 2.1502 | 1.7768 | 2.5957 | 40.21 | 51.60 | 0.5695 |
| 1.0666 | 1.6856 | 1.0676 | 0.8410 | 1.3162 | 40.96 | 57.22 | 0.8130 | |
| 0.6245 | 1.0594 | 0.6190 | 0.4856 | 0.7686 | 42.56 | 67.91 | 1.2675 | |
| 5000 | 2.1715 | 2.4491 | 2.1387 | 1.8641 | 2.4501 | 40.16 | 53.52 | 0.6680 |
| 1.0666 | 1.4626 | 1.0627 | 0.9261 | 1.2111 | 40.68 | 60.44 | 0.9880 | |
| 0.6245 | 0.9476 | 0.6224 | 0.5268 | 0.7226 | 41.94 | 71.78 | 1.4920 | |
| 8000 | 2.1715 | 2.3873 | 2.1558 | 1.9541 | 2.3842 | 40.10 | 55.16 | 0.7530 |
| 1.0666 | 1.2874 | 1.0645 | 0.9721 | 1.1652 | 40.28 | 64.87 | 1.2295 | |
| 0.6245 | 0.8366 | 0.6209 | 0.5616 | 0.6840 | 41.67 | 75.96 | 1.7145 | |
| 10,000 | 2.1715 | 2.3371 | 2.1548 | 1.9770 | 2.3495 | 40.02 | 55.52 | 0.7750 |
| 1.0666 | 1.2592 | 1.0612 | 0.9782 | 1.1495 | 40.26 | 65.82 | 1.2780 | |
| 0.6245 | 0.8086 | 0.6226 | 0.5694 | 0.6784 | 41.27 | 77.59 | 1.8160 | |
| 50,000 | 2.1715 | 2.1990 | 2.1558 | 2.0857 | 2.2296 | 40.14 | 62.15 | 1.1005 |
| 1.0666 | 1.1207 | 1.0653 | 1.0356 | 1.0961 | 40.04 | 77.32 | 1.8640 | |
| 0.6245 | 0.7092 | 0.6245 | 0.6058 | 0.6436 | 40.14 | 86.99 | 2.3425 | |
| 100,000 | 2.1715 | 2.1709 | 2.1608 | 2.1146 | 2.2087 | 40.00 | 65.19 | 1.2595 |
| 1.0666 | 1.1011 | 1.0655 | 1.0454 | 1.0861 | 40.00 | 81.30 | 2.0650 | |
| 0.6245 | 0.6962 | 0.6242 | 0.6115 | 0.6372 | 40.04 | 89.26 | 2.4610 | |
| Rock | Channels | b Value | Confidence Limits | Standard Deviation | Data Volume | ||
|---|---|---|---|---|---|---|---|
| Lower | Upper | Width = Upper − Lower | |||||
| Red sandstone | 1 | 1.5105 | 1.4016 | 1.6250 | 0.2234 | 0.0469 | 6368 |
| 2 | 1.6539 | 1.4712 | 1.8541 | 0.3829 | 0.0750 | 2434 | |
| 3 | 1.8771 | 1.6670 | 2.1121 | 0.4452 | 0.0781 | 2030 | |
| 4 | 1.6674 | 1.5356 | 1.8081 | 0.2725 | 0.0532 | 4677 | |
| 5 | 1.7288 | 1.5892 | 1.8786 | 0.2893 | 0.0548 | 4317 | |
| 6 | 1.6653 | 1.5180 | 1.8238 | 0.3058 | 0.0597 | 3742 | |
| Marble | 1 | 1.4081 | 1.3278 | 1.4914 | 0.1637 | 0.0360 | 11,376 |
| 2 | 1.3400 | 1.2553 | 1.4278 | 0.1725 | 0.0391 | 10,026 | |
| 3 | 1.3614 | 1.2897 | 1.4353 | 0.1456 | 0.0327 | 14,139 | |
| 4 | 1.3050 | 1.2541 | 1.3571 | 0.1030 | 0.0237 | 27,372 | |
| 5 | 1.3358 | 1.2686 | 1.4049 | 0.1364 | 0.0310 | 15,875 | |
| 6 | 1.3399 | 1.2558 | 1.4272 | 0.1714 | 0.0389 | 10,155 | |
| Granite | 1 | 1.1973 | 1.1443 | 1.2514 | 0.1071 | 0.0257 | 24,435 |
| 2 | 1.1897 | 1.1392 | 1.2412 | 0.1020 | 0.0246 | 27,154 | |
| 3 | 1.1575 | 1.1074 | 1.2086 | 0.1011 | 0.0247 | 27,340 | |
| 4 | 1.1566 | 1.1098 | 1.2042 | 0.0944 | 0.0231 | 31,333 | |
| 5 | 1.1602 | 1.1130 | 1.2083 | 0.0953 | 0.0232 | 30,764 | |
| 6 | 1.1669 | 1.1143 | 1.2206 | 0.1063 | 0.0259 | 24,673 | |
| Limestone | 1 | 1.0767 | 0.8617 | 1.3100 | 0.4483 | 0.1123 | 1592 |
| 2 | 1.0980 | 0.8963 | 1.3159 | 0.4197 | 0.1044 | 1812 | |
| 3 | 1.0212 | 0.7795 | 1.2852 | 0.5057 | 0.1291 | 1244 | |
| 4 | 1.1382 | 0.9565 | 1.3335 | 0.3770 | 0.0924 | 2178 | |
| 5 | 1.0485 | 0.8060 | 1.3140 | 0.5080 | 0.1284 | 1247 | |
| 6 | 1.1170 | 0.9017 | 1.3511 | 0.4494 | 0.1109 | 1582 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, C.; Chen, D.; He, W.; Liu, H.; Liu, X. Research on Maximum Likelihood b Value and Confidence Limits Estimation in Doubly Truncated Apparent Frequency–Amplitude Distribution in Rock Acoustic Emission Tests. Mathematics 2022, 10, 2409. https://doi.org/10.3390/math10142409
Xia C, Chen D, He W, Liu H, Liu X. Research on Maximum Likelihood b Value and Confidence Limits Estimation in Doubly Truncated Apparent Frequency–Amplitude Distribution in Rock Acoustic Emission Tests. Mathematics. 2022; 10(14):2409. https://doi.org/10.3390/math10142409
Chicago/Turabian StyleXia, Changgen, Daolong Chen, Wei He, Huini Liu, and Xiling Liu. 2022. "Research on Maximum Likelihood b Value and Confidence Limits Estimation in Doubly Truncated Apparent Frequency–Amplitude Distribution in Rock Acoustic Emission Tests" Mathematics 10, no. 14: 2409. https://doi.org/10.3390/math10142409
APA StyleXia, C., Chen, D., He, W., Liu, H., & Liu, X. (2022). Research on Maximum Likelihood b Value and Confidence Limits Estimation in Doubly Truncated Apparent Frequency–Amplitude Distribution in Rock Acoustic Emission Tests. Mathematics, 10(14), 2409. https://doi.org/10.3390/math10142409





