Dynamics of Triple Diffusive Free Convective MHD Fluid Flow: Lie Group Transformation

Abstract

This analysis is interested in the dynamic flow of incompressible triple diffusive fluid flowing through a linear stretched surface. The current study simulates when Boussinesq approximation and MHD are significant. As for originality, a comparative study of all the results for opposing and assisting flow cases is provided. Lie-group transformation is utilized to determine symmetry depletions of partial differential equations. The transformed system of ordinary differential equations is solved using the Runge-Kutta shooting technique. The impacts of magnetic parameter, buoyancy ratio parameter of temperature and concentration, and Lewis number on velocity, temperature, and concentration are depicted through graphs. We observed that the magnetic field parameter decelerates in velocity distribution for both fluid flow cases. Additionally, the same phenomenon was noticed with the buoyancy ratio parameters on both salt concentration distributions. Finally, the influence of heat and mass transfer rates decreases for both fluid flow cases with an increase in Lewis number.

1. Introduction

The flow of mass and heat transfer has many applications in science, industry, technical processes, and many theoretical or experimental disciplines. As examples, take aerospace, power generation, automotive, materials, and chemical processing industries [1,2,3]. Magneto-hydro dynamics (MHD) is one of the branches of physics used to analyze the fluids dynamics with the help of magnetic effects. Its applications have been extensive in numerous disciplines ranging from the study of solar winds [4] to MHD-driven biomedical sensors [5] and actuators [6,7]. Massoudi et al. [8] examined the impacts of a nanofluid’s thermal radiation and magnetic field inside a nonagon inclined cavity embedded in a porous medium. Massoudi et al. [9] used a MHD W-shaped inclined cavity saturated with Ag/Al₂O₃ hybrid nanofluid for uniform heat generation/absorption. Lie theory is a field of group theory that deals with continuous symmetry. It has a component which is close to identity transformation. Sophie Lie devised symmetry analysis, also known as Lie group analysis, to identify point transformations that allow a differential equation to be transferred to itself. Almost every known accurate integration technique for ordinary and differential equations is gathered in this transformation [9]. The Lie group transformation is a method of determining all aspects of a differential equation that does not require any extempore hypotheses or foreknowledge of the equation.

For most nonlinear differential equations, the approximate solutions are numerical due to the complexity of the problems [10]. He et al. [11] discussed on new analytical methods for cleaning up the solution of nonlinear equations. Massoudi et al. [12] studied numerical techniques on magneto natural convection of SWCNT nanofluid inside a T-inverted cavity. There are many general methods for solving linear and nonlinear partial differential equations. The Lie group theory, explained in [13], is the usual approach. Symmetry groups are invariant transformations that do not change the structure of the equations. Using this transformation, one can find the exact solution of differential equations developed by Sophie Lie about one century ago. Nowadays, the method is used widely. It creates a new solution from an existing one, rather than looking for so-called similar solutions [14]. This transformation has an n-independent variable partial differential system that can be converted to a system of $n-1$ independent variables, and if $n=2$, then the situation is considered best. It is one of the most effective tools for developing similarity transformations. Scaling transformation is the most common tool used to apply to the boundary layer equation in fluid dynamics. By reducing the number of independent variables, this transformation converts a system of nonlinear coupled partial differential equations regulating fluid motion into a system of coupled ordinary differential equations. Using nanofluid, Uddin et al. [15] utilized this transformation to analyze the boundary layer in MHD fluid flow on a stretched surface. MHD heat transfer in thermal slip using a semi-infinite domain and Carreau fluid was discussed by Rehman et al. [16]. Using this transformation, many researchers gave exact solutions to their problems [17,18].

The fluid motion created by the buoyancy forces is called free convection. Heat transfer in free convection depends on fluid circulation over and around the object, which is induced by temperature gradients, which create density gradients. In heat transfer, many applications were developed, such as food heating processing and cooling systems in which free convection is assertive. The sterilization process of food in cans and meat freezing are controlled by free convection. In the presence of a chemical reaction, researchers [19] analyzed an unsteady free convection MHD flow around a vertical cone in porous media with variable heat and mass flux. A lot of research is carried out in the area of free convection MHD flow [20,21,22,23,24,25].

In general, free convection is merely due to heat transfer and not in the mode of forced flow. In gas or liquid, the density differences are induced by temperature differences. Due to its numerous applications, the convective process has grown important over the last century. Bernard started the convective process experiments after that carried out by Rayleigh [26]. Triple diffusive free convection [27] develops when a fluid is applied to three density gradients with different diffusion rates. In this study, the triple diffusion is formulated by the diffusion of heat and species concentrations, a linear stability analysis for triple diffusive convection in Oldroyd-B fluid is carried out, and the expression of Rayleigh number for stationary and oscillatory convection is achieved [28]. Patil [29] examined a quadratic mixed convective nanofluid flow over a wedge by considering viscous dissipation. He observed that the rate of heat transfer increases with an increase in Biot number. In the normal mode theory, introducing a Maxwell fluid to a saturated porous layer causes triple diffusive convection [30]. In a time-dependent model, Khan et al. [31] investigated a triple diffusive natural convective flow along with a vertical plate. The heat transfer rate increased as the volume fraction distribution of nanoparticles increased. Triple diffusive convective importance was analyzed [32,33,34,35,36,37,38].

Few works have been performed using Lie group transformation analysis, as per the authors’ knowledge of the literature in most practical uses; however, the components of mass and heat are inextricably linked. The heat and mass diffusion components, on the other hand, are invariably coupled in most real-world applications. This fact prompted us to investigate the combined impacts of mass diffusion and heat on magnetohydrodynamic free-convective flow in the boundary layer. As far as we can tell, the findings of this work appear to be perfectly consistent with previous research, and due to their simplicity, easily transferable to relevant applications.

2. Mathematical Model and Formulation

The rate of mass change and heat transfer performance of an electrically conducting viscous fluid in a steady, triple-diffusive, two-dimensional hydro-magnetic flow follow. A uniformly strong magnetic field $B$ is introduced perpendicular to the flow direction. Except for the influences of density variation on concentration and temperature, all liquid properties are assumed to be uniform. The surface temperature should be maintained at $T_w$, higher than the constant. With the help of Lie group transformation analysis, we studied a triple-diffusive, free-convective, 2D, steady laminar flow through a stretching surface and its incompressible fluid flow model.

Under the pre-defined assumptions mentioned above, the governing equations are expressed as shown below [18].

$$\frac{\partial \overline{u}}{\partial \overline{x}}+\frac{\partial \overline{v}}{\partial \overline{y}}=0,$$

(1)

$$\overline{u}\frac{\partial \overline{u}}{\partial \overline{x}}+\overline{v}\frac{\partial \overline{u}}{\partial \overline{y}}=\vartheta \frac{{\partial }^2\overline{u}}{\partial {\overline{y}}^2}+\left[g{\beta }_T\left(T-T_{\infty }\right)+g{\beta }_{c_1}\left(C-C_{1\infty }\right)+g{\beta }_{c_2}\left(C-C_{2\infty }\right)-\frac{\sigma B^2}{\rho }\overline{u}\right],$$

(2)

$$\overline{u}\frac{\partial T}{\partial \overline{x}}+\overline{v}\frac{\partial T}{\partial \overline{y}}=\alpha \frac{{\partial }^{2}T}{\partial {\overline{y}}^2},$$

(3)

$$\overline{u}\frac{\partial C_1}{\partial \overline{x}}+\overline{v}\frac{\partial C_1}{\partial \overline{y}}=D_{S_1}\frac{{\partial }^2{C}_1}{\partial {\overline{y}}^2},$$

(4)

$$\overline{u}\frac{\partial C_2}{\partial \overline{x}}+\overline{v}\frac{\partial C_2}{\partial \overline{y}}=D_{S_2}\frac{{\partial }^2{C}_2}{\partial {\overline{y}}^2}.$$

(5)

Along the boundary conditions

$$\begin{array}{l}\overline{u}=u_w, \overline{v}=0, T=T_w, C_1=C_{1w}, C_2=C_{2w} \mathrm{at} \eta =0,\\ \overline{u}\to u_{\infty }, T\to T_{\infty }, C_1\to C_1{}_{\infty }, C_2\to C_2{}_{\infty } \mathrm{as} \eta \to \infty .\end{array}$$

(6)

To non-dimensionalize the above-mentioned Equations from (1) to (5) together with Equation (6), the following similarity transformations are considered.

$$\begin{array}{l}u=\frac{\overline{u}}{\sqrt{a\vartheta }},u=\frac{\overline{v}}{\sqrt{a\vartheta }},x=\frac{\overline{x}}{\sqrt{\raisebox{1ex}{$\vartheta $}\!\left/ \!\raisebox{-1ex}{$a$}\right.}},y=\frac{\overline{y}}{\sqrt{\raisebox{1ex}{$\vartheta $}\!\left/ \!\raisebox{-1ex}{$a$}\right.}}\\ \theta =\frac{T-T_{\infty }}{T_w-T_{\infty }}, {\varphi }_1=\frac{C_1-C_1{}_{\infty }}{C_1{}_w-C_1{}_{\infty }}, {\varphi }_2=\frac{C_2-C_2{}_{\infty }}{C_2{}_w-C_2{}_{\infty }}.\end{array}$$

(7)

We substitute above non-dimensional quantities into Equations (1)–(5), along with the boundary conditions (6), and then complete simplification results in the following non-dimensional differential equations:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(8)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{{\partial }^{2}u}{\partial y^2}-\frac{\sigma B^2}{\rho a}u+\lambda \theta +N{C}_1{\varphi }_1+N{C}_2{\varphi }_2,$$

(9)

$$u\frac{\partial \theta }{\partial x}+v\frac{\partial \theta }{\partial y}=\frac{1}{\mathrm{Pr}}\frac{{\partial }^2\theta }{\partial y^2},$$

(10)

$$u\frac{\partial {\varphi }_1}{\partial x}+v\frac{\partial {\varphi }_1}{\partial y}=\frac{D_{S_1}}{\nu }\frac{{\partial }^2{\varphi }_1}{\partial y^2},$$

(11)

$$u\frac{\partial {\varphi }_2}{\partial x}+v\frac{\partial {\varphi }_2}{\partial y}=\frac{D_{S_2}}{\nu }\frac{{\partial }^2{\varphi }_2}{\partial y^2}.$$

(12)

With the boundary conditions

$$\begin{array}{l}u=x, v=0, \theta =1, {\varphi }_1=1, {\varphi }_2=1 \mathrm{at} \eta =0,\\ u\to 0, \theta \to 0, {\varphi }_1\to 0, {\varphi }_2\to 0 \mathrm{as} \eta \to \infty ,\end{array}$$

(13)

where $\lambda =\frac{g{\beta }_T\Delta T}{a\sqrt{a\vartheta }},N{C}_1=\frac{g{\beta }_{C_1}\Delta C_1}{a\sqrt{a\vartheta }},N{C}_2=\frac{g{\beta }_{C_2}\Delta C_2}{a\sqrt{a\vartheta }}$ are the thermal, salt_1, and salt_2 solutal buoyancy ratios.

3. Scaling Transformations

The stream function $\psi$ is introduced before scaling modifications are applied, as demonstrated below [17]:

$$u=\frac{\partial \psi }{\partial y} \mathrm{and} v=-\frac{\partial \psi }{\partial x}$$

(14)

Replace the above Equation (14) in to (8)–(12) together with the boundary conditions (13). Obviously, Equation (8) is satisfied by them. Additionally, remaining equations are transformed as below:

$$\frac{\partial \psi }{\partial x}\frac{{\partial }^2\psi }{\partial x\partial y}-\frac{\partial \psi }{\partial x}\frac{{\partial }^2\psi }{\partial y^2}=\frac{{\partial }^3\psi }{\partial y^3}-\frac{\sigma B^2}{\rho a}\frac{\partial \psi }{\partial y}-\lambda \theta +N{C}_1{\varphi }_1+N{C}_2{\varphi }_2,$$

(15)

$$\frac{\partial \psi }{\partial y}\frac{\partial \theta }{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial \theta }{\partial y}=\frac{\alpha }{\nu }\frac{{\partial }^2\theta }{\partial y^2},$$

(16)

$$\frac{\partial \psi }{\partial y}\frac{\partial {\varphi }_1}{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial {\varphi }_1}{\partial y}=\frac{D_{S_1}}{\nu }\frac{{\partial }^2{\varphi }_1}{\partial y^2},$$

(17)

$$\frac{\partial \psi }{\partial y}\frac{\partial {\varphi }_2}{\partial x}-\frac{\partial \psi }{\partial x}\frac{\partial {\varphi }_2}{\partial y}=\frac{D_{S_2}}{\nu }\frac{{\partial }^2{\varphi }_2}{\partial y^2}.$$

(18)

With the boundary conditions

$$\begin{array}{l}\frac{\partial \psi }{\partial y}=x, \frac{\partial \psi }{\partial x}=0, \theta =1, {\varphi }_1=1, {\varphi }_2=1 \mathrm{at} \eta =0,\\ \frac{\partial \psi }{\partial y}\to 0, \theta \to 0, {\varphi }_1\to 0, {\varphi }_2\to 0 \mathrm{as} \eta \to \infty .\end{array}$$

(19)

Additionally,

$$e^{\epsilon \left(r_2-r_3\right)}\frac{\partial {\psi }^{*}}{\partial y^{*}}=1, e^{\epsilon \left(r_1-r_3\right)}=0, e^{-\epsilon r_4}{\theta }^{*}=0.$$

(20)

We suppose that $\epsilon$, as a smaller scale transformation parameter. Then, the transformation $F$ (a specified set of Lie-group transformation analysis) is reflected as shown below:

$$\begin{array}{l}F: x^{*}=x{e}^{\epsilon r_1}, y^{*}=y{e}^{\epsilon r_2}, {\psi }^{*}=\psi e^{\epsilon r_3},\\ {\theta }^{*}=\theta e^{\epsilon r_4}, {\varphi }_1{}^{*}={\varphi }_1{e}^{\epsilon r_5}, {\varphi }_2{}^{*}={\varphi }_2{e}^{\epsilon r_6},\end{array}$$

(21)

where $r_1,r_2,r_3,r_4,r_5,r_6$ are real numbers. The point of the transformation defined through (21) is to convert the coordinates as $\left(x,y,\psi ,\theta ,{\varphi }_1,{\varphi }_2\right)$ to $\left(x^{*},y^{*},{\psi }^{*},{\theta }^{*},{\varphi }_1{}^{*},{\varphi }_2{}^{*}\right)$. With the help of Lie group analysis mentioned in (15), Equations (15)–(18) are transformed as:

$$\begin{array}{l}{e}^{\epsilon \left(r_1+2r_2-2r_3\right)}\left[\frac{\partial {\psi }^{*}}{\partial x^{*}}\frac{{\partial }^2{\psi }^{*}}{\partial x^{*}\partial y^{*}}-\frac{\partial {\psi }^{*}}{\partial x^{*}}\frac{{\partial }^2{\psi }^{*}}{\partial y^{*}{}^2}\right]=e^{\epsilon \left(3r_2-r_3\right)}\frac{{\partial }^3{\psi }^{*}}{\partial y^{*}{}^3}-\frac{\sigma B^2}{\rho a}{e}^{\epsilon \left(r_2-r_3\right)}\\ -\lambda e^{\epsilon r_4}\theta +N{C}_1{e}^{\epsilon r_5}{\varphi }_1+N{C}_2{e}^{\epsilon r_6}{\varphi }_2,\end{array}$$

(22)

$$e^{\epsilon \left(r_1+r_2-r_3-r_5\right)}\left[\frac{\partial {\psi }^{*}}{\partial y^{*}}\frac{\partial {\theta }^{*}}{\partial x^{*}}-\frac{\partial {\psi }^{*}}{\partial x^{*}}\frac{\partial {\theta }^{*}}{\partial y^{*}}\right]=\frac{a}{\nu }{e}^{\epsilon \left(2r_2-r_4\right)}\frac{{\partial }^2{\theta }^{*}}{\partial y^{*}{}^2},$$

(23)

$$e^{\epsilon \left(r_1+r_2-r_3-r_5\right)}\left[\frac{\partial {\psi }^{*}}{\partial y^{*}}\frac{\partial {\varphi }_1{}^{*}}{\partial x^{*}}-\frac{\partial {\psi }^{*}}{\partial x^{*}}\frac{\partial {\varphi }_1{}^{*}}{\partial y^{*}}\right]=\frac{D_{S_1}}{\nu }{e}^{\epsilon \left(2r_2-r_5\right)}\frac{{\partial }^2{\varphi }_1{}^{*}}{\partial y^{*}{}^2},$$

(24)

$$e^{\epsilon \left(r_1+r_2-r_3-r_6\right)}\left[\frac{\partial {\psi }^{*}}{\partial y^{*}}\frac{\partial {\varphi }_2{}^{*}}{\partial x^{*}}-\frac{\partial {\psi }^{*}}{\partial x^{*}}\frac{\partial {\varphi }_2{}^{*}}{\partial y^{*}}\right]=\frac{D_{S_2}}{\nu }{e}^{\epsilon \left(2r_2-r_6\right)}\frac{{\partial }^2{\varphi }_2{}^{*}}{\partial y^{*}{}^2}.$$

(25)

Equations (22)–(25) will remain invariant after the translation, if the exponent of this converted system of equations which satisfies the resulting linear equations is as follows:

$$r_1=2r_2-2r_3=3r_2-r_3=r_2-r_3=r_4=r_5=r_6,$$

(26)

$$r_1+r_2-r_3-r_4=2r_2-r_4,$$

(27)

$$r_1+r_2-r_3-r_5=2r_2-r_5,$$

(28)

$$r_1+r_2-r_3-r_6=2r_2-r_6.$$

(29)

By solving above linear Equations (26)–(29) simultaneously, we find:

$$r_1=r_1, r_2=0, r_3=r_1, r_4=0, r_5=0, r_6=0.$$

(30)

Substituting the above values (30) into the scaling transformations given in (21), we get:

$$F: x^{*}=x{e}^{\epsilon r_1}, y^{*}=y, {\psi }^{*}=\psi e^{\epsilon r_1}, {\theta }^{*}=\theta , {\varphi }_1{}^{*}={\varphi }_1, {\varphi }_2{}^{*}={\varphi }_2.$$

(31)

The Taylor series expansions are:

$$\begin{array}{l}{x}^{*}-x=x\epsilon r_1, y^{*}-y=0, {\psi }^{*}-\psi =\psi \epsilon r_1, {\theta }^{*}-\theta =0, \\ {\varphi }_1{}^{*}-{\varphi }_1=0, {\varphi }_2{}^{*}-{\varphi }_2=0.\end{array}$$

A simple algebraic expression for the above transformations (31) with the help of Taylor series expansion leads to a mono parametric group of transformations in the form of the characteristic equation given below:

$$\frac{dx}{x{r}_1}=\frac{dy}{0}=\frac{d\psi }{\psi r_1}=\frac{d\theta }{0}=\frac{d{\varphi }_1}{0}=\frac{d{\varphi }_2}{0}.$$

(32)

From Equation (32), we can easily obtain new similarity transformations as:

$$y=\eta , \psi =x f\left(\eta \right), \theta =\theta \left(\eta \right), {\varphi }_1={\varphi }_1\left(\eta \right), {\varphi }_2={\varphi }_2\left(\eta \right),$$

(33)

where $\eta$ is the similarity variable and $f, \theta , {\varphi }_1, {\varphi }_2$ are the dependent variables. Now, we substitute the above quantities specified in Equation (33) into PDEs (16)–(18) in boundary conditions mentioned in (19). We obtain the set of ordinary differential equations as:

$$f^{‴}+f{f}^{″}-{(f^{\prime })}^2-M{f}^{\prime }+\lambda \theta +N{C}_1{\varphi }_1+N{C}_2{\varphi }_2=0,$$

(34)

$${\theta }^{″}+\mathrm{Pr}f{\theta }^{\prime }=0,$$

(35)

$${\varphi }_1{}^{″}+L{e}_{1}f{\varphi }_1{}^{\prime }=0,$$

(36)

$${\varphi }_2{}^{″}+L{e}_{2}f{\varphi }_2{}^{\prime }=0.$$

(37)

Together with the boundary conditions:

$$\begin{array}{l}{f}^{\prime }=1, f=0, \theta =1, {\varphi }_1=1, {\varphi }_2=1 \mathrm{at} \eta =0,\\ f^{\prime }\to 0, \theta \to 0, {\varphi }_1\to 0, {\varphi }_2\to 0 \mathrm{as} \eta \to \infty ,\end{array}$$

(38)

with the predefined parameters

$$\begin{array}{l}M=\frac{\sigma B^2}{\rho a}, \lambda =\frac{g{\beta }_T\Delta T}{a\sqrt{a\vartheta }}, N{C}_1=\frac{g{\beta }_{C_1}\Delta C_1}{a\sqrt{a\vartheta }}, N{C}_2=\frac{g{\beta }_{C_2}\Delta C_2}{a\sqrt{a\vartheta }}, \\ \mathrm{Pr}=\frac{\nu }{\alpha }, L{e}_1=\frac{\nu }{D_{S_1}}, L{e}_2=\frac{\nu }{D_{S_2}}.\end{array}$$

Furthermore, $\lambda >0$ and $\lambda <0$ represents buoyancy assisting flow and buoyancy opposing flow, respectively.

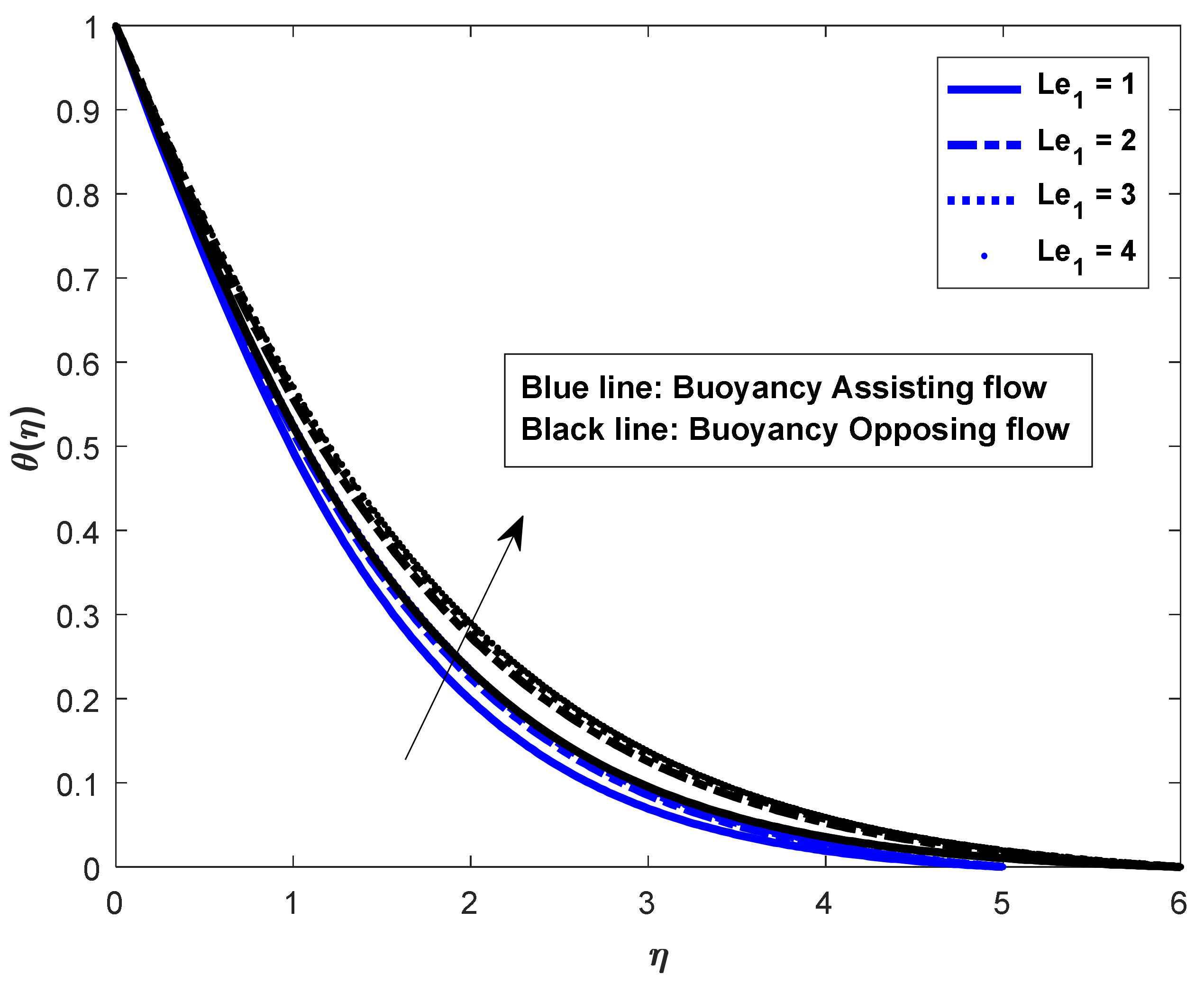
4. Numerical Results and Discussion

The effects of triple diffusive free convective magnetohydrodynamic fluid flow in a linearly stretching sheet were studied numerically. Lie group transformation analysis converts a collection of nonlinear partial differential equations and boundary situations into a set of ODEs. BVP4C resolved the system of the reduced nonlinear ODEs with corresponding boundary conditions in MATLAB.

Table 1. Comparison values of Nusselt number ${\theta }^{\prime }\left(0\right)$ for various values of Prandtl number when $M=\lambda =N{c}_1=N{c}_2=L{e}_1=L{e}_2=0$.

$\mathbf{Pr}$	${\mathit{\theta }}^{\prime }\left(0\right)$
	Ferdows et al. [17]	Present Results
1	0.9547	0.9546
2	1.4715	1.4711
3	1.8691	1.8672

shows a great correlation between the present results and the results of Ferdows et al. [17].

The influences of $M$ on the velocity $f^{\prime }\left(\eta \right)$, temperature $\theta \left(\eta \right)$, salt_1, and salt_2 concentration fields ${\varphi }_1\left(\eta \right),{\varphi }_2\left(\eta \right)$ on assisting flow $(\lambda >0)$ and opposing flow $(\lambda <0)$ are shown in Figure 1, Figure 2, Figure 3 and Figure 4. As illustrated in Figure 1, $f^{\prime }\left(\eta \right)$ the surface decreases in assisting and opposing flows. It can be seen that increasing the value of the magnetic field parameter decreases the momentum boundary layer thickness. This is because the strong magnetic field inside the boundary layer increases the Lorentz force, which strongly resists flow in the opposite direction. It is also worth noting that the presence of a magnetic field reduces velocity near the wall while increasing velocity far away. The effects of magnetic parameters on temperature and concentration distributions are shown in Figure 2, Figure 3 and Figure 4. As the value rises, the fluid becomes warmer, raising the temperature. The thickness of the thermal boundary layer is always increased by the presence of a magnetic field, and the concentration field is likewise increased by the magnetic parameter.

The influences of the Prandtl number are seen in Figure 5, Figure 6, Figure 7 and Figure 8. The dimensional velocity profile grows as the Prandtl number increases in the opposing flow case and reduces in the helping flow case, as seen in Figure 5. In contrast, in the natural convective flow of a regular fluid over a vertical surface, the thickness of the hydrodynamic boundary layer reduces as the Prandtl number grows, and the vertical flow velocity drops. It is worth noting that, unlike in the classical analysis of natural convection on a vertical surface, where the Prandtl number appears in the energy equation, the Prandtl number appears in the momentum equation in the present analysis and thus has a different effect on the velocity profiles than in the classical velocity profiles. The same phenomenon can be seen in the salt_1 and salt_2 concentration profiles (see Figure 7 and Figure 8). The temperature profile falls as the Prandtl number grows, as shown in Figure 6. An increase in the Prandtl number reduces the thermal boundary layer thickness, since the Prandtl number signifies the ratio of momentum diffusivity to thermal diffusivity. In heat transfer problems, $\mathrm{Pr}$ controls the thicknesses of the momentum and thermal boundary layers.

Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 illustrate the effects of buoyancy ratio parameters on velocity, temperature, and salt_1 and salt_2 concentration distributions. Increasing the values of buoyancy ratio parameters increases the velocity for smaller values of $\eta$, as shown in Figure 9 and Figure 13. From the graphical representations of Figure 10, Figure 11, Figure 12 and Figure 14, Figure 15, Figure 16 it is noticed that an increase in buoyancy ratio decreases the temperature and salt_1 and salt_2 concentration profiles in both assisting and opposing cases.

The velocity, temperature and concentration distributions $f^{\prime }\left(\eta \right), \theta \left(\eta \right), {\varphi }_1\left(\eta \right)$ and ${\varphi }_2\left(\eta \right)$ for various values of Lewis numbers $L{e}_2$ and $L{e}_1$ can be observed in Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24 for both the flow circumstances. In helping flows, the dimensionless concentration increases with increasing Lewis numbers inside the concentration boundary layer, whereas buoyancy opposes and resists flows. Lewis number determines the thickness of the concentration boundary layer physically. That is, the greater the Lewis number, the thinner the concentration boundary layer will be. For Lewis numbers, the dimensionless wall concentrations decline quickly to zero in both buoyancy assisting and opposing flows, and the inside wall concentration is equivalent to the ambient concentration. In fluid flow instances, the thickness of the thermal boundary layer decreases while the momentum boundary layer increases.

It is recognized that the friction factor rate was enhanced in both flow cases for an increase in Lewis numbers $L{e}_1$ and $L{e}_2.$ However, the influences of ${\theta }^{\prime }\left(0\right), {\varphi }_1{}^{\prime }\left(0\right),{{\varphi }^{\prime }}_2\left(0\right)$ decreased in both the flow cases with an increase in Lewis number. The friction factor coefficient decreased with increases in buoyancy ratio parameters $N{c}_1$ and $N{c}_2$, but the opposite behavior was observed in the cases of Nusselt and Sherwood numbers. The skin friction coefficient increased for an increase in magnetic field parameter, whereas the opposite phenomena could be observed in both cases’ mass and heat transfer rates. Finally, the Prandtl number increased the friction factor in assisting flow and decreased it in opposing flow. The same behavior can also be observed ${{\varphi }^{\prime }}_2\left(0\right)$ in both the assisting flow $(\lambda >0)$ and opposing flow $(\lambda <0)$ cases.

The $f^{″}\left(0\right), {\theta }^{\prime }\left(0\right)$ and ${\varphi }^{\prime }\left(0\right)$ plots for different values of the magnetic field parameter M are shown in Figure 25, Figure 26 and Figure 27. Figure 25 shows that as the value of $M$ increases, $f^{″}\left(0\right)$ is enhanced at a rate of 0.290386 $(\lambda >0)$ or 0.26876 $(\lambda <0)$. Similarly, for assisting and opposing flows, heat and mass transfer coefficients decrease at rates of −0.0235 and −0.02999, and −0.02286 and −0.02946, respectively. Due to the buoyancy force, surface shear stress is greater in assisting flow than in opposing flow.

The skin friction coefficient ${\theta }^{\prime }\left(0\right)$ and ${\varphi }^{\prime }\left(0\right)$ plots for different $\mathrm{Pr}$ values are shown in Figure 28, Figure 29 and Figure 30. As $\mathrm{Pr}$ grows, $f^{″}\left(0\right)$ increases in assisting flow and falls in opposing flow, as seen in Figure 28. The Sherwood number ${\varphi }^{\prime }\left(0\right)$ exhibits opposite behavior (Figure 30). However, in both fluid flow cases, ${\theta }^{\prime }\left(0\right)$ is increased (Figure 29).

Figure 31, Figure 32 and Figure 33 depict the friction factor coefficient, ${\theta }^{\prime }\left(0\right)$, and ${\varphi }^{\prime }\left(0\right)$ plots for different values of $N{c}_1$. Figure 31 represents that for increasing values of $N{c}_1$, the friction factor coefficient decreases in assisting and opposing flow cases. The rates of ${\theta }^{\prime }\left(0\right)$ and ${\varphi }^{\prime }\left(0\right)$ rise as the Prandtl number increases in both cases.

The $f^{″}\left(0\right), {\theta }^{\prime }\left(0\right)$ and ${\varphi }^{\prime }\left(0\right)$ plots for various values of the buoyancy ratio parameter $N{c}_2$ are shown in Figure 34, Figure 35 and Figure 36. Figure 34 shows that when $N{c}_2$ increases, the skin friction coefficient decreases at a rate of −0.31689 $(\lambda >0)$ or −0.32663 $(\lambda <0)$. For assisting and opposing flow, the Nusselt and Sherwood numbers escalate rates of 0.019164 and 0.022813, and 0.022813 and 0.026919, respectively.

Figure 37, Figure 38, Figure 39 and Figure 40 illustrate the shear stress, Nusselt number, and salt_1 and salt_2 Sherwood number plots for different values of Lewis number $L{e}_1$. Figure 37 shows that for increasing values of $L{e}_1$, the skin friction coefficient increases at 0.045962 (assisting flow) and 0.048975 $(\lambda <0)$ rates. The ${\theta }^{\prime }\left(0\right)$ is decreased at the rates of −0.00653 and −0.00881 in the fluid flow cases. The salt_1 Sherwood number for the Lewis number is increased in assisting and opposing flow cases, whereas the reverse trend can be observed for salt_2 Sherwood in both cases.

Figure 41, Figure 42, Figure 43 and Figure 44 illustrate the shear stress, Nusselt number, and salts_1 and salt_2 Sherwood number plots for different values of Lewis number $L{e}_2$. Figure 41 shows that increasing values of $L{e}_2$ $f^{″}\left(0\right)$ escalate in both fluid flow cases. The Nusselt number is decreased in both flow cases. Finally, the salt_1 Sherwood number decreased and the salt_2 Sherwood number increased in both assisting and opposing flow cases.

5. Concluding Remarks

A steady, incompressible, and laminar boundary layer was used to investigate the effects of triple diffusion on boundary layer flow, heat, and mass transfer through a linearly stretching sheet. Numerical findings for surface ${\theta }^{\prime }\left(0\right)$ and ${\varphi }^{\prime }\left(0\right)$ were provided for various values of the governing parameters. The following are the investigation’s principal findings:

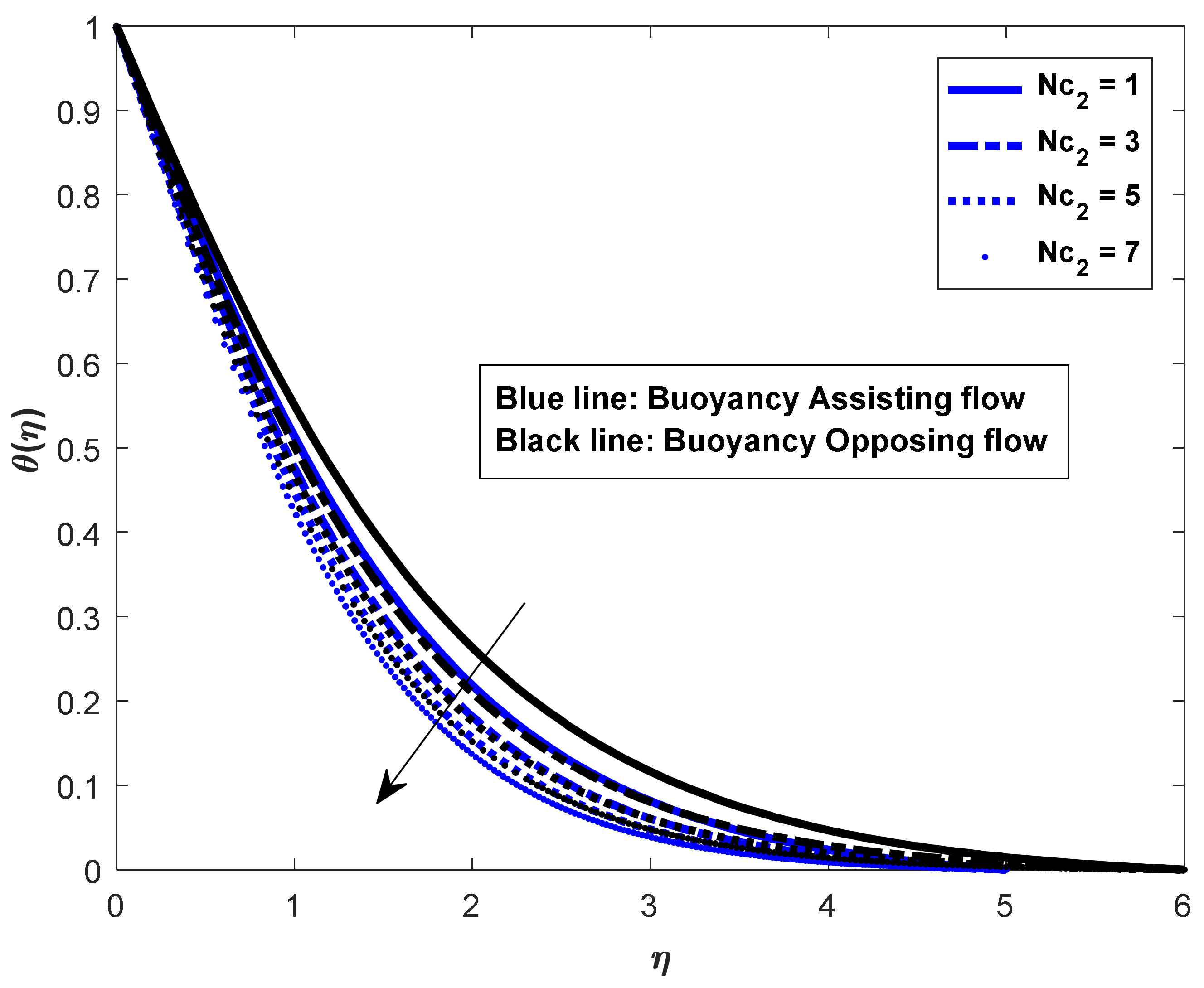
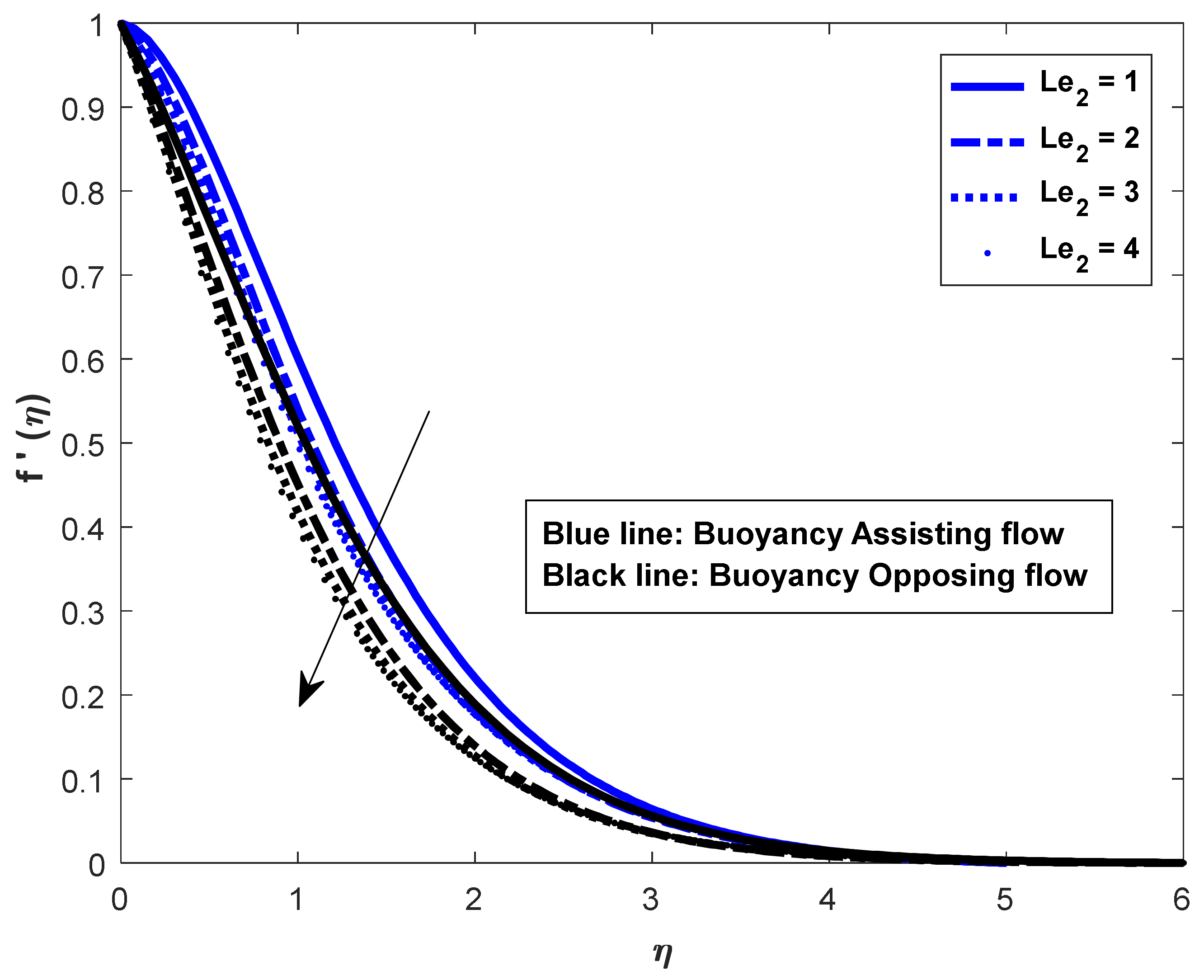
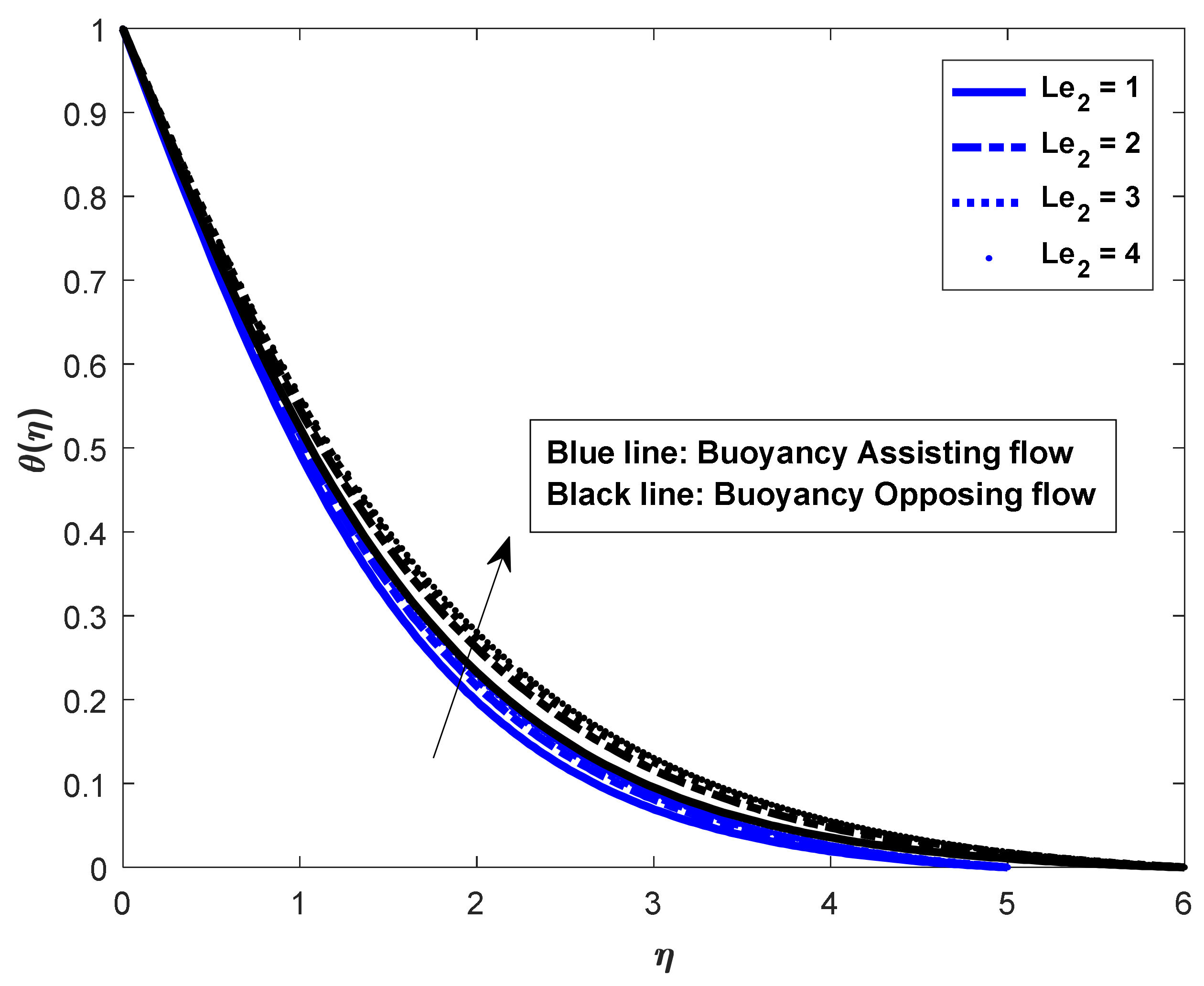
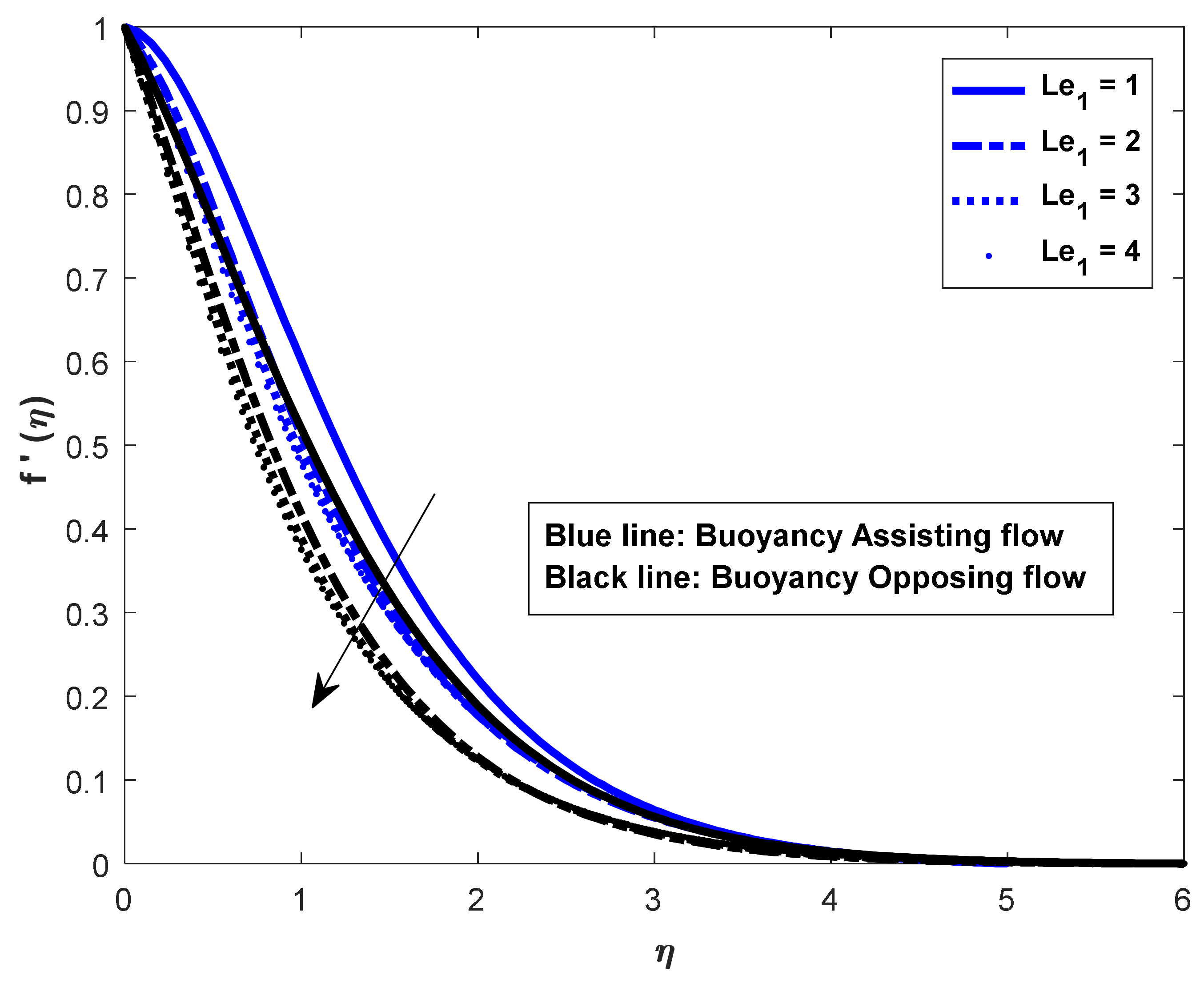
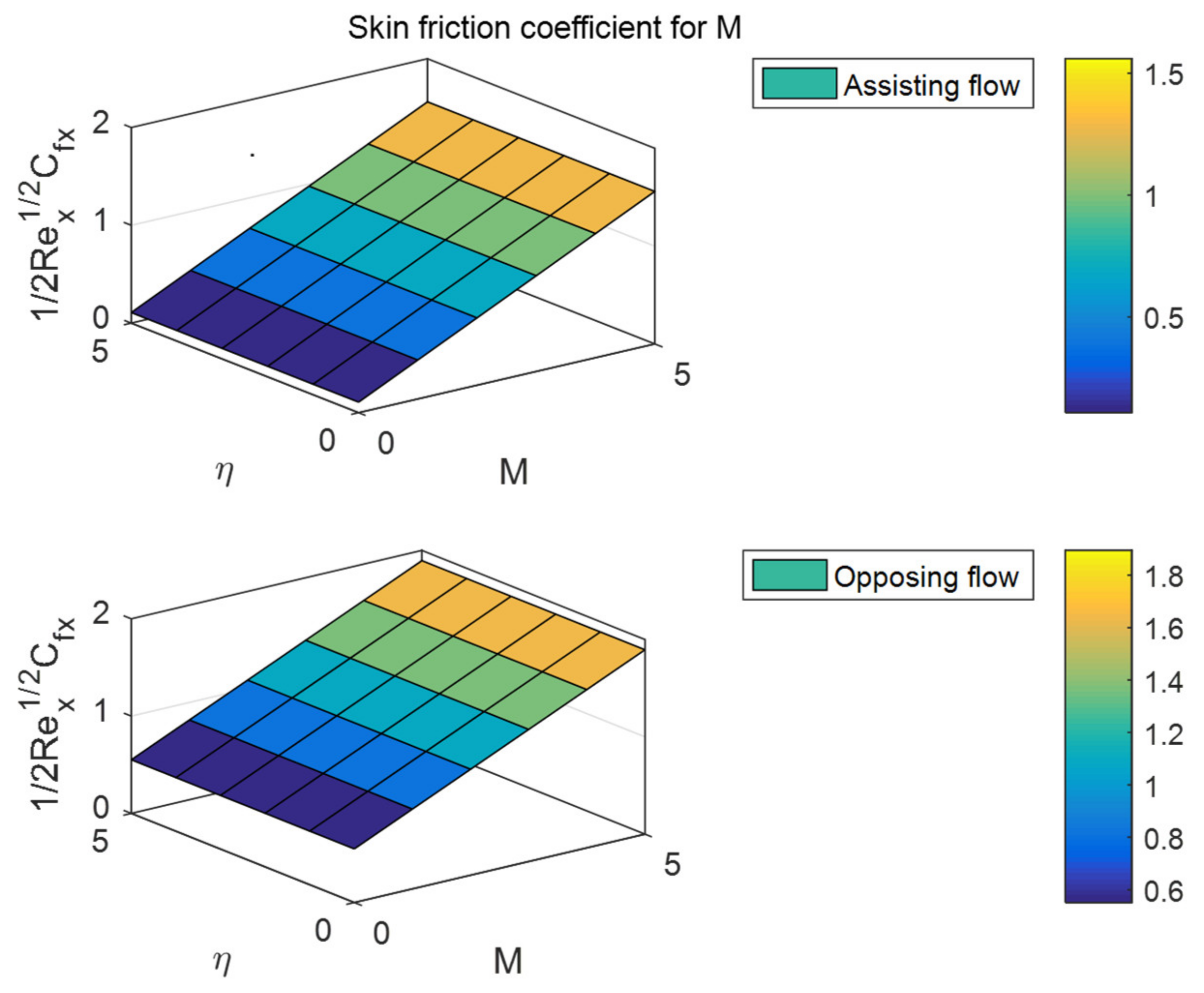
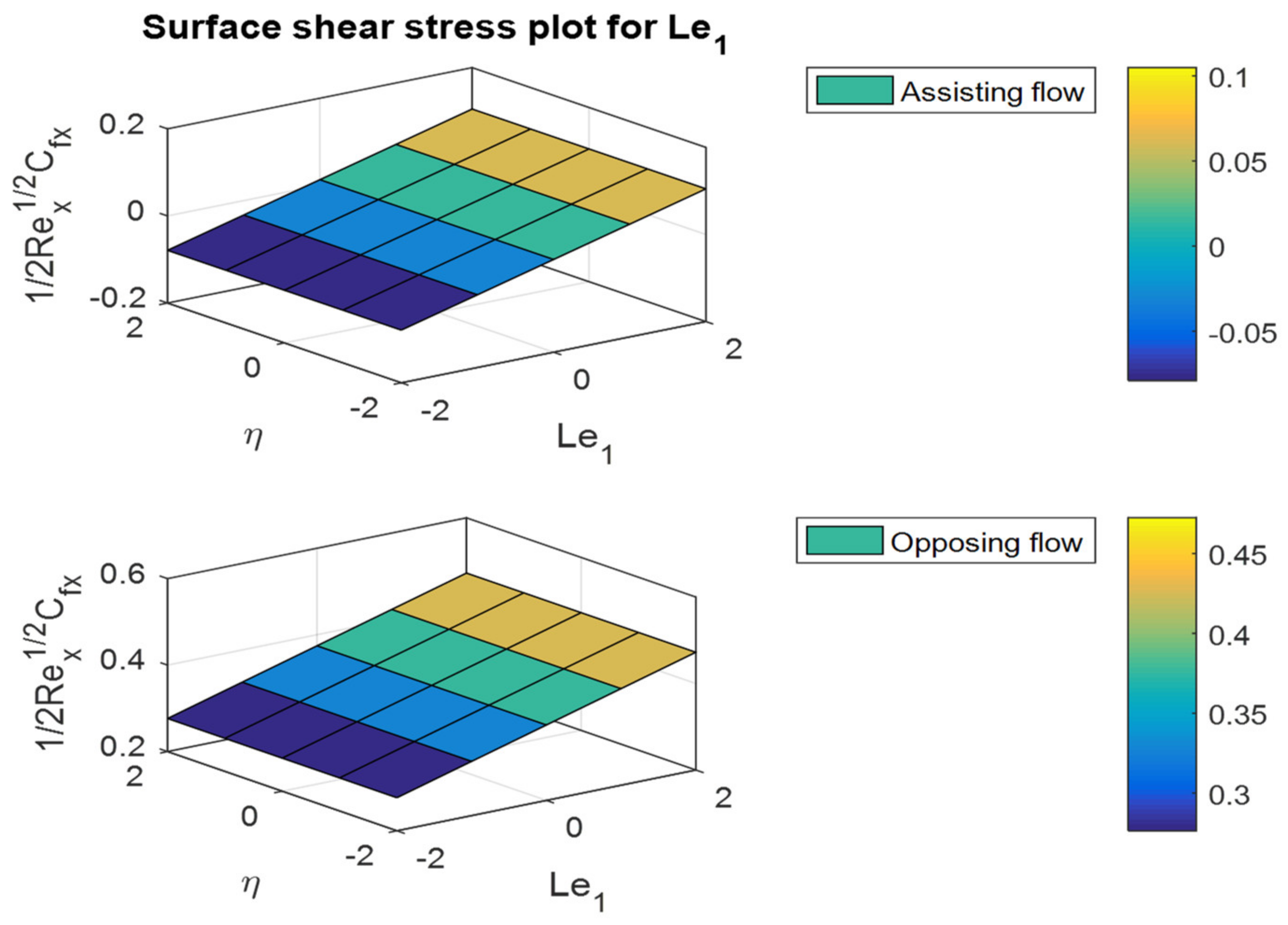
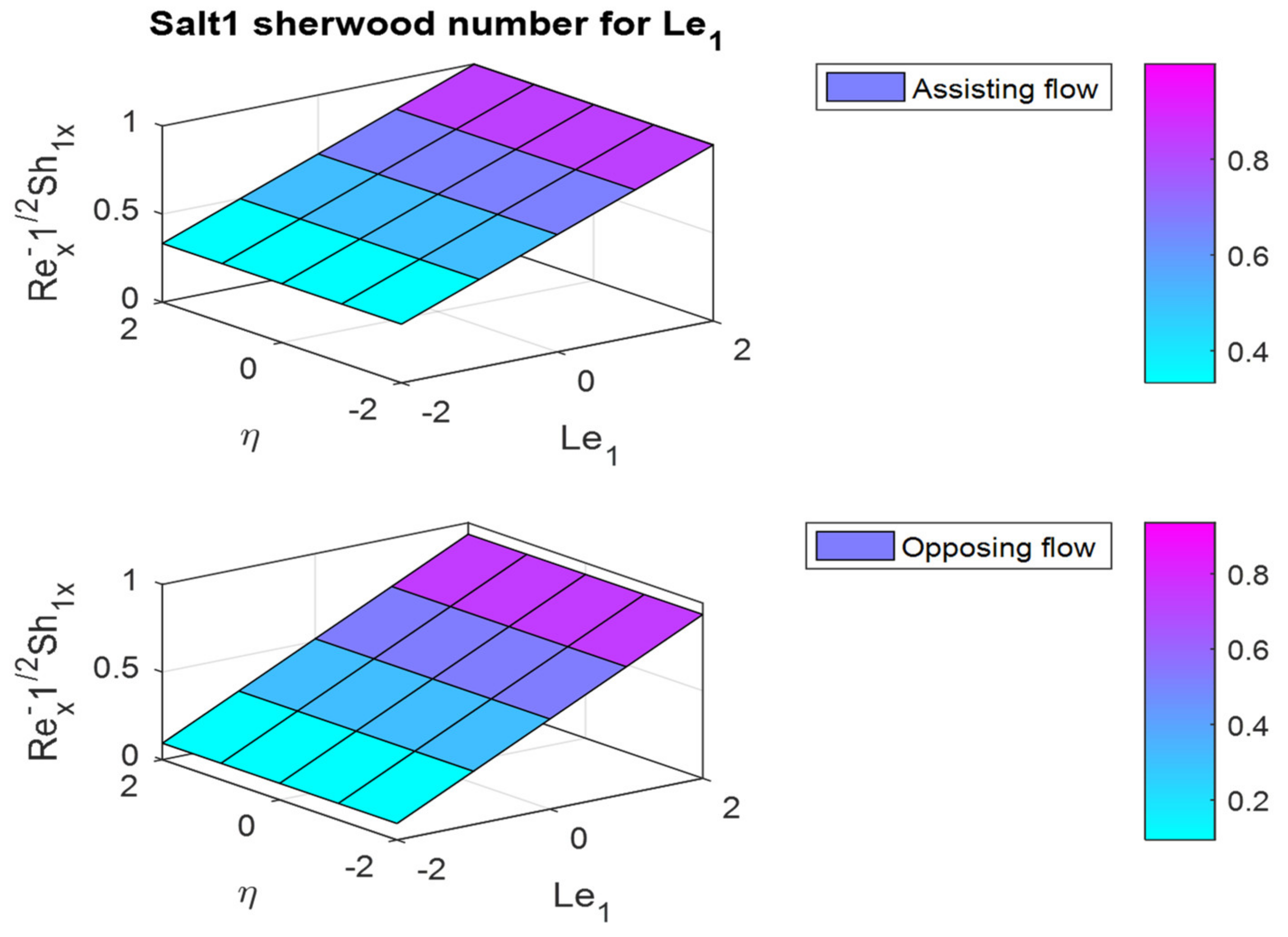
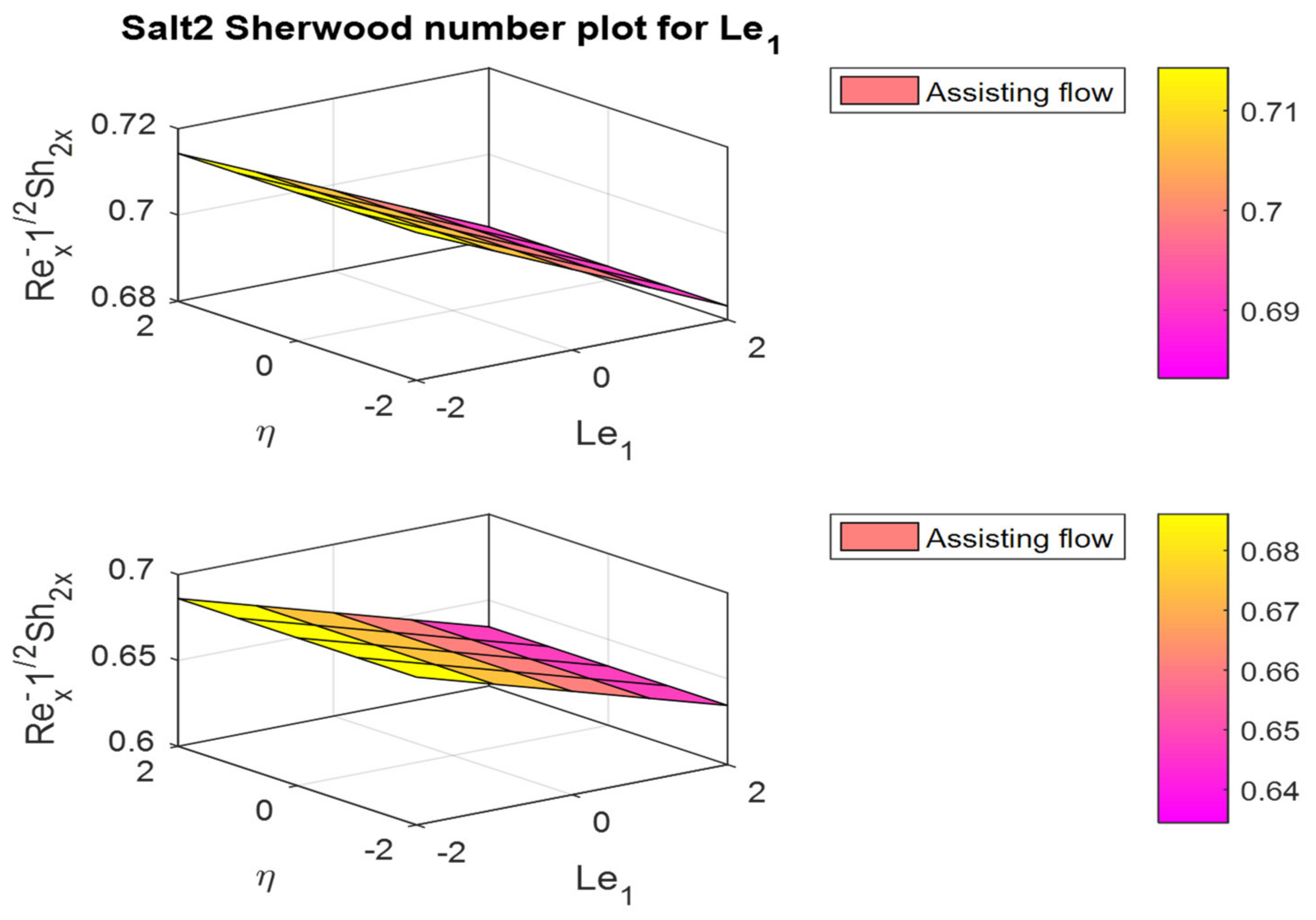
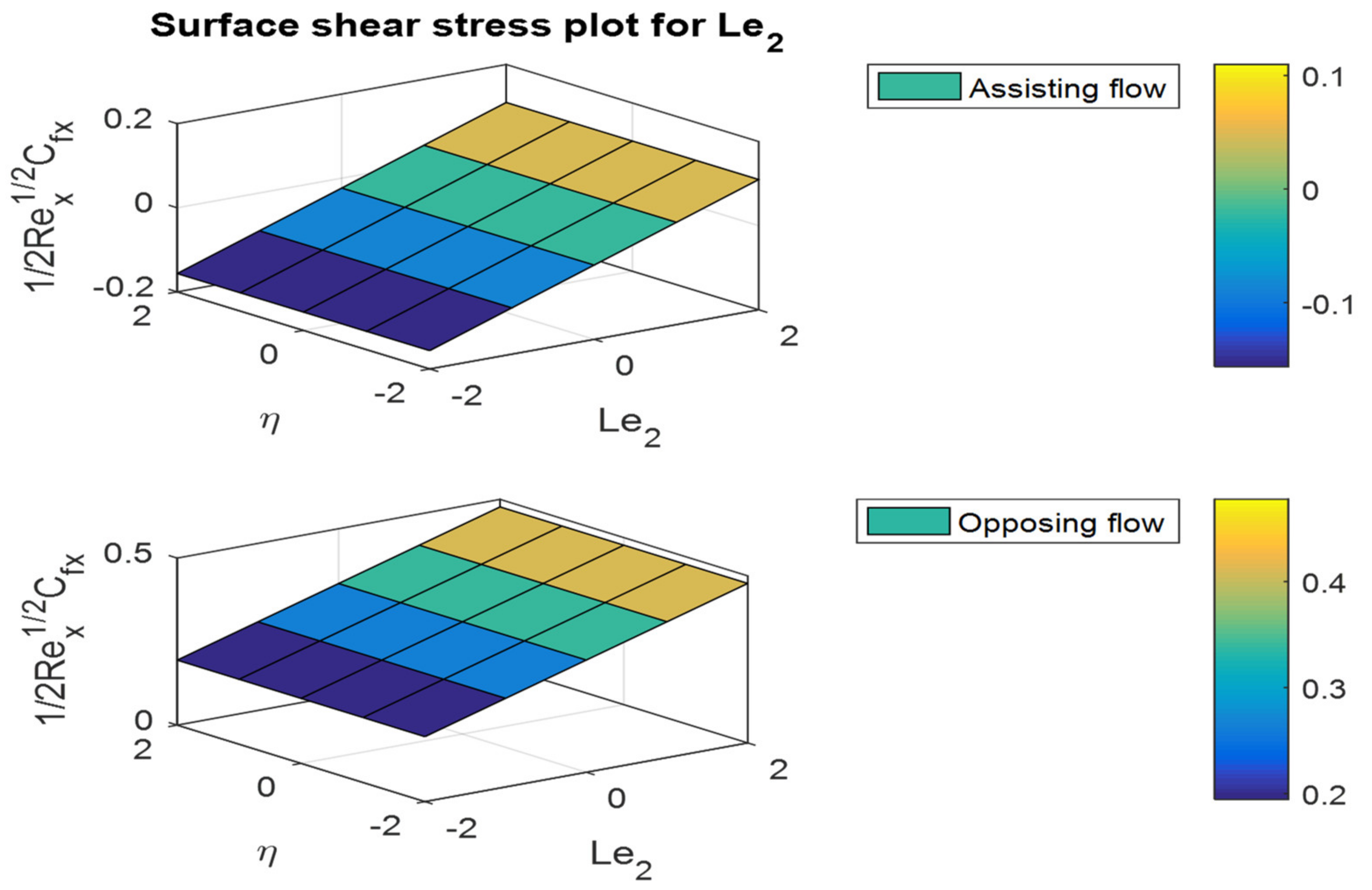
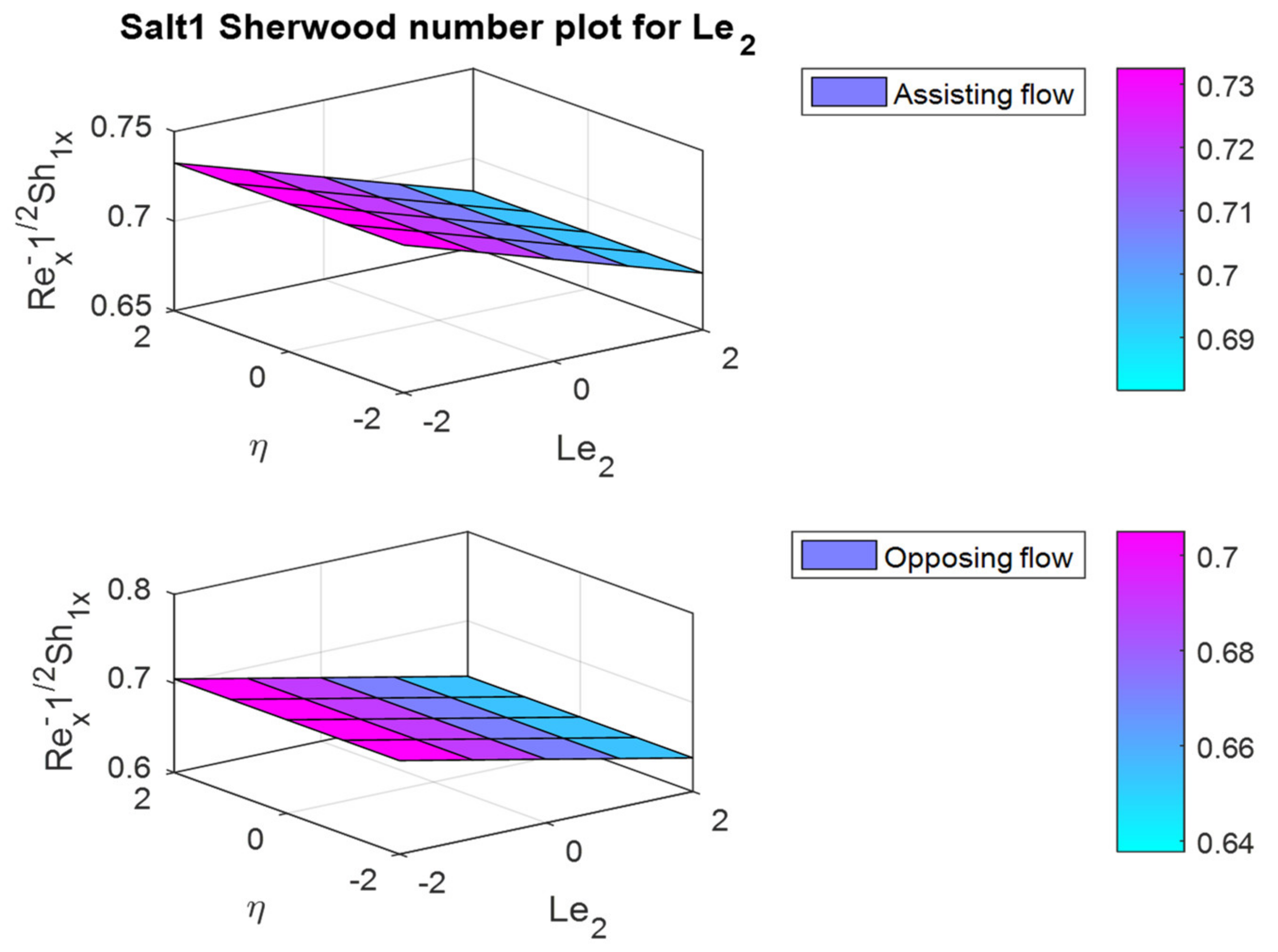
• The friction factor rate is enhanced in both fluid flow cases for increases in Lewis numbers $L{e}_1$ and $L{e}_2$.
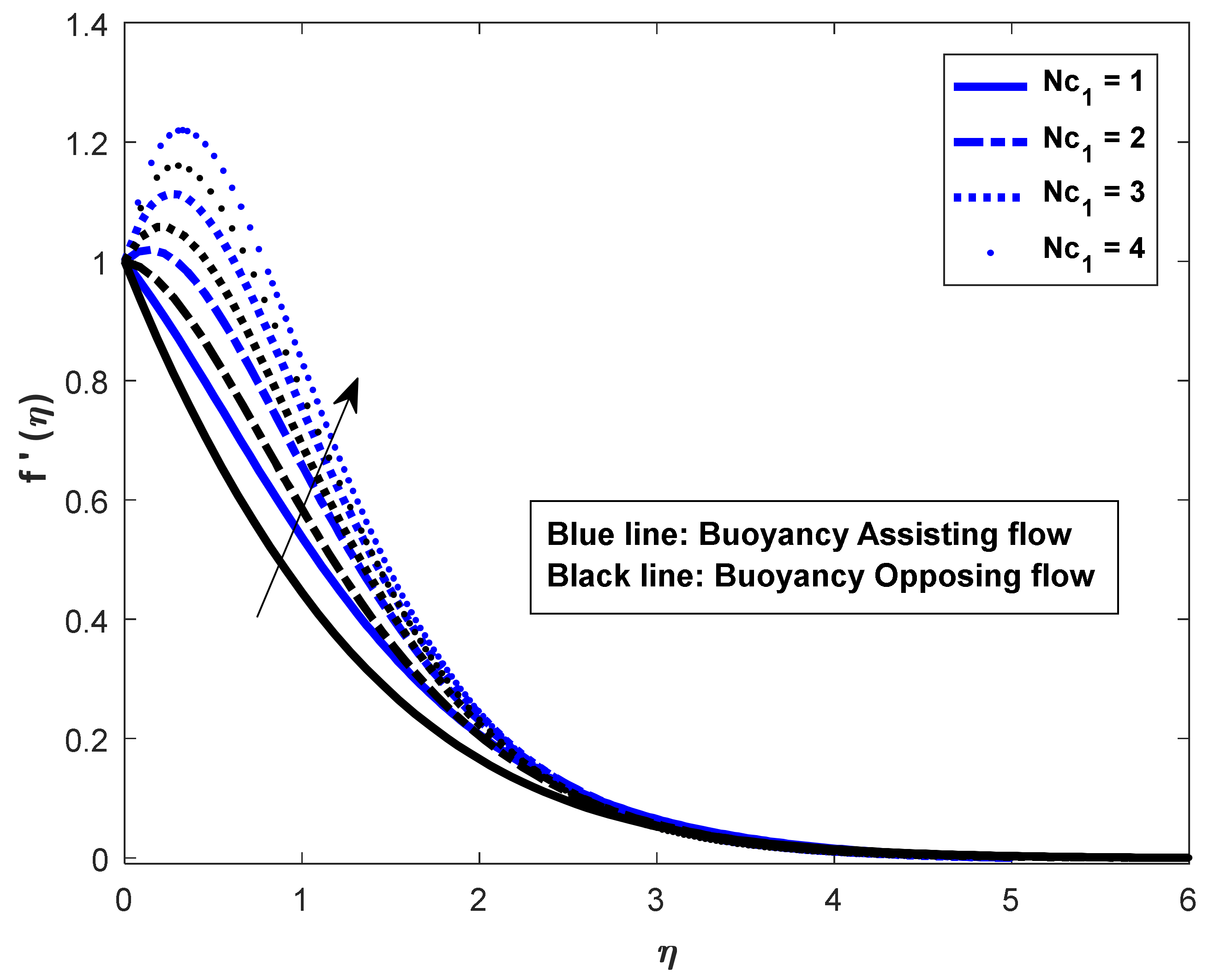
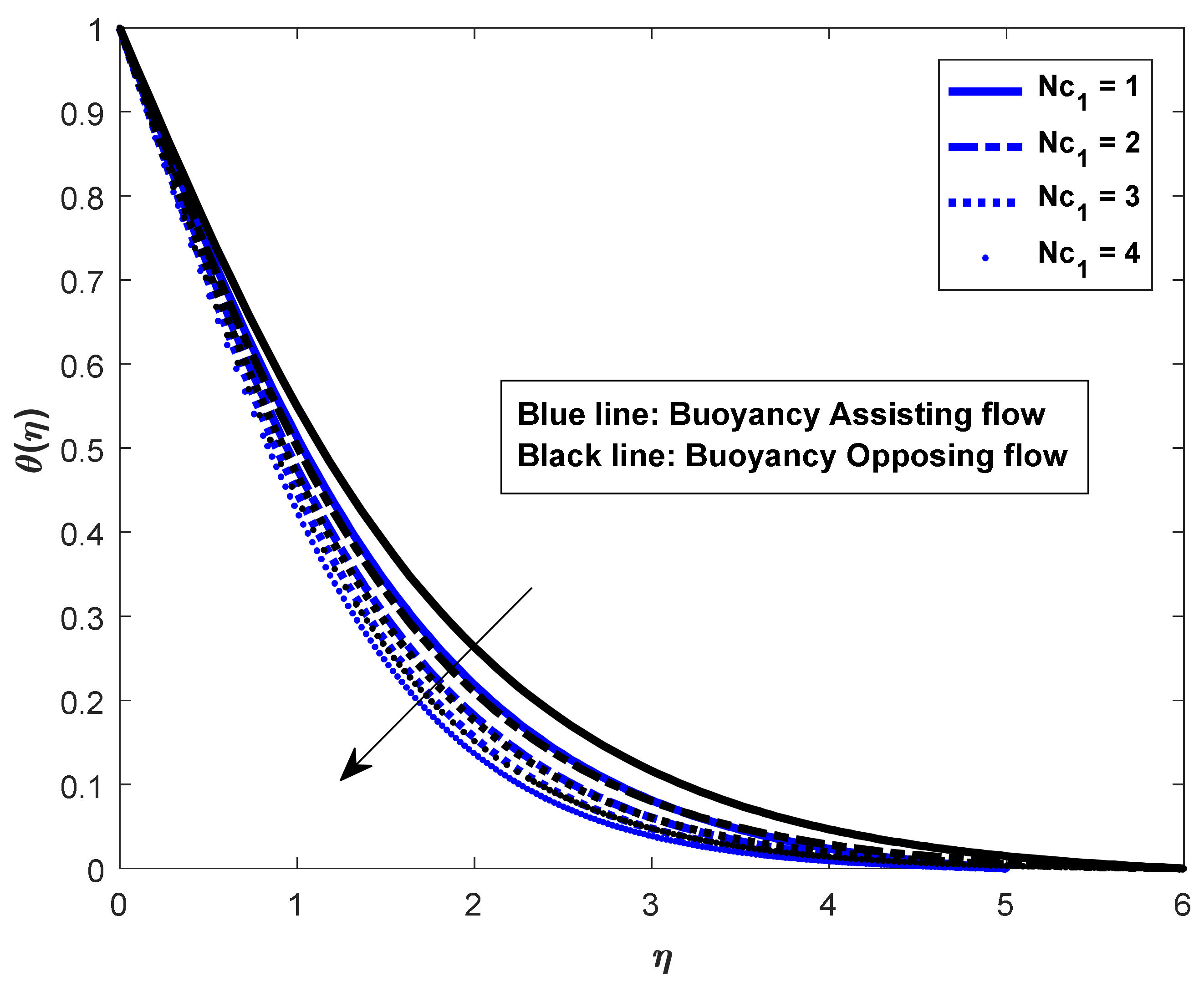
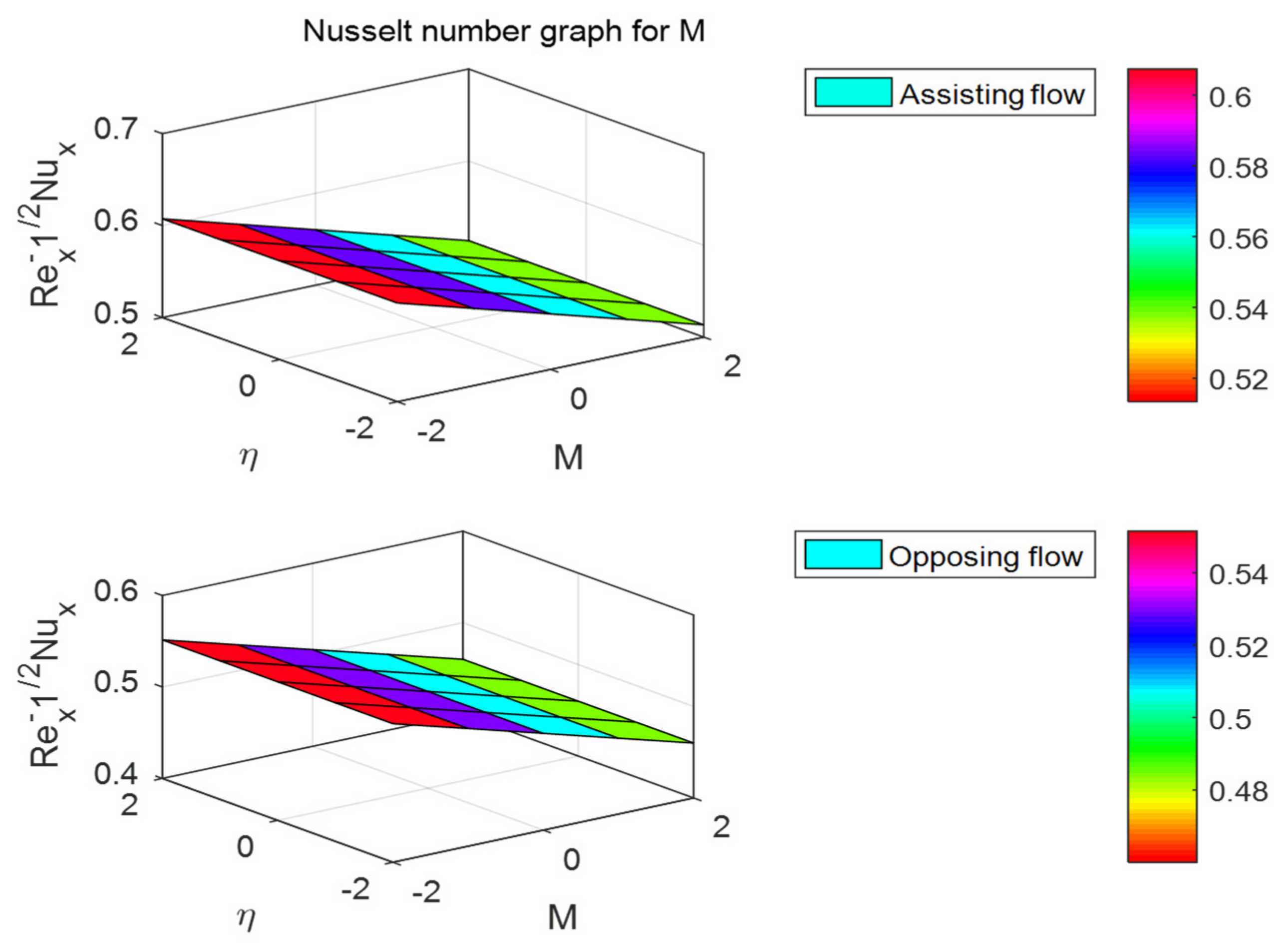
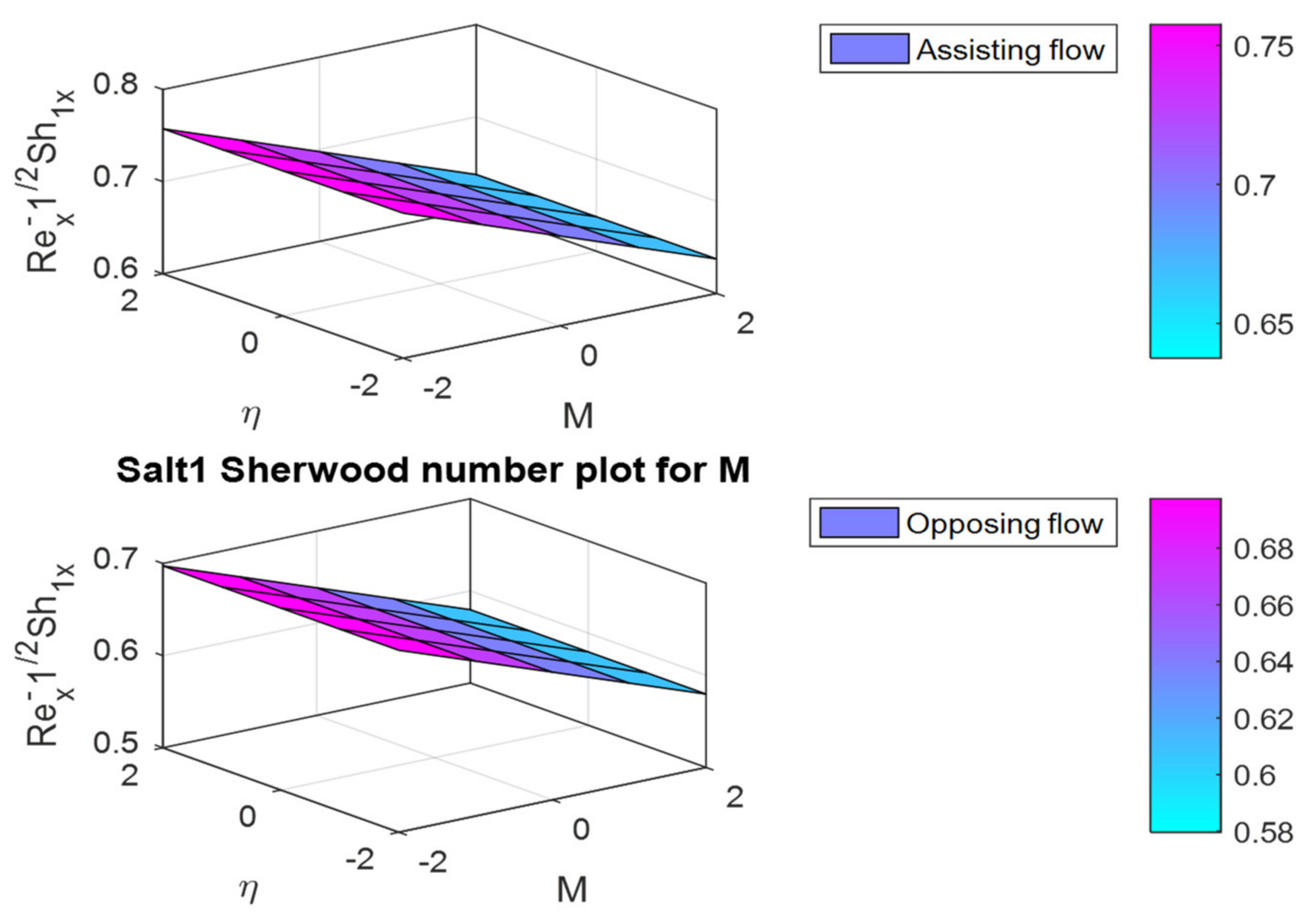
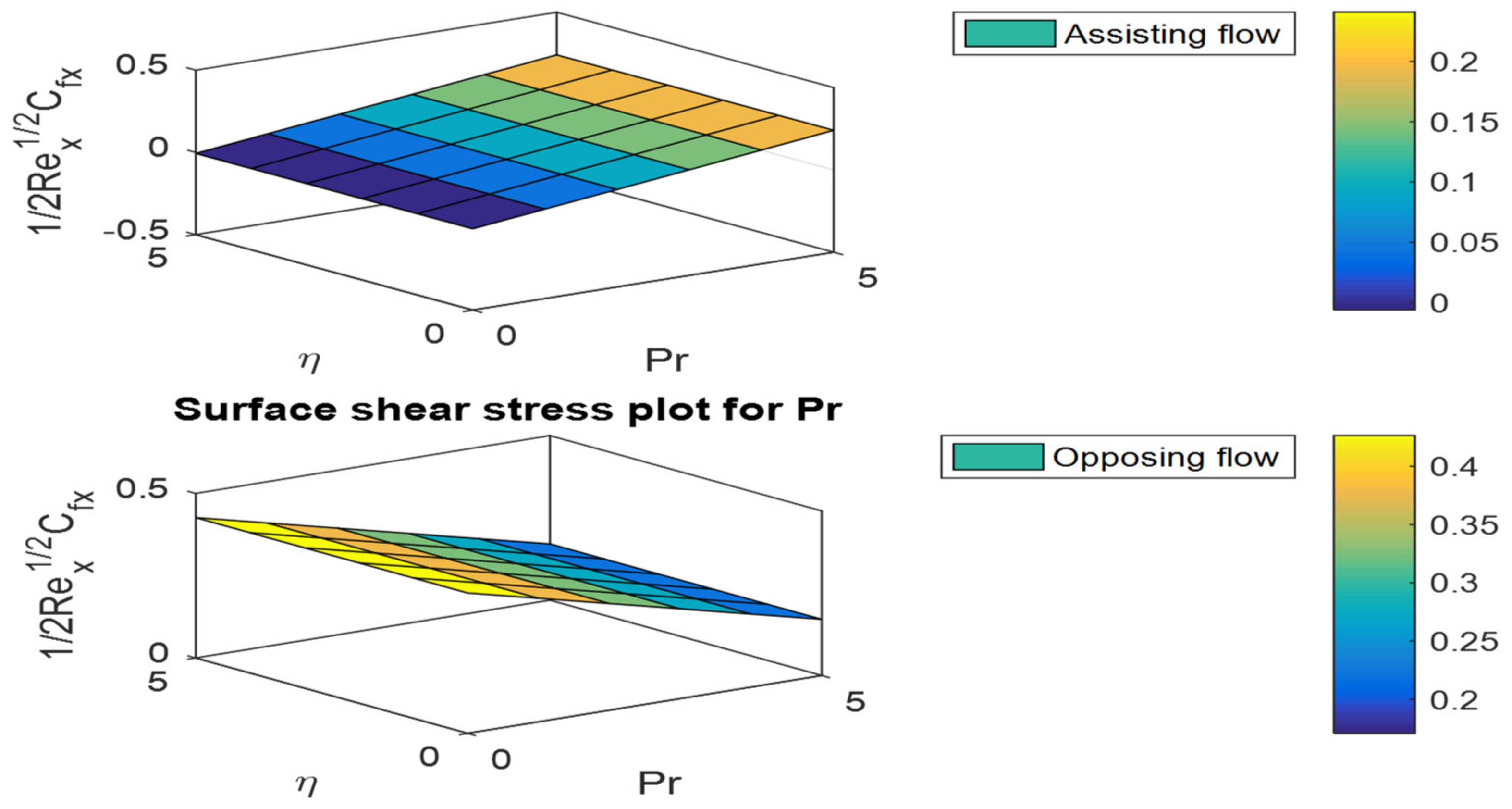
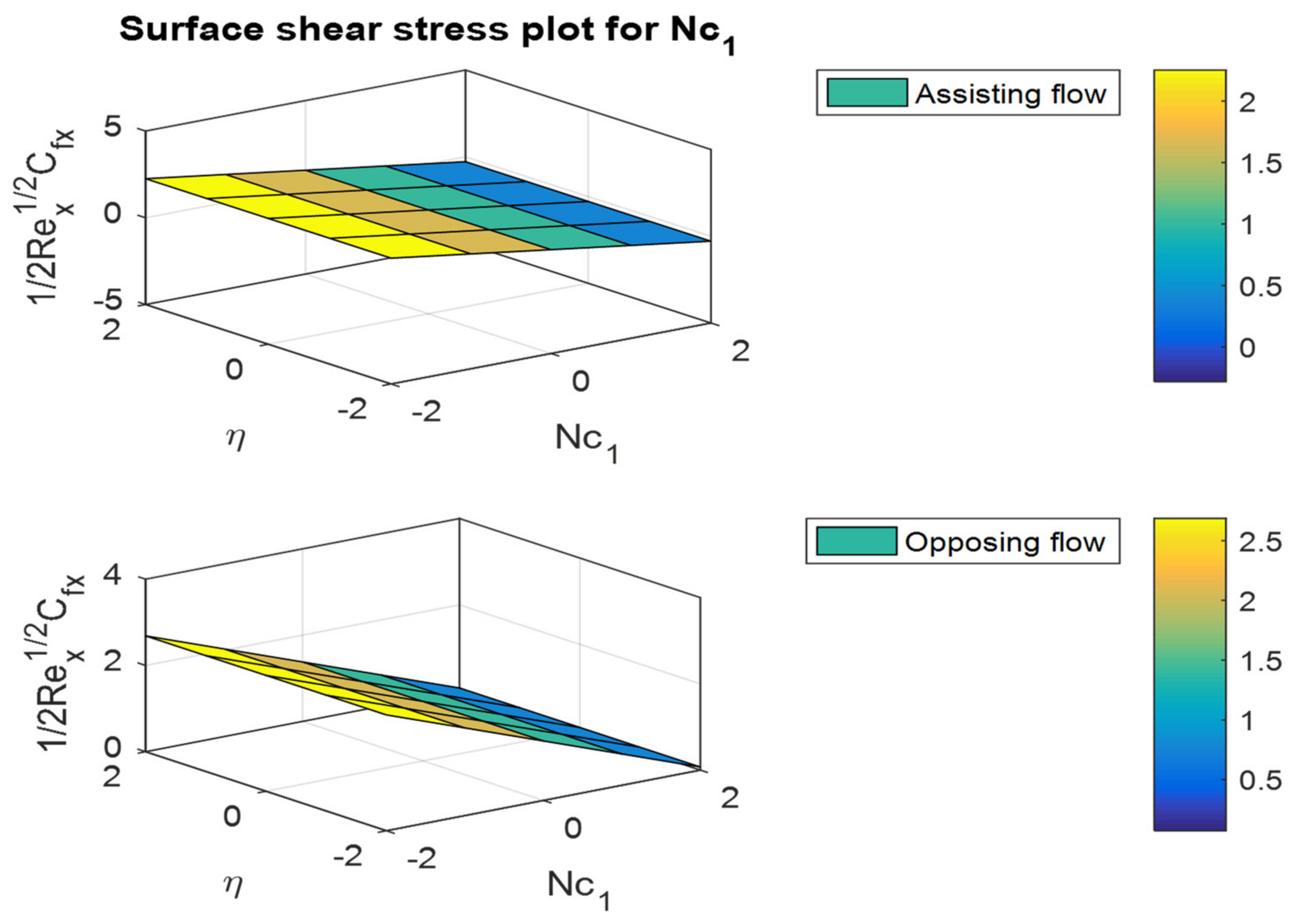
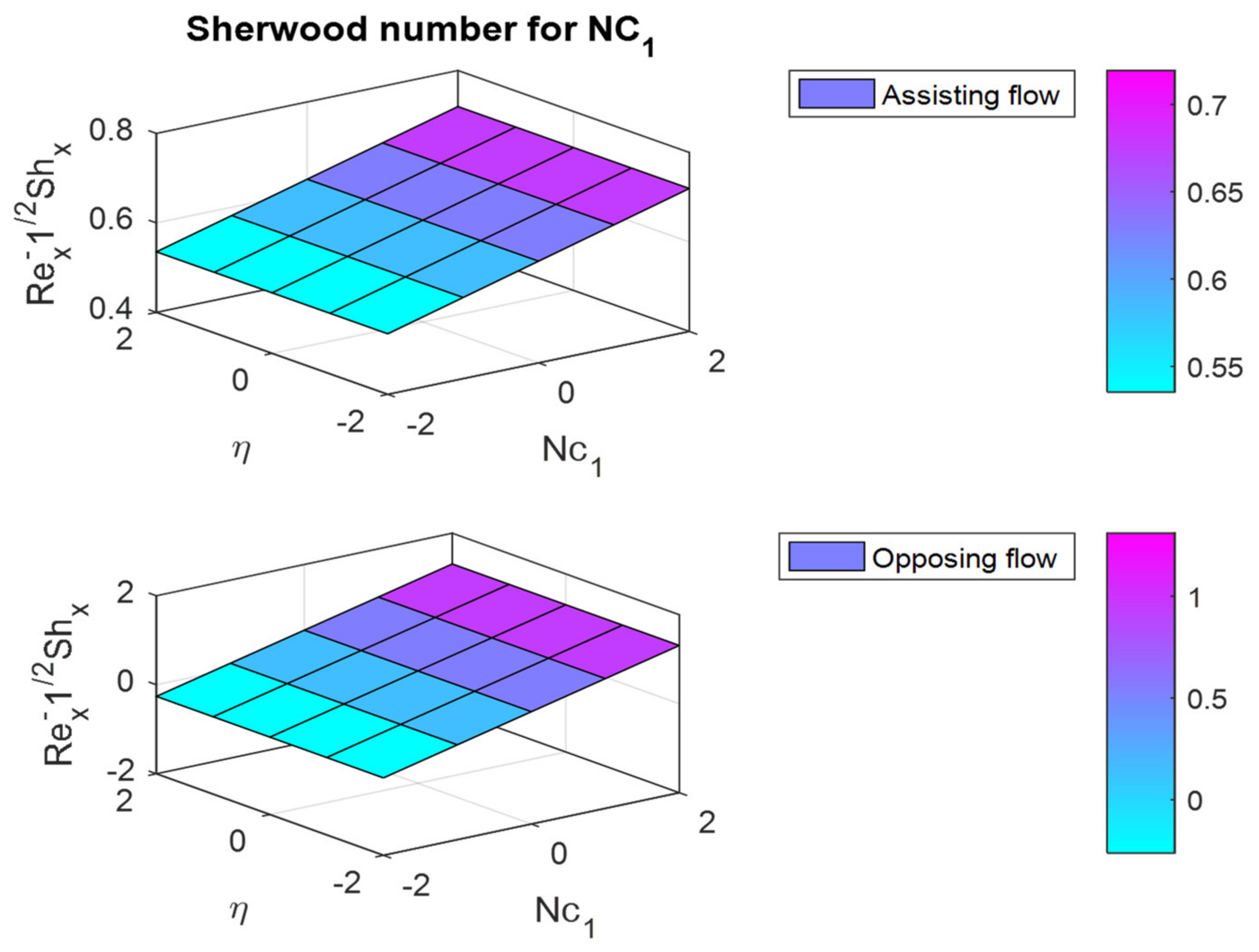
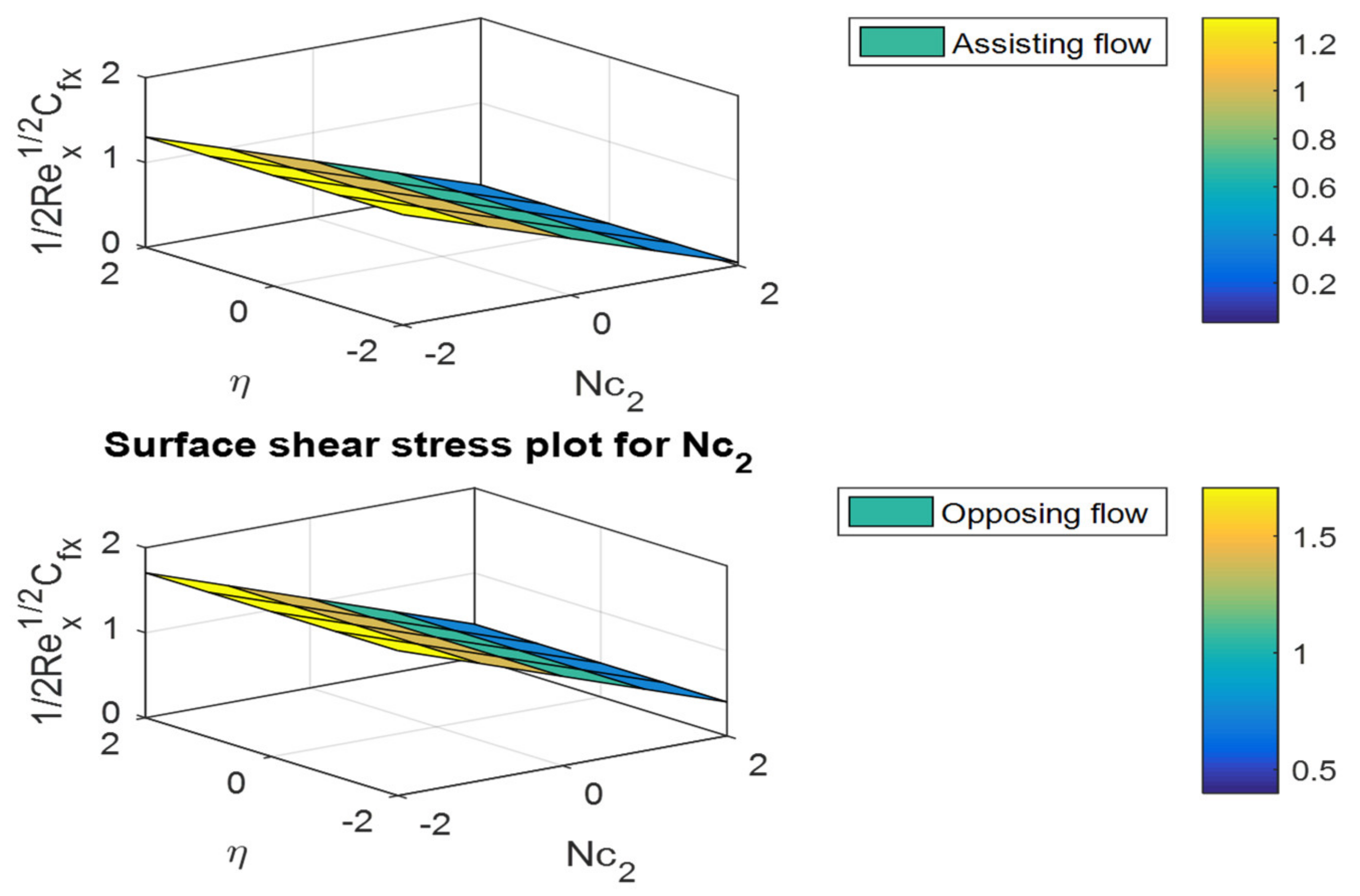
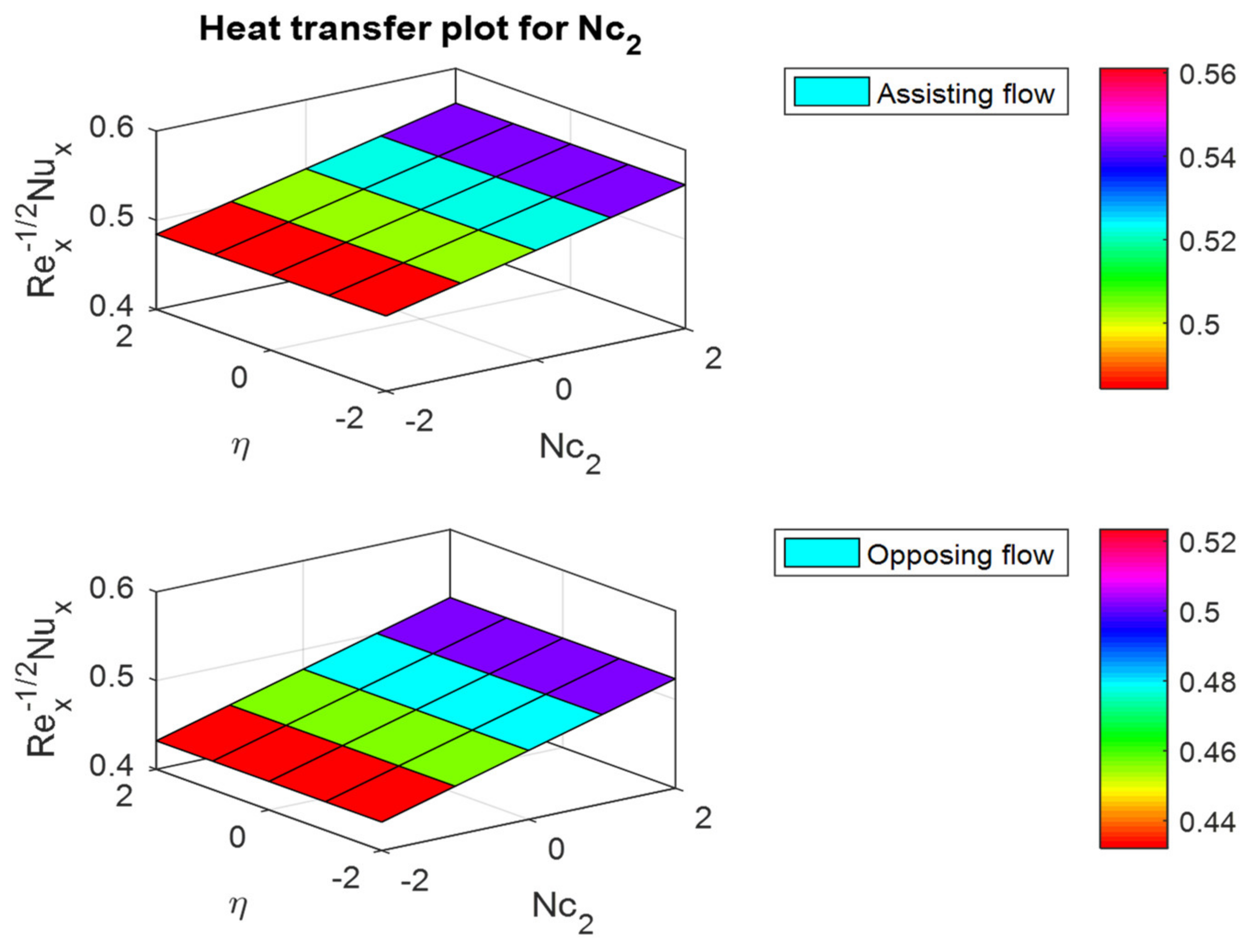
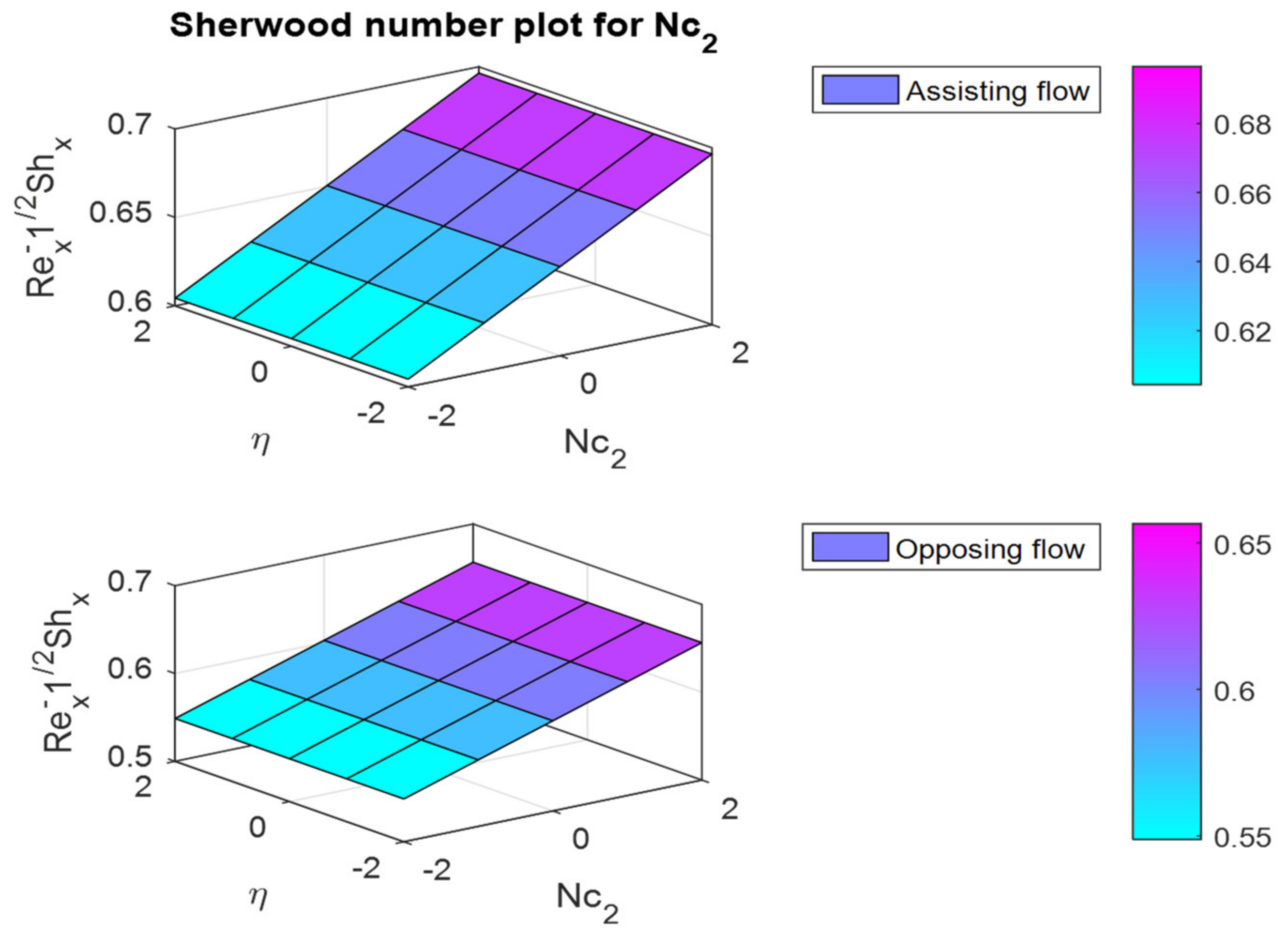
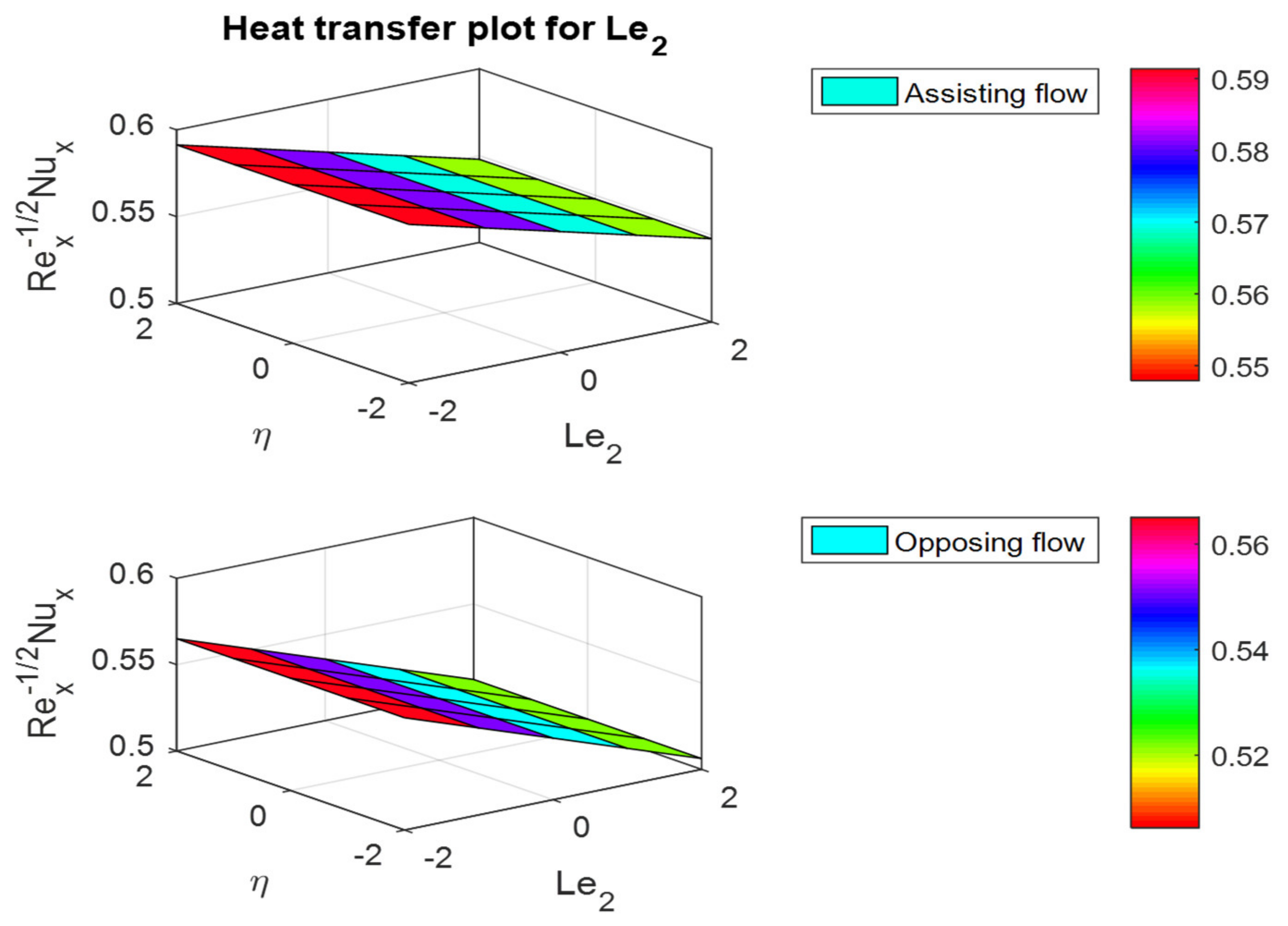
• The friction factor coefficient decreases with increases in buoyancy ratio parameters $N{c}_1$ and $N{c}_2$, but the opposite behavior can be observed for the Nusselt and Sherwood numbers.
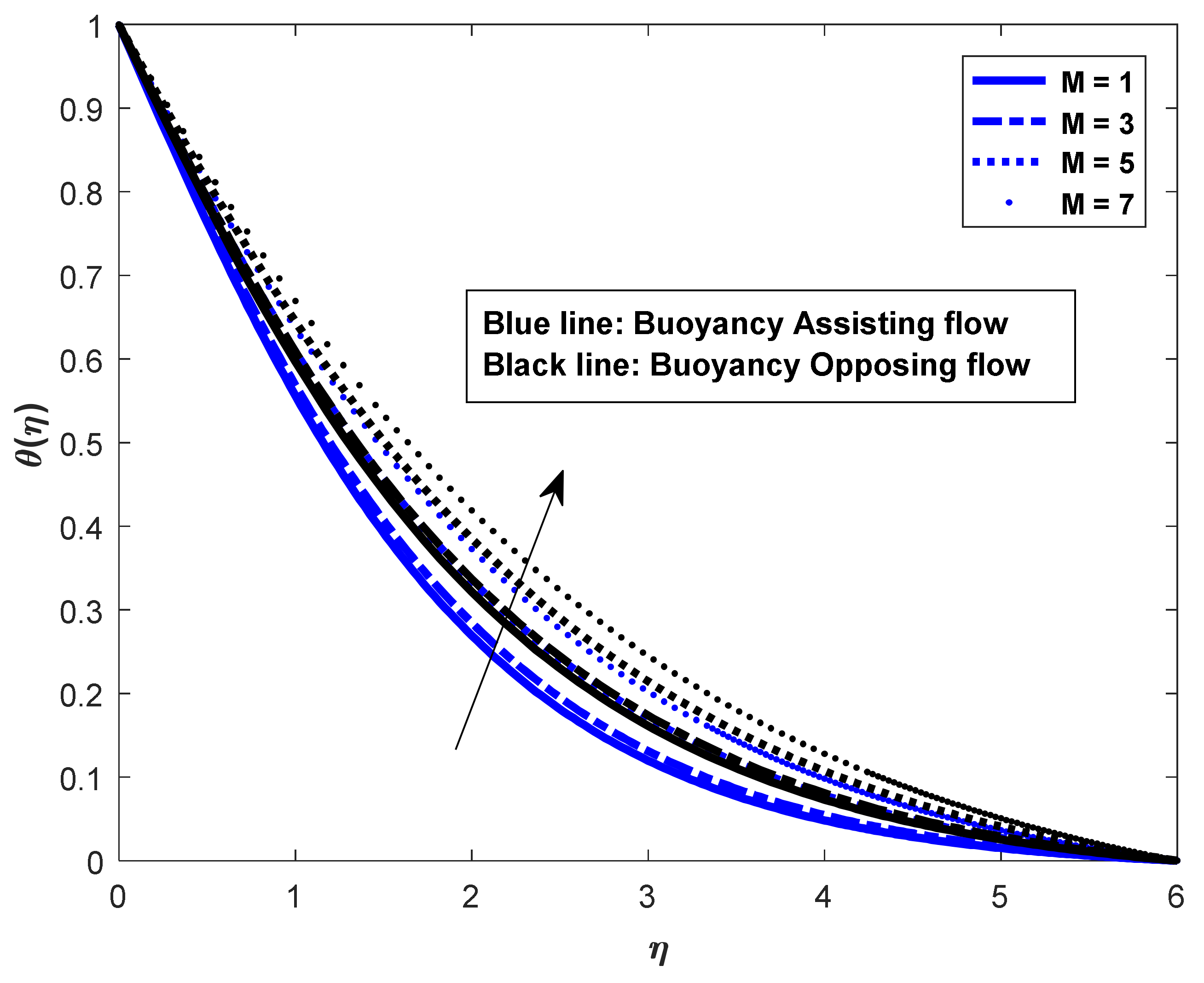
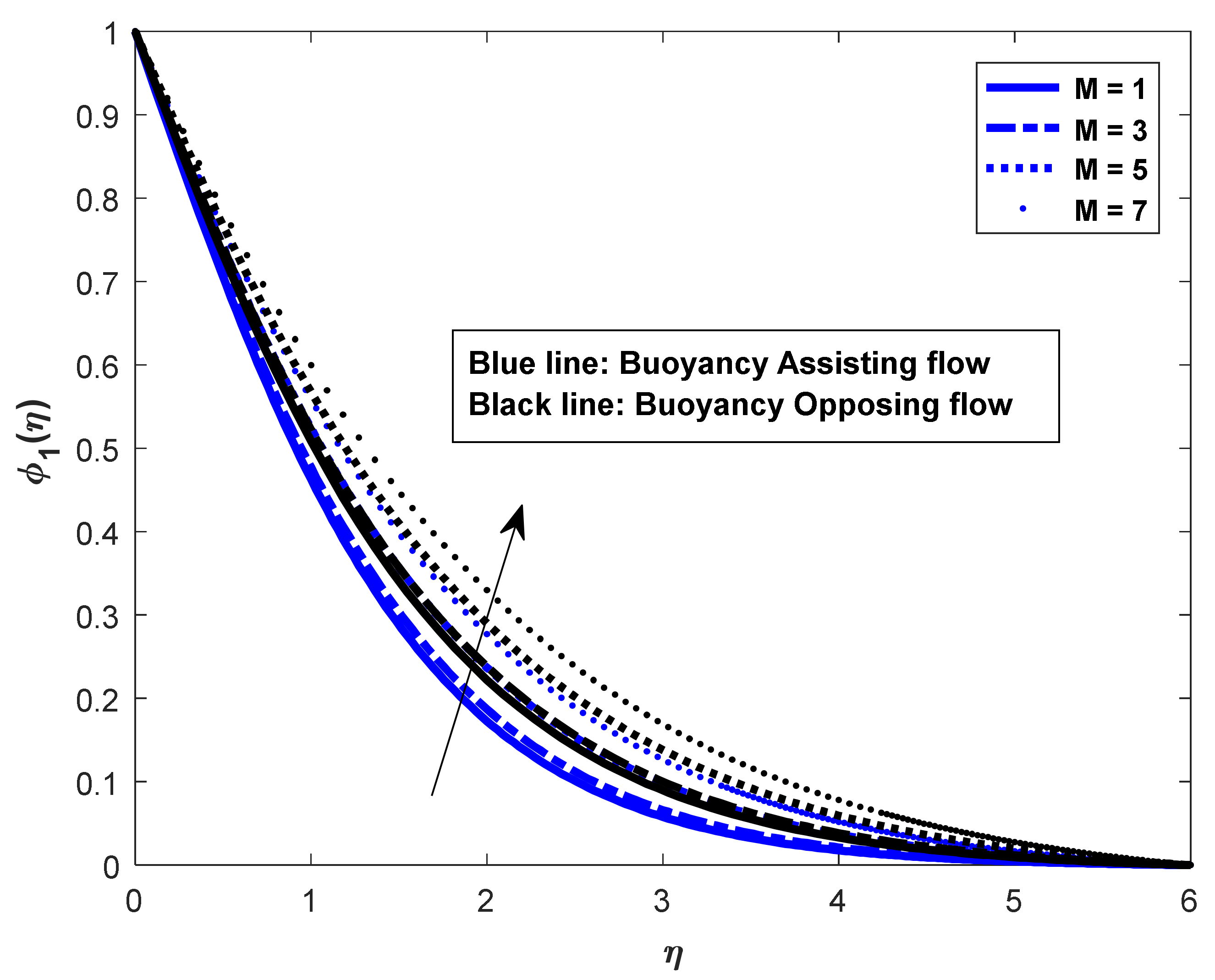
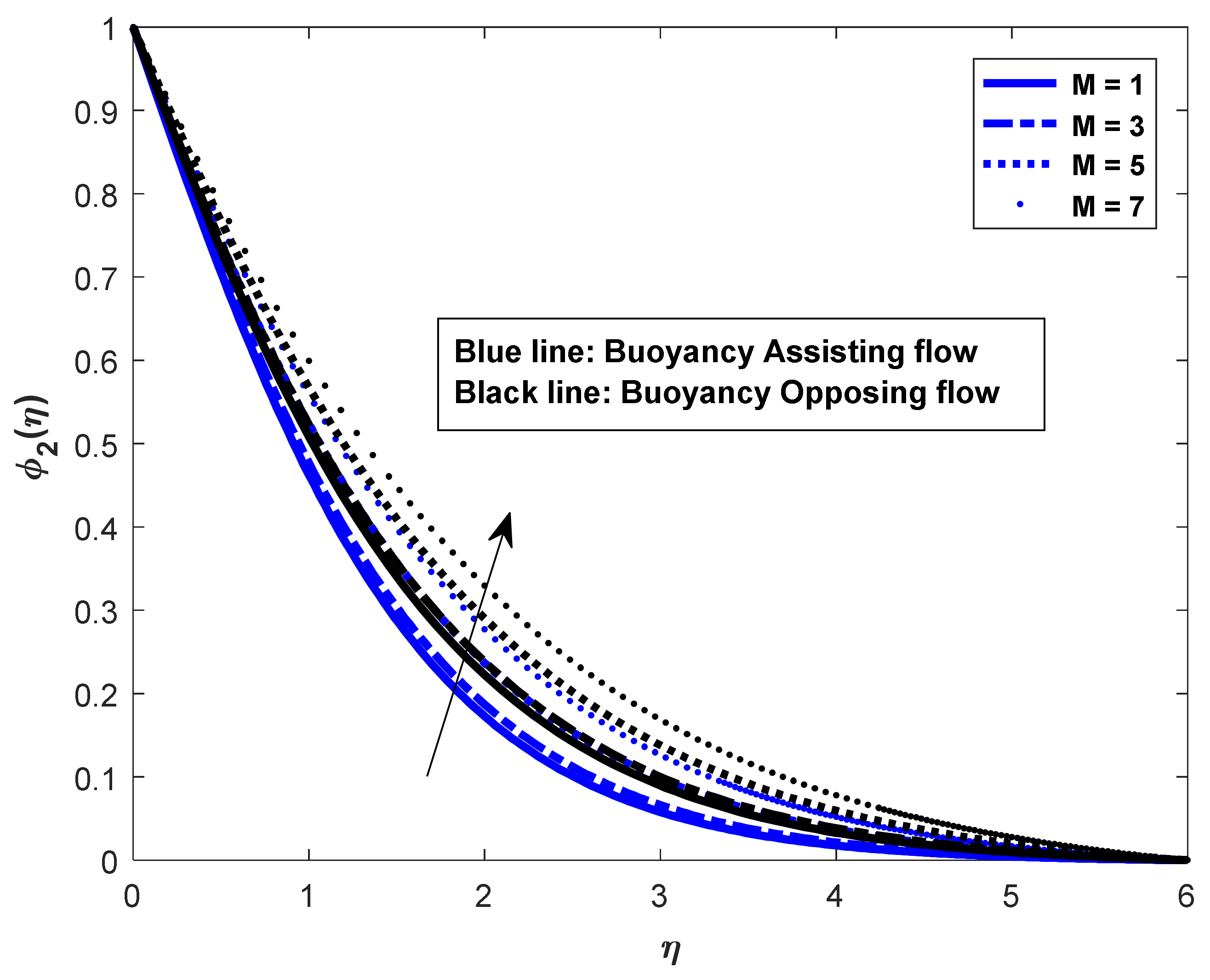
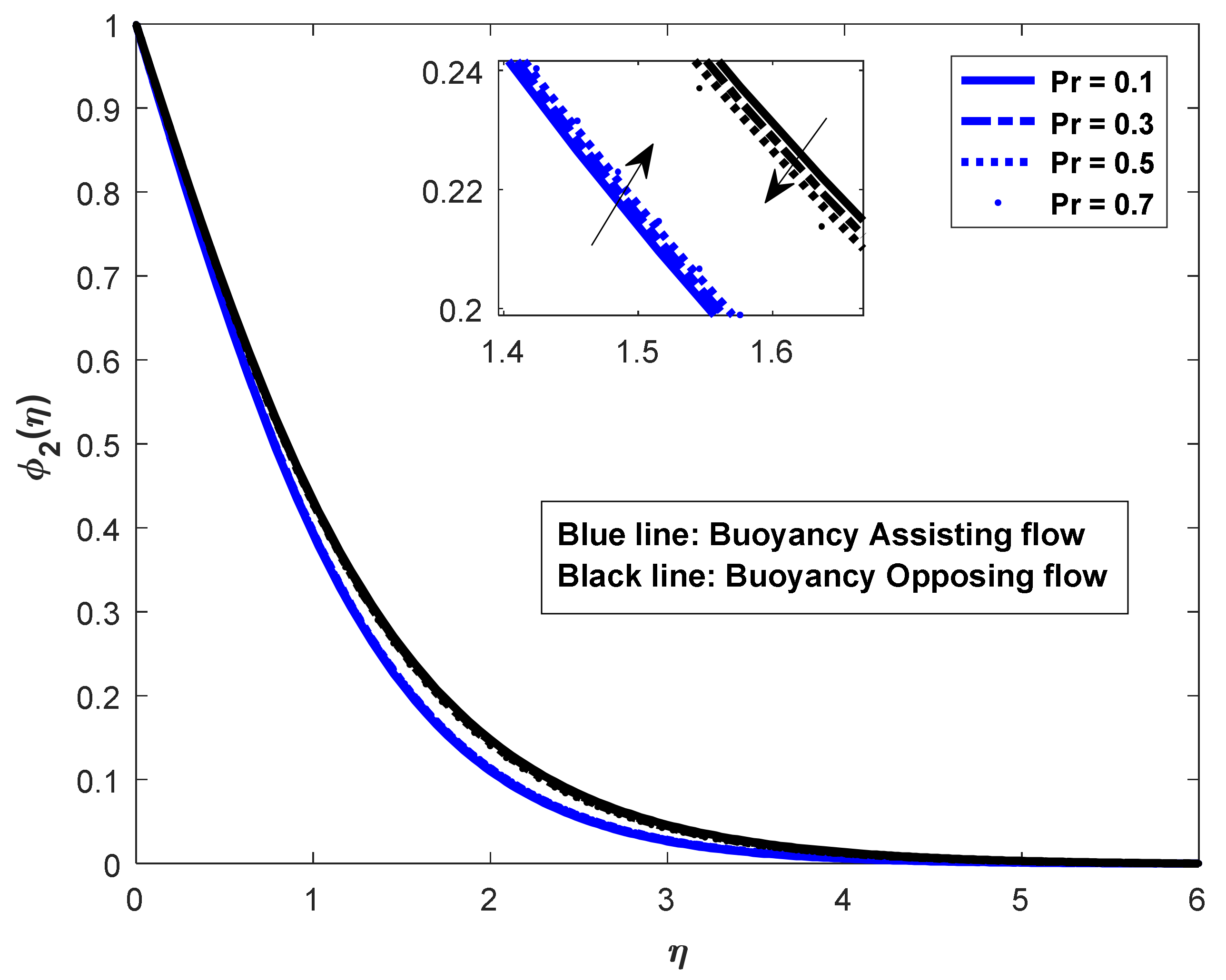
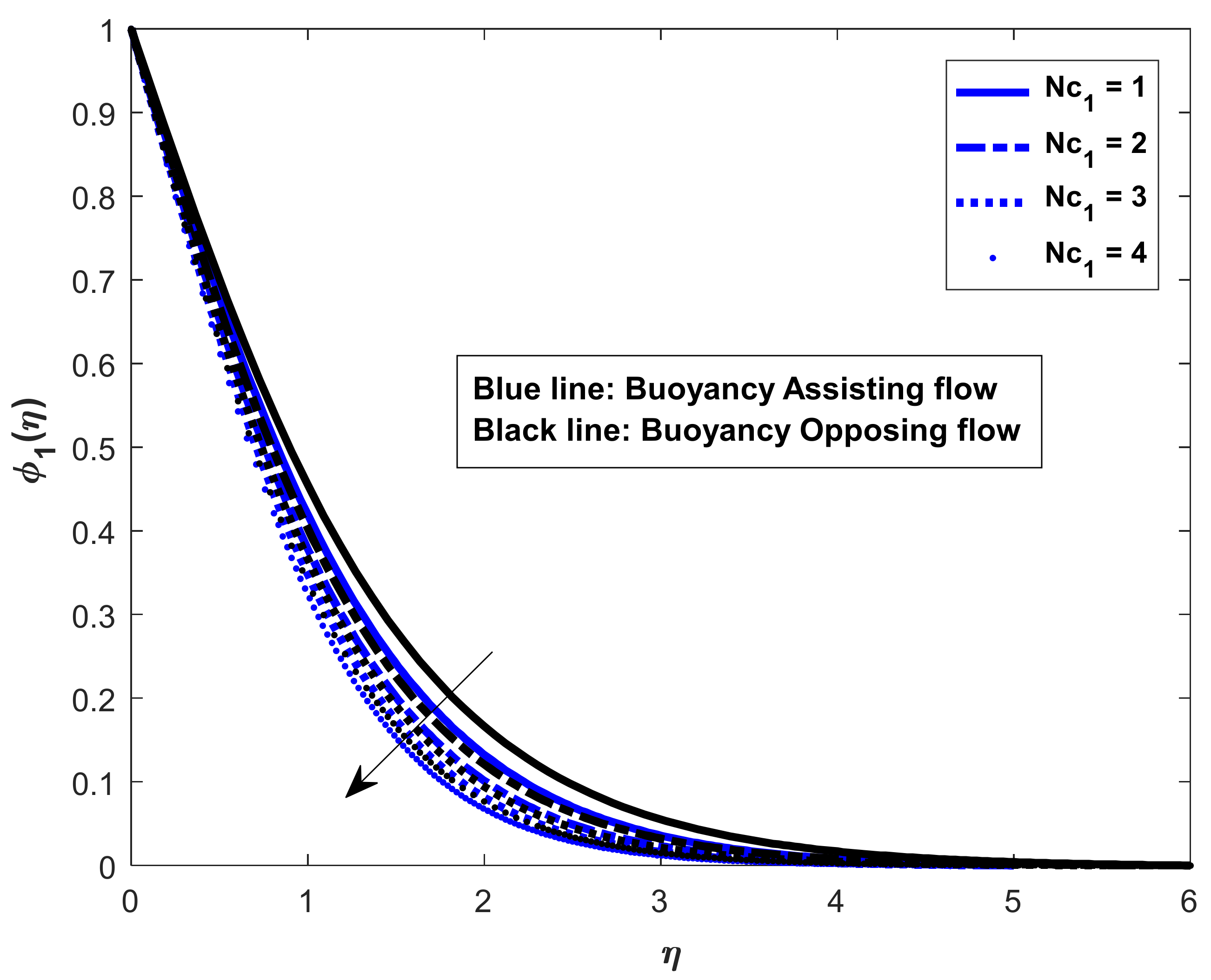
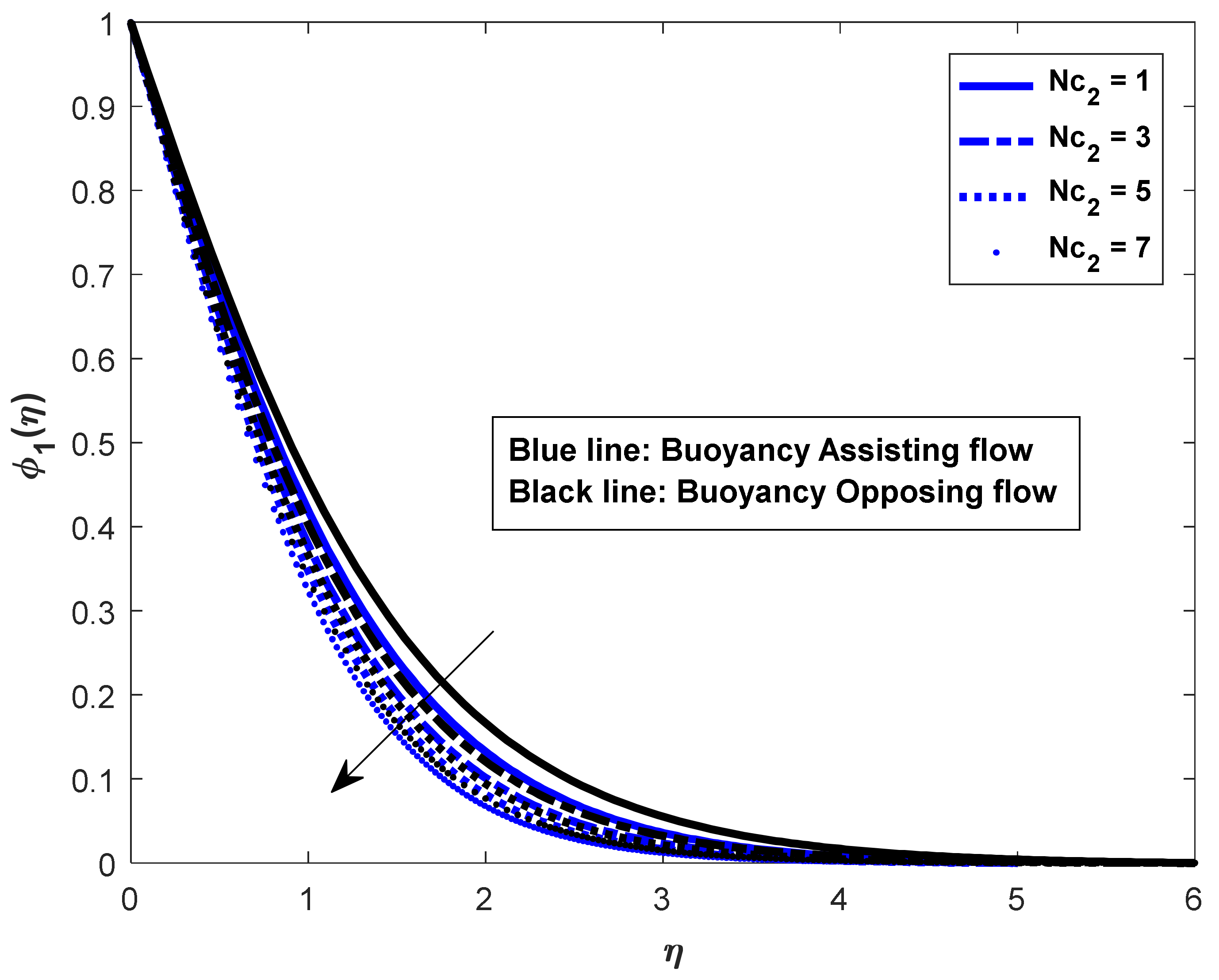
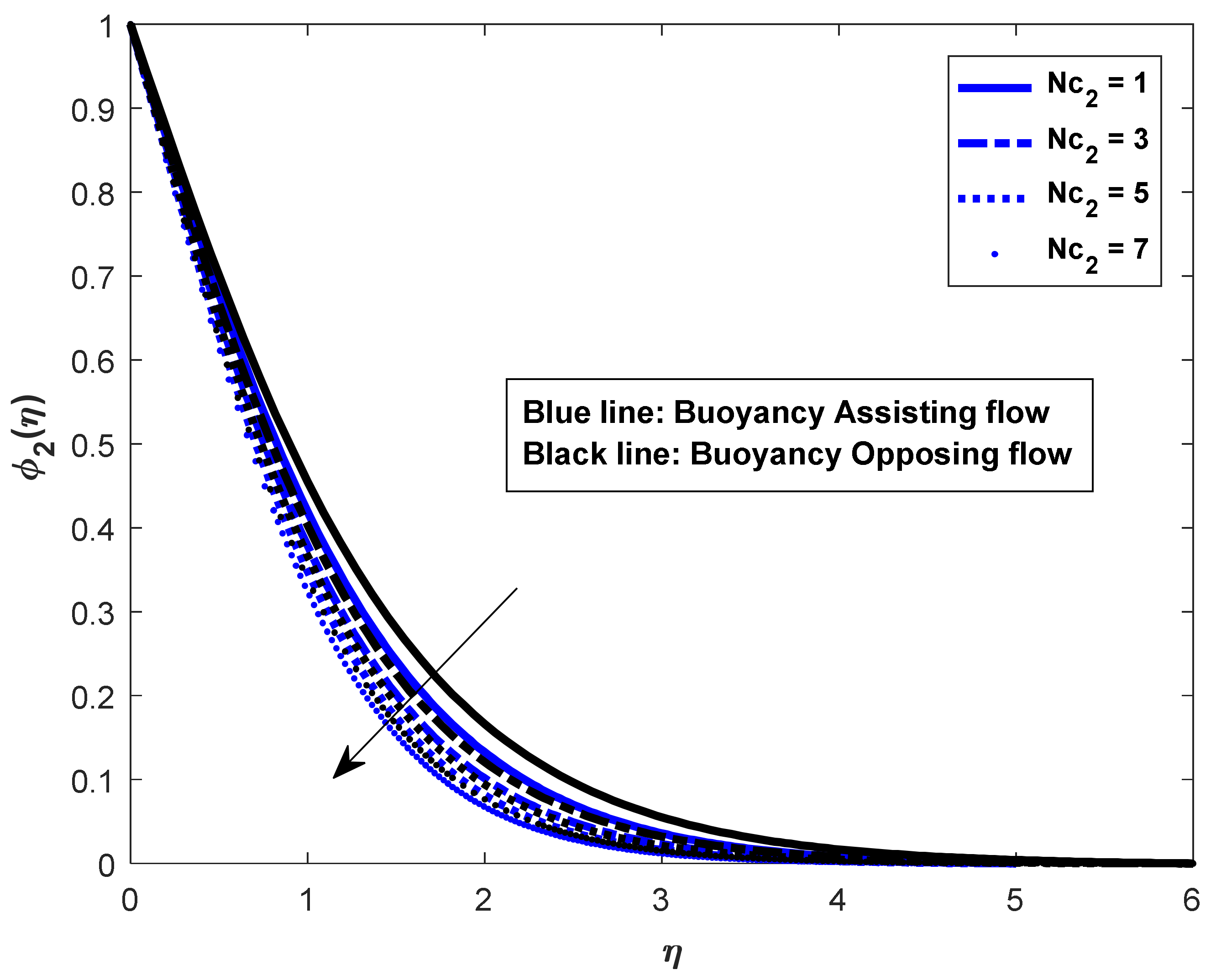
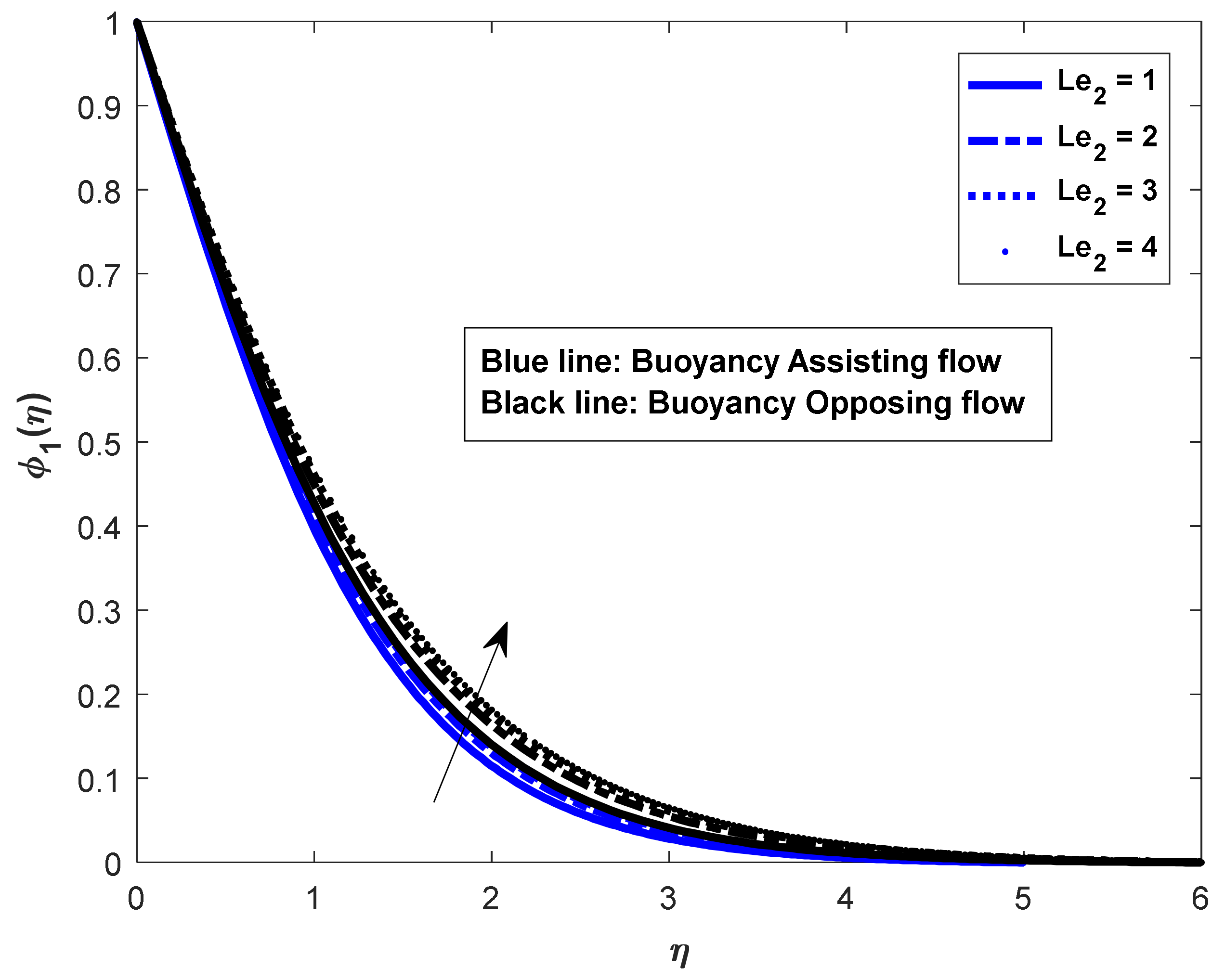
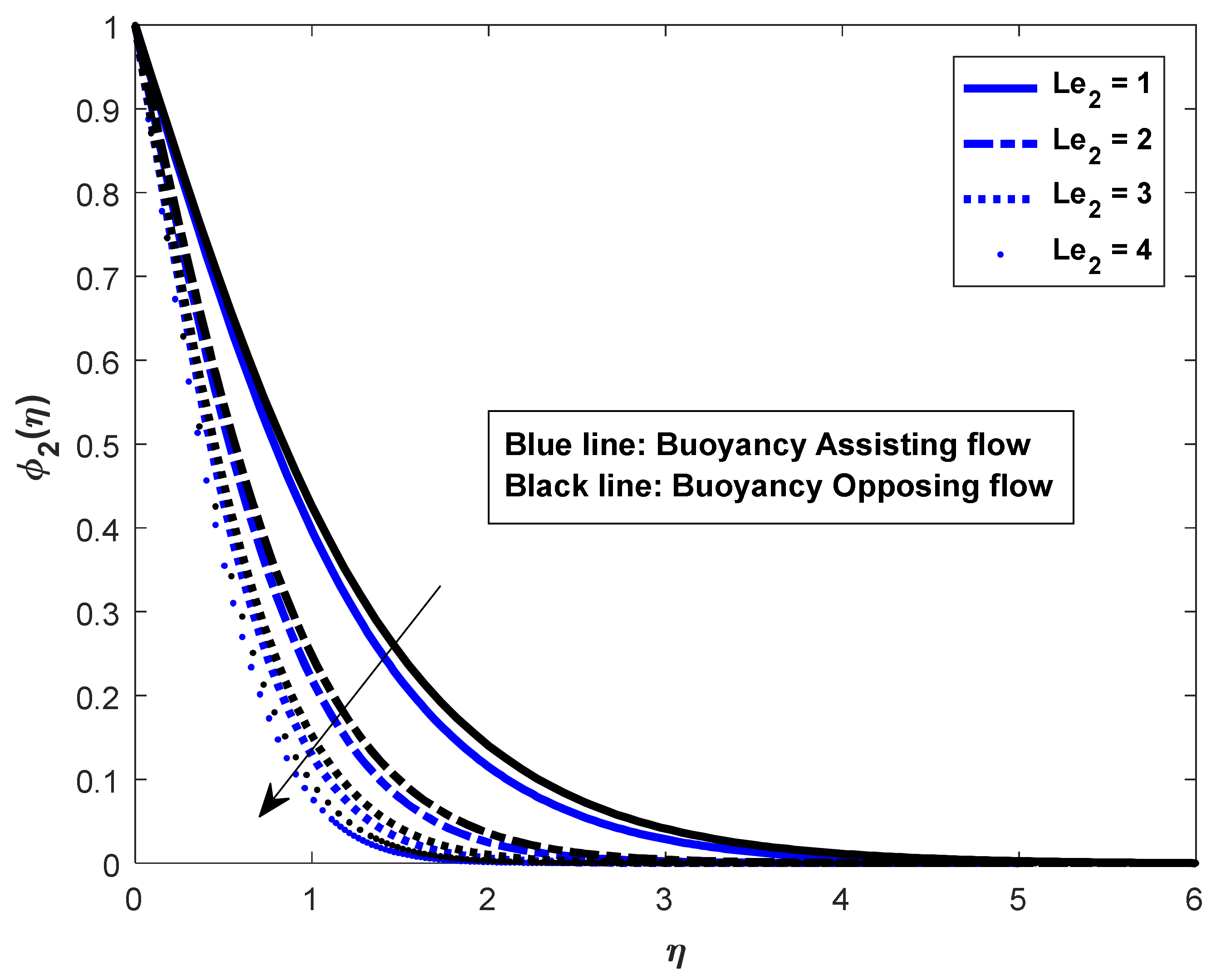
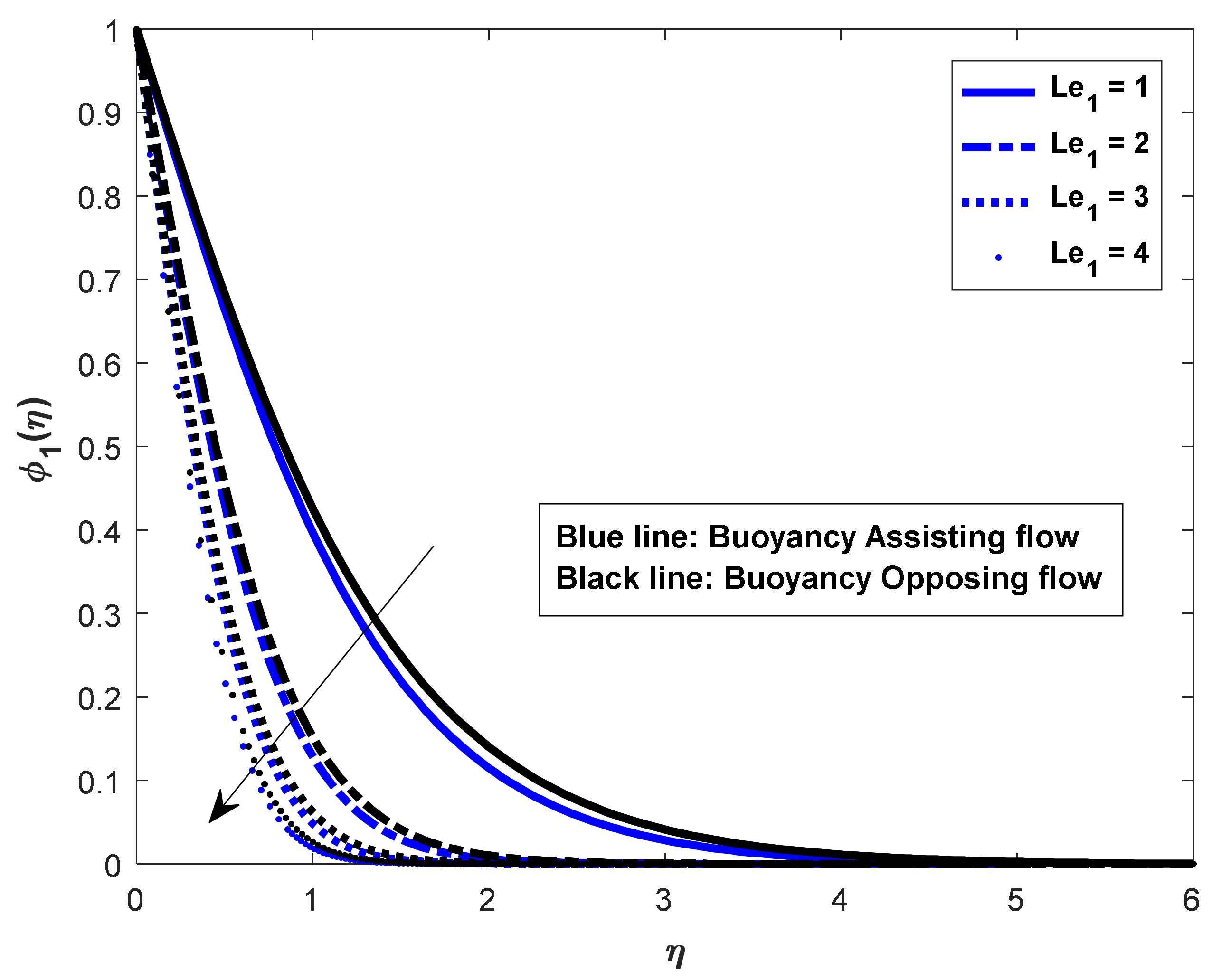
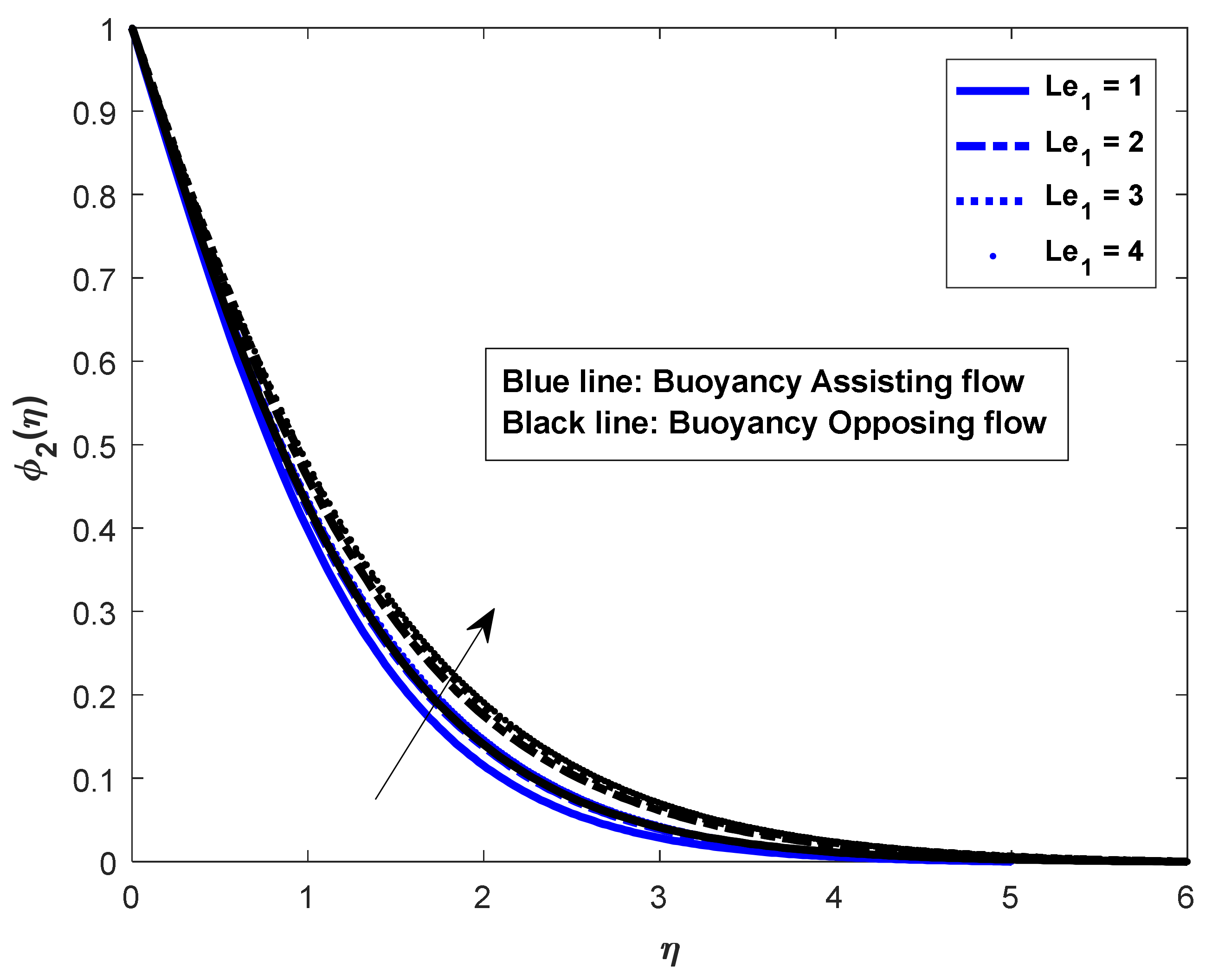
• In the assisting flow case, the dimensionless concentration rises as the Lewis number rises; for buoyancy, the opposing flow case also remains the same.
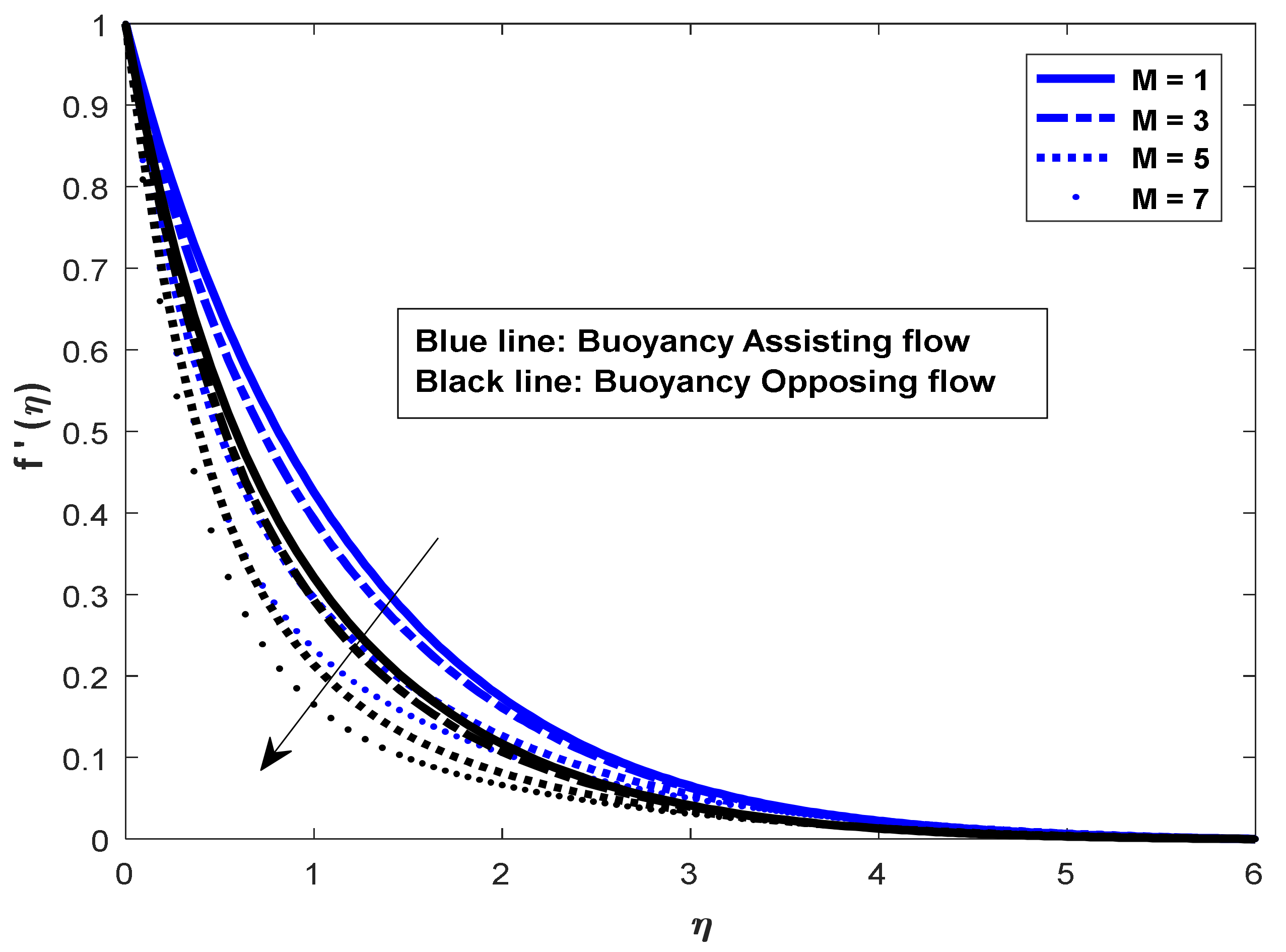
• The magnetic field parameter decreased the velocity distribution by the effect of Lorentz force.
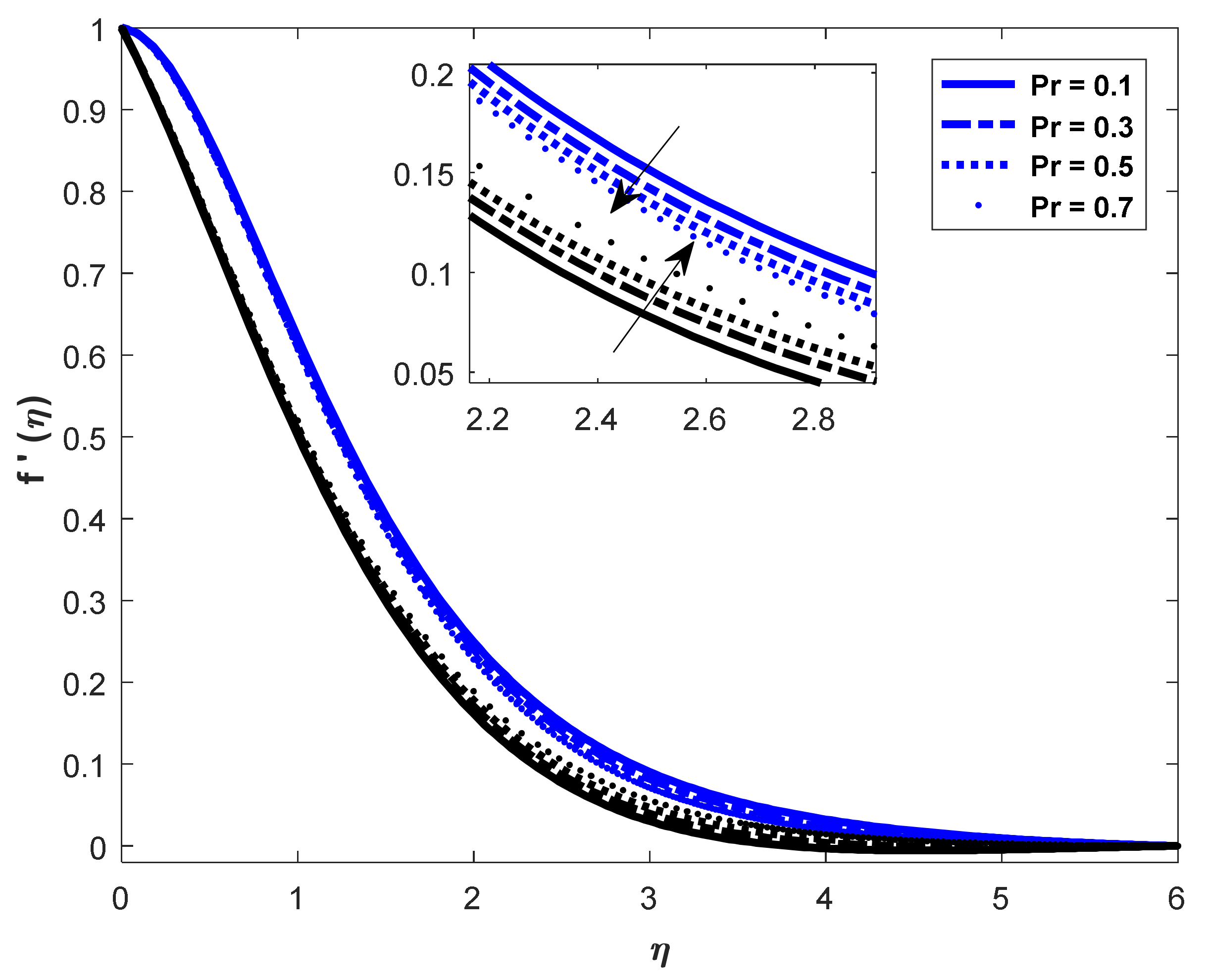
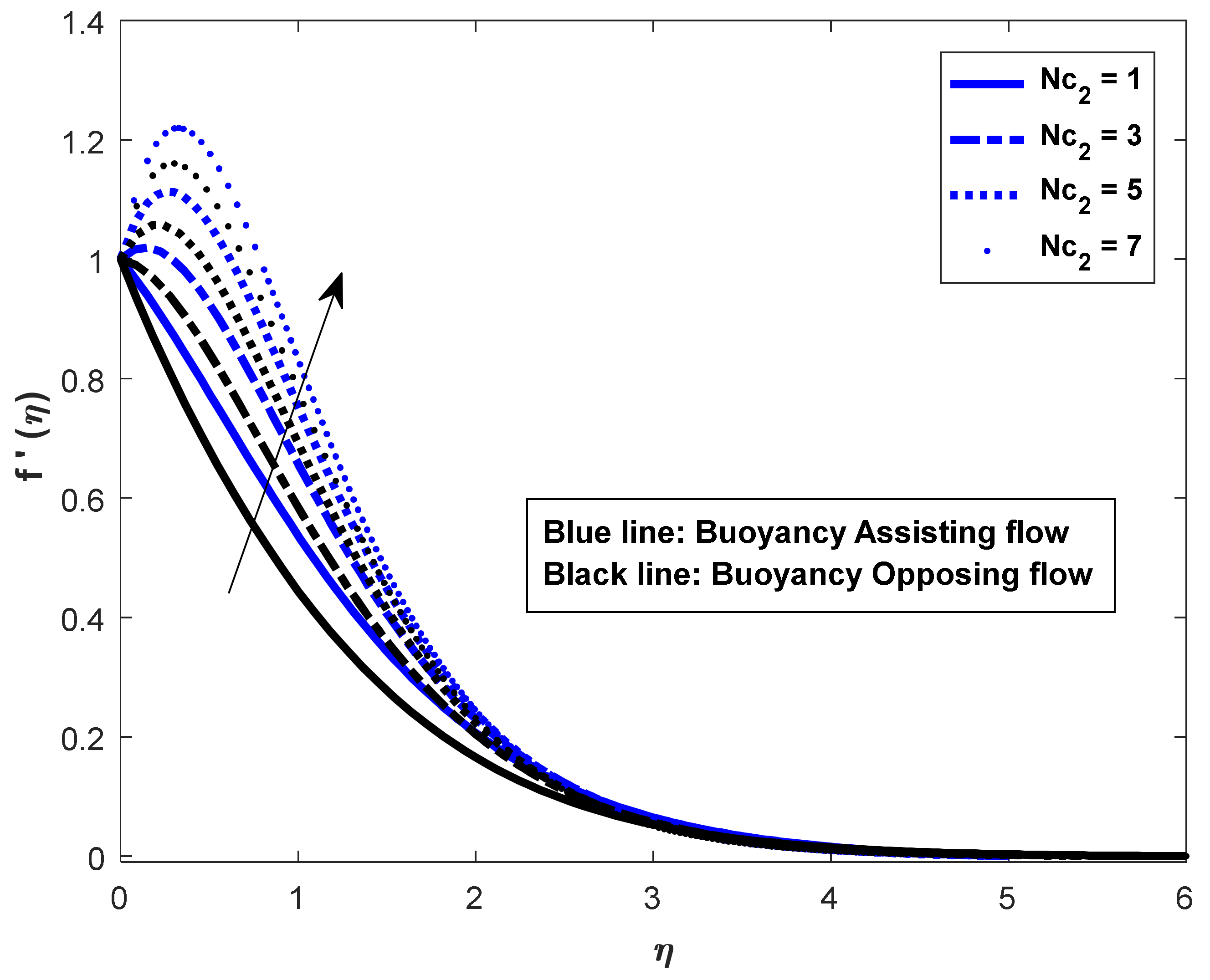
• In both assisting and opposing flow instances, the Prandtl number increases the skin friction coefficient in assisting flow and decreases it in opposing flow in heat and mass transfer rates.

6. Limitations and Future Scope

6.1. Limitations

• The flow was considered as not time-dependent and incompressible.
• The turbulence due to the hematite nanoparticles interaction was neglected.
• Away from the object’s surface, viscous effects can be considered negligible, and potential flow can be assumed.
• The viscosity, conductivity, and density properties were constant.

6.2. Future Scope

• Triple diffusion analysis can include variable viscosity and nonlinear convection flow properties.
• Variable conductivity and unsteady nonlinear flow characteristics of various flow characteristics with chemical species in the triple diffusion process.
• The investigations mentioned above could also be extended by using various techniques, such as mess-free methods, the finite-difference scheme, the spectral element method, the finite element method, the Keller-box method, homotopy analysis, and spectral methods.