Product Design Scheme Generation and Optimization Decisions While Considering Remanufacturability
Abstract
:1. Introduction
2. Literature Review
3. Scheme Generation Based on Improved Axiomatic Design
3.1. Analysis of Tree Topology Mapping Process
- (1)
- Taking axiomatic design as the guideline and supporting its design concept, it provides concrete implementation means from function domain to method domain for axiomatic design to make the mapping process clearer.
- (2)
- Based on a certain knowledge base, it can guide the whole mapping process through a variety of design experience, knowledge information, and past design cases.
3.2. Establishment of Scheme Generation Process Model
- (1)
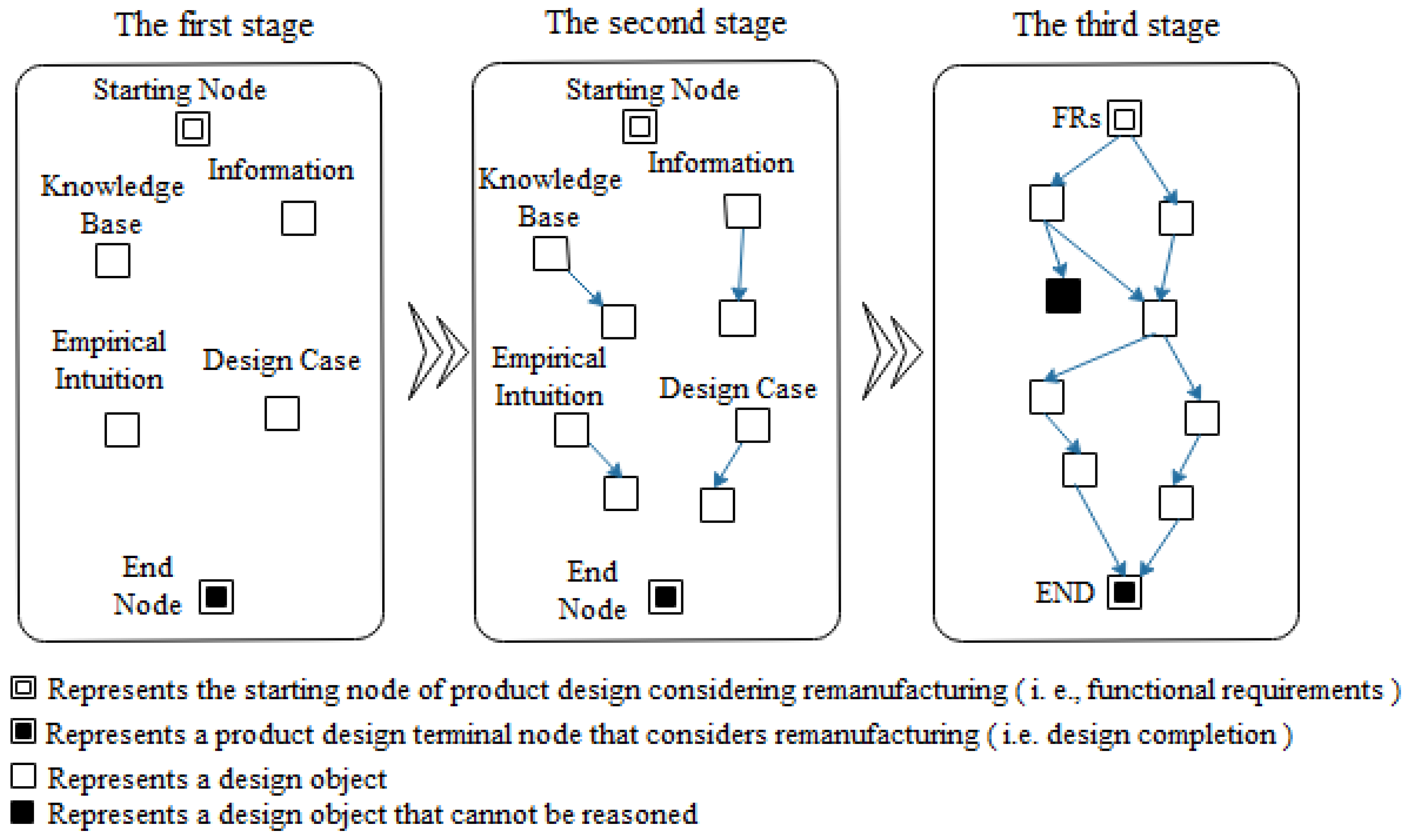
- The scheme generation process model is a weighted directed graph, M = {V(M), E(M), G(M)}, which is defined as follows:
- V(M) represents the set of nodes, V(M) = {FR, ED, DP, D(M)}, where FR (functional requirement set) is the starting node; ED (terminal node) indicates the end of the design; DP (terminal node-set) represents the design object; and D(M) (dead point set) represents objects that cannot be inferred or designed incorrectly.
- E(M) = {(Vi, Vj)} represents the set of directed arcs of different elements in V(M). One of the directed arcs from nodes Vi to Vj can be represented by an ordered dual (Vi, Vj). The directivity of the directed arcs enables the design objects to be connected to form a scheme network.
- G(M) = {g (Vi, Vj)} = {gi, j} is the set of function weights.
- (2)
- The scheme represents the set of feasible paths from the initial node FR to the terminal node DP. As long as the path from FR to DP can be connected, it is called the feasible path.
3.3. The Scheme Generation Model Incorporating the Tree Topological Mapping Process Is Established
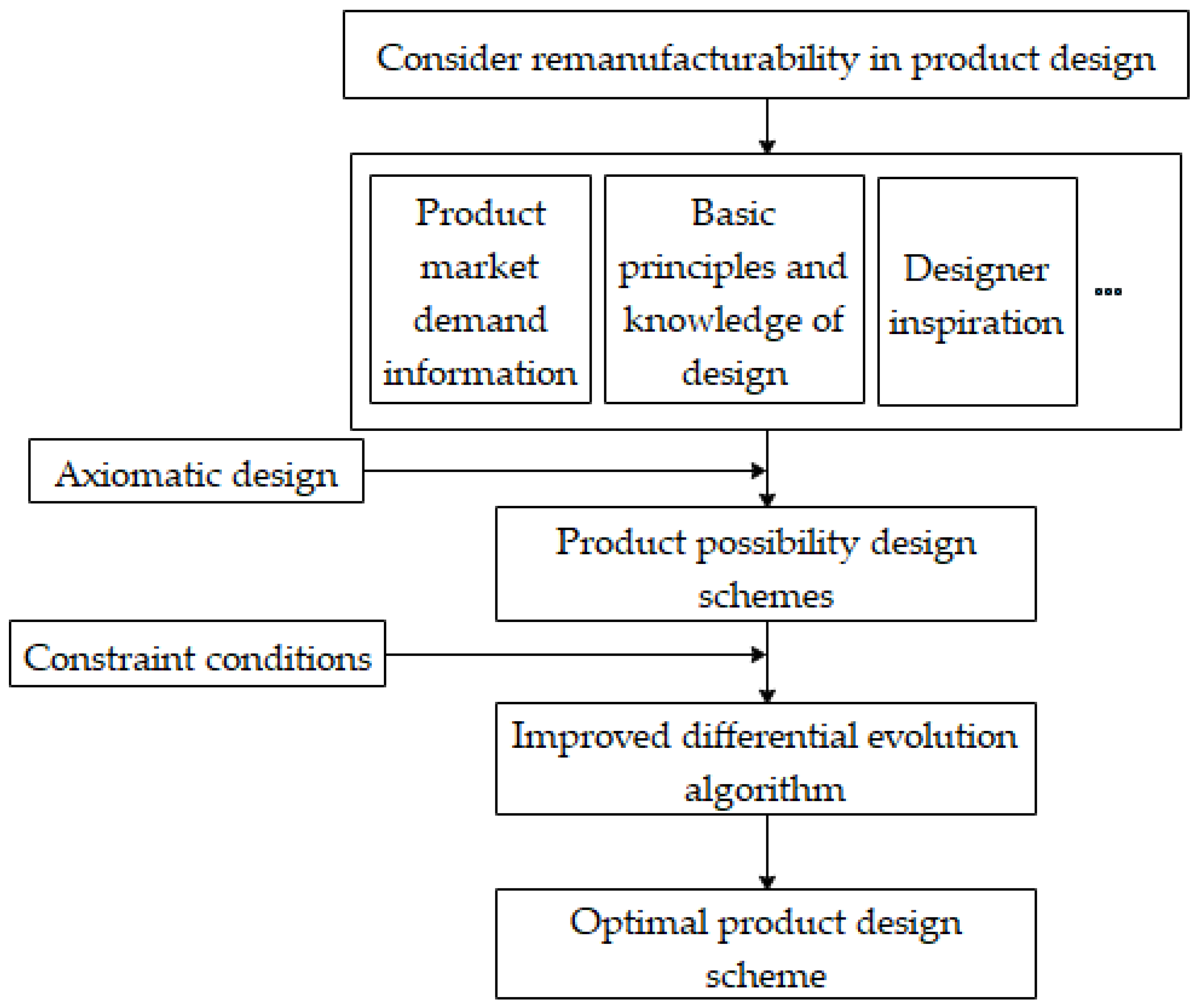
- (1)
- Knowledge base is established. The knowledge base is composed of expert knowledge, customer requirements, existing achievements, and technical requirements as input.
- (2)
- Total functional requirement FR0 is determined. The design requirements and knowledge base are used to solve FR0, graph M0 is employed to describe the generation process, and the total design method DP0 is then obtained.
- (3)
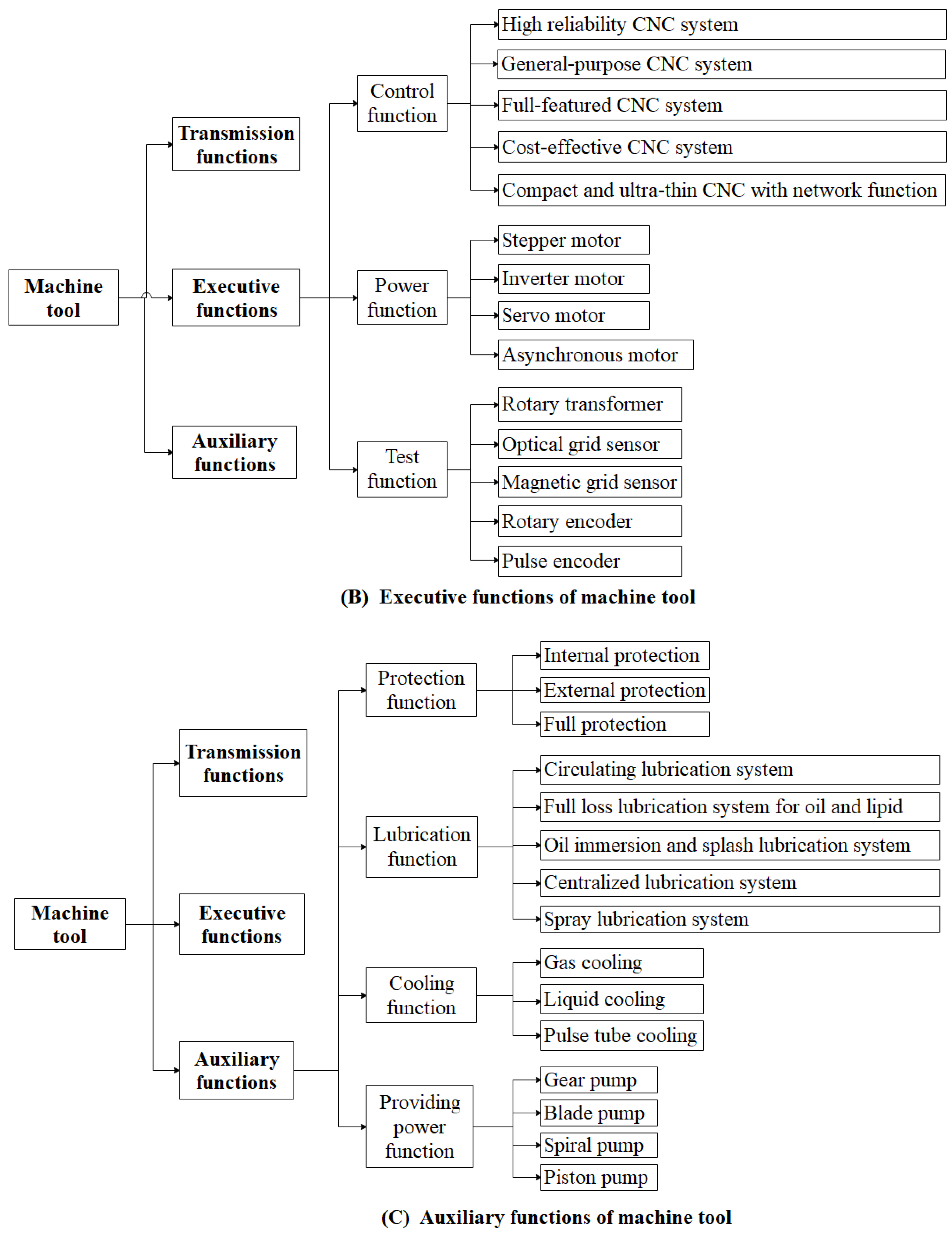
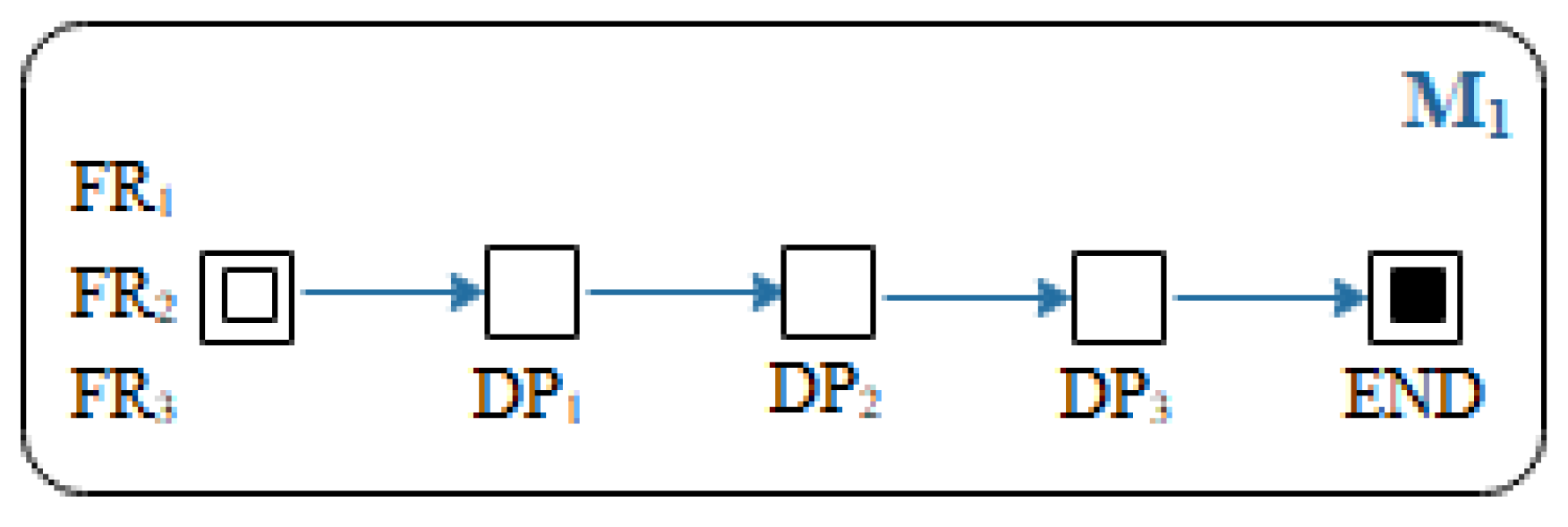
- The subfunctional requirements FR1 and FR2 are solved. DP0 is decomposed to obtain FR1 and FR2, represented as the starting nodes of M1 in Figure 5. The possible design methods are found in the knowledge base, and the feasible design methods DP11, DP21, and DP22 are selected according to the constraints of remanufacturability criteria and design requirements.
- (4)
- Compatibility judgment. The compatibility of FR1 and FR2 is judged. The compatible nodes continue to be decomposed downward, while redundant nodes are eliminated. Therefore, the design matrix of the feasible design method is obtained using Equations (1) and (2).
- (5)
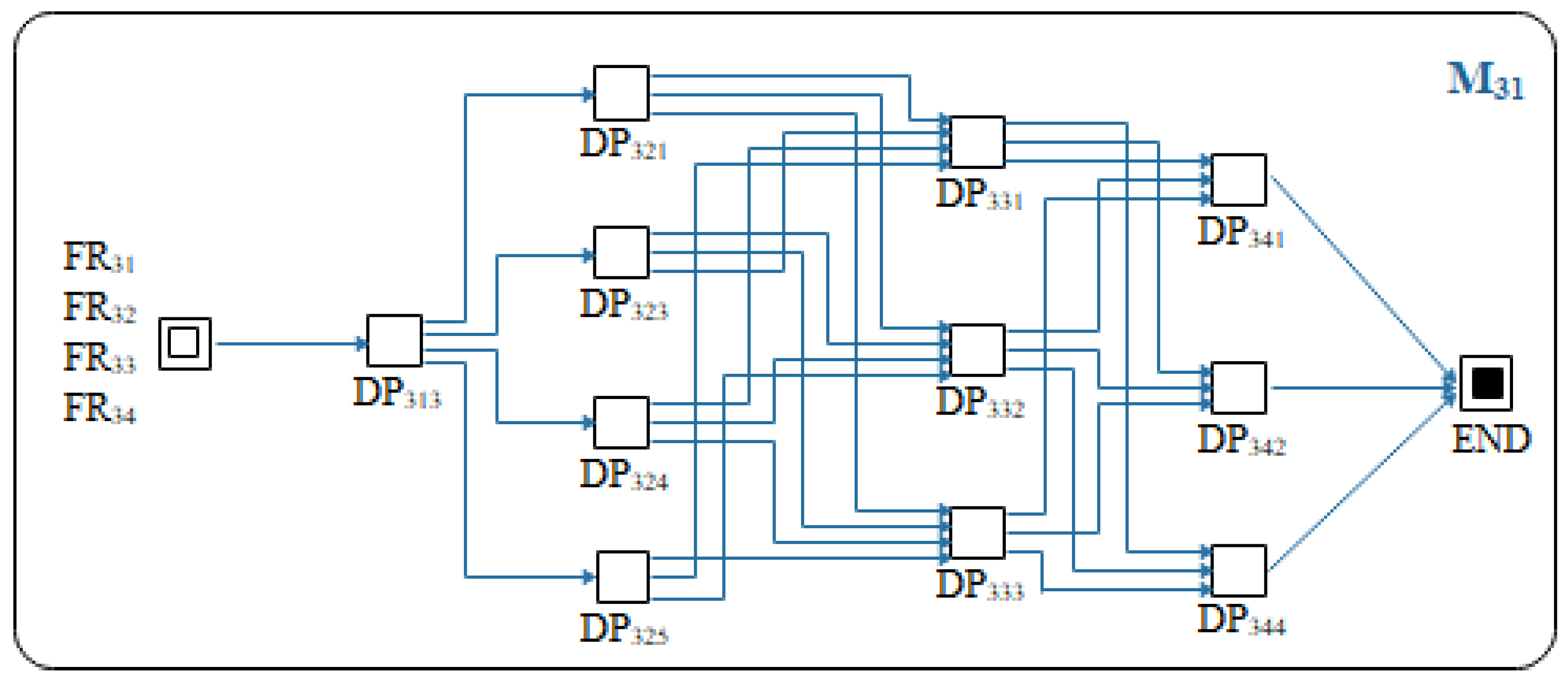
- Decompose DP11, DP21, and DP22. The design methods DP11, DP21, and DP22 are decomposed respectively to obtain the subfunctional requirements, which are expressed in the starting nodes of M11, M21, and M22 in Figure 5.
- (6)
- Repeat the above steps to decompose downward until it cannot be decomposed further, and then stop the cycle.
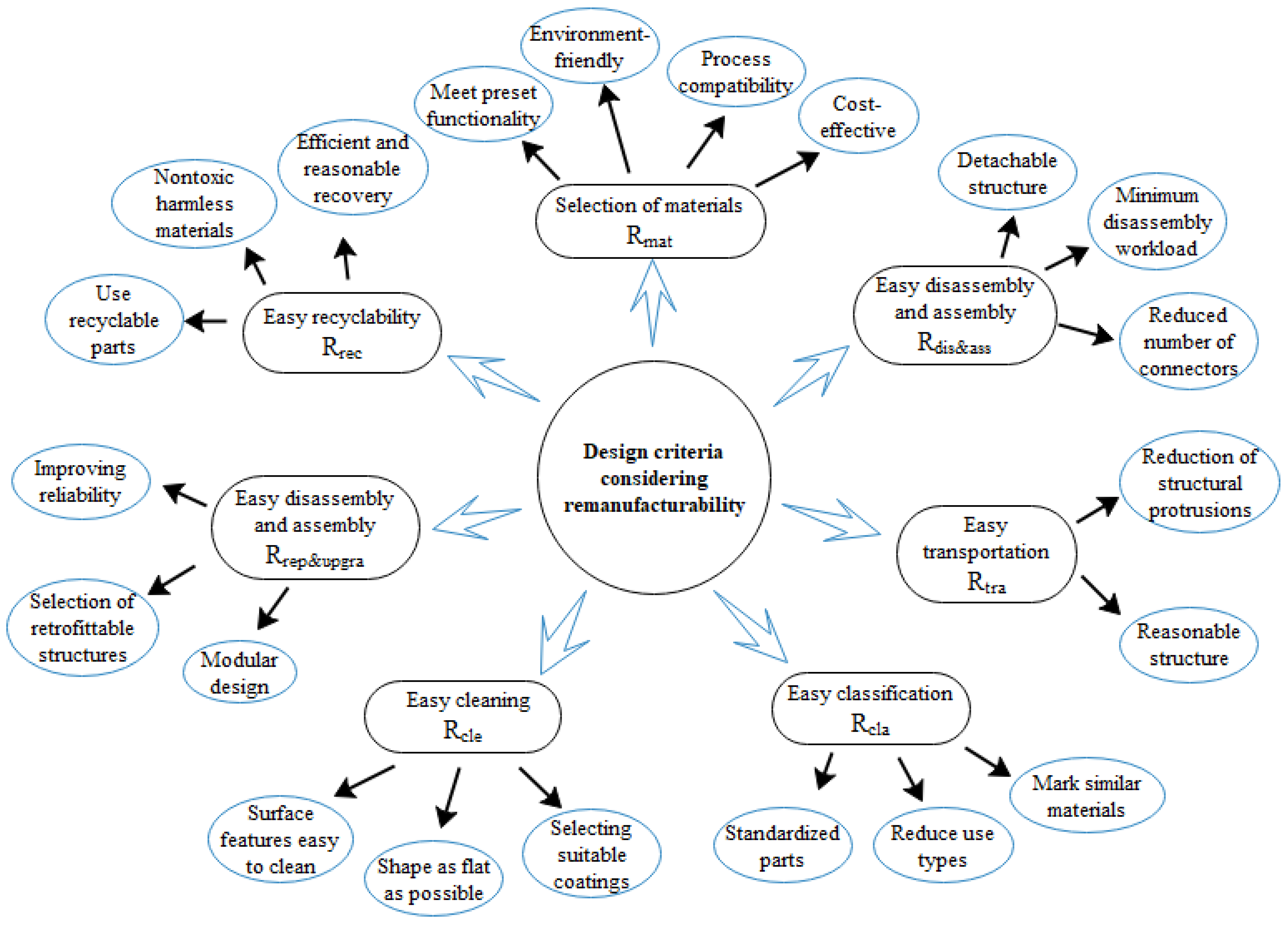
3.4. Design Constraint Criteria While Considering Remanufacturability
4. Scheme Optimization Based on Differential Evolution Algorithm
4.1. Establishment of Evaluation Index System
- (1)
- Functional indicator ()
- (2)
- Economic indicator ()
- (3)
- Stability indicator ()
- (4)
- Environmental indicator ()
- (5)
- Comprehensive evaluation index ()
4.2. EW-AHP Method to Determine the Weight of Indicators
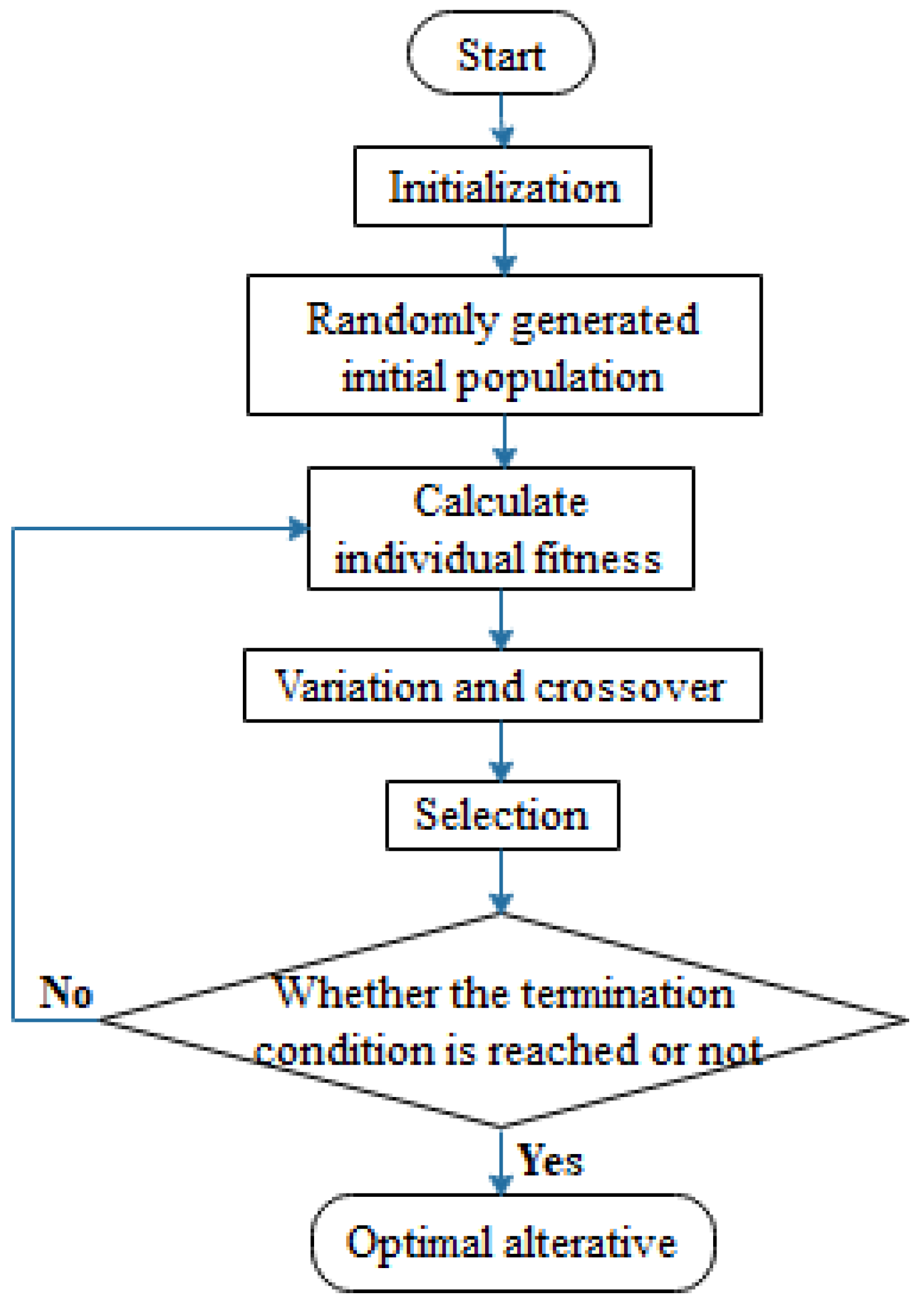
4.3. Optimization of Scheme
- (1)
- Parameter initialization
- (2)
- Random generation of an initial population
- (3)
- Calculate individual fitness
- (4)
- Variation
- (5)
- Cross
- (6)
- Detection of boundary conditions
- (7)
- Choice
5. Case Analysis
5.1. Scheme Generation Process
- (1)
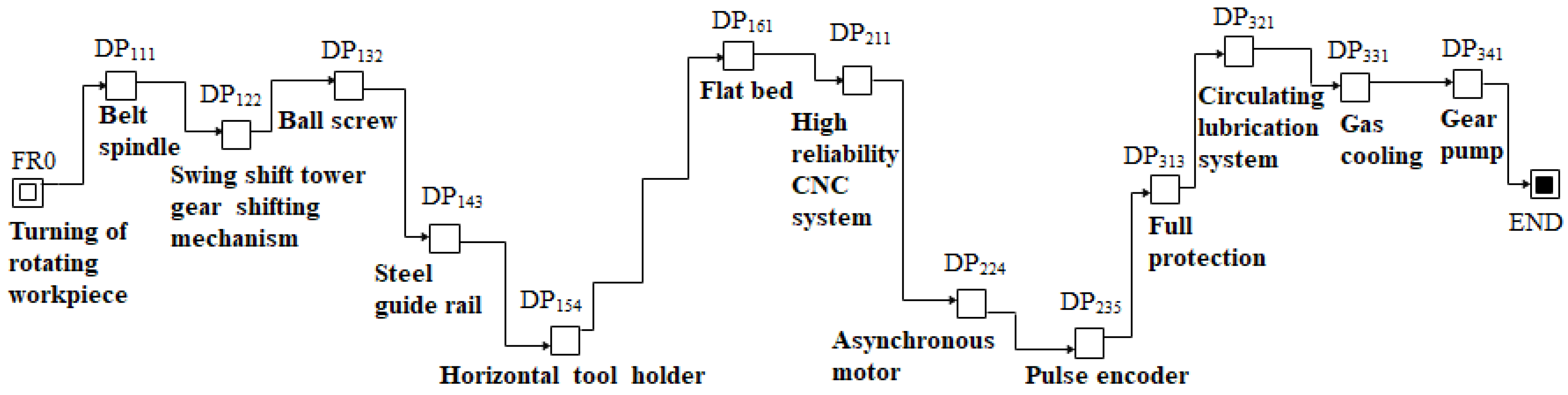
- Firstly, the total functional requirements of lathe FR0 were determined, and then the lathe knowledge base was used to analyze the scheme generation process model.
- (2)
- (3)
- The total function was decomposed using tree topology mapping to obtain the subfunctions FR1, FR2, and FR3. According to the subfunctions, the feasible design parameters DP1, DP2, and DP3 were obtained. Among them, DP1 and DP2 were interrelated with DP2 and DP3. The scheme generation process diagram M1 is shown in Figure 10. Table 3 is the list of FR1, FR2, and FR3; and Table 4 is the list of its terminal nodes.
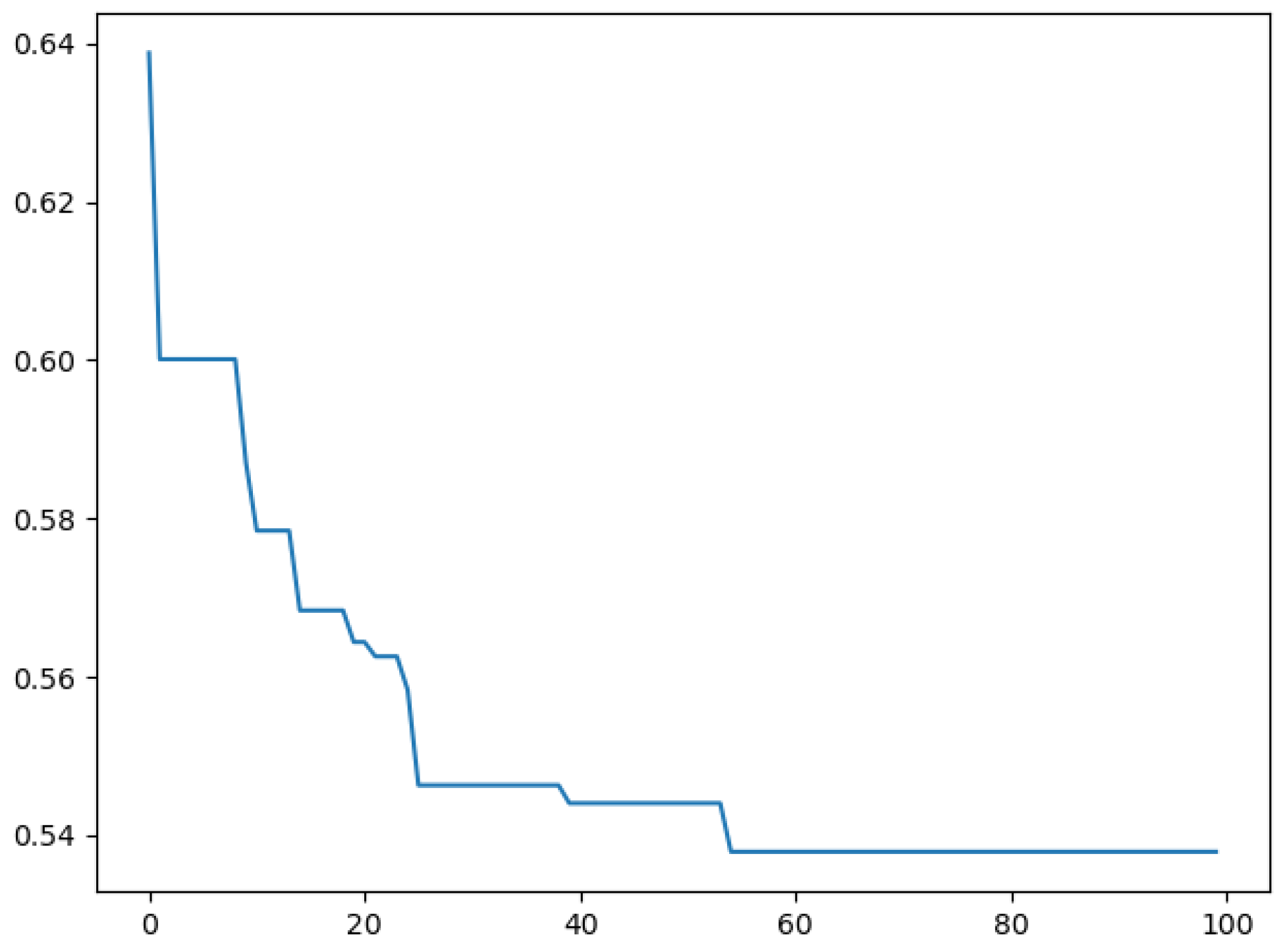
5.2. Scheme-Optimization Process
6. Discussion
- (1)
- Research on remanufacturability of existing products mainly relies on the accumulation of knowledge and experience of designers, and there is no unified evaluation standard, resulting in a strong subjectivity of such research. Future research can be undertaken for objective remanufacturability constraint criteria to increase the accuracy of decision making.
- (2)
- The four evaluation indicators established were only judged by simple formulas without a detailed explanation of each index. Future research can put forward more detailed evaluation indicators to further improve the accuracy of judgment.
- (3)
- The case analysis only considered the optimization of a machine tool remanufacturability design scheme, and the amount of data was small, resulting in a final fitting result that may not have been the optimal result. The employment of big data analtyics in the future will provide the possibility of building a more comprehensive, stable, efficient, and intelligent product design scheme optimization.
7. Conclusions
- (1)
- The Z-shaped mapping in axiomatic design was improved to a tree topology mapping process, which not only took axiomatic design as the guiding principle, but also provided the functional domains to the specific implementation method of the domain method. Based on a certain knowledge base, the entire scheme-generation process was guided, and the hierarchical relationship and mapping process of FRS and DPS were clearly expressed.
- (2)
- Aiming at the problem that product design does not consider the inherent value of end-of-life products, remanufacturing was integrated into product design, and the remanufacturing constraint criteria were established to limit the method decisions in the process of scheme generation. Remanufacturing was considered in the stage of product design to improve the remanufacturability, thus reducing resource waste and environmental pollution.
- (3)
- The combination of EW and AHP was used to calculate the weight of the index, the differential evolution algorithm was used to optimize the scheme, the “survival of the fittest” was used to guide the search to identify the optimal solution, and the Python programming language was used to automatically solve the optimization design scheme.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.G.; Ao, X.Y.; Jiang, Z.G.; Zhang, H.; Cai, W. A remanufacturing cost prediction model of used parts considering failure characteristics. Robot. Comput. Integr. Manuf. 2019, 59, 291–296. [Google Scholar] [CrossRef]
- Liu, Q.T.; Shang, Z.Y.; Ding, K.; Guo, L.; Zhang, L. Multi-process routes based remanufacturability assessment and associated application on production decision. J. Clean. Prod. 2019, 240, 118114. [Google Scholar] [CrossRef]
- Peters, K. Methodological issues in life cycle assessment for remanufactured products: A critical review of existing studies and an illustrative case study. J. Clean. Prod. 2016, 126, 21–37. [Google Scholar] [CrossRef]
- Fatimah, Y.A.; Biswas, W.K. Sustainability Assessment of Remanufactured Computers. Procedia CIRP 2016, 40, 150–155. [Google Scholar] [CrossRef] [Green Version]
- Christophe, F.; Bernard, A.; Coatanéa, É. RFBS: A model for knowledge representation of conceptual design. CIRP Ann. Manuf. Technol. 2010, 59, 155–158. [Google Scholar] [CrossRef]
- Deng, Y.M.; Zhu, Y.W. Function to structure/material mappings for conceptual design synthesis and their supportive strategies. Int. J. Adv. Manuf. Technol. 2009, 44, 1063–1072. [Google Scholar] [CrossRef]
- Yang, T.; Gao, X.; Dai, F. New Hybrid AD Methodology for Minimizing the Total Amount of Information Content: A Case Study of Rehabilitation Robot Design. Chin. J. Mech. Eng. 2020, 33, 86. [Google Scholar] [CrossRef]
- Sarath, C.; Renjith, K.; Park, G. A Design Framework for Additive Manufacturing: Integration of Additive Manufacturing Capabilities in the Early Design Process. Int. J. Precis. Eng. Manuf. 2020, 21, 329–345. [Google Scholar]
- Li, W.J.; Song, Z.H.; Mao, E.R.; Suh, S. Using Extenics to Describe Coupled Solutions in Axiomatic Design. J. Eng. Des. 2019, 30, 1–31. [Google Scholar] [CrossRef]
- Ren, S.D.; Gui, F.Z.; Zhao, Y.W.; Xie, Z.W. Accelerating preliminary low-carbon design for products by integrating TRIZ and Extenics methods. Adv. Mech. Eng. 2017, 9, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Yeo, S.H.; Mak, M.W.; Balon, S.A.P. Analysis of decision-making methodologies for desirability score of conceptual design. J. Eng. Des. 2004, 15, 195–208. [Google Scholar] [CrossRef]
- Lin, M.C.; Wang, C.C.; Chen, M.S.; Chang, C.A. Using AHP and TOPSIS approaches in customer-driven product design process. Comput. Ind. 2008, 59, 17–31. [Google Scholar] [CrossRef]
- Wan, L.; Du, C. An approach to evaluation of environmental benefits for ecological mining areas based on ant Colony algorithm. Earth Sci. Inform. 2021, 14, 797–808. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, Z.G.; Zhang, X.G.; Wang, Y.N. A fault feature characterization based method for remanufacturing process planning optimization. J. Clean. Prod. 2017, 161, 708–719. [Google Scholar] [CrossRef]
- Yan, J.F.; Guo, C.F. An Improved Differential Evolution and Its Application in Function Optimization Problem. Adv. Mat. Res. 2011, 267, 632–634. [Google Scholar] [CrossRef]
- Hatcher, G.D.; Ijomah, W.L.; Windmill, J.F.C. Design for remanufacture: A literature review and future research needs. J. Clean. Prod. 2011, 19, 2004–2014. [Google Scholar] [CrossRef]
- Omwando, T.A.; Otieno, W.A.; Farahani, S.; Ross, A.D. A Bi-Level fuzzy analytical decision support tool for assessing product remanufacturability. J. Clean. Prod. 2018, 174, 1534–1549. [Google Scholar] [CrossRef]
- Jiang, Z.G.; Wang, H.; Zhang, H.; Wang, Y.; Gong, Q.S. Hybrid Multi-attribute Decision Making for Remanufacturing Design Based on Subjectivity Reduction. J. Nanjing Univ. Aeronaut. Astronaut. 2020, 52, 73–78. [Google Scholar]
- Ijomah, W.L.; Mcmahon, C.A.; Hammond, G.P. Development of robust design-for-remanufacturing guidelines to further the aims of sustainable development. Int. J. Prod. Res. 2007, 45, 4513–4536. [Google Scholar] [CrossRef]
- Chiodo, J.D.; Ijomah, W.L. Use of active disassembly technology to improve remanufacturing productivity: Automotive application. Int. J. Comput. Integr. Manuf. 2014, 27, 361–371. [Google Scholar] [CrossRef]
- Soh, S.L.; Ong, S.L.; Nee, A.Y.C. Design for assembly and disassembly for remanufacturing. Assem. Autom. 2016, 36, 12–24. [Google Scholar] [CrossRef]
- Geda, M.W.; Kwong, C.K.; Jiang, H. Fastening method selection with simultaneous consideration of product assembly and disassembly from a remanufacturing perspective. Int. J. Adv. Manuf. Technol. 2019, 101, 1481–1493. [Google Scholar] [CrossRef]
- Fegade, V.; Shrivatsava, R.L.; Kale, A.V. Design for Remanufacturing: Methods and their Approaches. Mater. Today Proc. 2015, 2, 1849–1858. [Google Scholar] [CrossRef]
- Wu, C.H. Product-design and pricing strategies with remanufacturing. Eur. J. Oper. Res. 2012, 222, 204–215. [Google Scholar] [CrossRef]
- Zhang, X.G.; Tang, Y.J.; Zhang, H.; Jiang, Z.G.; Cai, W. Remanufacturability evaluation of end-of-life products considering technology, economy and environment: A review. Sci. Total Environ. 2021, 764, 142922. [Google Scholar] [CrossRef]
- Zhang, X.G.; Wang, Y.L.; Xiang, Q.; Zhang, H.; Jiang, Z.G. Remanufacturability evaluation method and application for used engineering machinery parts based on fuzzy-EAHP. J. Manuf. Syst. 2020, 57, 133–147. [Google Scholar] [CrossRef]




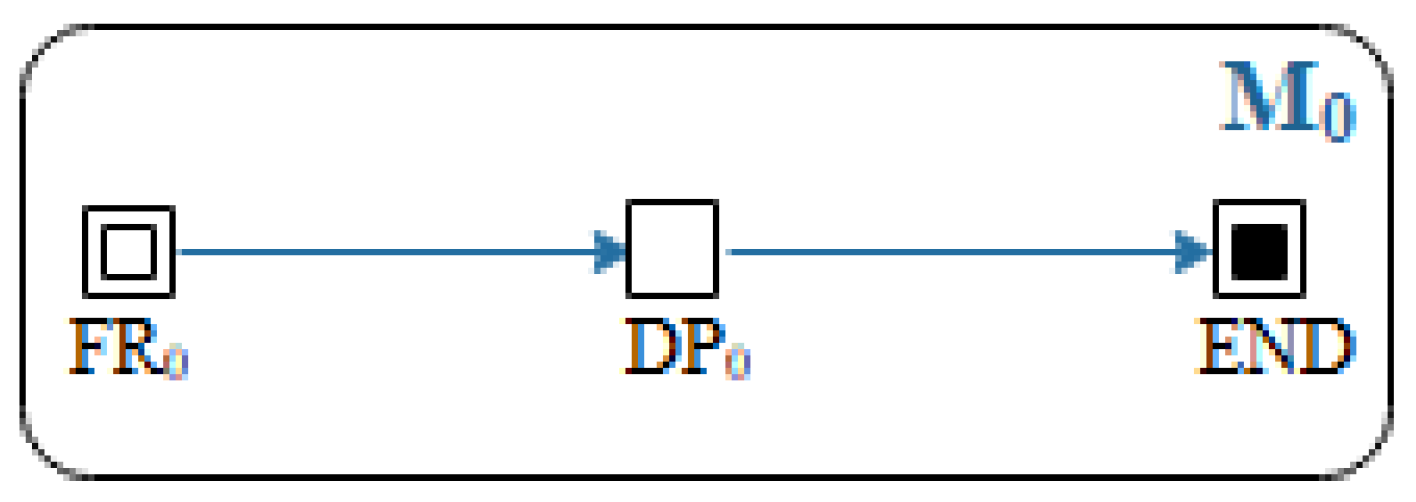



| Source of Function Requirements (FRS) | Design Requirements |
|---|---|
| FR0 | Turning the rotating workpiece |
| Name | Feasible Design Method | Whether It Could Be Broken Down |
|---|---|---|
| Turning mechanism | DP0 | Yes |
| Source of Function Requirements (FRS) | DP0 Turning Mechanism |
|---|---|
| Code name | Description of FR |
| FR1 | Transmission function |
| FR2 | Executive function |
| FR3 | Auxiliary function |
| Name | Feasible Design Method | Whether It Could Be Broken Down |
|---|---|---|
| Mechanical device | DP1 | Yes |
| Electrical device | DP2 | Yes |
| Auxiliary devices | DP3 | Yes |
| Source of Function Requirements (FRS) | DP1 Mechanical Device |
|---|---|
| Code name | Description of FR |
| FR11 | Rotating work piece function |
| FR12 | Coordinated transmission component function |
| FR13 | Servo drive function |
| FR14 | Guide function |
| FR15 | Tool drive function |
| FR16 | Supporting and providing track function |
| Name | Feasible Design Method | Whether It Could Be Broken Down |
|---|---|---|
| Belt spindle | DP111 | No |
| Straight junction spindle | DP112 | No |
| Motorized spindle | DP114 | No |
| Sliding gear transmission mechanism | DP121 | No |
| Swing shift tower gear shifting mechanism | DP122 | No |
| Multiplying variable speed mechanism | DP124 | No |
| Return crank gear variable speed mechanism | DP126 | No |
| Ball screw | DP132 | No |
| Sliding screw | DP134 | No |
| Static pressure screw | DP135 | No |
| Linear guide | DP141 | No |
| Linear roller guideway | DP142 | No |
| Steel guide rail | DP143 | No |
| Swallowtail groove guide rail | DP146 | No |
| Row turret | DP151 | No |
| Electric tool holder | DP152 | No |
| Vertical tool holder | DP153 | No |
| Horizontal tool holder | DP154 | No |
| Flat bed | DP161 | No |
| Inclined bed | DP162 | No |
| Horizontal bed inclined guide bed | DP163 | No |
| Upright bed | DP164 | No |
| Source of Function Requirements (FRS) | DP2 Electrical Equipment |
|---|---|
| Code name | Description of FR |
| FR21 | Control function |
| FR22 | Power function |
| FR23 | Test function |
| Name | Feasible Design Method | Whether It Could Be Broken Down |
|---|---|---|
| High-reliability Computer Numerical Control (CNC) system | DP211 | No |
| General-purpose CNC system | DP212 | No |
| Cost-effective CNC system | DP214 | No |
| Inverter motor | DP222 | No |
| Servo motor | DP223 | No |
| Asynchronous motor | DP224 | No |
| Rotary transformer | DP231 | No |
| Optical grid sensor | DP232 | No |
| Magnetic grid sensor | DP233 | No |
| Pulse encoder | DP235 | No |
| Source of Function Requirements (FRS) | DP3 Auxiliary Device |
|---|---|
| Code name | Description of FR |
| FR31 | Protection function |
| FR32 | Lubrication function |
| FR33 | Cooling function |
| FR34 | Providing power function |
| Name | Feasible Design Method | Whether It Could Be Broken Down |
|---|---|---|
| Full protection | DP313 | No |
| Circulating lubrication system | DP321 | No |
| Oil immersion and splash lubrication system | DP323 | No |
| Centralized lubrication system | DP324 | No |
| Spray lubrication system | DP325 | No |
| Gas cooling | DP331 | No |
| Liquid cooling | DP332 | No |
| Pulse tube cooling | DP333 | No |
| Gear pump | DP341 | No |
| Blade pump | DP342 | No |
| Piston pump | DP 344 | No |
| 1 | 0.5 | 0.25 | 0.5 | |
| 2 | 1 | 0.67 | 2 | |
| 4 | 1.5 | 1 | 1.33 | |
| 2 | 0.5 | 0.75 | 1 |
| Feasible Design Method | Functionality | Cost | Failure Rate | Environmental |
|---|---|---|---|---|
| Belt spindle | E | 3200 | 0.012 | 0.15 |
| Straight junction spindle | D | 3300 | 0.014 | 0.19 |
| Motorized spindle | C | 3500 | 0.017 | 0.23 |
| Slip gear change mechanism | E | 2450 | 0.005 | 0.23 |
| Swing shift tower gear shifting mechanism | E | 2500 | 0.003 | 0.19 |
| Multiplying variable speed mechanism | D | 2850 | 0.012 | 0.31 |
| Return crank gear variable speed mechanism | C | 3200 | 0.015 | 0.27 |
| Ball screw | D | 710 | 0.015 | 0.19 |
| Sliding screw | C | 1080 | 0.033 | 0.27 |
| Static pressure screw | D | 980 | 0.027 | 0.23 |
| Linear guide | C | 890 | 0.029 | 0.39 |
| Linear roller guideway | C | 730 | 0.032 | 0.27 |
| Steel guide rail | D | 650 | 0.021 | 0.15 |
| Swallow tail groove guide rail | D | 600 | 0.027 | 0.23 |
| Row turret | C | 1750 | 0.006 | 0.31 |
| Electric tool holder | C | 2310 | 0.007 | 0.35 |
| Vertical tool holder | D | 1800 | 0.007 | 0.23 |
| Horizontal tool holder | D | 1650 | 0.002 | 0.19 |
| Flat bed | E | 5500 | 0.003 | 0.23 |
| Inclined bed | C | 6500 | 0.007 | 0.27 |
| Horizontal bed inclined guide bed | C | 6300 | 0.011 | 0.31 |
| Upright bed | D | 6350 | 0.005 | 0.23 |
| High-reliability CNC system | D | 7800 | 0.003 | 0.35 |
| General-purpose CNC system | E | 3500 | 0.015 | 0.15 |
| Cost-effective CNC system | E | 5650 | 0.013 | 0.27 |
| Inverter motor | D | 730 | 0.014 | 0.19 |
| Servo motor | E | 800 | 0.009 | 0.23 |
| Asynchronous motor | D | 680 | 0.007 | 0.19 |
| Rotary transformer | C | 860 | 0.037 | 0.35 |
| Optical grid sensor | D | 1020 | 0.044 | 0.31 |
| Magnetic grid sensor | E | 930 | 0.019 | 0.23 |
| Pulse encoder | E | 780 | 0.021 | 0.27 |
| Circulating lubrication system | D | 2600 | 0.017 | 0.15 |
| Oil immersion and splash lubrication system | C | 4200 | 0.023 | 0.31 |
| Centralized lubrication system | C | 4500 | 0.022 | 0.43 |
| Spray lubrication system | D | 3400 | 0.019 | 0.23 |
| Gas cooling | E | 2780 | 0.011 | 0.19 |
| Liquid cooling | D | 3600 | 0.014 | 0.27 |
| Pulse tube cooling | E | 3560 | 0.013 | 0.23 |
| Gear pump | D | 390 | 0.008 | 0.15 |
| Blade pump | C | 450 | 0.009 | 0.19 |
| Piston pump | B | 560 | 0.009 | 0.19 |
| Parameter Name | Crossover Probability (CR) | Generation | Population Size | f |
|---|---|---|---|---|
| Value | 0.3 | 100 | 50 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, S.; Jiang, Z.; Zhang, X.; Wang, Y. Product Design Scheme Generation and Optimization Decisions While Considering Remanufacturability. Mathematics 2022, 10, 2477. https://doi.org/10.3390/math10142477
Xing S, Jiang Z, Zhang X, Wang Y. Product Design Scheme Generation and Optimization Decisions While Considering Remanufacturability. Mathematics. 2022; 10(14):2477. https://doi.org/10.3390/math10142477
Chicago/Turabian StyleXing, Shixiong, Zhigang Jiang, Xugang Zhang, and Yan Wang. 2022. "Product Design Scheme Generation and Optimization Decisions While Considering Remanufacturability" Mathematics 10, no. 14: 2477. https://doi.org/10.3390/math10142477
APA StyleXing, S., Jiang, Z., Zhang, X., & Wang, Y. (2022). Product Design Scheme Generation and Optimization Decisions While Considering Remanufacturability. Mathematics, 10(14), 2477. https://doi.org/10.3390/math10142477








