Fractional Advection Diffusion Models for Radionuclide Migration in Multiple Barriers System of Deep Geological Repository

Abstract

Based on the multiple barriers concept of deep geological disposal of high-level waste, fractional advection diffusion equations for radionuclide migration in multiple layers low-permeability porous media are proposed in this work. The presented fractional advection diffusion models in terms of different definitions of fractional derivative are analytically addressed via the Laplace integral transform method. This work provides a theoretical foundation for further simulations of radionuclide migration in the multiple barriers system of the high-level waste repository.

1. Introduction

Deep geological repository (DGR) is the internationally preferred option for the permanent disposal of high-level waste (HLW). In general, DGR is built in stable geological layers, such as clay and granite formations, to protect humans and the environment from the possible adverse consequences of HLW as it may remain radioactive [1]. In China, the site-selection process for HLW repository has commenced since the last century and the Beishan granitic region has been selected as the final DGR site [2]. Meanwhile, the multiple barriers concept is provided for the deep geological disposal of HLW. Most importantly, for the long timescales not less than ten thousand years, the stability of the multiple barriers system must be demonstrated. A quantitative description of the geochemical properties of the multiple barriers system must be investigated by analyzing the transport processes of radionuclides. In addition, advection and diffusion are the two limiting processes for radionuclide migration miscible with deep groundwater through the multiple barriers system. However, multiple barriers often have ultra-low permeability, and the particle transport in these barriers arises anomalous transport behaviors [3]. These complex processes in the multiple barriers system of DGR may not be adequately described by the conventional approaches, such as the classical advection–diffusion equation models. Therefore, appropriate mathematical models should be developed to characterize the anomalous transport process of radionuclides in low-permeability porous media.

The fractional dynamic approach is emerging as a novel description of anomalous transport processes [4,5,6]. Numerous researchers have applied the fractional derivative models to describe the turbulent flow [7], non-Darcian flow [8,9,10], transient flow [11], atmospheric pollutant dispersion [12,13], solute transport [14], and contaminant migration [15,16]. Moreover, fractional diffusion models, in terms of different definitions of a fractional derivative, also have been considered to depict the advective-dispersive transport in single porous media [17,18,19]. Advection diffusion models can be solved by analytical methods as well as numerical methods [20,21].

Motivated by the aforementioned works, this work makes an attempt to propose fractional advection diffusion models for radionuclide anomalous migration in multiple barriers system of deep geological repository. The rest of this work is organized as follows: In Section 2, the fractional advection diffusion models for radionuclide anomalous transport in multiple barriers system of DGR are developed and analytical addressed. In Section 3, the main conclusions are drawn.

2. Fractional Advection Diffusion Model: Two Adjacent Layers

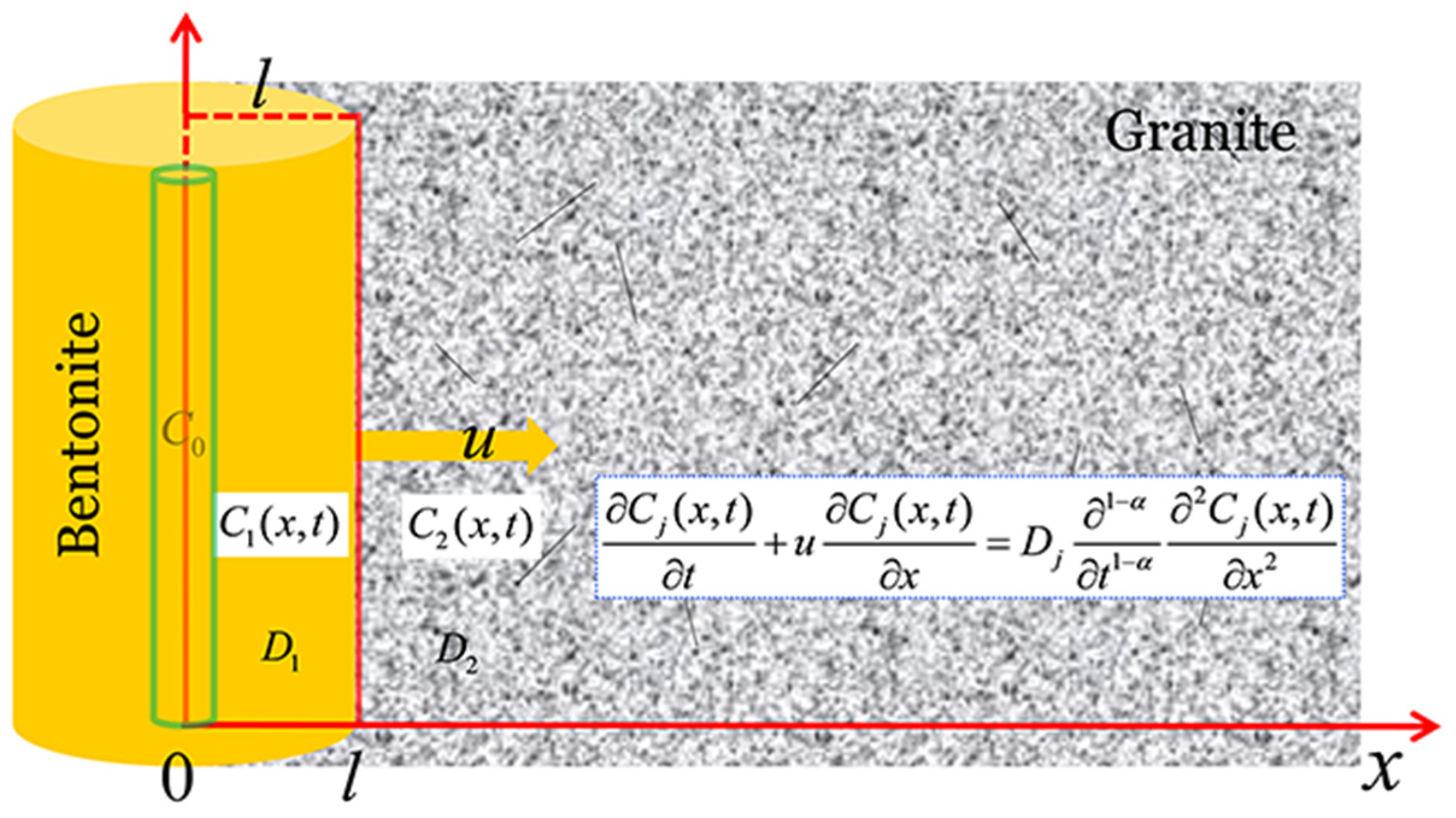
2.1. Geological Disposal Concept of HLW Repository

The principal concept of the HLW geological disposal depends on a combination of engineered and natural barriers, called a multiple barriers system. The main objective of this multiple barriers system is to prevent radionuclides from reaching the human environment. A representative illustration of the deep geological disposal concept of HLW repository is shown in Figure 1. The multiple barriers system is simplified as two adjacent layers to represent the engineered barrier (bentonite backfill) and natural barrier (granitic host rock). In subsequent arguments, the fractional advection diffusion models will be presented to modelling the radionuclide anomalous migration in each layer.

2.2. Fractional Advection Diffusion Equations

The diffusive flux arises due to diffusion that is approximated by the fractional Fick’s law [22]

$$J_{\mathrm{diff}}(x,t)=-D\frac{{\partial }^{1-\alpha }}{\partial t^{1-\alpha }}\left(\frac{\partial C(x,t)}{\partial x}\right).$$

(1)

In addition, there is an associated flux called advective flux resulting from fluid advection, i.e.,

$$J_{\mathrm{adv}}(x,t)=uC(x,t),$$

(2)

where $J(x,t)=J_{\mathrm{diff}}(x,t)+J_{\mathrm{adv}}(x,t)$ is the total flux, $C(x,t)$ is the concentration, D denotes the generalized diffusion coefficient $\left(m^2/s^{\alpha }\right)$, u is the average velocity of fluid flow $\left(m/s\right)$, and $\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}$ represents the fractional derivative in the definitions of Caputo [23], Caputo–Fabrizio [24] and Atangana–Baleanu [25] as follows.

$${}^C{D}^{\alpha }f(t)=\frac{1}{\Gamma (1-\alpha )}{\displaystyle {\int }_0^t\frac{f^{\prime }(\tau )}{{(t-\tau )}^{\alpha }}}d\tau$$

(3)

$${}^{CF}{D}^{\alpha }f(t)=\frac{1}{1-\alpha }{\displaystyle {\int }_0^t{f}^{\prime }}(\tau )\exp \left\{-\frac{\alpha (t-\tau )}{1-\alpha }\right\}d\tau , 0<\alpha \le 1.$$

(4)

$${}^{AB}{D}^{\alpha }f(t)=\frac{1}{1-\alpha }{\displaystyle {\int }_0^t{f}^{\prime }}(\tau )E_{\alpha }\left\{-\frac{\alpha {(t-\tau )}^{\alpha }}{1-\alpha }\right\}d\tau , 0<\alpha \le 1,$$

(5)

where $E_{\alpha }(x)={\displaystyle \sum _{k=0}^{\infty }\frac{x^k}{\Gamma (\alpha k+1)}}$ is the Mittag–Leffler function. Obviously, when $\alpha =1$ these fractional derivatives in Equations (3)–(5) reduce to the classical derivative of the first order; detailed derivations also can be referred to in reference [23,24,25].

Incorporating the above constitutive relations Equations (1) and (2) into the continuity equation, i.e.,

$$\frac{\partial C(x,t)}{\partial t}+\frac{\partial J(x,t)}{\partial x}=0$$

(6)

can lead to the one-dimensional fractional advection diffusion equation (FADE) for fluid flow and radionuclide migration in each layer, i.e.,

$$\{\begin{array}{c}\frac{\partial C\left(x,t\right)}{\partial t}+u\frac{\partial C\left(x,t\right)}{\partial x}=D\frac{{\partial }^{1-\alpha }}{\partial t^{1-\alpha }}\frac{{\partial }^{2}C\left(x,t\right)}{\partial x^2}\\ C\left(x,0\right)=0,\frac{\partial C\left(x,t\ge 0\right)}{\partial x}=0.\end{array}$$

(7)

which is subjected to the initial and boundary value conditions resulting from the engineering practice. In addition, results from the different features of the mentioned three fractional derivatives, we believe that the presented FADE models in terms of different fractional derivative definition can depict numerous anomalous transport processes arising from the engineering.

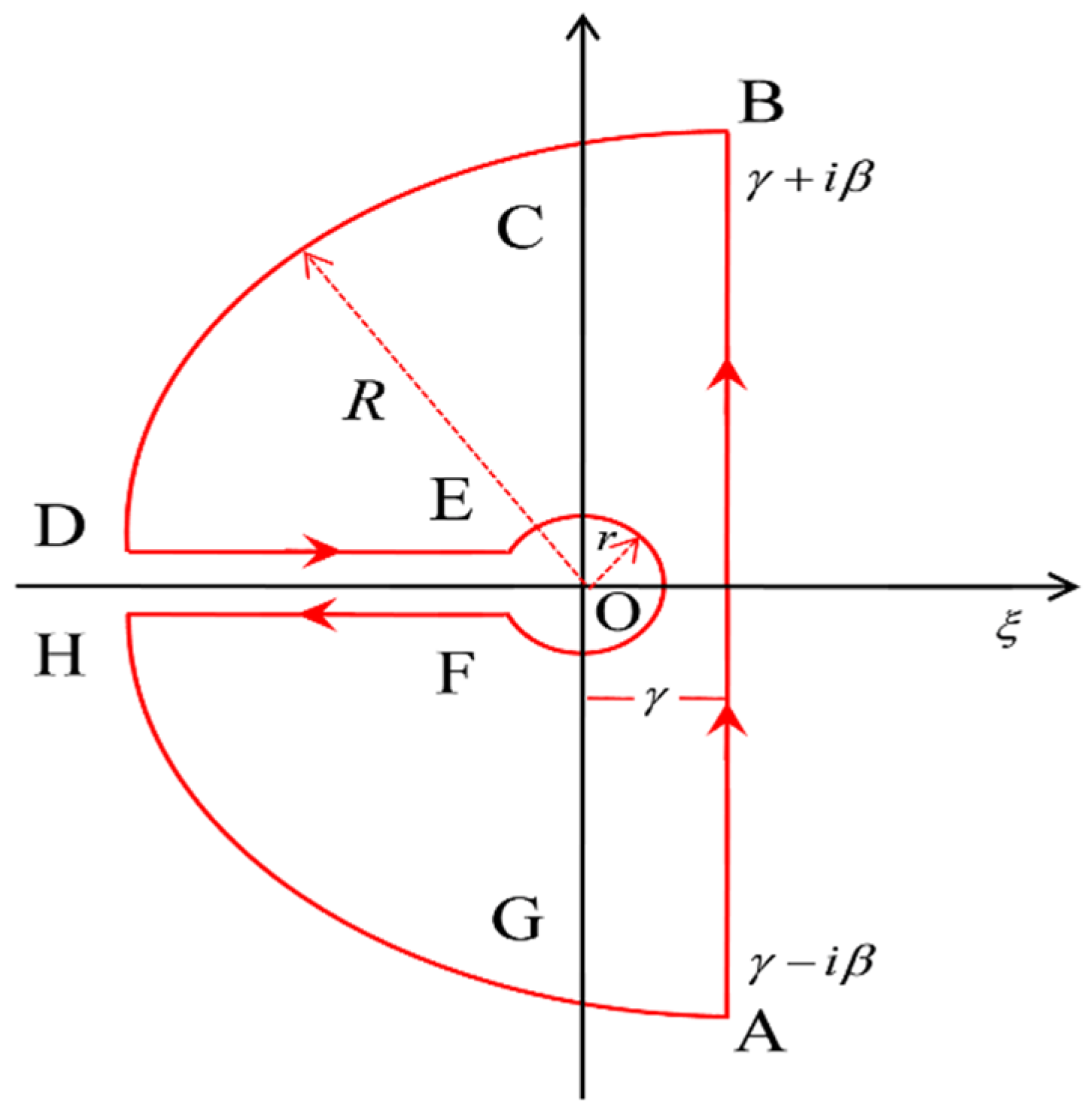
2.3. Analytical Solutions for FADE in Two Layers

Inverting the FADE (7) to a fractional diffusion equation via the transforms x′ = x − ut, then employing the Laplace transform with respect to t leads to

$$C_{x^{\prime }{x}^{\prime }}(x^{\prime },s)=Q(s)C(x^{\prime },s)$$

(8)

where s is Laplace variable, and the Laplace transforms of fractional derivative in terms of different definitions are given by

$$ℒ\left[\frac{{\partial }^{\alpha }f(t)}{\partial t^{\alpha }}\right](s)=\{\begin{array}{ll}{s}^{\alpha }ℒ\left[f(t)\right](s)-s^{\alpha -1}f(0),\hfill & \mathrm{Caputo} \mathrm{derivative};\hfill \\ \frac{sℒ\left[f(t)\right](s)-f(0)}{(1-\alpha )s+\alpha },\hfill & \mathrm{Caputo}\text{-}\mathrm{Fabrizio} \mathrm{derivative};\hfill \\ \frac{s^{\alpha }ℒ\left[f(t)\right](s)-s^{\alpha -1}f(0)}{(1-\alpha )s^{\alpha }+\alpha },\hfill & \mathrm{Atangana}\text{-}\mathrm{Baleanu} \mathrm{derivative}.\hfill \end{array}$$

(9)

Therefore, in the case of the fractional derivatives invoking the Caputo, Caputo–Fabrizio, and Atangana–Baleanu’s definitions, Q(s) in Equation (8) denotes the following different formulations, respectively.

$$Q(s)=\{\begin{array}{ll}\frac{s^{\alpha }}{D},\hfill & \mathrm{Caputo} \mathrm{derivative};\hfill \\ \frac{1-\alpha +\alpha s}{D},\hfill & \mathrm{Caputo}\text{-}\mathrm{Fabrizio} \mathrm{derivative};\hfill \\ \frac{(1-\alpha )s^{\alpha }+\alpha s}{D},\hfill & \mathrm{Atangana}\text{-}\mathrm{Baleanu} \mathrm{derivative}.\hfill \end{array}$$

(10)

The general solution of the second-order ordinary differential Equation (8) is known as

$$C(x^{\prime },s)=C_1\exp (\sqrt{Q}{x}^{\prime })+C_2\exp (-\sqrt{Q}{x}^{\prime }),$$

(11)

where $C_1$ and $C_2$ are parameters in terms of s and depend on the initial conditions.

As shown in Figure 1, the two adjacent bentonite and granite layers characterized by two different diffusion coefficients $D_1$ and $D_2$, respectively. The thickness of the first engineering barrier is $0\le x\le l$. The solutions in the Laplace domain for the presented FADE models in each layer can be derived as follows:

According to Equation (11), one can obtain

$$C_1(x^{\prime },s)=C_{11}\exp \left(\sqrt{Q_1}{x}^{\prime }\right)+C_{12}\exp \left(-\sqrt{Q_1}{x}^{\prime }\right), 0\le x\le l.$$

(12)

$$C_2(x^{\prime },s)=C_{21}\exp \left(-\sqrt{Q_2}{x}^{\prime }\right), l\le x\le \infty .$$

(13)

where $C_2(x^{\prime },s)$ is in the result of the convergent of concentration distribution for $x\to \infty$.

Assuming the initial diffusion concentration $C_1(0,t)=C_0$, the concentrations in each layer are continuous at the interface boundary $x=l$, i.e., $C_1(x=l,t)=C_2(x=l,t)$ and $C_{1x}(x=l,t)=C_{2x}(x=l,t)$. Based on these initial and boundary conditions, the parameters in Equations (12) and (13) are given by

$$C_{11}=\frac{C_0}{s}\frac{\left(\sqrt{Q_1}+\sqrt{Q_2}\right)\left[\sinh (2\sqrt{Q_1}l)+\cosh (2\sqrt{Q_1}l)\right]}{\sqrt{Q_1}-\sqrt{Q_2}+\left(\sqrt{Q_1}+\sqrt{Q_2}\right)\left[\cosh \left(2\sqrt{Q_1}l\right)+\sinh \left(2\sqrt{Q_1}l\right)\right]},$$

(14)

$$C_{12}=\frac{C_0}{s}\frac{\sqrt{Q_1}-\sqrt{Q_2}}{\sqrt{Q_1}-\sqrt{Q_2}+\left(\sqrt{Q_1}+\sqrt{Q_2}\right)\left[\cosh \left(2\sqrt{Q_1}l\right)+\sinh \left(2\sqrt{Q_1}l\right)\right]},$$

(15)

$$C_{21}=\frac{C_0}{s}\frac{2\sqrt{Q_1}\left[\sinh \left((\sqrt{Q_1}+\sqrt{Q_2})l\right)+\cosh \left((\sqrt{Q_1}+\sqrt{Q_2})l\right)\right]}{\sqrt{Q_1}-\sqrt{Q_2}+\left(\sqrt{Q_1}+\sqrt{Q_2}\right)\left[\cosh \left(2\sqrt{Q_1}l\right)+\sinh \left(2\sqrt{Q_1}l\right)\right]},$$

(16)

where $\sinh (x)$ and $\cosh (x)$ represent hyperbolic sine and cosine function, respectively.

Substituting $C_{11},C_{12},C_{21}$ into Equations (12) and (13) leads to

$$C_1(x^{\prime },s)=\frac{C_0}{s}\frac{\left(\sqrt{Q_1}+\sqrt{Q_2}\right)\left[\sinh (2\sqrt{Q_1}l)+\cosh (2\sqrt{Q_1}l)\right]\exp \left(\sqrt{Q_1}{x}^{\prime }\right)+\left(\sqrt{Q_1}-\sqrt{Q_2}\right)\exp \left(-\sqrt{Q_1}{x}^{\prime }\right)}{\sqrt{Q_1}-\sqrt{Q_2}+\left(\sqrt{Q_1}+\sqrt{Q_2}\right)\left[\cosh \left(2\sqrt{Q_1}l\right)+\sinh \left(2\sqrt{Q_1}l\right)\right]},$$

(17)

$$C_2(x^{\prime },s)=\frac{C_0}{s}\frac{2\sqrt{Q_1}\left[\sinh \left((\sqrt{Q_1}+\sqrt{Q_2})l\right)+\cosh \left((\sqrt{Q_1}+\sqrt{Q_2})l\right)\right]\exp \left(-\sqrt{Q_2}{x}^{\prime }\right)}{\sqrt{Q_1}-\sqrt{Q_2}+\left(\sqrt{Q_1}+\sqrt{Q_2}\right)\left[\cosh \left(2\sqrt{Q_1}l\right)+\sinh \left(2\sqrt{Q_1}l\right)\right]}.$$

(18)

Subsequently, one can apply the Bromwich–Hankel integration path shown in Figure 2 to obtain the inverse Laplace transform of Equations (17) and (18). Assuming $F_j(s)=C_j(x^{\prime },s)\exp (st),j=1,2$ and according to the residue theorem one can derive

$$\frac{1}{2\pi i}{\displaystyle {\int }_{\Gamma }{F}_j}(s)ds={\Sigma }_{k=1}^N\mathrm{Res}{F}_j(s_k),$$

(19)

where $\Gamma$ represents the Bromwich–Hankel integration path, and $\mathrm{Res}{F}_j(s_k)$ denotes the residues of $F_j(s)$ at the singular point $s_k$. $N$ is the number of singular points. When $R\to \infty$ and $r\to 0$ in $\mathrm{Res}{F}_j(s_k)$, Equation (19) is inverted to

$$\frac{1}{2\pi i}{\displaystyle {\int }_{\gamma -i\beta }^{\gamma +i\beta }{F}_j}(s)ds-\frac{1}{2\pi i}{\displaystyle {\int }_0^{\infty }\left[C_j\left(x^{\prime },W_{-}(\xi )\right)-C_j\left(x^{\prime },W_{+}(\xi )\right)\right]}\exp (-\xi t)d\xi ={\Sigma }_{k=1}^N\mathrm{Res}{F}_j(s_k),$$

(20)

where $W_{\pm }(\xi )=\xi e^{\pm i\pi }$. The first term of the left side of Equation (20) gives the inverse Laplace transform of $C_j(x^{\prime },s)$, i.e.,

$$C_j(x^{\prime },t)={\Sigma }_{k=1}^N\mathrm{Res}{F}_j(s_k)+\frac{1}{2\pi i}{\displaystyle {\int }_0^{\infty }\left[C_j(x^{\prime },W_{-}(\xi ))-C_j(x^{\prime },W_{+}(\xi ))\right]}\exp (-\xi t)d\xi .$$

(21)

It is noted that $F_j(s)$ only has one singular point $s=0$, accordingly,

$${\Sigma }_{k=1}^N\mathrm{Res}{F}_j(s_k)=\mathrm{Res}{F}_j(s=0)=\underset{s\to 0}{\lim }s{F}_j(s)=C_0.$$

(22)

Therefore, on the basis of Equations (21) and (22), the concentration distribution of each layer can be represented as

$$\frac{C_j(x,t)}{C_0}=1+\frac{1}{2\pi i}{{\displaystyle \int }}_0^{\infty }\left[M_j^{+}(x,\xi )-M_j^{-}(x,\xi )\right]\frac{\exp (-\xi t)}{\xi }d\xi , j=1,2,$$

(23)

where $j=1,2$ corresponding to the two adjacent layers $0\le x\le l$ and $l\le x\le \infty$, respectively.

Furthermore, $M_j^{\pm }(x,\xi )$ depends on the definitions of fractional derivative, and is expressed by

$$\begin{array}{ll}\hfill & M_1^{\pm }(x,\xi )\hfill \\ \hfill & =\frac{\left(k_1+k_2\right)\left[\sinh \left(2k_{1}l{U}_{\pm }^{\frac{1}{2}}(\xi )\right)+\cosh \left(2k_{1}l{U}_{\pm }^{\frac{1}{2}}(\xi )\right)\right]\exp \left(k_1{U}_{\pm }^{\frac{1}{2}}(\xi )x^{\prime }\right)+\left(k_1-k_2\right)\exp \left(-k_1{U}_{\pm }^{\frac{1}{2}}(\xi )x^{\prime }\right)}{k_1-k_2+\left(k_1+k_2\right)\left[\cosh \left(2k_1{U}_{\pm }^{\frac{1}{2}}(\xi )l\right)+\sinh \left(2k_{1}l{U}_{\pm }^{\frac{1}{2}}(\xi )\right)\right]}\hfill \end{array},$$

(24)

$$M_2^{\pm }(x,\xi )=\frac{2k_1\left[\sinh \left((k_1+k_2)l{U}_{\pm }^{\frac{1}{2}}(\xi )\right)+\cosh \left((k_1+k_2)l{U}_{\pm }^{\frac{1}{2}}(\xi )\right)\right]\exp \left(-k_2{U}_{\pm }^{\frac{1}{2}}(\xi )x^{\prime }\right)}{k_1-k_2+\left(k_1+k_2\right)\left[\cosh \left(2k_1{U}_{\pm }^{\frac{1}{2}}(\xi )l\right)+\sinh \left(2k_{1}l{U}_{\pm }^{\frac{1}{2}}(\xi )\right)\right]},$$

(25)

where $x^{\prime }=x-u\xi$, $k_1=\frac{1}{\sqrt{D_1}}$, $k_2=\frac{1}{\sqrt{D_2}}$ and $U_{\pm }(\xi )$ is given by

$$U_{\pm }(\xi )=\{\begin{array}{ll}{W}_{\pm }^{\alpha }(\xi ),\hfill & \mathrm{Caputo} \mathrm{derivative};\hfill \\ 1-\alpha +\alpha W_{\pm }(\xi ),\hfill & \mathrm{Caputo}\text{-}\mathrm{Fabrizio} \mathrm{derivative};\hfill \\ (1-\alpha )W_{\pm }^{\alpha }(\xi )+\alpha W_{\pm }(\xi ),\hfill & \mathrm{Atangana}\text{-}\mathrm{Baleanu} \mathrm{derivative}.\hfill \end{array}$$

(26)

As a consequence, the analytical solutions of the FADE model in each layer are derived. In actuality, the proposed FADE model is generalized from the classical ADE model using a fractional-derivative approach. Therefore, it is necessary to consider the consistency between the FADE and the ADE model in the particular case of the fractional-derivative order $\alpha =1$. Specifically, in the case of $\alpha =1$, the fractional advection diffusion model in Equation (7) reduces to the traditional ADE model. Meanwhile, the proposed FADE model in Equation (23) regresses back into ADE model for two-layer porous media. The analytical solutions of the classical ADE model are recovered from the solutions of FADE when the fractional derivative order $\alpha =1$, and is shown as follows:

$$\begin{array}{l}\frac{C_1(x,t)}{C_0}=1+\frac{1}{2\pi i}{{\displaystyle \int }}_0^{\infty }\left[M_1^{+}(x,\xi )-M_1^{-}(x,\xi )\right]\frac{\exp (-\xi t)}{\xi }d\xi \\ =1+\frac{1}{2\pi i}{{\displaystyle \int }}_0^{\infty }\left[\frac{k_1{k}_2\left(\sinh [k_1{\xi }^{\frac{1}{2}}(l+x-u\xi )]\right)}{k_1^2{\cosh }^2(k_1{\xi }^{\frac{1}{2}}l)-k_2^2{\sinh }^2(k_1{\xi }^{\frac{1}{2}}l)}\right]\frac{\exp (-\xi t)}{\xi }d\xi \end{array},$$

(27)

$$\begin{array}{l}\frac{C_2(x,t)}{C_0}=1+\frac{1}{2\pi i}{{\displaystyle \int }}_0^{\infty }\left[M_2^{+}(x,\xi )-M_2^{-}(x,\xi )\right]\frac{\exp (-\xi t)}{\xi }d\xi \\ =1+\frac{1}{2\pi i}{{\displaystyle \int }}_0^{\infty }\left[\frac{-2k_1\left(k_1\cosh (k_1{\xi }^{\frac{1}{2}}l)\sinh (\Phi )-k_2\sinh (k_1{\xi }^{\frac{1}{2}}l)\cosh (\Phi )\right)}{k_1^2{\cosh }^2(k_1{\xi }^{\frac{1}{2}}l)-k_2^2{\sinh }^2(k_1{\xi }^{\frac{1}{2}}l)}\right]\frac{\exp (-\xi t)}{\xi }d\xi \end{array},$$

(28)

where $\Phi =k_2{\xi }^{\frac{1}{2}}(x-u\xi )$.

It is worthwhile to note that the parameters, such as diffusion coefficients and advection velocity of the FADE model, need to be acquired from experimental data fitting or field measurements. Furthermore, the relations between the fractional derivative order with the geometric structure and fluid flow parameters of the selected porous media need to be confirmed. The development of understanding radionuclide anomalous migration in multiple layers low-permeability porous media is an ongoing research program involving the investigation of complex processes, usually involving coupled thermo-hydro-mechanical effects. The precise mechanism of the FADE model for radionuclide anomalous transport and the factors which control it remain controversial, and require further elucidation. The numerical simulation and concentration prediction of parameters determined by the FADE model are of great significance to the safety of the HLW repository, and are the main directions of further study.

3. Conclusions

This work attempts to develop a FADE model for radionuclide migration in multiple layers low-permeability porous media on the basis of the multiple barriers concept of deep geological disposal of HLW. The presented FADE models in terms of different definitions of fractional derivative among Caputo, Caputo–Fabrizio and Atangana–Baleanu are analytically addressed via the Laplace integral transform method. This work provides a theoretical foundation of fractional advection diffusion in multiple layers porous media. In addition, it should be pointed out that the applicability of the proposed theoretical FADE models for radionuclide migration in the multiple barriers system of the HLW repository needs to be further validated in comparison with the experimental and field data.