Impact of Regressand Stratification in Dataset Shift Caused by Cross-Validation
Abstract
:1. Introduction
- Delving into the use of regressand stratification in k-fcv and analyzing whether, despite not being generalized, it should be recommended when dealing with regression data.
- Establishing a direct comparison between k-fcv with and without stratification at three levels (amount of dataset shift introduced, quality of performance estimation and convergence speed) to determine in which aspects stratification offers advantages and the degree of improvement in each of them.
- Studying different amounts of strata in the output variable in order to check if they significantly affect the results obtained and recommend the most appropriate values.
- Analyzing if the effects of stratification on the results depend on the number of folds k in k-fcv, through the study of the values of k commonly used in the literature (2, 5 and 10).
- Drawing conclusions through experimentation with different regression paradigms, both classic and more recent, including decision trees, extreme learning machines and ensembles, among others.
2. On Dataset Shift Induced by Cross-Validation
3. Cross-Validation in Regression Problems
3.1. Standard Cross-Validation
| Algorithm 1 Standard cross-validation (CV). |
| Input: dataset D, number of folds k. Output: folds
|
3.2. Totally Stratified Cross-Validation
| Algorithm 2 Totally stratified cross-validation (TSCV). |
| Input: dataset D, number of folds k. Output: folds
|
3.3. Stratified Cross-Validation
| Algorithm 3t-stratified cross-validation (SCV ). |
| Input: dataset D, number of folds k, number of strata t. Output: folds
|
4. Experimental Framework
4.1. Real-World Datasets
4.2. Regression Algorithms
- Recursive partitioning and regression trees (RPART) [23]. It builds a decision tree from the dataset, in which the nodes are successively split into subnodes using a homogeneity-based threshold attribute value. The process stops when the last subset of samples is included in the tree or the maximum number of leaves is reached (known as tree pruning).
- k-nearest neighbors (NN) [43]. To estimate the output value for a sample, it computes the distances between such sample and all the training samples. Then, it selects the k closest samples to the query and averages their regressand values to obtain a single prediction.
- Extreme learning machine (ELM) [24]. It is a feedforward neural network with a hidden layer of nodes whose parameters do not need to be tuned. Its main advantage is that it produces good generalization performance in less time compared to traditional neural networks trained with backpropagation.
- Multivariate adaptive regression spline (MARS) [44]. It is a non-parametric algorithm based on two main stages. In the forward stage, it splits the data in several subsets and runs a linear regression model on each partition. In the backward stage, the model is pruned to avoid overfitting by removing the functions that contribute the least to performance.
- Generalized boosted regression modeling (GBM) [45]. It iteratively builds decision trees based on random subsets of the training samples using boosting. For each new tree, those samples poorly modeled by previous trees have a higher probability of being selected.
| Method | Parameters |
|---|---|
| RPART | min. split ; min. leaf ; complexity ; max. depth |
| NN | ; distance: Euclidean |
| ELM | neurons ; activation: radial basis; input weights: |
| MARS | degree ; pruning = backward |
| GBM | distribution = Gaussian; trees ; learning rate ; bag |
4.3. Methodology of Analysis
- CV, which does not consider any stratification;
- TSCV, which considers a total stratification of the samples;
- SCV with six different values of t (2, 5, 10, 20, 50 and 100), which allows for controlling the stratification degree.
5. Analysis of Results
5.1. Analysis of Induced Target Shift by Cross-Validation Schemes
- CV, which does not consider any stratification (row vs. CV);
- TSCV, which considers a maximum stratification (row vs. TSCV).
| Folds | CV | SCV | SCV | SCV | SCV | SCV | SCV | TSCV |
|---|---|---|---|---|---|---|---|---|
| 2-fcv | 0.0604 | 0.0491 | 0.0390 | 0.0280 | 0.0217 | 0.0150 | 0.0109 | 0.0055 |
| vs. CV | ✗ | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 |
| vs. TSCV | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 1.49E-8 * | ✗ |
| 5-fcv | 0.0754 | 0.0615 | 0.0491 | 0.0354 | 0.0273 | 0.0195 | 0.0155 | 0.0109 |
| vs. CV | ✗ | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 |
| vs. TSCV | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | ✗ |
| 10-fcv | 0.1002 | 0.0820 | 0.0656 | 0.0480 | 0.0378 | 0.0287 | 0.0246 | 0.0213 |
| vs. CV | ✗ | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 | 7.45E-9 |
| vs. TSCV | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 7.45E-9 * | 1.49E-8 * | ✗ |
5.2. Effect of Stratification in Error Bias Related to Target Shift
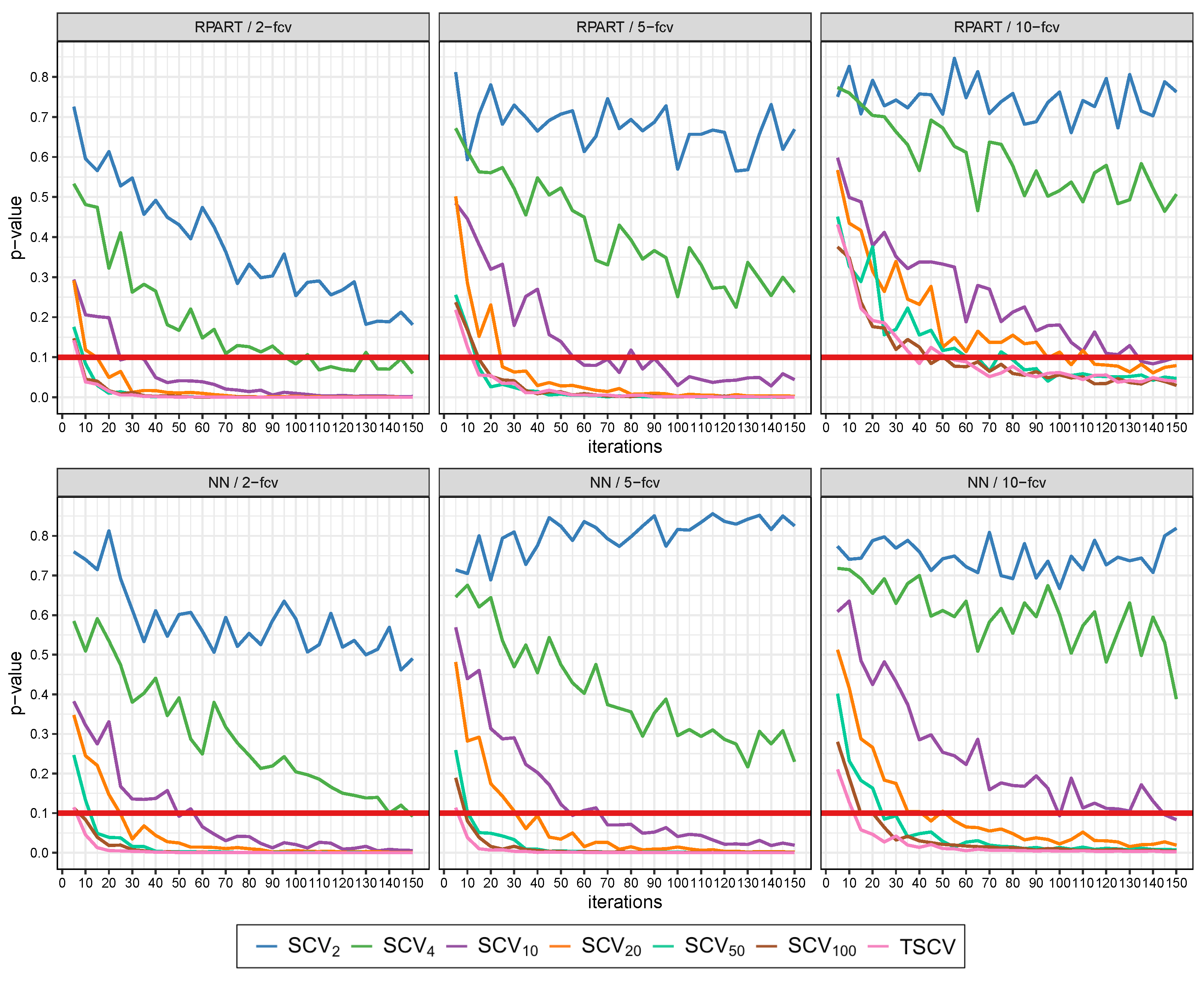
5.3. Convergence Speed of Stratification Schemes against CV
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Liao, S.; Jiang, S.; Ding, L.; Lin, H.; Wang, W. Fast cross-validation for kernel-based algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 1083–1096. [Google Scholar] [CrossRef] [PubMed]
- Rad, K.; Maleki, A. A scalable estimate of the out-of-sample prediction error via approximate leave-one-out cross-validation. J. R. Stat. Soc. Ser. B Stat. Methodol. 2020, 82, 965–996. [Google Scholar] [CrossRef]
- Qi, C.; Diao, J.; Qiu, L. On estimating model in feature selection with cross-validation. IEEE Access 2019, 7, 33454–33463. [Google Scholar] [CrossRef]
- Jiang, G.; Wang, W. Error estimation based on variance analysis of k-fold cross-validation. Pattern Recognit. 2017, 69, 94–106. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Volume 2, pp. 1137–1143. [Google Scholar]
- Krstajic, D.; Buturovic, L.; Leahy, D.; Thomas, S. Cross-validation pitfalls when selecting and assessing regression and classification models. J. Cheminform. 2014, 6, 10. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Torres, J.; Sáez, J.; Herrera, F. Study on the impact of partition-induced dataset shift on k-fold cross-validation. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1304–1312. [Google Scholar] [CrossRef]
- Maldonado, S.; López, J.; Iturriaga, A. Out-of-time cross-validation strategies for classification in the presence of dataset shift. Appl. Intell. 2022, 52, 5770–5783. [Google Scholar] [CrossRef]
- Wei, T.; Wang, J.; Chen, H.; Chen, L.; Liu, W. L2-norm prototypical networks for tackling the data shift problem in scene classification. Int. J. Remote Sens. 2021, 42, 3326–3352. [Google Scholar] [CrossRef]
- Moreno-Torres, J.G.; Raeder, T.; Alaíz-Rodríguez, R.; Chawla, N.V.; Herrera, F. A unifying view on dataset shift in classification. Pattern Recognit. 2012, 45, 521–530. [Google Scholar] [CrossRef]
- Nikzad-Langerodi, R.; Andries, E. A chemometrician’s guide to transfer learning. J. Chemom. 2021, 35, e3373. [Google Scholar] [CrossRef]
- Huyen, C. Designing Machine Learning Systems: An Iterative Process for Production-Ready Applications; O’Reilly Media: Sebastopol, CA, USA, 2022. [Google Scholar]
- Li, Y.; Murias, M.; Major, S.; Dawson, G.; Carlson, D. On target shift in adversarial domain adaptation. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Naha, Japan, 16–18 April 2019; Volume 89, pp. 616–625. [Google Scholar]
- Redko, I.; Courty, N.; Flamary, R.; Tuia, D. Optimal transport for multi-source domain adaptation under target shift. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Naha, Japan, 16–18 April 2019; Volume 89, pp. 849–858. [Google Scholar]
- Podkopaev, A.; Ramdas, A. Distribution-free uncertainty quantification for classification under label shift. In Proceedings of the 37th Conference on Uncertainty in Artificial Intelligence, Online, 27–30 July 2021; pp. 844–853. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Kang, S.; Kang, P. Locally linear ensemble for regression. Inf. Sci. 2018, 432, 199–209. [Google Scholar] [CrossRef]
- Carrizosa, E.; Mortensen, L.; Romero Morales, D.; Sillero-Denamiel, M. The tree based linear regression model for hierarchical categorical variables. Expert Syst. Appl. 2022, 203, 117423. [Google Scholar] [CrossRef]
- Dhanjal, C.; Baskiotis, N.; Clémençon, S.; Usunier, N. An empirical comparison of V-fold penalisation and cross-validation for model selection in distribution-free regression. Pattern Anal. Appl. 2016, 19, 41–53. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.; Spector, P. Submodel selection and evaluation in regression. The x-random case. Int. Stat. Rev. 1992, 60, 291–319. [Google Scholar] [CrossRef]
- Baxter, C.W.; Stanley, S.J.; Zhang, Q.; Smith, D.W. Developing artificial neural network models of water treatment processes: A guide for utilities. J. Environ. Eng. Sci. 2002, 1, 201–211. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ding, S.; Zhao, H.; Zhang, Y.; Xu, X.; Nie, R. Extreme learning machine: Algorithm, theory and applications. Artif. Intell. Rev. 2015, 44, 103–115. [Google Scholar] [CrossRef]
- Baringhaus, L.; Gaigall, D. Efficiency comparison of the Wilcoxon tests in paired and independent survey samples. Metrika 2018, 81, 891–930. [Google Scholar] [CrossRef]
- Xu, L.; Hu, O.; Guo, Y.; Zhang, M.; Lu, D.; Cai, C.; Xie, S.; Goodarzi, M.; Fu, H.; She, Y. Representative splitting cross validation. Chemom. Intell. Lab. Syst. 2018, 183, 29–35. [Google Scholar] [CrossRef]
- May, R.; Maier, H.; Dandy, G. Data splitting for artificial neural networks using SOM-based stratified sampling. Neural Netw. 2010, 23, 283–294. [Google Scholar] [CrossRef]
- Diamantidis, N.; Karlis, D.; Giakoumakis, E. Unsupervised stratification of cross-validation for accuracy estimation. Artif. Intell. 2000, 116, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Snee, R. Validation of regression models: Methods and examples. Technometrics 1977, 19, 415–428. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Zuo, M.J.; Tiwari, M.K. A data clustering algorithm for stratified data partitioning in artificial neural network. Expert Syst. Appl. 2012, 39, 7004–7014. [Google Scholar] [CrossRef]
- Joseph, V.R.; Vakayil, A. SPlit: An optimal method for data splitting. Technometrics 2022, 64, 166–176. [Google Scholar] [CrossRef]
- Wu, W.; May, R.; Dandy, G.C.; Maier, H.R. A method for comparing data splitting approaches for developing hydrological ANN models. In Proceedings of the International Congress on Environmental Modelling and Software, Leipzig, Germany, 1–5 June 2012; p. 394. [Google Scholar]
- Wu, W.; May, R.; Maier, H.; Dandy, G. A benchmarking approach for comparing data splitting methods for modeling water resources parameters using artificial neural networks. Water Resour. Res. 2013, 49, 7598–7614. [Google Scholar] [CrossRef]
- Zheng, F.; Maier, H.; Wu, W.; Dandy, G.; Gupta, H.; Zhang, T. On lack of robustness in hydrological model development due to absence of guidelines for selecting calibration and evaluation data: Demonstration for data-driven models. Water Resour. Res. 2018, 54, 1013–1030. [Google Scholar] [CrossRef]
- Chapaneri, S.; Jayaswal, D. Covariate shift adaptation for structured regression with Frank-Wolfe algorithms. IEEE Access 2019, 7, 73804–73818. [Google Scholar] [CrossRef]
- Chen, X.; Monfort, M.; Liu, A.; Ziebart, B. Robust covariate shift regression. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; Volume 51, pp. 1270–1279. [Google Scholar]
- Sugiyama, M.; Nakajima, S.; Kashima, H.; Buenau, P.; Kawanabe, M. Direct importance estimation with model selection and its application to covariate shift adaptation. Adv. Neural Inf. Process. Syst. 2007, 20, 1–8. [Google Scholar]
- Shimodaira, H. Improving predictive inference under covariate shift by weighting the log-likelihood function. J. Stat. Plan. Inference 2000, 90, 227–244. [Google Scholar] [CrossRef]
- Kanamori, T.; Hido, S.; Sugiyama, M. A least-squares approach to direct importance estimation. J. Mach. Learn. Res. 2009, 10, 1391–1445. [Google Scholar]
- Huang, J.; Smola, A.J.; Gretton, A.; Borgwardt, K.M.; Schölkopf, B. Correcting sample selection bias by unlabeled data. Adv. Neural Inf. Process. Syst. 2006, 19, 601–608. [Google Scholar]
- Zhang, K.; Zheng, V.W.; Wang, Q.; Kwok, J.T.; Yang, Q.; Marsic, I. Covariate shift in Hilbert space: A solution via sorrogate kernels. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; Volume 28, pp. 388–395. [Google Scholar]
- Zeng, X.; Martinez, T.R. Distribution-balanced stratified cross-validation for accuracy estimation. J. Exp. Theor. Artif. Intell. 2000, 12, 1–12. [Google Scholar] [CrossRef]
- Curteanu, S.; Leon, F.; Mircea-Vicoveanu, A.M.; Logofatu, D. Regression methods based on nearest neighbors with adaptive distance metrics applied to a polymerization process. Mathematics 2021, 9, 547. [Google Scholar] [CrossRef]
- Raj, N.; Gharineiat, Z. Evaluation of multivariate adaptive regression splines and artificial neural network for prediction of mean sea level trend around northern australian coastlines. Mathematics 2021, 9, 2696. [Google Scholar] [CrossRef]
- Boehmke, B.; Greenwell, B. Gradient Boosting. In Hands-On Machine Learning with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019; pp. 221–246. [Google Scholar]
- Dimitrova, D.; Kaishev, V.; Tan, S. Computing the Kolmogorov-Smirnov distribution when the underlying CDF is purely discrete, mixed, or continuous. J. Stat. Softw. 2020, 95, 1–42. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]

| Dataset | at | sa | Dataset | at | sa |
|---|---|---|---|---|---|
| abalone | 8 | 4177 | friedman | 5 | 1200 |
| airfoil | 5 | 1503 | laser | 4 | 993 |
| anacalt | 7 | 4052 | machinecpu | 6 | 209 |
| autompg8 | 7 | 392 | mortgage | 15 | 1049 |
| baseball | 16 | 337 | plastic | 2 | 1650 |
| concrete | 8 | 1030 | quake | 3 | 2178 |
| coolingeff | 8 | 768 | realestate | 6 | 414 |
| dailerons | 5 | 7129 | stock | 9 | 950 |
| dee | 6 | 365 | traffic | 17 | 135 |
| delevators | 6 | 9517 | treasury | 15 | 1049 |
| elength | 2 | 495 | wankara | 9 | 321 |
| emaintenance | 4 | 1056 | watertoxicity | 8 | 546 |
| fish | 6 | 908 | wizmir | 9 | 1461 |
| forest | 12 | 517 | yacht | 6 | 308 |
| Parameter | Values | # |
|---|---|---|
| Datasets | See Table 1 | 28 |
| Folds | and 10 | 3 |
| Partitioning | CV, TSCV and SCV () | 8 |
| Seed | Random without replacement in [1, 1,000,000] | 1000 |
| Regression | RPART, NN, ELM, MARS, GBM | 5 |
| Metric | RMSE (performance) and (target shift) | 2 |
| Metric | Error | Standard Deviation | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RPART | CV | SCV | SCV | SCV | SCV | SCV | SCV | TSCV | CV | SCV | SCV | SCV | SCV | SCV | SCV | TSCV |
| 2-fcv | 9.2947E-2 | 9.2766E-2 | 9.2609E-2 | 9.2355E-2 | 9.2156E-2 | 9.1978E-2 | 9.1991E-2 | 9.1875E-2 | 3.3380E-3 | 3.3012E-3 | 3.1851E-3 | 3.0756E-3 | 2.9521E-3 | 2.8680E-3 | 2.8328E-3 | 2.7992E-3 |
| vs. CV | ✗ | 2.44E-4 | 1.51E-5 | 7.45E-9 | 5.22E-7 | 2.46E-7 | 1.54E-6 | 2.76E-6 | ✗ | 1.71E-1 | 1.87E-3 | 5.83E-4 | 2.75E-5 | 1.88E-6 | 7.45E-8 | 1.26E-6 |
| vs. TSCV | 2.76E-6 * | 4.77E-6 * | 7.96E-6 * | 1.35E-4 * | 7.16E-4 * | 3.27E-1 * | 1.26E-1 * | ✗ | 1.26E-6 * | 4.10E-7 * | 1.20E-4 * | 7.92E-4 * | 3.66E-5 * | 2.02E-1 * | 9.73E-1 | ✗ |
| 5-fcv | 9.0102E-2 | 9.0086E-2 | 9.0023E-2 | 8.9920E-2 | 8.9815E-2 | 8.9701E-2 | 8.9705E-2 | 8.9653E-2 | 1.9316E-3 | 1.9204E-3 | 1.9172E-3 | 1.8594E-3 | 1.8275E-3 | 1.7749E-3 | 1.7593E-3 | 1.7456E-3 |
| vs. CV | ✗ | 3.62E-1 | 4.21E-5 | 1.29E-3 | 1.88E-6 | 1.10E-5 | 1.77E-5 | 4.83E-5 | ✗ | 2.64E-1 | 3.05E-1 | 4.41E-3 | 4.73E-4 | 1.06E-4 | 3.66E-5 | 3.18E-5 |
| vs. TSCV | 4.83E-5 * | 9.32E-5 * | 2.74E-4 * | 3.81E-4 * | 8.86E-3 * | 5.37E-1 * | 7.35E-2 * | ✗ | 3.18E-5 * | 1.20E-4 * | 5.53E-5 * | 4.41E-3 * | 1.70E-3 * | 5.64E-2 * | 6.62E-1 * | ✗ |
| 10-fcv | 8.9141E-2 | 8.9143E-2 | 8.9137E-2 | 8.9071E-2 | 8.9021E-2 | 8.8974E-2 | 8.8957E-2 | 8.8945E-2 | 1.5020E-3 | 1.5006E-3 | 1.4981E-3 | 1.4373E-3 | 1.4092E-3 | 1.3977E-3 | 1.3674E-3 | 1.3662E-3 |
| vs. CV | ✗ | 9.55E-1 | 2.64E-2 | 4.06E-3 | 1.36E-2 | 1.67E-2 | 1.03E-2 | 1.36E-2 | ✗ | 8.67E-1 | 5.67E-1 | 3.18E-5 | 6.32E-5 | 3.66E-5 | 1.35E-4 | 5.68E-6 |
| vs. TSCV | 1.36E-2 * | 8.86E-3 * | 2.64E-2 * | 1.79E-2 * | 8.15E-2 * | 1.09E-1 * | 6.30E-1 * | ✗ | 5.68E-6 * | 6.32E-5 * | 2.76E-6 * | 8.75E-4 * | 6.55E-3 * | 3.74E-3 * | 9.73E-1 | ✗ |
| NN | CV | SCV | SCV | SCV | SCV | SCV | SCV | TSCV | CV | SCV | SCV | SCV | SCV | SCV | SCV | TSCV |
| 2-fcv | 8.6539E-2 | 8.6454E-2 | 8.6336E-2 | 8.6196E-2 | 8.6106E-2 | 8.5954E-2 | 8.5849E-2 | 8.5689E-2 | 3.0571E-3 | 3.0134E-3 | 3.0113E-3 | 3.0113E-3 | 2.9897E-3 | 2.9681E-3 | 2.9352E-3 | 2.9453E-3 |
| vs. CV | ✗ | 6.98E-2 | 7.92E-4 | 4.77E-6 | 6.56E-7 | 4.77E-6 | 2.46E-7 | 4.10E-7 | ✗ | 5.95E-2 | 1.57E-1 | 6.62E-2 | 1.56E-2 | 3.06E-4 | 3.66E-5 | 2.81E-2 |
| vs. TSCV | 4.10E-7 * | 4.77E-6 * | 1.94E-4 * | 3.42E-4 * | 1.29E-3 * | 2.47E-2 * | 2.18E-1 * | ✗ | 2.81E-2 * | 4.51E-2 * | 2.18E-2 * | 1.67E-2 * | 5.34E-2 * | 9.93E-2 * | 6.14E-1 * | ✗ |
| 5-fcv | 8.1336E-2 | 8.1350E-2 | 8.1270E-2 | 8.1197E-2 | 8.1136E-2 | 8.1016E-2 | 8.0928E-2 | 8.0752E-2 | 1.8602E-3 | 1.8664E-3 | 1.8340E-3 | 1.8393E-3 | 1.7967E-3 | 1.7092E-3 | 1.6800E-3 | 1.6733E-3 |
| vs. CV | ✗ | 4.51E-1 * | 1.79E-2 | 6.32E-5 | 5.53E-5 | 1.20E-4 | 8.20E-5 | 6.32E-5 | ✗ | 5.22E-1 * | 3.74E-1 | 5.64E-2 | 4.25E-4 | 1.55E-3 | 6.32E-5 | 1.17E-3 |
| vs. TSCV | 6.32E-5 * | 5.53E-5 * | 1.72E-4 * | 5.26E-4 * | 1.72E-4 * | 2.90E-3 * | 1.55E-3 * | ✗ | 1.17E-3 * | 3.81E-4 * | 9.54E-3 * | 7.92E-4 * | 9.00E-2 * | 2.64E-2 * | 9.55E-1 * | ✗ |
| 10-fcv | 7.9092E-2 | 7.9089E-2 | 7.9092E-2 | 7.9071E-2 | 7.9063E-2 | 7.9006E-2 | 7.8983E-2 | 7.8874E-2 | 1.3628E-3 | 1.3489E-3 | 1.3409E-3 | 1.3100E-3 | 1.2730E-3 | 1.2442E-3 | 1.2360E-3 | 1.2129E-3 |
| vs. CV | ✗ | 9.55E-1 * | 2.95E-1 | 1.27E-2 | 4.78E-3 | 2.04E-3 | 3.16E-3 | 4.73E-4 | ✗ | 6.14E-1 | 1.57E-1 | 2.90E-3 | 2.44E-4 | 1.54E-6 | 1.26E-6 | 3.18E-5 |
| vs. TSCV | 4.73E-4 * | 5.83E-4 * | 1.70E-3 * | *1.06E-3 | 4.06E-3 * | 9.54E-3 * | 1.03E-2 * | ✗ | 3.18E-5 * | 1.88E-6 * | 1.42E-3 * | 2.04E-3 * | 2.04E-2 * | 4.77E-2 * | 3.99E-1 * | ✗ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sáez, J.A.; Romero-Béjar, J.L. Impact of Regressand Stratification in Dataset Shift Caused by Cross-Validation. Mathematics 2022, 10, 2538. https://doi.org/10.3390/math10142538
Sáez JA, Romero-Béjar JL. Impact of Regressand Stratification in Dataset Shift Caused by Cross-Validation. Mathematics. 2022; 10(14):2538. https://doi.org/10.3390/math10142538
Chicago/Turabian StyleSáez, José A., and José L. Romero-Béjar. 2022. "Impact of Regressand Stratification in Dataset Shift Caused by Cross-Validation" Mathematics 10, no. 14: 2538. https://doi.org/10.3390/math10142538
APA StyleSáez, J. A., & Romero-Béjar, J. L. (2022). Impact of Regressand Stratification in Dataset Shift Caused by Cross-Validation. Mathematics, 10(14), 2538. https://doi.org/10.3390/math10142538







