Traffic Missing Data Imputation: A Selective Overview of Temporal Theories and Algorithms
Abstract
:1. Introduction
2. Analysis of Methods
2.1. Research Methods
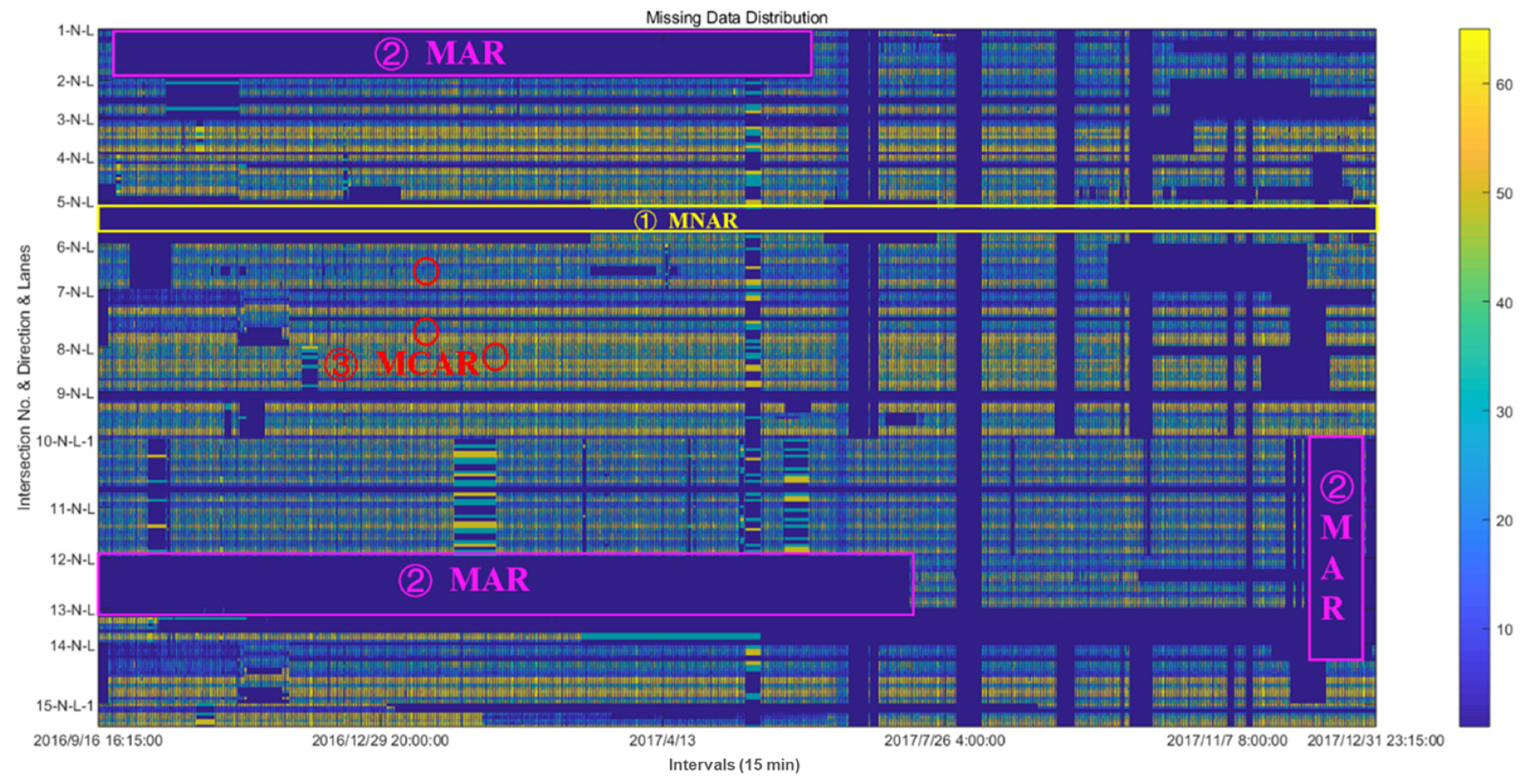
2.2. Missing Pattern
- MNAR: The missing data are regular. It usually means that there are some faults in detectors.
- MAR: The points of missing traffic data are related to nearby points. They usually occur as a group at special intervals, but the position of each group is random.
- MCAR: The missing data are isolated, random, and independent.
2.3. Assumption
- Data are lost randomly.
- Missing data are at low missing rates.
- Missing data are assumed to have determined attributes or patterns.
- Missing data are mostly influenced by historical data, neighboring data, or spatial data, without consideration of variations from interval to interval, from day to day, or from upstream to downstream.
2.4. Imputation Style
- Singular choice imputation (SCI)
- 2.
- Multiple choice imputation (MCI)
2.5. Applicable Conditions
- Offline imputation with moderate-to-high datasets
- 2.
- Online imputation with light-to-moderate datasets
2.6. Limitations
- Compared with the tensor-based method [23], CM [27], and KM [28], vector and matrix methods share partial spatiotemporal information so that the results seem to be good when the main features are achieved by chance. However, without sufficient information incorporated, most cases will fail, especially in extreme conditions, since daily periodicity similarity, local interval fluctuation, variation from day to day, and spatial influence between upstream and downstream should be considered.
- When data are integrated from multiple shorter-term observations, the main reason for missing data is the error at the stage of processing data. Additionally, the stage of data aggregation can lead to data loss. Moreover, the repeated and error data are considered as missing data to be imputed.
- Most methods focus on spatiotemporal feature learning, but they cannot perform very well in urban traffic. This is because being divided by signal phases and the length of the phase time of traffic lights, the turning movements can influence the variation in traffic flows both in temporal and spatial aspects [8].
- It is worth studying the quantity of sparsity detector and location optimization with a consideration of missing data imputation under different missing rates and the relationship of their threshold conditions with the number of partially missing detectors, the number of invalid detectors, and missing rates [96].
- Although the imputation methods are various, it is vital to investigate the performance of each method under different traffic conditions and their application and invalid conditions.
2.7. Public Datasets
3. Missing Data Imputing Methods with Mathematical Formulation
3.1. PPCA-Based Missing Data Imputing
3.2. GMM-Based Missing Data Imputing
3.3. KNN-Based Missing Data Imputing
3.4. Copula-Based Missing Data Imputing
3.5. Tensor-Based Missing Data Imputing
3.6. ARIMA-Based Missing Data Imputing
3.7. Random Forest-Based Missing Data Imputing
3.8. LSTM-Based Missing Data Imputing
4. Test and Results
4.1. Test Data
4.2. Test and Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- You, L.; Tunçer, B.; Zhu, R.; Xing, H.; Yuen, C. A Synergetic Orchestration of Objects, Data, and Services to Enable Smart Cities. IEEE Internet Things J. 2019, 6, 10496–10507. [Google Scholar] [CrossRef]
- You, L.; Zhao, F.; Cheah, L.; Jeong, K.; Zegras, P.C.; Ben-Akiva, M. A Generic Future Mobility Sensing System for Travel Data Collection, Management, Fusion, and Visualization. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4149–4160. [Google Scholar] [CrossRef]
- Sun, B.; Jiao, P. Spatio-temporal segmented traffic flow prediction with ANPRS data based on improved XGBoost. J. Adv. Transp. 2021, 2021, 5559562. [Google Scholar] [CrossRef]
- You, L.; Tuncer, B.; Xing, H. Harnessing multi-source data about public sentiments and activities for informed design. IEEE Trans. Knowl. Data Eng. 2018, 31, 343–356. [Google Scholar] [CrossRef]
- Turner, S.; Albert, L.; Gajewski, B.; Eisele, W. Archived intelligent transportation system data quality: Preliminary analyses of San Antonio TransGuide data. Transp. Res. Rec. 2000, 1719, 77–84. [Google Scholar] [CrossRef]
- Conklin, J.H.; Smith, B.L. The use of local lane distribution patterns for the estimation of missing data in transportation management systems. Transp. Res. Rec. 2002, 1811, 50–56. [Google Scholar]
- Van Buuren, S. Flexible Imputation of Missing Data; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Qu, L.; Li, L.; Zhang, Y.; Hu, J. PPCA-based missing data imputation for traffic flow volume: A systematical approach. IEEE Trans. Intell. Transp. Syst. 2009, 10, 512–522. [Google Scholar]
- Vlahogianni, E.I.; Golias, J.C.; Karlaftis, M.G. Short-term traffic forecasting: Overview of objectives and methods. Transp. Rev. 2004, 24, 533–557. [Google Scholar] [CrossRef]
- Van Lint, J.W.C.; Hoogendoorn, S.P.; Van Zuylen, H.J. Accurate freeway travel time prediction with state-space neural networks under missing data. Transp. Res. Part C Emerg. Technol. 2005, 13, 347–369. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.Y.; Wang, K.; Lin, W.; Xu, X.; Chen, C. Data-driven intelligent transportation systems: A survey. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1624–1639. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Y.; Li, L.; Hu, J.; Zhang, Z. The retrieval of intra-day trend and its influence on traffic prediction. Transp. Res. Part C Emerg. Technol. 2012, 22, 103–118. [Google Scholar] [CrossRef]
- You, L.; He, J.; Wang, W.; Cai, M. Autonomous Transportation Systems and Services Enabled by the Next-Generation Network. IEEE Netw. 2022, 3, 66–72. [Google Scholar] [CrossRef]
- Kim, J.O.; Curry, J. The treatment of missing data in multivariate analysis. Sociol. Methods Res. 1977, 6, 215–240. [Google Scholar] [CrossRef]
- Raaijmakers, Q.A.W. Effectiveness of different missing data treatments in surveys with Likert-type data: Introducing the relative mean substitution approach. Educ. Psychol. Meas. 1999, 59, 725–748. [Google Scholar] [CrossRef]
- Grzymala-Busse, J.W.; Hu, M. A comparison of several approaches to missing attribute values in data mining. In Proceedings of the International Conference on Rough Sets and Current Trends in Computing, Banff, AB, Canada, 16–19 October 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 378–385. [Google Scholar]
- Chen, J.; Shao, J. Nearest neighbor imputation for survey data. J. Off. Stat. 2000, 16, 113–131. [Google Scholar]
- Nguyen, L.N.; Scherer, W.T. Imputation Techniques to Account for Missing Data in Support of Intelligent Transportation Systems Applications; Center for Transportation Studies, University of Virginia: Charlottesville, VA, USA, 2003. [Google Scholar]
- Gold, D.L.; Turner, S.M.; Gajewski, B.J.; Spiegelman, C. Imputing missing values in its data archives for intervals under 5 minutes. In Proceedings of the Transportation Research Board 80th Annual Meeting, Washington, DC, USA, 7–11 January 2001. [Google Scholar]
- Zhong, M.; Lingras, P.; Sharma, S. Estimation of missing traffic counts using factor, genetic, neural, and regression techniques. Transp. Res. Part C Emerg. Technol. 2004, 12, 139–166. [Google Scholar] [CrossRef]
- Sun, B.; Sun, T.; Zhang, Y.; Jiao, P. Urban traffic flow online prediction based on multi-component attention mechanism. IET Intell. Transp. Syst. 2020, 14, 1249–1258. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y. Data imputation using least squares support vector machines in urban arterial streets. IEEE Signal Processing Lett. 2009, 16, 414–417. [Google Scholar] [CrossRef]
- Tan, H.; Feng, G.; Feng, J.; Wang, W.; Zhang, Y.J.; Li, F. A tensor-based method for missing traffic data completion. Transp. Res. Part C Emerg. Technol. 2013, 28, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Zhang, G.; Wang, Y.; Wang, H.; Liu, F. A hybrid approach to integrate fuzzy C-means based imputation method with genetic algorithm for missing traffic volume data estimation. Transp. Res. Part C Emerg. Technol. 2015, 51, 29–40. [Google Scholar] [CrossRef]
- Tan, H.; Wu, Y.; Shen, B.; Jin, P.J.; Ran, B. Short-term traffic prediction based on dynamic tensor completion. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2123–2133. [Google Scholar] [CrossRef]
- Duan, Y.; Lv, Y.; Liu, Y.L.; Wang, F.Y. An efficient realization of deep learning for traffic data imputation. Transp. Res. Part C Emerg. Technol. 2016, 72, 168–181. [Google Scholar] [CrossRef]
- Ma, X.; Luan, S.; Du, B.; Yu, B. Spatial copula model for imputing traffic flow data from remote microwave sensors. Sensors 2017, 17, 2160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bae, B.; Kim, H.; Lim, H.; Liu, Y.; Han, L.D.; Freeze, P.B. Missing data imputation for traffic flow speed using spatio-temporal cokriging. Transp. Res. Part C Emerg. Technol. 2018, 88, 124–139. [Google Scholar] [CrossRef]
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Smith, B.L.; Scherer, W.T.; Conklin, J.H. Exploring Imputation Techniques for Missing Data in Transportation Management Systems. Transp. Res. Rec. 2003, 1836, 132–142. [Google Scholar] [CrossRef]
- Dailey, D.J. Improved Error Detection for Inductive Loop Sensors; Transportation Research Board: Washington, DC, USA, 1993. [Google Scholar]
- Nihan, N.L. Aid to determining freeway metering rates and detecting loop errors. J. Transp. Eng. 1997, 123, 454–458. [Google Scholar] [CrossRef]
- Ghosh, B.; Basu, B.; O’Mahony, M.M. Time-series modelling for forecasting vehicular traffic flow in Dublin. In Proceedings of the 84th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 9–13 January 2005. [Google Scholar]
- Zhong, M.; Sharma, S.; Liu, Z. Assessing robustness of imputation models based on data from different jurisdictions: Examples of Alberta and Saskatchewan, Canada. Transp. Res. Rec. 2005, 1917, 116–126. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Optimized and meta-optimized neural networks for short-term traffic flow prediction: A genetic approach. Transp. Res. Part C Emerg. Technol. 2005, 13, 211–234. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E. Rényi entropy and divergence for VARFIMA processes based on characteristic and impulse response functions. Chaos Solitons Fractals 2022, 160, 112268. [Google Scholar] [CrossRef]
- Van Der Voort, M.; Dougherty, M.; Watson, S. Combining Kohonen maps with ARIMA time series models to forecast traffic flow. Transp. Res. Part C Emerg. Technol. 1996, 4, 307–318. [Google Scholar] [CrossRef] [Green Version]
- Williams, B.M. Multivariate vehicular traffic flow prediction: Evaluation of ARIMAX modeling. Transp. Res. Rec. 2001, 1776, 194–200. [Google Scholar] [CrossRef]
- Kamarianakis, Y.; Prastacos, P. Forecasting traffic flow conditions in an urban network: Comparison of multivariate and univariate approaches. Transp. Res. Rec. 2003, 1857, 74–84. [Google Scholar] [CrossRef]
- Min, X.; Hu, J.; Zhang, Z. Urban traffic network modeling and short-term traffic flow forecasting based on GSTARIMA model. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; IEEE: New York City, NY, USA, 2010; pp. 1535–1540. [Google Scholar]
- Min, W.; Wynter, L. Real-time road traffic prediction with spatiotemporal correlations. Transp. Res. Part C Emerg. Technol. 2011, 19, 606–616. [Google Scholar] [CrossRef]
- Stathopoulos, A.; Karlaftis, M.G. A multivariate state space approach for urban traffic flow modeling and prediction. Transp. Res. Part C Emerg. Technol. 2003, 11, 121–135. [Google Scholar] [CrossRef]
- Gazis, D.; Liu, C. Kalman filtering estimation of traffic counts for two network links in tandem. Transp. Res. Part B Methodol. 2003, 37, 737–745. [Google Scholar] [CrossRef]
- Ni, D.; Leonard, J.D. Markov chain monte carlo multiple imputation using bayesian networks for incomplete intelligent transportation systems data. Transp. Res. Rec. 2005, 1935, 57–67. [Google Scholar] [CrossRef]
- Sun, S.; Yu, G.; Zhang, C. Short-term traffic flow forecasting using sampling Markov Chain method with incomplete data. In IEEE Intelligent Vehicles Symposium; IEEE: Piscataway, NJ, USA, 2004; pp. 437–441. [Google Scholar]
- Sun, S.; Zhang, C.; Yu, G. A Bayesian network approach to traffic flow forecasting. IEEE Trans. Intell. Transp. Syst. 2006, 7, 124–132. [Google Scholar] [CrossRef]
- Kamarianakis, Y.; Shen, W.; Wynter, L. Real-time road traffic forecasting using regime-switching space-time models and adaptive LASSO. Appl. Stoch. Models Bus. Ind. 2012, 28, 297–315. [Google Scholar] [CrossRef]
- Sun, S.; Huang, R.; Gao, Y. Network-scale traffic modeling and forecasting with graphical lasso and neural networks. J. Transp. Eng. 2012, 138, 1358–1367. [Google Scholar] [CrossRef] [Green Version]
- Allison, P.D. Missing Data; Sage Publications: Thousand Oaks, CA, USA, 2001. [Google Scholar]
- Holt, C.C. Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast. 2004, 20, 5–10. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar]
- Acurna, E.; Rodriguez, C. The treatment of missing values and its effect in the classifier accuracy, classification, clustering, and data mining applications. In Proceedings of the Meeting of the International Federation of Classification Societies (IFCS), Chicago, IL, USA, 15–18 July 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 639–647. [Google Scholar]
- Liu, P.; Lei, L.; Zhang, X.F. A comparison study of missing value processing methods. Comput. Sci. 2004, 31, 155–156. [Google Scholar]
- Chen, C.; Kwon, J.; Rice, J.; Skabardonis, A.; Varaiya, P. Detecting errors and imputing missing data for single-loop surveillance systems. Transp. Res. Rec. 2003, 1855, 160–167. [Google Scholar] [CrossRef]
- Al-Deek, H.M.; Venkata, C.; Chandra, S.R. New algorithms for filtering and imputation of real-time and archived dual-loop detector data in I-4 data warehouse. Transp. Res. Rec. 2004, 1867, 116–126. [Google Scholar] [CrossRef]
- Kim, H.; Lovell, D.J. Traffic information imputation using a linear model in vehicular ad hoc networks. In Proceedings of the 2006 IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006; pp. 1406–1411. [Google Scholar]
- Boyles, S. Comparison of Interpolation Methods for Missing Traffic Volume Data; Transportation Research Board: Washington, DC, USA, 2011. [Google Scholar]
- Castrillon, F.; Guin, A.; Guensler, R.; Laval, J. Comparison of modeling approaches for imputation of video detection data in intelligent transportation systems. Transp. Res. Rec. 2012, 2308, 138–147. [Google Scholar] [CrossRef]
- Yin, W.; Murray-Tuite, P.; Rakha, H. Imputing erroneous data of single-station loop detectors for nonincident conditions: Comparison between temporal and spatial methods. J. Intell. Transp. Syst. 2012, 16, 159–176. [Google Scholar] [CrossRef]
- Wang, J.; Zou, N.; Chang, G.L. Travel time prediction: Empirical analysis of missing data issues for advanced traveler information system applications. Transp. Res. Rec. 2008, 2049, 81–91. [Google Scholar] [CrossRef]
- Henrickson, K.; Zou, Y.; Wang, Y. Flexible and robust method for missing loop detector data imputation. Transp. Res. Rec. 2015, 2527, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Sharma, S.; Datla, S. Imputation of missing traffic data during holiday periods. Transp. Plan. Technol. 2008, 31, 525–544. [Google Scholar] [CrossRef]
- Chang, G.; Zhang, Y.; Yao, D. Missing data imputation for traffic flow based on improved local least squares. Tsinghua Sci. Technol. 2012, 17, 304–309. [Google Scholar] [CrossRef]
- Zhong, M.; Sharma, S. Matching hourly, daily, and monthly traffic patterns to estimate missing volume data. Transp. Res. Rec. 2006, 1957, 32–42. [Google Scholar] [CrossRef]
- Zhong, M.; Sharma, S.; Lingras, P. Matching patterns for updating missing values of traffic counts. Transp. Plan. Technol. 2006, 29, 141–156. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, Y.; Hu, J.; Li, L. Mining for similarities in urban traffic flow using wavelets. In Proceedings of the 2007 IEEE Intelligent Transportation Systems Conference, Seattle, WA, USA, 30 September–3 October 2007; pp. 119–124. [Google Scholar]
- Li, D.; Gu, H.; Zhang, L. A fuzzy c-means clustering algorithm based on nearest-neighbor intervals for incomplete data. Expert Syst. Appl. 2010, 37, 6942–6947. [Google Scholar] [CrossRef]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–22. [Google Scholar]
- Liu, P.; Lei, L. A review of missing data treatment methods. Int. J. Intel. Inf. Manag. Syst. Tech. 2005, 1, 412–419. [Google Scholar]
- Qu, L.; Zhang, Y.; Hu, J.; Jia, L.; Li, L. A BPCA based missing value imputing method for traffic flow volume data. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; pp. 985–990. [Google Scholar]
- Li, L.; Li, Y.; Li, Z. Efficient missing data imputing for traffic flow by considering temporal and spatial dependence. Transp. Res. Part C Emerg. Technol. 2013, 34, 108–120. [Google Scholar] [CrossRef]
- Song, Y.; Miller, H.J. Exploring traffic flow databases using space-time plots and data cubes. Transportation 2012, 39, 215–234. [Google Scholar] [CrossRef]
- Yang, J.; Han, L.D.; Freeze, P.B.; Chin, S.M.; Hwang, H.L. Short-term freeway speed profiling based on longitudinal spatiotemporal dynamics. Transp. Res. Rec. 2014, 2467, 62–72. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Li, L.; Zhang, Y.; Jin, M. Comparison on PPCA, KPPCA and MPPCA based missing data imputing for traffic flow. In Proceedings of the International Conference on Transportation Information and Safety (ICTIS), American Society of Civil Engineers, Wuhan, China, 29 June–2 July 2013. [Google Scholar]
- Haworth, J.; Cheng, T. Non-parametric regression for space–time forecasting under missing data. Comput. Environ. Urban Syst. 2012, 36, 538–550. [Google Scholar] [CrossRef] [Green Version]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Ku, W.C.; Jagadeesh, G.R.; Prakash, A.; Srikanthan, T. A clustering-based approach for data-driven imputation of missing traffic data. In Proceedings of the 2016 IEEE Forum on Integrated and Sustainable Transportation Systems (FISTS), Beijing, China, 10–12 July 2016; pp. 1–6. [Google Scholar]
- Duan, Y.; Lv, Y.; Kang, W.; Zhao, Y. A deep learning based approach for traffic data imputation. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 912–917. [Google Scholar]
- Laña, I.; Olabarrieta, I.I.; Vélez, M.; Ser, J.D. On the imputation of missing data for road traffic forecasting: New insights and novel techniques. Transp. Res. Part C Emerg. Technol. 2018, 90, 18–33. [Google Scholar] [CrossRef]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cinar, Y.G.; Mirisaee, H.; Goswami, P.; Gaussier, E.; Aït-Bachir, A. Period-aware content attention RNNs for time series forecasting with missing values. Neurocomputing 2018, 312, 177–186. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.; Wang, Y.; Ran, B. Missing value imputation for traffic-related time series data based on a multi-view learning method. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2933–2943. [Google Scholar] [CrossRef]
- Zhuang, Y.; Ke, R.; Wang, Y. Innovative method for traffic data imputation based on convolutional neural network. IET Intell. Transp. Syst. 2018, 13, 605–613. [Google Scholar] [CrossRef]
- Rodrigues, F.; Henrickson, K.; Pereira, F.C. Multi-output Gaussian processes for crowdsourced traffic data imputation. IEEE Trans. Intell. Transp. Syst. 2018, 99, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Luengo, J.; García, S.; Herrera, F. A study on the use of imputation methods for experimentation with Radial Basis Function Network classifiers handling missing attribute values: The good synergy between RBFNs and EventCovering method. Neural Netw. 2010, 23, 406–418. [Google Scholar] [CrossRef]
- Luengo, J.; García, S.; Herrera, F. On the choice of the best imputation methods for missing values considering three groups of classification methods. Knowl. Inf. Syst. 2012, 32, 77–108. [Google Scholar] [CrossRef]
- Hu, T.; Mahmassani, H.S.; Rothery, R.W. Dynasmart-Dynamic Network Assignment-Simulation Model for Advanced Road Telematics; Center for Transportation Research, University of Texas: Austin, TX, USA, 1992. [Google Scholar]
- Ben-Akiva, M.; Bierlaire, M.; Koutsopoulos, H.; Mishalani, R. DynaMIT: A simulation-based system for traffic prediction. In Proceedings of the DACCORD Short Term Forecasting Workshop, Delft, The Netherlands, 1 February 1998; pp. 1–12. [Google Scholar]
- Fellendorf, M.; Vortisch, P. Microscopic traffic flow simulator VISSIM. In Fundamentals of Traffic Simulation; Springer: New York, NY, USA, 2010; pp. 63–93. [Google Scholar]
- Cameron, G.D.B.; Duncan, G.I.D. PARAMICS—Parallel microscopic simulation of road traffic. J. Supercomput. 1996, 10, 25–53. [Google Scholar] [CrossRef]
- Wang, F.Y. Parallel control and management for intelligent transportation systems: Concepts, architectures, and applications. IEEE Trans. Intell. Transp. Syst. 2010, 11, 630–638. [Google Scholar] [CrossRef]
- Muralidharan, A.; Horowitz, R. Imputation of ramp flow data for freeway traffic simulation. Transp. Res. Rec. 2009, 2099, 58–64. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, Z.; Li, L. Missing traffic data: Comparison of imputation methods. IET Intell. Transp. Syst. 2014, 8, 51–57. [Google Scholar] [CrossRef]
- Chen, H.; Grant-Muller, S.; Mussone, L.; Montgomery, F. A study of hybrid neural network approaches and the effects of missing data on traffic forecasting. Neural Comput. Appl. 2001, 10, 277–286. [Google Scholar] [CrossRef]
- Ma, X.; Luan, S.; Ding, C.; Liu, H.; Wang, Y. Spatial Interpolation of Missing Annual Average Daily Traffic Data Using Copula-Based Model. IEEE Intell. Transp. Syst. Mag. 2019, 11, 158–170. [Google Scholar] [CrossRef]
- Chen, M.; Yu, G.; Chen, P.; Wang, Y. A copula-based approach for estimating the travel time reliability of urban arterial. Transp. Res. Part C Emerg. Technol. 2017, 82, 1–23. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, P.; Zheng, J.; Zhu, J.; Yu, G.; Wang, Y.; Liu, H.X. Missing data detection and imputation for urban ANPR system using an iterative tensor decomposition approach. Trans. Res. Part C Emerg. Technol. 2019, 107, 337–355. [Google Scholar] [CrossRef]
- Chen, X.; Yang, J.; Sun, L. A nonconvex low-rank tensor completion model for spatiotemporal traffic data imputation. Trans. Res. Part C Emerg. Technol. 2020, 117, 102673. [Google Scholar] [CrossRef]
- Fard, M.R.; Mohaymany, A.S. A copula-based estimation of distribution algorithm for calibration of microscopic traffic models. Trans. Res. Part C Emerg. Technol. 2019, 98, 449–470. [Google Scholar] [CrossRef]













| Dataset | City, Country | Duration | Time Resolution | Spatial Coverage | Data Type |
|---|---|---|---|---|---|
| PeMS (Li et al., 2018 [83]) | California, USA | 1 June 2011–31 August 2011 | 5 min | Three detectors in S Valley Free Way in Santa Clara, CA, USA | Traffic flow data |
| Communications Commission (Chen et al., 2017 [97]) | Guangzhou, China | 1 August 2016–30 September 2016 | 10 min | 214 road segments in urban expressways and arterials | Traffic speed data |
| ANPR systems’ data (Zhang et al., 2019 [98]) | China | 1 December 2017–31 December 2017 | 30 min | Traffic management department of a city | Missing data cases |
| Birmingham parking data (Chen et al., 2020 [99]) | Birmingham, England | 4 October 2016–19 December 2016 | 30 min | 30 car parks | 14.89% missing values |
| Hangzhou metro passenger flow data (Chen et al., 2020 [99]) | Hangzhou, China | 1 October 2019–25 October 2019 | 10 min | 80 metro stations | Incoming passenger flow |
| Seattle freeway traffic speed data (Chen et al., 2020 [99]) | Seattle, USA | 1 January 2015–28 January 2015 | 5 min | 323 loop detectors | Freeway traffic speed data |
| Remote Traffic Microwave Sensors (Bae et al., 2018 [28]) | Knoxville, USA | 1 December 2015– | 5 min | Two major highways in the Knoxville region, I-40 and I-75 | Traffic count, speed, and occupancy information |
| Changshou Road (Chen et al., 2017 [97]) | Shanghai, China | 25 August 2008–29 August 2008 | - | Section consists of seven signalized intersections | Travel time data |
| FHWA (Fard and Mohaymany [100]) | Los Angeles, USA | 2004– | 60 min | Southern section of the US101 highway | Location, speed, acceleration, and type of vehicles |
| AADT (Ma et al., 2019 [96]) | California, USA | 2010– | - | 253 road segments with 7218 data collection sites | Traffic count data |
| Microwave sensors (Ma et al., 2017 [27]) | Beijing, China | 1 June 2015–7 June 2015 | 2 min | Two ring expressways | Latitude and longitude, timestamp, traffic flow, speed, and occupancy |
| Open Data portal (Laña et al., 2018 [80]) | Madrid, Spain | 2014–2016 | 1 min | 3600 ATRs in urban freeways | Resolution data |
| Detector ID | Location | Direction |
|---|---|---|
| 1 | 241.59 | North to South |
| 2 | 241.20 | North to South |
| 3 | 240.83 | North to South |
| 4 | 240.43 | North to South |
| 5 | 240.34 | North to South |
| 6 | 239.82 | North to South |
| 7 | 238.97 | North to South |
| 8 | 238.76 | North to South |
| 9 | 238.37 | North to South |
| 10 | 238.18 | North to South |
| 11 | 237.87 | North to South |
| 12 | 235.50 | North to South |
| Missing Ratio | 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | |
|---|---|---|---|---|---|---|---|---|---|---|
| PPCA | NRMSE | 14.76 | 12.17 | 13.61 | 13.62 | 14.09 | 17.27 | 22.00 | 22.96 | 24.67 |
| NMAE | 9.41 | 8.18 | 8.54 | 8.96 | 9.85 | 13.31 | 17.65 | 18.39 | 19.81 | |
| GMM | NRMSE | 30.61 | 31.06 | 36.13 | 48.46 | 50.91 | 53.21 | 55.23 | 59.06 | 62.17 |
| NMAE | 22.35 | 24.79 | 29.13 | 40.52 | 41.66 | 44.41 | 46.29 | 54.16 | 58.12 | |
| KNN | NRMSE | 16.62 | 15.09 | 16.93 | 18.06 | 20.81 | 16.52 | 16.94 | 30.19 | 33.13 |
| NMAE | 10.07 | 9.23 | 10.22 | 10.47 | 13.09 | 10.68 | 10.74 | 20.96 | 24.13 | |
| Copula | NRMSE | 32.31 | 29.05 | 34.18 | 33.83 | 34.32 | 31.07 | 33.47 | 34.13 | 34.14 |
| NMAE | 24.23 | 22.39 | 25.93 | 25.67 | 26.28 | 24.02 | 25.05 | 25.88 | 25.95 | |
| Tensor | NRMSE | 18.69 | 12.90 | 18.09 | 23.37 | 28.22 | 14.59 | 15.92 | 27.09 | 29.26 |
| NMAE | 10.79 | 8.34 | 10.13 | 12.82 | 17.03 | 9.67 | 9.70 | 19.76 | 22.07 | |
| ARIMA | NRMSE | 28.81 | 23.25 | 27.95 | 26.67 | 28.04 | 25.76 | 26.66 | 27.44 | 27.81 |
| NMAE | 22.07 | 19.10 | 22.15 | 21.55 | 22.32 | 20.08 | 20.46 | 21.55 | 22.13 | |
| Random Forest | NRMSE | 30.61 | 33.43 | 36.78 | 41.11 | 41.62 | 39.98 | 40.82 | 43.13 | 46.91 |
| NMAE | 22.35 | 25.18 | 32.73 | 31.08 | 32.06 | 31.22 | 30.70 | 34.22 | 38.12 | |
| LSTM | NRMSE | 12.40 | 14.80 | 20.03 | 28.43 | 33.53 | 37.36 | 40.68 | 41.86 | 43.12 |
| NMAE | 8.06 | 9.69 | 15.18 | 20.32 | 24.36 | 28.51 | 30.68 | 31.72 | 33.10 | |
| LSTM-M | NRMSE | 11.92 | 15.26 | 19.37 | 28.61 | 32.59 | 38.15 | 40.01 | 41.29 | 42.33 |
| NMAE | 7.54 | 10.02 | 14.24 | 19.97 | 23.46 | 29.21 | 30.27 | 31.06 | 32.13 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Zhu, S.; Hao, R.; Sun, B.; Xie, J. Traffic Missing Data Imputation: A Selective Overview of Temporal Theories and Algorithms. Mathematics 2022, 10, 2544. https://doi.org/10.3390/math10142544
Sun T, Zhu S, Hao R, Sun B, Xie J. Traffic Missing Data Imputation: A Selective Overview of Temporal Theories and Algorithms. Mathematics. 2022; 10(14):2544. https://doi.org/10.3390/math10142544
Chicago/Turabian StyleSun, Tuo, Shihao Zhu, Ruochen Hao, Bo Sun, and Jiemin Xie. 2022. "Traffic Missing Data Imputation: A Selective Overview of Temporal Theories and Algorithms" Mathematics 10, no. 14: 2544. https://doi.org/10.3390/math10142544
APA StyleSun, T., Zhu, S., Hao, R., Sun, B., & Xie, J. (2022). Traffic Missing Data Imputation: A Selective Overview of Temporal Theories and Algorithms. Mathematics, 10(14), 2544. https://doi.org/10.3390/math10142544






