Performance Analysis of Multi-Cell Association in Downlink MU-MIMO System with Arbitrary Beamforming

Abstract

This article deals with the analysis of the multi-cell association setup, and it exploits the possibility of enhancing coverage in the envisioned sixth generation (6G) large-scale cellular networks. Specifically, we propose a simple, effective approach for finding a closed-form solution to the coverage probability of a given user in a multi-cell association regime of downlink multiple-user multiple-input multiple-output (MU-MIMO) systems. In particular, a Rayleigh fading channel is considered, wherein the transmitter has only the knowledge of the second-order statistics of the channel. The proposed work uses an indefinite quadratic formulation method and thereby investigates the effect of cell association in a correlated downlink broadcast channel with co-channel interference, additive white noise, and multiple transceiver antenna elements. In the results, we show that a predefined signal-to-interference-plus-noise ratio (SINR) threshold dictates an effective multi-cell association setup, and we identify the region in which a multi-cell association performs better that a single association-based network. The derived theoretical expressions in this paper are validated by the same means of simulation.

1. Introduction

Several research frontiers are being investigated for beyond fifth generation (B5G) wireless communications networks in order to address the challenging spectrum demands extrapolated in [1]. One such frontier is coined as the cell-free multiple-input multiple-output (MIMO) systems with distributed antennas and a central processing unit [2,3]. Another frontier deals with a selection-based mobile station (MS) association scheme in a multi-tier heterogeneous cellular network (HCN) [4]. Furthermore, the dense deployment of small cells operating at distinct frequency bands in HCNs explores the possibilities of decoupled access schemes [5]. In the existing systems, a multi-order simultaneous connectivity has been proposed in the twelfth release of long term evolution (LTE) [6] and for 5G communication systems [7,8]. In such a setup, the MS can be associated effectively with multiple small cells and macrocells, broadly coined herein as base stations (BSs), in both uplink and downlink modes [9,10]. In parallel, a frontier is also concerned with the incorporation of efficient beamforming techniques [11] for the multi-antenna nodes to help balance the supply and demand of the envisioned wireless data. The latter two research directions motivate the proposed work.

Noting the potential of a multi-cell association in communication systems, Kim and Popovski [7] worked on the reliable double association in the uplink scenario. They characterized the performance metrics using a framework of homogeneous Poisson point processes (PPP) and the stochastic geometry approach [12], i.e., a stationary process. Furthermore, Lema et al., in [10], point to a realizable limitation in the uplink double association due to the power budget constraints of the user equipment. Nevertheless, [7,10] postulate that both the system reliability as well as the user connectivity experience can be tremendously enhanced by the simultaneous multi-cell association. However, the performance analysis of the multi-cell association with the transmit beamforming aspects were not considered in [7,10].

In the context of a simultaneous multi-cell association in a downlink communication system, the power constraints mentioned in [10] can be easily relaxed, and the MS can efficiently select the set of serving BSs based on the network geometries and the configuration parameters [13]. Hence, in a downlink HCN, a hybrid association scheme with the MS operating in either single or dual connectivity mode was investigated in [14] without, however, considering the antenna diversity at the BS. Moreover, an extension in [15] dealt with the interference management scheme in a co-channel interference (CCI) setup of dual connectivity mode. Further, the authors in [16] present an in-depth analysis of dual-connectivity in the LTE-Advanced system setup and make use of channel state information-reference signals (CSI-RS) to effect cell selection and re-selection. Traffic scheduling aspects of dual connectivity were also examined in [17]. Furthermore, several recent research investigations point towards the usability of dual-connectivity in downlink communication systems; a pedagogical overview is summarized well in [18]. These works are based on the signal-to-interference-plus-noise ratio (SINR) analysis; however, they do not characterize the key performance indicators (KPIs) with statistical channel state information on the transmit side.

From the aspect of mathematical tractability involved in the characterization of network KPIs, an indefinite quadratic form (IQF) approach was introduced in [19], which included the characterization of the outage probability, i.e., the cumulative distribution function (CDF), of the instantaneous SINR for the multi-user MIMO (MU-MIMO) systems. The work, however, was limited to an orthonormal set of transmit beamformers. The condition of the orthonormal beamformers was later relaxed in the covariance shaping-based scheme in [20]. A recent work [21], proposes a method for multi-cell association in a single receiver antenna system; the model, therefore, is not applicable for the multi-antenna multi-user multi-cell association scenario, and hence, covariance shaping cannot be performed on such system. Thus, existing works do not provide the distribution of SINR in a multi-cell association regime under generic network parameters.

In the proposed work, we primarily extend the literature on simultaneous multi-cell association in MU-MIMO systems by:

• Incorporating transmit and receive antenna diversity into the system design and thereby analyzing the coverage probability of a given user associated with several cells.
• Deriving exact closed-form expressions under the assumption of only the statistical CSI’s availability in a downlink broadcast scenario.
• Providing a generic framework for which several precoding and equalization schemes can be employed. Furthermore, a scheme of repeated, as well as distinct, eigenvalue structures of channel weight matrices is outlined.

We achieve the aforementioned goals by firstly formulating the SINR expression of a given user in a canonical quadratic form, and then by incorporating the residue theory approach to achieve the closed-form expression of the coverage probability of a given user in multi-user multi-cell association setup. The availability of such a closed-form expression can assist in the adaptive beamforming design under the coverage probability maximization problem; this, however, is not done herein.

The material is structured as follows: In Section 2, we outline the system model. Section 3 deals with the characterization procedure of the coverage probability. The performance evaluation is given in Section 4. This is followed by conclusions, acknowledgments, and references.

Notations: $\left|\mathit{a}\right|$, $\left|\mathbf{A}\right|$, and ${∥\mathbf{a}∥}^2$ denote the absolute value of scalar a, the determinant of matrix A and the square of norm-2 of vector a, respectively. In ${\{a;\mathbf{a}\}}_{c;k}$, the subscript notation ‘c’ indicates the associated cell, whereas ‘k’ represents the intended kth user, which is associated with the cth cell. The notation ${\left(\right)}^H$ represents the conjugate transposition, and ${\left(\right)}^{\frac{H}{2}}$ is the short representation of ${({\left(\right)}^{\frac{1}{2}})}^H$. The quadratic form is defined as ${∥\mathbf{a}∥}_{\mathbf{A}}^2\stackrel{△}{=}{\mathbf{a}}^H\mathbf{A}\mathbf{a}$.

2. System Model

A downlink single data stream intended for the kth user, $k\in \{1,2,\dots ,K\}$, simultaneously associated with C cells is considered in this work, as shown in Figure 1. The base station (BS) and mobile station (MS) have antennas of an array of sizes N and M, respectively. Moreover, the BS can be conventional and/or a flying-cell denoted by drone. The data symbol intended for the kth user associated with the cth cell, $c\in \{1,2,\dots ,C\}$, is ${\mathit{s}}_{ck}$, and the transmit beamformer ${\mathbf{w}}_{ck}$ modulates ${\mathit{s}}_{ck}$ before transmission. Additionally, $\mathbb{E}\left\{\right|{\mathit{s}}_{ck}{|}^2\}=1$ is assumed. Therefore, the kth MS associated with the cth cell observes:

$${\mathit{y}}_{ck}={\mathbf{v}}_k{\mathbf{H}}_{ck}{\mathbf{w}}_{ck}{s}_{ck}+\sum _{i=1,i\ne k}^K{\mathbf{v}}_k{\mathbf{H}}_{ck}{\mathbf{w}}_{ci}{s}_{ci}+z_{ck},$$

(1)

where ${\mathbf{v}}_k$ is a receive beamforming vector, $\parallel {\mathbf{v}}_k{\parallel }^2=1$, and the additive term $z_{ck}\sim \mathcal{CN}(0,{\sigma }_{ck}^2)$, more specifically $z_{ck}={\mathbf{v}}_k{\mathbf{n}}_{ck}$, and ${\mathbf{n}}_{ck}$ is a zero-mean independent and identically distributed (i.i.d.) vector with the variance ${\sigma }_{ck}^2$. Additionally, a conventional Kronecker structured model [22] for the channel covariances is assumed in which the transmit correlation (${\mathbf{T}}_{ck}$) and receive correlation (${\mathbf{R}}_{ck}$) are separable, and the model for the channel matrix ${\mathbf{H}}_{ck}$ is:

$${\mathbf{H}}_{ck}={\mathbf{R}}_{ck}^{\frac{1}{2}}{\overline{\mathbf{H}}}_{ck}{\mathbf{T}}_{ck}^{\frac{1}{2}},$$

(2)

where the elements of ${\overline{\mathbf{H}}}_{ck}$ are i.i.d. complex Gaussian random variables with zero-mean and unit variance.

Hence, the instantaneous SINR of the kth MS associated with the cth cell is:

$$\begin{array}{ccc}\hfill {\gamma }_{ck}& =& {\displaystyle \frac{|{\mathbf{v}}_k{\mathbf{H}}_{ck}{\mathbf{w}}_{ck}{|}^2}{{\sigma }_{ck}^2+{\sum }_{i=1,i\ne k}^K{\left|{\mathbf{v}}_k{\mathbf{H}}_{ck}{\mathbf{w}}_{ci}\right|}^2}},\hfill \\ & =& {\displaystyle \frac{|{\mathbf{v}}_k{\mathbf{R}}_{ck}^{\frac{1}{2}}{\overline{\mathbf{H}}}_{ck}{\overline{\mathbf{w}}}_{ck}{|}^2}{{\sigma }_{ck}^2+{\sum }_{i=1,i\ne k}^K{\left|{\mathbf{v}}_k{\mathbf{R}}_{ck}^{\frac{1}{2}}{\overline{\mathbf{H}}}_{ck}{\overline{\mathbf{w}}}_{ci}\right|}^2}},\hfill \end{array}$$

(3)

where ${\overline{\mathbf{w}}}_{ck}={\mathbf{T}}_{ck}^{\frac{1}{2}}{\mathbf{w}}_{ck}$.

Now, by representing ${\overline{\mathbf{H}}}_{ck}$ in a vectorized form, ${\overline{\mathbf{h}}}_{ck}=\mathrm{vec}\left({\overline{\mathbf{H}}}_{\mathbf{ck}}^T\right)\in {\mathbb{C}}^{NM\times 1}$, the composite channel and beamvector terms of the signal and interference parts of the above expression are ${\overline{\mathbf{H}}}_{ck}{\overline{\mathbf{w}}}_{ck}=\left({\mathbf{I}}_M\otimes {\overline{\mathbf{w}}}_{ck}^T\right){\overline{\mathbf{h}}}_{ck}$ and ${\overline{\mathbf{H}}}_{ck}{\overline{\mathbf{w}}}_{ci}=\left({\mathbf{I}}_M\otimes {\overline{\mathbf{w}}}_{ci}^T\right){\overline{\mathbf{h}}}_{ck}$, respectively. Thus, we express ${\gamma }_{ck}$ in the canonical quadratic form as:

$${\gamma }_{ck}={\displaystyle \frac{\parallel {\overline{\mathbf{h}}}_{ck}{\parallel }_{{\mathbf{A}}_{ck}}^2}{{\sigma }_{ck}^2+{\parallel {\overline{\mathbf{h}}}_{ck}\parallel }_{{\mathbf{B}}_{ck}}^2}},$$

(4)

where ${\mathbf{A}}_{ck}$ and ${\mathbf{B}}_{ck}$ are $\in {\mathbb{C}}^{NM\times NM}$ Hermitian matrices given by:

$$\begin{array}{ccc}\hfill {\mathbf{A}}_{ck}& =& {\left({\mathbf{I}}_M\otimes {\overline{\mathbf{w}}}_{ck}^T\right)}^H{\mathbf{R}}_{ck}^{\frac{H}{2}}{\mathbf{v}}_k^H{\mathbf{v}}_k{\mathbf{R}}_{ck}^{\frac{1}{2}}\left({\mathbf{I}}_M\otimes {\overline{\mathbf{w}}}_{ck}^T\right),\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill {\mathbf{B}}_{ck}& =& \sum _{i=1,i\ne k}^K{\left({\mathbf{I}}_M\otimes {\overline{\mathbf{w}}}_{ci}^T\right)}^H{\mathbf{R}}_{ck}^{\frac{H}{2}}{\mathbf{v}}_k^H{\mathbf{v}}_k{\mathbf{R}}_{ck}^{\frac{1}{2}}\left({\mathbf{I}}_M\otimes {\overline{\mathbf{w}}}_{ci}^T\right).\hfill \end{array}$$

(6)

Herein, we define the following two special cases for the aforementioned weight matrices.

2.1. Receive Beamforming Used for Covariance Shaping

The aim for this case is to project a transmitted signal in an orthogonal subspace using a receive beamforming scheme. Hence, incorporation of the covariance shaping scheme [20] yields simplified weight matrices given by:

$$\begin{array}{ccc}\hfill {\mathbf{A}}_{ck}& =& {{\Psi }_{ck}^{\frac{1}{2}}\mathbf{w}}_{ck}^{}{\mathbf{w}}_{ck}^H{\Psi }_{ck}^{\frac{H}{2}},\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\mathbf{B}}_{ck}& =& \sum _{i=1,i\ne k}^K{\Psi }_{ck}^{\frac{1}{2}}{\mathbf{w}}_{ci}^{}{\mathbf{w}}_{ci}^H{\Psi }_{ck}^{\frac{H}{2}}\hfill \end{array}$$

(8)

where ${\Psi }_{ck},\forall c,k$ is ${\Psi }_{ck}={\left(({\mathbf{I}}_N\otimes {\mathbf{v}}_{ck}){\Sigma }_{ck}({\mathbf{I}}_N\otimes {\mathbf{v}}_{ck}^H)\right)}^T$, and ${\Sigma }_k$ is the channel covariance matrix obtained from the vectored channel, i.e., $\mathrm{vec}\left({\mathbf{H}}_{ck}\right)\sim \mathcal{CN}(\mathbf{0},{\Sigma }_{ck})$.

2.2. MS having Single Antenna Element

For the case in which the MS is a single antenna device, the weight matrices only include the transmit beamforming vectors, and they are given by:

$$\begin{array}{ccc}\hfill {\mathbf{A}}_{ck}& =& {{\mathit{R}}_{ck}^{\frac{1}{2}}\mathbf{w}}_{ck}^{}{\mathbf{w}}_{ck}^H{\mathit{R}}_{ck}^{\frac{H}{2}},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\mathbf{B}}_{ck}& =& \sum _{i=1,i\ne k}^K{\mathit{R}}_{ck}^{\frac{1}{2}}{\mathbf{w}}_{ci}^{}{\mathbf{w}}_{ci}^H{\mathit{R}}_{ck}^{\frac{H}{2}}.\hfill \end{array}$$

(10)

3. Characterization of Multi-Cell Association Coverage Probability l

In this section, we employ an indefinite quadratic formulation to characterize the coverage probability expression of a given user simultaneously associated with multiple BSs. To this end, we use (3) and affix a predefined threshold level of the kth user associated with the cth cell, denoted as ${\zeta }_{ck}$. Consequently, the outage probability of the kth user simultaneously associated with all C cells is $O_k\left({\left\{{\zeta }_{ck}\right\}}_{c=1}^C\right)$. Inversely, the CCDF representing the coverage probability is ${\overline{O}}_k\left({\left\{{\zeta }_{ck}\right\}}_{c=1}^C\right)$, and it defined as:

$$\begin{array}{ccc}\hfill {\overline{O}}_k\left({\left\{{\zeta }_{ck}\right\}}_{c=1}^C\right)& =& 1-\mathrm{Pr}\left({\gamma }_{1k}<{\zeta }_{1k},\dots ,{\gamma }_{Ck}<{\zeta }_{Ck}\right),\hfill \\ & =& 1-\prod _{c=1}^C{F}_{ck}\left({\zeta }_{ck}\right),\hfill \end{array}$$

(11)

where the independence of all associated links is assumed in the second equality, and $F_{ck}\left({\zeta }_{ck}\right)$ identifies the outage probability of the kth user associated with the cth link. More formally, $F_{ck}\left({\zeta }_{ck}\right)$ is defined as follows:

$$\begin{array}{ccc}\hfill {\mathit{F}}_{ck}\left({\zeta }_{ck}\right)& =& \mathrm{Pr}\left({\gamma }_{ck}<{\zeta }_{ck}\right),\hfill \\ & =& \mathrm{Pr}\left({\sigma }_{ck}^2{\zeta }_{ck}+{\parallel {\overline{\mathbf{h}}}_{ck}\parallel }_{{\mathbf{P}}_{ck}}^2>0\right),\hfill \\ & =& \mathrm{Pr}\left({\sigma }_{ck}^2{\zeta }_{ck}+{\parallel {\tilde{\mathbf{h}}}_{ck}\parallel }_{{\Lambda }_{ck}}^2>0\right),\hfill \\ & =& {\int }_{-\infty }^{\infty }p\left({\tilde{\mathbf{h}}}_{ck}\right)u\left({\sigma }_{ck}^2{\zeta }_{ck}-{\parallel {\tilde{\mathbf{h}}}_{ck}\parallel }_{{\Lambda }_{ck}}^2\right)d{\tilde{\mathbf{h}}}_{ck}\hfill \end{array}$$

(12)

where the second equality is from the property of the sum of the quadratic forms, and the unitary Hermitian matrix is define as ${\mathbf{P}}_{ck}={\mathbf{A}}_{ck}-{\zeta }_{ck}{\mathbf{B}}_{ck}$. In the third equality, we perform the eigenvalue decomposition $\mathbf{P}={\mathbf{U}}_p\Lambda {\mathbf{U}}_p^H$ and do the whitening transformation ${\tilde{\mathbf{h}}}_k={\mathbf{U}}_p^{\frac{H}{2}}{ħ}_k$. Further, ${\Lambda }_{ck}$ is a diagonal matrix with indefinite eigenvalues that are a function of ${\zeta }_{ck}$, ${\mathbf{w}}_{ck}$, and ${\mathbf{v}}_k$. Lastly, the fourth equality is in terms of the unit step function u(.) and probability density function (PDF) of the channel, as follows:

$$\begin{array}{ccc}\hfill u\left(x\right)& =& \frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{e^{x(j\omega +\beta )}}{j\omega +\beta }d\omega ;\beta >0\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill p\left({\tilde{\mathbf{h}}}_{ck}\right)& =& \frac{1}{{\pi }^T}{e}^{-{∥{\tilde{\mathbf{h}}}_{ck}∥}^2}\hfill \end{array}$$

(14)

where $T=NM$.

Now, the CDF is modeled as follows:

$$\begin{array}{ccc}\hfill {\mathit{F}}_{ck}\left({\zeta }_{ck}\right)& =& \frac{1}{2{\pi }^{T+1}}{\int }_{-\infty }^{\infty }\frac{e^{{\sigma }_{ck}^2{\zeta }_{ck}(j\omega +\beta )}}{j\omega +\beta }{\int }_{-\infty }^{\infty }{e}^{-{∥{\tilde{\mathbf{h}}}_{ck}∥}_{\mathbf{I}-{\Lambda }_{ck}}^2}d{\tilde{\mathbf{h}}}_{ck}d\omega \hfill \end{array}$$

(15)

Here, we employ an indefinite quadratic formulation approach [23] to achieve closed-form expressions of $F_{ck}\left({\zeta }_{ck}\right)$ based on the structure of the eigenvalues given in the diagonal matrix ${\Lambda }_{ck}$. Specifically, the two cases are given by:

3.1. Multiplicity of Eigenvalues

If the diagonal matrix ${\Lambda }_{ck}$ has L distinct eigenvalues, and each distinct eigenvalue has a multiplicity of S, then the closed-form expression is obtained as follows:

$${\mathit{F}}_{ck}\left({\zeta }_{ck}\right)=1+\sum _{l=1}^L\sum _{s=1}^S\frac{{\alpha }_{\{s,l\},ck}}{\Gamma \left(s\right)}\frac{1}{|{\lambda }_{l,ck}{|}^s}{e}^{-\frac{{\sigma }_{ck}^2{\zeta }_{ck}}{{\lambda }_{l,ck}}}\mathit{u}\left(\frac{{\zeta }_{ck}}{{\lambda }_{l,ck}}\right)$$

(16)

where ${\alpha }_{\{s,l\},ck}$ is the partial fraction expansion coefficient:

$$\begin{array}{ccc}\hfill {\alpha }_{\{s,l\},ck}& =& \frac{1}{(S-s)!}\underset{(j\omega +\beta )⟶\frac{-1}{{\lambda }_{l,ck}}}{lim}\frac{{\mathit{d}}^{S-s}}{d{(j\omega +\beta )}^{S-s}}\hfill \\ & & \times \left(\frac{1}{(j\omega +\beta )}\prod _{\overline{l}=1,\overline{l}\ne l}^L\frac{{{\lambda }_{\overline{l},ck}}^{\overline{S}}}{{\left((j\omega +\beta )+\frac{1}{{\lambda }_{\overline{l},ck}}\right)}^{\overline{S}}}\right).\hfill \end{array}$$

(17)

Proof. 

The proof is given in Appendix A. □

3.2. Distinct Eigenvalues

For the case of the non-repeating eigenvalues of the diagonal matrix ${\Lambda }_{ck}$, the closed-form expression of $F_{ck}\left({\zeta }_{ck}\right)$ is given by:

$${\mathit{F}}_{ck}\left({\zeta }_{ck}\right)=1-\sum _{t=1}^T\frac{{\lambda }_{t,ck}^{T-1}}{{\prod }_{i=1,i\ne t}^T({\lambda }_{t,ck}-{\lambda }_{i,ck})}{e}^{-\frac{{\sigma }_{ck}^2{\zeta }_{ck}}{{\lambda }_{t,ck}}}\mathit{u}\left(\frac{{\zeta }_{ck}}{{\lambda }_{t,ck}}\right).$$

(18)

Here, ${\lambda }_{tck}$ is tth diagonal element of ${\Lambda }_{ck}$.

Proof. 

The proof is given in Appendix A. □

The summation limit, i.e., $T=NM$, identifies the antenna diversity at the BS and MS. Similarly, the closed-form expressions of the outage probability of the remaining users simultaneously associated with multiple BSs are characterized and furnished in (11).

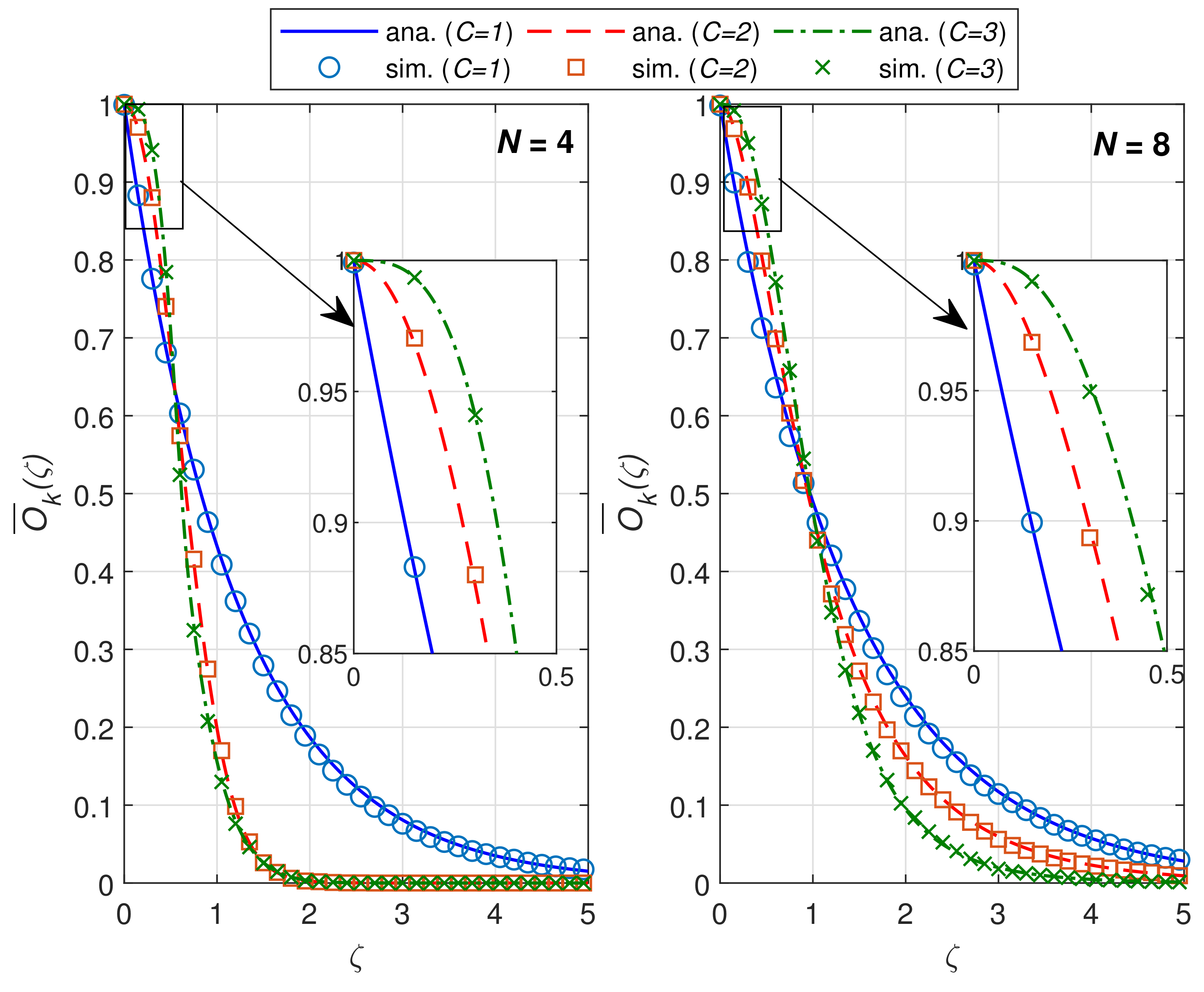
4. Performance Evaluation

This section provides the validation of the derived results using Monte Carlo simulations. In the simulation setup, we (i) consider a MU-MIMO system wherein the coverage probability of kth user, i.e., ${\overline{O}}_k\left(\left\{\zeta \right\}\right)$, is a function of C and N under a network configuration of K = 3 and M = 2; (ii) assume distinct transmit and receive correlation matrices for each user and each association. The matrices are a function of the correlation coefficient ${\rho }_{c;k}$ such that ${\mathbf{R}}_{c;k\{i,j\}}={\rho }_{c;k}^{|i-j|}$ with $0<{\rho }_{c;k}<1,\forall c,k$; (iii) set the noise variance as ${\sigma }_{c;k}^2$ = 10 dBm; and (iv) use transmit and receive beamforming vectors from the Gaussian codebook. Furthermore, the total number of simulation runs is set to 10,000.

In Figure 2, we show the effect of the multi-cell association C on the coverage probability given in (11) against the predefined threshold $\zeta$. Herein, $\zeta$ is considered the same for all associations and links for generalization. It is observed that the coverage probability is dependent on the antenna diversity and, more importantly, on the total number of cell associations C. Specifically, at low threshold values, more cell associations reap better results, whereas, at higher threshold values, conventional single association networks give better results. Moreover, as the number of transmit antennas increases, the range of the threshold values for which a multi-cell association is beneficial also increases. Similarly, in Figure 3, a massive MIMO setup with $N>>K$ is considered. Here, the conventional single association network shows less coverage probability than in the cases of $C=2$ and $C=3$. Both figures indicate that the Monte Carlo simulation agrees strongly with the theoretical results, and hence, validate the proposed work.

In Figure 4, the coverage probability of a single antenna kth user simultaneously associated with two cells and K = 3 is considered. It is observed that an increase in the transmit antenna diversity yields significant performance gains initially, and the rate of increase in the coverage probability saturates at around $N\ge 32$ under the considered setting. This behavior is portrayed in a graphical depiction in Figure 5 at $\zeta =2$. The pattern is apparent at other values of $\zeta$ after the inflection point at $\zeta$ = 0.3.

5. Conclusions

In this paper, the problem of simultaneous multi-cell association is modeled and characterized. It is shown that the performance indexes of a dense multi-tier cellular network can greatly benefit from multi-association, depending on the set SINR threshold level. Multi-cell association is also dependent on the number of transmit antennas, and, as the antenna array size increases, the useful range to incorporate multi-cell association also increases. As an extension of this work, transmit and receive beamforming schemes can be investigated by setting the derived closed-form expressions as an objective function in the optimization problem.