On Some Properties of Signed Cayley Graph Sn
Abstract
:1. Introduction
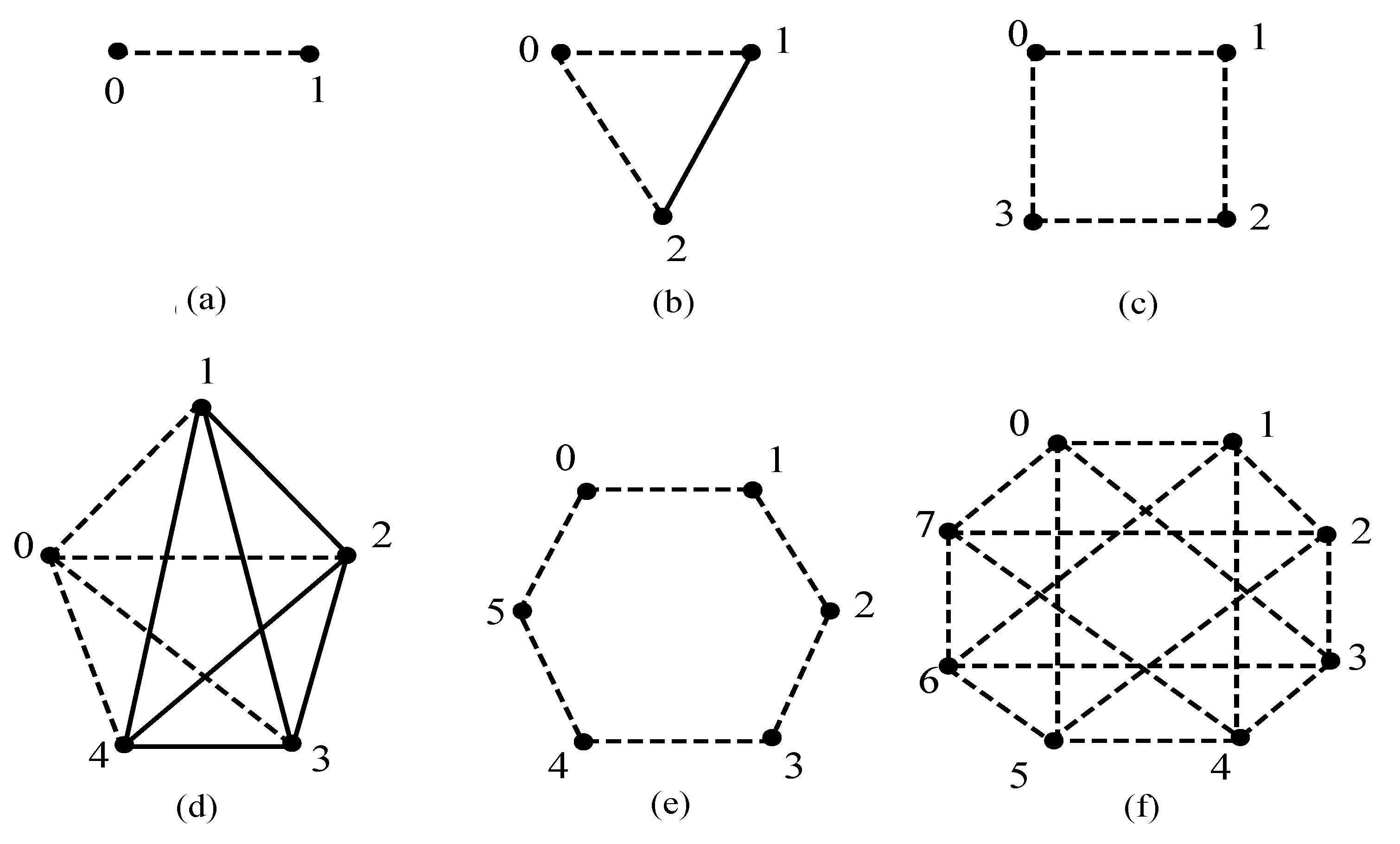
2. Some Properties of
2.1. Balancing in
- and ,
- and ,
- and .
2.2. Clusterability in
2.3. Sign-Compatibility in
2.4. -Consistency of
- Each fundamental cycle relative to T is positive, and
- The two end vertices of any common path between each pair of fundamental cycles relative to T have the same mark.
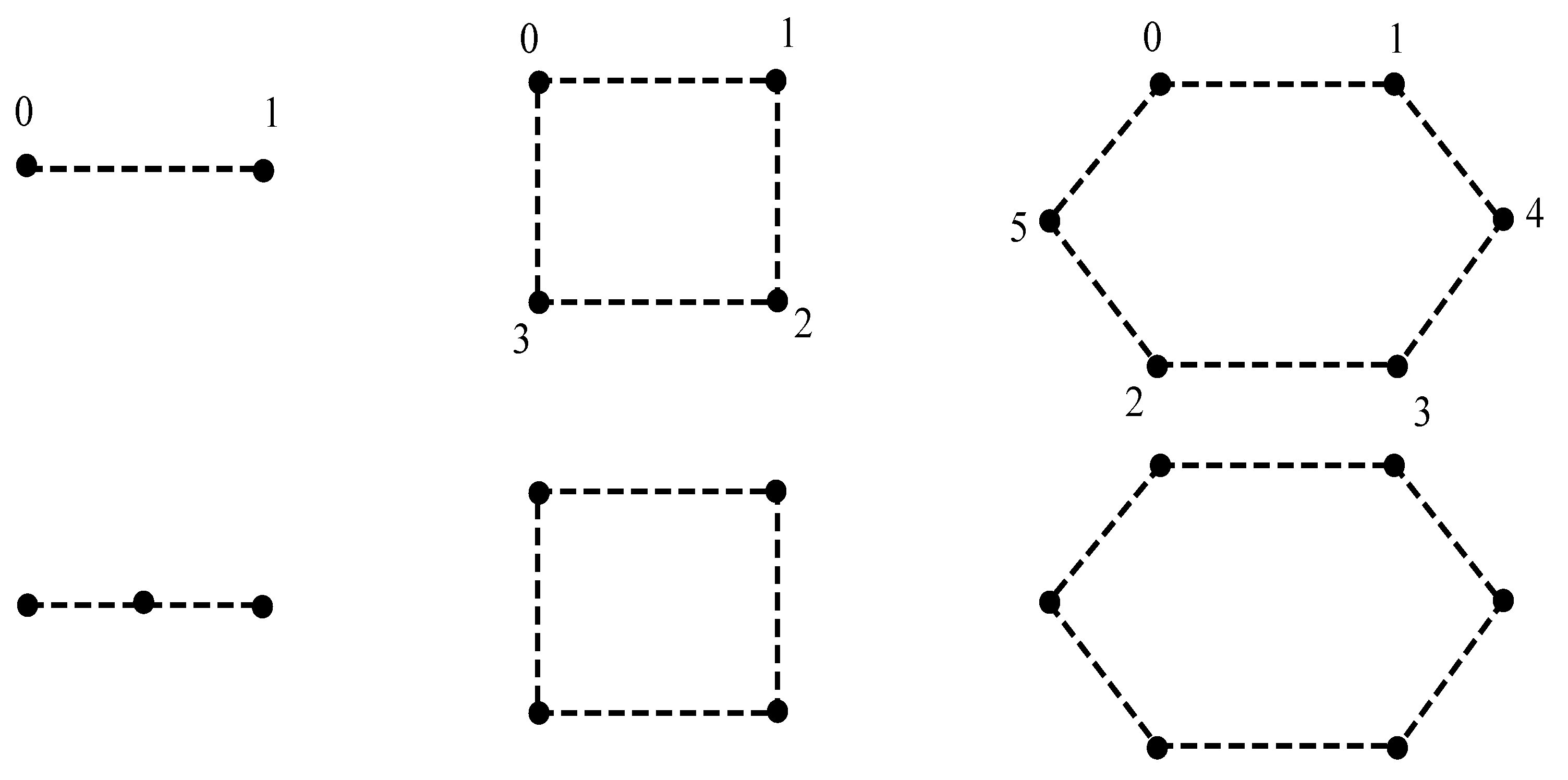
3. Balance in Certain Derived Signed Graphs
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harary, F. Graph Theory; Addison-Wesley Publ. Comp.: Boston, MA, USA, 1969. [Google Scholar]
- West, D.B. Introduction to Graph Theory; Prentice-Hall of India Pvt. Ltd.: Delhi, India, 1996. [Google Scholar]
- Zaslavsky, T. A mathematical bibliography of signed and gain graphs and allied areas. Electron. J. Combin. 2018, DS8. [Google Scholar] [CrossRef]
- Zaslavsky, T. Glossary of signed and gain graphs and allied areas. Electron. J. Combin. 1998, DS9. Available online: https://www.combinatorics.org/files/Surveys/ds9/ds9v1-1998.pdf (accessed on 11 July 2022).
- Harary, F. On the notion of balance of a signed graph. Mich. Math. 1953, 2, 143–146. [Google Scholar] [CrossRef]
- Zaslavsky, T. Signed analogs of bipartite graphs. Discret. Math. 1998, 179, 205–216. [Google Scholar] [CrossRef] [Green Version]
- Sharma, P.; Acharya, M. Balanced signed total graphs of commutative ring. Graphs Comb. 2016, 32, 1585–1597. [Google Scholar] [CrossRef]
- Davis, J.A. Clustering and structural balance in graphs. Hum. Relat. 1967, 20, 181–187. [Google Scholar] [CrossRef]
- Acharya, B.D. A characterization of consistent marked graphs. Natl. Acad. Sci. Lett. 1983, 6, 431–440. [Google Scholar]
- Sinha, D. New Frontiers in the Theory of Signed Graphs. Ph.D. Thesis, University of Delhi, New Delhi, India, 2005. [Google Scholar]
- Sinha, D.; Acharya, M. Characterization of signed graphs whose iteratied line graphs are balanced and S-consistent. Bull. Malays. Math. Sci. Soc. 2016, 39, 297–306. [Google Scholar] [CrossRef]
- Zaslavsky, T. Consistency in the naturally vertex-signed line graph of a signed graph. Bull. Malays. Math. Sci. Soc. 2016, 39, 307–314. [Google Scholar] [CrossRef] [Green Version]
- Behzad, M.; Chartrand, G.T. Line coloring of signed graphs. Elem. Math. 1969, 24, 49–52. [Google Scholar]
- Gill, M.K. Contribution to Some Topics in Graph Theory and It’s Applications. Ph.D. Thesis, Indian Institute of Technology, Bombay, India, 1969. [Google Scholar]
- Acharya, M.; Sinha, D. Common-edge signed graphs. AKCE Int. J. Graphs Comb. 2006, 3, 115–130. [Google Scholar]
- Sinha, D.; Dhama, A. On The Unitary Cayley Ring Signed Graphs Sn⊕. J. Interconnect. Netw. 2013, 14, 1350020. [Google Scholar] [CrossRef]
- Evans, A.B.; Fricke, G.H.; Maneri, C.C.; McKee, T.A.; Perkel, M. Representations of graphs modulo n. J. Graph Theory 1994, 18, 801–815. [Google Scholar] [CrossRef]
- Sinha, D.; Dhama, A. Unitary Cayley Meet Signed Graphs. Electron. Notes Discret. Math. 2017, 63, 425–434. [Google Scholar] [CrossRef]
- Sinha, D.; Garg, P. On the unitary Cayley signed graphs. Electron. J. Comb. 2011, 18, P229. [Google Scholar] [CrossRef] [Green Version]
- Dejter, I.J.; Giudici, R.E. On unitary Cayley graphs. J. Comb. Math. Comb. Comput. 1995, 18, 121–124. [Google Scholar]
- Sampathkumar, E. Point-signed and line-signed graphs. Natl. Acad. Sci. Lett. 1984, 7, 91–93. [Google Scholar]
- Sinha, D.; Dhama, A. Sign-Compatibility of common-edge signed graphs and 2-path signed graphs. Graph Theory Notes N. Y. 2013, 65, 55–61. [Google Scholar]
- Acharya, M.; Sinha, D. Characterizations of line signed graphs. Natl. Acad. Sci. Lett. 2005, 28, 31–34. [Google Scholar]
- Acharya, M. ×-line signed graph of a signed graph. J. Comb. Math. Comb. Comput. 2009, 69, 103–111. [Google Scholar] [CrossRef]
- Hoede, C. A characterization of consistent marked graphs. Graph Theory 1992, 16, 17–23. [Google Scholar] [CrossRef] [Green Version]
- Acharya, M.; Sinha, D. A characterization of signed graphs whose line signed graphs and jump signed graphs are switching equivalent. Graph Theory Notes N. Y. 2003, 44, 30–34. [Google Scholar]
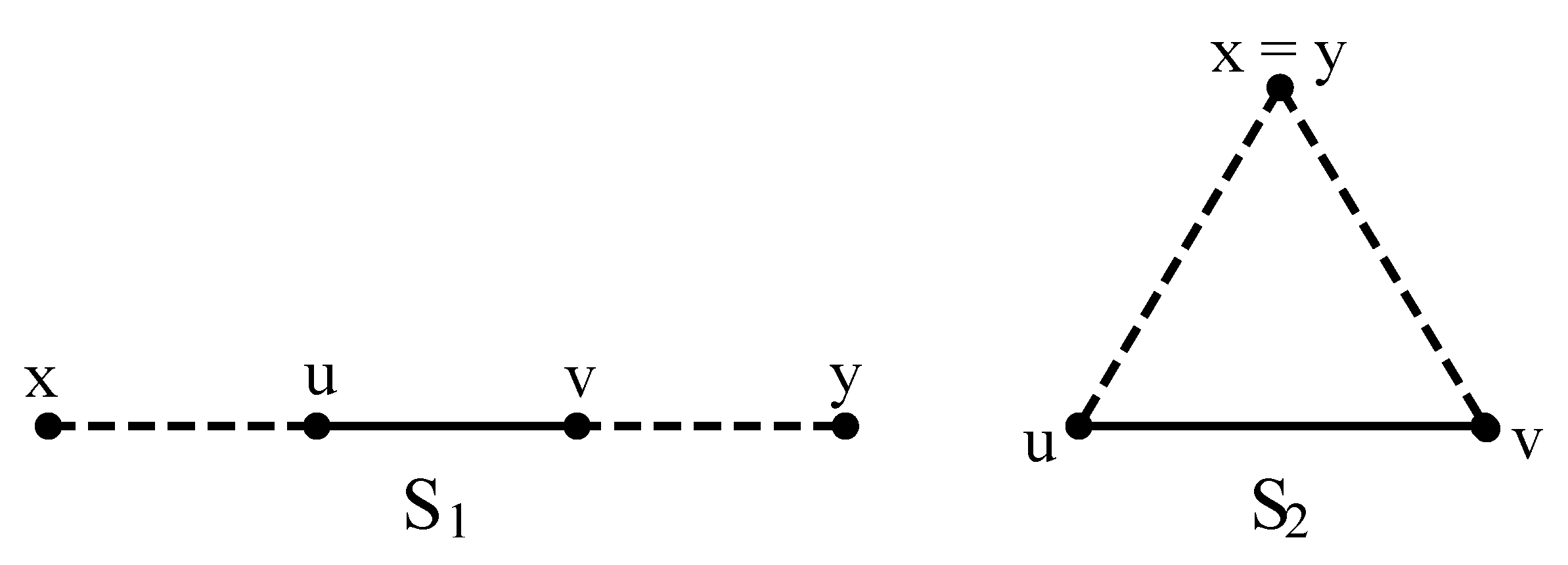

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinha, D.; Wardak, O.; Dhama, A. On Some Properties of Signed Cayley Graph Sn. Mathematics 2022, 10, 2633. https://doi.org/10.3390/math10152633
Sinha D, Wardak O, Dhama A. On Some Properties of Signed Cayley Graph Sn. Mathematics. 2022; 10(15):2633. https://doi.org/10.3390/math10152633
Chicago/Turabian StyleSinha, Deepa, Obaidullah Wardak, and Ayushi Dhama. 2022. "On Some Properties of Signed Cayley Graph Sn" Mathematics 10, no. 15: 2633. https://doi.org/10.3390/math10152633
APA StyleSinha, D., Wardak, O., & Dhama, A. (2022). On Some Properties of Signed Cayley Graph Sn. Mathematics, 10(15), 2633. https://doi.org/10.3390/math10152633






