New Localized Structure for (2+1) Dimensional Boussinesq-Kadomtsev-Petviashvili Equation
Abstract
:1. Introduction
2. Variable Separation Approach for Boussinesq-Kadomtsev-Petviashvili Equation
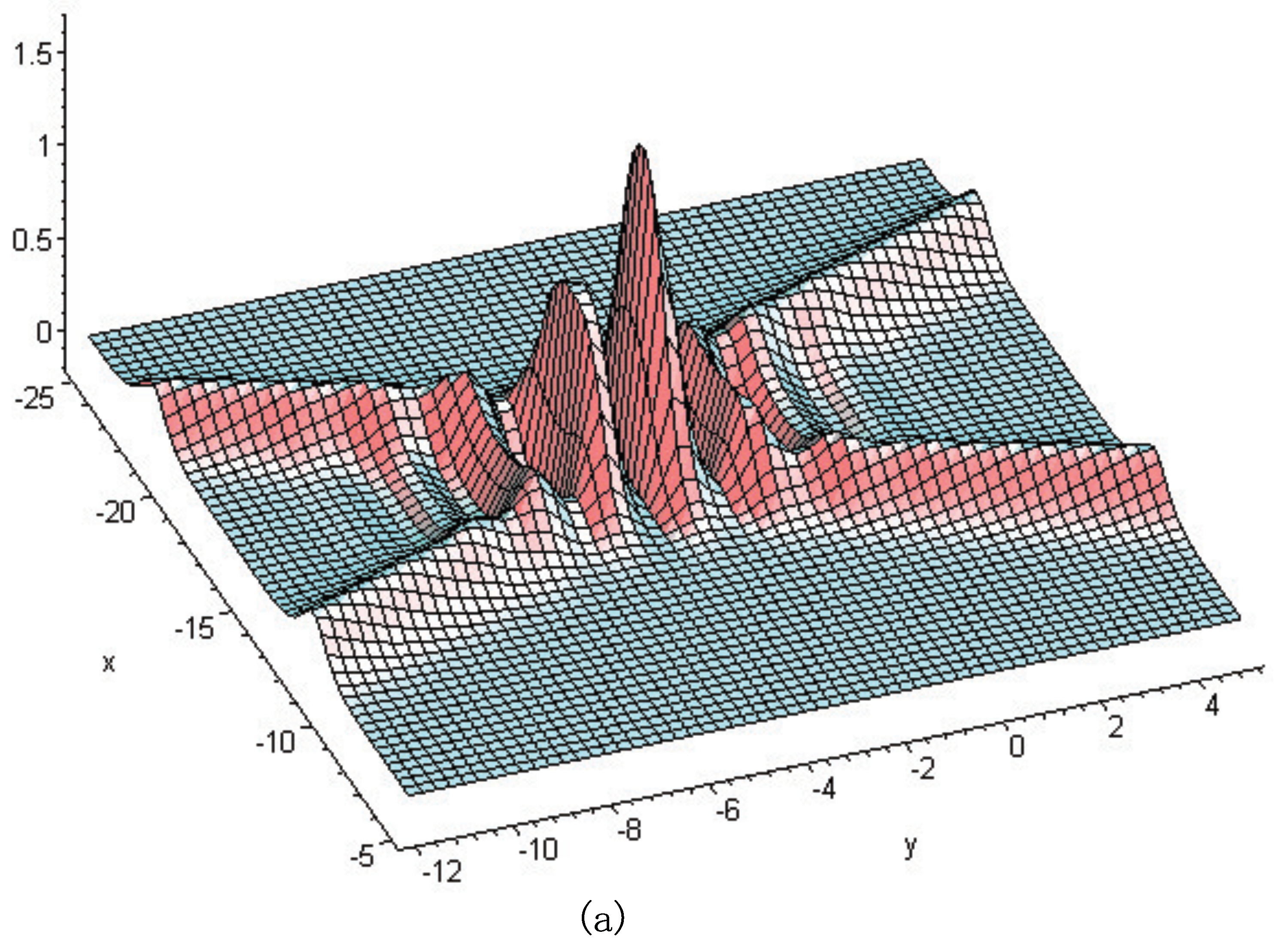
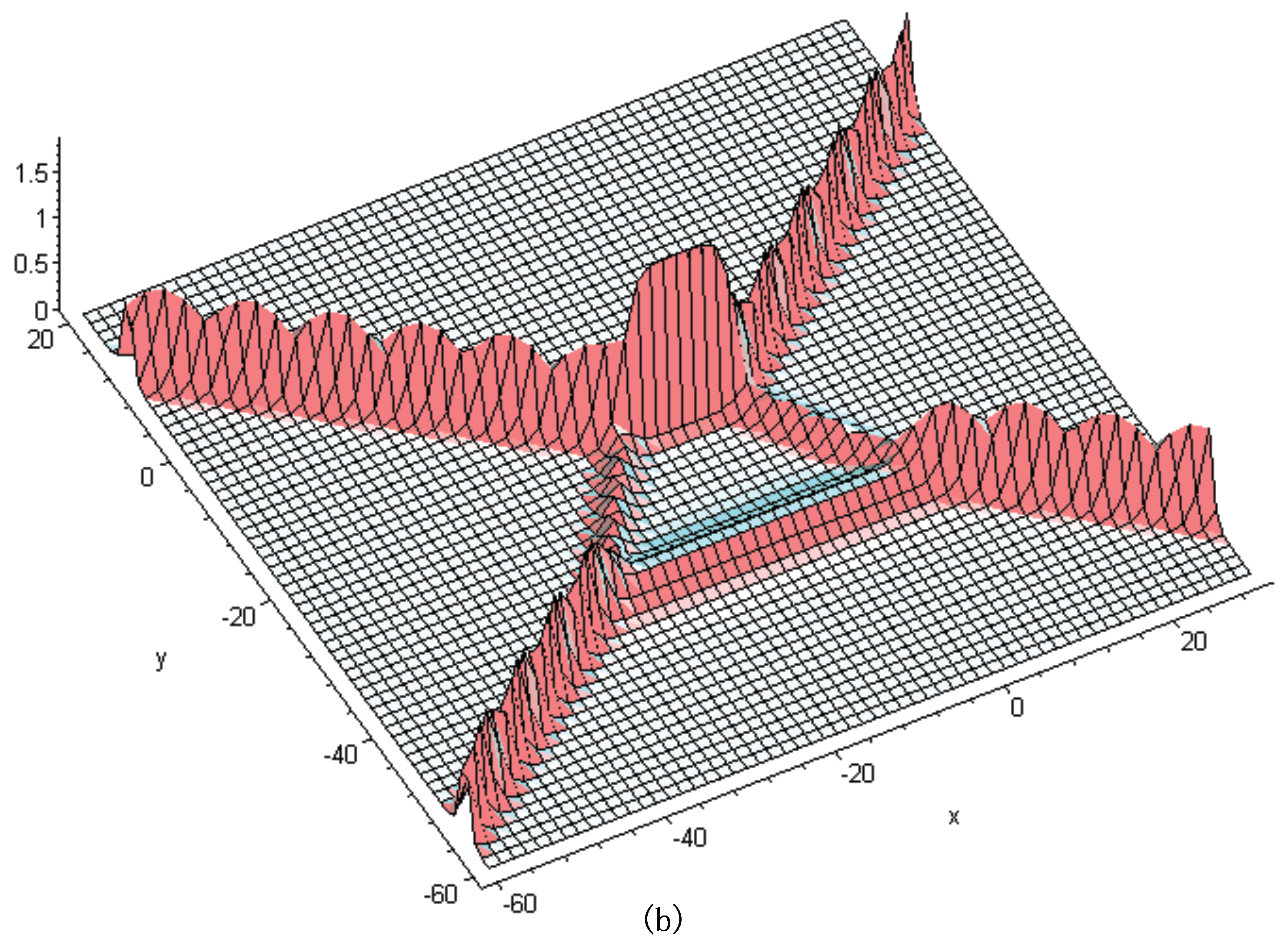
3. Soliton Excitations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yemélé, D.; Kenmogné, F. Compact envelope dark solitary wave in a discrete nonlinear electrical transmission line. Phys. Lett. A 2009, 373, 3801–3809. [Google Scholar] [CrossRef]
- Currie, J.F.; Krumhansl, J.A.; Bishop, A.R.; Trullinger, S.E. Statistical mechanics of one-dimensional solitary-wave-bearing scalar fields: Exact results and ideal-gas phenomenology. Phys. Rev. B 1980, 22, 477–496. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Baleanu, S.S.D.; Zafar, A. Specific wave structures of a fifth-order nonlinear water wave equation. J. Ocean. Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Baleanu, D.; Salahshour, S.; Akinyemi, L. Optical solitons of a high-order nonlinear Schrödinger equation involving nonlinear dispersions and Kerr effect. Opt. Quant. Electron. 2022, 54, 177. [Google Scholar] [CrossRef]
- Hosseini, K.; Matinfar, M.; Mirzazadeh, M. Soliton Solutions of High-Order Nonlinear Schrödinger Equations with Different Laws of Nonlinearities. Regul. Chaot. Dyn. 2021, 26, 105–112. [Google Scholar] [CrossRef]
- Rasheed, N.M.; Al-Amr, M.O.; Az-Zo’bi, E.A.; Tashtoush, M.A.; Akinyemi, L. Stable Optical Solitons for the Higher-Order Non-Kerr NLSE via the Modified Simple Equation Method. Mathematics 2021, 9, 1986. [Google Scholar] [CrossRef]
- Sun, J.-Q.; Qin, M.-Z. Multi-symplectic methods for the coupled 1D nonlinear Schrödinger system. Comput. Phys. Commun. 2003, 155, 221–235. [Google Scholar] [CrossRef]
- Hasegawa, A.; Matsumoto, M. Optical Solitons in Fibers; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Yang, J. Multisolitons perturbation theory for the Manakov equations and its applications to nonlinear optics. Phys. Rev. E 1999, 59, 2393–2405. [Google Scholar] [CrossRef] [Green Version]
- Ablowitz, M.J.; Segur, H. Solitions and the Inverse Scattering Transform; SIAM: Philadelphia, PA, USA, 1981. [Google Scholar]
- Hirota, R. Exact n-soliton solutions of the wave equation of long waves in shallow-water and in nonlinear lattices. J. Math. Phys. 1973, 14, 810–814. [Google Scholar] [CrossRef]
- Yan, Z.Y. Abundant families of Jacobi elliptic function solutions of the (2+1)-dimensional integrable Davey–Stewartson-type equation via a new method. Chaos Solitons Fract. 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Lou, S.Y. On the coherent structures of Nizhnik-Novikov- Veselov equation. Phys. Lett. A 2000, 277, 94–100. [Google Scholar] [CrossRef]
- Tang, X.Y.; Chen, C.L.; Lou, S.Y. Localized solutions with chaotic and fractal behaviours in a (2+1)-dimensional dispersive long-wave system. J. Phys. A Math. Gen. 2002, 35, L293–L301. [Google Scholar] [CrossRef]
- Tang, X.Y.; Lou, S.Y.; Zhang, Y. Localized excitations in (2+1)-dimensional systems. Phys. Rev. E 2002, 66, 046601–046604. [Google Scholar] [CrossRef]
- Lou, S.Y. (2+1)-dimensional compacton solutions with and without completely elastic interaction properties. J. Phys. A Math. Gen. 2002, 35, 10619–10628. [Google Scholar] [CrossRef]
- Tang, X.Y.; Lou, S.Y. Extended multilinear variable separation approach and multivalued localized excitations for some (2+1)-dimensional integrable systems. J. Math. Phys. 2003, 44, 4000–4025. [Google Scholar] [CrossRef]
- Date, E.; Jimbo, M.; Kashiwara, M.; Miwa, T. Transformation groups for soliton equations. IV. A new hierarchy of soliton equations of KP type. Phys. D 1982, 4, 343–365. [Google Scholar] [CrossRef]
- Ma, H.C.; Wang, Y.; Qin, Z.Y. New exact complex traveling wave solutions for (2+1)-dimensional BKP equation. Appl. Math. Comput. 2009, 208, 564–568. [Google Scholar] [CrossRef]
- Xie, Y.G.; Zhou, B.W.; Tang, S.Q. Bifurcations of travelling wave solutions for the generalized (2+1)-dimensional Boussinesq–Kadomtsev–Petviashvili equation. Appl. Math. Comput. 2010, 217, 2433–2447. [Google Scholar] [CrossRef]
- Zhang, H.Q. A note on exact complex travelling wave solutions for (2+1)-dimensional B-type Kadomtsev–Petviashvili equation. Appl. Math. Comput. 2010, 216, 2771–2777. [Google Scholar] [CrossRef]
- Cheng, H.J.; Hu, Y.X. Exact solutions of the generalized (2+1)-dimensional BKP equation by the -expansion method and the first integral method. Mathematics 2017, 2, 562–579. [Google Scholar] [CrossRef]
- Akinyemi, L.; Şenol, M.; Az-Zo’bi, E.; Veeresha, P.; Akpan, U. Novel soliton solutions of four sets of generalized (2+1)-dimensional Boussinesq–Kadomtsev–Petviashvili-like equations. Mod. Phys. Lett. B 2022, 36, 2150530. [Google Scholar] [CrossRef]
- Ma, W.; Qin, Z.; Lü, X. Lump solutions to dimensionally reduced p-gKP and p-gBKP equations. Nonlinear Dyn. 2016, 84, 923–931. [Google Scholar] [CrossRef]
- Ma, W. Lump solutions to the Kadomtsev-Petviashviliequation. Phys. Lett. A 2015, 379, 1975–1978. [Google Scholar] [CrossRef]
- Peng, W.; Tian, S.; Zhang, T. Analysis on lump, lumpoff and rogue waves with predictability to the (2+1)-dimensional B-type Kadomtsev-Petviashvili equation. Phys. Lett. A 2018, 382, 2701–2708. [Google Scholar] [CrossRef]
- Lou, S.Y. Dromions, dromion lattices, breathers and instantons of the Davey-Stevvartson equation. Phys. Scr. 2002, 65, 7–12. [Google Scholar] [CrossRef]
- Mu, G.; Qin, Z.Y.; Grimshaw, R. Dynamics of Rogue Waves on a Multisoliton Background in a Vector Nonlinear Schrödinger Equation. SIAM J. Appl. Math. 2015, 75, 1–20. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, G.; Zhu, Y.; Feng, T. New Localized Structure for (2+1) Dimensional Boussinesq-Kadomtsev-Petviashvili Equation. Mathematics 2022, 10, 2634. https://doi.org/10.3390/math10152634
Mu G, Zhu Y, Feng T. New Localized Structure for (2+1) Dimensional Boussinesq-Kadomtsev-Petviashvili Equation. Mathematics. 2022; 10(15):2634. https://doi.org/10.3390/math10152634
Chicago/Turabian StyleMu, Gui, Yan Zhu, and Tingfu Feng. 2022. "New Localized Structure for (2+1) Dimensional Boussinesq-Kadomtsev-Petviashvili Equation" Mathematics 10, no. 15: 2634. https://doi.org/10.3390/math10152634