Sparse Index Tracking Portfolio with Sector Neutrality

Abstract

As a popular passive investment strategy, a sparse index tracking strategy has advantages over a full index replication strategy because of higher liquidity and lower transaction costs. Sparsity and nonnegativity constraints are usually assumed in the construction of portfolios in sparse index tracking. However, none of the existing studies considered sector risk exposure of the portfolios that prices of stocks in one sector may fall at the same time due to sudden changes in policy or unexpected events that may affect the whole sector. Therefore, sector neutrality appeals to be critical when building a sparse index tracking portfolio if not using full replication. The statistical approach to sparse index tracking is a constrained variable selection problem. However, the constrained variable selection procedure using Lasso fails to produce a sparse portfolio under sector neutrality constraints. In this paper, we propose a high-dimensional constrained variable selection method using TLP for building index tracking portfolios under sparsity, sector neutrality and nonnegativity constraints. Selection consistency is established for the proposed method, and the asymptotic distribution is obtained for the sparse portfolio weights estimator. We also develop an efficient iteration algorithm for the weight estimation. We examine the performance of the proposed methodology through simulations and an application to the CSI 300 index of China. The results demonstrate the validity and advantages of our methodology.

1. Introduction

Despite various types and goals, portfolio managing strategies can be classified into two main groups according to styles, namely, active and passive strategies. The former ones attempt to beat the market by exploiting market inefficiency, whereas the latter ones prefer to follow the market. However, the majority of actively managed funds do not outperform the market in the long run [1]. On the contrary, passive funds provide market-level profits without taking an active risk. Passive funds become more popular in recent years. U.S. equity index fund assets have surpassed the assets of their actively managed counterparts for the first time, according to Morningstar’s latest fund flows report. This trend is also growing in other parts of the world.

The most commonly used passive investing strategy is index tracking, which aims to mimic the performance of a specified basket of underlying assets. Without exposure to active risk, an index tracking fund needs to follow the targeting index as closely as possible. The performance of an index tracker is measured by tracking error [2], which is defined as the divergence between the index tracker and the targeting index. Tracking error gives investors a sense of how “tight” the index tracker goes after the index. Smaller tracking error means less exposure to active risk.

A straightforward method to construct an index tracking portfolio is full replication, which is to buy appropriate quantities of all assets composing the index. Theoretically, the performance of a full replication portfolio should match that of the targeting index perfectly. However, full replication portfolios often incur higher transaction and administration costs than portfolios of relatively fewer stocks. An alternative to full replication is sparse index tracking, which is to replicate the performance of an index by holding a representative sample of the securities in the index [3,4,5]. The challenge of building a sparse index tracking portfolio lies in the trade-off between transaction costs and tracking efficiency. A sparse index tracking portfolio manager attempts to hold as few securities as possible to reduce the transaction costs and eliminate potential illiquid stocks and curb the tracking error to maintain tracking efficiency at the same time. Sparse index portfolios are often constructed via portfolio optimization. Such an algorithm-driven portfolio aims to minimize the tracking error in both training samples and testing samples. Specifically, index tracking optimization needs to incorporate certain constraints, such as no short selling and balance among industrial sectors. The latter constraint aims at taming sector risk of sparse portfolios that a set of factors particular to a sector drags down the sector’s overall performance in financial risk management. Upon the occurrence of events affecting the entire sector, such as sudden policy changes or technology innovation, the stock prices of many of the companies in the same sector may undergo drastic changes simultaneously. Unbalanced allocation of assets among different sectors can result in the failure of index tracking for a portfolio. In Table 1, we present several periods when sector risk appears for China CSI300 Index. The table shows the performance of the index, the sector gainers and losers during the selected period. The large divergence between the index and the gainers or losers indicates that inappropriate exposure to sector risk can inflate the tracking error and undermine the portfolio performance. To manage the sector risk with index tracking, it is necessary to build a sector-neutral portfolio in which the total weight of stocks within each sector remains the same as that in the index. In particular, a sector-neutral strategy means not to overweight or underweight any given sector compared to its weight in the index, so as to ensure the performance of the portfolio will be stable and accordingly will be not affected by style switch in the market. Therefore, a sector-neutral portfolio can closely fit and help track the performance of a benchmark index, and essentially it turns out to be a passive investment strategy.

Table 1. The periods with sector risk for CSI300 index from 2014 to 2018.

Period	CSI300	Gainer		Loser
October 2018–November 2018	−4.16%	Financials	2.50%	Consumer Staple	−13.18%
February 2018–March 2018	−5.23%	Information	6.44%	Financials	−9.17%
June 2017–August 2017	9.75%	Consumer Staple	17.51%	Utilities	−3.77%
October 2015–December 2015	8.19%	Information	26.40%	Energy	3.18%
November 2012–January 2013	17.01%	Financials	30.92%	Consumer Staple	−5.94%

To overcome the drawbacks of full replication and accommodate the sector risk in traditional sparse portfolios, we propose a novel method to construct sparse index-tracking portfolios, assuming that short positions are forbidden and no cash is allowed in the constructed portfolios. Finally, we formulate the sparse index tracking problem with sector neutrality as the minimization of the tracking error under constraints of nonnegativity, sparsity, and sector neutrality.

2. Literature Review

There is a vast amount of research on quantitative methods for index tracking. Ref. [6] studied the traditional Markowitz asset allocation problem and proposed an algorithm for designing a sparse index fund. This algorithm yields a locally optimal index portfolio with a fixed number of securities. Ref. [7] investigated the relation between error measures in statistical tracking and asset allocation restrictions expressed as admissible weight ranges. It addressed the relationship between tracking errors caused by active portfolio management and given tactical asset allocation ranges. Ref. [8] imposed the no-short-sale constraint on the Markowitz mean-variance optimization and gave an insightful explanation and demonstration of why the constraints help. Ref. [9] considered maximizing the index fund’s tracking accuracy by rebalancing the composition of the index fund’s tracking portfolio in response to new market information and cash deposits and withdrawals from investors. Ref. [10] investigated the inclusion of portfolio liquidity constraints for the construction of index tracking portfolios and proposed two liquidity modelling approaches for index tracking.

Many statistical regularization methods have been applied to the index tracking problem recently. In general, a sparse index tracking portfolio can be constructed via variable selection, which removes non-informative features and yields sparse models, especially for the high-dimensional data, and consequently facilitates inference, interpretability and prediction. Ref. [11] formulated sparse index tracking problem as an optimization problem that minimizes the tracking error, subject to the number of selected assets less than or equal to a preset threshold. Ref. [12] formulated the index tracking as a regression problem whose objective was to minimise the tracking error and adds a $L_0$ penalty on weights corresponding to the amount to invest in each stock, then solved the optimization problem with stochastic neural networks. Ref. [13] investigated the applications of sparse auto-encoder deep-learning architectures with $L_1$ regularization in selecting representative stocks from the index constituents. Ref. [14] analyzed the constraints effect on covariance regularization for index tracking, and developed an $L_1$ and $L_2$ norm constrained minimum-variance portfolio. Ref. [15] reformulated the classical Markowitz mean-variance framework as a constrained least-squares regression problem and added a penalty function to construct a sparse index tracking portfolio. They emphasized that adding an $L_1$ penalty on weights to the objective function may bring several advantages, including promoting sparsity and stabilizing the out-of-sample performance. Ref. [16] offered deep mathematical insights into the utility approximations with the gross-exposure constraint and gave a theoretical justification for the empirical results by [8]. These approaches consist in solving index tracking problems through constraining portfolio norms, for example, the $L_1$ norm as implied in Lasso and the $L_2$ norm as imposed in ridge regression. Besides, many other variable selection methods introduced in various fields can be applied to the index tracking problems as well. Truncated $L_1$ penalty (TLP) [17] has advantages over Lasso [18] in that Lasso gives biased parameter estimates and possibly inconsistent variable selection. Intuitively, unlike Lasso which penalizes all variables, TLP does not penalize variables of large values, and thus enables us to incorporate more complicated constraints into optimization as in Section 3. We asserted in Section 1 that the novelty of our method lies in the construction of a sparse index tracking portfolio with exposure to sector risk. Sector neutrality can be achieved by constrained variable selection procedures. The constrained Lasso [19] introduced additional equality and inequality constraints to the traditional Lasso method for asset allocation, which generalized the work of [16]. However, with the constrained Lasso, the nonnegativity and sector neutrality constraints nullify the Lasso penalty and cause the method fails to give sparsity. More details will be discussed further in Section 3. Ref. [20] followed and added a ridge term into the objective function in constrained Lasso so that it may work in a high-dimensional case where sparsity is necessary.

Computationally solving a constrained variable selection problem is not an easy task, especially when complex penalty functions and constraints are used. The alternating direction method of multipliers (ADMM) algorithm [21] is an efficient and scalable optimization algorithm for convex optimization. Ref. [22] exploited the structure of distributed optimization framework and illustrated this framework via applications such as $L_1$ mean and variance filtering. The idea of the ADMM algorithm is to break the original optimization into iterations of easier problems. However, optimization with the TLP term is not a convex problem. To solve this nonconvex problem, ref. [17] presented an efficient algorithm based on a difference of convex (DC) decomposition [23] and a coordinate descent (CD) algorithm [24,25]. The DC method decomposes the nonconvex constraint into a difference of two convex functions to produce a sequence of approximating convex constraints. Thus the original nonconvex optimization is broken down into a series of convex optimization problems. In minimization of a multivariate function, the CD algorithm iteratively minimizes the objective function with respect to each coordinate direction until convergence. This is an efficient algorithm for large-scale convex optimization problems.

In this paper, we propose a novel method to solve the sparse index tracking problem with sector neutrality. An error bound for variable selection is obtained for the method, and then variable selection consistency and asymptotic distribution are established for effective inference. An efficient minimization algorithm is developed by combining the ADMM algorithm, DC decomposition and CD algorithm. The new procedure is tested via numerical simulations under different data generation settings. An application is given to index tracking in the Chinese stock market. Both the numerical experiments and application confirm the good performance of our method in general.

This paper is organized as follows. Section 3 formulates the sparse index tracking with sector neutrality as an optimization problem under constraints. Section 4 discusses the theory for high-dimensional constrained variable selection. Section 5 describes the algorithm for the optimization problem. Section 6 presents the results of the simulated experiments. Section 7 shows the application of the proposed method to index tracking portfolio construction. Summary and discussion are given in Section 8. Technical proofs and some tables are relegated to the Appendix A.

3. Methodology

From a statistical point of view, index tracking is a linear regression problem:

$$\begin{array}{c}\hfill \mathit{Y}=\mathit{X}\mathbf{\beta }+\mathbf{ϵ},\end{array}$$

(1)

with the response $\mathit{Y}\in {\mathbb{R}}^{n\times 1}$ and the covariates $\mathit{X}\in {\mathbb{R}}^{n\times p}$, where n is the sample size and p is the dimension of covariates. $\mathbf{\beta }\in {\mathbb{R}}^p$ is the parameter of covariates $\mathit{X}$, and $\mathbf{ϵ}$ is the error term, we assume $\mathbf{ϵ}\sim N(0,{\sigma }^{2}I)$, where I is the identity matrix. In index tracking, $\mathit{Y}$ and $\mathit{X}$ represent the returns of an index and its constituents, respectively, and $\mathbf{\beta }$ is the weight vector of the index’s constituents.

Suppose that there are q sectors. We rewrite the covariates $\mathit{X}=({\mathit{X}}_1,\cdots ,{\mathit{X}}_q)$, where ${\mathit{X}}_i=({\mathit{X}}_{i,1},\cdots ,{\mathit{X}}_{i,g_i})$ are the covariates in the i-th sector, and $g_i$ is the number of stocks in the i-th sector, $i\in \{1,\cdots ,q\}$. Accordingly, we write $\mathbf{\beta }={({\mathbf{\beta }}_1^{\top },\cdots ,{\mathbf{\beta }}_q^{\top })}^{\top }$, and ${\mathbf{\beta }}_i={({\beta }_{i,1},\cdots ,{\beta }_{i,g_i})}^{\top }$.

For sparse index tracking, three categories of constraints are under consideration:

(1)

the sparsity constraint within sector: ${\sum }_{i=1}^q{\sum }_{j=1}^{g_i}J\left({\beta }_{i,j}\right)\le K$;

(2)

the sector neutrality constraint: ${\sum }_{j=1}^{g_i}{\beta }_{i,j}={\omega }_i$, for $i\in \{1,\cdots ,q\}$;

(3)

the nonnegativity constraint: ${\beta }_{i,j}\ge 0$, for $i\in \{1,\cdots ,q\},j\in \{1,\cdots ,g_i\}$.

Here ${\omega }_i$ are constants satisfying ${\sum }_{i=1}^q{\omega }_i=1$. Each ${\omega }_i$ is the sum of the original constituent weights in the i-th sector. These original non-sparse weights are pre-specified by portfolio managers and hence are known in advance from the definition of the index.

The penalty function $J(·)$ needs to be chosen carefully. The Lasso penalty is widely used in variable selection problems because of its ease of computation. Nevertheless, it turns out that the Lasso penalty fails to yield a sparse portfolio under sector neutrality and nonnegativity constraints for index tracking, as explained below. Under the nonnegativity constraint, the Lasso penalty ${\sum }_{i=1}^q{\sum }_{j=1}^{g_i}\left|{\beta }_{i,j}\right|$ becomes ${\sum }_{i=1}^q{\sum }_{j=1}^{g_i}{\beta }_{i,j}$, while the sector neutrality constraint makes this sum a constant: ${\sum }_{i=1}^q{\sum }_{j=1}^{g_i}{\beta }_{i,j}={\sum }_{i=1}^q{\omega }_i=1$. Therefore, the Lasso penalty becomes invalid and gives no penalty on the portfolio size.

To solve this problem, we take $J(·)$ to be the truncated $L_1$ penalty (TLP) function [17], which can achieve sparse portfolio selection under the sector neutrality and nonnegativity constraints. TLP can be thought of as a truncated version of the $L_1$ penalty approximating the $L_0$-function. As a piecewise linear function, TLP permits efficient computation and adaptive variable selection. TLP is defined as

$$J\left(\right|z\left|\right)=min(\frac{\left|z\right|}{\tau },1),$$

where $\tau >0$ is a tuning parameter controlling the degree of approximation. With the TLP function, the estimation of coefficients $\mathbf{\beta }$ is obtained by minimization:

$$\begin{array}{c}\hfill \underset{\mathbf{\beta }}{min}\mathrm{TE}\left(\mathbf{\beta }\right)+\lambda \sum _{i=1}^q\sum _{j=1}^{g_i}J\left(\right|{\beta }_{i,j}\left|\right).\end{array}$$

(2)

where $\mathrm{TE}\left(\mathbf{\beta }\right)$ is the tracking error. This is the dual problem corresponding to the constrained primal problem

$$\underset{\mathbf{\beta }}{min}\mathrm{TE}\left(\mathbf{\beta }\right),\mathrm{subject}\mathrm{to}\sum _{i=1}^q\sum _{j=1}^{g_i}J\left(\right|{\beta }_{i,j}\left|\right)\le K.$$

The dual problem is not equivalent to the constrained primal problem in general. However, with the TLP as the penalty function, the two optimization problems are equivalent [17]. In the remainder of the paper, we will consider only the unconstrained dual problem for its computational advantages. Minimization of (2) reduces to a general weighted Lasso problem, which can be solved by many efficient algorithms [18,26,27].

The tracking error $\mathrm{TE}\left(\mathbf{\beta }\right)$ can assume many forms [28], for example, the empirical tracking error (ETE), defined as

$$\begin{array}{c}\hfill \mathrm{TE}\left(\mathbf{\beta }\right)=\frac{1}{n}{\parallel \mathit{Y}\mathbf{y}-\mathit{X}\mathbf{\beta }\parallel }_2^2.\end{array}$$

(3)

With TLP and the empirical tracking error, we can rewrite (2) as

$$\begin{array}{c}\hfill \begin{array}{ccc}\underset{\mathbf{\beta }}{min}\hfill & & f\left(\mathbf{\beta }\right)=n^{-1}{\parallel \mathit{Y}-\mathit{X}\mathbf{\beta }\parallel }_2^2+\lambda \sum _{i=1}^q\sum _{j=1}^{g_i}min\{\frac{|{\beta }_{i,j}|}{\tau },1\},\hfill \\ \mathrm{subject}\mathrm{to}:\hfill & & \\ & & \sum _{j=1}^{g_i}{\beta }_{i,j}={\omega }_i,i\in \{1,\cdots ,q\},\hfill \\ & & {\beta }_{i,j}\ge 0,i\in \{1,\cdots ,q\},j\in \{1,\cdots ,g_i\}.\hfill \end{array}\end{array}$$

(4)

4. Theory

Let us first introduce some notations. The true value of $\mathbf{\beta }$ is denoted by ${\mathbf{\beta }}^{*}$. Without loss of generality, we assume that the last component ${\beta }_{i,g_i}^{*}$ of ${\mathbf{\beta }}_i^{*}$ is nonzero for $i\in \{1,\cdots ,q\}$. By virtue of the sector neutrality constraint, we can solve for the last component ${\beta }_{i,g_i}$ in each sector:

$${\beta }_{i,g_i}=w_i-\sum _{j=1}^{g_i-1}{\beta }_{i,j},i\in \{1,\cdots ,q\}.$$

(5)

We write

$$\begin{array}{cc}\hfill {\mathbf{\beta }}_{-q}& ={({\beta }_{1,1},\cdots ,{\beta }_{1,g_1-1},\cdots ,{\beta }_{q,1},\cdots ,{\beta }_{q,g_q-1})}^{\top },\hfill \\ \hfill {\mathit{X}}_{-q}& =(X_{1,1},\cdots ,X_{1,g_1-1},\cdots ,X_{q,1},\cdots ,X_{q,g_q-1}),\hfill \\ \hfill {\mathit{X}}_G& =(X_{1,1}-X_{1,g_1},\cdots ,X_{1,g_1-1}-X_{1,g_1},\cdots ,\hfill \\ & X_{q,1}-X_{q,g_q},\cdots ,X_{q,g_q-1}-X_{q,g_q}).\hfill \end{array}$$

For any subscripts set $\mathcal{A}\subset \{(i,j):i\in \{1,\cdots ,q\},j\in \{1,\cdots ,g_i-1\}\}$, we use ${\mathit{X}}_{\mathcal{A}}$ to denote the matrix consisting of the columns of ${\mathit{X}}_G$ with subscripts in $\mathcal{A}$; likewise, ${\mathbf{\beta }}_{\mathcal{A}}$ comprises all the elements of ${\mathbf{\beta }}_{-q}$ with subscripts in $\mathcal{A}$.

Let

$${\mathcal{A}}^{*}=\{(i,j):{\beta }_{i,j}^{*}>0,i\in \{1,\cdots ,q\},j\in \{1,\cdots ,g_i-1\}\}$$

be the set of subscripts of all nonzero true coefficients in ${\mathbf{\beta }}_{-q}^{*}$. We denote the cardinality of ${\mathcal{A}}^{*}$ as $p_0=\left|{\mathcal{A}}^{*}\right|$, and the minimal value of nonzero true coefficients as ${\gamma }_{min}=min\{{\beta }_{i,j}^{*}:{\beta }_{i,j}^{*}>0,i\in \{1,\cdots ,q\},j\in \{1,\cdots ,g_i\}\}$.

By (5), the regression Equation (1) can be rewritten as

$$\begin{array}{cc}\hfill \mathit{Y}-\sum _{i=1}^q{w}_i{\mathit{X}}_{i,g_i}& ={\mathit{X}}_{-q}{\mathbf{\beta }}_{-q}^{*}-\sum _{i=1}^q{\mathit{X}}_{i,g_i}\sum _{j=1}^{g_i-1}{\beta }_{i,j}^{*}+\mathbf{ϵ}\hfill \\ \hfill & ={\mathit{X}}_G{\mathbf{\beta }}_{-q}^{*}+\mathbf{ϵ}\hfill \\ \hfill & ={\mathit{X}}_{{\mathcal{A}}^{*}}{\mathbf{\beta }}_{{\mathcal{A}}^{*}}^{*}+\mathbf{ϵ}.\hfill \end{array}$$

(6)

Define

$${\widehat{\mathbf{\beta }}}_{{\mathcal{A}}^{*}}^{ols}={\left({\mathit{X}}_{{\mathcal{A}}^{*}}^{\top }{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}^{-1}{\mathit{X}}_{{\mathcal{A}}^{*}}^{\top }(\mathit{Y}-\sum _{i=1}^q{w}_i{\mathit{X}}_{i,g_i}).$$

We expand ${\widehat{\mathbf{\beta }}}_{{\mathcal{A}}^{*}}^{ols}$ to be the oracle estimator ${\widehat{\mathbf{\beta }}}^{ols}$ by letting ${\widehat{\beta }}_{i,j}^{ols}=0$ if ${\beta }_{i,j}^{*}=0$, and obtaining ${\widehat{\beta }}_{i,g_i}^{ols}$ by Equation (5).

Let ${\widehat{\mathbf{\beta }}}^{tlp}$ be the global minimizer of (4), and let

$$\widehat{\mathcal{A}}=\{(i,j):{\widehat{\beta }}_{i,j}^{tlp}>0,i\in \{1,\cdots ,q\},j\in \{1,\cdots ,g_i-1\}\}.$$

be the estimated set of nonzero coefficients.

We now give two key assumptions when establishing theoretical results regarding the error bound and asymptotic distribution of the coefficient estimator, and model selection consistency.

Assumption 1.

For some constants $d_0>0$ and $\alpha >1$, $C_{min}\ge d_0{\sigma }^2\frac{logp}{n}$, where

$$C_{min}=\underset{\left\{{\mathbf{\beta }}_{\mathcal{A}}:\left|\mathcal{A}\right|\le \alpha |{\mathcal{A}}^{*}|,\mathcal{A}\ne {\mathcal{A}}^{*}\right\}}{inf}\frac{{∥{\mathit{X}}_{{\mathcal{A}}^{*}}{\mathbf{\beta }}_{{\mathcal{A}}^{*}}^{*}-{\mathit{X}}_{\mathcal{A}}{\mathbf{\beta }}_{\mathcal{A}}∥}_2^2}{max\left(|{\mathcal{A}}^{*}\setminus \mathcal{A}|,1\right)}.$$

Assumption 2.

For some constants $d_1>0$ and $d_2>0$,

$$d_1\le {\eta }_{min}\left(\frac{1}{n}{\mathit{X}}^{\top }\mathit{X}\right)\le {\eta }_{max}\left(\frac{1}{n}{\mathit{X}}^{\top }\mathit{X}\right)\le d_2,$$

where ${\eta }_{min}(·)$ and ${\eta }_{max}(·)$ denote the minimum and maximum eigenvalues of a matrix, respectively.

Theorem 1.

Assume that Assumption 1 holds, and $0<\tau \le \sqrt{{\displaystyle \frac{\lambda }{(n+1){\eta }_{max}\left(\frac{1}{n}{\mathit{X}}^{\top }\mathit{X}\right)}}}$. Then $Pr\left[{\widehat{\mathbf{\beta }}}^{tlp}\ne {\widehat{\mathbf{\beta }}}^{ols}\right]$ is upper bounded by

$$\begin{array}{cc}\hfill min& \left\{\frac{\sqrt{2}{p}_0{n}^{1/2}\tau }{\sigma \sqrt{\pi }{\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}exp\left(-\frac{n{\left({\gamma }_{min}-\tau \right)}^2}{2{\sigma }^2{\eta }_{min}^{-1}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}\right),\right.\hfill \\ & \left.p_0\Phi \left(-\frac{n^{1/2}\left({\gamma }_{min}-\tau \right)}{\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}\right)\right\}\hfill \\ & +4exp\left(-\left(\frac{n{C}_{min}}{20{\sigma }^2}-(\alpha +1)log(p+1)-\frac{n\lambda }{4{\sigma }^2}\right)\right)\hfill \\ & +4exp\left(-\left(\frac{(\alpha -1)n\lambda }{6\alpha {\sigma }^2}-\left(1+\frac{1}{\alpha }\right)(log(p+1)-\frac{5}{3})\right)\right)\hfill \\ & +p_0\Phi \left(-{\displaystyle \frac{n^{1/2}({\gamma }_{min}-\tau )}{\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}}\right)+q\Phi \left(-{\displaystyle \frac{n^{1/2}({\gamma }_{min}-\tau )}{p_0^{1/2}\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}}\right),\hfill \end{array}$$

where $\Phi (·)$ is the distribution function of $N(0,1)$.

Theorem 2.

Assume there are constants $a_{\gamma }$, $a_C$, $a_{\lambda }$, $a_{p_0}$ and $a_{lp}$ satisfying

$$\begin{array}{cc}& a_{p_0}\ge 0,a_{lp}\ge 0,a_{p_0}<a_{\gamma },a_{\lambda }<a_{\gamma },a_{lp}-1<a_{\lambda },a_{\lambda }<a_C\mathit{and}\hfill \\ & {\gamma }_{min}\asymp n^{-\frac{1-a_{\gamma }}{2}},C_{min}\asymp n^{a_C},\lambda \asymp n^{a_{\lambda }},p_0\asymp n^{a_{p_0}},log\left(p\right)\asymp n^{a_{lp}},\hfill \end{array}$$

where for two sequences $\left\{h_n\right\}$ and $\left\{g_n\right\}$ we say $h_n\asymp g_n$ if both sequences $\frac{h_n}{g_n}$ and $\frac{g_n}{h_n}$ are bounded. Also assume that the conditions of Theorem 1 and Assumption 2 hold. Then

(A) 

Selection consistency:

$$Pr[\widehat{\mathcal{A}}\ne {\mathcal{A}}^{*}]\le Pr[{\widehat{\mathbf{\beta }}}^{tlp}\ne {\widehat{\mathbf{\beta }}}^{ols}]\to 0,\mathrm{as}n,p\to \infty .$$

(B) 

Asymptotic distribution: Let $F_n\left(t\right)$ denote the distribution function of

$\sqrt{n}{\left(\frac{{\mathit{X}}_{{\mathcal{A}}^{*}}^{\top }{\mathit{X}}_{{\mathcal{A}}^{*}}}{n}\right)}^{\frac{1}{2}}\left({\widehat{\mathbf{\beta }}}_{{\mathcal{A}}^{*}}^{tlp}-{\mathbf{\beta }}_{{\mathcal{A}}^{*}}^{*}\right)$, and ${\Phi }_{p_0}\left(t\right)$ the distribution function of $p_0$-dimensional standard multivariate normal distribution. We have

$$\underset{n\to \infty }{lim}\underset{t\in {\mathbb{R}}^{p_0}}{sup}\left|F_n\left(t\right)-{\Phi }_{p_0}\left(t\right)\right|=0.$$

(7)

Remark 1.

Theorems 1 and 2 stabilize the index tracking problem. They encourage the non-negativity and sector neutrality in constructing sparse index tracking portfolios in high dimensional cases and allow practical and empirical work with only a moderate size of training data. The proofs of Theorems 1 and 2 are displayed in Appendix A.1.

5. Computation

The minimization of (4) with TLP can be treated as a sequence of weighted Lasso problems [17] and can be solved iteratively. However, the sector neutrality constraint and the nonnegativity constraint in (4) are not easy to handle directly. Fortunately, the alternating direction method of multipliers (ADMM) algorithm [21,22] can be applied to solve the constrained minimization problem (4).

We are now to put our optimization problem in the ADMM framework. First, using the Lagrangian multiplier method, we transform the original optimization into minimization of the objective function

$$\begin{array}{c}\hfill f\left(\mathbf{\beta }\right)=n^{-1}{\parallel \mathit{Y}-\mathit{X}\mathbf{\beta }\parallel }_2^2+\lambda \sum _{i=1}^q\sum _{j=1}^{g_i}min\{\frac{|{\beta }_{i,j}|}{\tau },1\}\end{array}$$

(8)

over the new parameter space $\mathcal{C}$:

$$\begin{array}{ccc}\hfill & & \mathcal{C}=\{\mathbf{\beta }:{\beta }_{i,j}\ge 0,\sum _{j=1}^{g_i}{\beta }_{i,j}={\omega }_i,i\in \{1,\cdots ,q\},j\in \{1,\cdots ,g_i\}\}.\hfill \end{array}$$

It is straightforward to verify that the new parameter space $\mathcal{C}$ is convex and the objective function f in (8) is a convex loss function plus a piecewise linear regularization function. Using the results in [21,29], our optimization problem is equivalent to

$$\begin{array}{ccc}\hfill \underset{\mathbf{\beta }}{min}& & f\left(\mathbf{\beta }\right)+{\mathbb{I}}_{\mathcal{C}}\left(\mathbf{\alpha }\right)\hfill \\ \hfill \mathrm{subject}\mathrm{to}:& & {\beta }_{i,j}={\alpha }_{i,j},i\in \{1,\cdots ,q\},j\in \{1,\cdots ,g_i\},\hfill \end{array}$$

(9)

where ${\mathbb{I}}_{\mathcal{C}}\left(\alpha \right)$ is the indicator function of space $\mathcal{C}$ (i.e., ${\mathbb{I}}_{\mathcal{C}}\left(\alpha \right)$ = 0 for $\alpha \in \mathcal{C}$, and ${\mathbb{I}}_{\mathcal{C}}\left(\alpha \right)=\infty$ for $\alpha \notin \mathcal{C}$). This is a standard starting form of the ADMM algorithm. Before following three steps in the ADMM algorithm, we write the augmented Lagrangian for (9),

$$\begin{array}{c}\hfill h\left(\mathbf{\beta }\right)=n^{-1}{\parallel \mathit{Y}-\mathit{X}\mathbf{\beta }\parallel }_2^2+\lambda \sum _{i=1}^q\sum _{j=1}^{g_i}min\{\frac{|{\beta }_{i,j}|}{\tau },1\}+\frac{\rho }{2}{\parallel \mathbf{\beta }-\mathbf{\alpha }+\mathbf{\mu }\parallel }_2^2,\end{array}$$

(10)

where $\mathbf{\mu }$ is a scaled dual variable associated with the constraint $\mathbf{\beta }=\mathbf{\alpha }$. Here $\rho >0$ is a penalty parameter.

In each iteration of ADMM, we perform alternating minimization of the augmented Lagrangian over $\mathbf{\beta }$ and $\mathbf{\alpha }$. At the k-th iteration we update variables $\mathbf{\beta }$, $\mathbf{\alpha }$ and $\mathbf{\mu }$ by the following steps:

$$\begin{array}{cc}\hfill {\mathbf{\beta }}^{k+1}=& arg\underset{\mathbf{\beta }}{min}{n}^{-1}{\parallel \mathit{Y}-\mathit{X}\mathbf{\beta }\parallel }_2^2+\lambda \sum _{i=1}^q\sum _{j=1}^{g_i}min\{\frac{|{\beta }_{i,j}|}{\tau },1\}+\frac{\rho }{2}{\parallel \mathbf{\beta }-{\mathbf{\alpha }}^k+{\mathbf{\mu }}^k\parallel }_2^2\hfill \end{array}$$

(11)

$${\mathbf{\alpha }}^{k+1}=\prod _{\mathcal{C}}({\mathbf{\beta }}^{k+1}+{\mathbf{u}}^k)$$

(12)

$${\mathbf{\mu }}^{k+1}={\mathbf{\mu }}^k+({\mathbf{\beta }}^{k+1}-{\mathbf{\alpha }}^{k+1}),$$

(13)

where ${\prod }_{\mathcal{C}}$ denotes the Euclidean projection onto space $\mathcal{C}$. In the first step of ADMM, we fix $\mathbf{\alpha }$ and $\mathbf{\mu }$ and update the value of $\mathbf{\beta }$ by minimization of the augmented Lagrangian; in the second step, we fix $\mathbf{\beta }$ and $\mathbf{\mu }$ and update the value of $\mathbf{\alpha }$ by projection onto space $\mathcal{C}$; and finally, we we fix $\mathbf{\alpha }$ and $\mathbf{\beta }$ and update the dual variable $\mathbf{\mu }$. Algorithm 1 summarizes the framework of our algorithm and the details are referred to Appendix A.2.

Algorithm 1 ADMM algorithm for the minimization of (10).

(Initialization) Let ${\mathbf{\beta }}^0$, ${\mathbf{\alpha }}^0$, ${\mathbf{\mu }}^0$$\in {\mathbb{R}}^p$ be the initial parameter vectors; (Iteration) At each iteration k, Update $\mathbf{\beta }$ using Algorithm A1 (see Appendix A.2), $\mathbf{\alpha }$ by the projection (12), and $\mathbf{\mu }$ by direct calculation (13); (Termination) Stop when $\mathbf{\beta }$, $\mathbf{\alpha }$, $\mathbf{\mu }$ converge.

6. Simulation Results

In this section, we show the performance of our estimation procedure via simulations and discuss the selection of appropriate tuning parameters $\lambda$, $\tau$ and $\rho$ in the augmented Lagrangian (10).

The detailed information about the simulation study, including the model and its variations, the methods to conduct the experiments and the choice of tuning parameters are given in Appendix A.3.

The performance of various methods is evaluated by both variable selection performance and estimation accuracy. In terms of variable selection, we use four criteria: the mean true positive(TP), the mean false positive(FP), positive selection rate(PSR), and negative selection rate(NSR) [30], respectively. The true positive(TP) is defined as $\#TP={\sum }_{i=1}^q{\sum }_{j=1}^{g_i}I({\beta }_{i,j}^{*}\ne 0,{\widehat{\beta }}_{i,j}\ne 0)$, which counts the variables with true non-zero coefficients and estimated non-zero coefficients. The false positive (FP) is defined as $\#FP={\sum }_{i=1}^q{\sum }_{j=1}^{g_i}I({\beta }_{i,j}^{*}=0,{\widehat{\beta }}_{i,j}\ne 0)$, which counts the variables with true zero coefficients but estimated as non-zero coefficients. Additionally, PSR is the ratio of TP and the total number of the true non-zero coefficients. Similar to PSR, NSR is the ratio of FP and the total number of the true zero coefficients. Regarding estimation accuracy, we adopt the mean and the standard deviation of model errors (ME) as criteria, where the model error is defined as $ME\left(\widehat{\mathbf{\beta }}\right)={(\widehat{\mathbf{\beta }}-{\mathbf{\beta }}^{*})}^{\top }\mathbb{E}\left(\mathit{X}{\mathit{X}}^{\top }\right)(\widehat{\mathbf{\beta }}-{\mathbf{\beta }}^{*})$, and the expectation is taken only with respect to new observation $(\mathit{X},\mathbf{y})$. The running time of each method is evaluated using the machine with Intel Core i5 CPU, 2.4 GHz, 8 GB RAM. All methods were implemented in R.

6.1. Case 1

In this case $n>p$, five methods are compared. The first one is our method, named as constrained TLP method (CTLP). The second method uses the Lasso penalty for sparsity constraint instead of TLP, and we name it the constrained $L_1$ method (C$L_1$). This method will fail to give a sparse portfolio because of the neutrality constraint, as is pointed out in Section 3; we present the results of C$L_1$ here for confirmation. The third method uses TLP for the sparsity constraint, but ignores the sector neutrality, and we refer to this method as TLP. The fourth and fifth methods are the index tracking procedures in the following form,

$$\begin{array}{ccc}\hfill \underset{\beta }{min}& & \mathrm{TE}\left(\mathbf{\beta }\right)+{\lambda \parallel \mathbf{\beta }\parallel }_0\hfill \\ \\ \hfill \mathrm{subject}\mathrm{to}& & {\mathbf{\beta }}^{\top }\mathbf{1}=\mathbf{1}\mathrm{and}\mathbf{\beta }>0,\hfill \end{array}$$

with $\mathrm{TE}\left(\mathbf{\beta }\right)$ being empirical tracking error (ETE) and Huber empirical tracking error (HETE), which are denoted by ETE and HETE, respectively. In ETE, $\mathrm{TE}\left(\mathbf{\beta }\right)$ is defined in (3), while in HETE, $\mathrm{TE}\left(\mathbf{\beta }\right)=\frac{1}{n}{\mathbf{1}}^{\top }\mathbf{\varphi }(\mathbf{y}-\mathit{X}\mathbf{\beta })$ where $\mathbf{\varphi }\left(\mathbf{x}\right)={(\varphi \left(x_1\right),\cdots ,\varphi \left(x_n\right))}^{\top }$, and

$$\begin{array}{c}\hfill \varphi \left(x\right)=\left\{\begin{array}{cc}{x}^2\hfill & \mathrm{if}\left|x\right|\le M\hfill \\ M\left(2\right|x|-M)\hfill & \mathrm{if}\left|x\right|>M,\hfill \end{array}\right.\end{array}$$

(14)

with M being the Huber parameter. Note that ETE and HETE methods ignore the sector-neutral constraints. These two methods can be carried out using R-package sparseIndexTracking [31].

We first investigate the case when the covariates $\mathit{X}$ have an independent structure. Table 2 shows the simulation results for both $\sigma =1$ and $\sigma =3$ settings. For the $\sigma =1$ setting, methods CTLP and C$L_1$ have smaller model errors than ETE and HETE, and the model errors of ETE and HETE are much smaller than that of TLP. When it comes to the variable selection ability, all methods correctly select non-zero variables. CTLP, ETE and HETE perform similarly, and better than C$L_1$ in that C$L_1$ tends to select too many trivial variables and thus fails to produce sparse portfolios, which confirms our earlier assertion. On the other hand, TLP makes the fewest mistakes in selecting both trivial and non-trivial variables. When the variance of error terms becomes larger, the simulated data are noisier. For the $\sigma =3$ setting, CTLP and C$L_1$ still have the smallest model error while TLP performs quite poorly in terms of model errors. Every method selects almost all nontrivial variables except for TLP, which selects slightly fewer nontrivial and trivial variables.

Table 2. The comparison of five methods in the case of $n>p$, independent correlation matrix.

	Method	ME	SE	TP	FP	PSR	NSR	Runtime (s)
$\sigma =1$	CTLP	0.0742	0.0025	14	18.85	100.00%	21.92%	2.78
	C$L_1$	0.0741	0.0025	14	52.36	100.00%	60.88%	1.10
	TLP	0.1650	0.0042	14	6.77	100.00%	7.87%	0.12
	ETE	0.0858	0.0026	14	18.76	100.00%	21.81%	0.02
	HETE	0.0924	0.0026	14	18.8	100.00%	21.86%	1.45
$\sigma =3$	CTLP	0.6415	0.0202	13.98	15.64	99.86%	18.19%	1.66
	C$L_1$	0.6712	0.0198	13.98	31.55	99.86%	36.69%	1.00
	TLP	1.2989	0.0338	13.55	7.52	96.79%	8.74%	0.11
	ETE	0.7673	0.0215	13.95	18.74	99.64%	21.79%	0.02
	HETE	0.9818	0.0278	13.9	19.33	99.29%	22.48%	1.47

Now we investigate the simulation settings when the covariates $\mathit{X}$ have $AR\left(1\right)$ correlation, without and with group structures. Similar conclusions can be reached from Table 3 and Table 4. In the large signal-to-noise ratio setting ($\sigma =1$), the model errors of CTLP and C$L_1$ are similar and smaller than that of their competitors. Besides, CTLP, ETE and HETE maintain a good balance between selections of trivial and nontrivial variables whereas C$L_1$ selects too many trivial variables. TLP gives good variable selection results but has poor estimation accuracy. In the small signal-to-noise ratio setting ($\sigma =3$), the model errors of all five methods become larger than those in the case of the large signal-to-noise ratio setting above. However, the relative performances of the five methods are similar in terms of model errors and variable selection ability as well.

Table 3. The comparison of five methods in the case of $n>p$, $AR\left(1\right)$ correlation matrix without group structure.

	Method	ME	SE	TP	FP	PSR	NSR	Runtime (s)
$\sigma =1$	CTLP	0.0697	0.0024	14	16.65	100.00%	19.36%	2.81
	C$L_1$	0.0696	0.0024	14	51.04	100.00%	59.35%	1.10
	TLP	0.1382	0.0043	14	6.74	100.00%	7.84%	0.14
	ETE	0.0796	0.0025	14	16.22	100.00%	18.86%	0.02
	HETE	0.0884	0.0026	14	16.21	100.00%	18.85%	1.49
$\sigma =3$	CTLP	0.5956	0.0171	13.98	12.92	99.86%	15.02%	1.95
	C$L_1$	0.6161	0.0179	13.97	29.21	99.79%	33.97%	1.12
	TLP	1.0480	0.0268	13.81	7.26	98.64%	8.44%	0.13
	ETE	0.7136	0.0196	13.95	16.2	99.64%	18.84%	0.02
	HETE	0.9427	0.0285	13.91	17.73	99.36%	20.62%	1.43

Table 4. The comparison of five methods in the case of $n>p$, $AR\left(1\right)$ correlation matrix with group structure.

	Method	ME	SE	TP	FP	PSR	NSR	Runtime (s)
$\sigma =1$	CTLP	0.0651	0.0020	14	15.26	100.00%	17.74%	2.75
	C$L_1$	0.0651	0.0020	14	50.32	100.00%	58.51%	1.04
	TLP	0.1337	0.0039	14	6.28	100.00%	7.30%	0.14
	ETE	0.0765	0.0022	14	15.32	100.00%	17.81%	0.02
	HETE	0.0841	0.0025	14	15.4	100.00%	17.91%	1.42
$\sigma =3$	CTLP	0.5740	0.0171	13.99	13.36	99.93%	15.53%	1.96
	C$L_1$	0.5836	0.0185	13.99	44.79	99.93%	52.08%	1.20
	TLP	0.9061	0.0276	13.89	10.65	99.21%	12.38%	0.13
	ETE	0.6742	0.0203	13.96	17.07	99.71%	19.85%	0.02
	HETE	0.9259	0.0253	13.9	17.05	99.29%	19.83%	1.49

From the last columns in Table 2, Table 3 and Table 4 we see that CTLP takes more time than other methods in training because of additional loops required to satisfy the sector neutrality constraint. In contrast, TLP and ETE consume the least time among all methods.

6.2. Case 2

When $p>n$, the variable selection becomes a high-dimensional problem and necessitates sparsity. Theoretically, the C$L_1$ method with the Lasso penalty fails to yield sparse models due to sector neutrality and nonnegativity constraints. However, we can solve the convex optimization problem using some common convex optimizers like CVXR [32] to obtain an approximate solution C$L_1^{*}$. Table 5, Table 6 and Table 7 present the results of this case.

Table 5. The comparison of four methods in the case of $n<p$, independent correlation matrix.

	Method	ME	SE	TP	FP	PSR	NSR	Runtime (s)
$\sigma =1$	CTLP	0.1352	0.0114	13.61	18.27	97.21%	21.24%	2.35
	C$L_1^{*}$	0.1758	0.0101	13.65	19.10	97.50%	22.21%	0.64
	TLP	0.3433	0.0299	11.09	12.77	79.21%	14.85%	0.10
	ETE	0.1724	0.0134	13.34	18.39	95.29%	21.38%	0.07
	HETE	0.1772	0.0134	13.32	18.2	95.14%	21.16%	0.33
$\sigma =3$	CTLP	0.9915	0.0441	10.53	12.08	75.21%	14.05%	2.73
	C$L_1^{*}$	0.9599	0.0437	11.31	17.34	80.78%	20.16%	0.63
	TLP	1.7058	0.0816	6.08	4.25	43.43%	4.94%	0.04
	ETE	1.0885	0.0432	10.01	16.54	71.50%	19.23%	0.03
	HETE	1.2494	0.0507	9.8	15.73	70.00%	18.29%	0.40

Table 6. The comparison of four methods in the case of $n<p$, $AR\left(1\right)$ correlation matrix without group structure.

	Method	ME	SE	TP	FP	PSR	NSR	Runtime (s)
$\sigma =1$	CTLP	0.1268	0.0088	13.69	14.68	97.79%	17.07%	2.17
	C$L_1^{*}$	0.1328	0.0062	13.79	16.86	98.50%	19.60%	0.65
	TLP	0.3060	0.0261	11.87	11.02	84.79%	12.81%	0.10
	ETE	0.1643	0.0111	13.36	15.02	95.43%	17.47%	0.06
	HETE	0.1628	0.0110	13.33	14.71	95.21%	17.10%	0.31
$\sigma =3$	CTLP	1.0728	0.0772	10.79	11.67	77.07%	13.57%	2.67
	C$L_1^{*}$	0.8185	0.0304	11.24	15.54	80.29%	18.07%	0.64
	TLP	1.8885	0.0644	7.03	4.53	50.21%	5.27%	0.05
	ETE	1.0795	0.0439	10.86	15.4	77.57%	17.91%	0.03
	HETE	1.2447	0.0507	10.39	15.27	74.21%	17.76%	0.37

Table 7. The comparison of four methods in the case of $n<p$, $AR\left(1\right)$ correlation matrix with group structure.

	Method	ME	SE	TP	FP	PSR	NSR	Runtime (s)
$\sigma =1$	CTLP	0.1189	0.0067	13.71	16.23	97.93%	18.87%	2.03
	C$L_1^{*}$	0.1328	0.0082	13.66	16.66	97.57%	19.37%	0.63
	TLP	0.2726	0.0229	12.94	15.04	92.43%	17.49%	0.10
	ETE	0.1600	0.0100	13.62	16.03	97.29%	18.64%	0.05
	HETE	0.1625	0.0104	13.57	16	96.93%	18.60%	0.32
$\sigma =3$	CTLP	1.0246	0.0526	10.7	11.09	76.43%	12.90%	2.24
	C$L_1^{*}$	0.8340	0.0472	11.36	15.41	81.14%	17.92%	0.62
	TLP	1.9927	0.0993	6.72	4.12	48.00%	4.79%	0.05
	ETE	1.0223	0.0412	10.88	14.78	77.71%	17.19%	0.03
	HETE	1.0964	0.0404	10.53	13.94	75.21%	16.21%	0.39

The results are similar to that of the low-dimensional case, but all four methods have larger model errors and select fewer nontrivial variables. In the large signal-to-noise ratio setting ($\sigma =1$), CTLP has smaller model errors than other methods. CTLP, ETE and HETE have a similar ability in variable selection. TLP has larger model errors and it tends to select fewer nontrivial variables. The average model error of C$L_1^{*}$ is between CTLP and other methods. It usually selects about 20% trivial variables as in tables if we consider the numbers less than ${10}^{-4}$ as 0. As the accuracy of numbers increases, more trivial variables are selected. No estimated coefficients of variables are exactly 0 with moderate accuracy, which proves that C$L_1^{*}$ is just an approximate solution and the $L_1$ term does not work. In the small signal-to-noise ratio setting ($\sigma =3$), there is no significant difference between CTLP and ETE in terms of model errors, but CTLP selects fewer trivial variables. As to the other two methods, HETE gives less accurate estimation, and TLP performs less well in terms of both variable selection and estimation. Although C$L_1^{*}$ yields the smallest model errors, it cannot provide the exact solution with the sparsity that we need. All five methods run faster than in the $p<n$ case due to the smaller sample size. CTLP is still the slowest one while ETE is the fastest one.

In conclusion, although CTLP takes more time to run, it performs similarly or better than the competitors in terms of both model errors and variable selection ability.

7. Real Data Results

Now we are to apply the proposed methodology to sparse index tracking for the CSI 300 Index. In this application, we use the daily return series of the CSI 300 Index and all stocks in this index from 2014 to 2018. The CSI 300 is a capitalization-weighted stock market index designed to replicate the performance of the top 300 stocks traded in the Shanghai and Shenzhen stock exchanges. The index is compiled by the China Securities Index and is considered a blue chip index for Mainland China stock exchanges. The return series, the methodology of the CSI 300 Index, the names and weights of the index constituents, and the corresponding sectors are available from China Securities Index (http://www.csindex.com.cn/) (accessed on 31 September 2018).

According to the guidelines for the industry classification by the Global Industry Classification Standard (GICS) and the weights of constituents making up the CSI 300 Index, the stocks can be divided into 11 major sectors, including Materials, Communication services, Real estate, Industrials, Utilities, Financials, Consumer Discretionary, Energy, Consumer Staples, Information Technology and Health Care. In the composition of the CSI 300 index, the constituents, as well as their weights, are reviewed every six months. As a consequence, every six months, the stock numbers and the weights of sectors will change. Due to its dynamic properties, we must update our model periodically. We train and tune the model on the first day after constituent adjustment is implemented with the daily return series of the index and its renewed constituents before half a year. The total weights within sectors are calculated based on the renewed weights as well. Then the model will be tested with daily return series before the next adjustment day. These steps are in accordance with the practical procedure.

We treat the estimated coefficients as the weights of stocks in building an index-tracking portfolio. The daily tracking error or prediction error is adopted to evaluate the model performance. The daily tracking error measures the deviation of the index daily return from the portfolio daily return, defined as $\mathit{error}={\widehat{r}}_t-r_t$, where $r_t$ is the daily return of the index, ${\widehat{r}}_t$ is the daily return of the constructed portfolio. We will compare our method CTLP with TLP, ETE and HETE as described in Section 6.1 in terms of tracking errors. Since the training sample size is smaller than the number of index constituents, there is no exact solution without sparsity, but an approximate solution by a common convex optimizer. Thus, we show the C$L_1^{*}$ solution as in Section 6.2. For an additional comparison in the Lasso family, we give the performance of standard sparse group lasso [33] by SGL. To give a more intuitive view of the advantages of the proposed method, we also present the performance of portfolios created by traditional methods, including equal-weighted portfolio (EW) and inverse volatility weighted portfolio (IVW). Both portfolios consist of 300 stocks. The weights in the EW portfolio are equal while the weights in the IVW portfolio are inversely proportional to their historical volatility.

The CSI 300 index has been adjusted eight times from December 2014 to November 2018. Each time the constituents of the index were adjusted, we update the model and test it with the return series for the next six months. Table 8 presents the mean and standard deviation of the daily tracking errors in each test set. It also shows the number of stocks building the portfolio. We highlight the method with the smallest mean daily tracking error in each period. It is clear that in a majority of periods, CTLP has the smallest mean tracking error among its competitors. Even in the period, such as 2017H1 and 2017H2, when CTLP is not the best, it is still very close to the best one. In terms of the standard deviation of tracking errors, CTLP has a slightly larger standard deviation than ETE and HETE, but significantly smaller than TLP. However, TLP and HETE tend to yield sparser portfolios than CTLP and ETE. As to tracking errors, C$L_1^{*}$ performs not bad. But it has difficulties to give a sparse portfolio in several periods which violates our motivation to propose this research. The standard sparse group lasso (SGL) may provide negative coefficients but satisfy sector-neutral constraints. Although it has sparse enough solutions, its tracking errors are the largest. The traditional EW and IVW portfolios are not sparse and yield unstable performance. In some periods they track the index tightly, while in other periods they produce large tracking errors. We also present the average runtime of the first four methods in Table 9, indicating that CTLP and HETE run more slowly than the other four methods. Even though the computation of CTLP requires longer computation time due to additional sector neutral constraints, it is still worthwhile for its competitive performance and the fact that this computation is not a frequent task.

Table 8. The performance of the selected portfolio. By different methods in eight periods. Mean, Std. Dev and Num stand for the mean, the standard deviation of tracking error and the number of stocks in the portfolio. In the columns of period, for example, 2018H1 stands for the first half year of 2018.

Period	Method	Mean	Std. Dev	Num	Period	Method	Mean	Std. Dev	Num
2018H2	CTLP	0.018%	0.0016	124	2016H2	CTLP	0.015%	0.0013	107
	C$L_1^{*}$	0.028%	0.0016	297		C$L_1^{*}$	0.027%	0.0007	300
	SGL	0.123%	0.0126	57		SGL	−0.073%	0.0056	65
	TLP	0.081%	0.0046	42		TLP	0.020%	0.0020	52
	ETE	0.031%	0.0013	188		ETE	0.023%	0.0009	219
	HETE	0.026%	0.0013	98		HETE	0.016%	0.0011	128
	EW	0.091%	0.0064	300		EW	−0.016%	0.0022	300
	IVW	0.087%	0.0066	300		IVW	0.055%	0.0060	300
2018H1	CTLP	0.008%	0.0031	116	2016H1	CTLP	0.002%	0.0022	75
	C$L_1^{*}$	0.014%	0.0017	126		C$L_1^{*}$	0.025%	0.0021	120
	SGL	0.043%	0.0093	57		SGL	0.062%	0.0109	90
	TLP	0.024%	0.0051	34		TLP	0.031%	0.0033	49
	ETE	0.022%	0.0013	129		ETE	0.031%	0.0018	140
	HETE	0.024%	0.0013	79		HETE	0.033%	0.0017	121
	EW	0.018%	0.0086	300		EW	0.052%	0.0040	300
	IVW	0.027%	0.0079	300		IVW	0.052%	0.0035	300
2017H2	CTLP	−0.008%	0.0019	123	2015H2	CTLP	0.055%	0.0034	117
	C$L_1^{*}$	−0.005%	0.0015	296		C$L_1^{*}$	0.064%	0.0021	130
	SGL	−0.095%	0.0060	35		SGL	0.195%	0.0208	84
	TLP	−0.040%	0.0035	25		TLP	0.135%	0.0087	51
	ETE	−0.012%	0.0013	220		ETE	0.064%	0.0017	179
	HETE	−0.017%	0.0016	84		HETE	0.062%	0.0019	121
	EW	−0.015%	0.0048	300		EW	0.076%	0.0049	300
	IVW	0.020%	0.0040	300		IVW	−0.935%	0.0479	300
2017H1	CTLP	−0.014%	0.0012	129	2015H1	CTLP	0.060%	0.0032	120
	C$L_1^{*}$	−0.016%	0.0009	299		C$L_1^{*}$	−0.011%	0.0020	147
	SGL	0.050%	0.0058	11		SGL	−0.358%	0.0153	58
	TLP	−0.024%	0.0032	33		TLP	−0.166%	0.0075	22
	ETE	−0.010%	0.0009	177		ETE	0.004%	0.0018	166
	HETE	−0.011%	0.0012	83		HETE	−0.009%	0.0024	90
	EW	0.017%	0.0023	300		EW	0.009%	0.0041	300
	IVW	0.015%	0.0017	300		IVW	0.045%	0.0176	300

Bold means the method has the smallest mean daily tracking error in this period.

Table 9. The average runtime of different methods.

	CTLP	C${\mathit{L}}_1^{*}$	SGL	TLP	ETE	HETE
Runtime (s)	47.60	0.75	0.14	18.48	1.67	46.78

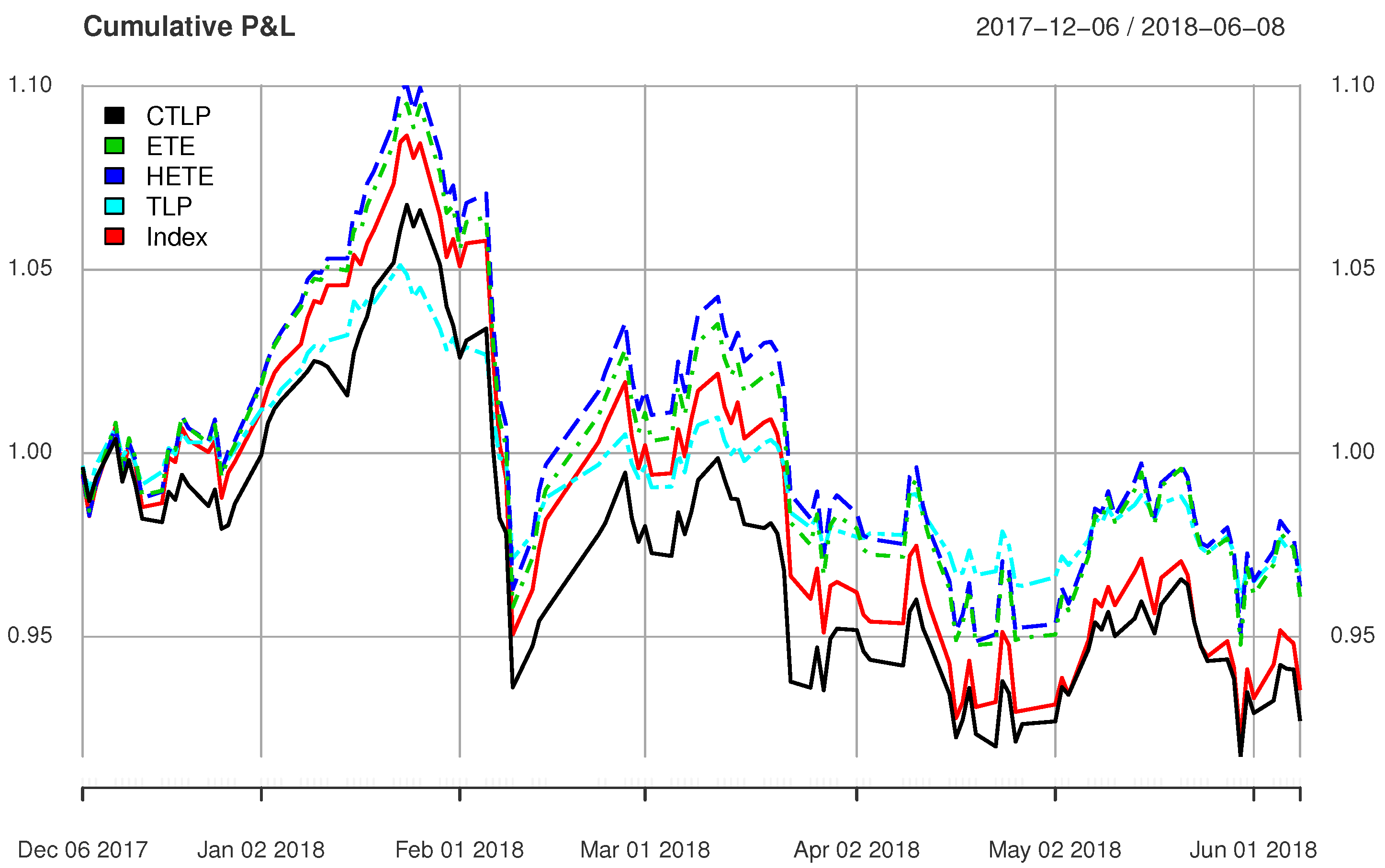
As illustration, we display analysis results for the most recent two periods – the first and second half of 2018, in Figure 1 and Figure 2, Table 10 and Table 11. Figure 1 and Figure 2 draw the cumulative profit and loss of CTLP, TLP, ETE, HETE and the index. The closer of the cumulative profit and loss line to the red line, which represents that of the index, the better the method. It is clear that the CTLP replicates the index the best among all four methods. Table 10 and Table 11 present the number of stocks and the total weights of different sectors. Compared with the index, all portfolios built by five methods are sparse. However, the portfolio given by TLP consists of such a small number of stocks that it cannot track the index well. In the TLP portfolio, some sectors even have zero weights. CTLP and C$L_1^{*}$ selected a portfolio with sector weights strictly equal to that of the index because of the sector neutrality constraint, whereas ETE and HETE produced sparse portfolios with sector weights only roughly equal to that of the index.

Figure 1. The cumulative profit and loss of portfolios built by different methods and the index in 2018H1.

Figure 2. The cumulative profit and loss of portfolios built by different methods and the index in 2018H2.

Table 10. The number of stocks and the sum of weights within sectors in selected portfolio by different methods and the index in 2018H1.

Sector	Number of Stocks						Sum of Weights
	Index	CTLP	C${\mathit{L}}_1^{*}$	TLP	ETE	HETE	Index	CTLP	C${\mathit{L}}_1^{*}$	TLP	ETE	HETE
Materials	25	11	14	3	12	7	0.062	0.062	0.062	0.004	0.068	0.077
Communication	2	1	2	0	1	1	0.008	0.008	0.008	0.000	0.004	0.005
Real Estate	20	6	8	2	6	5	0.057	0.057	0.057	0.074	0.049	0.056
Industrials	60	14	22	5	22	10	0.137	0.137	0.137	0.117	0.133	0.131
Utilities	8	3	2	1	4	3	0.025	0.025	0.025	0.006	0.041	0.047
Financials	58	22	24	10	27	17	0.353	0.353	0.353	0.340	0.323	0.323
Consumer dis.	42	12	17	4	19	12	0.114	0.114	0.114	0.103	0.127	0.139
Energy	11	3	5	0	5	3	0.023	0.023	0.023	0.000	0.026	0.008
Consumer sta.	14	5	6	1	7	5	0.075	0.075	0.075	0.070	0.085	0.078
Information	42	16	18	5	17	8	0.100	0.100	0.100	0.088	0.065	0.050
Health Care	18	8	8	3	9	8	0.047	0.047	0.047	0.198	0.079	0.086

Table 11. The number of stocks and the sum of weights within sectors in selected portfolio by different methods and the index in 2018H2.

Sector	Number of Stocks						Sum of Weights
	Index	CTLP	C${\mathit{L}}_1^{*}$	TLP	ETE	HETE	Index	CTLP	C${\mathit{L}}_1^{*}$	TLP	ETE	HETE
Materials	36	9	35	5	23	9	0.067	0.067	0.067	0.094	0.066	0.063
Communications	2	1	2	0	1	0	0.006	0.006	0.006	0.000	0.005	0.000
Real Estate	17	5	17	1	12	7	0.050	0.050	0.050	0.005	0.058	0.065
Industrials	57	14	57	10	25	12	0.122	0.122	0.122	0.132	0.118	0.128
Utilities	10	4	10	0	7	3	0.027	0.027	0.027	0.184	0.034	0.038
Financials	59	24	59	11	41	25	0.368	0.368	0.368	0.000	0.334	0.330
Consumer dis.	37	14	36	5	25	13	0.107	0.107	0.107	0.439	0.120	0.113
Energy	13	2	13	1	7	1	0.026	0.026	0.026	0.035	0.024	0.018
Consumer sta.	13	8	13	4	10	5	0.082	0.082	0.082	0.045	0.079	0.066
Information	34	10	33	4	23	14	0.080	0.080	0.080	0.046	0.098	0.108
Health Care	22	10	22	1	14	9	0.063	0.063	0.063	0.015	0.063	0.071

In summary, the proposed CTLP method demonstrates its advantages over the competitive methods in sparse index tracking. The sector neutrality constraint of CTLP guarantees the resulted sparse portfolio has the same sector risk exposure as the index. Most of the time, the CTLP method also gives smaller tracking errors. In addition, the non-negativity and sparsity of the CTLP portfolios are often desired properties in practical applications.

8. Summary

Motivated by a sparse index tracking problem, we propose a new method to do sparse variable selection under constraints. Our methodology extends the traditional variable selection with added constraints. Constraints either represent the lower dimensional structure of the data or special characteristics of practical applications.

In the sparse index tracking problem, sparsity, sector neutrality, and nonnegativity constraints are necessary to build an efficient, sector-risk neutral portfolio with lower transaction costs to track the performance of the index. We proved the consistency and asymptotic distribution for the constrained high-dimensional variable selection using our method. We also developed an efficient algorithm for the estimation of the stock weights of the sparse portfolio. Both simulations and the real application confirmed the validity and advantages of the new methodology.

In portfolio management applications, additional constraints may be incorporated into index tracking, for example, low volatility or size neutrality constraints. We leave these problems for future investigations.

Appendix A.1. Proof of Theorems

Proof of Theorem 1.

For $(i,j)\in {\mathcal{A}}^{*}$, by the definition of ${\widehat{\mathbf{\beta }}}_{{\mathcal{A}}^{*}}^{ols}$, the variance of ${\widehat{\beta }}_{i,j}^{ols}$ is a diagonal entry of matrix ${\sigma }^2{\left({\mathit{X}}_{{\mathcal{A}}^{*}}^{\top }{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}^{-1}$. Therefore,

$$\begin{array}{cc}\hfill Pr[{\widehat{\beta }}_{i,j}^{ols}\le \tau ]& =Pr[n^{1/2}({\widehat{\beta }}_{i,j}^{ols}-{\beta }_{i,j}^{*})\le -n^{1/2}({\beta }_{i,j}^{*}-\tau )]\hfill \\ & \le \Phi \left(-{\displaystyle \frac{n^{1/2}({\gamma }_{min}-\tau )}{\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}}\right).\hfill \end{array}$$

The variance of ${\widehat{\beta }}_{i,g_i}^{ols}$ is ${\sigma }^2{\mathit{v}}_i^{\top }{\left({\mathit{X}}_{{\mathcal{A}}^{*}}^{\top }{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}^{-1}{\mathit{v}}_i$, where ${\mathit{v}}_i$ is the coefficient vector for the linear combination of ${\mathbf{\beta }}_{i,j}^{*}$ on the right hand side of Equation (5) using only nonzero values of ${\mathbf{\beta }}^{*}$. Note that ${\mathit{v}}_i$ is a $p_0$-dimensional vector consisting of 0’s and $-1$’s only, The variance of ${\widehat{\beta }}_{i,g_i}^{ols}$ is bounded above by $p_0{\sigma }^2{\eta }_{min}^{-1}\left({\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)$. Thus,

$$\begin{array}{cc}\hfill Pr[{\widehat{\beta }}_{i,g_i}^{ols}\le \tau ]& =Pr[n^{1/2}({\widehat{\beta }}_{i,g_i}^{ols}-{\beta }_{i,g_i}^{*})\le -n^{1/2}({\beta }_{i,g_i}^{*}-\tau )]\hfill \\ & \le \Phi \left(-{\displaystyle \frac{n^{1/2}({\gamma }_{min}-\tau )}{p_0^{1/2}\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}}\right).\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill Pr[{\widehat{\beta }}_{i,j}^{ols}& \le \tau \mathrm{for}\mathrm{some}(i,j)\mathrm{with}{\beta }_{i,j}^{*}>0]\hfill \\ & \le p_0\Phi \left(-{\displaystyle \frac{n^{1/2}({\gamma }_{min}-\tau )}{\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}}\right)+q\Phi \left(-{\displaystyle \frac{n^{1/2}({\gamma }_{min}-\tau )}{p_0^{1/2}\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}}\right).\hfill \end{array}$$

Using theorem 5 of [34] for the global minimizer of (4) without constraints in (4), we obtain an upper bound for $Pr\left[{\widehat{\mathbf{\beta }}}^{ols}\ne {\widehat{\mathbf{\beta }}}^{tlp}\right]$:

$$\begin{array}{cc}\hfill min& \left\{\frac{\sqrt{2}{p}_0{n}^{1/2}\tau }{\sigma \sqrt{\pi }{\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}exp\left(-\frac{n{\left({\gamma }_{min}-\tau \right)}^2}{2{\sigma }^2{\eta }_{min}^{-1}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}\right),\right.\hfill \\ & \left.p_0\Phi \left(-\frac{n^{1/2}\left({\gamma }_{min}-\tau \right)}{\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}\right)\right\}\hfill \\ & +4exp\left(-\left(\frac{n{C}_{min}}{20{\sigma }^2}-(\alpha +1)log(p+1)-\frac{n\lambda }{4{\sigma }^2}\right)\right)\hfill \\ & +4exp\left(-\left(\frac{(\alpha -1)n\lambda }{6\alpha {\sigma }^2}-\left(1+\frac{1}{\alpha }\right)(log(p+1)-\frac{5}{3})\right)\right)\hfill \\ & +p_0\Phi \left(-{\displaystyle \frac{n^{1/2}({\gamma }_{min}-\tau )}{\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}}\right)+q\Phi \left(-{\displaystyle \frac{n^{1/2}({\gamma }_{min}-\tau )}{p_0^{1/2}\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}}\right),\hfill \end{array}$$

which completes the proof.    □

Proof of Theorem 2.

We firstly show that $P\left[{\widehat{\mathbf{\beta }}}^{ols}\ne {\widehat{\mathbf{\beta }}}^{tlp}\right]\to 0$ as $n\to \infty$. From Mill’s ratio [35] it follows that

$$\Phi (-x)\le \frac{1}{\sqrt{2\pi }}\frac{1}{x}{e}^{-\frac{x^2}{2}},x>0.$$

Hence,

$$\begin{array}{cc}& \Phi \left(-\frac{n^{1/2}\left({\gamma }_{min}-\tau \right)}{\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}\right)\hfill \\ & \le \frac{1}{\sqrt{2\pi }}\frac{\sigma }{n^{1/2}{d}_1^{1/2}({\gamma }_{min}-\tau )}exp\left(-\frac{n{d}_1{({\gamma }_{min}-\tau )}^2}{2{\sigma }^2}\right),\hfill \end{array}$$

and

$$\begin{array}{cc}& \Phi \left(-\frac{n^{1/2}\left({\gamma }_{min}-\tau \right)}{p_0^{1/2}\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}\right)\hfill \\ & \le \frac{1}{\sqrt{2\pi }}\frac{p_0^{1/2}\sigma }{n^{1/2}{d}_1^{1/2}({\gamma }_{min}-\tau )}exp\left(-\frac{n{d}_1{({\gamma }_{min}-\tau )}^2}{2p_0{\sigma }^2}\right).\hfill \end{array}$$

Since ${\gamma }_{min}\asymp n^{-\frac{1-a_{\gamma }}{2}}$, $\lambda \asymp n^{a_{\lambda }}$, $p_0\asymp n^{p_0}$, $a_{\gamma }>a_{\lambda }$, $a_{\gamma }>a_{p_0}\ge 0$, it follows that

$$\begin{array}{cc}\hfill & max\left\{\frac{\sqrt{2}{p}_0{n}^{1/2}\tau }{\sigma \sqrt{\pi }{\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}exp\left(-\frac{n{\left({\gamma }_{min}-\tau \right)}^2}{2{\sigma }^2{\eta }_{min}^{-1}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}\right),\right.\hfill \\ & \left.p_0\Phi \left(-\frac{n^{1/2}\left({\gamma }_{min}-\tau \right)}{\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}\right)\right\}\hfill \\ \hfill \le & max\left\{\frac{\sqrt{2}{p}_0{n}^{1/2}{d}_2^{1/2}\tau }{\sigma \sqrt{\pi }},\frac{p_0^{3/2}\sigma }{\sqrt{2\pi }{n}^{1/2}{d}_1^{1/2}({\gamma }_{min}-\tau )}\right\}exp\left(-\frac{n{d}_1{({\gamma }_{min}-\tau )}^2}{2{\sigma }^2}\right)\hfill \\ \hfill & \to 0.\hfill \end{array}$$

(A1)

Similarly,

$$\begin{array}{cc}\hfill & q\Phi \left(-{\displaystyle \frac{n^{1/2}({\gamma }_{min}-\tau )}{p_0^{1/2}\sigma {\eta }_{min}^{-1/2}\left(\frac{1}{n}{\mathit{X}}_{{\mathcal{A}}^{*}}^T{\mathit{X}}_{{\mathcal{A}}^{*}}\right)}}\right)\hfill \\ \hfill & \le \frac{p_0}{\sqrt{2\pi }}\frac{p_0^{1/2}\sigma }{n^{1/2}{d}_1^{1/2}({\gamma }_{min}-\tau )}exp\left(-\frac{n{d}_1{({\gamma }_{min}-\tau )}^2}{2p_0{\sigma }^2}\right)\to 0.\hfill \end{array}$$

(A2)

Because $a_{lp}-1<a_{\lambda }<a_C$ and $a_{lp}\ge 0$, it follows that

$$\left(\frac{n{C}_{min}}{20{\sigma }^2}-(\alpha +1)log(p+1)-\frac{n\lambda }{4{\sigma }^2}\right)\to \infty ,$$

(A3)

and

$$\left(\frac{(\alpha -1)n\lambda }{6\alpha {\sigma }^2}-\left(1+\frac{1}{\alpha }\right)(log(p+1)-\frac{5}{3})\right)\to \infty .$$

(A4)

Combining the limits (A1)–(A4), we obtain the selection consistency from Theorem 1.

   Asymptotic properties: From Equation (6) we know that ${\widehat{\beta }}_{{\mathcal{A}}^{*}}^{ols}$ has a multivariate normal distribution with mean ${\beta }_{{\mathcal{A}}^{*}}^{*}$ and covariance matrix $\frac{{\sigma }^2}{n}{\left(\frac{{\mathit{X}}_{{\mathcal{A}}^{*}}^{\top }{\mathit{X}}_{{\mathcal{A}}^{*}}}{n}\right)}^{-1}$. By the selection consistency in part (A) we obtain the asymptotic distribution (7).   □

Appendix A.2. The Details of Algorithm

The objective function in the first minimization step (11) is a quadratic function plus a TLP function. This is a non-convex minimization which can be solved by the difference of the convex (DC) method [17,23]. The DC method is used to decompose a non-convex function into the difference of convex functions so that the algorithms and properties of convex optimization can be applied. By DC decomposition and some calculations, the minimization subproblem (11) is equivalent to minimize (A5) with regard to $\mathbf{\beta }$,

$$\begin{array}{c}\hfill h^{\left(m\right)}\left(\mathbf{\beta }\right)=L\left(\mathbf{\beta }\right)+\frac{\lambda }{\tau }\sum _{i=1}^q\sum _{j=1}^{g_i}\left|{\beta }_{i,j}\right|\mathbb{I}({\widehat{\beta }}_{i,j}^{(m-1)}\le \tau ).\end{array}$$

(A5)

Let us begin with the DC decomposition of the objective function $h\left(\mathbf{\beta }\right)=h_1\left(\mathbf{\beta }\right)-h_2\left(\mathbf{\beta }\right)$, where

$$\begin{array}{ccc}& & h_1\left(\mathbf{\beta }\right)=L\left(\mathbf{\beta }\right)+\lambda \sum _{j=1}^p{J}_1\left(\right|{\beta }_{i,j}\left|\right),h_2\left(\mathbf{\beta }\right)=\lambda \sum _{i=1}^q\sum _{j=1}^{g_i}{J}_2\left(\right|{\beta }_{i,j}\left|\right)\hfill \\ & & L\left(\mathbf{\beta }\right)=n^{-1}{\parallel \mathit{Y}-\mathit{X}\mathbf{\beta }\parallel }_2^2+\frac{\rho }{2}{\parallel \mathbf{\beta }-{\mathbf{\alpha }}^k+{\mathbf{\mu }}^k\parallel }_2^2\hfill \\ & & J_1\left(\right|{\beta }_{i,j}\left|\right)=\frac{|{\beta }_{i,j}|}{\tau },J_2\left(\right|{\beta }_{i,j}\left|\right)=max\{\frac{|{\beta }_{i,j}|}{\tau }-1,0\}.\hfill \end{array}$$

It is clear that $L\left(\mathbf{\beta }\right)$ is a convex function of $\mathbf{\beta }$. Using the DC decomposition, a sequence of linear approximations $h^{\left(m\right)}\left(\mathbf{\beta }\right)$ of $h\left(\mathbf{\beta }\right)$ is constructed. Let $\nabla h_2$ be the subgradient of $h_2$. At the m-th iteration, replacing $h_2\left(\mathbf{\beta }\right)$ by its majorization, we obtain

$$\begin{array}{c}\hfill h^{\left(m\right)}\left(\mathbf{\beta }\right)=h_1\left(\mathbf{\beta }\right)-(h_2({\widehat{\mathbf{\beta }}}^{(m-1)})+\left(\right|\mathbf{\beta }|-|{\widehat{\mathbf{\beta }}}^{(m-1)}{\left|\right)}^{\top }\nabla h_2\left(\right|{\widehat{\mathbf{\beta }}}^{(m-1)}\left|\right)),\end{array}$$

where $\left|\mathbf{\beta }\right|$ denotes the vector obtained by replacing each component of $\mathbf{\beta }$ with its absolute value. After ignoring the terms that are independent of $\mathbf{\beta }$, the $h^{\left(m\right)}\left(\mathbf{\beta }\right)$ becomes

$$\begin{array}{c}\hfill h^{\left(m\right)}\left(\mathbf{\beta }\right)=L\left(\mathbf{\beta }\right)+\frac{\lambda }{\tau }\sum _{i=1}^q\sum _{j=1}^{g_i}\left|{\beta }_{i,j}\right|\mathbb{I}({\widehat{\beta }}_{i,j}^{(m-1)}\le \tau ).\end{array}$$

(A6)

Minimizing (A6) gives the updated value ${\widehat{\mathbf{\beta }}}^{\left(m\right)}$. Repeat the process procedure until convergence.

Then, for the minimizing of (A6), we can use the adaptive weights ${\lambda }_{i,j}=\frac{\lambda }{\tau }\mathbb{I}\left(\right|{\widehat{\beta }}_{i,j}^{(m-1)}|\le \tau )$, (A6) can be rewritten as

$$\begin{array}{c}\hfill h^{\left(m\right)}\left(\mathbf{\beta }\right)=L\left(\mathbf{\beta }\right)+\sum _{i=1}^q\sum _{j=1}^{g_i}{\lambda }_{i,j}\left|{\beta }_{i,j}\right|.\end{array}$$

(A7)

Note that the second term in (A7) is a separable function in variable $\mathbf{\beta }$. This property enables us to use coordinate descent algorithm [24,25] for minimization. Similar to the results of regular Lasso [36], the updating formula for $\mathbf{\beta }$ is

$$\begin{array}{c}\hfill {\beta }_{i,j}\leftarrow {(\frac{2}{n}{\mathit{X}}_{i,j}^T{\mathit{X}}_{i,j}+\rho )}^{-1}S(Z_{i,j},{\lambda }_{i,j}),\end{array}$$

(A8)

were $Z_{i,j}=\frac{2}{n}{\mathit{X}}_{i,j}^T{\mathbf{r}}_{i,j}-\rho (-{\alpha }_{i,j}+{\mu }_{i,j})$, ${\mathbf{r}}_{i,j}=\mathit{Y}-{\mathit{X}}_{-(i,j)}{\mathbf{\beta }}_{-(i,j)}$, ${\mathit{X}}_{i,j}$ is the j-th column of ${\mathit{X}}_i$, ${\mathit{X}}_{-(i,j)}$ is the matrix $\mathit{X}$ with the j-th column of ${\mathit{X}}_i$ deleted, and ${\mathbf{\beta }}_{-(i,j)}$ is defined similarly. $S(z,\lambda )=\mathrm{Sign}\left(z\right)\left(\right|z|-\lambda )$ is the soft-thresholding operator. Updating Formula (A8) is cycled through all variables in turn. Repeated iteration of (A8) until convergence gives the estimate ${\widehat{\mathbf{\beta }}}^{\left(m\right)}$.

Finally, with the inner iteration (A8) and outer iteration Algorithm A1, we solve the minimization subproblem (11).

We summarize the DC algorithm for minimization (11) below.

Algorithm A1 DC algorithm for the minimization of (11).

(Initialization) Use ${\mathbf{\beta }}^k$ in k-th ADMM iteration as the initial estimate ${\widehat{\mathbf{\beta }}}^{\left(0\right)}$. (Iteration) At m-th DC iteration, compute ${\widehat{\mathbf{\beta }}}^{\left(m\right)}$ by minimizing (A5). (Termination) Stop when $|h({\widehat{\mathbf{\beta }}}^{(m-1)})-h({\widehat{\mathbf{\beta }}}^{\left(m\right)})|<ϵ$ and no components of ${\widehat{\mathbf{\beta }}}^{\left(m\right)}$ is at $\pm \tau$.

Next, we note that computing the projection (12) directly is not easy. Let ${\mathcal{C}}_1=\{\beta :{\sum }_{j=1,\cdots ,g_i}{\beta }_j={\omega }_i,i=1,\cdots ,q\}$. We divide the projection into two easier sequential projections: the first one is the projection from ${\mathbb{R}}^p$ onto space ${\mathcal{C}}_1$, and the second one is the projection from ${\mathcal{C}}_1$ to $\mathcal{C}$. The Theorem A1 below will guarantee the equivalence between the direct projection on $\mathcal{C}$ and the two sequential projections.

Theorem A1.

In Euclidean space, projection onto space $\mathcal{C}$$\mathbf{\beta }\stackrel{{\prod }_{\mathcal{C}}}{\to }{\mathbf{\beta }}_2$ is equivalent to the sequential projections onto space ${\mathcal{C}}_1$ and space $\mathcal{C}$:

$$\begin{array}{c}\hfill \mathbf{\beta }\stackrel{{\prod }_{{\mathcal{C}}_1}}{\to }{\mathbf{\beta }}_1\stackrel{{\prod }_{\mathcal{C}}}{\to }{\mathbf{\beta }}_2.\end{array}$$

(A9)

There exists a closed-form solution for ${\mathbf{\beta }}_1={\prod }_{{\mathcal{C}}_1}\mathbf{\beta }$.

Let ${\mathbf{\beta }}_1={({\beta }_{11},\cdots ,{\beta }_{1p})}^{\top }$. Assume there are $m_i$ elements in the i-th group $g_i$. We have

$$\begin{array}{c}\hfill {\beta }_{1j}={\beta }_j+\frac{{\omega }_i-{\sum }_{j=1}^{g_i}{\beta }_j}{m_i},i\in \{1,\cdots ,q\},j\in \{1,\cdots ,g_i\}.\end{array}$$

(A10)

The computation of the second projection is given in the proof of Theorem A1. The composition of these two sequential projections updates the value of $\mathbf{\alpha }$. The third step (13) is a direct calculation.

Proof of Theorem A1.

Without loss of generality, we assume that all variables belong to the same group. The proof is similar to the case when the number of groups for variables is more than 1. The parameter space ${\mathcal{C}}_1$ becomes ${\mathcal{C}}_1=\{\mathbf{\beta }:{\sum }_j{\beta }_j=1\}$.

Denote ${\mathbf{\beta }}_1={\prod }_{{\mathcal{C}}_1}\mathbf{\beta }$, and ${\mathbf{\beta }}_2={\prod }_{\mathcal{C}}{\mathbf{\beta }}_1$, where ${\mathbf{\beta }}_1={({\beta }_{11},\cdots ,{\beta }_{1p})}^{\top }$, and ${\mathbf{\beta }}_2={({\beta }_{21},\cdots ,{\beta }_{2p})}^{\top }$. The closed-form formula for ${\prod }_{{\mathcal{C}}_1}$ is given by (A10).

Now we are to calculate the projection ${\prod }_{{\mathcal{C}}_2}$. We assume that ${\mathbf{\beta }}_1$ has u positive elements, v zero elements, and $p-u-v$ negative elements:

$$\left\{\begin{array}{cc}{\beta }_{1j}>0\hfill & 1\le j\le u\hfill \\ {\beta }_{1j}=0\hfill & u+1\le j\le u+v\hfill \\ {\beta }_{1j}<0\hfill & u+v+1\le j\le p.\hfill \end{array}\right.$$

(A11)

Let $c_u={\displaystyle \frac{1-{\sum }_{j=1}^u{\beta }_{1j}}{u}}$. The projection ${\mathbf{\beta }}_2={\prod }_{\mathcal{C}}{\mathbf{\beta }}_1$ is given by

$${\beta }_{2j}=\left\{\begin{array}{cc}{\beta }_{1j}+c_u\hfill & 1\le j\le u\hfill \\ 0\hfill & u+v+1\le j\le p.\hfill \end{array}\right.$$

(A12)

It is possible that some of ${\beta }_{2j}$, $1\le j\le u$ are negative. If this is the case, we will repeat the above procedure (A11) and (A12) until there are no negative elements in ${\mathbf{\beta }}_2$. This completes the proof. □

Appendix A.3. The Details of Simulation

In the simulation study, we consider the model $\mathbf{y}=\mathit{X}\mathbf{\beta }+\sigma \mathbf{ϵ}$. The covariates $\mathit{X}$ are generated from a multivariate normal distribution with all marginal distributions being standard normal distribution $N(0,1)$. The correlation matrix of $\mathit{X}$ is denoted by $\mathit{R}$.

We assume three settings for the correlation matrix $\mathit{R}$:

(1)

Independence structure: $\mathit{R}$ is the identity matrix;

(2)

$AR\left(1\right)$ correlation without group structure: $\mathit{R}={\left(r_{j,l}\right)}_{j,l=1}^p$, where $r_{j,l}=0.5^{|j-l|}$ for $j,l=1,\cdots ,p$;

(3)

$AR\left(1\right)$ correlation with group structure: $\mathit{R}={\left(r_{j,l}\right)}_{j,l=1}^p$, where $r_{j,l}=0.5^{|j-l|}$ for $j,l=1,\cdots ,g_i$ and $r_{j,l}=0$ for $j=1,\cdots g_i$ and $l=1,\cdots ,g_{i^{\prime }}$, $i\ne i^{\prime }$.

As to the dimension of the covariates $\mathit{X}$, two cases $n<p$ and $n>p$ will be considered. We use $p=100$. The parameter vector $\mathbf{\beta }$ is divided into 5 groups, with 20 elements in each group. The numbers of non-zero elements in each group are 3, 3, 1, 2, and 5, respectively. The true values of $\mathbf{\beta }$ are

$$\begin{array}{c}\hfill {\mathbf{\beta }}^0=(\underbrace{0.12,0.04,0.05,\begin{array}{c}\underbrace{0,\cdots ,0}\\ 17\end{array}},\underbrace{0.09,0.02,0.03,\begin{array}{c}\underbrace{0,\cdots ,0}\\ 17\end{array}},\underbrace{0.17,\begin{array}{c}\underbrace{0,\cdots ,0}\\ 19\end{array}},\\ \hfill \underbrace{0.2,0.12,\begin{array}{c}\underbrace{0,\cdots ,0}\\ 18\end{array}},\underbrace{0.02,0.04,0.03,0.02,0.05,\begin{array}{c}\underbrace{0,\cdots ,0}\\ 15\end{array}}).\end{array}$$

The sum of coefficients for each group are ${\gamma }_1=0.21$, ${\gamma }_2=0.14$, ${\gamma }_3=0.17$, ${\gamma }_4=0.32$, and ${\gamma }_5=0.16$, respectively. Besides, the numbers of zero elements in each group are 17, 17, 19, 18, and 15, respectively. The sample size n is set to be 50 and 2000, for low- and high-dimensional cases. The distribution of error term $\mathbf{ϵ}$ is the normal distribution $N(0,0.{05}^2)$, and the scaling parameter $\sigma$ takes two values: $\sigma =1$ and $\sigma =3$.

In each experiment, we randomly divide a dataset into training, tuning, and testing sets of 60%, 20%, and 20% of original sample sizes, respectively. We repeat the experiment 100 times and report the means of ME, TP, FP, PSR, NSR and the standard error of ME for each of the simulation settings.

As to tuning parameter selection, we will use five-fold cross-validation. The optimal choice of tuning parameters $\lambda$ and $\tau$ can be found by grid search [17]. Finding an optimal value for $\rho$ is not a straightforward problem [22], however, ref. [21] provides many heuristics that work well in practice. Here, we find out that a good choice of $\rho$ is around 1.