DL-Aided Underground Cavity Morphology Recognition Based on 3D GPR Data
Abstract
:1. Introduction
- (i)
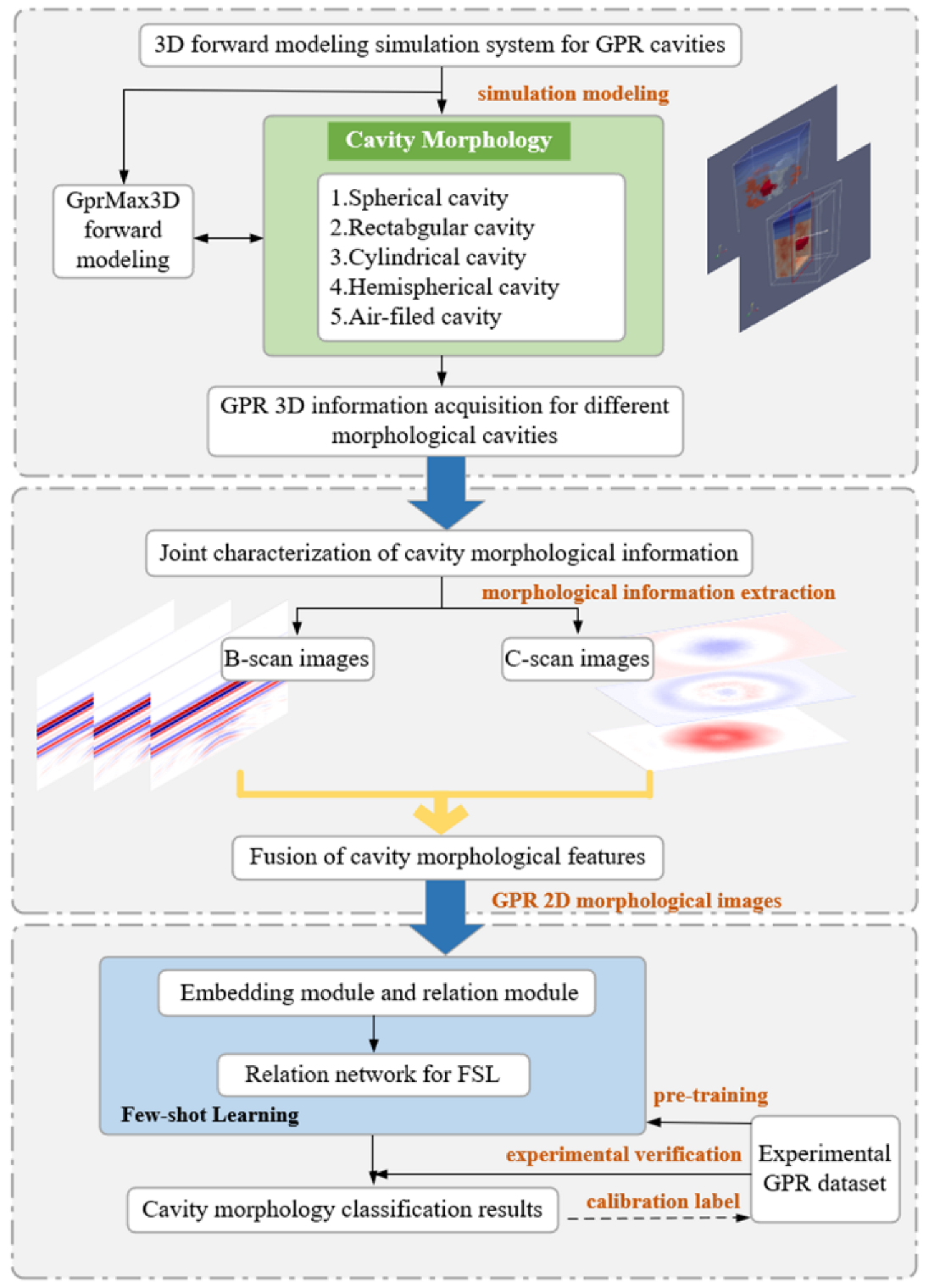
- First, a joint characterization algorithm was developed for cavity morphology that generates 2D morphological images and fully exploits 3D GPR spatial information;
- (ii)
- Second, we implemented a novel few-shot learning (FSL) network for cavity morphology classification and embedded a relation network (RelationNet) into the FSL model to adapt to different few-sample cavity scenarios.
2. Literature Review
3. Imaging Scheme of 3D GPR Data
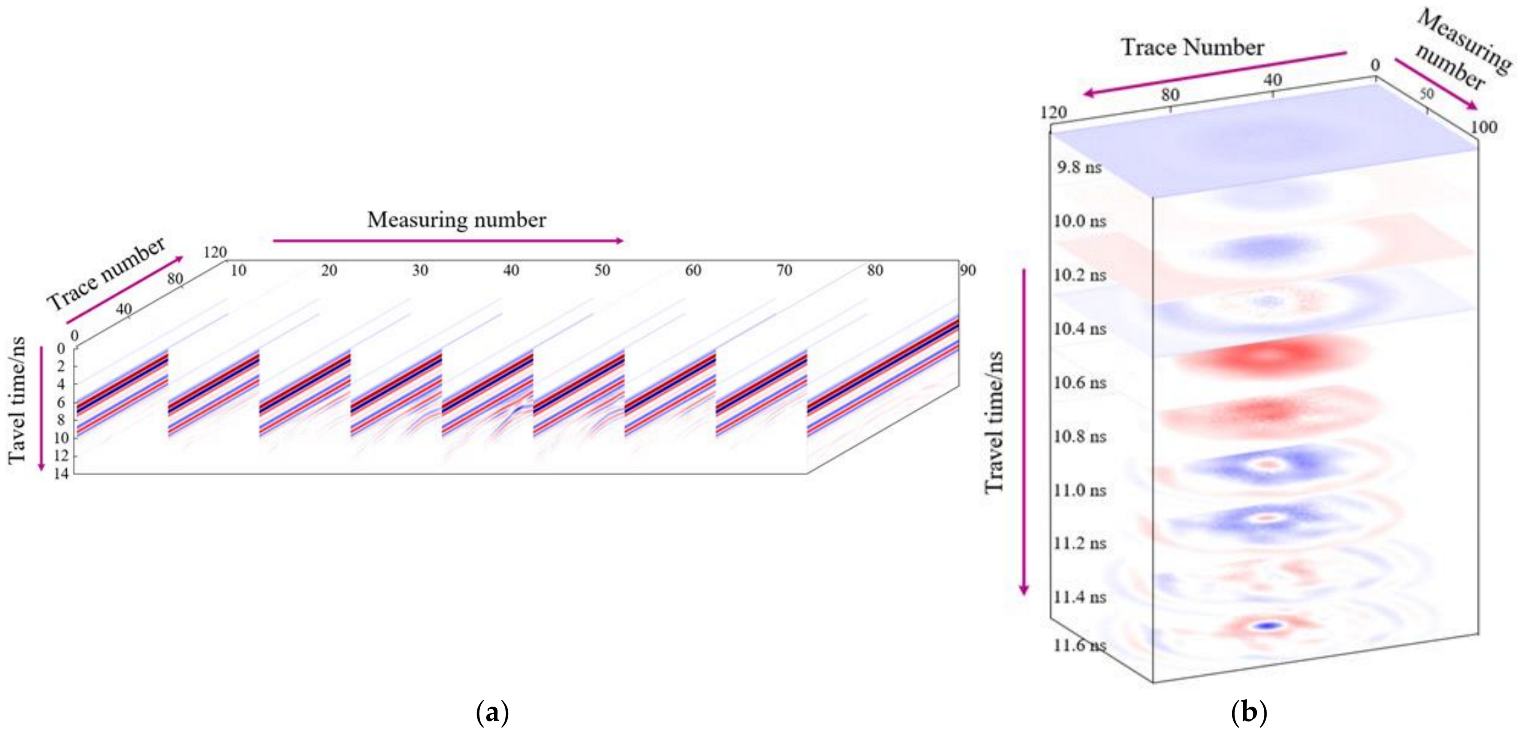
3.1. The 3D GPR Data Format
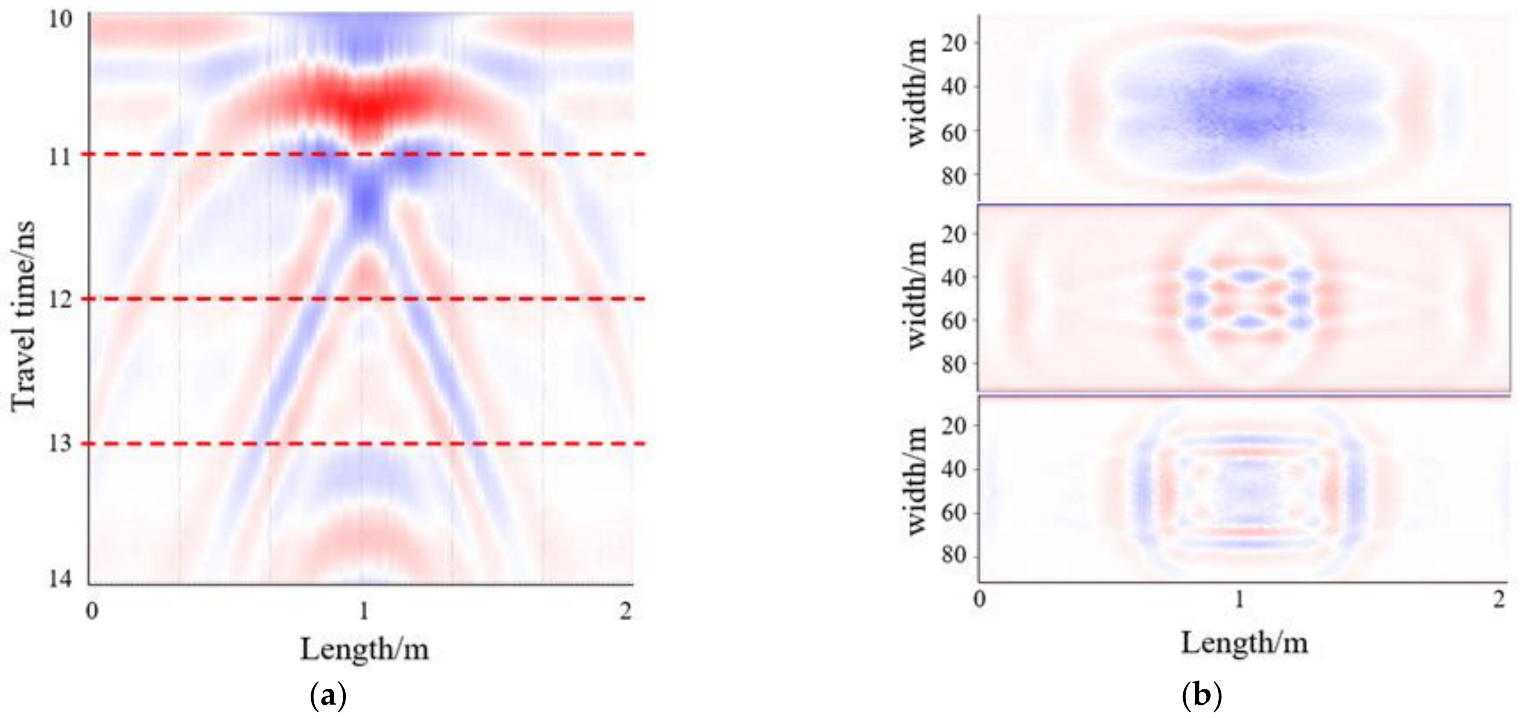
3.2. GPR Morphological Data Extraction
3.3. The 2D Morphological Image Generation
4. Few-Shot Learning Designed for Morphology Classification
4.1. FSL Definition
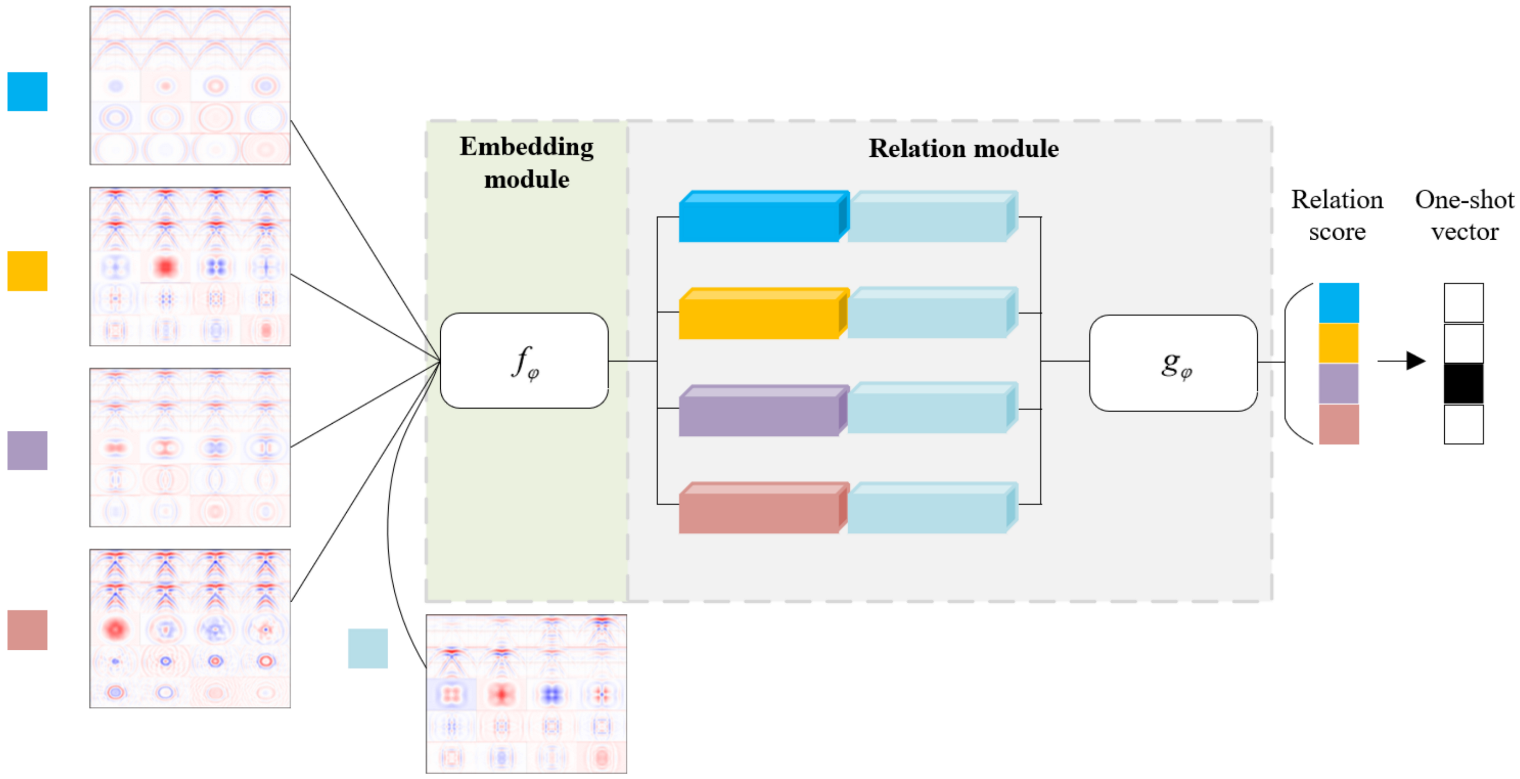
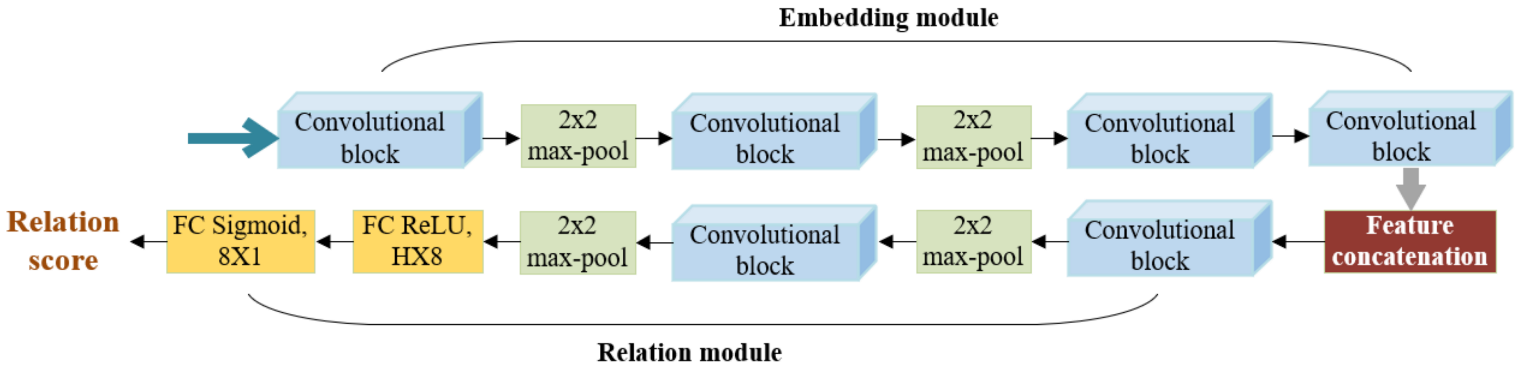
4.2. Relation Network Architecture and Relation Score Computation
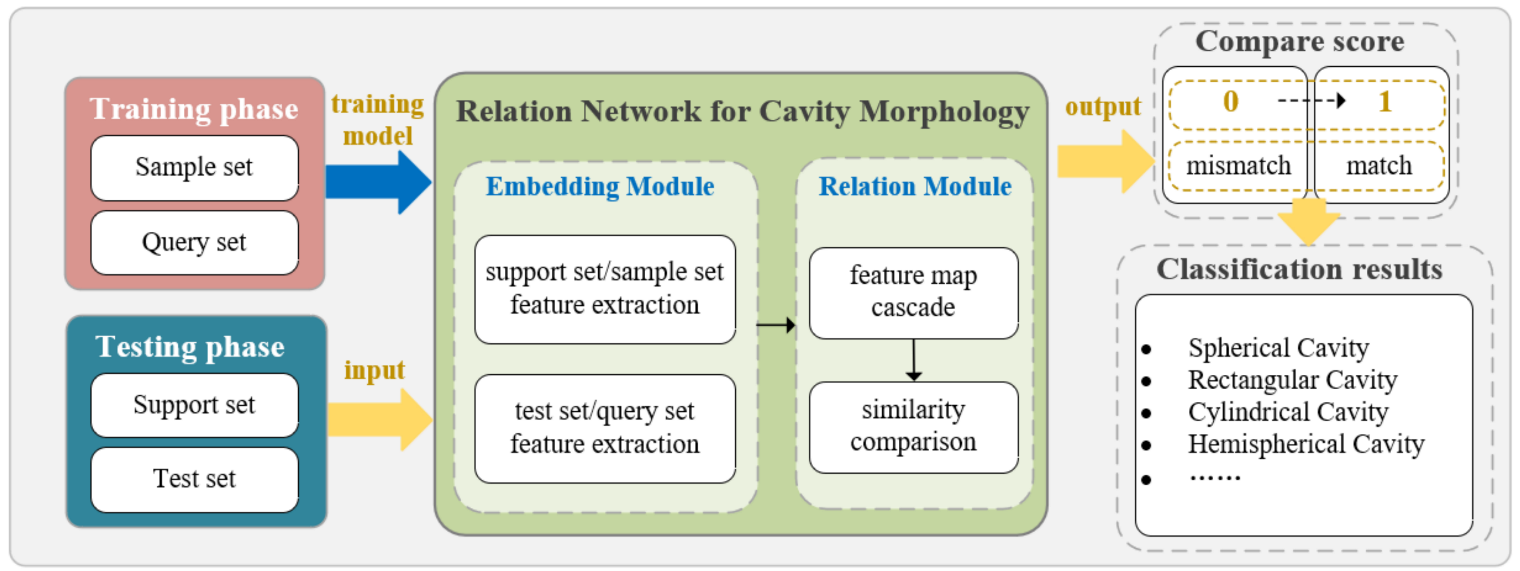
4.3. RelationNet-Based Cavity Morphology Classification Scheme
5. Experiments and Results
5.1. Experimental Settings
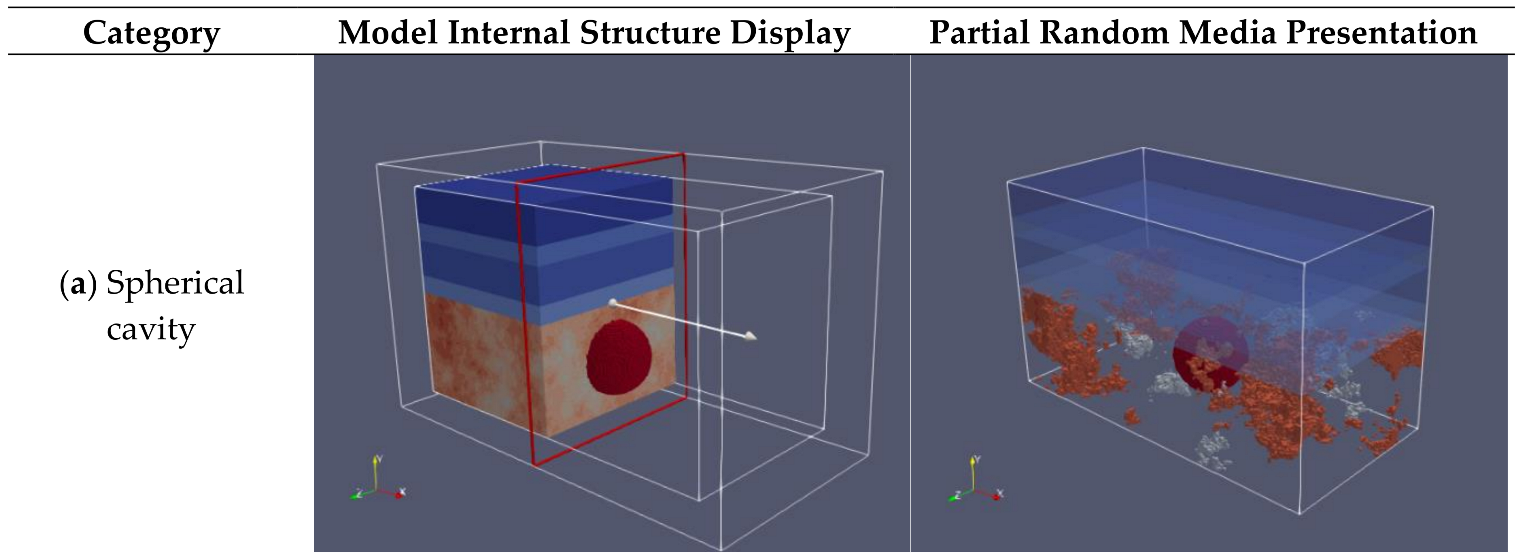
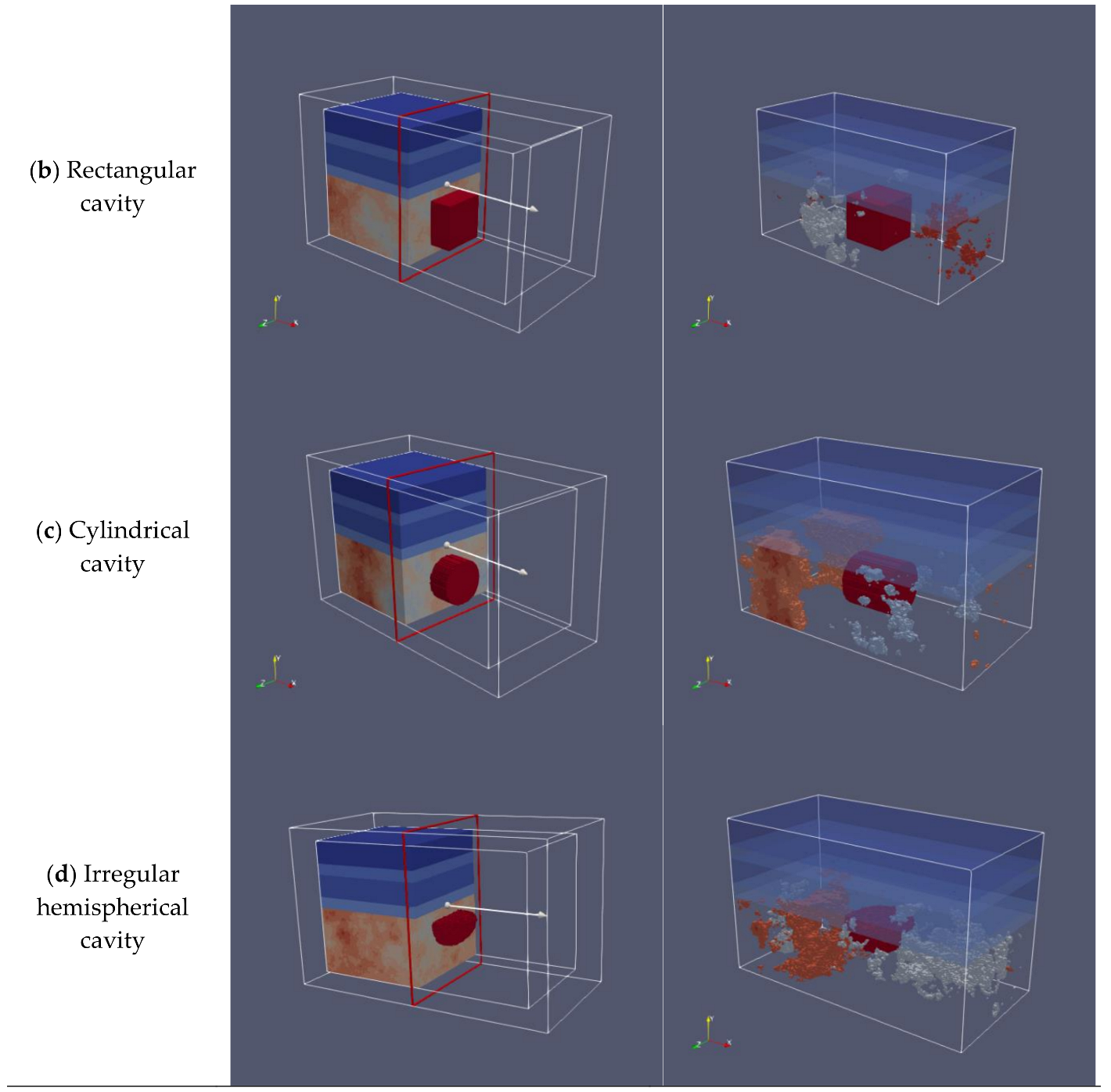
5.2. The 3D GPR Cavity Data Acquisition
5.3. Classification Results and Analysis
5.4. Comparison Experiments
5.4.1. RelationNet Evaluation on Different Embedding Backbones
5.4.2. RelationNet Evaluation on Different Benchmark Datasets
5.4.3. Performance Comparison of Different FSL Networks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Gutiérrez, F.; Parise, M.; Waele, J.; Jourde, H. A review on natural and human-induced geohazards and impacts in karst. Earth Sci. Rev. 2014, 138, 61–88. [Google Scholar]
- Garcia-Garcia, F.; Valls-Ayuso, A.; Benlloch-Marco, J.; Valcuende-Paya, M. An optimization of the work disruption by 3D cavity mapping using GPR: A new sewerage project in Torrente (Valencia, Spain). Constr. Build. Mater. 2017, 154, 1226–1233. [Google Scholar] [CrossRef] [Green Version]
- Jol, H.M. Ground Penetrating Radar Theory and Applications; Elseviere: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Meyers, R.; Smith, D.; Jol, H.; Peterson, C. Evidence for eight great earthquake-subsidence events detected with ground-penetrating radar, Willapa barrier, Washington. Geology 1996, 24, 99–102. [Google Scholar] [CrossRef]
- Qin, Y.; Huang, C. Identifying underground voids using a GPR circular-end bow-tie antenna system based on a support vector machine. Int..J. Remote Sens. 2016, 37, 876–888. [Google Scholar] [CrossRef]
- Park, B.; Kim, J.; Lee, J.; Kang, M.-S.; An, Y.-K. Underground object classification for urban roads using instantaneous phase analysis of Ground-Penetrating Radar (GPR) Data. Remote Sens. 2018, 10, 1417. [Google Scholar] [CrossRef] [Green Version]
- Hong, W.-T.; Lee, J.-S. Estimation of ground cavity configurations using ground penetrating radar and time domain reflectometry. Nat. Hazards 2018, 92, 1789–1807. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, W. Curvelet transform-based identification of void diseases in ballastless track by ground-penetrating radar. Struct. Control Health Monit. 2019, 26, e2322–e2339. [Google Scholar] [CrossRef]
- Chen, J.; Li, S.; Liu, D.; Li, X. AiRobSim: Simulating a Multisensor Aerial Robot for Urban Search and Rescue Operation and Training. Sensors 2020, 20, 5223–5242. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Li, S.; Chen, J.; Kamat, V.R. Detecting, locating, and characterizing voids in disaster rubble for search and rescue. Adv. Eng. Inform. 2019, 42, 100974–100982. [Google Scholar] [CrossRef]
- Rasol, M.; Pais, J.; Pérez-Gracia, V.; Solla, M.; Fernandes, F.; Fontul, S.; Ayala-Cabrera, D.; Schmidt, F.; Assadollahi, H. GPR monitoring for road transport infrastructure: A systematic review and machine learning insights. Constr. Build. Mate. 2022, 324, 126686. [Google Scholar] [CrossRef]
- Liu, Z.; Gu, X.; Yang, H.; Wang, L.; Chen, Y.; Wang, D. Novel YOLOv3 Model With Structure and Hyperparameter Optimization for Detection of Pavement Concealed Cracks in GPR Images. IEEE T Intell. Transp. Syst. 2022, 1, 1–11. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Mizutani, T.; Meguro, K.; Hirano, T. Detecting Subsurface Voids From GPR Images by 3-D Convolutional Neural Network Using 2-D Finite Difference Time Domain Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3061–3073. [Google Scholar] [CrossRef]
- Yamashita, Y.; Kamoshita, T.; Akiyama, Y.; Hattori, H.; Kakishita, Y.; Sadaki, T.; Okazaki, H. Improving efficiency of cavity detection under paved road from GPR data using deep learning method. In Proceedings of the 13th SEGJ International Symposium, Tokyo, Japan, 12–14 November 2018; Society of Exploration Geophysicists and Society of Exploration Geophysicists of Japan: Tykyo, Japan, 2019; pp. 526–529. [Google Scholar]
- Ni, Z.-K.; Zhao, D.; Ye, S.B.; Fang, G. City road cavity detection using YOLOv3 for ground-penetrating radar. In Proceedings of the18th International Conference on Ground Penetrating Radar, Golden, CO, USA, 14–19 June 2020; Society of Exploration Geophysicists: Houston, TX, USA, 2020; pp. 2159–6832. [Google Scholar]
- Liu, H.; Shi, Z.; Li, J.; Liu, C.; Meng, X.; Du, Y.; Chen, J. Detection of road cavities in urban cities by 3D ground-penetrating radar. Geophysics 2021, 86, WA25–WA33. [Google Scholar] [CrossRef]
- Feng, J.; Yang, L.; Hoxha, E.; Xiao, J. Improving 3D Metric GPR Imaging Using Automated Data Collection and Learning-based Processing. IEEE Sens. J. 2022, 1–13. [Google Scholar] [CrossRef]
- Luo, T.; Lai, W. GPR pattern recognition of shallow subsurface air voids. Tunn. Undergr. Sp. Tech. 2020, 99, 103355–103366. [Google Scholar] [CrossRef]
- Kim, N.; Kim, S.; An, Y.-K.; Lee, J.-J. Triplanar imaging of 3-D GPR data for deep-learning-based underground object detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4446–4456. [Google Scholar] [CrossRef]
- Kang, M.-S.; Kim, N.; Im, S.B.; Lee, J.-J.; An, Y.-K. 3D GPR image-based UcNet for enhancing underground cavity detectability. Remote Sens. 2019, 11, 2545–2562. [Google Scholar] [CrossRef] [Green Version]
- Kang, M.-S.; Kim, N.; Lee, J.-J.; An, Y.-K. Deep learning-based automated underground cavity detection using three-dimensional ground penetrating radar. Struct. Health Monit. 2020, 19, 173–185. [Google Scholar] [CrossRef]
- Khudoyarov, S.; Kim, N.; Lee, J.-J. Three-dimensional convolutional neural network–based underground object classification using three-dimensional ground penetrating radar data. Struct. Health Monit. 2020, 19, 1884–1893. [Google Scholar] [CrossRef]
- Kim, N.; Kim, K.; An, Y.-K.; Lee, H.-J.; Lee, J.-J. Deep learning-based underground object detection for urban road pavement. Int. J. Pavement Eng. 2020, 21, 1638–1650. [Google Scholar] [CrossRef]
- Kim, N.; Kim, S.; An, Y.-K.; Lee, J.-J. A novel 3D GPR image arrangement for deep learning-based underground object classification. Int. J. Pavement Eng. 2021, 22, 740–751. [Google Scholar] [CrossRef]
- Abhinaya, A. Using Machine Learning to Detect Voids in an Underground Pipeline Using in-Pipe Ground Penetrating Radar. Master’s Thesis, University of Twente, Enschede, Holland, 2021. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Liu, Z.; Wu, W.; Gu, X.; Li, S.; Wang, L.; Zhang, T. Application of combining YOLO models and 3D GPR images in road detection and maintenance. Remote Sens. 2021, 13, 1081–1099. [Google Scholar] [CrossRef]
- Lu, J.; Gong, P.; Ye, J.; Zhang, C. Learning from very few samples: A survey. arXiv 2020, arXiv:2009.02653. [Google Scholar]
- Yang, S.; Liu, L.; Xu, M. Free lunch for few-shot learning: Distribution calibration. arXiv 2021, arXiv:2101.06395. [Google Scholar]
- Wang, Y.; Yao, Q.; Kwok, J.; Ni, L. Generalizing from a few examples: A survey on few-shot learning. ACM Comput. Surv. 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Santoro, A.; Bartunov, S.; Botvinick, M.; Wierstra, D.; Lillicrap, T. One-shot learning with memory-augmented neural networks. arXiv 2016, arXiv:1605.06065. [Google Scholar]
- Munkhdalai, T.; Yu, H. Meta networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–17 August 2017. [Google Scholar]
- Ravi, S.; Larochelle, H. Optimization as a model for few-shot learning. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–17 August 2017. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Kavukcuoglu, K.; Wierstra, D. Matching networks for one shot learning. Adv. Neural Inf. Process. Syst. 2016, 29, 3630–3638. [Google Scholar]
- Sung, F.; Yang, Y.; Zhang, L.; Xiang, T.; Torr, P.; Hospedales, T. Learning to compare: Relation network for few-shot learning. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1199–1208. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. ICML Deep. Learn. Workshop 2015, 2, 2015. [Google Scholar]
- Li, W.; Wang, L.; Xu, J.; Huo, J.; Gao, Y.; Luo, J. Revisiting local descriptor based image-to-class measure for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, California, CA, USA, 16–20 June 2019; pp. 7260–7268. [Google Scholar]
- Wertheimer, D.; Tang, L.; Hariharan, B. Few-shot classification with feature map reconstruction networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 8012–8021. [Google Scholar]
- Kang, D.; Kwon, H.; Min, J.; Cho, M. Relational Embedding for Few-Shot Classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 8822–8833. [Google Scholar]
- Zhang, C.; Cai, Y.; Lin, G.; Shen, C. Deepemd: Few-shot image classification with differentiable earth mover’s distance and structured classifiers. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Seattle, WA, USA, 13–19 June 2020; pp. 12203–12213. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Li, W.; Dong, C.; Tian, P.; Qin, T.; Yang, X.; Wang, Z.; Huo, J.; Shi, Y.; Wang, L.; Gao, Y.; et al. LibFewShot: A Comprehensive Library for Few-shot Learning. arXiv 2021, arXiv:2109.04898. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Bertinetto, L.; Henriques, J.; Torr, P.; Vedaldi, A. Meta-learning with differentiable closed-form solvers. arXiv 2018, arXiv:1805.08136. [Google Scholar]
- Chen, W.-Y.; Liu, Y.-C.; Kira, Z.; Wang, Y.-C.; Huang, J.-B. A closer look at few-shot classification. arXiv 2019, arXiv:1904.04232. [Google Scholar]
- Ren, M.; Triantafillou, E.; Ravi, S.; Snell, J.; Swersky, K.; Tenenbaum, J.; Larochelle, H.; Zemel, R. Meta-learning for semi-supervised few-shot classification. arXiv 2018, arXiv:1803.00676, 2018. [Google Scholar]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for ground penetrating radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef] [Green Version]
- Giannakis, I.; Giannopoulos, A.; Warren, C. A realistic FDTD numerical modeling framework of ground penetrating radar for landmine detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 37–51. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]







| System Parameters | Value |
|---|---|
| Spatial resolution/m | 0.01 |
| Time window/ns | 14 |
| Initial coordinate of transmit antenna/m | (0.45, 1.0, 0.0) |
| Initial coordinate of receive antenna/m | (0.35, 1.0, 0.0) |
| Antenna step distance/m | (0.01, 0, 0) |
| Measuring point number | 100 |
| Excitation signal type | Ricker |
| Excitation signal frequency/MHz | 800 |
| System Parameters | Relative Permittivity | Conductivity (S/m) |
|---|---|---|
| Air | 1 | 0 |
| Asphalt | 6 | 0.005 |
| Concrete (dry) | 9 | 0.05 |
| Gravel | 12 | 0.1 |
| System Parameters | Precision | Recall | F-Score |
|---|---|---|---|
| Spherical | 99.15 | 97.5 | 98.32 |
| Rectangular | 100 | 98.33 | 99.16 |
| Cylindrical | 99.16 | 98.33 | 98.74 |
| Hemispherical | 96 | 100 | 97.96 |
| Embedding Backbones | Four-Way One-Shot | Four-Way Five-Shot |
|---|---|---|
| Conv64F | 78.097 | 88.934 |
| ResNet12 | 69.467 | 72.500 |
| ResNet18 | 69.926 | 79.865 |
| Embedding Backbones | Four-Way One-Shot | Four-Way Five-Shot |
|---|---|---|
| miniImageNet | 78.097 | 88.934 |
| tieredImageNet | 77.086 | 97.328 |
| FSL Networks | Four-Way One-Shot | Four-Way Five-Shot |
|---|---|---|
| ProtoNet | 70.965 | 85.221 |
| R2D2 | 76.562 | 88.659 |
| BaseLine | 66.103 | 83.505 |
| RelationNet | 78.097 | 88.934 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, F.; Liu, X.; Fan, X.; Guo, Y. DL-Aided Underground Cavity Morphology Recognition Based on 3D GPR Data. Mathematics 2022, 10, 2806. https://doi.org/10.3390/math10152806
Hou F, Liu X, Fan X, Guo Y. DL-Aided Underground Cavity Morphology Recognition Based on 3D GPR Data. Mathematics. 2022; 10(15):2806. https://doi.org/10.3390/math10152806
Chicago/Turabian StyleHou, Feifei, Xu Liu, Xinyu Fan, and Ying Guo. 2022. "DL-Aided Underground Cavity Morphology Recognition Based on 3D GPR Data" Mathematics 10, no. 15: 2806. https://doi.org/10.3390/math10152806
APA StyleHou, F., Liu, X., Fan, X., & Guo, Y. (2022). DL-Aided Underground Cavity Morphology Recognition Based on 3D GPR Data. Mathematics, 10(15), 2806. https://doi.org/10.3390/math10152806






