A Thermal-Hydrological-Mechanical-Chemical Coupled Mathematical Model for Underground Coal Gasification with Random Fractures
Abstract
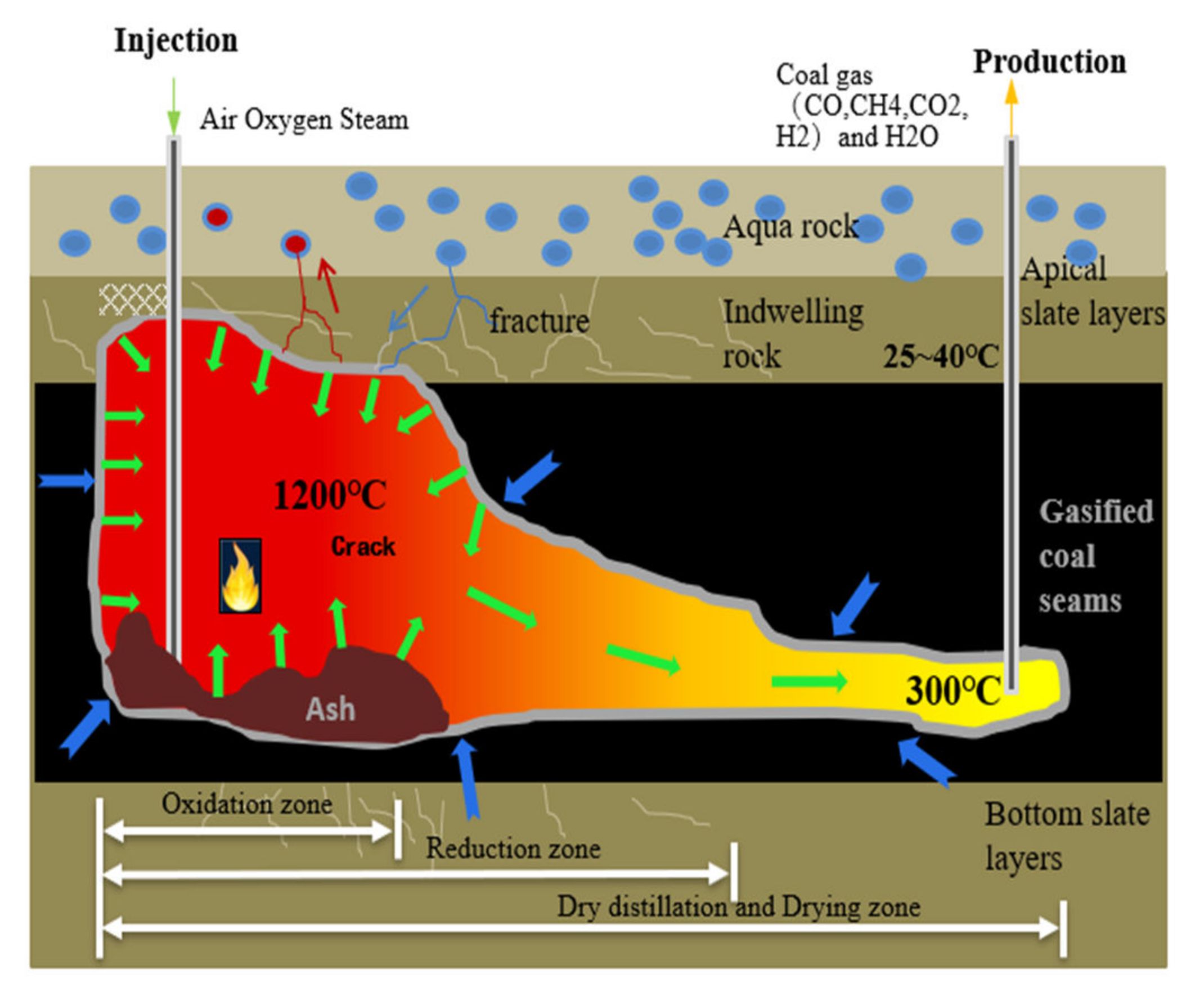
:1. Introduction
2. A Thermal-Hydrological-Mechanical-Chemical Coupled Mathematical Model for Underground Coal Gasification
2.1. Coal Seam Deformation Equation
2.2. Gas Transport Equation
2.3. Chemical Reaction Processes
2.4. Mixed Gaseous Species Transport Equation
2.5. Energy Equations
2.6. Petrophysical and Mechanical Properties
2.7. Cross-Coupling Equations
3. Numerical Analysis of Thermal-Hydrological-Mechanical-Chemical Coupling Process of Coal Gasification
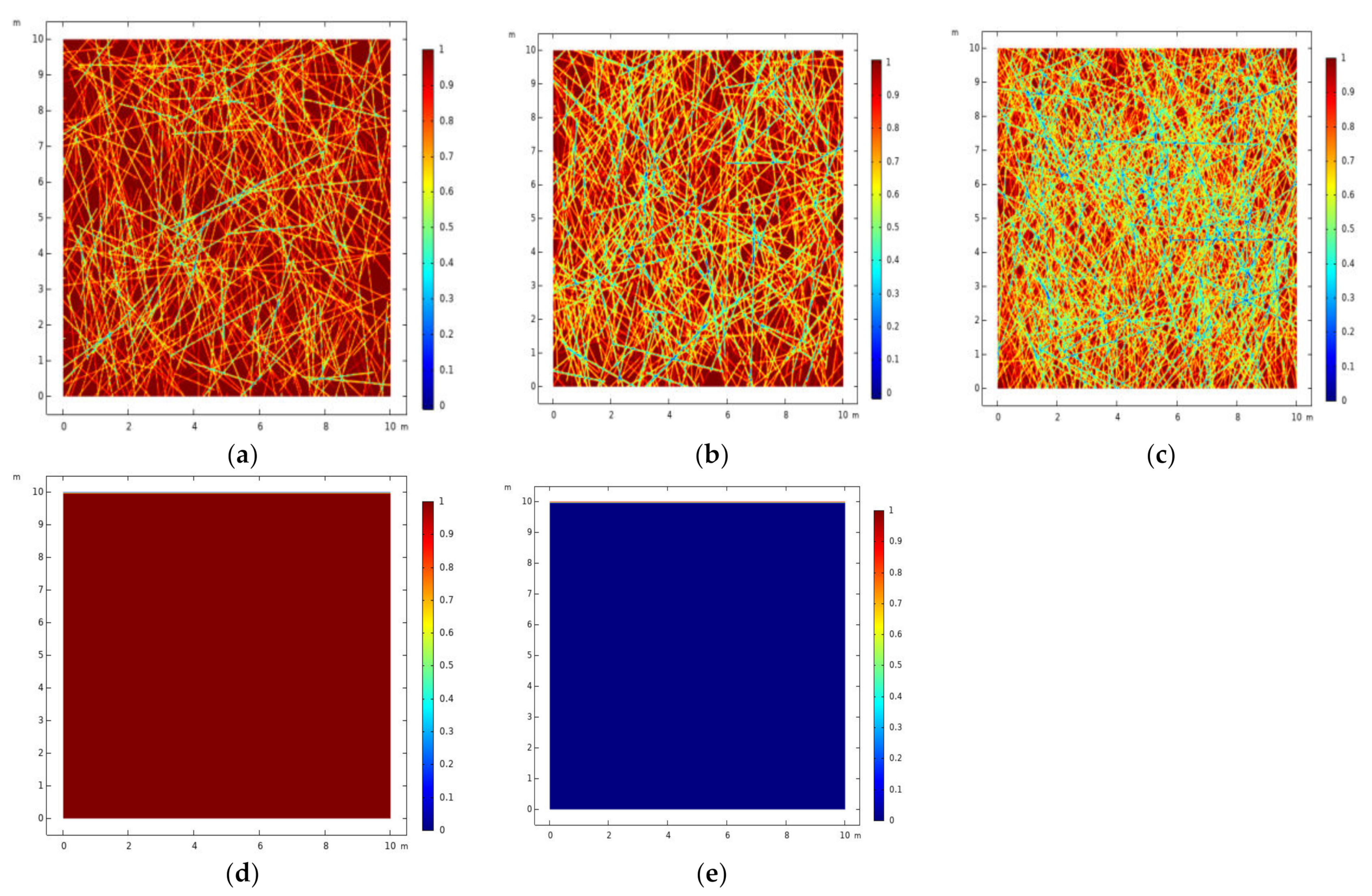
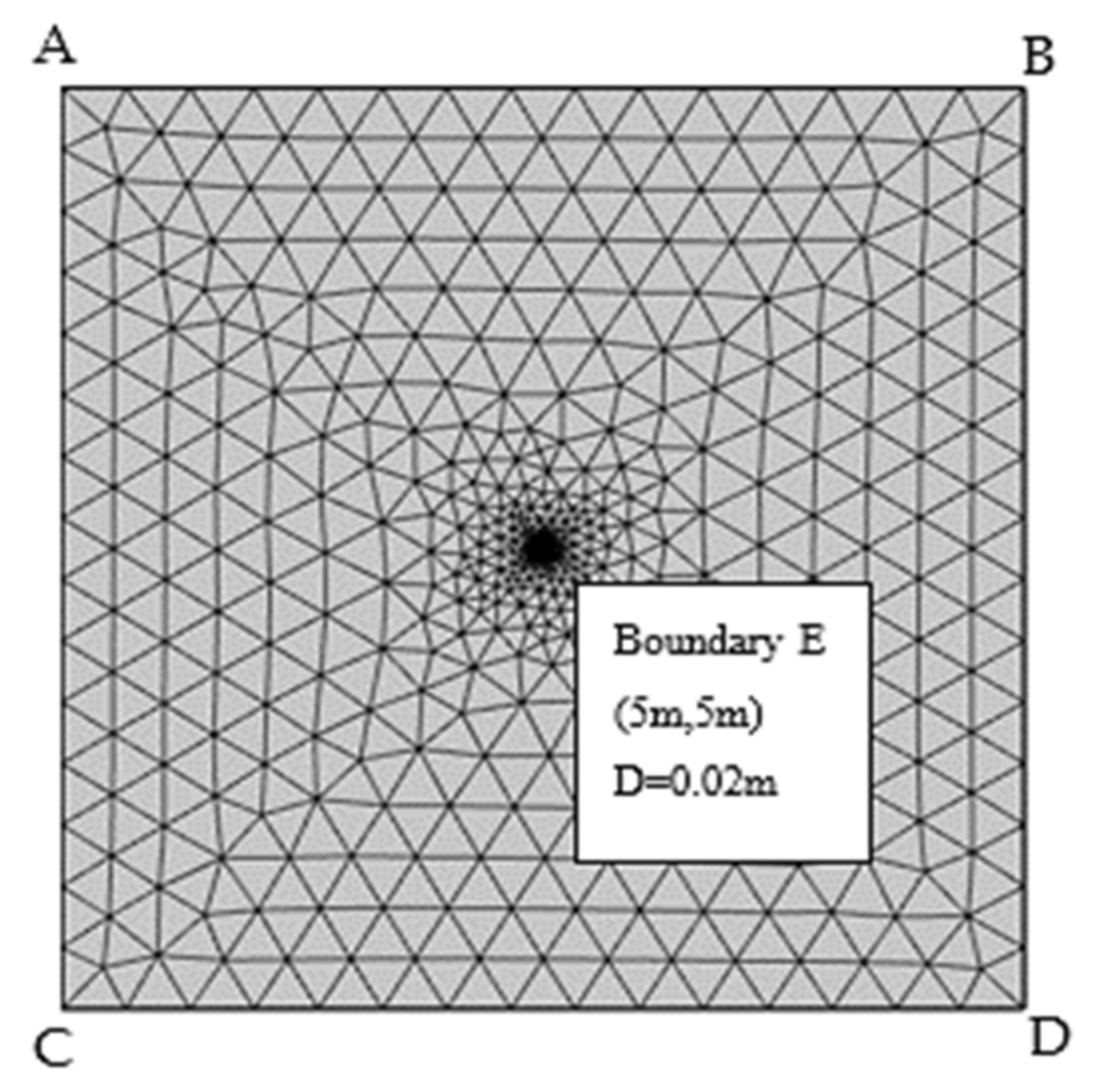
3.1. Establishment of Geometric Model
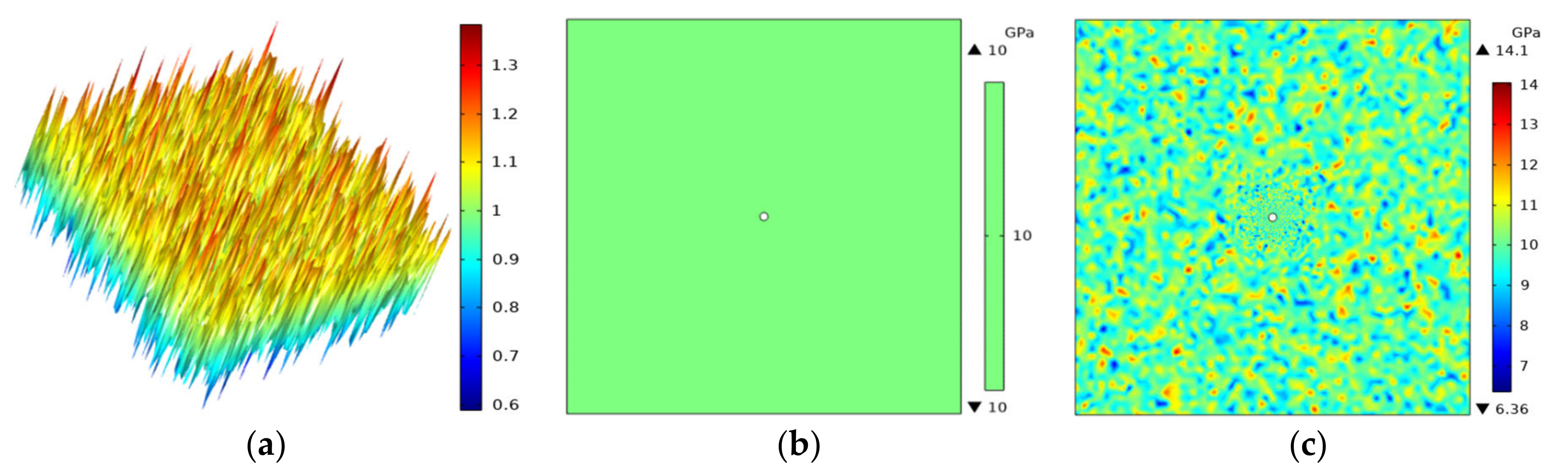
3.2. The Relationship between Coal Rock Mechanics and Temperature
3.3. Temperature Analysis of Fractured Rocks of Different Densities
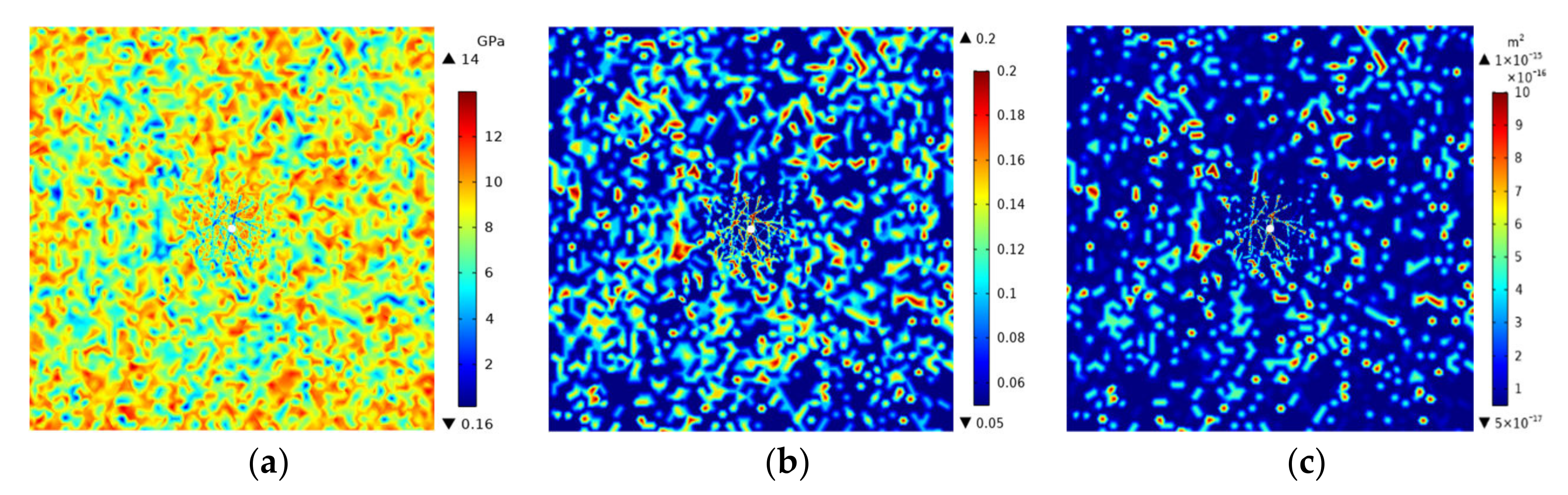
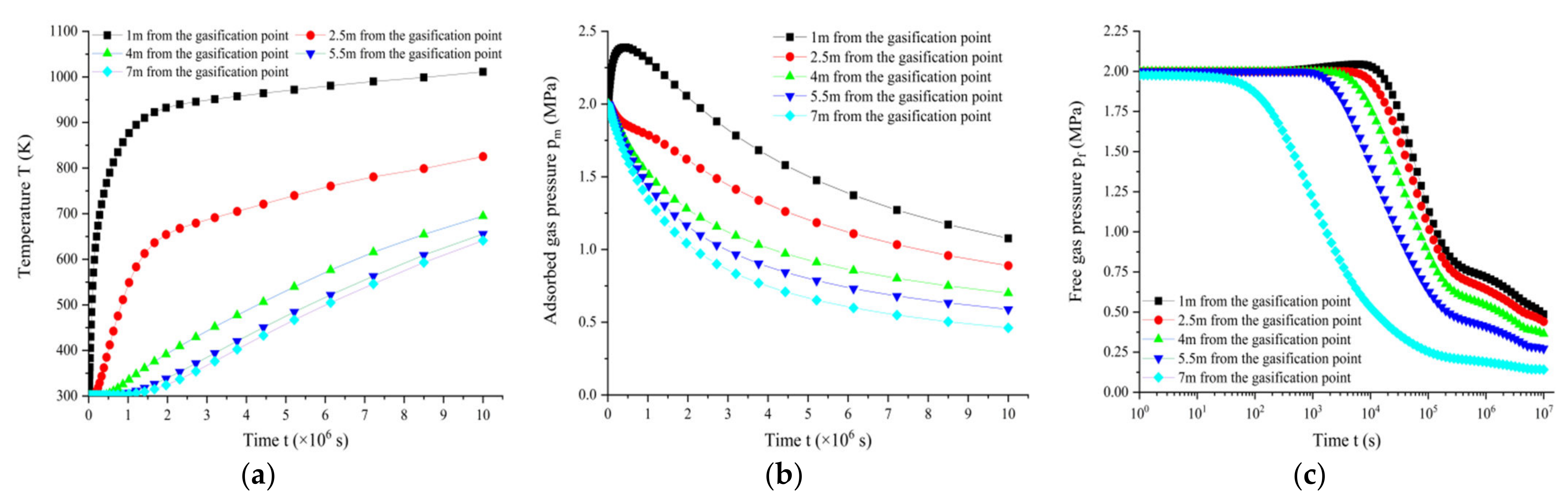
3.4. Analysis of Temperature, Air Pressure, Stress-Strain and Gasification Point Distance
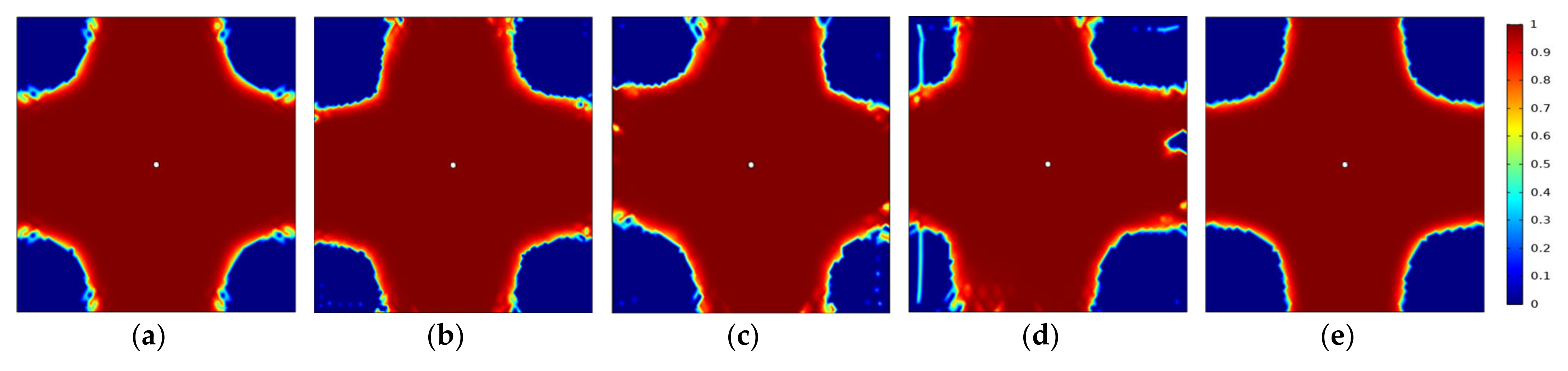
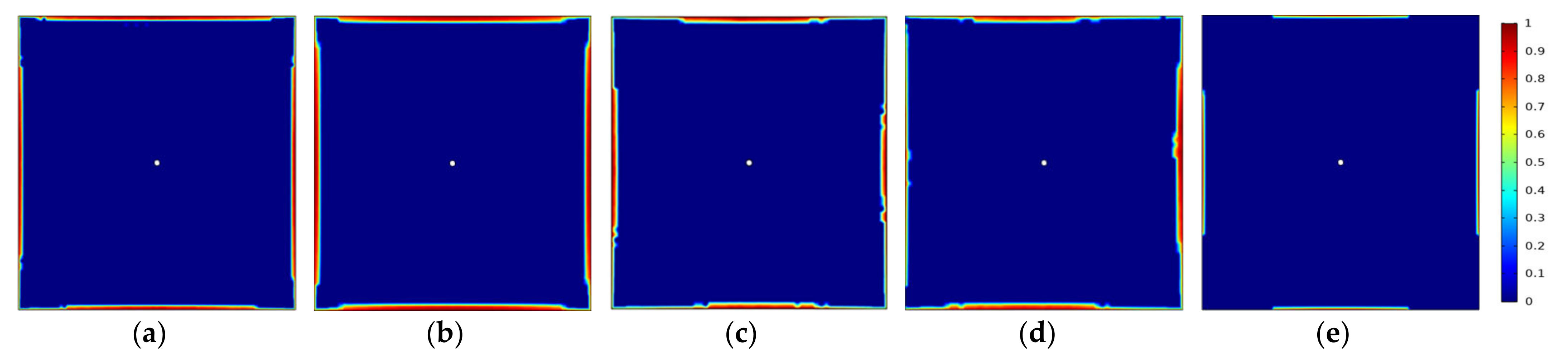
3.5. Coal Underground Gasification Gas Concentration Distribution
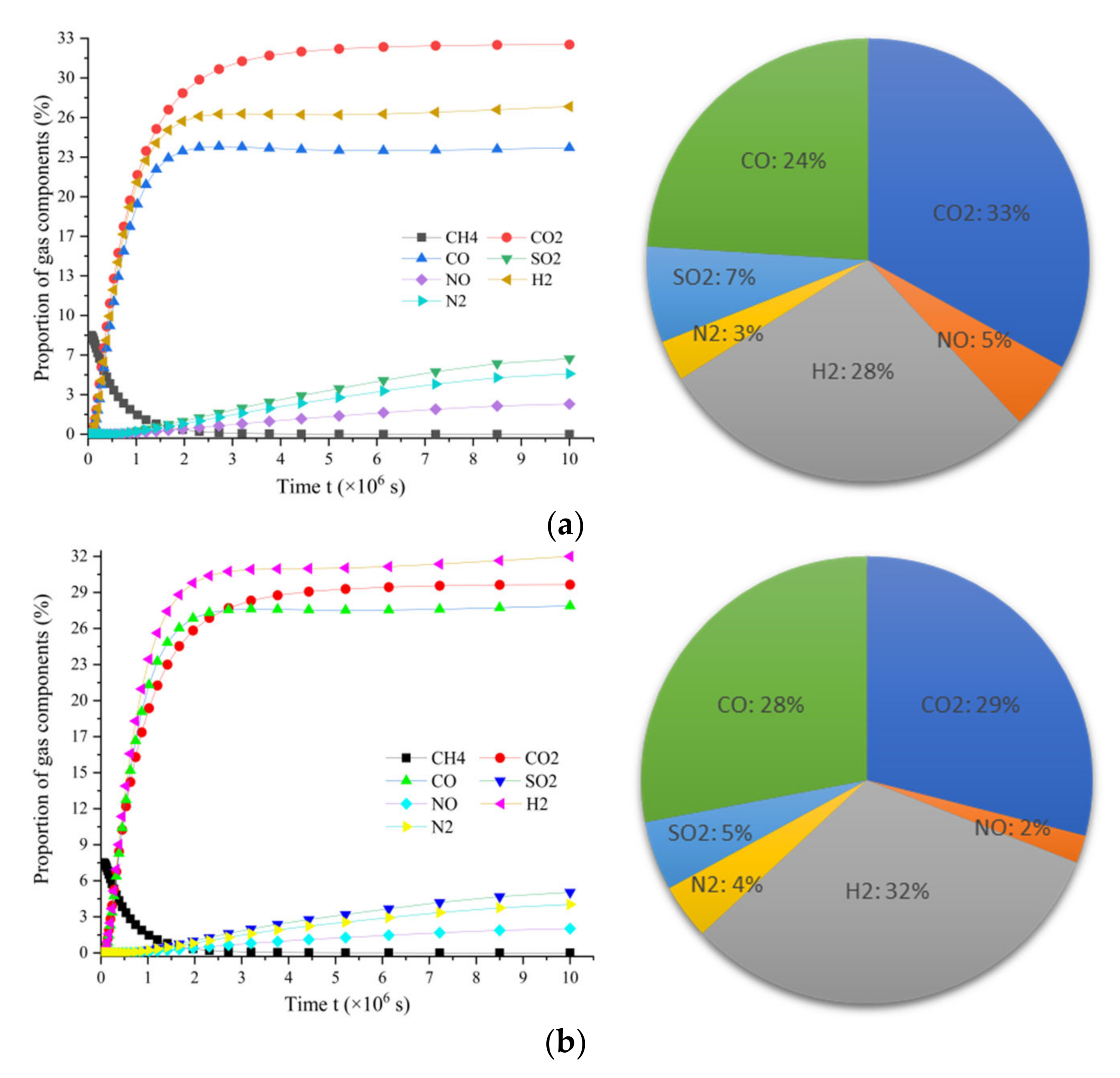
3.5.1. Proportions of Gas Products with Different Water-to-Oxygen Ratios
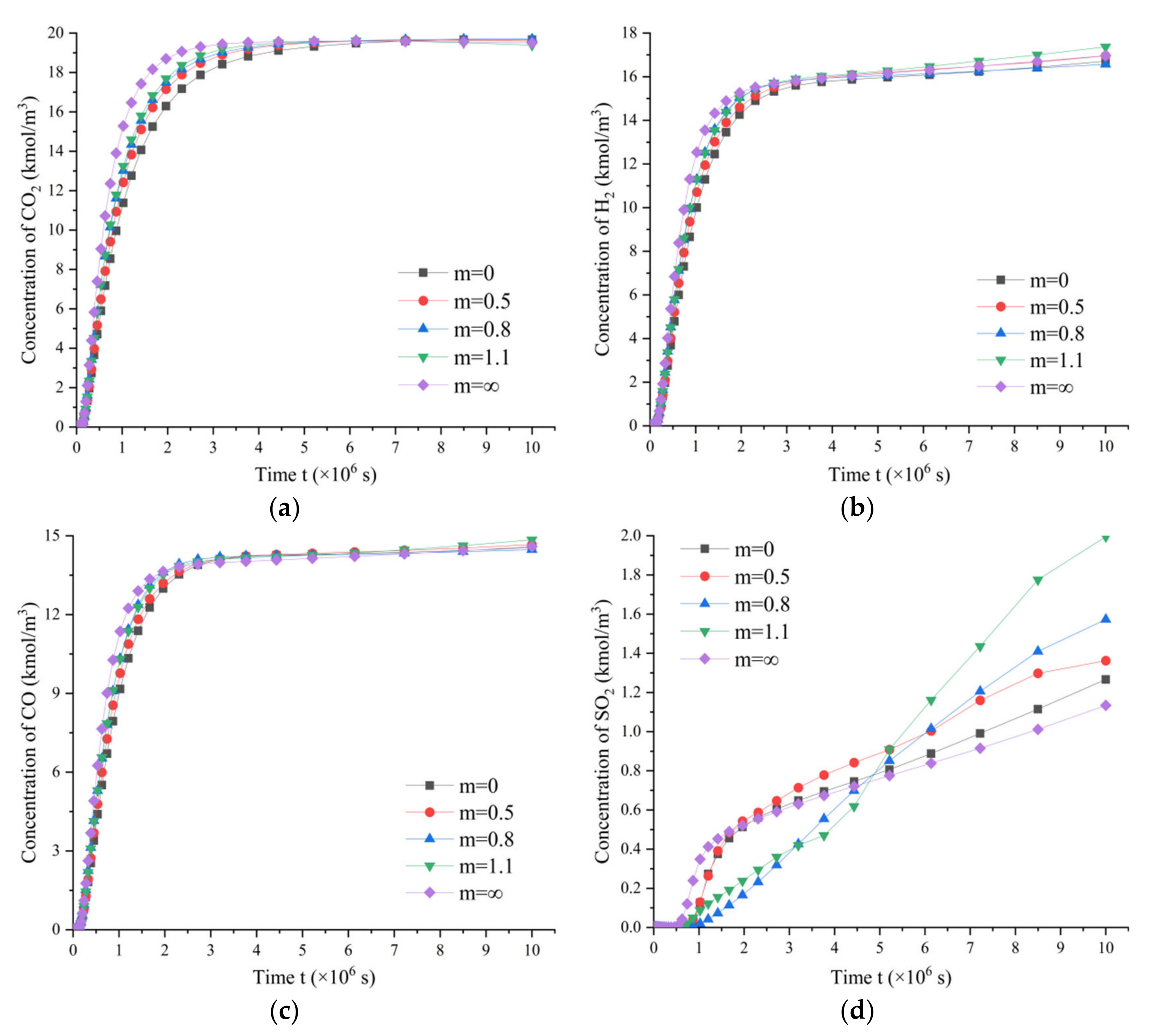
3.5.2. Variation of Gas Component Concentrations in Coal Rocks with Different Fracture Densities
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| K | Volume modulus of the coal matrix (GPa) |
| Ks | Volume modulus of coal particles (GPa) |
| E | Young’s modulus of coal matrix (GPa) |
| Es | Young’s modulus of coal particles (GPa) |
| ν | Poisson’s ratio |
| α | Biot factor |
| αT | Coefficient of thermal expansion (1/K) |
| p | Gas pressure (MPa) |
| T | Seam temperature (K) |
| Tar | Reference temperature of gas adsorption and desorption (K) |
| Ta | Standard temperature at standard atmospheric pressure (K) |
| Ah | Evaporation coefficient of water vapor (kg/(m3·K)) |
| Sv* | Amount of change in the reaction of water vapor (kg/(m3·s)) |
| εL | Adsorption strain under unlimited pore pressure |
| εs | Volumetric strain due to gas adsorption or desorption |
| εv | Volumetric strain |
| ui | Volume displacement in i direction (m) |
| σt | Tensile strength (MPa) |
| c1 | Pressure constant (1/MPa) |
| PL | Langmuir pressure constant at Tar temperature (MPa) |
| QHi | Enthalpy of reactions for each chemical reaction i (kJ/mol) |
| ρa | Gas density at standard atmospheric pressure (kg/m3) |
| φ | Rock friction angle (°) |
| rj | Different reaction rate j (mol/(m3·s)) |
| Cp | Specific heat capacity (J/(kg·K)) |
| k | Permeability (m2) |
| ρs | Seam density (kg/m3) |
| D | Damage variable |
| xf | The sub-coefficient of gas |
| Mg | Gas molar mass (kg/mol) |
| Mv | Water vapor molar mass (kg/mol) |
| τ | Adsorption gas desorption time (s) |
| t | Total time (s) |
| R | Universal gas constant (J/(mol·K)) |
| mb | Absorbed gas content in matrix (kg/m3) |
| v | Seepage velocity (m/s) |
| μ | Dynamic viscosity (Pa·s) |
| Tref | Reference temperature of environment (K) |
| Th0 | Reference temperature of water evaporation (K) |
| mv | Water in the coal rock changes from liquid to gaseous at high temperatures (kg/(m3)) |
| ci | Concentrations of different gas components i (mol/m3) |
| Sg* | Amount of change in the reaction of gas (kg/(m3·s)) |
| Aφ | Pore increase factor of moisture volatilization (1/K) |
| Vsg | Volume of adsorbed gas per unit mass coal seam |
| m | Fracture density |
| fi | Volume force in i direction (kg/m3) |
| σc | Compressive strength (MPa) |
| c2 | Temperature constant (1/K) |
| VL | Langmuir volume constant at Tar temperature (m3/kg) |
| D | Diffusion coefficient of the gas produced in the coal rock (m2/s) |
| κeff | Equivalent thermal conductivity (W/(m·K)) |
| (ρCp)eff | Equivalent specific heat capacity (J/(m3·K)) |
| Reaction rate coefficient | |
| κ | Thermal conductivity (W/(m·K)) |
| Porosity | |
| Ea | Apparent activation energy (kJ/mol) |
| A | Pre-exponential factor (1/s) |
| xv | The sub-coefficient of water vapor |
| Subscript | |
| 0 | Initial value of the variable |
| s | Solid phase |
| f | The fracture system of coal or free gas |
| g | Gas phase including free gas, adsorbed gas |
| m | The matrix system of coal or adsorbed gas |
| v | Water vapor |
References
- Khan, M.; Mmbaga, J.; Shirazi, A.; Trivedi, J.; Liu, Q.; Gupta, R. Modelling underground coal gasification—A review. Energies 2015, 8, 12603–12668. [Google Scholar] [CrossRef]
- Seifi, M.; Abedi, J.; Chen, Z. Application of porous medium approach to simulate UCG process. Fuel 2014, 116, 191–200. [Google Scholar] [CrossRef]
- Xie, J.; Xin, L.; Hu, X.; Cheng, W.; Liu, W.; Wang, Z. Technical application of safety and cleaner production technology by underground coal gasification in China. J. Clean. Prod. 2020, 250, 119487. [Google Scholar] [CrossRef]
- Wiatowski, M.; Kapusta, K.; Stańczyk, K.; Stańczyk, K. Efficiency assessment of underground gasification of ortho- and meta-lignite: High-pressure ex situ experimental simulations. Fuel 2019, 236, 221–227. [Google Scholar] [CrossRef]
- Perkins, G. Underground coal gasification—Part I: Field demonstrations and process performance. Prog. Energy Combust. 2018, 67, 158–187. [Google Scholar] [CrossRef]
- Liang, J.; Wang, Z.; Liang, K.; Li, Y. Progress and technology of underground coal gasification. J. Coal Soc. 2020, 45, 393–402. [Google Scholar]
- Liu, S.; Zhang, S.; Niu, M.; Yu, L. Technology process and application prospect of underground coal gasification. Geosci. Front. 2016, 23, 97–102. [Google Scholar]
- Li, H.; Guo, G.; Zheng, N. Influence of coal types on overlying strata movement and deformation in underground coal gasification without shaft and prediction method of surface subsidence. Process Saf. Environ. 2018, 120, 302–312. [Google Scholar] [CrossRef]
- Nourozieh, H.; Kariznovi, M.; Chen, Z.; Abedi, J. Simulation study of underground coal gasification in Alberta reservoirs: Geological structure and process modeling. Energy Fuels 2010, 24, 3540–3550. [Google Scholar] [CrossRef]
- Elahi, S.M.; Nassir, M.; Chen, Z. Effect of various coal constitutive models on coupled thermo-mechanical modeling of underground coal gasification. J. Pet. Sci. Eng. 2017, 154, 469–478. [Google Scholar] [CrossRef]
- Perkins, G.; Sahajwalla, V. Steady-state model for estimating gas production from underground coal gasification. Energy Fuels 2008, 22, 3902–3914. [Google Scholar] [CrossRef]
- Cui, Y.; Liang, J.; Wang, X. Numerical simulation on UCG process based on non-steady flow in porous media transport. J. China Coal Soc. 2014, 39, 231–238. [Google Scholar]
- Perkins, G. Underground coal gasification—Part II: Fundamental phenomena and modeling. Prog. Energy Combust. Sci. 2018, 67, 234–274. [Google Scholar] [CrossRef]
- Wiatowski, M.; Stańczyk, K.; Świądrowski, J.; Kapusta, K.; Cybulski, K.; Krause, E.; Grabowski, J.; Rogut, J.; Howaniec, N.; Smoliński, A. Semi-technical underground coal gasification (UCG) using the shaft method in Experimental Mine “Barbara”. Fuel 2012, 99, 170–179. [Google Scholar] [CrossRef]
- Gao, W.; Zagorščak, R.; Thomas, H.R. Insights into solid-gas conversion and cavity growth during Underground Coal Gasification (UCG) through Thermo-Hydraulic-Chemical (THC) modelling. Int. J. Coal Geol. 2021, 237, 103711. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, L.; Tang, F.; He, Y. Fracture evolution of overlying strata over combustion cavity under thermalmechanical interaction during underground coal gasification. J. China Coal Soc. 2012, 37, 1292–1298. [Google Scholar]
- Huang, W.; Wang, Z.; Xia, Y.; Xin, L. Numerical simulation of strip mining under thermal-mechanical coupling of underground coal gasification. Coal Sci. Technol. 2020, 1–8. Available online: http://kns.cnki.net/kcms/detail/11.2402.TD.20201218.1107.010.html (accessed on 25 June 2022).
- Najafi, M.; Jalali, S.M.E.; KhaloKakaie, R. Thermal–mechanical–numerical analysis of stress distribution in the vicinity of underground coal gasification (UCG) panels. Int. J. Coal Geol. 2014, 134–135, 1–16. [Google Scholar] [CrossRef]
- Seifi, M.; Chen, Z.; Abedi, J. Numerical simulation of underground coal gasification using the CRIP method. Can. J. Chem. Eng. 2011, 89, 1528–1535. [Google Scholar] [CrossRef]
- Andrianopoulos, E.; Korre, A.; Durucan, S. Chemical process modelling of underground coal gasification and evaluation of produced gas quality for end use. Energy Procedia 2015, 76, 444–453. [Google Scholar] [CrossRef]
- Vidana Pathiranagei, S.; Gratchev, I.; Kong, R. Engineering properties of four different rocks after heat treatment. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 16. [Google Scholar] [CrossRef]
- Xin, L.; Han, L.; Feng, M.; Li, K.; Wu, J.; Li, J. Study on thermal damage characteristics of similar overburden materials in underground coal gasification. Min. Res. Dev. 2021, 41, 52–57. [Google Scholar]
- Ludwik-Pardała, M.; Stańczyk, K. Underground coal gasification (UCG): An analysis of gas diffusion and sorption phenomena. Fuel 2015, 150, 48–54. [Google Scholar] [CrossRef]
- Kang, J.; Zhou, F.; Xia, T.; Ye, G. Numerical modeling and experimental validation of anomalous time and space subdiffusion for gas transport in porous coal matrix. Int. J. Heat Mass Transf. 2016, 100, 747–757. [Google Scholar] [CrossRef]
- Gao, W.; Zagorščak, R.; Thomas, H.R. Numerical study of ground deformation during underground coal gasification through coupled flow-geomechanical modelling. Fuel 2022, 315, 122833. [Google Scholar] [CrossRef]
- Xia, T.; Zhou, F.; Gao, F.; Kang, J.; Liu, J.; Wang, J. Simulation of coal self-heating processes in underground methane-rich coal seams. Int. J. Coal Geol. 2015, 141–142, 1–12. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, C.H.; Liu, J.; Qu, H.Y.; Elsworth, D. A model of coal–gas interaction under variable temperatures. Int. J. Coal Geol. 2011, 86, 213–221. [Google Scholar] [CrossRef]
- Wang, J.G.; Liu, J.; Kabir, A. Combined effects of directional compaction, non-Darcy flow and anisotropic swelling on coal seam gas extraction. Int. J. Coal Geol. 2013, 109–110, 1–14. [Google Scholar] [CrossRef]
- Gür, M.; Canbaz, E.D. Analysis of syngas production and reaction zones in hydrogen oriented underground coal gasification. Fuel 2020, 269, 117331. [Google Scholar] [CrossRef]
- Li, H.; Shen, S.; Shi, Z.; Shan, W.; Chang, S.; Guo, C.; Bai, Y.; Yan, L.; Li, F. Effect of the upstream gas on the evolved coal gas in the dry distillation zone of the fixed bed gasifier. Energy 2019, 180, 421–428. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, X. Modeling of contaminant transport in underground coal gasification. Energy Fuel 2009, 23, 193–201. [Google Scholar] [CrossRef]
- Janoszek, T.; Masny, W. CFD simulations of Allothermal steam gasification process for hydrogen production. Energies 2021, 14, 1532. [Google Scholar] [CrossRef]
- Gao, W.; Zagorščak, R.; Thomas, H.R.; An, N. Simulation of underground coal gasification based on a coupled thermal-hydraulic-chemical model. Combust. Theory Model. 2021, 26, 110–134. [Google Scholar] [CrossRef]
- Gao, W.; Zagorščak, R.; Thomas, H.R. Insights into ground response during underground coal gasification through thermo-mechanical modeling. Int. J. Numer. Anal. Methods 2022, 46, 3–22. [Google Scholar] [CrossRef]
- Samdani, G.; Ganesh, A.; Aghalayam, P.; Sapru, R.K.; Lohar, B.L.; Mahajani, S. Kinetics of heterogeneous reactions with coal in context of underground coal gasification. Fuel 2017, 199, 102–114. [Google Scholar] [CrossRef]
- Yuan, L.; Smith, A.C. Numerical study on effects of coal properties on spontaneous heating in longwall gob areas. Fuel 2008, 87, 3409–3419. [Google Scholar] [CrossRef]
- Kang, J.; Zhang, D.; Zhou, F.; Li, H.; Xia, T. Numerical modeling and experimental validation of fractional heat transfer induced by gas adsorption in heterogeneous coal matrix. Int. J. Heat Mass Transf. 2019, 128, 492–503. [Google Scholar] [CrossRef]
- Guo, W.; Liu, H.; Chang, Z.; Cao, D.; Liu, S. Study on effects of thermal resistance and thermal buoyancy on oxygen flow patterns during underground coal gasification. ACS Omega 2021, 6, 32977–32986. [Google Scholar] [CrossRef]
- Jowkar, A.; Sereshki, F.; Najafi, M. A new model for evaluation of cavity shape and volume during Underground Coal Gasification process. Energy 2018, 148, 756–765. [Google Scholar] [CrossRef]
- Liu, X. Study on high temperature burnt surrounding rock movement and failure mechanism in UCG. China Univ. Min. Technol. 2019. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Li, C.; Li, B.; Zhao, H.; Li, R.; Qi, Q. Variation characteristics of coal-rock mechanical properties under varying temperature conditions for Shanxi Linfen coalbed methane well in China. J. Pet. Explor. Prod. Technol. 2021, 11, 2905–2915. [Google Scholar] [CrossRef]
- Sadasivam, S.; Zagorščak, R.; Thomas, H.R.; Kapusta, K.; Stańczyk, K. Experimental study of methane-oriented gasification of semi-anthracite and bituminous coals using oxygen and steam in the context of underground coal gasification (UCG): Effects of pressure, temperature, gasification reactant supply rates and coal rank. Fuel 2020, 268, 117330. [Google Scholar] [CrossRef]
- Konstantinou, E.; Marsh, R. Experimental study on the impact of reactant gas pressure in the conversion of coal char to combustible gas products in the context of Underground Coal Gasification. Fuel 2015, 159, 508–518. [Google Scholar] [CrossRef]



| Reaction Rate | α | A (1/s) | Ea (kJ/mol) | Reaction Enthalpy (kJ/mol) |
|---|---|---|---|---|
| [32,33] r1 | 0 | 5.4 × 103 | 78.24 | +100 |
| [34] r2 = k2Co2 | 0 | 1 × 109 | 159.4 | −110 |
| [11] r3 = k3Co2 | 1 | 2.503 × 1017 | 179.4 | −393.8 |
| [32] r4 = k4CH2O | 0.5 | 85.93 | 231 | +131.4 |
| [11,32] r5 = k5CH2 | 1 | 2.337 × 10−6 | 150 | −74.9 |
| [34] r6 = k6Cco2 | 0.5 | 0.8593 | 211 | +162.4 |
| [33] r7 = k7Cco2CH2 | 0 | 2.75 × 1010 | 193 | +98.3 |
| [32] r8 = k8CcoCH2o | 0 | 27.8 | 12.6 | +41 |
| [11] r9 = k9CcoCo2 | 0 | 3.98 × 1019 | 167.4 | −285.1 |
| [11,33] r10 = k10Co2CH2 | −1 | 2.5 × 1018 | 167.4 | −242 |
| [33] r11 = k11Co2CcH4 | 0 | 4.4 × 1015 | 125.5 | −256 |
| [34] r12 = k12CH2OCcH4 | 0 | 31.2 | 30 | −248 |
| Number | Fracture Density m | Towards the Mean/° | Towards Standard Deviation | Trace Length Mean/m | Trace Length Standard Deviation | Mean Gap Width/mm | Gap Width Standard Deviation |
|---|---|---|---|---|---|---|---|
| 1 | 0 | - | - | - | - | - | - |
| 2 | 0.5 | 90 | 40 | 1 | 5 | 2 | 1 |
| 3 | 0.8 | 90 | 40 | 1 | 5 | 2 | 1 |
| 4 | 1.1 | 90 | 40 | 1 | 5 | 2 | 1 |
| 5 | ∞ | - | - | - | - | - | - |
| Defined Conditions | Coal Seam Deformation | Water Vapor, Gas Seepage | Temperature Transfer Heat | Gas Diffusion | ||
|---|---|---|---|---|---|---|
| Displacement | Stress | |||||
| Initial conditions | Ux = U y = 0 | 0 | pv0 = 1 MPa, p0 = 2 MPa | T0 = 300 K | Cco2(0) = 10 mol/m3 Co2(0) = 5 mol/m3 CH2O(0) = 5 mol/m3 CH2(0) = 5 mol/m3 CCO(0) = 5 mol/m3 | |
| Boundary conditions | AB | Uy = 0 | 0 | p = 1 atm | Thermal insulation | outflow |
| AC | Ux = 0 | 0 | p = 1 atm | Thermal insulation | outflow | |
| CD | Uy = 0 | 0 | p = 1 atm | Thermal insulation | outflow | |
| BD | Uy = 0 | 0 | p = 1 atm | Thermal insulation | outflow | |
| Boundary E | Free displacement | 0 | No flux | T = 1273.13 K | Co2 = 20 mol/m3 CH2O = 20 mol/m3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Yang, X.; Shang, X.; Yang, H. A Thermal-Hydrological-Mechanical-Chemical Coupled Mathematical Model for Underground Coal Gasification with Random Fractures. Mathematics 2022, 10, 2835. https://doi.org/10.3390/math10162835
Zhang Z, Yang X, Shang X, Yang H. A Thermal-Hydrological-Mechanical-Chemical Coupled Mathematical Model for Underground Coal Gasification with Random Fractures. Mathematics. 2022; 10(16):2835. https://doi.org/10.3390/math10162835
Chicago/Turabian StyleZhang, Zhizhen, Xiao Yang, Xiaoji Shang, and Huai Yang. 2022. "A Thermal-Hydrological-Mechanical-Chemical Coupled Mathematical Model for Underground Coal Gasification with Random Fractures" Mathematics 10, no. 16: 2835. https://doi.org/10.3390/math10162835
APA StyleZhang, Z., Yang, X., Shang, X., & Yang, H. (2022). A Thermal-Hydrological-Mechanical-Chemical Coupled Mathematical Model for Underground Coal Gasification with Random Fractures. Mathematics, 10(16), 2835. https://doi.org/10.3390/math10162835








