A Creative Statistical Model of Geometric Area Index Number for Adequate Estimation of ESG, DESG Goals Achievement, and Other Macroeconomic (Im)balances Dynamics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Literature Review and the Theoretical Frameworks of the Assessment of the Socio-Economic Dynamic
2.2. An Original Methodology for Geometric Area Index Number (GAIN)
3. Results and Discussions
3.1. ”3-gon” GAIN or Inscribed Equilateral Triangle
3.2. ”4-gon” GAIN or Carré Magique
3.3. ”5-gon” GAIN or “Strategical and Conjunctural Pentagon”
3.4. ”6-gon” GAIN or “Perrenial Hexagon”
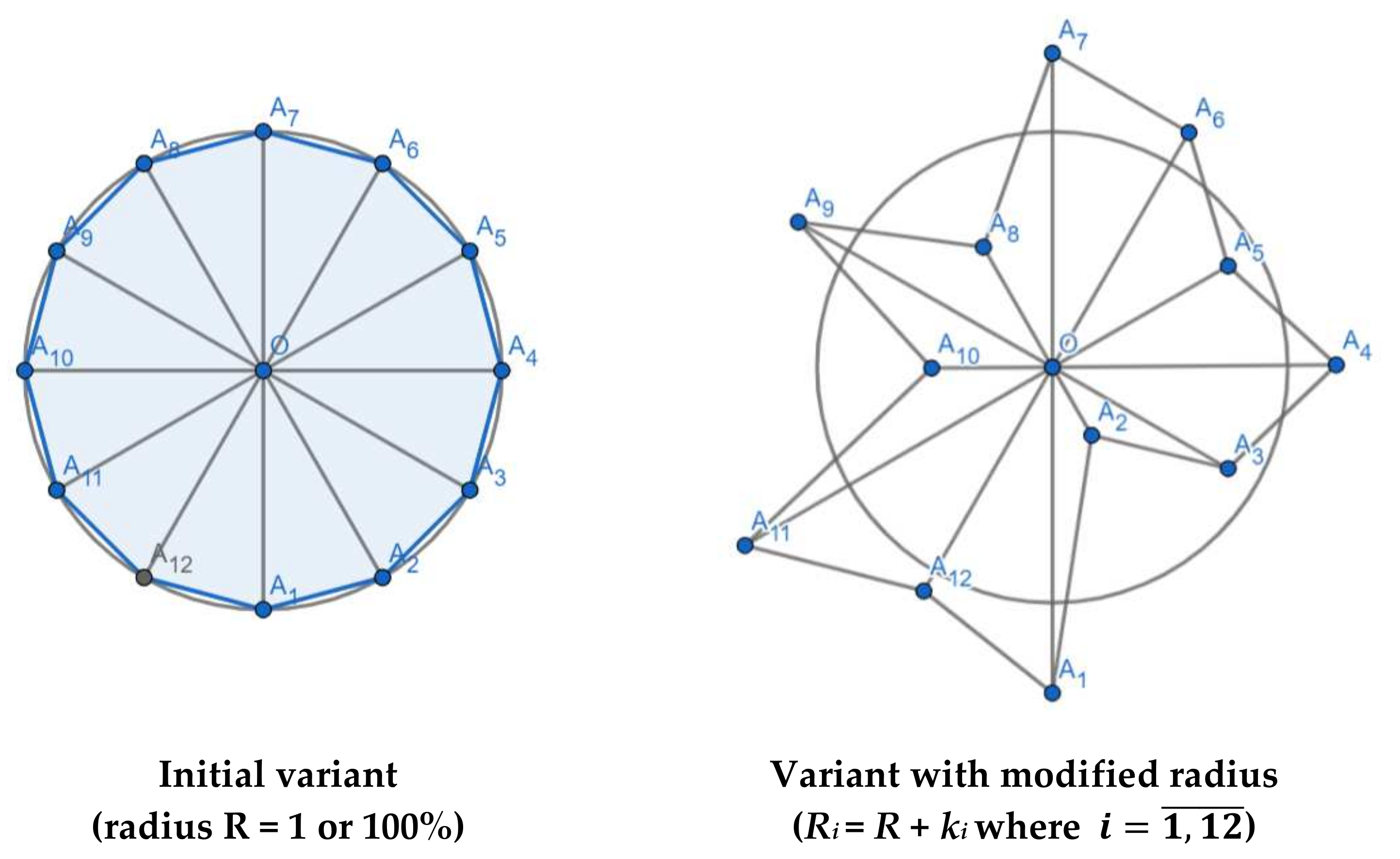
3.5. “12-gon” GAIN or “First Acceptable IN as Dodecagon in Terms of Decision Risk”
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CIN | Composite index number |
| CPI | Consumer price index |
| DESG | Demographic, Economic, Social, Governance |
| ESG | Economic, Social, Governance |
| GAIN | Geometric area index number |
| HPI | House price index |
| IN | Index number |
| INM | Index numbers’ method |
| IPPI | Index of producer price in industry |
| MID | Macroeconomic imbalances dynamics. |
| N-GONS | Regular polygons |
References
- Dumitriu, A. History of Logic; Wells, K., Ed.; Abacus Press: London, UK, 1977. [Google Scholar]
- Barbilian, D. Receptări şi Repere în Filosofia Ştiinţei. In Opere. II Proză; Barbu, I., Ed.; Univers enciclopedic: Bucharest, Romania, 2000; pp. 315–316. [Google Scholar]
- Katz, V.J. A History of Mathematics: An Introduction, 3rd ed.; Addison-Wesley: Boston, MA, USA, 2009; p. 41. Available online: https://edisciplinas.usp.br/pluginfile.php/6075667/mod_resource/content/1/Victor%20J.%20Katz%20-%20A%20History%20of%20Mathematics-Pearson%20%282008%29.pdf (accessed on 14 March 2022).
- Clark, G.N.; Fleetwood, W. The Occasion of Fleetwood’s “Chronicon Preciosum”. Engl. Hist. Rev. 1936, 51, 686–690. Available online: http://www.jstor.org/stable/554442 (accessed on 24 March 2022). [CrossRef]
- Fleetwood, W. Chronicon Preciosum, or, an Account of English Gold and Silver Money; the Price of Corn and Other Commodities; and of the Stipends, Salaries, Wages, Jointures, Portions, Day Labour, &c. in England, for Six Hundred Years, Shewing from the Decrease of the Value of Money, and from the Increase of the Value of Corn and Other Commodities &c, that a Fellow, Who Has an Estate in Land of Inheritance or a Perpetual Pension of Five Pounds per Annum, may Conscientiously Keep his Fellowship, and Ought not to be Compelled the Leave the Same, though the Statutes of his College (Founded between the Years 1440 and 1460) Did then Vacate His Fellowship on such a Condition; Osborne, T., Ed.; Gray’s-Inn: London, UK, 1745; (originally published in 1707); Available online: https://books.google.ro/books?id=TC45AAAAMAAJ&pg=PP7&redir_esc=y#v=onepage&q&f=false (accessed on 23 March 2022).
- Fisher, I. The Making of Index-Numbers: A Study of Their Varieties, Tests, and Reliability; Houghton Mifflin Company: New York, NY, USA, 1922. [Google Scholar]
- Diewert, W.E. The early history of price index research. In Essays in Index Number Theory; Diewert, W.E., Nakamura, A.O., Eds.; North-Holland: Amsterdam, The Netherlands, 1993; Volume 1, pp. 33–65. [Google Scholar]
- Diewert, W.E. Index Numbers. In The New Palgrave Dictionary of Economics, 3rd ed.; Macmillan Publishers Ltd.: New York, NY, USA, 2018. [Google Scholar]
- Ralph, J.; O’Neill, R.; Winton, J. A Practical Introduction to Index Numbers; John Wiley & Sons Ltd.: Chichester, UK, 2015. [Google Scholar]
- O’Neill, R.; Ralph, J.A.; Smith, P. The Origins of Inflation Measurement: 1700–1879. In Inflation; Palgrave Macmillan: Cham, Switzerland, 2017; Available online: https://doi.org/10.1007/978-3-319-64125-6_3 (accessed on 26 March 2022). [CrossRef]
- Dutot, C. Réflections Politiques sur les Finances et le Commerce; Les Frères , V., Prevost, N., Eds.; La Haye: London, UK, 1738; Volume 1. [Google Scholar]
- Custodi, P. Del Valore e Della Proporzione dei Metalli Monetati. In Scrittori Classici Italiani di Economia Politica; Destefanis, G.G.: Milan, Italy, 1804; Volume 13, pp. 297–366, (originally published in 1764). [Google Scholar]
- Young, A. An Inquiry into the Progressive Value of Money in England as Marked by the Price of Agricultural Products; Hatchards–Piccadilly: London, UK, 1812. [Google Scholar]
- Săvoiu, G. Universul Preţurilor şi Indicii Interpret; Editura Independenţa Economicǎ: Piteşti, Romania, 2001. [Google Scholar]
- Săvoiu, G.; Matei, S. Transdisciplinarity of Logic’s History. ESMSJ 2022, 10, 12–20. [Google Scholar]
- Bowley, A.L. Irving Fisher, The Making of Index-Numbers: A Study of their Varieties, Tests, and Reliability. Econ. J. 1923, 33, 90–93. [Google Scholar] [CrossRef]
- Fisher, I.; Bowley, A.L. Professor Bowley on Index-Numbers. Econ. J. 1923, 33, 246–252. [Google Scholar] [CrossRef]
- Croxton, F.E.; Cowden, D.J. Applied General Statistics; Prentice-Hall, Inc.: New York, NY, USA, 1939. [Google Scholar]
- Eichhorn, W.; Voeller, J. Theory of the Price Index; Springer: Berlin, Germany, 1976. [Google Scholar]
- Eichhorn, W. What is an Economic Index? An Attempt of an Answer. In Theory and Applications of Economic Indices; Eichhorn, W., Henn, R., Opitz, O., Shephard, R.W., Eds.; Physica Verlag: Wurzburg, Germany, 1978; pp. 3–42. [Google Scholar]
- Levell, P. Is the Carli index flawed? Assessing the case for the new retail price index RPIJ. J. R. Stat. Soc. Ser. A 2015, 178, 303–336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yule, G.U. Discussion of Mr. Flux’s Paper. J. R. Stat. Soc. 1921, 84, 199–202. [Google Scholar]
- White, G. IndexNumR: A Package for Index Number Calculation. 2020. Available online: https://cran.r-project.org/web/packages/IndexNumR/vignettes/indexnumr.html (accessed on 21 March 2022).
- Savoiu, G.; Iorga-Siman, I. The Concept of Time in the Physical Way of Thinking, and Its Impact on Knowledge and the Evaluation of Inflation as an Economic Phenomenon. ESMSJ 2011, 1, 25–35. Available online: https://esmsj.upit.ro/No2_2011.html (accessed on 21 March 2022).
- Graf, B. Consumer Price Index Manual, Concepts and Methods; International Monetary Fund: Washington, DC, USA, 2020; Available online: https://www.elibrary.imf.org/view/books/069/25164-9781484354841-en/back-1.xml (accessed on 28 March 2022).
- Smarandache, F.; Săvoiu, G. Neutrosophic Index Numbers: Neutrosophic Logic Applied in the Statistical Indicators Theory; Critical Review A Publication of Society for Mathematics of Uncertainty; Center for Mathematics of Uncertainty Creighton University: Omaha, NE, USA, 2015; Volume 10, pp. 67–101. [Google Scholar]
- Banerjee, K.S. A Unified Statistical Approach to the Index Number Problem. Econometrica 1961, 29, 591–601. [Google Scholar] [CrossRef]
- Crowell, R. The Evolving Quest for a Grand Unified Theory of Mathematics. 2022. Available online: https://www.scientificamerican.com/article/the-evolving-quest-for-a-grand-unified-theory-of-mathematics/ (accessed on 15 March 2022).
- Frenkel, E. Lectures on the Langlands program and conformal field theory. In Frontiers in Number Theory, Physics, and Geometry II; Springer: Berlin/Heidelberg, Germany, 2007; pp. 387–533. [Google Scholar]
- Langlands, R.P. An essay on the dynamics and statistics of critical field theories. Société Mathématique Can. 1996, 3, 1945–1995. Available online: http://www.sunsite.ubc.ca/DigitalMathArchive/Langlands/pdf/cms-ps.pdf (accessed on 11 March 2022).
- Diewert, W.E. The Consumer Price Index and Index Number Purpose. J. Econ. Soc. Meas. 2001, 27, 167–248. [Google Scholar] [CrossRef] [Green Version]
- Gowers, T. Mathematics: A Very Short Introduction; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Săvoiu, G. Statistica: Un Mod Ştiinţific de Gândire; Editura Universitară: Bucharest, Romania, 2007. [Google Scholar]
- Hirschmann, A. National Power and the Structure of Foreign Trade; University of California Press: Berkeley, CA, USA, 1945. [Google Scholar]
- Herfindahl, O. Concentration in the Steel Industry; Columbia University: New York, NY, USA, 1950. [Google Scholar]
- Hirschmann, A. The Paternity of an Index. Am. Econ. Rev. 1964, 54, 761. [Google Scholar]
- Săvoiu, G.; Iorga Simăn, I.; Crăciuneanu, V. The Phenomenon of Concentration—Diversification in Contemporary Globalization. Rom. Stat. Rev. 2012, 60, 16–27. [Google Scholar]
- Bondarenko, P. Herfindahl-Hirschman index. Encyclopedia Britannica. 10 October 2019. Available online: https://www.britannica.com/topic/Herfindahl-Hirschman-index (accessed on 29 March 2022).
- Frisch, M. Don Juan oder Die Liebe zur Geometrie [Don Juan or the Love of Geometry]. In A comedy in Five Acts, 1st ed.; Suhrkamp: Frankfurt, Germany, 1953. [Google Scholar]
- Blåsjö, V. Jakob Steiner’s Systematische Entwickelung: The Culmination of Classical Geometry. Math. Intel. 2009, 31, 21–29. [Google Scholar] [CrossRef]
- Ball, W.W.R. A Short Account of the History of Mathematics; The Project Gutenberg EBook of A Short Account of the History of Mathematics, EBook #31246; Dover Publications, Inc.: New York, NY, USA, 1908; (revised May 2010); Available online: https://www.gutenberg.org/files/31246/31246-pdf (accessed on 3 May 2022).
- Cajori, F. A History of Mathematics; The Project Gutenberg EBook of A History of Mathematics, EBook #31061; Macmillan & Co. Ltd.: London, UK, 1909; (revised January 2010); Available online: http://mis.kp.ac.rw/admin/admin_panel/kp_lms/files/digital/SelectiveBooks/Mathematics/A%20History%20of%20Mathematics.pdf (accessed on 21 May 2022).
- Heath, T.A. History of Greek Mathematics. II from Aristarchus to Diophantus; Clarenton Press: Oxford, UK, 1921. [Google Scholar]
- Ivor, T. Selections Illustrating the History of Greek Mathematics from Aristarchus to Pappus; William Heineman Ltd.: London, UK, 1941; Volume 2. [Google Scholar]
- Wells, D. The Penguin Dictionary of Curious and Interesting Geometry; Penguin Books: London, UK, 1991. [Google Scholar]
- Knorr, W.R. Archimedes and the Elements: Proposal for a Revised Chronological Ordering of the Archimedean Corpus. Granul. Matter 1978, 19, 211–290. Available online: http://www.jstor.org/stable/41133526 (accessed on 28 May 2022). [CrossRef]
- Roser, M. Human Development Index (HDI). 2014. Available online: https://ourworldindata.org/human-development-index (accessed on 25 May 2022).
- Prados de la Escosura, L. Augmented Human Development in the Age of Globalisation. Econ. Hist. Rev. 2021, 74, 946–975. Available online: https://onlinelibrary.wiley.com/doi/full/10.1111/ehr.13064 (accessed on 30 May 2022). [CrossRef]
- Săvoiu, G.; Gogu, E.; Taicu, M. Hierarchies of Asociative Dynamics, Starting From Romania’s Macro-Economic Imbalances in the EU-28. What Does Romania’s Economic Evolution in the EU-28 Look Like? Rom. Stat. Rev. 2017, 3, 35–46. [Google Scholar]
- Kaldor, N. Speculation and economic stability. In The Economics of Futures Trading; Palgrave Macmillan: London, UK, 1939; pp. 111–123. [Google Scholar]
- Kaldor, N. A Model of Economic Growth. Econ. J. 1957, 67, 591–624. [Google Scholar] [CrossRef]
- Kaldor, N. Strategic Factors in Economic Development; Ithaca: New York, NY, USA, 1967. [Google Scholar]
- Stoleru, L.G. L’Équilibre et la Croissance Économique, Principes de Macroéconomie; Dunod: Paris, France, 1967. [Google Scholar]
- Stoleru, L.G. Economie, Comprendre L’avenir; Dunod: Paris, France, 1999. [Google Scholar]
- Korka, M.; Tușa, E. International Business Statistics, 2nd ed.; ASE Publishers: Bucharest, Romania, 2004. [Google Scholar]
- Săvoiu, G. Situaţii Statistice Financiar-Contabile şi Sisteme de Indicatori Statistici Derivaţi [Financial and Accountancy Statistical Situations and Systems of Derived Statistical Indicators]; Universitara Publishers: Bucharest, Romania, 2013. [Google Scholar]
- Săvoiu, G. Systems of Industrial Indicators—In a Context Dominated by the National Forecasting Commission’s Anticipations. Rom. Stat. Rev. Suppl. 2017, 65, 121–129. [Google Scholar]
- Orcibal, J. Dei agricultura: Le carré magique SATOR AREPO, sa valeur et son origine. Rev. Hist. Relig. 1954, 146, 51–66. [Google Scholar] [CrossRef]
- Săvoiu, G.; Ţaicu, M. Foreign Direct Investment Models, based on Country Risk for Some Post-socialist Central and Eastern European Economies. Procedia Econ. Financ. 2014, 10, 249–260. [Google Scholar] [CrossRef] [Green Version]
- Khalid, B.; Naumova, E. Digital transformation SCM in view of Covid-19 from Thailand SMEs perspective. In Global Challenges of Digital Transformation of Markets; de la Poza, E., Barykin, S.E., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2021; pp. 49–66. [Google Scholar]
- Barykin, S.Y.; Kapustina, I.V.; Sergeev, S.M.; Kalinina, O.V.; Vilken, V.V.; de la Poza, E.; Putikhin, Y.Y.; Volkova, L.V. Developing the physical distribution digital twin model within the trade network. Acad. Strateg. Manag. J. 2021, 20, 1–24. [Google Scholar]
- Duignan, B. Occam’s Razor. Encyclopedia Britannica. 28 May 2021. Available online: https://www.britannica.com/topic/Occams-razor (accessed on 20 May 2022).
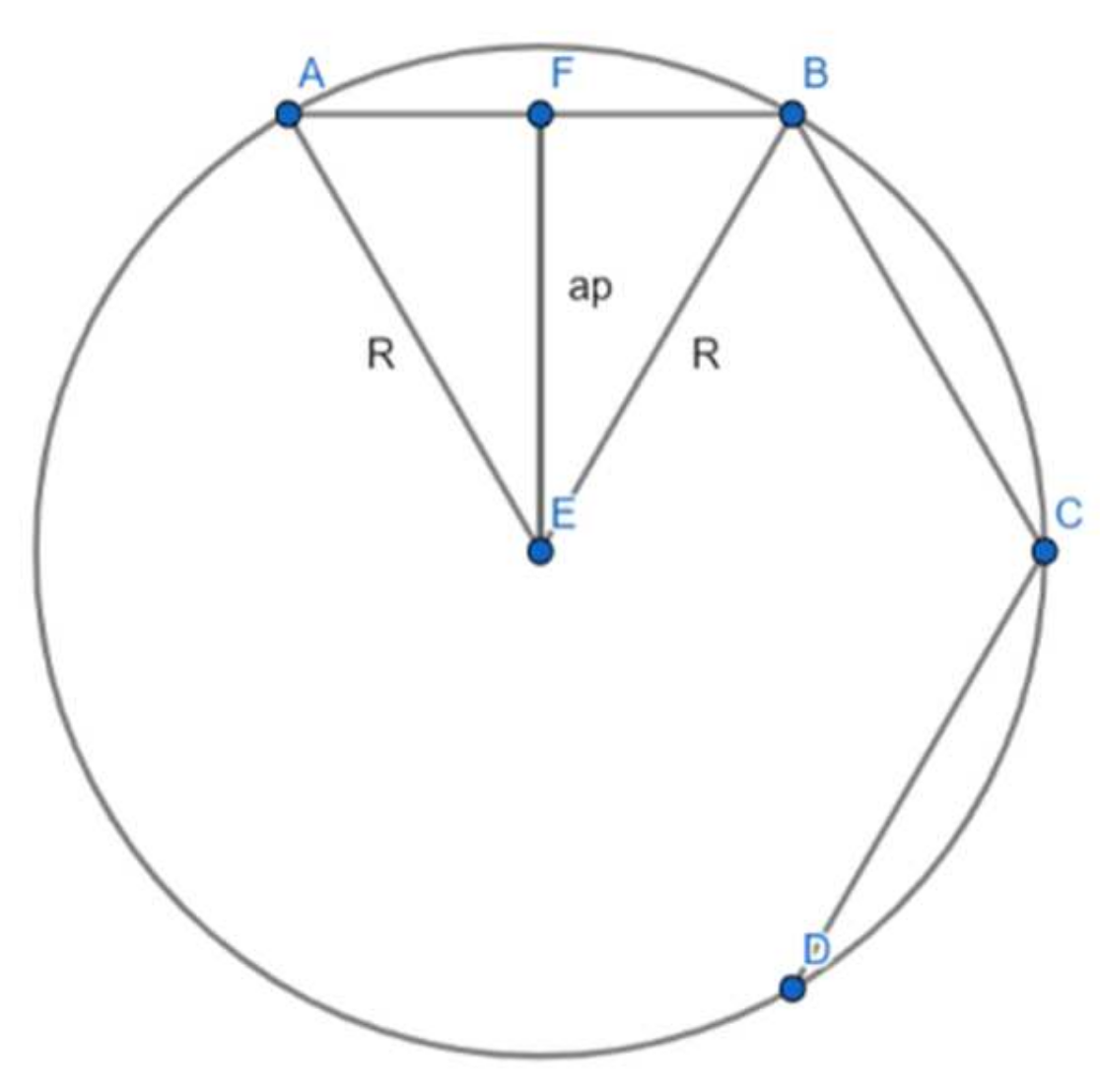

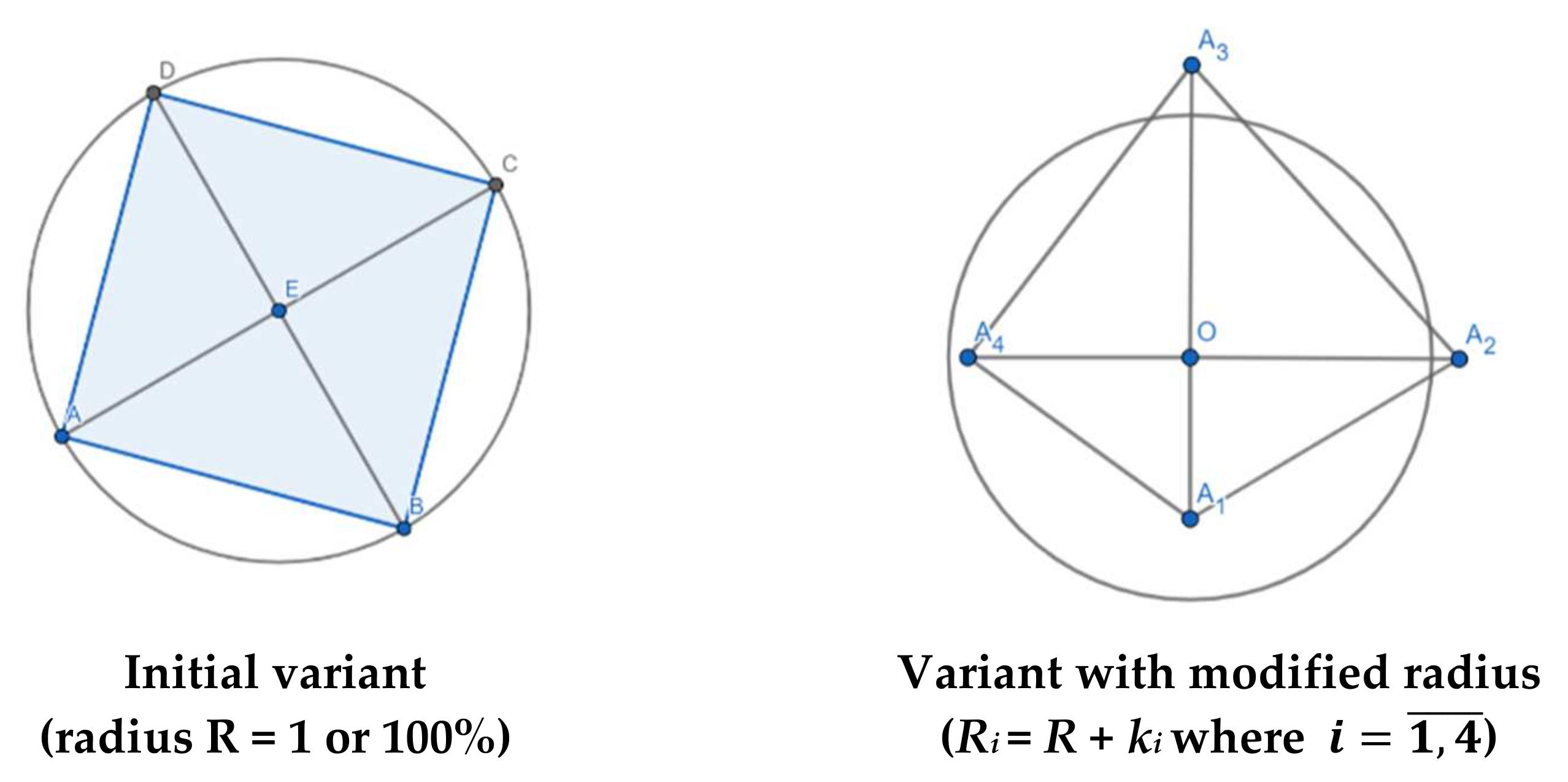
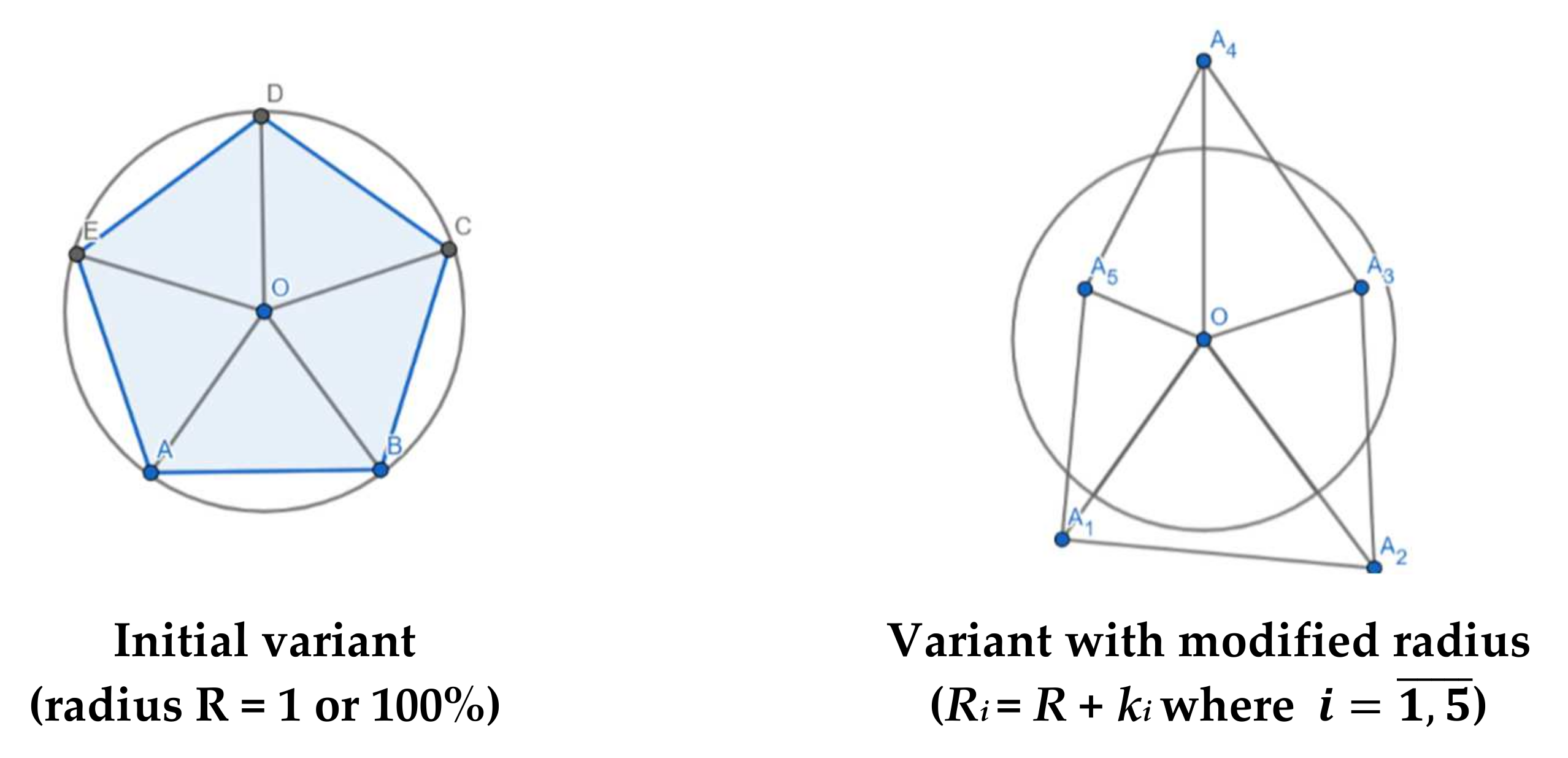
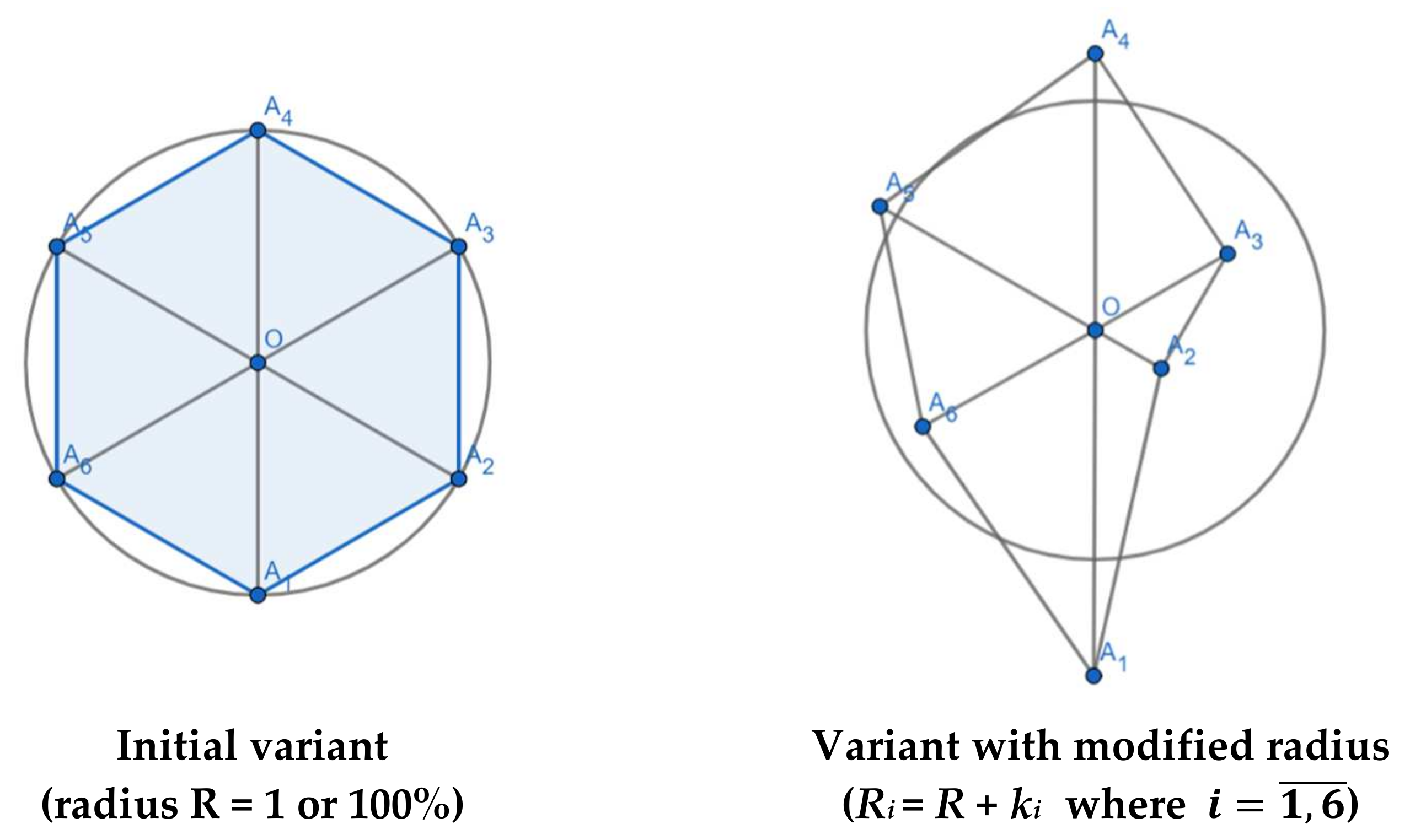
| n Lines. (Sides, Angles) | Ancient Greek Denomination for Regular Polygons (“n-gons”) | Inscribed Polygon Area (Radius R = 1) | % from Inscribed Circle’s Area (π)* | Error’s Level (%) | Obs. |
|---|---|---|---|---|---|
| 3 | Trigon (Triangle) | 1.29903810 | 41.3496671 | 58.6503329 | >50% |
| 4 | Tetragon (Square) | 2.0000000000 | 63.6619772 | 36.3380228 | >33% |
| 5 | Pentagon | 2.3776412907 | 75.6826728 | 24.3173272 | >20% |
| 6 | Hexagon | 2.5980762114 | 82.6993343 | 17.3006657 | >10% |
| 7 | Heptagon | 2.7364101886 | 87.1026415 | 12.8973585 | >10% |
| 8 | Octagon | 2.8284271245 | 90.0316316 | 9.9683683 | >5% |
| 9 | Enneagon (Nonagon) | 2.8925442436 | 92.0725428 | 7.9274572 | >5% |
| 10 | Decagon | 2.9389262615 | 93.5489283 | 6.4510717 | >5% |
| 11 | Hendecagon | 2.9735244960 | 94.6502244 | 5.3497756 | >5% |
| 12 | Dodecagon | 2.9999999999 | 95.4820244 | 4.5179756 | <5% |
| 13 | Triskaidecagon | 3.0207006183 | 96.1518870 | 3.8481130 | <5% |
| 14 | Tetradecagon | 3.0371861738 | 96.6766385 | 3.3233615 | <5% |
| 15 | Pentadecagon | 3.0505248231 | 97.1012209 | 2.8987791 | <3% |
| 16 | Hexadecagon | 3.0614674589 | 97.4495358 | 2.5504642 | <3% |
| 17 | Heptadecagon | 3.0705541626 | 97.7387746 | 2.2612254 | <3% |
| 18 | Octadecagon | 3.0781812899 | 97.9815535 | 2.0184465 | <3% |
| 19 | Enneadecagon (Nonadecagon) | 3.0846449574 | 98.1872985 | 1.8127015 | <2% |
| 20 | Icosagon | 3.0901699437 | 98.3631643 | 1.6368357 | <2% |
| 21 | Icosi(kai)henagon | 3.0949293313 | 98.5146603 | 1.4853397 | <2% |
| 22 | Icosi(kai)digon | 3.0990581242 | 98.6460838 | 1.3539162 | <2% |
| 23 | Icosi(kai)trigon | 3.1026628683 | 98.7608264 | 1.2391736 | <2% |
| 24 | Icosi(kai)tetragon | 3.1058285412 | 98.8615929 | 1.1384071 | <2% |
| 25 | Icosi(kai)pentagon | 3.1086235896 | 98.9505621 | 1.0494379 | <2% |
| 26 | Icosi(kai)hexagon | 3.1111036357 | 99.0295044 | 0.9704956 | <1% |
| 27 | Icosi(kai)heptagon | 3.1133142550 | 99.0998706 | 0.9001294 | <1% |
| 28 | Icosi(kai)octagon | 3.1152930754 | 99.1628584 | 0.8371416 | <1% |
| 29 | Icosi(kai)enneagon Icosi(kai)nonagon | 3.1170713831 | 99.2194637 | 0.7805363 | <1% |
| 30 | Triacontagon | 3.1186753623 | 99.2705199 | 0.7294801 | <1% |
| … | … | ||||
| 40 | Tetracontagon | 3.1286893008 | 99.5892735 | 0.4107265 | <1% |
| … | … | ||||
| 50 | Pentacontagon | 3.1333308391 | 99.7370182 | 0.2629818 | <1% |
| … | … | ||||
| 100 | Hectogon | 3.1395259765 | 99.9342156 | 0.0657844 | <0.1% |
| … | … | ||||
| 1000 | Chiliagon | 3.1415719828 | 99.999342 | 0.000658 | <0.001% |
| … | … | ||||
| 10000 | Myriagon | 3.1415924469 | 99.9999934 | 0.0000066 | <0.00001% |
| … | … | ||||
| N** | “n-gon” inscribed in a circle with radius R = 1 | ): 2π | ): 2π] |
| Selected Economic Equilibria (Indicators) | Values * for the Regular Trigon (2020) | Values * for the Second Irregular Trigon (2021) | Real Terms IN (2021) | Error’s Level (%) |
|---|---|---|---|---|
| Harmonized Index of Consumer Prices (HICP) | 105.97 1 or 100% | 111.59 111.59:105.97 = 1.0530 or 105.30% | 1.0530 or 105.30% | 58.65 |
| House price index (HPI) | 127.80 1 or 100% | 142.51 142.51:127.80 = 1.115 or 111.51% | 1.1151 or 111.51% | 58.65 |
| Index of Producer Price in Industry (IPPI) | 101.9 1 or 100% | 111.9 111.9:101.9 = 1.0981 or 109.81% | 1.0981 or 109.81% | 58.65 |
| Selected Economic Equilibria (Indicators) | Values * for the Regular Carré Magique (2020) | Values * for the Second Irregular Carré Magique (2021) | Real Terms IN (2021) | Error’s Level (%) |
|---|---|---|---|---|
| Gross Domestic Product Index (Real Terms GDPI) | 2046.21 (billions of constant prices) 1 or 100% | 2198.47 (billions of constant prices) 2198.47:2046.21 = 1.0744 or 107.44% | 1.0744 or 107.44% | 36.34 |
| 1/GDP Deflator Index (1/GDDPI) (2019 = 100%) | 1/1.05091 = 0.95156 1 or 100% | 1/1.05394 = 0.94882 0.94882:0.95156 = 0.9971 0.9971 or 99.71% | 0.9971 or 99.71% | 36.34 |
| Employment Index (ILO definition) (EI) | 32.529 (billions of persons) 1 or 100% | 32.366 32.366:32.529 = 0.995 or 99.50% | 0.995 or 99.50% | 36.34 |
| Coverage Dynamics of Imports by Exports Index (CDIEI) (2006 = 100%) | Imports IN= 84.231 Exports IN = 87.039 CIEI = 1.0333 or 103.33% 1 or 100% | Imports IN = 103.841 Exports IN = 98.714 CIEI = 0.9506 or 95.06% 95.06:103.33 = 0.92 | 0.920 or 92.0% | 36.34 |
| Selected Economic Equilibria (Indicators) | The Fifth IN Value of the Regular Strategical Pentagon in GBP (2020) | The Fifth IN Value of the Second Irregular Strategical Pentagon in GBP (2021) | Real Terms IN (2021/ 2020) | Error’s Level (%) |
|---|---|---|---|---|
| Minimum vs. Median Hourly Earnings Index (MMHEI) | Minimum value = 8.72 Median value = 14.90 (GBP/H) MMHEI = 0.585234899 | Minimum value = 8.91 Median value = 15.65 (GBP/H) MMHEI = 0.569329073 | 0.9728 or 97.28% | 24.32 |
| Selected Economic Equilibria (Indicators) | Values * in the Regular Perennial Hexagon (2019–2020) | Values * in the Second Irregular Perennial Hexagon (2020–2021) | Real Terms IN (2020–2021) | Error’s Level (%) |
|---|---|---|---|---|
| Public Expenditure for Environment Protection Index (Real Terms PEEPI) | 12.5 (GBP billions) 1 or 100% | 13.0 (GBP billions) 13.0:12.5 = 1.04 | 1.04 or 104.0% | 17.30 |
| Selected Economic Equilibria (Indicators) | Values * for the Regular Dodecagon (2020) | Values * for the Second Irregular Dodecagon (2021) | Real IN Value (2021) | Error’s Level (%) |
|---|---|---|---|---|
| Total Investment from GDP (%) Index (TINV/GDPI) | 16.693 1 or 100% | 17.091 17.091: 16.693 = 1.0238 or 102.38% | 1.0238 or 102.38% | 4.52 |
| Gross National Savings from GDP (%) Index [(GNS/GDP)I] | 14.192 1 or 100% | 14.504 14.504:14.192 = 1.0220 or102.20% | 1.0220 or 102.20% | 4.52 |
| 1/General Government Gross Debt Index—% of GDP (1/GGGDI) | 102.608 1 or 100% | 95.348 1: (95.348:102.608) = 1.0761 or 107.61% | 1.0761 or 107.61% | 4.52 |
| Productivity Index (2019 = 100%) | Output per hour Worked = 101.9% 1 or 100% | Output per hour Worked = 102.6% 102.6:101.9 = 1.0069 | 1.0069 or 100.69 | 4.52 |
| Index of Economic Freedom (IEF) | Score IEF = 78.4 1 or 100% | Score IEF = 72.7 72.7:78.4 = 0.9273 or 92.73% | 0.9273 or 92.73% | 4.52 |
| Euromoney’s Country Risk Index (ECRI) | Score ECR = 64.37 1 or 100% | Score ECR = 64.23 64.23:64.37 = 0.9978 or 99.78% | 0.9978 or 99.78% | 4.52 |
| n | Interval for Regular Polygons (“n-gons” Numerical Limits) | Major Scope or Aim | Error’s Level (%) | * Obs. |
|---|---|---|---|---|
| 3–11 | From Hendecagon to Tetragon (Square) | Prospective (Foresight) | (5.35–36.34%) | LT MT |
| 12–26 | From Icosi(kai)hexagon to Dodecagon | Decision (Statistics) | (0.97–4.52) | MT ST |
| 27–100 | From Hectogon to Icosi(kai)heptagon | More precise calculus | (0.07–0.90) | ST VST |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savoiu, G.; Matei, S.; Čudanov, M.; Gogu, E. A Creative Statistical Model of Geometric Area Index Number for Adequate Estimation of ESG, DESG Goals Achievement, and Other Macroeconomic (Im)balances Dynamics. Mathematics 2022, 10, 2853. https://doi.org/10.3390/math10162853
Savoiu G, Matei S, Čudanov M, Gogu E. A Creative Statistical Model of Geometric Area Index Number for Adequate Estimation of ESG, DESG Goals Achievement, and Other Macroeconomic (Im)balances Dynamics. Mathematics. 2022; 10(16):2853. https://doi.org/10.3390/math10162853
Chicago/Turabian StyleSavoiu, Gheorghe, Sandra Matei, Mladen Čudanov, and Emilia Gogu. 2022. "A Creative Statistical Model of Geometric Area Index Number for Adequate Estimation of ESG, DESG Goals Achievement, and Other Macroeconomic (Im)balances Dynamics" Mathematics 10, no. 16: 2853. https://doi.org/10.3390/math10162853







