A Nonlinear Multigrid Method for the Parameter Identification Problem of Partial Differential Equations with Constraints
Abstract
:1. Introduction
2. Inversion Model
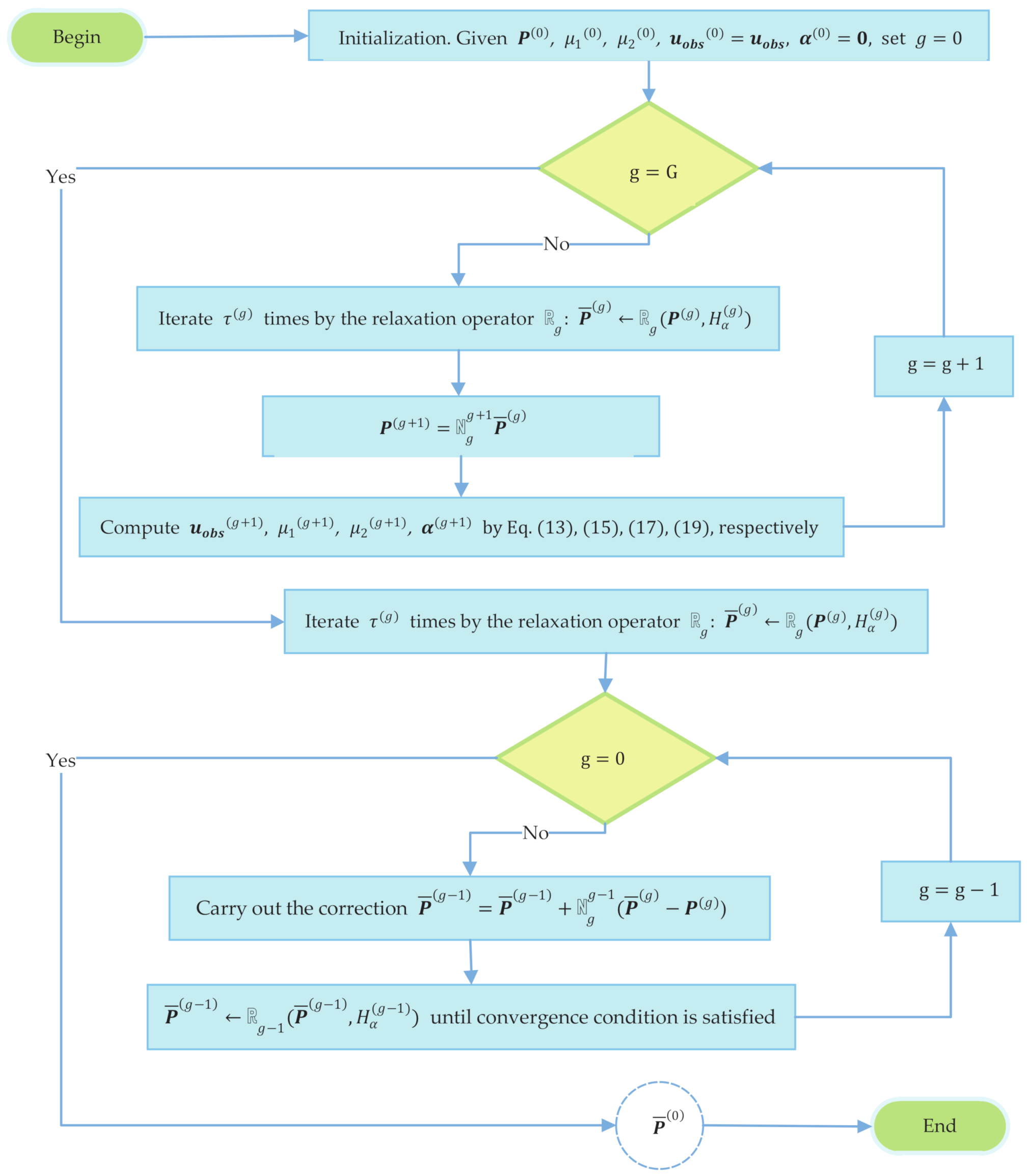
3. Multigrid Method with Constraints
4. An Application
4.1. Mathematical Model
4.2. Simulation Test
5. Conclusions
- It is fast, accurate, and noise-resistant;
- It is faster and less likely to fall into local minima compared to the multigrid method without constraints and fixed-grid method with constraints;
- It has stronger anti-noise ability, higher precision, and better stability than the multigrid method without constraints and fixed-grid method with constraints.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, L.; Soldevila, F.; Moretti, C.; d’Arco, A.; Boniface, A.; Shao, X.; de Aguiar, H.B.; Gigan, S. Large field-of-view non-invasive imaging through scattering layers using fluctuating random illumination. Nat. Commun. 2022, 13, 1447. [Google Scholar] [CrossRef] [PubMed]
- Boniface, A.; Dong, J.; Gigan, S. Non-invasive focusing and imaging in scattering media with a fluorescence-based transmission matrix. Nat. Commun. 2020, 11, 6154. [Google Scholar] [CrossRef] [PubMed]
- Göppel, S.; Frikel, J.; Haltmeier, M. Feature Reconstruction from Incomplete Tomographic Data without Detour. Mathematics 2022, 10, 1318. [Google Scholar] [CrossRef]
- Siddique, S.; Chow, J.C.L. Application of nanomaterials in biomedical imaging and cancer therapy. Nanomaterials 2020, 10, 1700. [Google Scholar] [CrossRef]
- Tromp, J. Seismic wavefield imaging of Earth’s interior across scales. Nat. Rev. Earth Environ. 2020, 1, 40–53. [Google Scholar] [CrossRef]
- Bringout, G.; Erb, W.; Frikel, J. A new 3D model for magnetic particle imaging using realistic magnetic field topologies for algebraic reconstruction. Inverse Probl. 2020, 36, 124002. [Google Scholar] [CrossRef]
- Yan, B.; Chen, B.; Harp, D.R.; Jia, W.; Pawar, R.J. A robust deep learning workflow to predict multiphase flow behavior during geological CO2 sequestration injection and Post-Injection periods. J. Hydrol. 2022, 607, 127542. [Google Scholar] [CrossRef]
- Kadeethum, T.; O’Malley, D.; Fuhg, J.N.; Choi, Y.; Lee, J.; Viswanathan, H.S.; Bouklas, N. A framework for data-driven solution and parameter estimation of PDEs using conditional generative adversarial networks. Nat. Comput. Sci. 2021, 1, 819–829. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Niderla, K.; Kozłowski, E.; Król, K.; Wyrwisz, J.M.; Skrzypek-Ahmed, S.; Gołąbek, P. Logistic regression with wave preprocessing to solve inverse problem in industrial tomography for technological process control. Energies 2021, 14, 8116. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kozłowski, E.; Kłosowski, G. Electrical impedance tomography in 3D flood embankments testing–elastic net approach. Trans. Inst. Meas. Control 2020, 42, 680–690. [Google Scholar] [CrossRef]
- Jadamba, B.; Khan, A.A.; Richards, M.; Sama, M.; Tammer, C. Analyzing the role of the Inf-Sup condition for parameter identification in saddle point problems with application in elasticity imaging. Optimization 2020, 69, 2577–2610. [Google Scholar] [CrossRef]
- Jadamba, B.; Khan, A.A.; Richards, M.; Sama, M. A convex inversion framework for identifying parameters in saddle point problems with applications to inverse incompressible elasticity. Inverse Probl. 2020, 36, 074003. [Google Scholar] [CrossRef]
- Adeli, E.; Rosić, B.; Matthies, H.G.; Reinstädler, S.; Dinkler, D. Comparison of Bayesian methods on parameter identification for a viscoplastic model with damage. Metals 2020, 10, 876. [Google Scholar] [CrossRef]
- Frikel, J.; Haltmeier, M. Efficient regularization with wavelet sparsity constraints in photoacoustic tomography. Inverse Probl. 2018, 34, 024006. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Król, K.; Kozłowski, E.; Wołowiec, T.; Cholewa-Wiktor, M.; Bednarczuk, P. Application of electrical tomography imaging using machine learning methods for the monitoring of flood embankments leaks. Energies 2021, 14, 8081. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kłosowski, G.; Hoła, A.; Sikora, J.; Wołowiec, T.; Tchórzewski, P.; Skowron, S. Comparison of machine learning methods in electrical tomography for detecting moisture in building walls. Energies 2021, 14, 2777. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kłosowski, G.; Hoła, A.; Hoła, J.; Sikora, J.; Tchórzewski, P.; Skowron, Ł. Historical buildings dampness analysis using electrical tomography and machine learning algorithms. Energies 2021, 14, 1307. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kozłowski, E.; Kłosowski, G.; Niderla, K. Logistic regression for machine learning in process tomography. Sensors 2019, 19, 3400. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kłosowski, G. Identification of moisture inside walls in buildings using machine learning and ensemble methods. Int. J. Appl. Electrom. 2022, 69, 375–388. [Google Scholar] [CrossRef]
- Kłosowski, G.; Rymarczyk, T. Ensemble learning for monitoring process in electrical impedance tomography. Int. J. Appl. Electrom. 2022, 69, 169–178. [Google Scholar] [CrossRef]
- Markl, M.; Alley, M.T.; Pelc, N.J. Balanced phase-contrast steady-state free precession (PC-SSFP): A novel technique for velocity encoding by gradient inversion. Magn. Reson. Imaging 2003, 49, 945–952. [Google Scholar] [CrossRef] [PubMed]
- Liu, T. A wavelet multiscale-homotopy method for the parameter identification problem of partial differential equations. Comput. Math. Appl. 2016, 71, 1519–1523. [Google Scholar] [CrossRef]
- Schweiger, M.; Arridge, S.R.; Nissilä, I. Gauss-Newton method for image reconstruction in diffuse optical tomography. Phys. Med. Biol. 2005, 50, 2365. [Google Scholar] [CrossRef] [PubMed]
- Pan, W.; Innanen, K.A.; Margrave, G.F.; Fehler, M.C.; Fang, X.; Li, J. Estimation of elastic constants for HTI media using Gauss-Newton and full-Newton multiparameter full-waveform inversion. Geophysics 2016, 81, R275–R291. [Google Scholar] [CrossRef]
- Lee, C.; Jeong, D.; Yang, J.; Kim, J. Nonlinear multigrid implementation for the two-dimensional Cahn-Hilliard equation. Mathematics 2020, 8, 97. [Google Scholar] [CrossRef]
- Liu, T. A multigrid-homotopy method for nonlinear inverse problems. Comput. Math. Appl. 2020, 79, 1706–1717. [Google Scholar] [CrossRef]
- Oh, S.; Milstein, A.B.; Bouman, C.A.; Webb, K.J. A general framework for nonlinear multigrid inversion. IEEE Trans. Image Process. 2005, 14, 125–140. [Google Scholar]
- Liu, T. Parameter estimation with the multigrid-homotopy method for a nonlinear diffusion equation. J. Comput. Appl. Math. 2022, 413, 114393. [Google Scholar] [CrossRef]
- Ye, J.C.; Bouman, C.A.; Webb, K.J.; Millane, R.P. Nonlinear multigrid algorithms for Bayesian optical diffusion tomography. IEEE Trans. Image Process. 2001, 10, 909–922. [Google Scholar]
- Marlevi, D.; Kohr, H.; Buurlage, J.; Gao, B.; Batenburg, K.J.; Colarieti-Tosti, M. Multigrid reconstruction in tomographic imaging. IEEE Trans. Radiat. Plasma 2020, 4, 300–310. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Duan, Y.; Yin, K.; Tai, X.C. An efficient multi-grid method for TV minimization problems. Inverse Probl. Imag. 2021, 15, 1199–1221. [Google Scholar] [CrossRef]
- Zhang, Y.; Bi, H.; Yang, Y. A multigrid correction scheme for a new Steklov eigenvalue problem in inverse scattering. Int. J. Comput. Math. 2020, 97, 1412–1430. [Google Scholar] [CrossRef]
- Edjlali, E.; Bérubé-Lauzière, Y. Lq-Lp optimization for multigrid fluorescence tomography of small animals using simplified spherical harmonics. J. Quant. Spectrosc. Ra. 2018, 205, 163–173. [Google Scholar] [CrossRef]
- Javaherian, A.; Holman, S. A multi-grid iterative method for photoacoustic tomography. IEEE Trans. Med. Imaging 2017, 36, 696–706. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Lin, J.; Zikatanov, L.T. An adaptive multigrid method based on path cover. SIAM J. Sci. Comput. 2019, 41, 220–241. [Google Scholar] [CrossRef]
- Braun, E.C.; Bretti, G.; Natalini, R. Parameter estimation techniques for a chemotaxis model inspired by Cancer-on-Chip (COC) experiments. Int. J. Nonlin. Mech. 2022, 140, 103895. [Google Scholar] [CrossRef]
- Braun, E.C.; Bretti, G.; Natalini, R. Mass-preserving approximation of a chemotaxis multi-domain transmission model for microfluidic chips. Mathematics 2021, 9, 688. [Google Scholar] [CrossRef]
- Bretti, G.; De Ninno, A.; Natalini, R.; Peri, D.; Roselli, N. Estimation algorithm for a hybrid PDEODE model inspired by immunocompetent Cancer-on-Chip experiment. Axioms 2021, 10, 243. [Google Scholar] [CrossRef]
- Christiansen, R.; Morosini, A.; Enriquez, E.; Muñoz, B.; Klinger, F.L.; Martinez, M.P.; Suárez, A.O.; Kostadinoff, J. 3D litho-constrained inversion model of southern Sierra Grande de San Luis: New insights into the Famatinian tectonic setting. Tectonophysics 2019, 756, 1–24. [Google Scholar] [CrossRef]
- Aragao, O.; Sava, P. Elastic full-waveform inversion with probabilistic petrophysical model constraints. Geophysics 2020, 85, 101–111. [Google Scholar] [CrossRef]
- Mahmoodi, O.; Smith, R.S.; Spicer, B. Using constrained inversion of gravity and magnetic field to produce a 3D litho-prediction model. Geophys. Prospect. 2017, 65, 1662–1679. [Google Scholar] [CrossRef]
- Gao, L.; Sadeghi, M.; Ebtehaj, A. Microwave retrievals of soil moisture and vegetation optical depth with improved resolution using a combined constrained inversion algorithm: Application for SMAP satellite. Remote Sens. Environ. 2020, 239, 111662. [Google Scholar] [CrossRef]
- Ebtehaj, A.; Bras, R.L. A physically constrained inversion for high-resolution passive microwave retrieval of soil moisture and vegetation water content in L-band. Remote Sens. Environ. 2019, 233, 111346. [Google Scholar] [CrossRef]
- Abubakar, A.; Habashy, T.M.; Pan, G.D.; Li, M. Application of the multiplicative regularized Gauss-Newton algorithm for three-dimensional microwave imaging. IEEE Trans. Antenn. Propag. 2012, 60, 2431–2441. [Google Scholar] [CrossRef]
- Yan, Z.; Zhong, S.; Lin, L.; Cui, Z. Adaptive Levenberg-Marquardt algorithm: A new optimization strategy for Levenberg-Marquardt neural networks. Mathematics 2021, 9, 2176. [Google Scholar] [CrossRef]
- Zhang, R.; Li, F.; Luo, X. Multiscale compression algorithm for solving nonlinear ill-posed integral equations via Landweber iteration. Mathematics 2020, 8, 221. [Google Scholar] [CrossRef]
- Liu, T. Porosity reconstruction based on Biot elastic model of porous media by homotopy perturbation method. Chaos Solitons Fractals 2022, 158, 112007. [Google Scholar] [CrossRef]




| Noise Level | MGCS | MG | FGCS |
|---|---|---|---|
| 30 dB | 531.191 | 633.275 | 1038.302 |
| 25 dB | 586.140 | 623.060 | 1002.997 |
| 20 dB | 571.452 | × | 1071.707 |
| 15 dB | 569.270 | × | × |
| Noise Level | MGCS | MG | FGCS |
|---|---|---|---|
| 30 dB | 0.0213 | 0.0635 | 0.0373 |
| 25 dB | 0.0297 | 0.0813 | 0.0415 |
| 20 dB | 0.0331 | × | 0.0493 |
| 15 dB | 0.0593 | × | × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Yu, J.; Zheng, Y.; Liu, C.; Yang, Y.; Qi, Y. A Nonlinear Multigrid Method for the Parameter Identification Problem of Partial Differential Equations with Constraints. Mathematics 2022, 10, 2938. https://doi.org/10.3390/math10162938
Liu T, Yu J, Zheng Y, Liu C, Yang Y, Qi Y. A Nonlinear Multigrid Method for the Parameter Identification Problem of Partial Differential Equations with Constraints. Mathematics. 2022; 10(16):2938. https://doi.org/10.3390/math10162938
Chicago/Turabian StyleLiu, Tao, Jiayuan Yu, Yuanjin Zheng, Chao Liu, Yanxiong Yang, and Yunfei Qi. 2022. "A Nonlinear Multigrid Method for the Parameter Identification Problem of Partial Differential Equations with Constraints" Mathematics 10, no. 16: 2938. https://doi.org/10.3390/math10162938
APA StyleLiu, T., Yu, J., Zheng, Y., Liu, C., Yang, Y., & Qi, Y. (2022). A Nonlinear Multigrid Method for the Parameter Identification Problem of Partial Differential Equations with Constraints. Mathematics, 10(16), 2938. https://doi.org/10.3390/math10162938








