Constructing a Class of Frozen Jacobian Multi-Step Iterative Solvers for Systems of Nonlinear Equations
Abstract
:1. Introduction
2. Constructing New Methods
2.1. The Third-Order FJA
2.1.1. Convergence Analysis
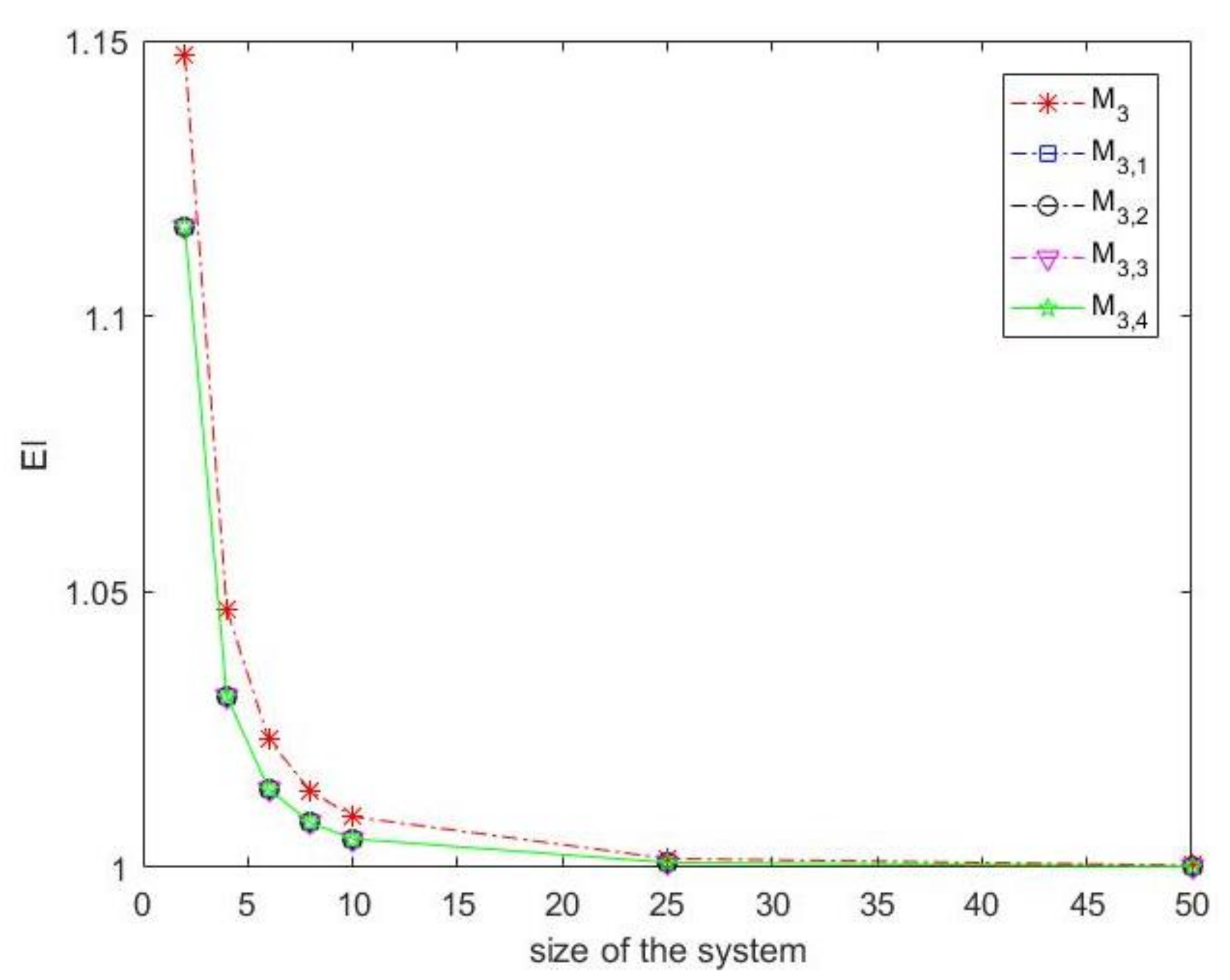
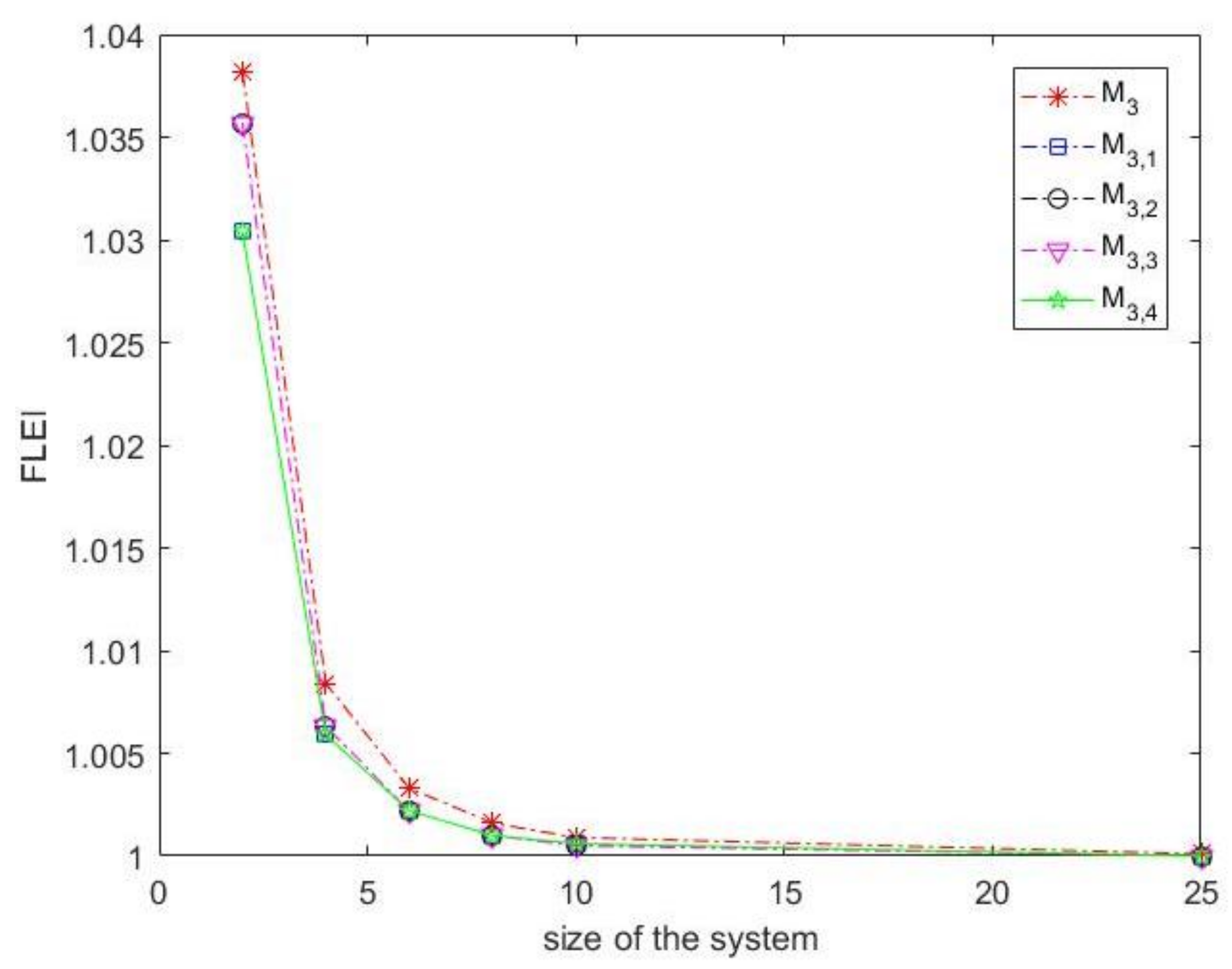
2.1.2. The Computational Efficiency
2.2. The Fourth-Order FJA
2.2.1. Convergence Analysis
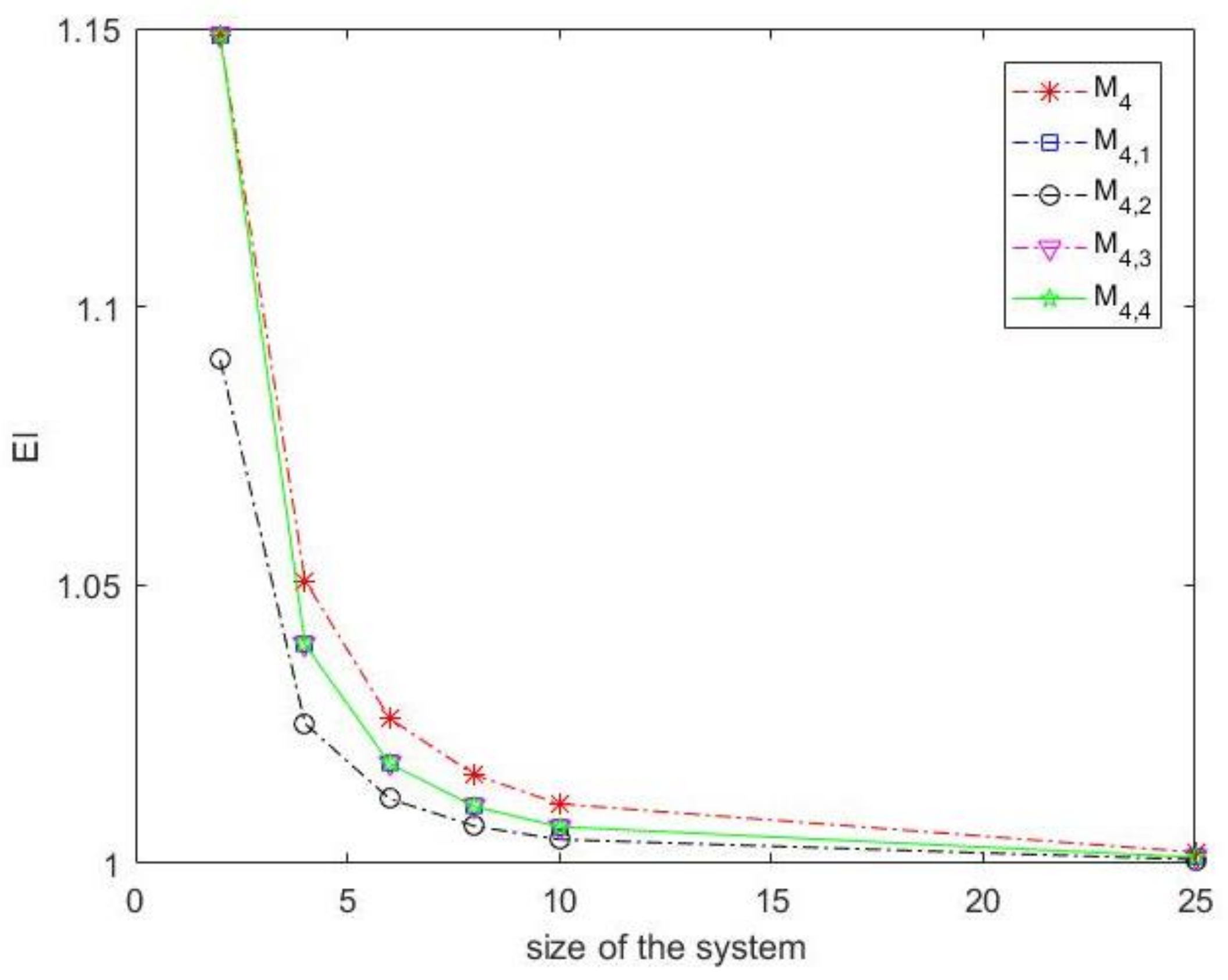
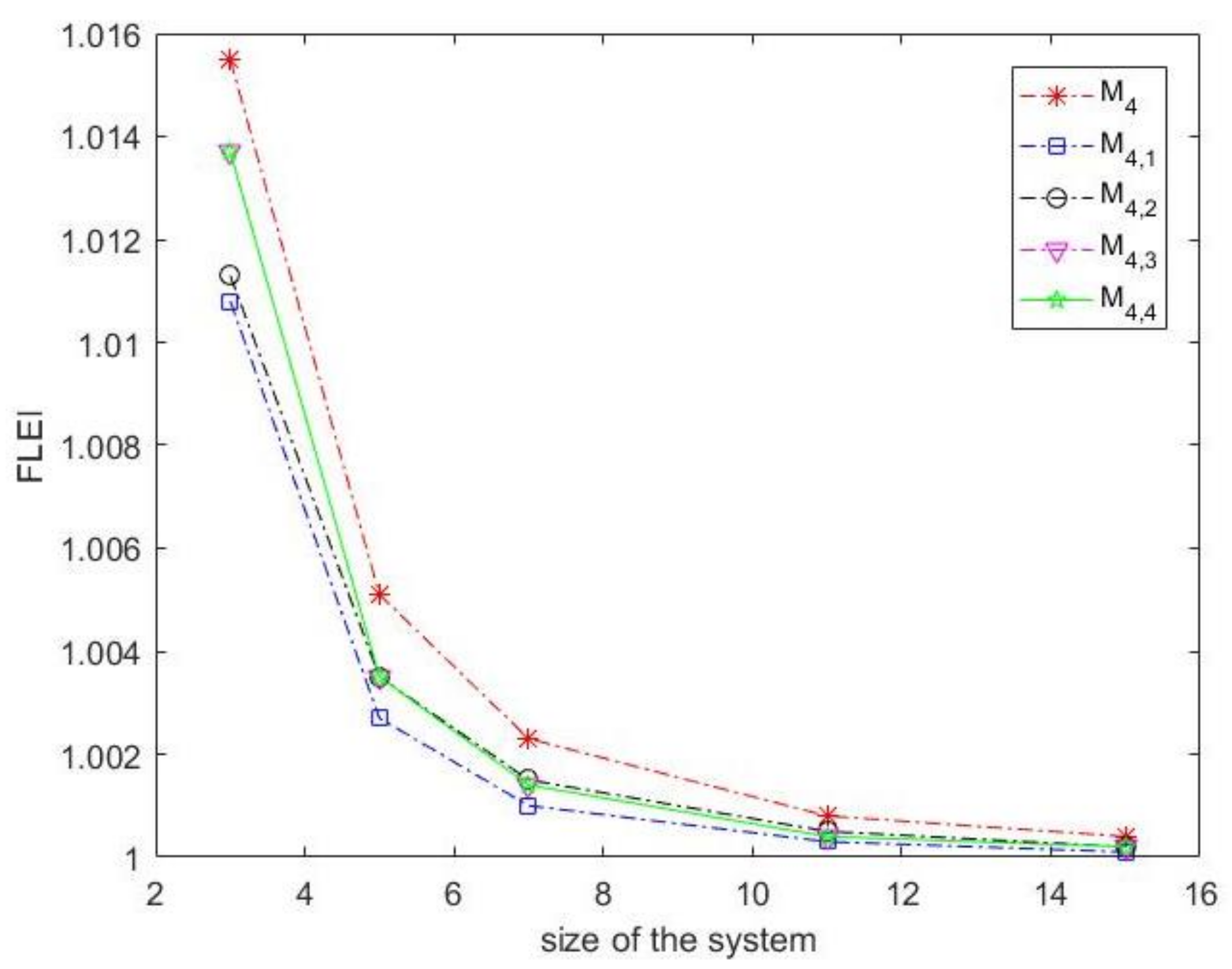
2.2.2. The Computational of Efficiency
3. Numerical Results
4. Another Comparison
- First. The fourth-order method given by Qasim et al. [25], ,
- Second. The fourth-order Newton-like method by Amat et al. [26], ,.
- Third. The fifth-order iterative method by Ahmad et al. [28], ,.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fay, T.H.; Graham, S.D. Coupled spring equations. Int. J. Math. Educ. Sci. Technol. 2003, 34, 65–79. [Google Scholar] [CrossRef]
- Petzold, L. Automatic selection of methods for solving stiff and non stiff systems of ordinary differential equations. SIAM J. Sci. Stat. Comput. 1983, 4, 136–148. [Google Scholar] [CrossRef]
- Ehle, B.L. High order A-stable methods for the numerical solution of systems of D.E.’s. BIT Numer. Math. 1968, 8, 276–278. [Google Scholar] [CrossRef]
- Wambecq, A. Rational Runge-Kutta methods for solving systems of ordinary differential equations. Computing 1978, 20, 333–342. [Google Scholar] [CrossRef]
- Liang, H.; Liu, M.; Song, M. Extinction and permanence of the numerical solution of a two-prey one-predator system with impulsive effect. Int. J. Comput. Math. 2011, 88, 1305–1325. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Mak, M.K. Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates. Appl. Math. Comput. 2014, 236, 184–194. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, L.; Han, Z. Stability analysis of two new SIRs models with two viruses. Int. J. Comput. Math. 2018, 95, 2026–2035. [Google Scholar] [CrossRef]
- Kröger, M.; Schlickeiser, R. Analytical solution of the SIR-model for the temporal evolution of epidemics, Part A: Time-independent reproduction factor. J. Phys. A Math. Theor. 2020, 53, 505601. [Google Scholar] [CrossRef]
- Ullah, M.Z.; Behl, R.; Argyros, I.K. Some high-order iterative methods for nonlinear models originating from real life problems. Mathematics 2020, 8, 1249. [Google Scholar] [CrossRef]
- Argyros, I.K. Concerning the “terra incognita” between convergence regions of two Newton methods. Nonlinear Anal. 2005, 62, 179–194. [Google Scholar] [CrossRef]
- Drexler, M. Newton Method as a Global Solver for Non-Linear Problems. Ph.D Thesis, University of Oxford, Oxford, UK, 1997. [Google Scholar]
- Guti’errez, J.M.; Hern’andez, M.A. A family of Chebyshev-Halley type methods in Banach spaces. Bull. Aust. Math. Soc. 1997, 55, 113–130. [Google Scholar] [CrossRef]
- Cordero, A.; Jordán, C.; Sanabria, E.; Torregrosa, J.R. A new class of iterative processes for solving nonlinear systems by using one divided differences operator. Mathematics 2019, 7, 776. [Google Scholar] [CrossRef]
- Stefanov, S.M. Numerical solution of systems of non linear equations defined by convex functions. J. Interdiscip. Math. 2022, 25, 951–962. [Google Scholar] [CrossRef]
- Lee, M.Y.; Kim, Y.I.K. Development of a family of Jarratt-like sixth-order iterative methods for solving nonlinear systems with their basins of attraction. Algorithms 2020, 13, 303. [Google Scholar] [CrossRef]
- Cordero, A.; Jordán, C.; Sanabria-Codesal, E.; Torregrosa, J.R. Design, convergence and stability of a fourth-order class of iterative methods for solving nonlinear vectorial problems. Fractal Fract. 2021, 5, 125. [Google Scholar] [CrossRef]
- Amiri, A.; Cordero, A.; Darvishi, M.T.; Torregrosa, J.R. A fast algorithm to solve systems of nonlinear equations. J. Comput. Appl. Math. 2019, 354, 242–258. [Google Scholar] [CrossRef]
- Argyros, I.K.; Sharma, D.; Argyros, C.I.; Parhi, S.K.; Sunanda, S.K. A family of fifth and sixth convergence order methods for nonlinear models. Symmetry 2021, 13, 715. [Google Scholar] [CrossRef]
- Singh, A. An efficient fifth-order Steffensen-type method for solving systems of nonlinear equations. Int. J. Comput. Sci. Math. 2018, 9, 501–514. [Google Scholar] [CrossRef]
- Ullah, M.Z.; Serra-Capizzano, S.; Ahmad, F. An efficient multi-step iterative method for computing the numerical solution of systems of nonlinear equations associated with ODEs. Appl. Math. Comput. 2015, 250, 249–259. [Google Scholar] [CrossRef]
- Pacurar, M. Approximating common fixed points of Pres̆ic-Kannan type operators by a multi-step iterative method. An. St. Univ. Ovidius Constanta 2009, 17, 153–168. [Google Scholar]
- Rafiq, A.; Rafiullah, M. Some multi-step iterative methods for solving nonlinear equations. Comput. Math. Appl. 2009, 58, 1589–1597. [Google Scholar] [CrossRef]
- Aremu, K.O.; Izuchukwu, C.; Ogwo, G.N.; Mewomo, O.T. Multi-step iterative algorithm for minimization and fixed point problems in p-uniformly convex metric spaces. J. Ind. Manag. Optim. 2021, 17, 2161. [Google Scholar] [CrossRef]
- Soleymani, F.; Lotfi, T.; Bakhtiari, P. A multi-step class of iterative methods for nonlinear systems. Optim. Lett. 2014, 8, 1001–1015. [Google Scholar] [CrossRef]
- Qasim, U.; Ali, Z.; Ahmad, F.; Serra-Capizzano, S.; Ullah, M.Z.; Asma, M. Constructing frozen Jacobian iterative methods for solving systems of nonlinear equations, associated with ODEs and PDEs using the homotopy method. Algorithms 2016, 9, 18. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Grau, À.; Grau-Sánchez, M. Maximum efficiency for a family of Newton-like methods with frozen derivatives and some applications. Appl. Math. Comput. 2013, 219, 7954–7963. [Google Scholar] [CrossRef]
- Kouser, S.; Rehman, S.U.; Ahmad, F.; Serra-Capizzano, S.; Ullah, M.Z.; Alshomrani, A.S.; Aljahdali, H.M.; Ahmad, S.; Ahmad, S. Generalized Newton multi-step iterative methods GMNp,m for solving systems of nonlinear equations. Int. J. Comput. Math. 2018, 95, 881–897. [Google Scholar] [CrossRef]
- Ahmad, F.; Tohidi, E.; Ullah, M.Z.; Carrasco, J.A. Higher order multi-step Jarratt-like method for solving systems of nonlinear equations: Application to PDEs and ODEs. Comput. Math. Appl. 2015, 70, 624–636. [Google Scholar] [CrossRef]
- Kaplan, W.; Kaplan, W.A. Ordinary Differential Equations; Addison-Wesley Publishing Company: Boston, MA, USA, 1958. [Google Scholar]
- Emmanuel, E.C. On the Frechet derivatives with applications to the inverse function theorem of ordinary differential equations. Aian J. Math. Sci. 2020, 4, 1–10. [Google Scholar]
- Ortega, J.M.; Rheinboldt, W.C.; Werner, C. Iterative Solution of Nonlinear Equations in Several Variables; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Behl, R.; Bhalla, S.; Magre nán, A.A.; Kumar, S. An efficient high order iterative scheme for large nonlinear systems with dynamics. J. Comput. Appl. Math. 2022, 404, 113249. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Solutions of the Equations and Systems of Equations; Prentice-Hall: England Cliffs, NJ, USA; New York, NY, USA, 1964. [Google Scholar]
- Montazeri, H.; Soleymani, F.; Shateyi, S.; Motsa, S.S. On a new method for computing the numerical solution of systems of nonlinear equations. J. Appl. Math. 2012, 2012, 751975. [Google Scholar] [CrossRef]
- Darvishi, M.T. A two-step high order Newton-like method for solving systems of nonlinear equations. Int. J. Pure Appl. Math. 2009, 57, 543–555. [Google Scholar]
- Hernández, M.A. Second-derivative-free variant of the Chebyshev method for nonlinear equations. J. Optim. Theory Appl. 2000, 3, 501–515. [Google Scholar] [CrossRef]
- Babajee, D.K.R.; Dauhoo, M.Z.; Darvishi, M.T.; Karami, A.; Barati, A. Analysis of two Chebyshev-like third order methods free from second derivatives for solving systems of nonlinear equations. J. Comput. Appl. Math. 2010, 233, 2002–2012. [Google Scholar] [CrossRef]
- Noor, M.S.; Waseem, M. Some iterative methods for solving a system of nonlinear equations. Comput. Math. Appl. 2009, 57, 101–106. [Google Scholar] [CrossRef]
- Sharma, J.R.; Guha, R.K.; Sharma, R. An efficient fourth order weighted-Newton method for systems of nonlinear equations. Numer. Algorithms 2013, 62, 307–323. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Barati, A. A fourth-order method from quadrature formulae to solve systems of nonlinear equations. Appl. Math. Comput. 2007, 188, 257–261. [Google Scholar] [CrossRef]
- Soleymani, F. Regarding the accuracy of optimal eighth-order methods. Math. Comput. Modell. 2011, 53, 1351–1357. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. A modified Newton-Jarratt’s composition. Numer. Algorithms 2010, 55, 87–99. [Google Scholar] [CrossRef]
- Shin, B.C.; Darvishi, M.T.; Kim, C.H. A comparison of the Newton–Krylov method with high order Newton-like methods to solve nonlinear systems. Appl. Math. Comput. 2010, 217, 3190–3198. [Google Scholar] [CrossRef]
- Waziri, M.Y.; Aisha, H.; Gambo, A.I. On performance analysis of diagonal variants of Newton’s method for large-scale systems of nonlinear equations. Int. J. Comput. Appl. 2011, 975, 8887. [Google Scholar]

| Methods | |||||
|---|---|---|---|---|---|
| No. of steps | 2 | 2 | 2 | 2 | 2 |
| Order of convergence | 3 | 3 | 3 | 3 | 3 |
| Functional evaluations | |||||
| The classical efficiency index (IE) | |||||
| No. of decompositions | 1 | 2 | 1 | 1 | 2 |
| Cost of decompositions | |||||
| Cost of linear systems (based on flops) | |||||
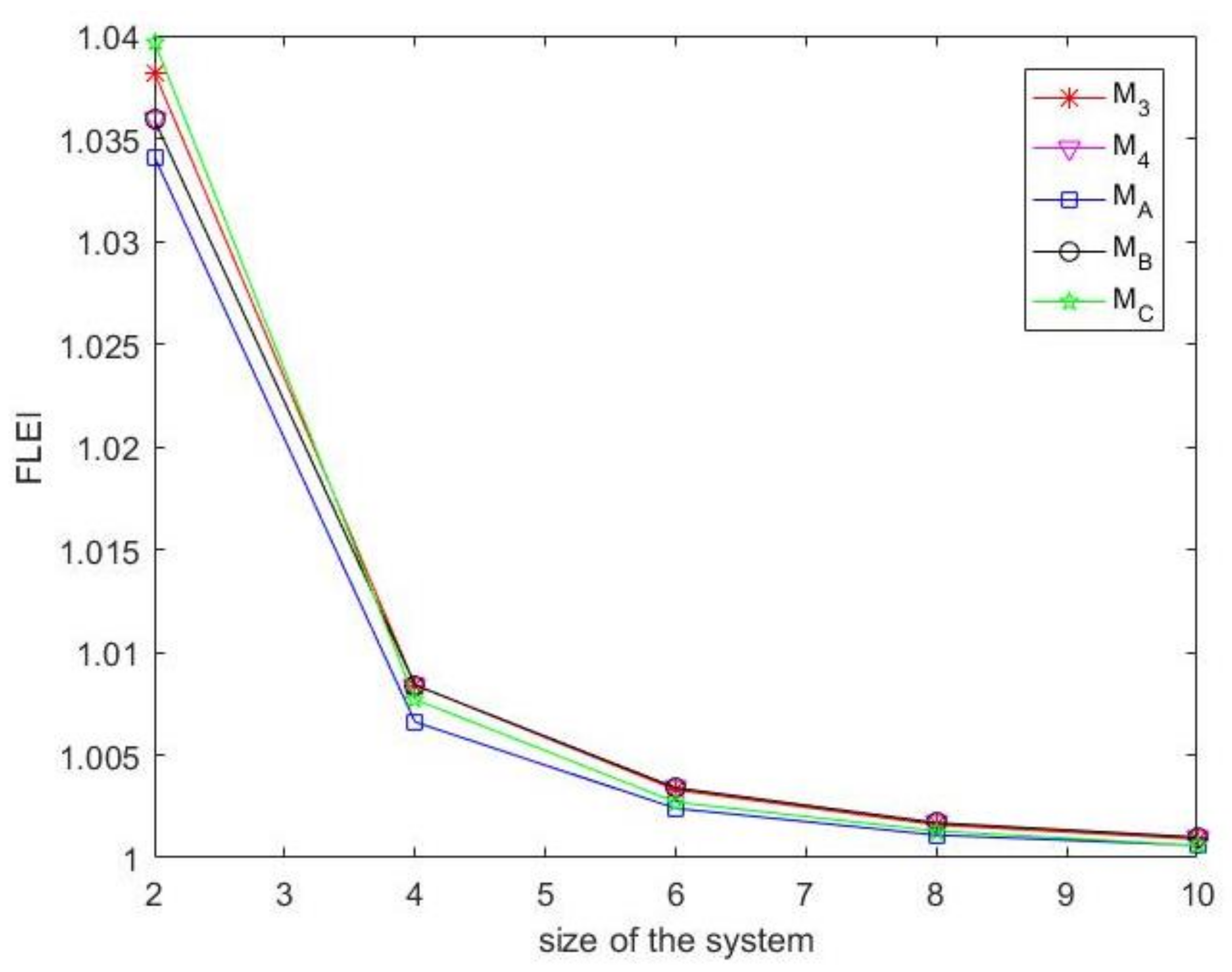
| Flops-like efficiency index (FLEI) |
| Methods | |||||
|---|---|---|---|---|---|
| No. of steps | 3 | 2 | 3 | 2 | 2 |
| Order of convergence | 4 | 4 | 4 | 4 | 4 |
| Functional evaluations | |||||
| The classical efficiency index (IE) | |||||
| No. of decompositions | 1 | 2 | 2 | 2 | 2 |
| Cost of decompositions | |||||
| Cost of linear systems (based on flops) | |||||
| Flops-like efficiency index (FLEI) |
| Methods | Experiment 1 | Experiment 2 | Experiment 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| n | cpu | n | cpu | n | cpu | ||||
| 50 | 4 | 7.7344 | 50 | 5 | 10.6250 | 50 | 5 | 10.4844 | |
| 100 | 5 | 59.6406 | 100 | 5 | 59.8594 | 100 | 5 | 60.0313 | |
| 50 | 4 | 11.0625 | 50 | 5 | 13.8125 | 50 | 5 | 14.1406 | |
| 100 | 4 | 69.4219 | 100 | 5 | 87.3594 | 100 | 5 | 87.4063 | |
| 50 | 4 | 18.7188 | 50 | 5 | 24.9375 | 50 | 5 | 21.5469 | |
| 100 | 5 | 157.2344 | 100 | 5 | 143.7344 | 100 | 5 | 146.2656 | |
| 50 | 4 | 20.7031 | 50 | 5 | 23.1563 | 50 | 5 | 24.2969 | |
| 100 | 5 | 153.1719 | 100 | 5 | 143.2969 | 100 | 5 | 145.4063 | |
| 50 | 4 | 13.1719 | 50 | 5 | 13.2500 | 50 | 4 | 11.0156 | |
| 100 | 4 | 73.2500 | 100 | 5 | 88.2031 | 100 | 4 | 70.2500 | |
| Methods | Experiment 1 | Experiment 2 | Experiment 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| n | cpu | n | cpu | n | cpu | ||||
| 50 | 4 | 12.2463 | 50 | 4 | 13.3218 | 50 | 4 | 11.5781 | |
| 100 | 4 | 78.1563 | 100 | 5 | 94.9063 | 100 | 4 | 74.2969 | |
| 50 | 4 | 23.6875 | 50 | 4 | 21.9531 | 50 | 4 | 21.7969 | |
| 100 | 4 | 151.9844 | 100 | 4 | 144.7656 | 100 | 4 | 140.8438 | |
| 50 | 3 | 15.3906 | 50 | 4 | 18.9531 | 50 | 4 | 18.6875 | |
| 100 | 4 | 121.6563 | 100 | 4 | 122.7344 | 100 | 4 | 118.5781 | |
| 50 | 3 | 12.2188 | 50 | 4 | 17.8750 | 50 | 4 | 15.2656 | |
| 100 | 4 | 97.5469 | 100 | 4 | 99.0469 | 100 | 4 | 97.1250 | |
| 50 | 3 | 16.4688 | 50 | 4 | 21.7344 | 50 | 4 | 20.7188 | |
| 100 | 3 | 109.1719 | 100 | 4 | 152.0156 | 100 | 4 | 140.2969 | |
| Methods | |||||
|---|---|---|---|---|---|
| No. of steps | 2 | 3 | 2 | 3 | 3 |
| Order of convergence | 3 | 4 | 4 | 4 | 5 |
| Functional evaluations | |||||
| The classical efficiency index (IE) | |||||
| No. of decompositions | 1 | 1 | 1 | 1 | 1 |
| Cost of decompositions | |||||
| Cost of linear systems (based on flops) | |||||
| Flops-like efficiency index (FLEI) |
| Methods | Experiment 1 | Experiment 2 | Experiment 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| n | CPU | n | CPU | n | CPU | ||||
| 50 | 4 | 7.7344 | 50 | 5 | 10.6250 | 50 | 5 | 10.4844 | |
| 100 | 5 | 59.6406 | 100 | 5 | 59.8594 | 100 | 5 | 60.0313 | |
| 50 | 4 | 12.2463 | 50 | 4 | 13.3218 | 50 | 4 | 11.5781 | |
| 100 | 4 | 78.1563 | 100 | 5 | 94.9063 | 100 | 4 | 74.2969 | |
| 50 | 6 | 23.1875 | 50 | 7 | 25.0625 | 50 | 6 | 25.4063 | |
| 100 | 6 | 139.5625 | 100 | 7 | 173.8125 | 100 | 6 | 150.8594 | |
| 50 | 4 | 15.2509 | 50 | 4 | 12.1563 | 50 | 4 | 12.9219 | |
| 100 | 4 | 76.1406 | 100 | 5 | 91.1719 | 100 | 4 | 71.6406 | |
| 50 | 4 | 23.4688 | 50 | 4 | 23.4854 | 50 | 4 | 22.1531 | |
| 100 | 4 | 139.9844 | 100 | 4 | 185.1406 | 100 | 4 | 138.4063 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Obaidi, R.H.; Darvishi, M.T. Constructing a Class of Frozen Jacobian Multi-Step Iterative Solvers for Systems of Nonlinear Equations. Mathematics 2022, 10, 2952. https://doi.org/10.3390/math10162952
Al-Obaidi RH, Darvishi MT. Constructing a Class of Frozen Jacobian Multi-Step Iterative Solvers for Systems of Nonlinear Equations. Mathematics. 2022; 10(16):2952. https://doi.org/10.3390/math10162952
Chicago/Turabian StyleAl-Obaidi, R. H., and M. T. Darvishi. 2022. "Constructing a Class of Frozen Jacobian Multi-Step Iterative Solvers for Systems of Nonlinear Equations" Mathematics 10, no. 16: 2952. https://doi.org/10.3390/math10162952
APA StyleAl-Obaidi, R. H., & Darvishi, M. T. (2022). Constructing a Class of Frozen Jacobian Multi-Step Iterative Solvers for Systems of Nonlinear Equations. Mathematics, 10(16), 2952. https://doi.org/10.3390/math10162952







