1. Introduction
Approximating a locally unique solution
of the nonlinear system
has many applications in engineering and mathematics [
1,
2,
3,
4]. In (
1), we have
n equations with
n variables. In fact,
F is a vector-valued function with
n variables. Several problems arising from the different areas in natural and applied sciences take the form of systems of nonlinear Equation (
1) that need to be solved, where
such that for all
,
is a scalar nonlinear function. Additionally, there are many real life problems for which, in the process of finding their solutions, one needs to solve a system of nonlinear equations, see for example [
5,
6,
7,
8,
9]. It is known that finding an exact solution
of the nonlinear system (
1) is not an easy task, especially when the equation contains terms consisting of logarithms, trigonometric and exponential functions, or a combination of transcendental terms. Hence, in general, one cannot find the solution of Equation (
1) analytically, therefore, we have to use iterative methods. Any iterative method starts from one approximation and constructs a sequence such that it converges to the solution of the Equation (
1) (for more details, see [
10]).
The most commonly used iterative method to solve (
1) is the classical Newton method, given by
where
is the Jacobian matrix of function
F, and
is the
k-th approximation of the root of (
1) with the initial guess
. It is well known that Newton’s method is a quadratic convergence method with the efficiency index
[
11]. The third and higher-order methods such as the Halley and Chebyshev methods [
12] have little practical value because of the evaluation of the second Frechèt-derivative. However, third and higher-order multi-step methods can be good substitutes because they require the evaluation of the function and its first derivative at different points.
In the recent decades, many authors tried to design iterative procedures with better efficiency and higher order of convergence than the Newton scheme, see, for example, ref. [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24] and references therein. However, the accuracy of solutions is highly dependent on the efficiency of the utilized algorithm. Furthermore, at each step of any iterative method, we must find the exact solution of an obtained linear system which is expensive in actual applications, especially when the system size
n is very large. However, the proposed higher-order iterative methods are futile unless they have high-order convergence. Therefore, the important aim in developing any new algorithm is to achieve high convergence order with requiring as small as possible the evaluations of functions, derivatives and matrix inversions. Thus, here, we focus on the technique of the frozen Jacobian multi-step iterative algorithms. It is shown that this idea is computationally attractive and economical for constructing iterative solvers because the inversion of the Jacobian matrix (regarding
-decomposition) is performed once. Many researchers have reduced the computational cost of these algorithms by frozen Jacobian multi-step iterative techniques [
25,
26,
27,
28].
In this work, we construct a new class of frozen Jacobian multi-step iterative methods for solving the nonlinear systems of equations. This is a high-order convergent algorithm with an excellent efficiency index. The theoretical analysis is presented completely. Further, by solving some nonlinear systems, the ability of the methods is compared with some known algorithms.
The rest of this paper is organized as follows. In the following section, we present our new methods with obtaining of their order of convergence. Additionally, their computational efficiency are discussed in general. Some numerical examples are considered in
Section 3 and
Section 4 to show the asymptotic behavior of these methods. Finally, a brief concluding remark is presented in
Section 5.
2. Constructing New Methods
In this section, two high-order frozen Jacobian multi-step iterative methods to solve systems of nonlinear equations are presented. These come by increasing the convergence in Newton’s method and simultaneously decreasing its computational costs. The framework of these Frozen Jacobian multi-step iterative Algorithms (FJA) can be described as
In (
2), for an
m-step method (
), one needs
m function evaluations and only one Jacobian evaluation. Further, the number of
decompositions is one. The order of convergence for such FJA method is
. In the right-hand side column of (
2), the algorithm is briefy described.
In the following subsections, by choosing two different values for m, a third- and a fourth-order frozen Jacobian multi-step iterative algorithm are presented.
2.1. The Third-Order FJA
First, we investigate case
, that is,
we denote this by
.
2.1.1. Convergence Analysis
In this part, we prove that the order of convergence of method (
3) is three. First, we need to definition of the Frechèt derivative.
Definition 1 ([
29]).
Let F be an operator which maps a Banach space X into a Banach space Y. If there exists a bounded linear operator T from X into Y such thatthen F is said to be Frechèt differentiable and .
For more details on the Frechèt differentiability and Frechèt derivative, we refer the interested readers to a review article by Emmanuel [30] and references therein. Theorem 1. Let be a Frechèt differentiable function at each point of an open convex neighborhood I of α, the solution of system . Suppose that is continuous and nonsingular in α, then, the sequence obtained using the iterative method (3) converges to α and its rate of convergence is three. Proof. Suppose that
using Taylor’s expansion [
31], we obtain
as
is the root of
F so
. As a matter of fact, one may yield the following equations of
and
in a neighborhood of
by using Taylor’s series expansions [
32],
wherein
and
I is the identity matrix whose order is the same as the order of the Jacobian matrix. Note that
. Using (
4) and (
5) we obtain
Since
, we find
By the definition of error term
, the error term of
as an approximation of
, that is,
is obtained from the second term of the right-hand side of Equation (
6). Similarly, the Taylor’s expansion of the function
is
From (
4) and (
7), we obtain
Clearly, the error Equation (
8) shows that the order of convergence of the frozen Jacobian multi-step iterative method (
3) is three. This completes the proof. □
2.1.2. The Computational Efficiency
In this section, we compare the computational efficiency of our third-order scheme (
3), denoted as
, with some existing third-order methods. We will assess the efficiency index of our new frozen Jacobian multi-step iterative method in contrast with the existing methods for systems of nonlinear equations, using two famous efficiency indices. The first one is the classical efficiency index [
33] as
where
p is the rate of convergence and
c stands for the total computational cost per iteration in terms of the number of functional evaluations, such that
where
r refers to the number of function evaluations needed per iteration and
m is the number of Jacobian matrix evaluations needed per iteration.
It is well known that the computation of factorization by any of the existing methods in the literature normally needs flops in floating point operations, while the floating point operations to solve two triangular systems needs flops.
The second criterion is the flops-like efficiency index (
) which was defined by Montazeri et al. [
34] as
where
p is the order of convergence of the method,
c denotes the total computational cost per loop in terms of the number of functional evaluations, as well as the cost of
factorization for solving two triangular systems (based on the flops).
As the first comparison, we compare
with the third-order method given by Darvishi [
35], which is denoted as
The second iterative method shown by
is the following third-order method introduced by Hernández [
36]
Another method is the following third-order iterative method given by Babajee et al. [
37],
,
Finally, the following third-order iterative method,
, ref. [
38] is considered
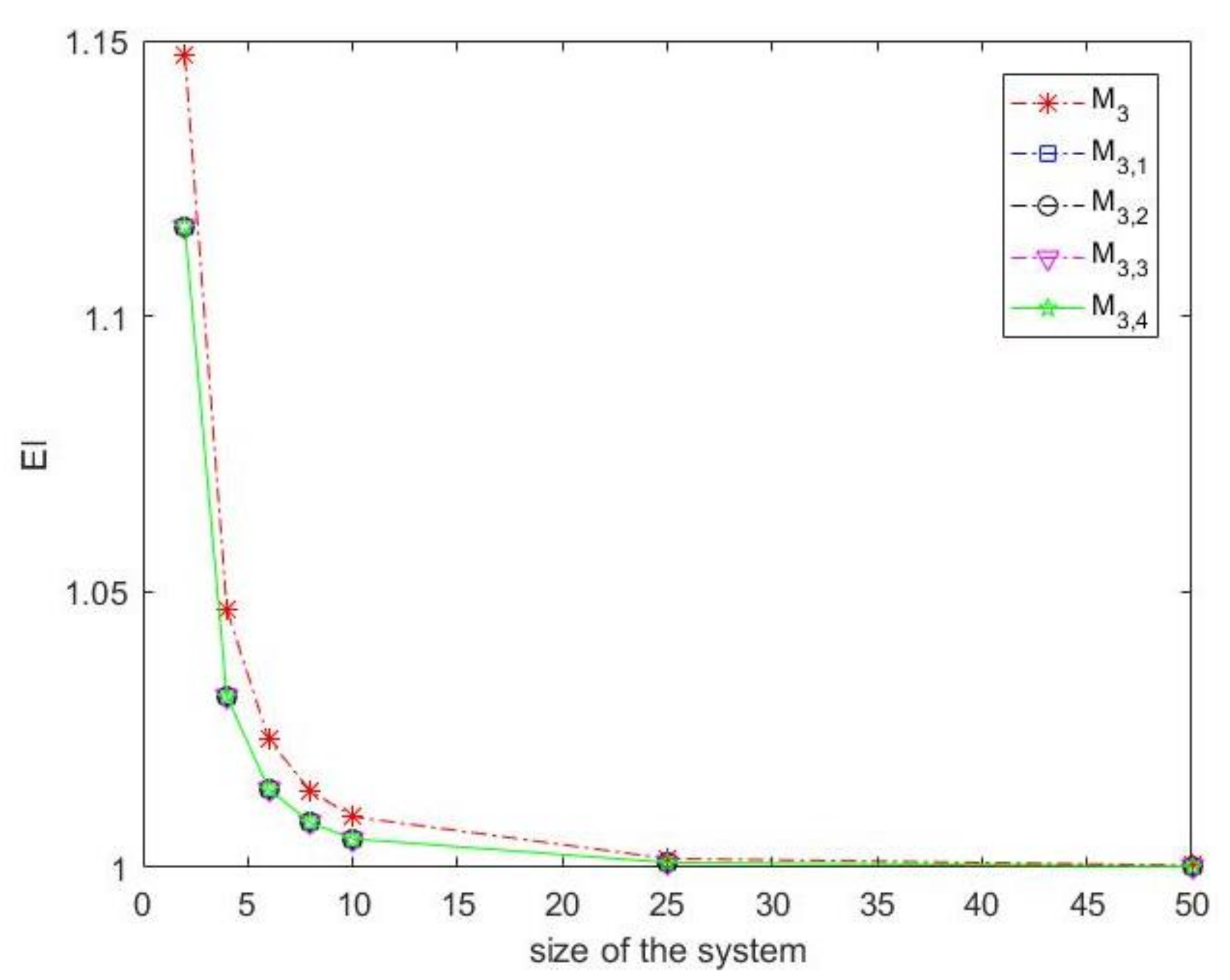
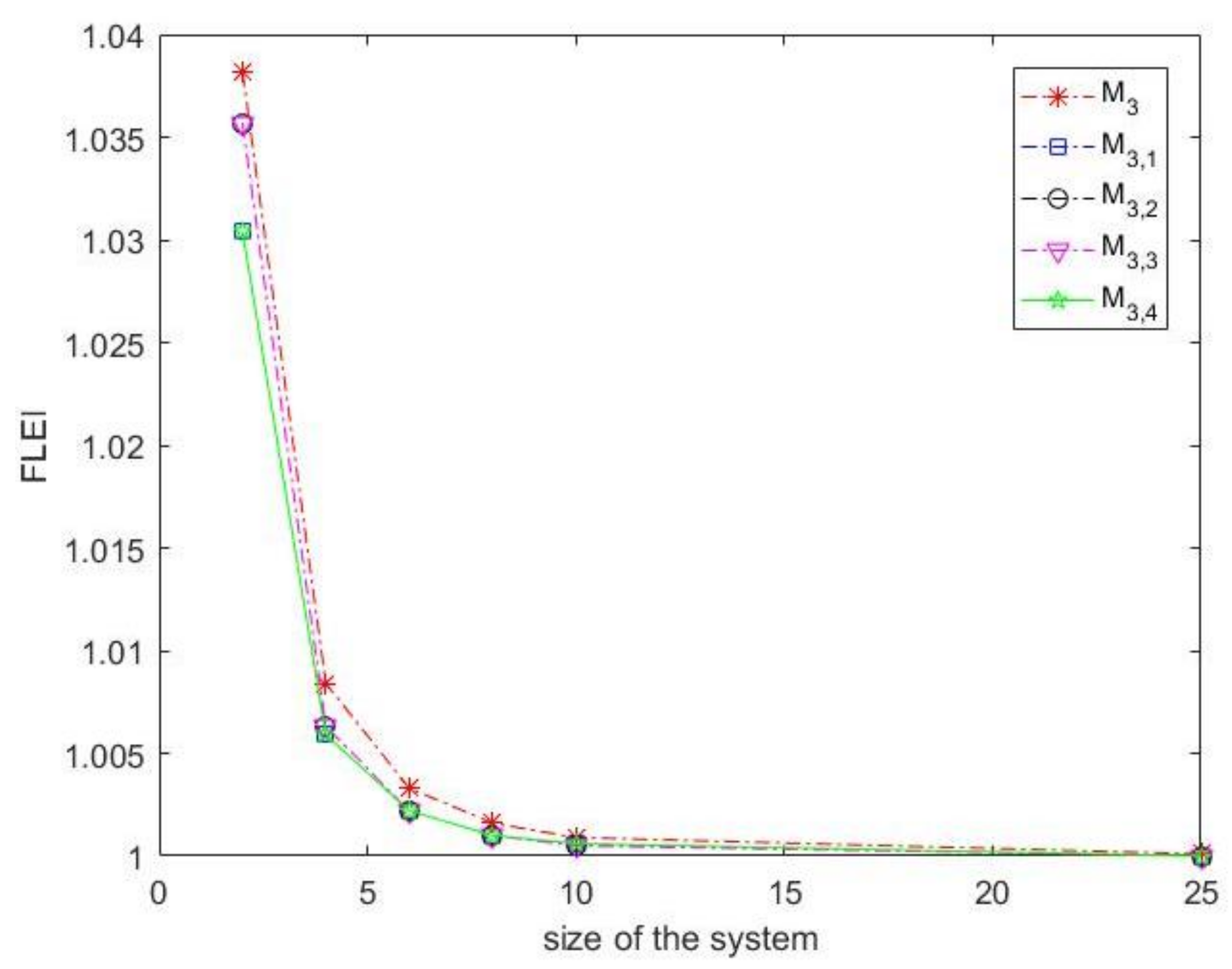
The computational efficiency of our third-order method revealed that our method,
, is the best one in respect with methods
,
,
and
, as presented in
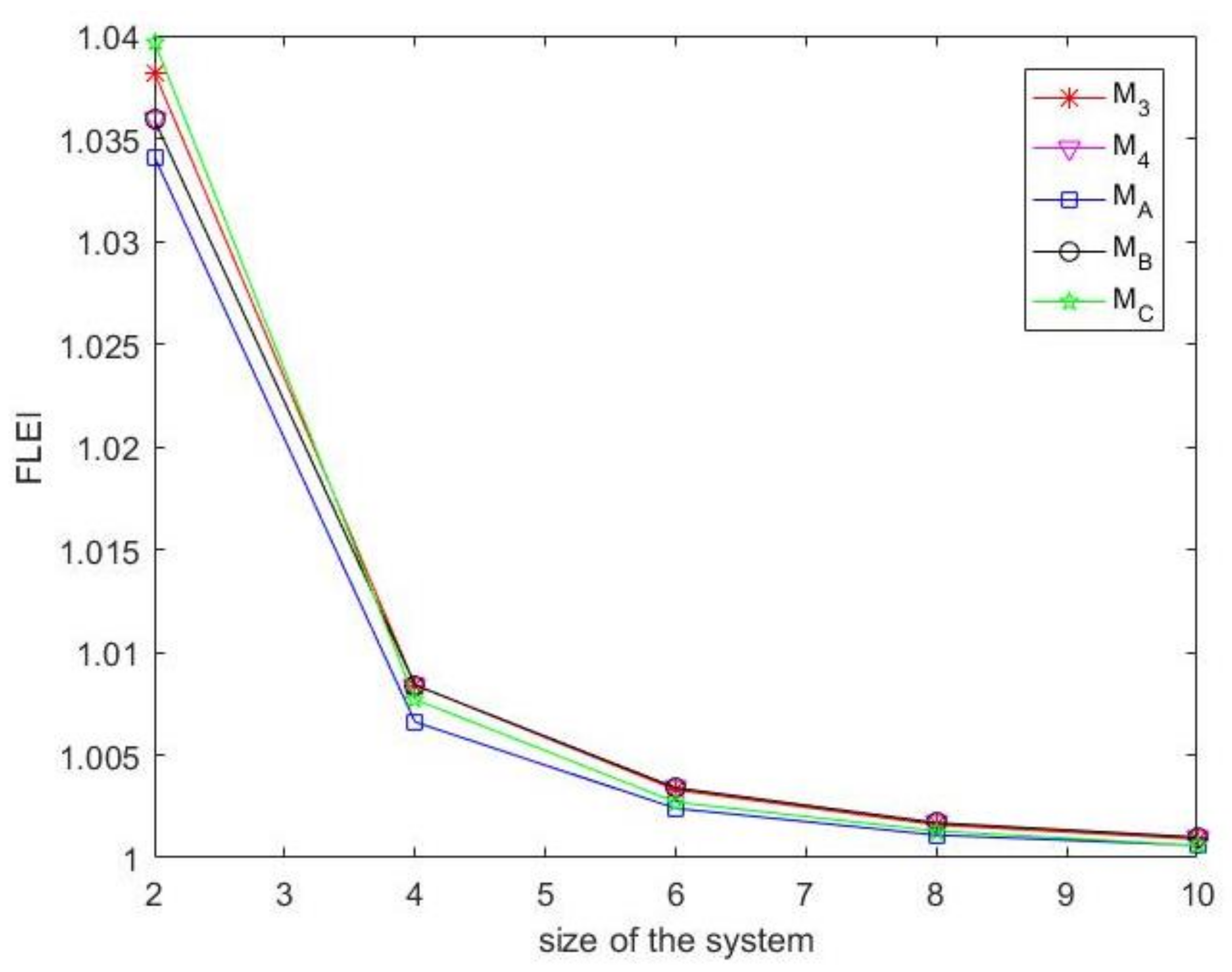
Table 1, and
Figure 1 and
Figure 2.
2.2. The Fourth-Order FJA
By setting
in FJA, the following three-step algorithm is deduced
.
In the following subsections, the order of convergence and efficiency indices are obtained for the method described in (
9).
2.2.1. Convergence Analysis
The frozen Jacobian three-step iterative process (
9) has the rate of convergence order four by using three evaluations of function
F and one first-order Frechèt derivative
F per full iterations. To avoid any repetition, we take a sketch of proof on this subject. Similar to the proof of Theorem 1, by setting
in (
8) we obtain
Therefore, from (
5) and (
10), we find
Since we have
from (
6) and (
11), the following result is obtained
This completes the proof, since error Equation (
12) shows that the order of convergence of the frozen Jacobian multi-step iterative method (
9) is four.
2.2.2. The Computational of Efficiency
Now, we compare the computational efficiency of our fourth-order scheme (
9), called by
, with some existing fourth-order methods. The considered methods are: the third-order method
given by Sharma et al. [
39],
the fourth-order iterative method
given by Darvishi and Barati [
40],
the fourth-order iterative method
given by Soleymani et al. [
34,
41],
and the following Jarratt fourth-order method
[
42],
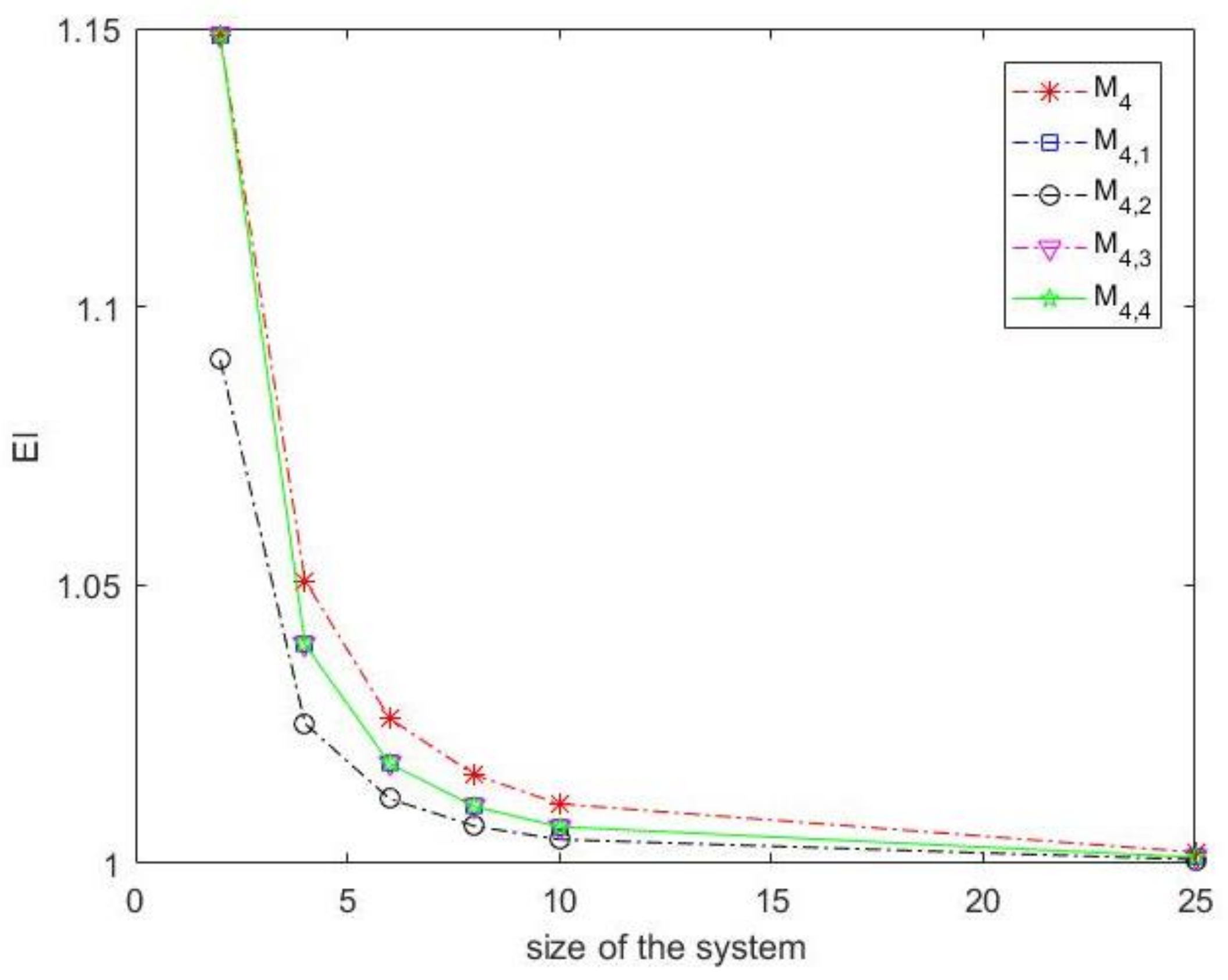
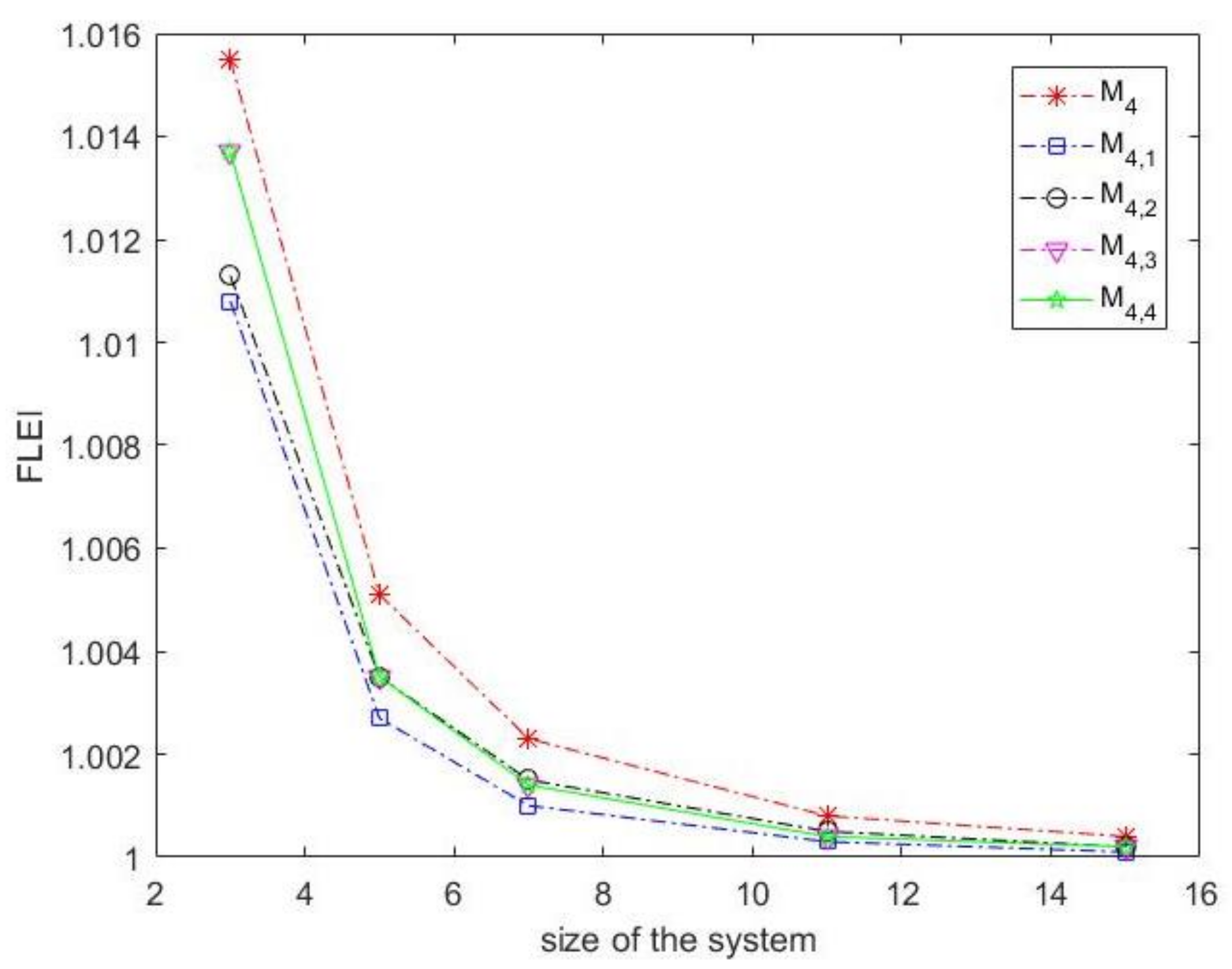
The computational efficiency of our fourth-order method showed that our method
is better than methods
,
,
and
as the comparison results are presented in
Table 2, and
Figure 3 and
Figure 4. As we can see from
Table 2, the indices of our method
are better than similar ones in methods
,
,
and
. Furthermore,
Figure 3 and
Figure 4 show the superiority of our method in respect with the another schemes.
3. Numerical Results
In order to check the validity and efficiency of our proposed frozen Jacobian multi-step iterative methods, three test problems are considered to illustrate convergence and computation behaviors such as efficiency index and some another indices of the frozen Jacobian multi-step iterative methods. Numerical computations have been performed using variable precision arithmetic that uses floating point representation of 100 decimal digits of mantissa in MATLAB. The computer specifications are: Intel(R) Core(TM) i7-1065G7 CPU 1.30 GHz with 16.00 GB of RAM on Windows 10 pro.
Experiment 1. We begin with the following nonlinear system of
n equations [
43],
The exact zero of
is
. To solve (
13), we set the initial guess as
. The stopping criterion is selected as
.
Experiment 2. The next test problem is the following system of nonlinear equations [
44],
The exact root of
is
. To solve (
14), the initial guess is taken as
. The stopping criterion is selected as
.
Experiment 3. The last test problem is the following nonlinear system [
9],
with the exact solution
. To solve (
15), the initial guess and the stopping criterion are respectively considered as
and
.
Table 3 shows the comparison results between our third-order frozen Jacobian two-step iterative method
and some third-order frozen Jacobian iterative methods, namely,
,
,
and
. For all test problems, two different values for
n are considered, namely,
. As this table shows, in all cases, our method works better than the others. Similarly, in
Table 4, CPU time and number of iterations are presented for our fourth-order method, namely,
and methods
,
,
and
. Similar to
, the CPU time for
is less than the CPU time for the other methods. These tables show superiority of our methods in respect with the other ones. In
Table 3 and
Table 4,
shows the number of iterations.
5. Conclusions
In this article, two new frozen Jacobian two- and three-step iterative methods to solve systems of nonlinear equations are presented. For the first method, we proved that the order of convergence is three, while for the second one, a fourth-order convergence is proved. By solving three different examples, one may see our methods work as well. Further, the CPU time of our methods is less than some selected frozen Jacobian multi-step iterative methods in the literature. Moreover, other indices of our methods such as number of steps, functional evaluations, the classical efficiency index, and so on, are better than these indices for other methods. This class of the frozen Jacobian multi-step iterative methods can be a pattern for new research on the frozen Jacobian iterative algorithms.