Day-Ahead Scheduling of On-Load Tap Changer Transformer and Switched Capacitors by Multi-Pareto Optimality
Abstract
:1. Introduction
1.1. Background
1.2. Aim and Contribution
1.3. Paper Organization
2. Related Studies
| References | Natures | Contributions | Drawbacks |
|---|---|---|---|
| Refs. [6,7] | Complex | Real-time voltage control method proposed using a linear approximation of ac power flow. | Local controller utilized lacking overall network stability. |
| Ref. [8] | Complex, coordinated | Voltage control through reactive power control using coordination between DGs and capacitor banks. | Demands expensive communication structures among local and central systems. |
| Ref. [9] | Very complex | A volt–var compensator proposed using coordinated control proposed with evolutionary optimization. | Unable to derive strategies for multi-energy microgrid scenarios. |
| Refs. [10,11] | Complex | A multi-agent system (MAS) is proposed to control the reactive power sources in a distribution system. | The communication among the multi-agents is even more complex than normal controllers and increases transition time. |
| Refs. [13,14] | Simple | Harmonic balance method proposed for voltage controllers using Q(V) control. | Two-end data are needed. Additionally, it cannot reflect the nature of large systems. |
| Ref. [15] | Complex | Model predictive controller (MPC) is used for coordinated control among the DGs and other voltage controllers. | Implementation of MPC is challenging and has high computation requirements and fine-tuned parameters. |
| Ref. [16] | Complex | Dynamic programming is used to establish a connection among DGs and OLTC with minimum switch operation. | Reliability depends on the quality of the communication system. PV power sources are not considered. |
| Ref. [19] | Complex | Cooperative controller is proposed for voltage control involving multiple feeders, loads, and DGs. | Suffers in the presence of microgrids and requires high communication bandwidth. |
| Ref. [21] | Very simple | Line drop compensator parameters are designed based on the current state of voltage regulators in presence of DG. | Only the OLTC control is considered, which reduces the effectiveness of the voltage regulation method. |
| Ref. [22] | Complex | Parameters of OLTC are designed in accordance with DG output in order to maintain the voltage profile. | Requires costly widespread communication facility. |
| Ref. [25] | Simple | Mixed integer non-linear programming (MILP) is used for volt–var control using capacitor banks and DGs. | MILP fails to address high-dimensional problems. Additionally, non-linear cases cannot be handled. |
| Ref. [26] | Very complex | Proper control parameters of volt–var compensators are obtained while keeping the voltage profiles at the desired range. | A coordinated complex control structure considers OLTC, voltage regulators, and capacitor banks at feeders and sub-stations. Difficulty in practical implementations. |
| Ref. [27] | Simple | Particle swarm optimization along with dynamic programming is used in solving reactive power control problems. | High-dimensional problems may face the local optima conditions. |
3. Problem Formulation
3.1. Objective Functions
3.1.1. Voltage Deviation at the Secondary Side of the Main Transformer
3.1.2. Voltage Deviation at the Ends of the Feeders
3.1.3. Total System Power Loss
3.2. Constraints
3.2.1. Voltage Constraints
3.2.2. OLTC Transformer Constraints
3.2.3. SC Constraints
4. Multi-Objective Optimization Algorithm
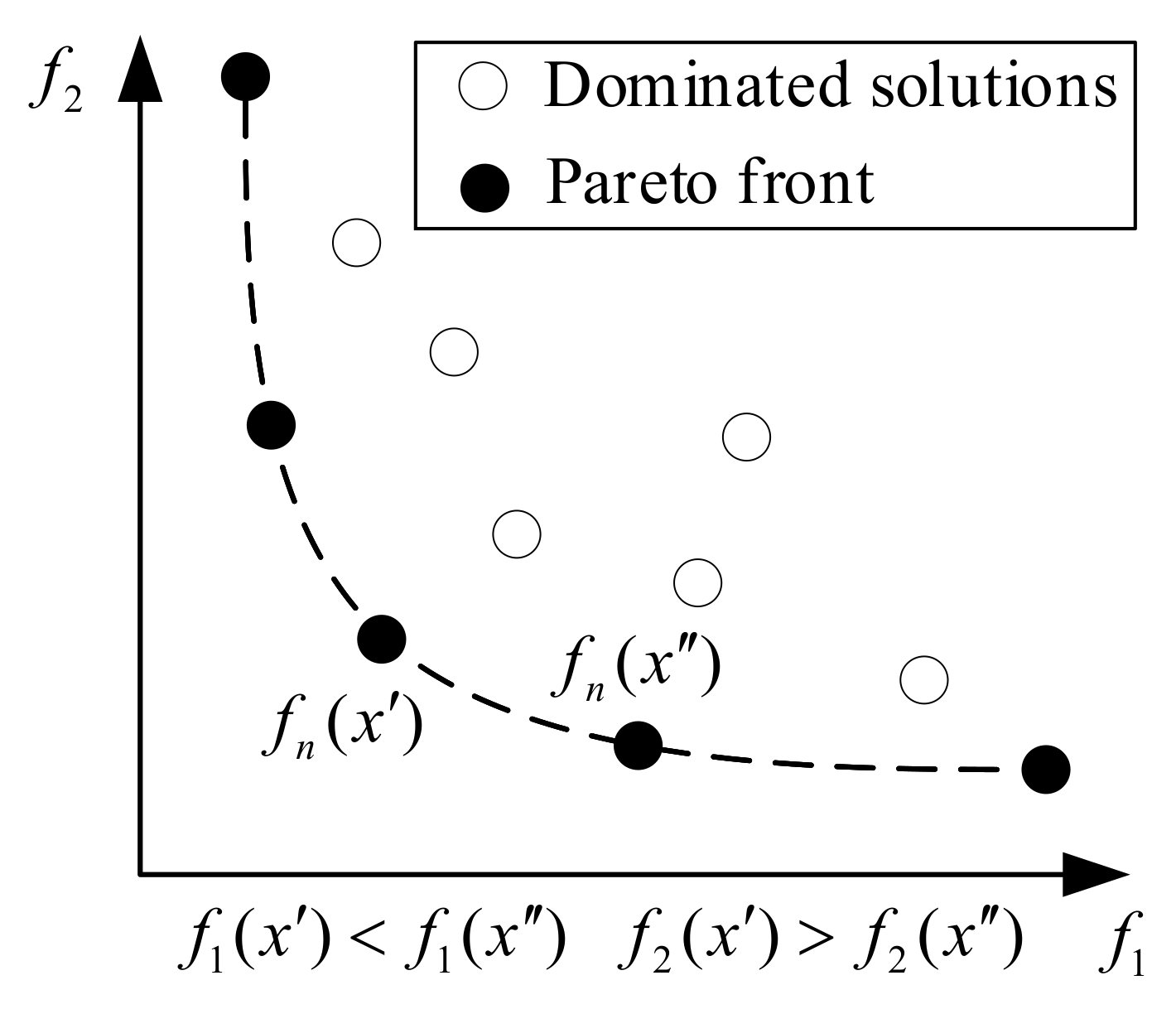
4.1. Pareto Optimality
4.2. MOPSO Algorithm
- Step 1
- Set the size of populations for particle swarms, the size of the external archive, and other parameters.
- Step 2
- Generate the position and velocity of each particle randomly.
- Step 3
- Evaluate the fitness of individual particles and store the first non-dominated solution in the external archive.
- Step 4
- Select one non-dominated solution as the Gbest from the external archive.
- Step 5
- Update the velocity and position of the particles using the PSO algorithm.
- Step 5
- Evaluate the fitness of each particle.
- Step 7
- Save new non-dominated solutions.
- Step 8
- Check whether the external archive is full.
- Step 9
- If the external archive is not full, the new solution is compared with the solutions stored in the external archive. If the new solution dominates any of the solutions in the archive, the dominated solutions are deleted, and the new non-dominated solution is stored.
- Step 10
- If the external archive is full, one solution in the most crowded hypercube is randomly removed, and the new non-dominated solution is stored.

4.3. Minimum Manhattan Distance Method
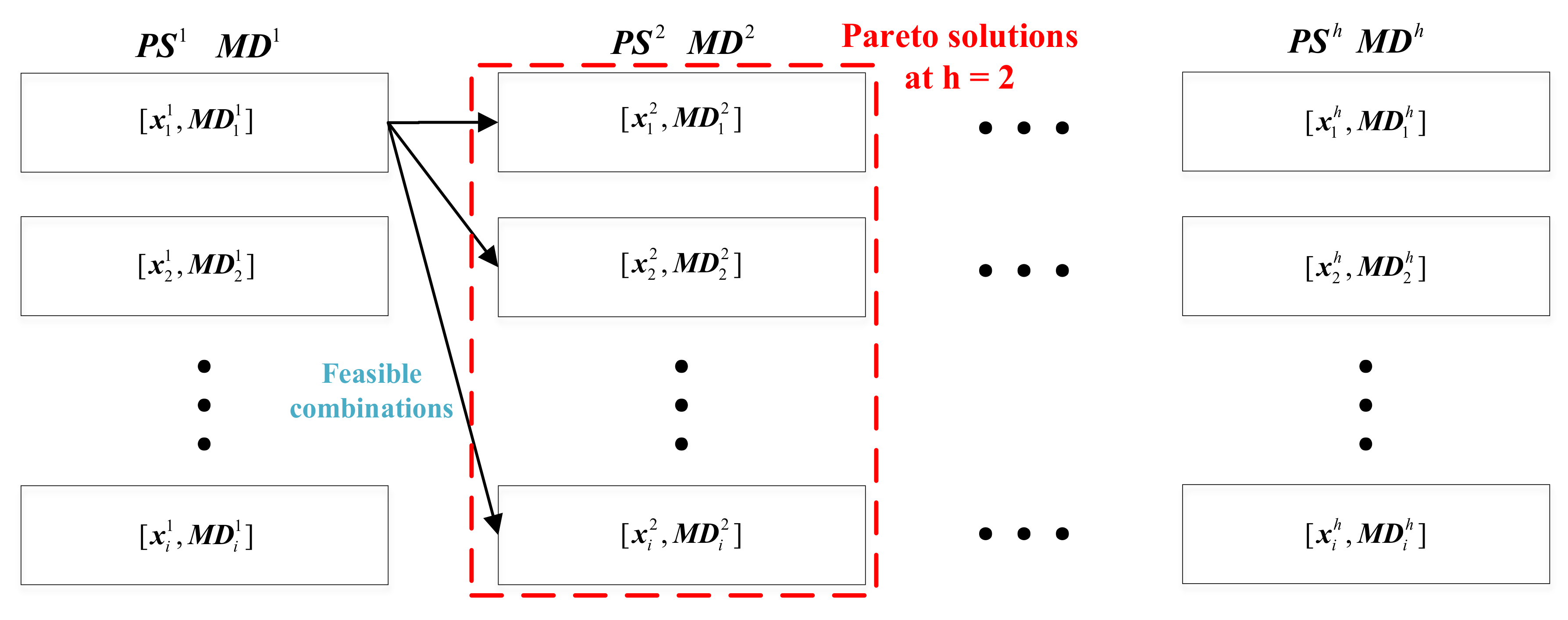
5. One-Day Scheduling Method
- Step 1
- Determine hourly Pareto front solutions of the OLTC transformer and SCs using the MOPSO algorithm, as shown in Equation (19).
- Step 2
- Calculate the distance of the hourly Pareto front solutions using the Manhattan distance method, as shown in Equation (20).
- Step 3
- Search for feasible one-day schedules that meet the switching constraint of the OLTC transformer as Equation (10) and the switching constraint of SCs as Equation (11) with the hourly Pareto front solutions, as shown in Equation (21).
- Step 4
- Calculate all possible one-day schedules using Step 3. Calculate the Manhattan distance for one-day schedules by summing the Manhattan distances corresponding to the hourly Pareto solutions, as shown in Equation (24).
- Step 5
- The schedule with the minimum Manhattan distance is selected from the above feasible solution sets, as shown in Equation (25).

6. Sample System and Simulation Results
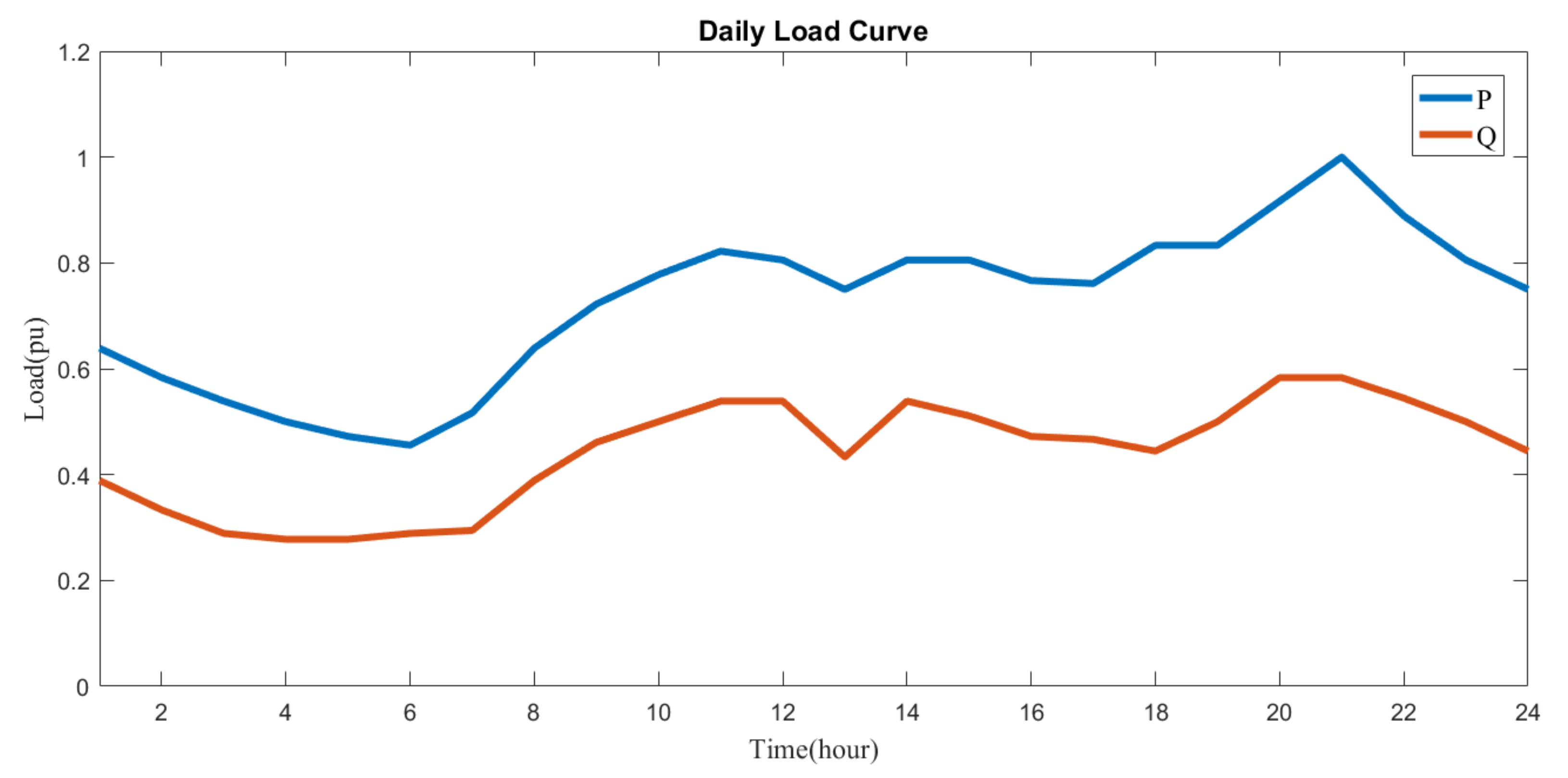
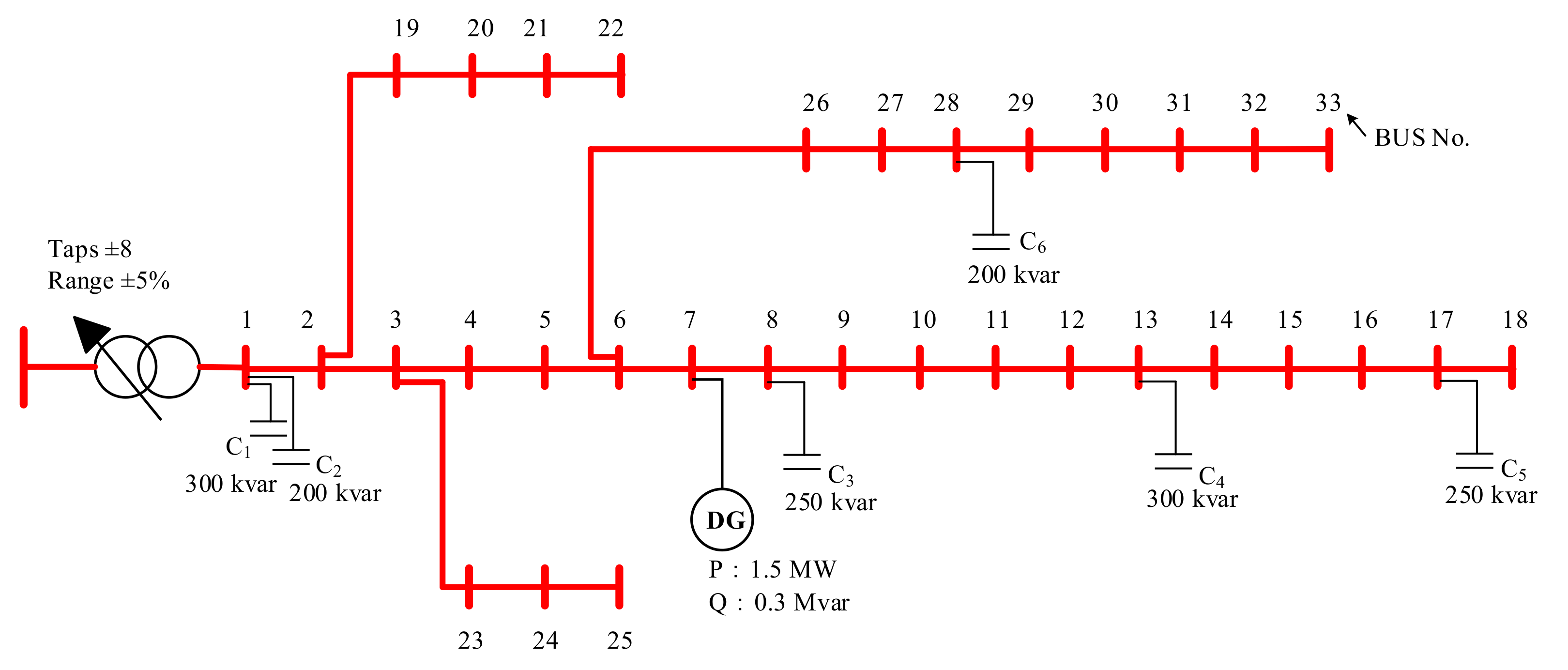
6.1. Sample System
6.2. Indicators for Validations
6.2.1. Voltage Deviations at All Buses
6.2.2. Voltage Variations
6.2.3. Total System Power Loss
6.2.4. Difference in Values
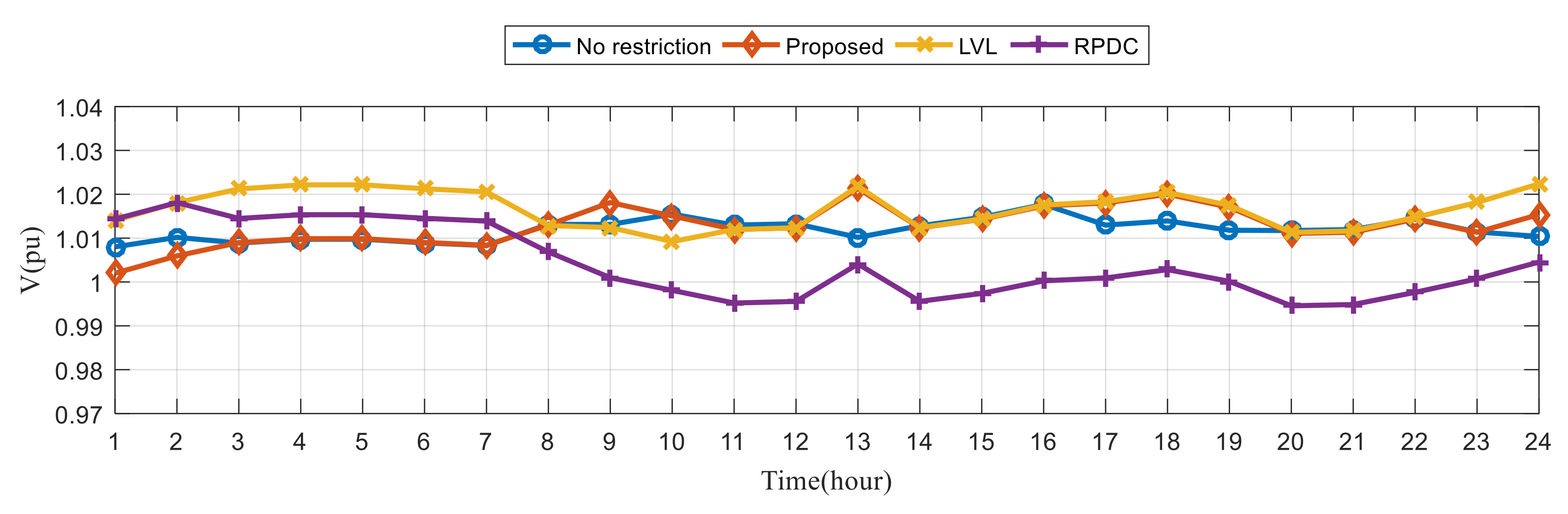
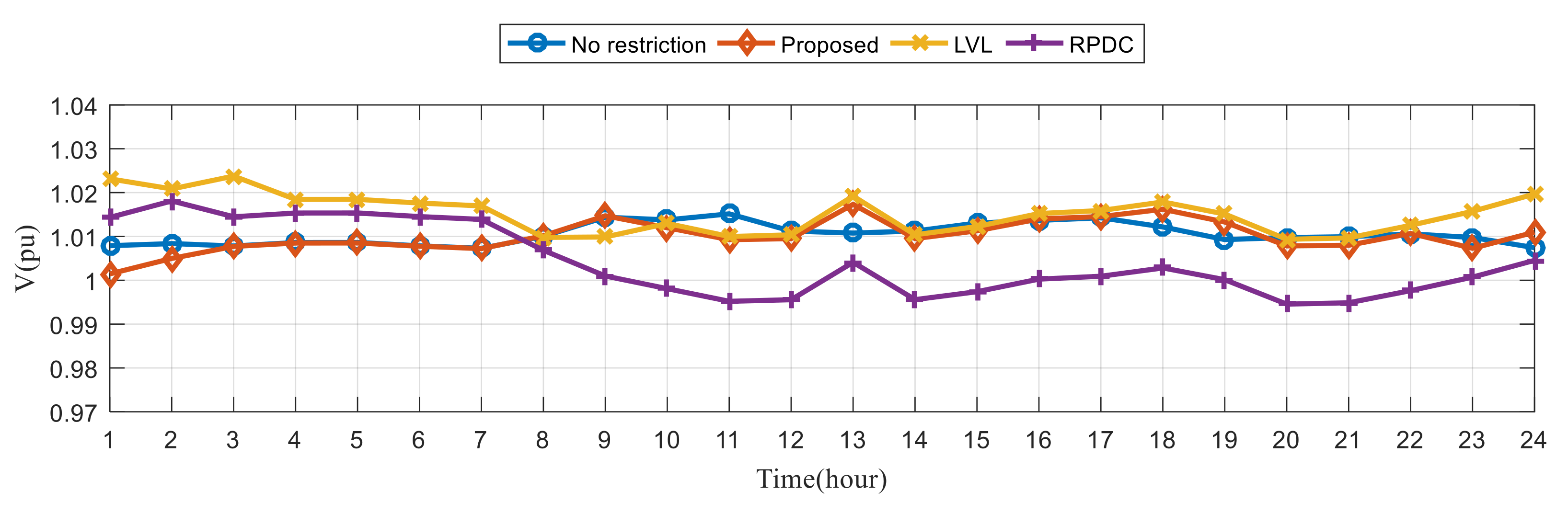
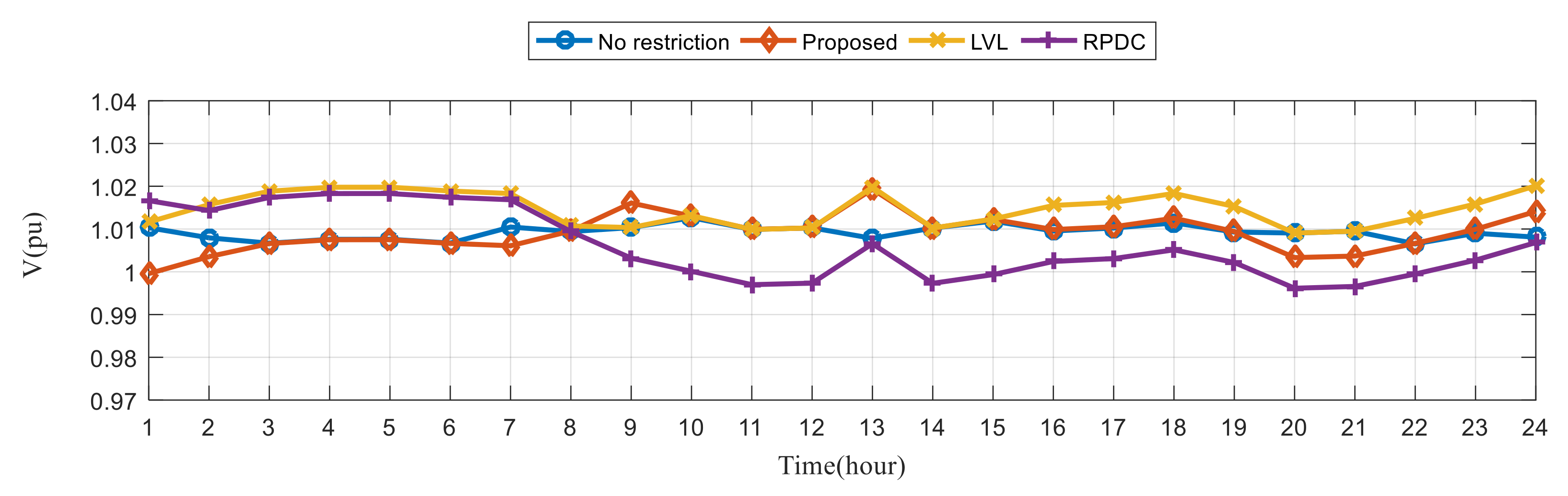
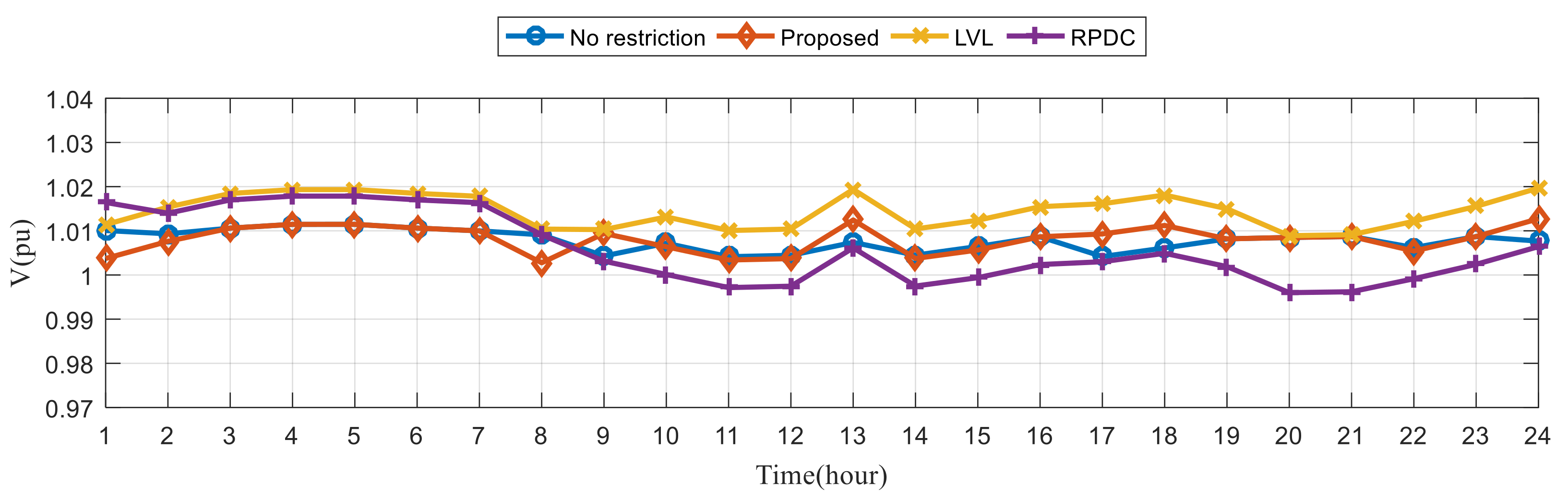
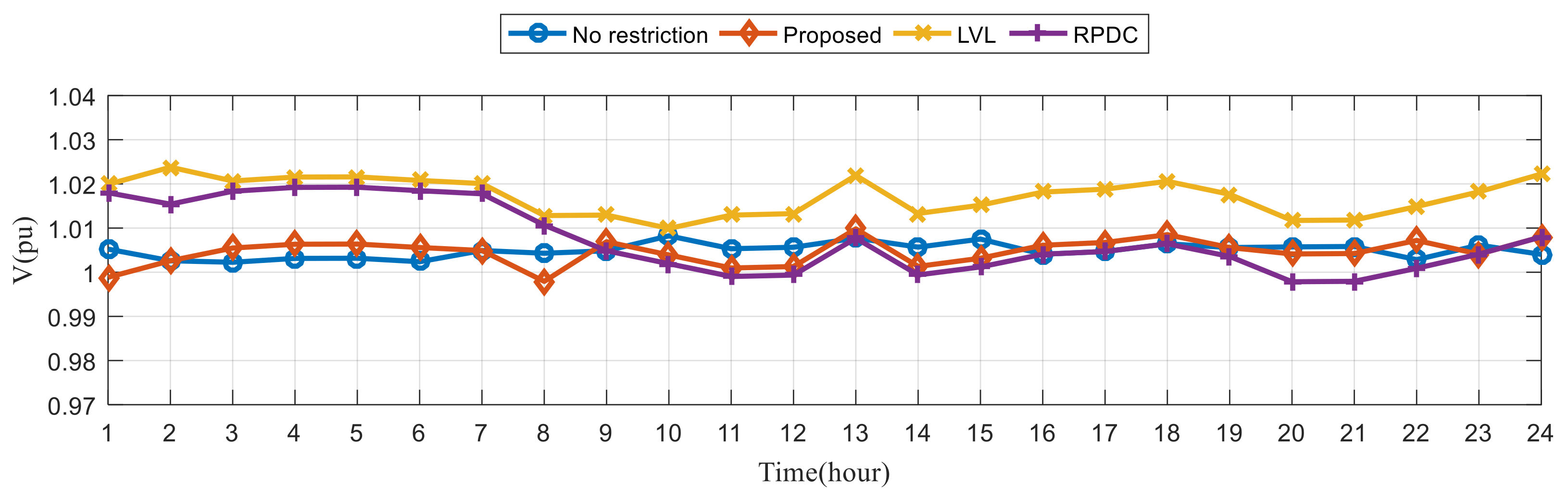
6.3. Simulation Results of Sample System
6.4. Performance Test of MOPSO and Other Algorithms
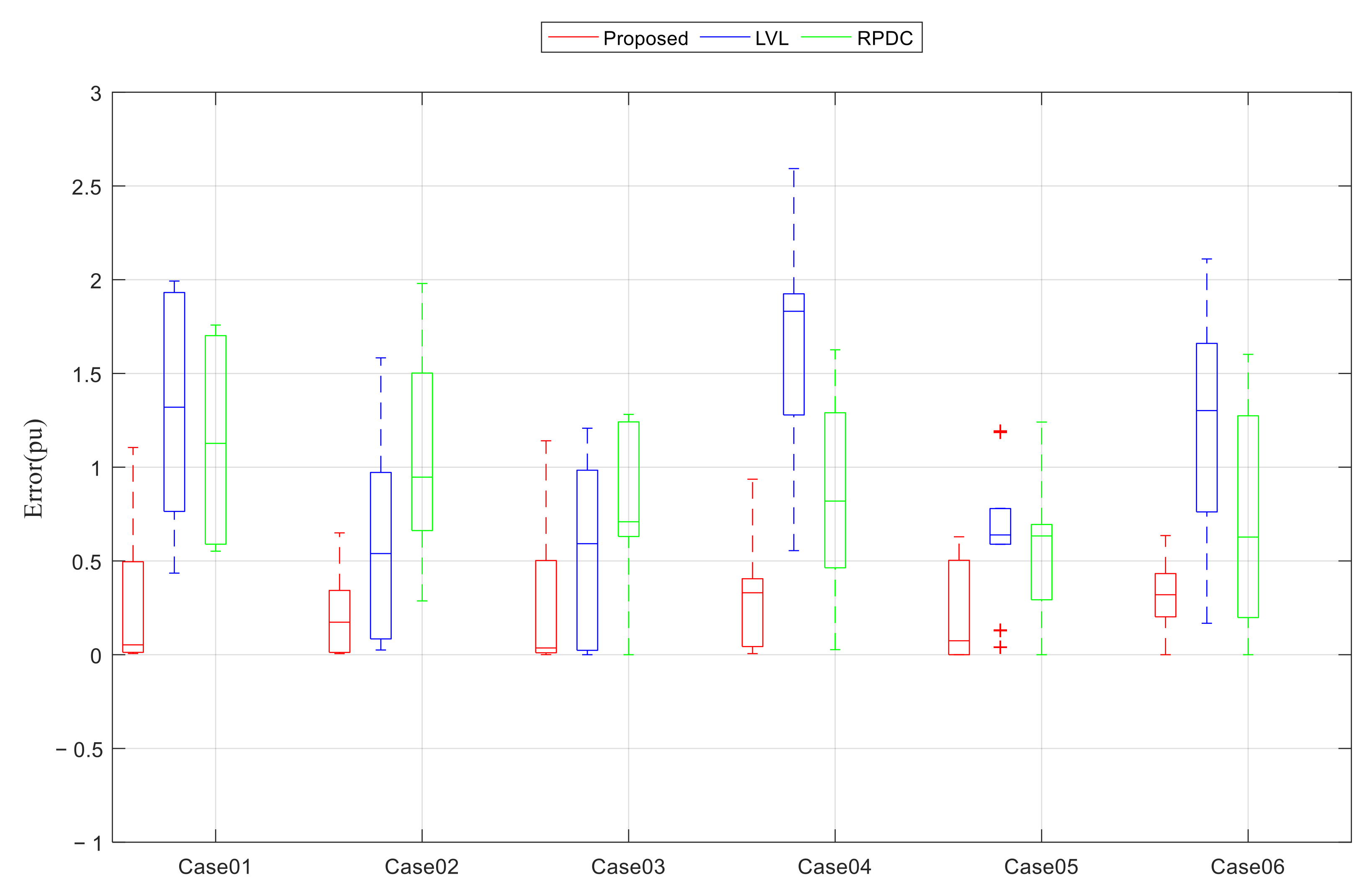
6.5. Simulation Results in IEEE 33 Bus System
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Renewable Capacity Statistics 2021; International Renewable Energy Agency (IRENA): Abu Dhabi, United Arab Emirates, 2021.
- Yoshizawa, S.; Hayashi, Y. Predictive Voltage Control Scheme Based on Estimation of Short-Time-Ahead Voltage Fluctuation in Distribution System with Pvs. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 916–924. [Google Scholar] [CrossRef]
- Park, J.-Y.; Nam, S.-R.; Park, J.-K. Control of a ULTC considering the dispatch schedule of capacitors in a distribution system. IEEE Trans. Power Syst. 2007, 22, 755–761. [Google Scholar] [CrossRef]
- Xiao, H.; Liu, G.; Huang, J.; Hou, S.; Zhu, L. Parameterized and centralized secondary voltage control for autonomous microgrids. Int. J. Electr. Power Energy Syst. 2022, 135, 107531. [Google Scholar] [CrossRef]
- Šulc, P.; Backhaus, S.; Chertkov, M. Optimal distributed control of reactive power via the alternating direction method of multipliers. IEEE Trans. Energy Convers. 2014, 29, 968–977. [Google Scholar] [CrossRef]
- Baker, K.; Bernstein, A.; Dall’anese, E.; Zhao, C.H. Network-Cognizant Voltage Droop Control for Distribution Grids. IEEE Trans. Power Syst. 2018, 33, 2098–2108. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Fusco, G.; Russo, M. Decentralized Control of Distributed Generation for Voltage Profile Optimization in Smart Feeders. IEEE Trans. Smart Grid 2013, 4, 1586–1596. [Google Scholar] [CrossRef]
- Elkhatib, M.E.; El Shatshat, R.; Salama, M.M. Decentralized reactive power control for advanced distribution automation systems. IEEE Trans. Smart Grid 2012, 3, 1482–1490. [Google Scholar] [CrossRef]
- Qiao, F.; Ma, J. Voltage/Var Control for Hybrid Distribution Networks Using Decomposition-Based Multiobjective Evolutionary Algorithm. IEEE Access 2020, 8, 12015–12025. [Google Scholar] [CrossRef]
- Elmitwally, A.; Elsaid, M.; Elgamal, M.; Chen, Z. A Fuzzy-Multiagent Self-Healing Scheme for a Distribution System with Distributed Generations. IEEE Trans. Power Syst. 2015, 30, 2612–2622. [Google Scholar] [CrossRef]
- Bedawy, A.; Yorino, N.; Mahmoud, K.; Zoka, Y.; Sasaki, Y. Optimal Voltage Control Strategy for Voltage Regulators in Active Unbalanced Distribution Systems Using Multi-Agents. IEEE Trans. Power Syst. 2020, 35, 1023–1035. [Google Scholar] [CrossRef]
- Kekatos, V.; Zhang, L.; Giannakis, G.B.; Baldick, R. Voltage regulation algorithms for multiphase power distribution grids. IEEE Trans. Power Syst. 2015, 31, 3913–3923. [Google Scholar] [CrossRef]
- Wurl, T.; Lindner, M.; Witzmann, R. Analysis of interactions between regulated distribution transformers (RDT) and local voltage control Q(V) by means of the harmonic balance method. Int. J. Electr. Power Energy Syst. 2020, 120, 105901. [Google Scholar] [CrossRef]
- Lindner, M.; Witzmann, R. Modelling and validation of an inverter featuring local voltage control Q(V) for transient stability and interaction analyses. Int. J. Electr. Power Energy Syst. 2018, 101, 280–288. [Google Scholar] [CrossRef]
- Valverde, G.; Van Cutsem, T. Model predictive control of voltages in active distribution networks. IEEE Trans. Smart Grid 2013, 4, 2152–2161. [Google Scholar] [CrossRef]
- Kim, Y.J.; Ahn, S.J.; Hwang, P.I.; Pyo, G.C.; Moon, S.I. Coordinated control of a DG and voltage control devices using a dynamic programming algorithm. IEEE Trans. Power Syst. 2013, 28, 42–51. [Google Scholar] [CrossRef]
- Mahmoud, K.; Abdel-Nasser, M.; Lehtonen, M.; Hussein, M.M. Optimal Voltage Regulation Scheme for PV-Rich Distribution Systems Interconnected with D-STATCOM. Electr. Power Compon. Syst. 2021, 48, 2130–2143. [Google Scholar] [CrossRef]
- Elkhatib, M.E.; El-Shatshat, R.; Salama, M.M.A. Novel coordinated voltage control for smart distribution networks with DG. IEEE Trans. Smart Grid 2011, 2, 598–605. [Google Scholar] [CrossRef]
- Farag, H.E.Z.; El-Saadany, E.F. A Novel Cooperative Protocol for Distributed Voltage Control in Active Distribution Systems. IEEE Trans. Power Syst. 2013, 28, 1645–1656. [Google Scholar] [CrossRef]
- Agalgaonkar, Y.P.; Pal, B.C.; Jabr, R.A. Distribution voltage control considering the impact of PV generation on tap changers and autonomous regulators. IEEE Trans. Power Syst. 2013, 29, 182–192. [Google Scholar] [CrossRef]
- Mufaris, A.L.M.; Baba, J.; Yoshizawa, S.; Hayashi, Y. Determination of dynamic line drop compensation parameters of voltage regulators for voltage rise mitigation. In Proceedings of the 2015 International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 319–325. [Google Scholar]
- Kim, M.; Hara, R.; Kita, H. Design of the optimal ULTC parameters in distribution system with distributed generations. IEEE Trans. Power Syst. 2009, 24, 297–305. [Google Scholar]
- Chen, Y.; Strothers, M.; Benigni, A. All-day coordinated optimal scheduling in distribution grids with PV penetration. Electr. Power Syst. Res. 2018, 164, 112–122. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, W.; Liang, J.; Cong, P.; Cai, Y. Coordinated day-ahead reactive power dispatch in distribution network based on real power forecast errors. IEEE Trans. Power Syst. 2015, 31, 2472–2480. [Google Scholar] [CrossRef]
- Ferraz, B.P.; Resener, M.; Pereira, L.A.; Lemos, F.A.; Haffner, S. MILP model for volt-var optimization considering chronological operation of distribution systems containing DERs. Int. J. Electr. Power Energy Syst. 2021, 129, 106761. [Google Scholar] [CrossRef]
- Ozdemir, G.; Baran, M. A new method for Volt–Var optimization with conservation voltage reduction on distribution systems. Electr. Eng. 2020, 102, 493–502. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kirtley, J.L.; Norford, L.K. Reactive Power Ancillary Service of Synchronous Dgs in Coordination with Voltage Control Devices. IEEE Trans. Smart Grid 2017, 8, 515–527. [Google Scholar] [CrossRef]
- Heydarianasl, M.; Rahmat, M.F. Design optimization of electrostatic sensor electrodes via MOPSO. Measurement 2020, 152, 107288. [Google Scholar] [CrossRef]
- Sivaranjani, R.; Roomi, S.M.M.; Senthilarasi, M. Speckle noise removal in SAR images using Multi-Objective PSO (MOPSO) algorithm. Appl. Soft Comput. 2019, 76, 671–681. [Google Scholar] [CrossRef]
- Ghorbani, N.; Kasaeian, A.; Toopshekan, A.; Bahrami, L.; Maghami, A. Optimizing a hybrid wind-PV-battery system using GA-PSO and MOPSO for reducing cost and increasing reliability. Energy 2018, 154, 581–591. [Google Scholar] [CrossRef]
- Qiu, G.X.; Zhan, D.P.; Jiang, Z.H.; Zhang, H.S. Optimisation of the MgO/Al2O3 ratio of high-alumina BF slag based on MOPSO algorithm. Ironmak. Steelmak. 2019, 46, 712–720. [Google Scholar] [CrossRef]
- Reyes-Sierra, M.; Coello, C.C. Multi-objective particle swarm optimizers: A survey of the state-of-the-art. Int. J. Comput. Intell. Res. 2006, 2, 287–308. [Google Scholar]
- Chiu, W.-Y.; Yen, G.G.; Juan, T.-K. Minimum Manhattan distance approach to multiple criteria decision making in multiobjective optimization problems. IEEE Trans. Evol. Comput. 2016, 20, 972–985. [Google Scholar] [CrossRef]
- Azimi, R.; Esmaeili, S. Multiobjective daily Volt/VAr control in distribution systems with distributed generation using binary ant colony optimization. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 613–629. [Google Scholar] [CrossRef]




| Parameter | MOPSO | PSO | GA |
|---|---|---|---|
| Number of iterations | 70 | 70 | 70 |
| Population size | 10 | 10 | 10 |
| Other related parameters | Cognitive parameter, Social parameter, | Cognitive parameter, Social parameter, | Elite count = 2 Crossover fraction = 0.8 Mutation rate = 0.1 Maximum survivalr ate = 2 |
| Case | DG Location | DG Capacity | Power Factor |
|---|---|---|---|
| Case 01 | BUS A3 | 5.2 MVA | 0.95 leading |
| Case 02 | 5.2 MVA | 0.9 lagging | |
| Case 03 | BUS A12 | 5.2 MVA | 0.95 leading |
| Case 04 | 1.3 MVA | 0.9 lagging | |
| Case 05 | BUS B12 | 5.2 MVA | 0.95 leading |
| Case 06 | 1.4 MVA | 0.9 lagging |
| Method | ||||
|---|---|---|---|---|
| Proposed method | 4.2577 | 1.6355 | 0.6848 | 0.0535 |
| LVL method | 6.1747 | 1.8514 | 0.6994 | 0.1347 |
| RPDC method | 5.6591 | 1.9719 | 0.7144 | 0.2740 |
| Method | ||||
|---|---|---|---|---|
| Proposed method | 4.03 | 1.4085 | 0.4936 | 0.0488 |
| LVL method | 6.5344 | 1.76 | 0.5354 | 0.1400 |
| RPDC method | 4.4974 | 1.8474 | 0.5447 | 0.2558 |
| Method | ||||
|---|---|---|---|---|
| Proposed method | 3.0383 | 1.6599 | 5.3044 | 0.0585 |
| LVL method | 5.4915 | 1.8389 | 5.2394 | 0.1295 |
| RPDC method | 4.5050 | 1.8929 | 5.3397 | 0.2022 |
| Method | ||||
|---|---|---|---|---|
| Proposed method | 3.19 | 1.925 | 0.124 | 0.0725 |
| LVL method | 8.3236 | 1.7831 | 0.1311 | 0.3874 |
| RPDC method | 4.4348 | 1.8509 | 0.1316 | 0.2074 |
| Method | ||||
|---|---|---|---|---|
| Proposed method | 4.4856 | 1.6258 | 6.4291 | 0.0445 |
| LVL method | 6.2075 | 1.7078 | 6.352 | 0.1588 |
| RPDC method | 5.283 | 1.7637 | 6.4586 | 0.1350 |
| Method | ||||
|---|---|---|---|---|
| Proposed method | 6.0427 | 1.6549 | 0.6645 | 0.0712 |
| LVL method | 9.2652 | 1.6531 | 0.655 | 0.2963 |
| RPDC method | 7.426 | 1.7118 | 0.6624 | 0.1664 |
| Algorithm | Best | Average | Worst | Standard Deviation |
|---|---|---|---|---|
| MOPSO | 0.4847 | 0.48502 | 0.4887 | 3.8010 × 10−5 |
| PSO | 0.4847 | 0.48698 | 0.5066 | 9.9358 × 10−4 |
| GA | 0.4847 | 0.48768 | 0.4934 | 2.2354 × 10−4 |
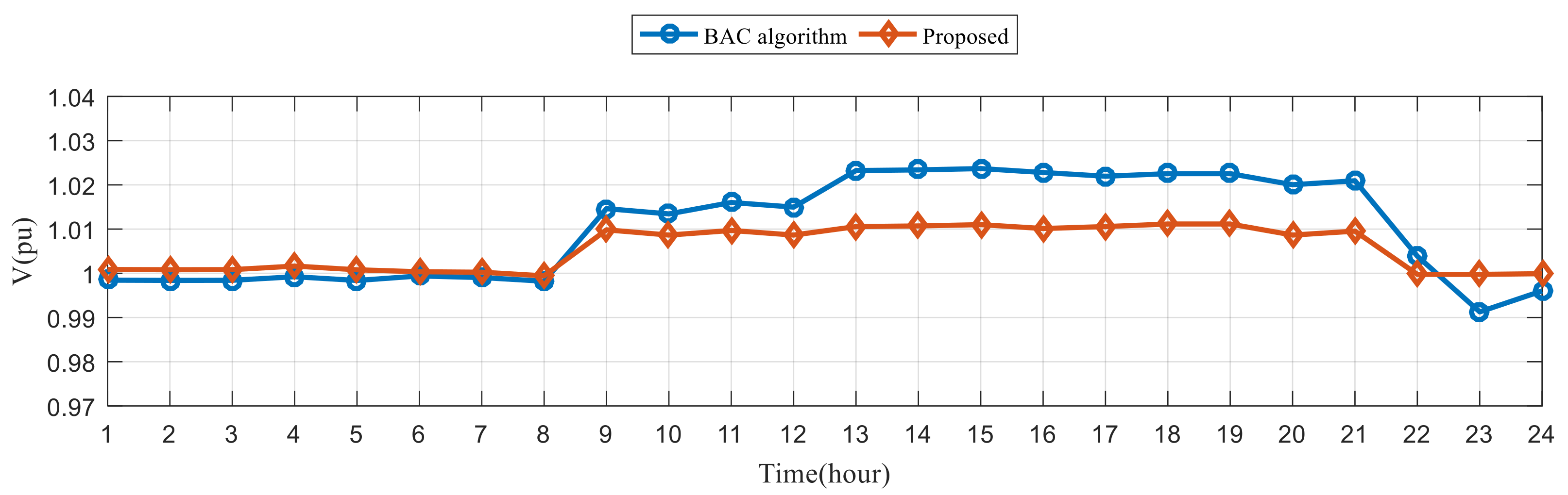
| Method | |||||
|---|---|---|---|---|---|
| BAC algorithm | 864.43 | 0.2872 | 0.0039 | 9 | 7 |
| Proposed method | 887.93 | 0.1369 | 0.0027 | 4 | 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, N.-C.; Zhong, P.-Y. Day-Ahead Scheduling of On-Load Tap Changer Transformer and Switched Capacitors by Multi-Pareto Optimality. Mathematics 2022, 10, 2969. https://doi.org/10.3390/math10162969
Yang N-C, Zhong P-Y. Day-Ahead Scheduling of On-Load Tap Changer Transformer and Switched Capacitors by Multi-Pareto Optimality. Mathematics. 2022; 10(16):2969. https://doi.org/10.3390/math10162969
Chicago/Turabian StyleYang, Nien-Che, and Pei-Yun Zhong. 2022. "Day-Ahead Scheduling of On-Load Tap Changer Transformer and Switched Capacitors by Multi-Pareto Optimality" Mathematics 10, no. 16: 2969. https://doi.org/10.3390/math10162969
APA StyleYang, N.-C., & Zhong, P.-Y. (2022). Day-Ahead Scheduling of On-Load Tap Changer Transformer and Switched Capacitors by Multi-Pareto Optimality. Mathematics, 10(16), 2969. https://doi.org/10.3390/math10162969







