Irreversibility Analysis in the Ethylene Glycol Based Hybrid Nanofluid Flow amongst Expanding/Contracting Walls When Quadratic Thermal Radiation and Arrhenius Activation Energy Are Significant
Abstract
:1. Introduction
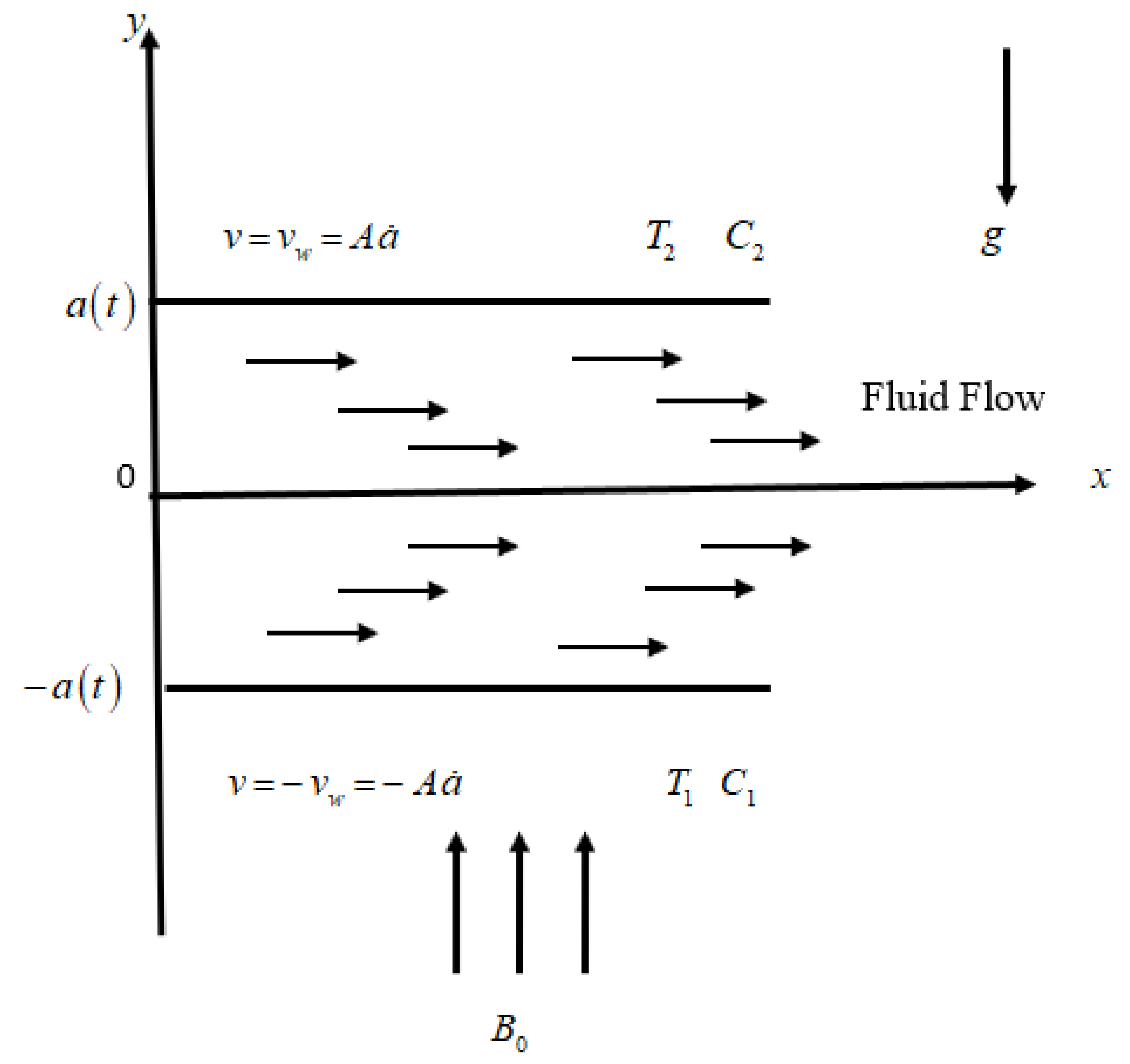
2. Formulation
2.1. Thermo-Physical Properties of Hybrid Nanofluid
2.2. Engineering Parameters of Concern
2.3. Entropy Generation and Bejan Number
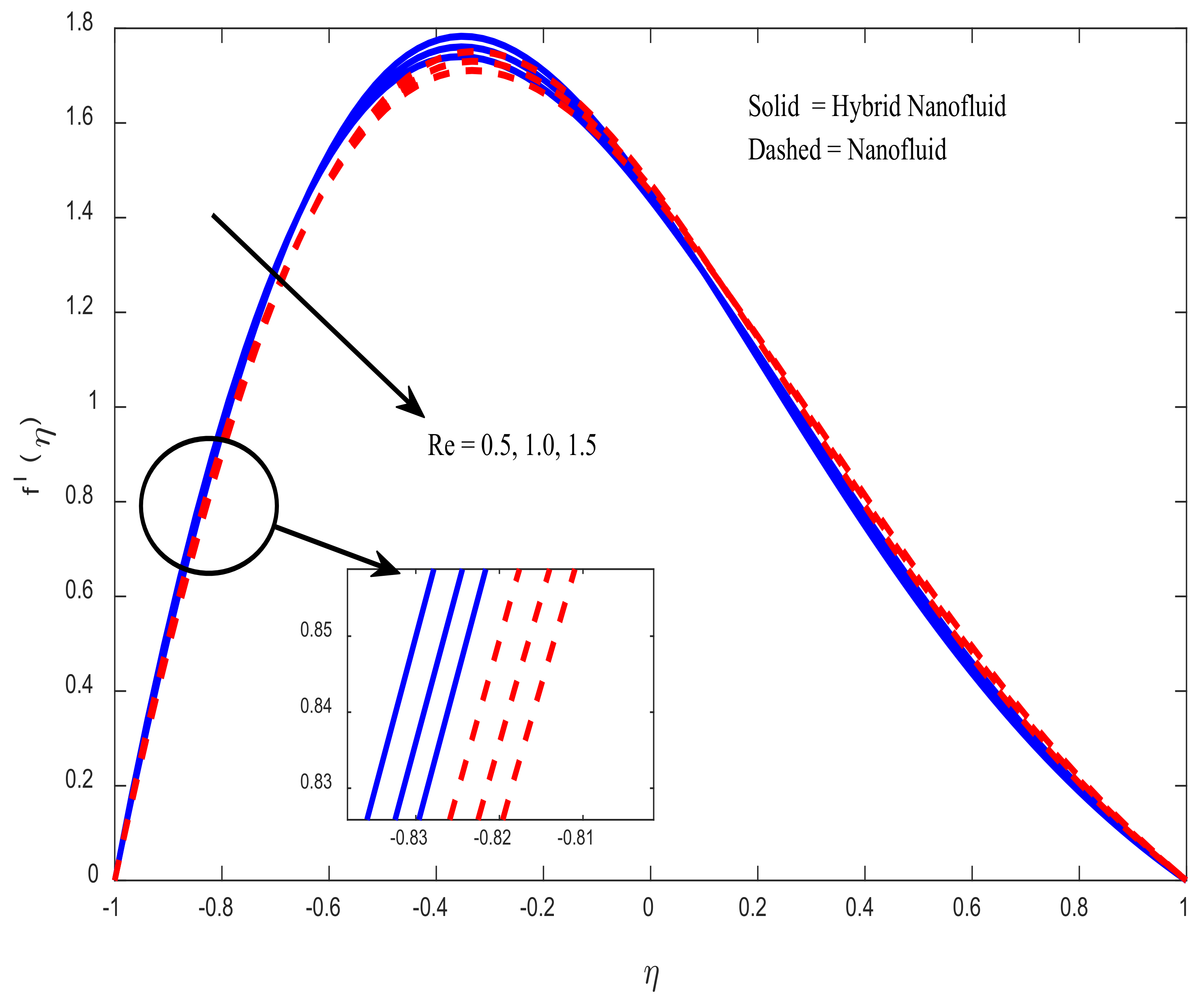
3. Validation
4. Discussion of Outcomes
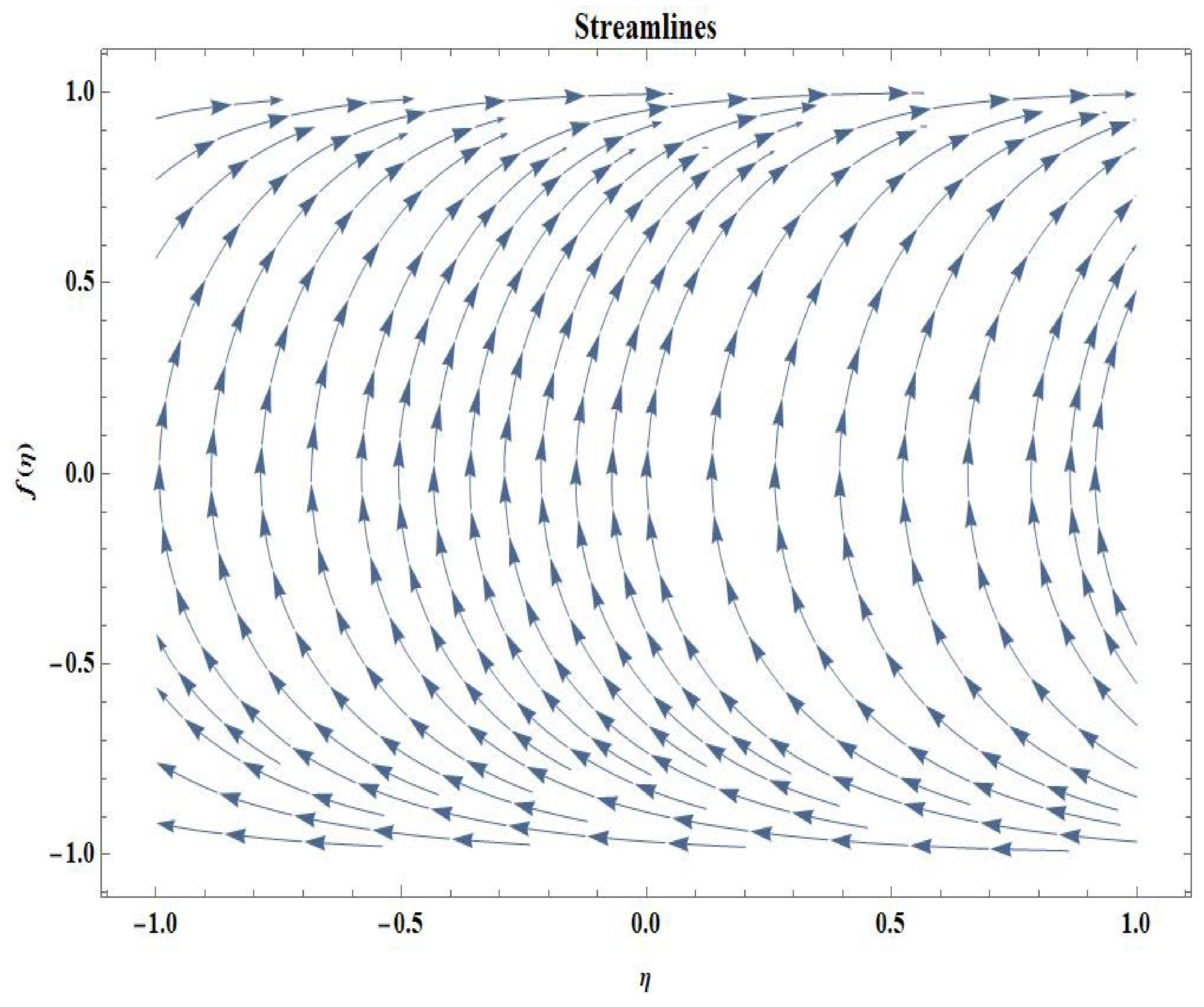
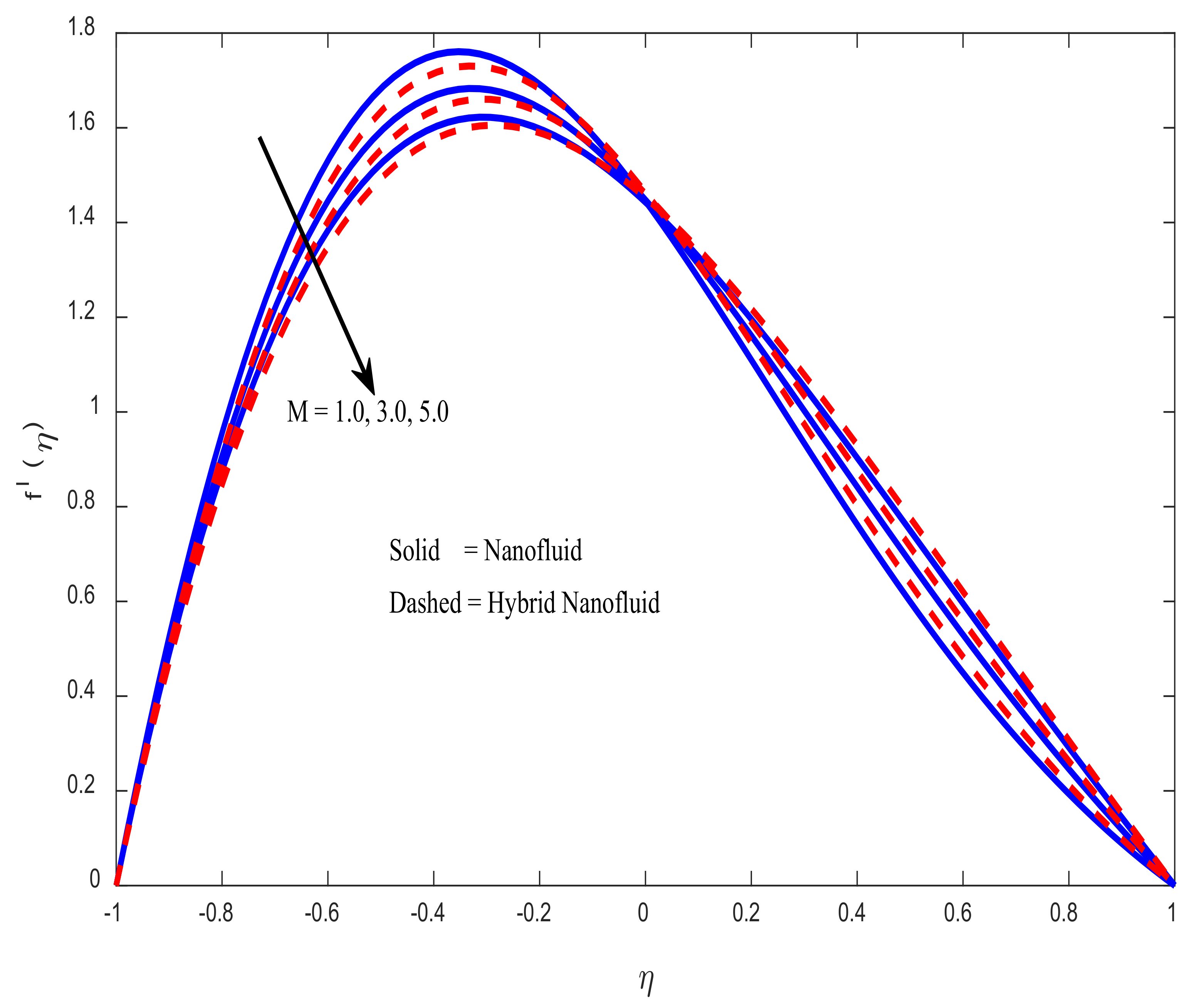
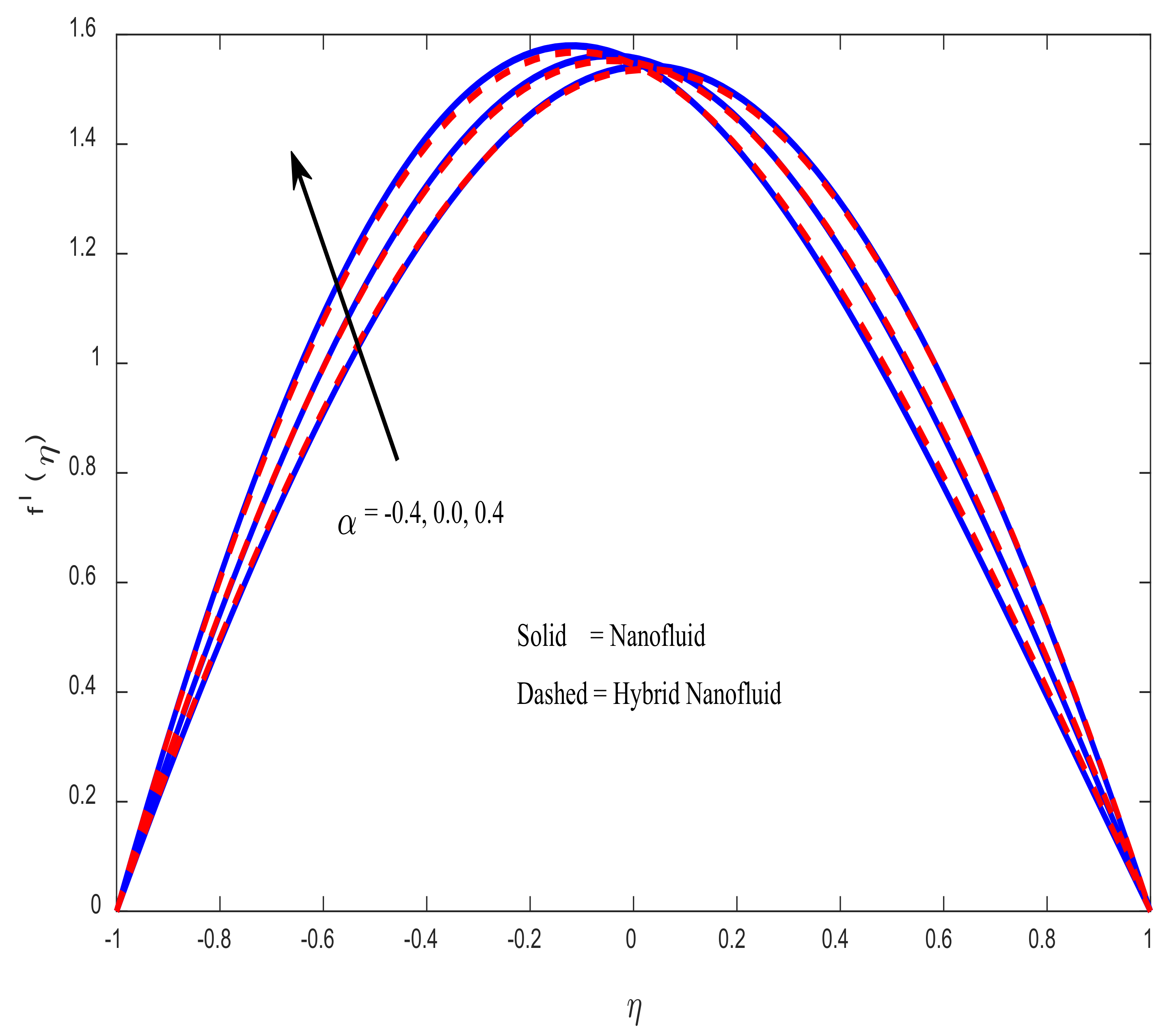
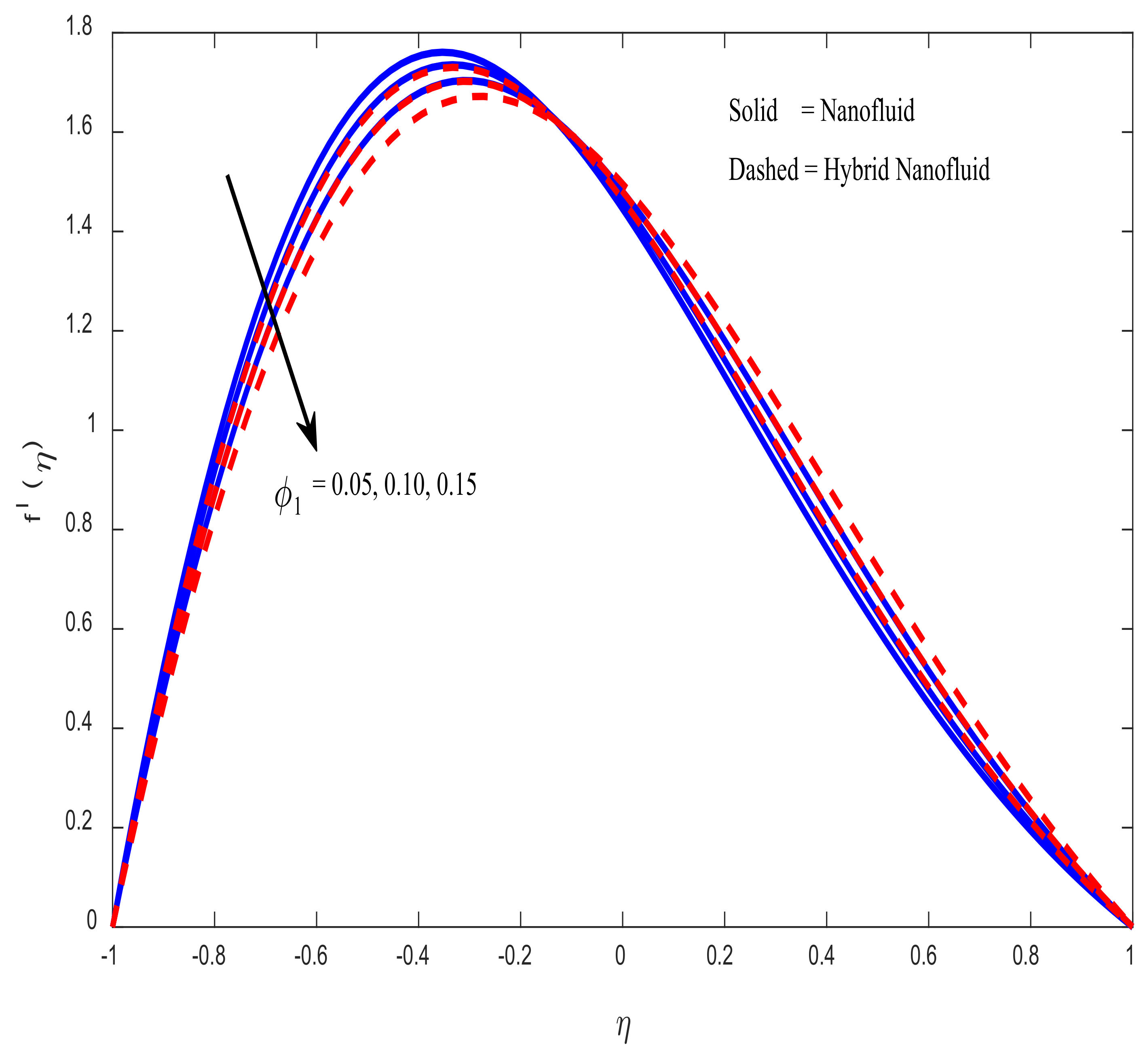
4.1. Velocity Profiles
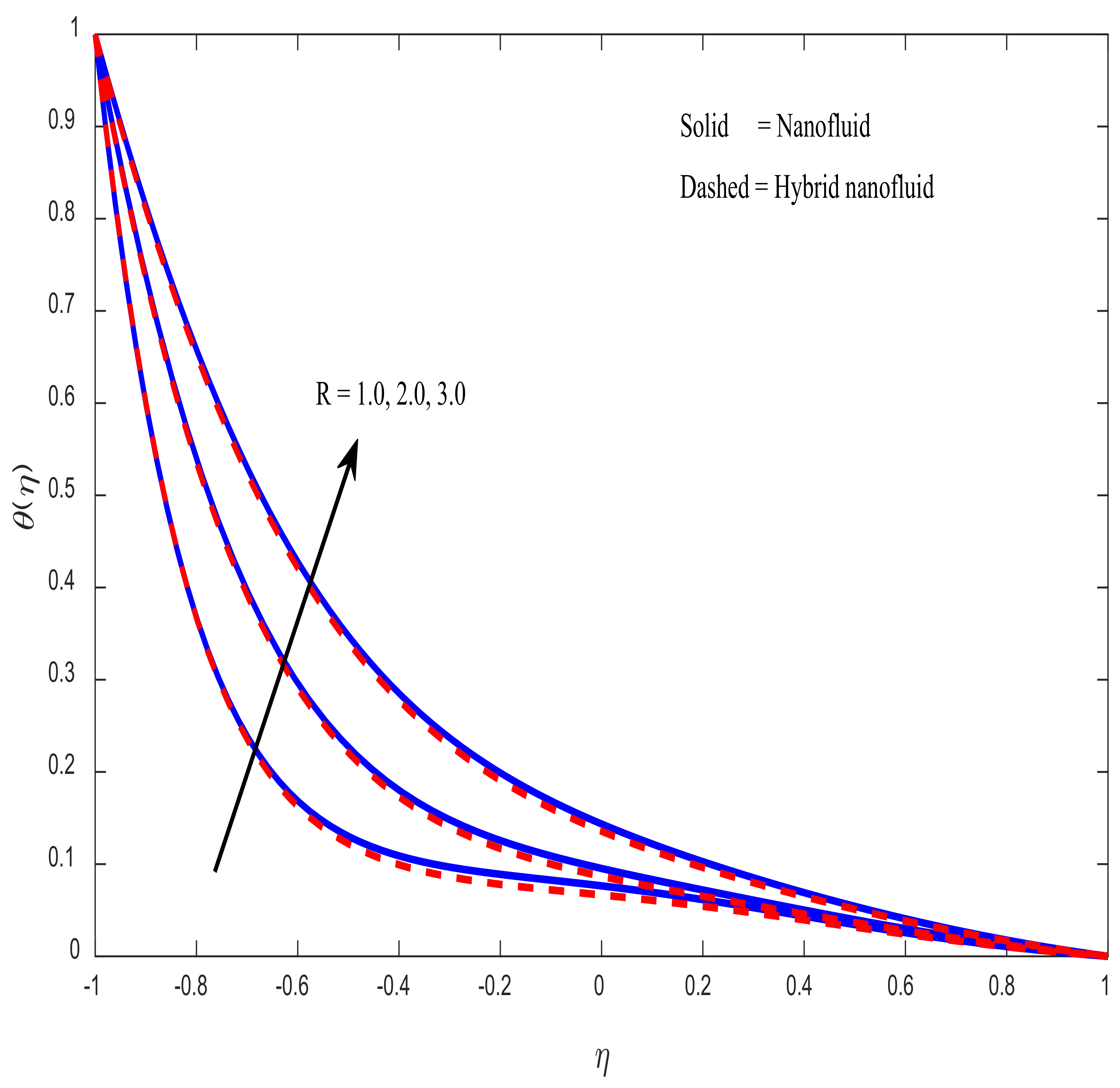
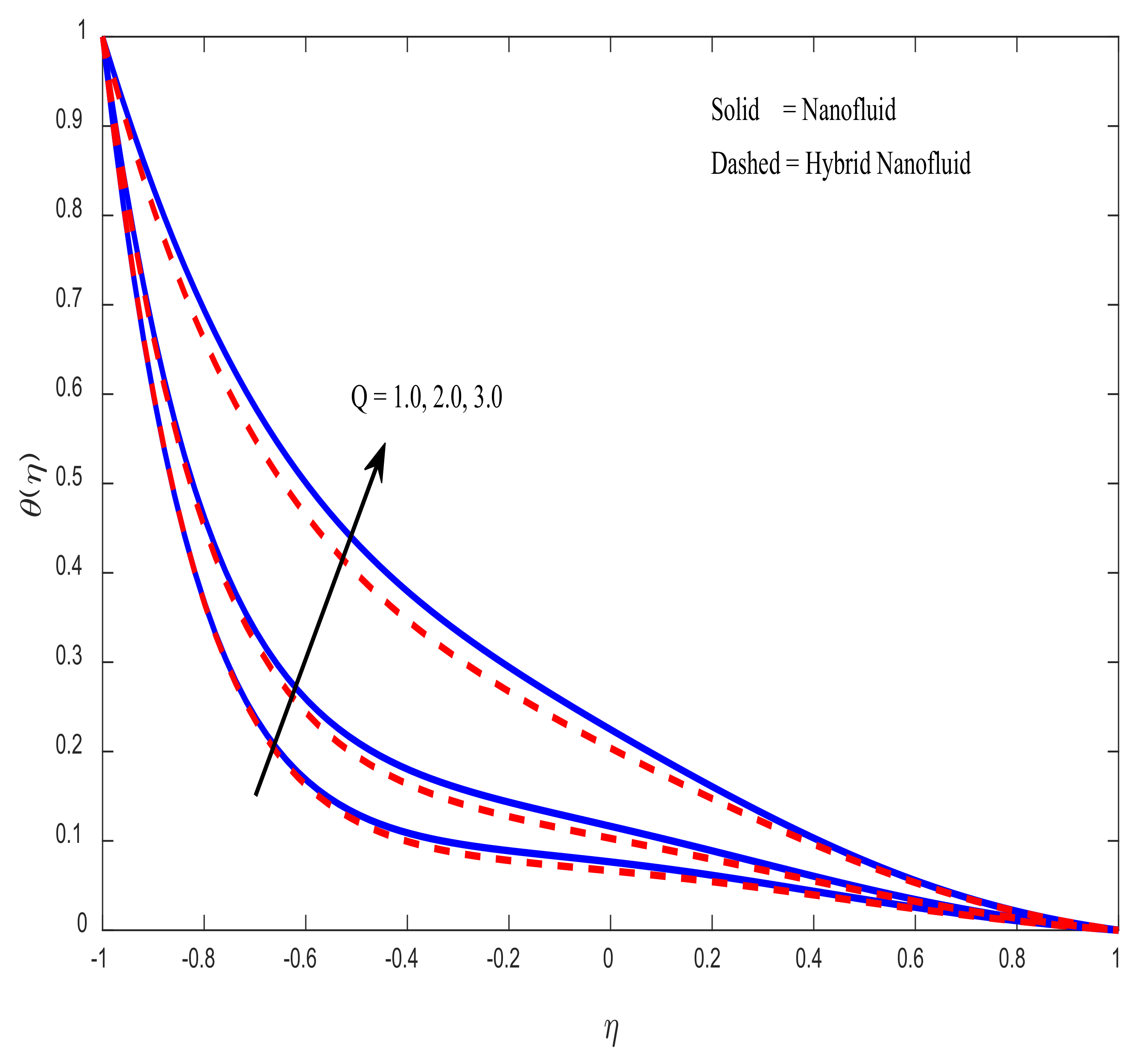
4.2. Temperature Profiles
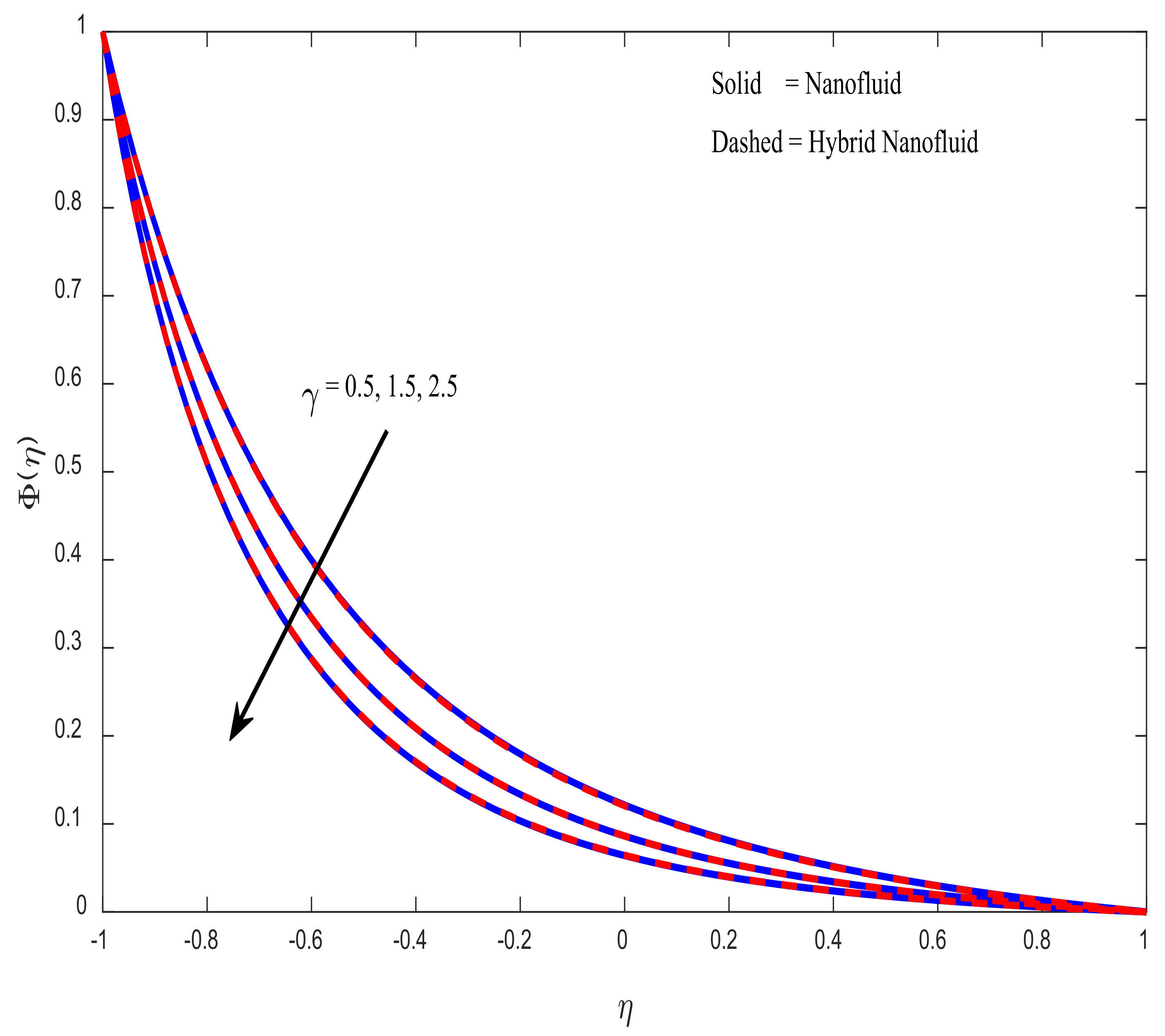
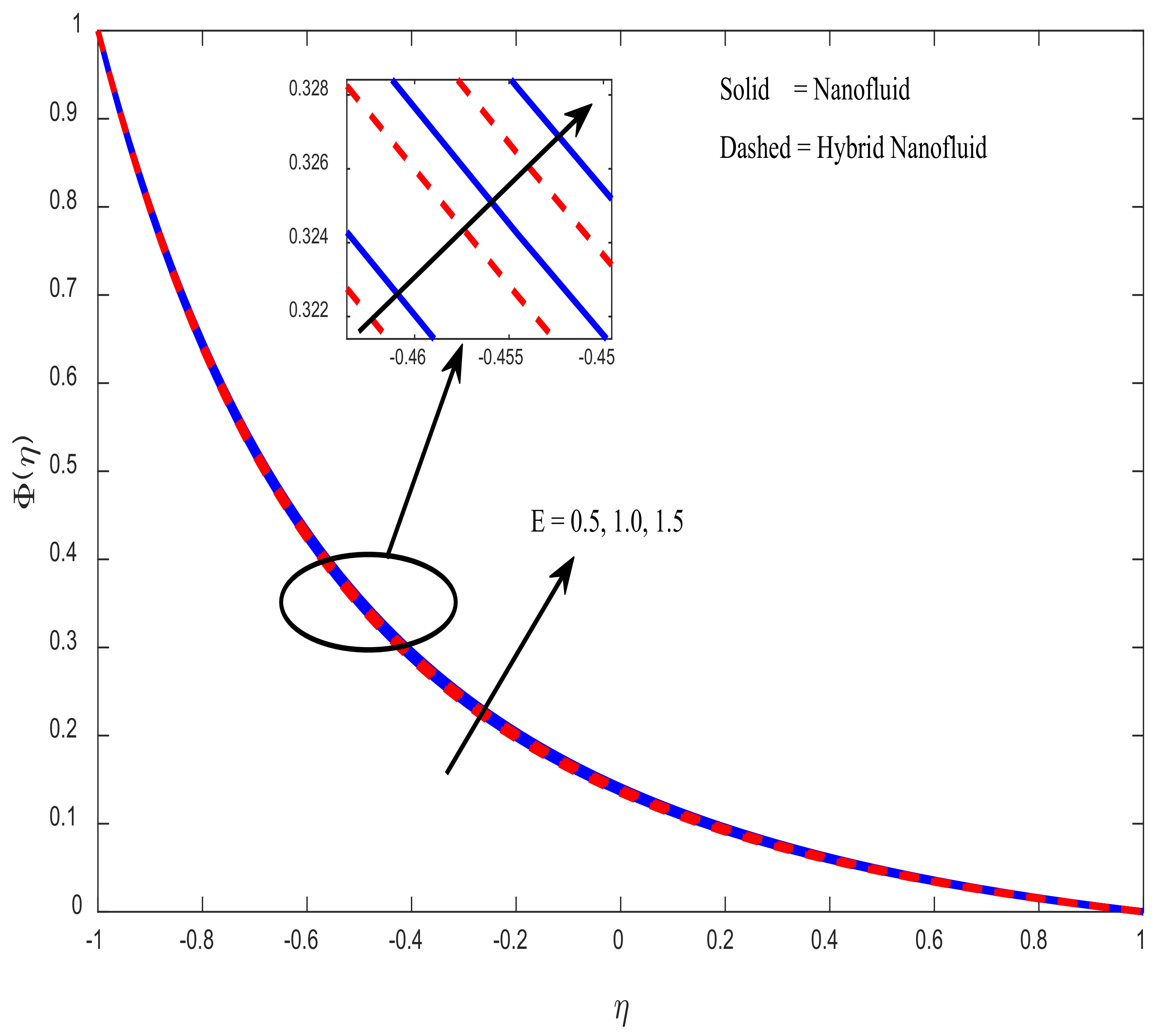
4.3. Concentration Profiles
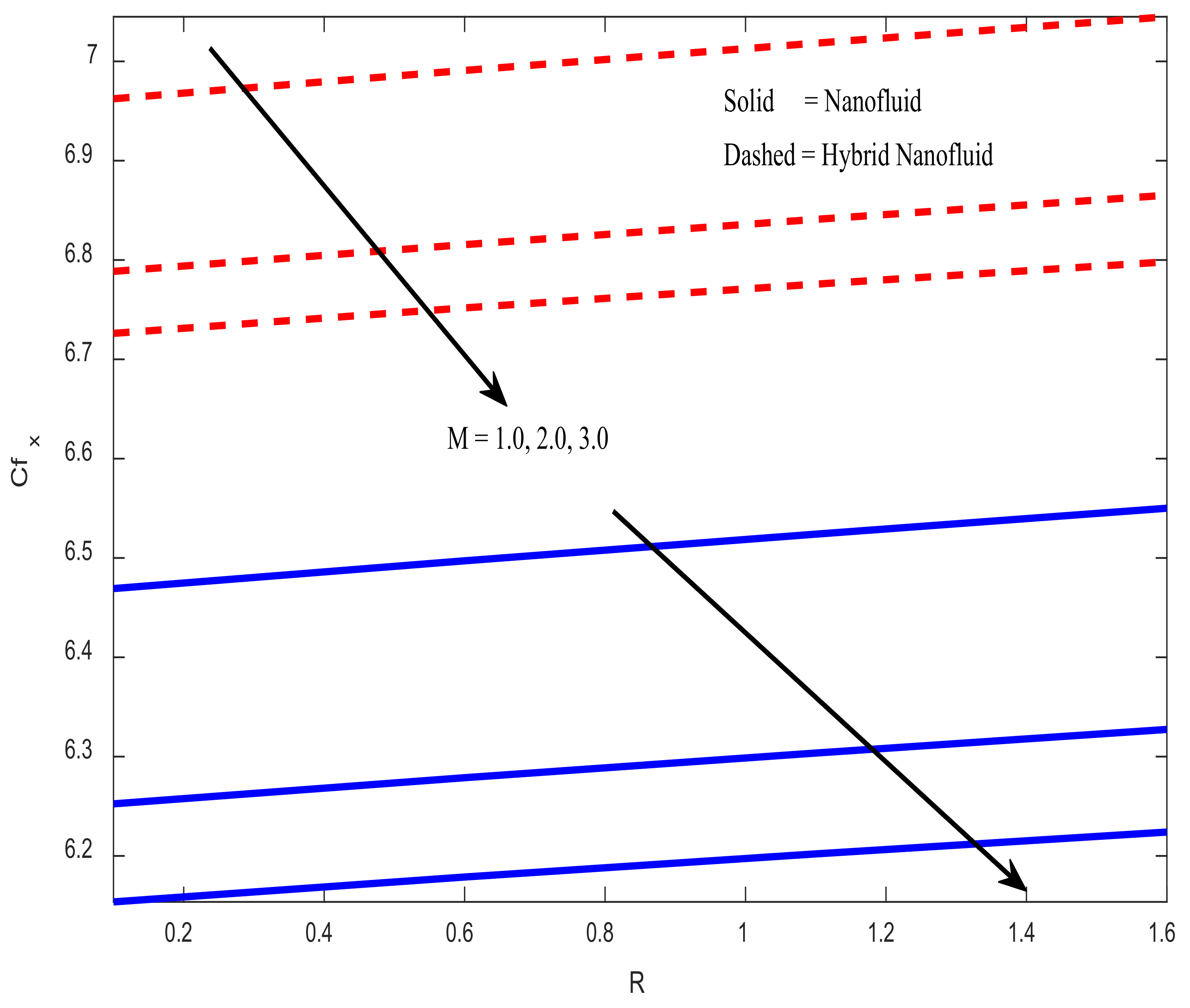
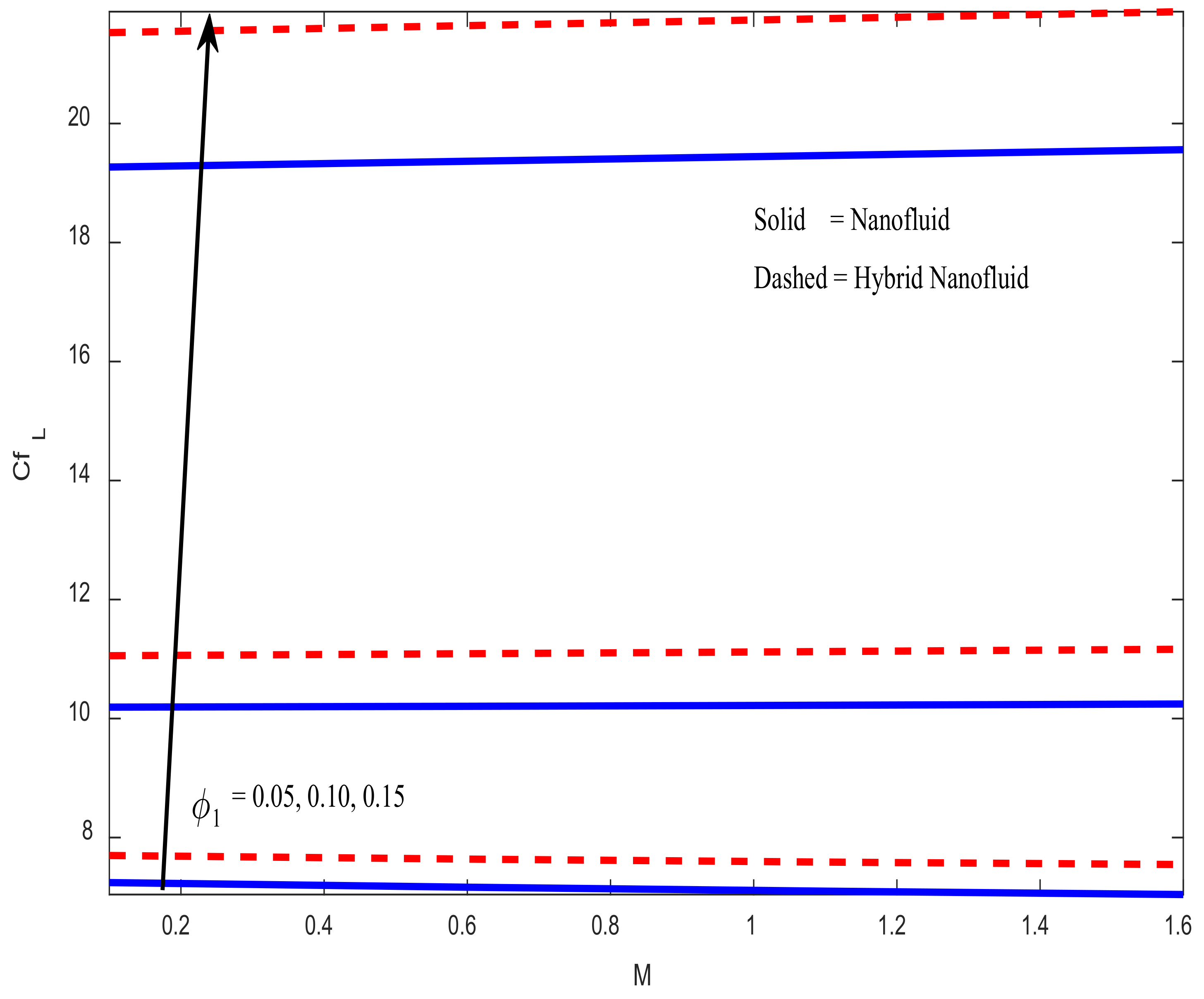
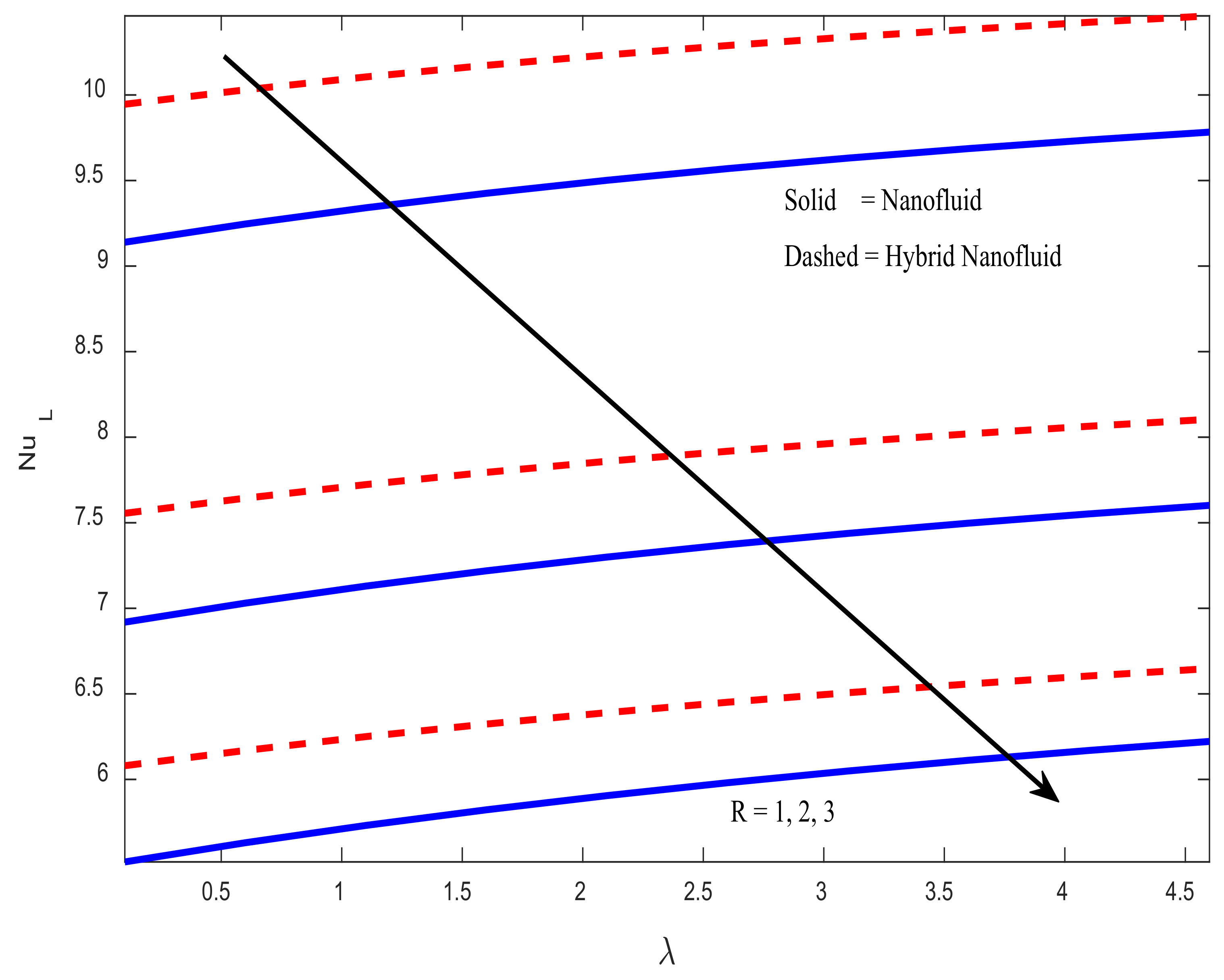
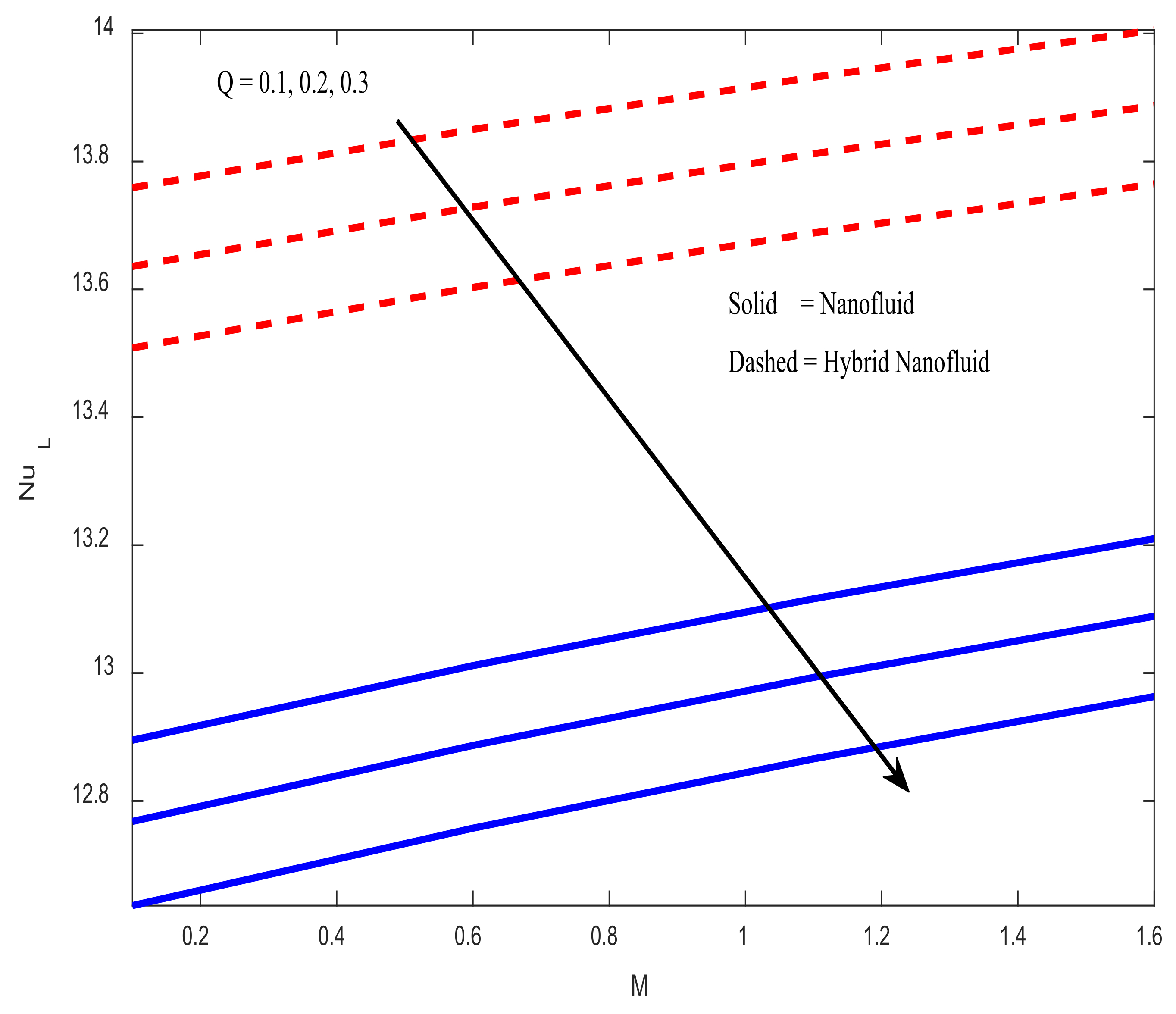
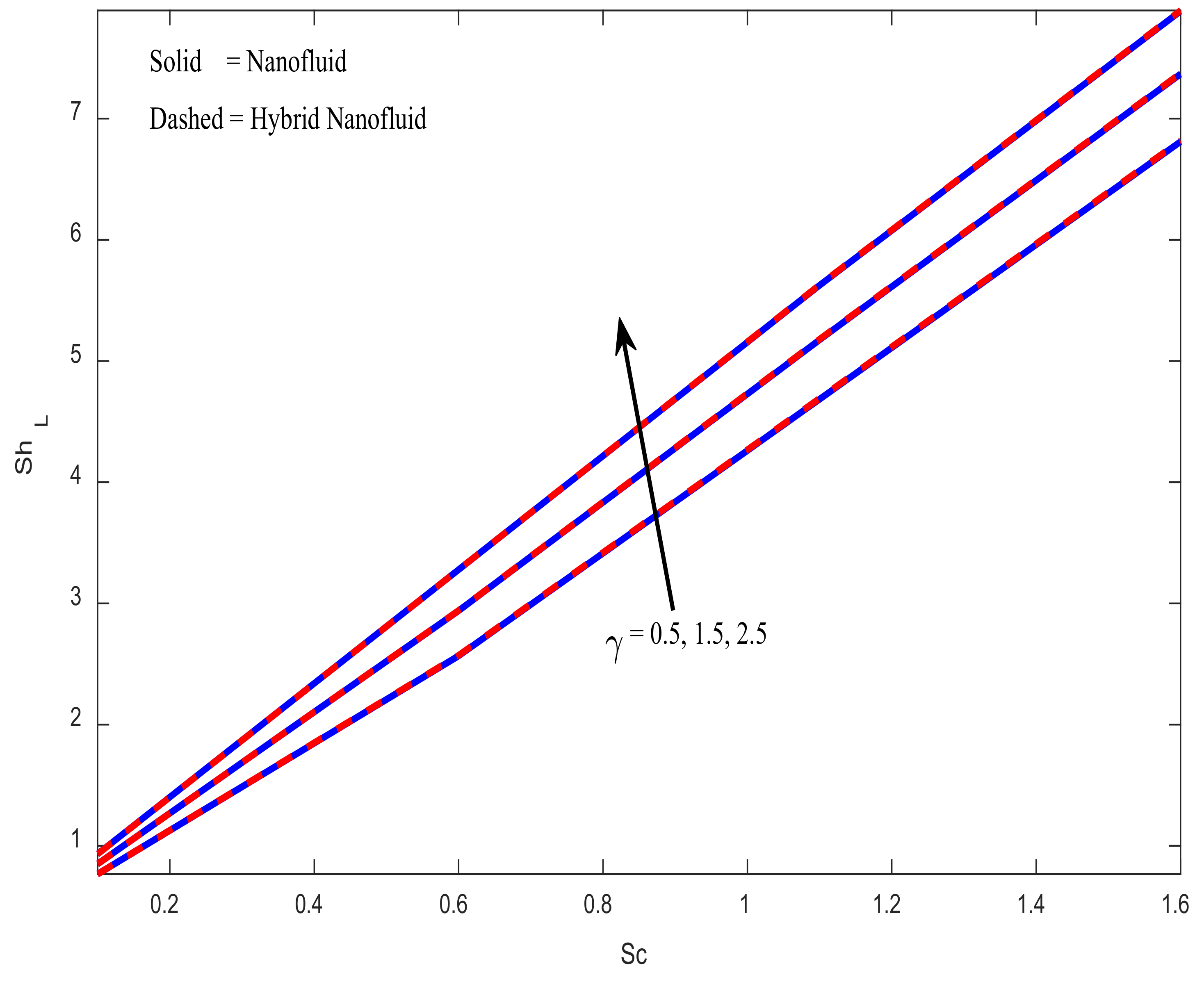
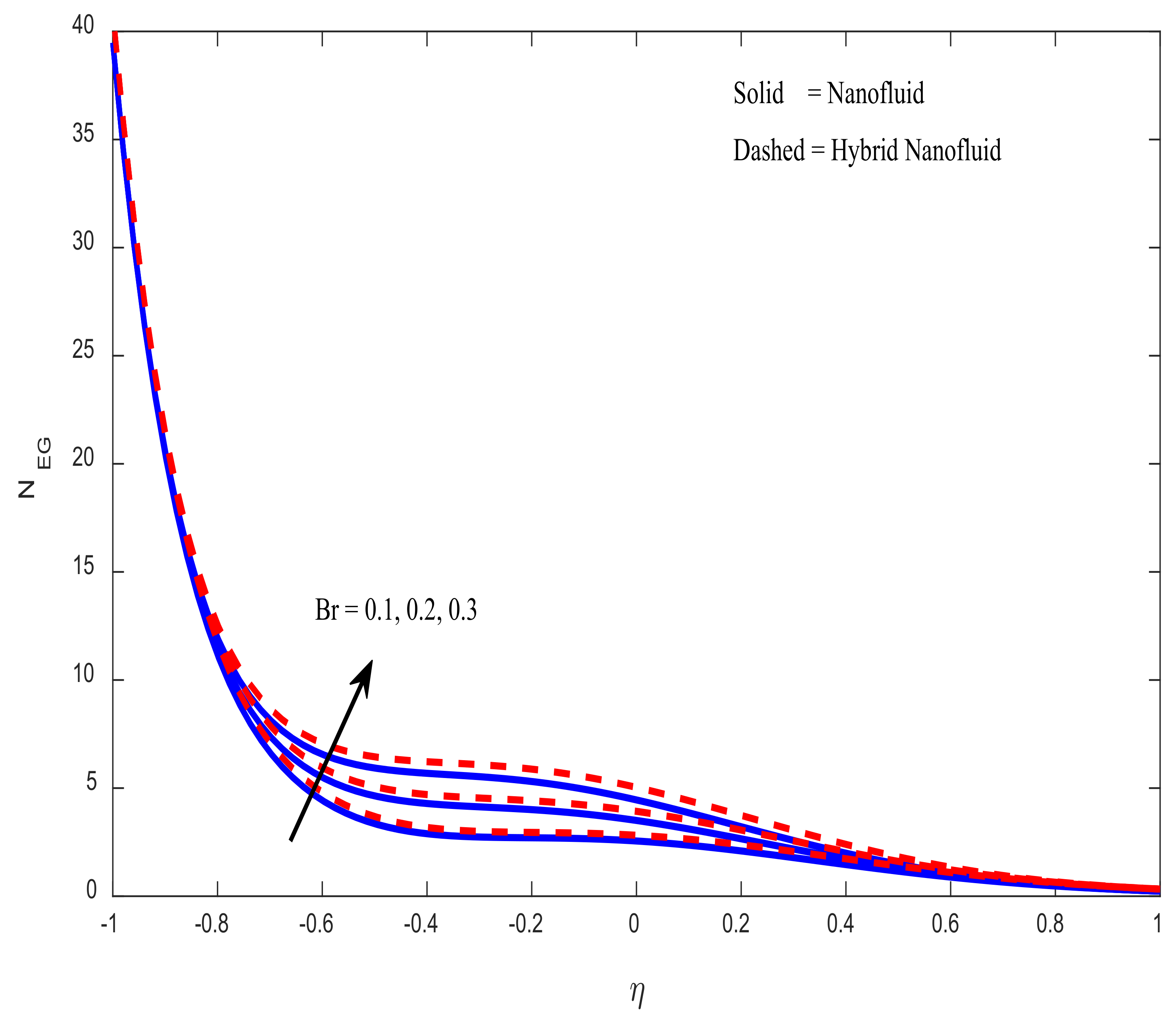
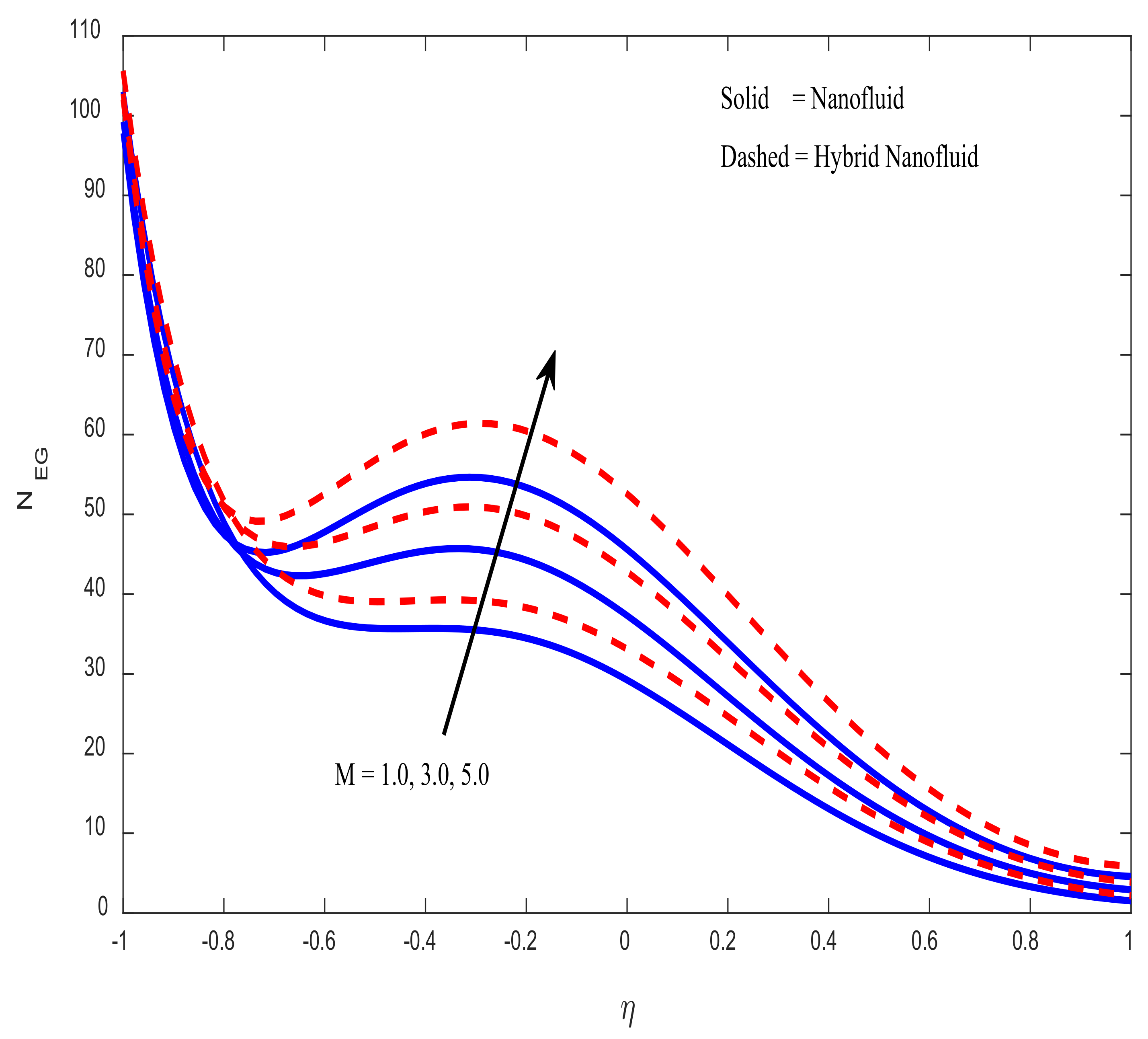
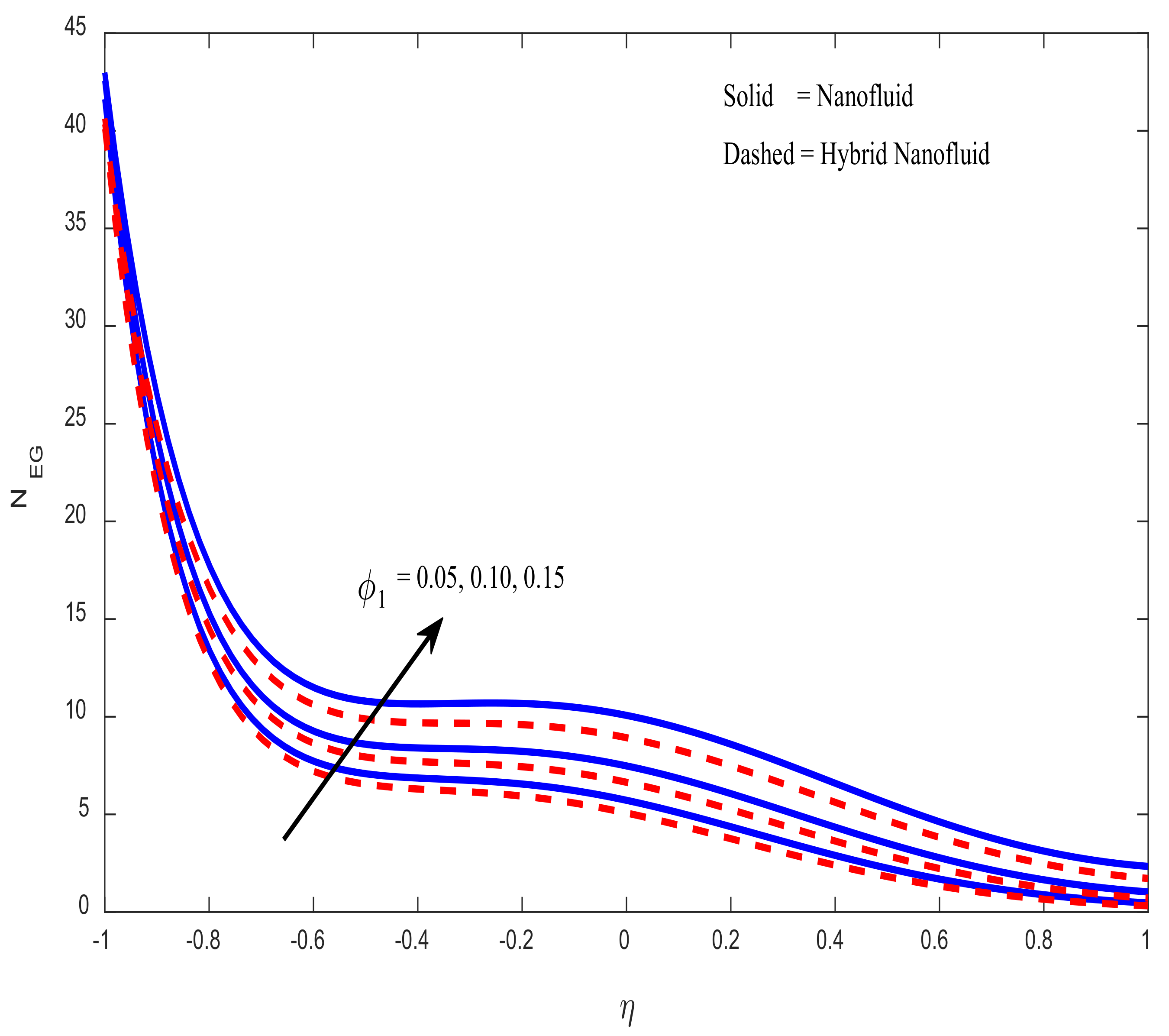
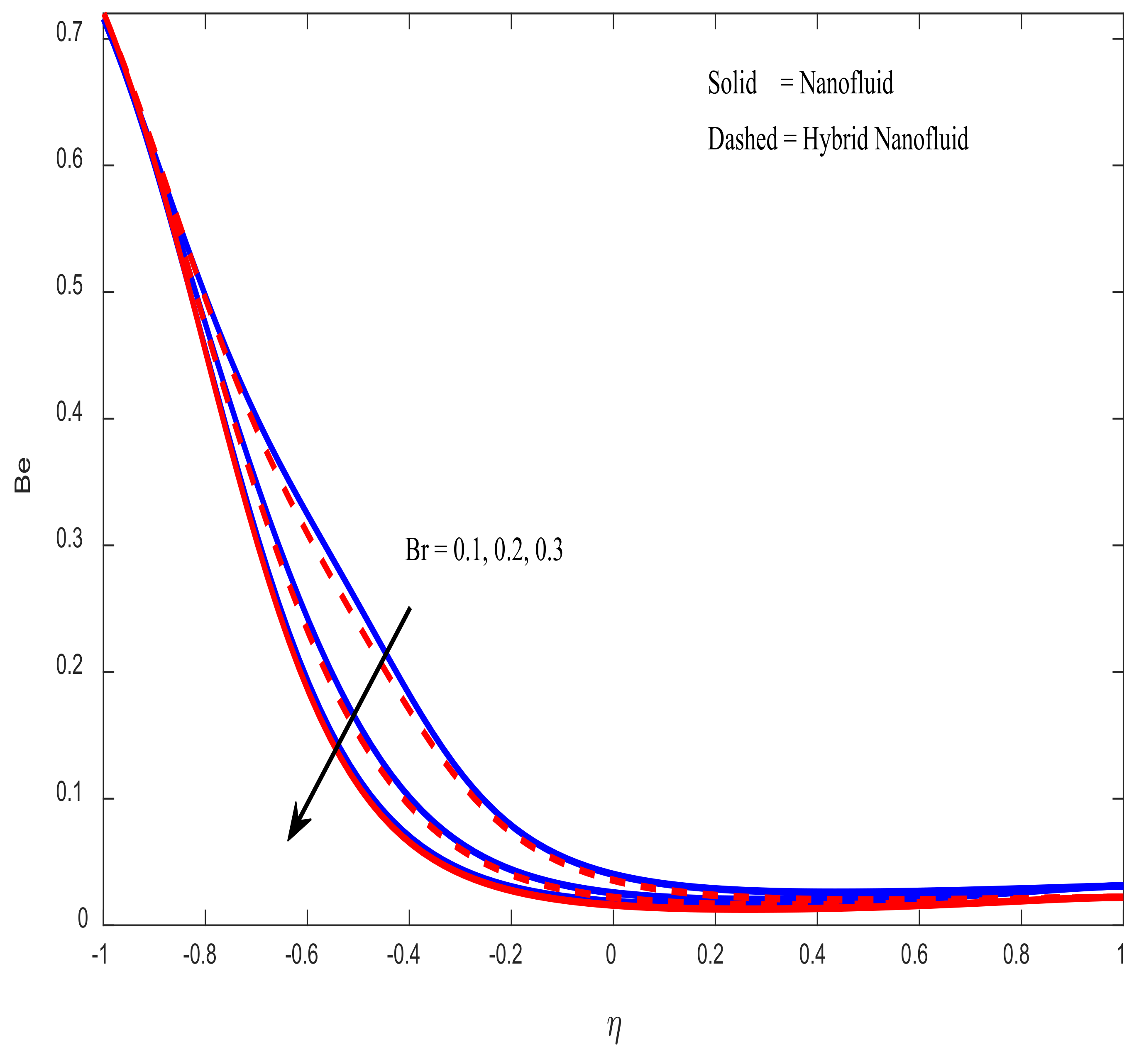
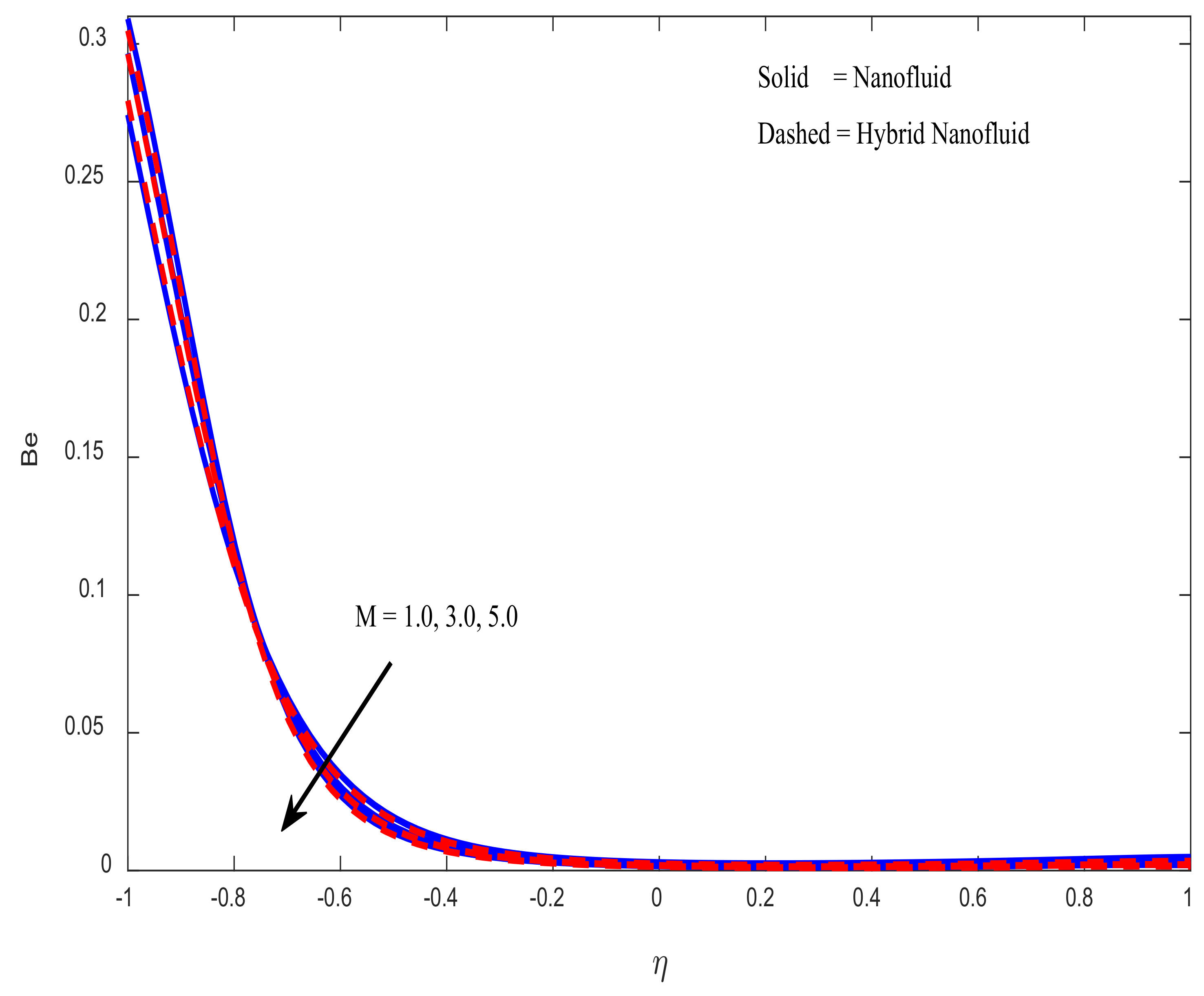
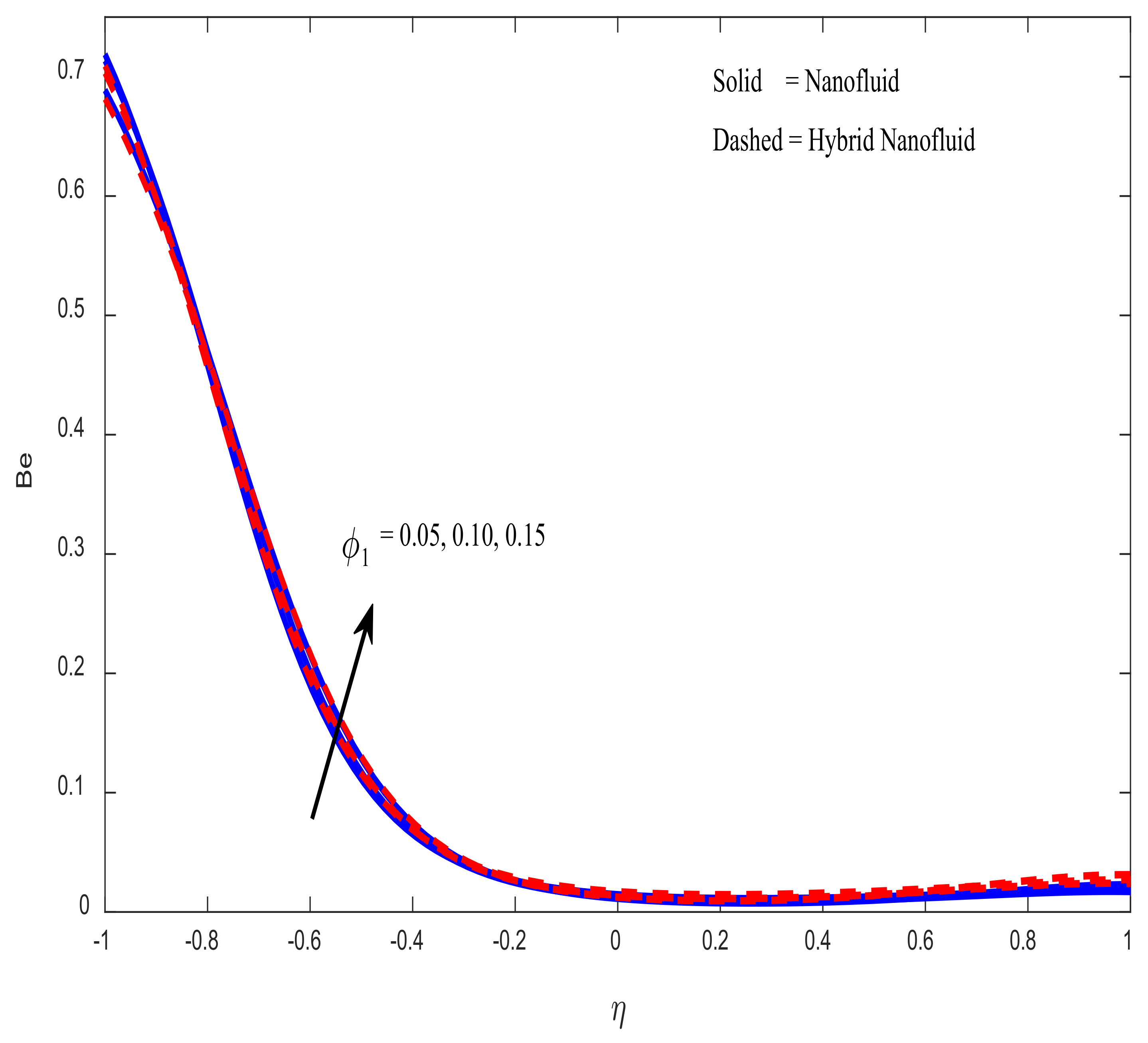
4.4. Engineering Parameters of Interest, Entropy Generation, and Bejan Number Profiles
5. Conclusions
- As the magnetic field parameter increases, the skin friction coefficient decreases. It is noticed that, when magnetic field parameter () takes an input in the range , skin friction coefficient decreases at a rate of 0.10847 (in the case of hybrid nanofluid) and 0.13105 (in the case of nanofluid) per unit value of magnetic field parameter.
- The rate of heat transfer reduces as the value of the heat source parameter increases. The heat transfer rate drops at a rate of 0.9734 (in the case of hybrid Nanofluid) and 0.97925 (in the case of nanofluid) when the heat source parameter () takes an input in the range .
- Increasing the value of results in a higher mass transfer rate but increasing the value has the opposite effect. The mass transfer rate decreases at a rate of 0.04669 (in the case of hybrid nanofluid) and 0.04721 (in the case of nanofluid) when activation energy () takes an input in the range .
- Entropy generation rises as the Brinkmann number rises. As the magnetic field parameter increases, there is a corresponding decrease in the fluid’s velocity.
- The Bejan number falls as the Brinkmann number and magnetic field increase.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Dynamic viscosity of the fluid | |
| Schmidt number | |
| The density of the fluid | |
| Prandtl number | |
| Thermal expansion coefficient | |
| Mean absorption coefficient | |
| Acceleration of gravity | |
| Kinematic viscosity | |
| Thermal conductivity | |
| Dimensionless velocity | |
| Heat capacity | |
| Velocity components in directions | |
| Activation energy parameter | |
| Nonlinear thermal convection parameter | |
| Suction/injection parameter | |
| Similarity variable | |
| Radiation parameter | |
| Stefan-Boltzmann constant | |
| Thermal Grashoff number | |
| Diffusion Grashoff number | |
| Buoyancy ratio parameter | |
| Molecular diffusivity | |
| Magnetic field Parameter | |
| Volumetric rate of heat source parameter | |
| Boltzmann constant | |
| Dimensional activation energy Parameter | |
| Heat source parameter | |
| Diffusion expansion coefficient | |
| Non-dimensional temperature | |
| Fitted rate constant | |
| Reaction rate constant | |
| Temperature difference parameter | |
| Mixed convection parameter | |
| Subscripts | |
| fluid | |
| Nanofluid | |
| Binary hybrid nanofluid |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Moraveji, A.; Toghraie, D. Computational fluid dynamics simulation of heat transfer and fluid flow characteristics in a vortex tube by considering the various parameters. Int. J. Heat Mass Transf. 2017, 113, 432–443. [Google Scholar] [CrossRef]
- Kavusi, H.; Toghraie, D. A comprehensive study of the performance of a heat pipe by using of various nanofluids. Adv. Powder Technol. 2017, 28, 3074–3084. [Google Scholar] [CrossRef]
- Mostafazadeh, A.; Toghraie, D.; Mashayekhi, R.; Akbari, O.A. Effect of radiation on laminar natural convection of nanofluid in a vertical channel with single-and two-phase approaches. J. Therm. Anal. Calorim. 2019, 138, 779–794. [Google Scholar] [CrossRef]
- Thameem Basha, H.; Sivaraj, R.; Subramanyam Reddy, A.; Chamkha, A.J. SWCNH/diamond-ethylene glycol nanofluid flow over a wedge, plate and stagnation point with induced magnetic field and nonlinear radiation–solar energy application. Eur. Phys. J. Spec. Top. 2019, 228, 2531–2551. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Abu-Hamdeh, N.H.; Goodarzi, M. Entropy optimization of first-grade viscoelastic nanofluid flow over a stretching sheet by using classical Keller-box scheme. Mathematics 2021, 9, 2563. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Alsulami, R.A.; Rawa, M.J.; Alazwari, M.A.; Goodarzi, M.; Safaei, M.R. A Significant Solar Energy Note on Powell-Eyring Nanofluid with Thermal Jump Conditions: Implementing Cattaneo-Christov Heat Flux Model. Mathematics 2021, 9, 2669. [Google Scholar] [CrossRef]
- Sabu, A.S.; Wakif, A.; Areekara, S.; Mathew, A.; Shah, N.A. Significance of nanoparticles’ shape and thermo-hydrodynamic slip constraints on MHD alumina-water nanoliquid flows over a rotating heated disk: The passive control approach. Int. Commun. Heat Mass Tran. 2021, 129, 105711. [Google Scholar] [CrossRef]
- Dawar, A.; Wakif, A.; Thumma, T.; Shah, N.A. Towards a new MHD non-homogeneous convective nanofluid flow model for simulating a rotating inclined thin layer of sodium alginate-based Iron oxide exposed to incident solar energy. Int. Commun. Heat Mass Tran. 2022, 130, 105800. [Google Scholar] [CrossRef]
- Balla, H.H.; Abdullah, S.; MohdFaizal, W.; Zulkifli, R.; Sopian, K. Numerical study of the enhancement of heat transfer for hybrid CuO-Cu nanofluids flowing in a circular pipe. J. Oleo Sci. 2013, 62, 533–539. [Google Scholar] [CrossRef]
- Iqbal, Z.; Azhar, E.; Maraj, E.N. Utilization of the computational technique to improve the thermophysical performance in the transportation of an electrically conducting Al2O3-Ag/H2O hybrid nanofluid. Eur. Phys. J. Plus 2017, 132, 1–13. [Google Scholar] [CrossRef]
- Mehryan, S.A.; Kashkooli, F.M.; Ghalambaz, M.; Chamkha, A.J. Free convection of hybrid Al2O3-Cu water nanofluid in a differentially heated porous cavity. Adv. Powder Technol. 2017, 28, 2295–2305. [Google Scholar] [CrossRef]
- Mashayekhi, R.; Khodabandeh, E.; Akbari, O.A.; Toghraie, D.; Bahiraei, M.; Gholami, M. CFD analysis of thermal and hydrodynamic characteristics of hybrid nanofluid in a new designed sinusoidal double-layered microchannel heat sink. J. Therm. Anal. Calorim. 2018, 134, 2305–2315. [Google Scholar] [CrossRef]
- Ruhani, B.; Barnoon, P.; Toghraie, D. Statistical investigation for developing a new model for rheological behavior of Silica–ethylene glycol/Water hybrid Newtonian nanofluid using experimental data. Phys. A Stat. Mech. Its Appl. 2019, 525, 616–627. [Google Scholar] [CrossRef]
- Mabood, F.; Yusuf, T.A.; Khan, W.A. Cu–Al2O3–H2O hybrid nanofluid flow with melting heat transfer, irreversibility analysis and nonlinear thermal radiation. J. Therm. Anal. Calorim. 2021, 143, 973–984. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Rostami, M.N.; Yousefi, M.; Dinarvand, S.; Pop, I.; Sheremet, M.A. Dual solutions for Casson hybrid nanofluid flow due to a stretching/shrinking sheet: A new combination of theoretical and experimental models. Chin. J. Phys. 2021, 71, 574–588. [Google Scholar] [CrossRef]
- Raju SS, K.; Babu, M.J.; Raju CS, K. Irreversibility analysis in hybrid nanofluid flow between two rotating disks with activation energy and cross-diffusion effects. Chin. J. Phys. 2021, 72, 499–529. [Google Scholar] [CrossRef]
- Mahesh, A.; Varma SV, K.; Raju CS, K.; Babu, M.J.; Vajravelu, K.; Al-Kouz, W. Significance of non-Fourier heat flux and radiation on PEG–Water based hybrid Nanofluid flow among revolving disks with chemical reaction and entropy generation optimization. Int. Commun. Heat Mass Transf. 2021, 127, 105572. [Google Scholar] [CrossRef]
- Abu Bakar, S.; Md Arifin, N.; Khashi’ie, N.S.; Bachok, N. Hybrid nanofluid flow over a permeable shrinking sheet embedded in a porous medium with radiation and slip impacts. Mathematics 2021, 9, 878. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Pop, I. Numerical computation of dusty hybrid nanofluid flow and heat transfer over a deformable sheet with slip effect. Mathematics 2021, 9, 643. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Magnetic Impact on the Unsteady Separated Stagnation-Point Flow of Hybrid Nanofluid with Viscous Dissipation and Joule Heating. Mathematics 2022, 10, 2356. [Google Scholar] [CrossRef]
- Mohd Sohut NF, H.; Soid, S.K.; Abu Bakar, S.; Ishak, A. Unsteady Three-Dimensional Flow in a Rotating Hybrid Nanofluid over a Stretching Sheet. Mathematics 2022, 10, 348. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Madhukesh, J.K.; Das, R.; Shah, N.A.; Yook, S.J. Thermodynamic activity of a ternary nanofluid flow passing through a permeable slipped surface with heat source and sink. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Multiple solutions of the unsteady hybrid nanofluid flow over a rotating disk with stability analysis. Eur. J. Mech. -B/Fluids 2022, 94, 121–127. [Google Scholar] [CrossRef]
- Khan, U.; Waini, I.; Zaib, A.; Ishak, A.; Pop, I. MHD mixed convection hybrid nanofluids flow over a permeable moving inclined flat plate in the presence of thermophoretic and radiative heat flux effects. Mathematics 2022, 10, 1164. [Google Scholar] [CrossRef]
- Chu, Y.M.; Bashir, S.; Ramzan, M.; Malik, M.Y. Model-based comparative study of magnetohydrodynamics unsteady hybrid nanofluid flow between two infinite parallel plates with particle shape effects. Math. Methods Appl. Sci. 2022. [Google Scholar] [CrossRef]
- Ashraf, M.Z.; Rehman, S.U.; Farid, S.; Hussein, A.K.; Ali, B.; Shah, N.A.; Weera, W. Insight into Significance of Bioconvection on MHD Tangent Hyperbolic Nanofluid Flow of Irregular Thickness across a Slender Elastic Surface. Mathematics 2022, 10, 2592. [Google Scholar] [CrossRef]
- Zhou, C.; Majdalani, J. Large injection and suction driven channel flows with expanding and contracting walls. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001; p. 2713. [Google Scholar]
- Raza, J.; Rohni, A.M.; Omar, Z. A note on some solutions of copper-water (Cu-water) nanofluids in a channel with slowly expanding or contracting walls with heat transfer. Math. Comput. Appl. 2016, 21, 24. [Google Scholar] [CrossRef]
- Ahmed, N.; Mohyud-Din, S.T.; Hassan, S.M. Flow and heat transfer of nanofluid in an asymmetric channel with expanding and contracting walls suspended by carbon nanotubes: A numerical investigation. Aerosp. Sci. Technol. 2016, 48, 53–60. [Google Scholar] [CrossRef]
- Saba, F.; Ahmed, N.; Khan, U.; Waheed, A.; Rafiq, M.; Mohyud-Din, S.T. Thermophysical analysis of water based (Cu–Al2O3) hybrid nanofluid in an asymmetric channel with dilating/squeezing walls considering different shapes of nanoparticles. Appl. Sci. 2018, 8, 1549. [Google Scholar] [CrossRef]
- Mollamahdi, M.; Abbaszadeh, M.; Sheikhzadeh, G.A. Analytical study of Al2O3-Cu/water micropolar hybrid nanofluid in a porous channel with expanding/contracting walls in the presence of magnetic field. Sci. Iran. 2018, 25, 208–220. [Google Scholar] [CrossRef]
- Ali, A.; Ali, Y.; Kumam, P.; Babar, K.; Ahmed, A.; Shah, Z. Flow of a nanofluid and heat transfer in channel with contracting/expanding walls. IEEE Access 2019, 7, 102427–102436. [Google Scholar] [CrossRef]
- Shah, N.A.; Wakif, A.; El-Zahar, E.R.; Ahmad, S.; Yook, S.J. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng. 2022, 35, 102046. [Google Scholar] [CrossRef]
- Sajjan, K.; Shah, N.A.; Ahammad, N.A.; Raju, C.S.K.; Kumar, M.D.; Weera, W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math. 2022, 7, 18416–18449. [Google Scholar] [CrossRef]
- Sarojamma, G.; Lakshmi, R.V.; Narayana, P.V.; Makinde, O.D. Non linear radiative flow of a micropolar nanofluid through a vertical channel with porous collapsible walls. In Defect and Diffusion Forum; Trans Tech Publications Ltd.: Bäch, Switzerland, 2018; Volume 387, pp. 498–509. [Google Scholar]
- Al-Kouz, W.; Mahanthesh, B.; Alqarni, M.S.; Thriveni, K. A study of quadratic thermal radiation and quadratic convection on viscoelastic material flow with two different heat source modulations. Int. Commun. Heat Mass Transf. 2021, 126, 105364. [Google Scholar] [CrossRef]
- Irfan, M.; Khan, M.; Khan, W.A.; Ahmad, L. Influence of binary chemical reaction with Arrhenius activation energy in MHD nonlinear radiative flow of unsteady Carreau nanofluid: Dual solutions. Appl. Phys. A 2019, 125, 1–11. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. Cattaneo–Christov based study of TiO2-CuO/EG Casson hybrid nanofluid flow over a stretching surface with entropy generation. Appl. Nanosci. 2018, 8, 685–698. [Google Scholar] [CrossRef]
- Dauenhauer, E.C.; Majdalani, J. Exact self-similarity solution of the Navier–Stokes equations for a porous channel with orthogonally moving walls. Phys. Fluids 2003, 15, 1485–1495. [Google Scholar] [CrossRef]

| S. No. | ||||
|---|---|---|---|---|
| 1 | 1114 | 5660 | 4250 | |
| 2 | 2415 | 495.2 | 686.2 | |
| 3 | 0.252 | 13 | 8.953 | |
| 4 | 0.0000055 | 0.01 | 2,380,000 |
| Bilal et al. [35] | Current Outcomes | ||
|---|---|---|---|
| 0 | 0.5 | 4.713254 | 4.713217 |
| 1 | 4.739148 | 4.739109 | |
| 2 | 4.820361 | 4.820342 | |
| 3 | 4.396271 | 4.396280 | |
| 2 | 0 | 1.842331 | 1.842323 |
| 0.3 | 3.653601 | 3.653614 | |
| 0.6 | 5.391148 | 5.391142 | |
| 1 | 7.593006 | 7.593001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lavanya, B.; Kumar, J.G.; Babu, M.J.; Raju, C.S.; Shah, N.A.; Junsawang, P. Irreversibility Analysis in the Ethylene Glycol Based Hybrid Nanofluid Flow amongst Expanding/Contracting Walls When Quadratic Thermal Radiation and Arrhenius Activation Energy Are Significant. Mathematics 2022, 10, 2984. https://doi.org/10.3390/math10162984
Lavanya B, Kumar JG, Babu MJ, Raju CS, Shah NA, Junsawang P. Irreversibility Analysis in the Ethylene Glycol Based Hybrid Nanofluid Flow amongst Expanding/Contracting Walls When Quadratic Thermal Radiation and Arrhenius Activation Energy Are Significant. Mathematics. 2022; 10(16):2984. https://doi.org/10.3390/math10162984
Chicago/Turabian StyleLavanya, Bommana, Jorige Girish Kumar, Macherla Jayachandra Babu, Chakravarthula Sivakrishnam Raju, Nehad Ali Shah, and Prem Junsawang. 2022. "Irreversibility Analysis in the Ethylene Glycol Based Hybrid Nanofluid Flow amongst Expanding/Contracting Walls When Quadratic Thermal Radiation and Arrhenius Activation Energy Are Significant" Mathematics 10, no. 16: 2984. https://doi.org/10.3390/math10162984
APA StyleLavanya, B., Kumar, J. G., Babu, M. J., Raju, C. S., Shah, N. A., & Junsawang, P. (2022). Irreversibility Analysis in the Ethylene Glycol Based Hybrid Nanofluid Flow amongst Expanding/Contracting Walls When Quadratic Thermal Radiation and Arrhenius Activation Energy Are Significant. Mathematics, 10(16), 2984. https://doi.org/10.3390/math10162984







