Developing a Variable Speed Limit Control Strategy for Mixed Traffic Flow Based on Car-Following Collision Avoidance Theory

Abstract

Variable speed limit (VSL) control is an effective technology to improve safety near freeway bottlenecks. This study aims to develop a control strategy for mixed traffic flow consisting of both human-driven vehicles (HDVs) and connected and automated vehicles (CAVs) based on collision avoidance theory. A microscopic simulation platform is first established, and four vehicle longitudinal dynamic models including Cruising model, Intelligent Driver Model (IDM), Adaptive Cruise Control model (ACC), Cooperative Cruise Control model (CACC) and one vehicle lateral dynamic model Minimizing Overall Braking Induced by Lane Changes model (MOBIL) are incorporated into the simulation platform. Then, a new VSL control strategy derived from collision avoidance theory is proposed for mixed traffic flow at the initial stage of CAVs’ popularization. Extensive simulation experiments are conducted, and surrogate safety measures and total travel time indicators are utilized to evaluate the safety and efficiency performances of the proposed VSL control. Results indicate that the proposed VSL control strategy can effectively improve the safety performance near freeway bottlenecks with an acceptable efficiency level.

1. Introduction

Freeway bottlenecks are usually caused by road geometric restrictions and traffic incidents such as traffic accidents and work zones. When the traffic demand is far greater than the capacity of the roadway, the consequent congestion and speed difference between the upstream and downstream may further increase collision risks. In order to alleviate the safety issue, the mainstream method is to reduce vehicle speed and increase speed homogenization by intelligent control strategies.

Variable speed limit (VSL) control, as one of the advanced traffic management technologies, has been extensively utilized to improve traffic safety on freeways via dynamically adjusting upstream speed limits posted on the variable message signs (VMS). The classical VSL control strategies can be divided into two types, i.e., model prediction control (MPC) and feedback-based control [1,2,3,4,5,6]. The performance of the MPC-based VSL control strategy depends on the accuracy of the predictive model. The feedback-based control strategy is simpler and easier to implement, whose objective is usually to obtain critical density at the bottleneck around the setpoint. More details can be referred to in the literature review section.

In recent years, intelligent transportation technologies have developed rapidly and can be generally divided into two directions: the intelligent road system and the intelligent vehicle system. The former provides the basis for vehicle-road collaboration and is able to further improve the effectiveness of traditional VSL controls, while the latter realizes the intelligence of vehicles through connected and automated technologies. The connected and automated vehicles (CAVs), as a representative of the intelligent vehicle system, can effectively reduce the response delay and operational errors of human-driven vehicles (HDVs). Therefore, it is recognized to be a promising technology to improve traffic safety and reduce traffic congestion and emissions.

Considerable previous studies have explored various VSL control strategies with intelligent road and vehicle systems, aiming to improve control effectiveness by taking advantage of vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) communication together with automated driving [7,8,9,10,11,12]. Nevertheless, CAVs are facing unavoidable challenges such as sensor failure, limited operational design domain and accurate trajectory prediction of other road users [13]. The popularization of CAVs will still take a long time due to these technical and safety issues, which means that the mixed traffic flow consisting of CAVs and HDVs will exist for the long term. For the initial stage of CAV application in the near future, HDVs still dominate in the mixed traffic flow with a large proportion, and VSL control methods need to take this special characteristic into account.

The primary objective of the current study is to propose a VSL control strategy for the initial stage of CAV popularization. More specifically, we focus on a general dynamic scenario of mixed traffic flow considering the driving behavior of car following and lane changing and develop the VSL control based on the collision avoidance theory. Four car-following models and one lane-changing model are embedded in the micro-simulation platform to capture the driving behaviors of HDVs and CAVs. Surrogate safety measures derived from time-to-collision (TTC), such as the time-exposure TTC (TET) and time-integrated TTC (TIT), are employed to evaluate the safety improvement performance of the proposed VSL control strategy. Meanwhile, the total travel time (TTT) is used to evaluate the efficiency. Taking into account the safe time gap of CAVs and different market penetration rates (MPRs), extensive simulation experiments are conducted and compared to verify the effectiveness of the proposed control strategy.

The rest of this paper is organized as follows: Section 2 presents the literature review. In Section 3, the simulation platform is introduced, and the VSL control strategy based on collision avoidance theory is proposed. The simulation experiments are designed in Section 4, and the simulation results are demonstrated in Section 5. The paper ends with conclusions in Section 6.

2. Literature Review

The early VSL control is mainly aimed at the conventional human-driven traffic flow, which can be divided into closed-loop control and open-loop one. The closed-loop control is a feedback logic-oriented control strategy. For example, Li et al. developed a VSL control strategy with the feedback logic by analyzing the risk of microscopic secondary collision [14]. Dörschel and Abel proposed a new directional feedback control through systematic analysis of the macroscopic traffic model, which is suitable for VSL control of a freeway [15]. Based on the analysis of the induction mechanism of the fundamental diagram of the freeway traffic flow, Frejo et al. proposed a new macroscopic VSL control model, which takes capacity, critical density, and compliance into account. The results show that the new model has better performance under low compliance when comparing the proposed model with two typical macroscopic models [16]. Based on the analysis of the macroscopic traffic model and the evolution law of the traffic fundamental diagram, Zhang et al. proposed an extended VSL control model for alleviating the impact of congestion and queuing problems caused by shock waves on the freeway [17]. In order to ensure the integral stability of the closed-loop system from input to state, Göksu et al. proposed a VSL controller, which utilized saturation feedback to ensure the integral input of traffic state to state stability. The controller was designed by using a traffic flow ordinary differential equation model and a two-phase fundamental diagram. A two-stage general Lyapunov function was established, and the robustness of the proposed controller was verified by numerical examples [18].

The open-loop control, also known as Model Predictive Control (MPC), utilizes a traffic flow model to predict trends in traffic flow evolution. Song and Wang proposed a VSL control method based on a high-precision collision prediction model to reduce the collision risk and traffic delays [19]. Zhang et al. proposed two control schemes based on feedback linearization and model prediction and combined VSL control with lane-changing control. The results show that both of the schemes can effectively improve the operating efficiency of the system and that the feedback linearization VSL control can provide better performance than model predictive control [20]. Hegyi et al. proposed a VSL strategy based on the model predictive control approach to optimally coordinate variable speed limits for freeway traffic with the aim of suppressing shock waves. The result shows that continuous speed limits via the coordinated control are effective against shock waves [3]. Mao et al. proposed an extended model-based VSL controller, which was also developed on the basis of the scheme of model predictive control to improve the connected environment. The results of numerical simulation show that the extended model-based VSL controller possesses greater significance in the reduction of total travel time [9]. Frejo et al. compared the effectiveness of the global and local model predictive control methods in a traffic network controller system consisting of ramp metering and variable speed limits. The results showed that the local techniques have a suboptimal behavior and the controller improves the local controller performance [2].

Since then, some studies have been devoted to developing and solving VSL control models based on algorithm optimization theory, mainly including the heuristic algorithm, reinforcement learning and deep reinforcement learning. In terms of the heuristic algorithm, Yu and Fan studied a VSL control problem at a partial lane closure bottleneck based on a genetic algorithm and established a multi-objective nonlinear integer model. They also evaluated and compared the solution quality of a genetic algorithm and sequential quadratic programming (SQP) algorithm. The numerical analysis results show that the VSL control model optimized by genetic algorithm is superior to that optimized by the SQP algorithm [21]. Wang et al. established an optimization model of VSL control for rainy days with the goal of minimizing accident incidence. The genetic algorithm is used to solve the VSL model [22]. Kušić et al. proposed a multi-agent reinforcement learning VSL control method based on W-learning algorithm. In this algorithm, two agents control two sections leading to the bottleneck area, and the performance of the control strategy is verified by simulation of two scenarios of dynamic and static traffic [23]. In terms of deep reinforcement learning, Wu et al. proposed a differential VSL (DVSL) control model based on deep reinforcement learning, which can achieve differentiated dynamic speed limits between lanes. The results show that the DVSL control model can help improve the safety and operation efficiency of freeways and reduce emissions [24]. Ke et al. proposed a VSL control strategy based on Double Deep Q-learning to reduce the total driving time on freeways [25]. Some researchers have also conducted different studies on various scenarios [26,27,28,29,30,31].

With the rapid development of CAV technology, the VSL control strategy combined with CAV has attracted widespread attention in recent years. Lu and Shladover proposed a VSL control method based on second-order METANET model prediction, which takes the market penetration rate of adaptive cruise control vehicles into account [32]. Grumert and Tapani proposed a VSL control system based on connected vehicles, whose goal was to allow the application of VSL control to any case for aperiodic bottleneck mitigation [33]. Gregurić et al. proposed an intelligent speed adaptation strategy that could induce vehicles to achieve a smooth speed conversion according to the suggested or imposed speed limit [34]. Yao et al. proposed a trajectory smoothing method based on the location-based individual VSL, which dynamically imposed speed limits on the identified target control vehicles through vehicle–infrastructure communication at adjacent lane control points [35]. Nezafat et al. proposed a feedback control method to manage the speed of connected vehicles from the upstream of a downhill freeway segment to avoid bottleneck formation due to changes in driver behavior [36]. Li et al. proposed a system combining CAVs with VSL control and simulated the safety gain brought by the system [37]. Meanwhile, the connected technology of CAV can make up for the shortcomings of human sight distance, especially when the visible range is affected by severe weather such as heavy fog. Zhao et al. proposed a VSL control system based on connected vehicles and then simulated different levels of visibility based on a driving simulator to examine the effectiveness of the proposed system. The results indicate that the developed system has a better performance in heavy fog conditions than that in light fog conditions [12]. Wu et al. proposed a VSL control method based on the different relationships between the car-following distance and the visual distance to reduce the risk of rear-end collisions in highway bottleneck sections under fog conditions [11]. Additionally, the previous study also indicates that near-maximum efficiency improvements can be obtained at relatively low CAV penetration rates [38]. Due to the aforementioned technical and safety issues of CAVs, the mixed traffic flow with a comparative low penetration rate is likely to be maintained for a long time. Therefore, it is necessary to develop specific VSL strategies applicable to this important and unavoidable period.

In summary, although a large number of studies have been conducted about VSL control strategies, the VSL control strategy is not fully explored for the mixed traffic flow consisting of CAVs and HDVs, especially for the initial stage of CAVs’ popularization in the near future. This study aims to bridge the research gap by proposing a new VSL control strategy based on the collision avoidance theory.

3. Methodology

This section presents the methodology of the current study. To simultaneously consider the car following and lane changing for simulation experiments, four typical car-following models and a lane-changing model are employed in the current study. The car-following models, including Cruising model, Intelligent Driver Model (IDM), Adaptive Cruise Control model (ACC), and Cooperative Cruise Control model (CACC) are introduced in Section 3.1. The vehicle lateral dynamic model Minimizing Overall Braking Induced by Lane Changes model (MOBIL), which models the lane-changing behaviors, is presented in Section 3.2. Section 3.3 details the VSL control strategy based on collision avoidance theory.

3.1. Car-Following Models

This study focuses on the safety performance of VSL control strategy in the mixed traffic flow composed of HDVs and CAVs. Four microscopic car-following models are used to model the longitudinal dynamic behaviors of HDVs and CAVs.

(1)

Cruise model

The control objective of cruise mode is to maintain the desired speed of the driver when the previous vehicle is not present or far away. In the simulation, it is used as the running mode of the leading vehicle of the fleet (no matter the leading vehicle is a HDV or a CAV). The specific calculation formula of acceleration in this mode is as follows:

$$a=k_0{v}_0-v,$$

(1)

where control gain $k_0$ is the parameter to determine the speed error rate of acceleration, which is set as 0.4 according to the previous study [39]; $v_0$ and $v$ denote the desired speed and current speed of the driver, respectively.

(2)

IDM model

A widely used microscopic vehicle dynamic model, Intelligent Driver Model (IDM), is incorporated to describe the car-following behavior of HDVs [40,41]. The authority of the IDM model has been proved that it can accurately reflect the one-dimensional dynamic behavior of HDVs. The model uses the desired speed and clearance distance to calculate dynamic acceleration, and the specific calculation formula is as follows:

$$a={\alpha }_m\left[1-{\left(\frac{v}{v_0}\right)}^4-{\left(\frac{s^{*}}{s}\right)}^2\right],$$

(2)

$$s^{*}=s_0+max\left[0,vT+\overline{L}+\frac{v\Delta v}{2\sqrt{{\alpha }_m\beta }}\right],$$

(3)

where $a$ is the acceleration of subject vehicle; ${\alpha }_m$ represents the absolute value of maximum acceleration; $v$ and $v_0$ denote the current speed and desired speed of the subject vehicle, respectively; $s$ is the net distance headway between the subject vehicle and the leading vehicle; $s_0$ is the minimum clearance distance at standstill; $T$ is the safe time gap; $\overline{L}$ is the average length of vehicles; $\Delta v$ is the speed difference between the subject vehicle and the leading vehicle; $\beta$ means the absolute value of desired deceleration.

(3)

ACC model

The ACC model developed by the California Partnership for Advanced Transportation and Highways (PATH) is used in this study. The PATH ACC model is derived from the real vehicle test and has been successfully commercialized to perform automated cruise driving without drivers’ input. Notably, the above-mentioned IDM model describes the car-following behavior of conventional vehicles humans (HDVs) while the ACC model can be considered as the initial version of autonomous driving. Similar to the traditional car-following model, the specific calculation formula for the acceleration of the ACC vehicle is:

$$a_i=k_1\left(x_{i-1}-x_i-t_{hw}{v}_i-L_{i-1}\right)+k_2\left(v_{i-1}-v_i\right),$$

(4)

where $a_i$ is the acceleration of the subject vehicle; $x_{i-1}$ and $v_{i-1}$ represent the position and speed of the leading vehicle, respectively; $x_i$ and $v_i$ represent the position and speed of the subject vehicle, respectively; $t_{hw}$ denotes the safe time gap; $L_{i-1}$ represents the length of leading vehicle; $k_1$ and $k_2$ are the model coefficients, which are calibrated as 0.23 and 0.07, respectively, according to the previous study [42].

(4)

CACC model

Milanés et al. conducted field tests on vehicles equipped with the cooperative adaptive cruise control system, which is the advanced version of the ACC system equipped with vehicle-to-vehicle communication functionality [42]. Under the control of the CACC model, the vehicle speed is calculated from the speed of the previous step, the gap error of the previous step and its derivative. The specific calculation formula is as follows:

$$e_i=x_{i-1}-x_i-t_{hw}{v}_i,$$

(5)

$$v_i=v_{iprev}+k_p{e}_i+k_d{e}_i^{\prime },$$

(6)

where $e_i$ represents the gap error of the $i\mathrm{th}$ vehicle; $x_i$ and $x_{i-1}$ represent the position of the $i\mathrm{th}$ vehicle and its preceding vehicle, respectively; $t_{hw}$ denotes the safe time gap; $v_i$ represents the speed of the subject vehicle. Equation (6) represents the speed calculation formula of CACC model, where $v_{iprev}$ is the speed of the subject vehicle at the previous time step; $e_i$ is the gap error of the $i\mathrm{th}$ vehicle; $e_i^{\prime }$ is the derivative of the clearance error of the $i\mathrm{th}$ vehicle; $k_p$ and $k_d$ represent the constant parameters adjusted for clearance error and clearance error derivative, which are set to 0.45 and 0.0125 according to previous studies [40,43].

Dynamic acceleration calculated by the Cruise model, IDM model and ACC model can further update the speed and position of the vehicle in the next step:

$$v=v_{prev}+a\Delta t,$$

(7)

$$x=x_{prev}+v\Delta t+a{\left(\Delta t\right)}^2/2,$$

(8)

where $x_{prev}$ and $v_{prev}$ represent the position and speed of the subject vehicle in the previous time step, respectively; $\Delta t$ denotes the simulation time step.

CACC further updates the position of the next step based on the speed calculated by the CACC model:

$$a_i=k_1\left(x_{i-1}-x_i-t_{hw}{v}_i-L_{i-1}\right)+k_2\left(v_{i-1}-v_i\right).$$

(9)

3.2. Lane-Changing Model

The Braking Overall Induced by Lane Changes (MOBIL) lane changing model proposed by Kesting et al. is applied to describe the lateral dynamics of vehicles in this study [44]. In this model, the driving benefit of a driver is represented by the vehicle’s acceleration. By comparing the acceleration gain of the vehicles affected by lane change in the current lane and the target lane, the overall acceleration gain of the local affected vehicle group is calculated to determine the lane changing demand. The lane changing executor should not only consider that it can achieve acceleration gain through lane change but should also consider other vehicles affected. Before and after lane change, the rear vehicle in the current lane will generate a positive lane changing gain, while the rear vehicle in the target lane will generate a negative lane changing gain. Only when the total acceleration gain of the system, consisting of the lane changing executer, the rear vehicle in the current lane and the rear vehicle in the target lane, reaches a certain degree (the system lane changing gain threshold), the lane changing requirements can be met. The specific calculation formula is as follows:

$$a_{sub}^{after}-a_{sub}^{before}+p_{alt}{a}_{cu{r}_f}^{after}-a_{cu{r}_f}^{before}+a_{ta{r}_f}^{after}-a_{ta{r}_f}^{before}>\Delta a+a_{bias},$$

(10)

where $a_{sub}^{before}$ and $a_{sub}^{after}$ are the acceleration of the subject vehicle before and after lane change; $a_{cu{r}_f}^{before}$ and $a_{cu{r}_f}^{after}$ are the acceleration of the rear vehicle in the current lane before and after lane change of the subject vehicle; $a_{ta{r}_f}^{before}$ and $a_{ta{r}_f}^{after}$ represent the acceleration of the rear vehicle in the target lane before and after lane change of the target vehicle; $p_{alt}$ denotes the altruistic factor; $\Delta a$ is the threshold of the overall benefit improvement of the system when lane changing demand decision making; $a_{bias}$ is the additional parameter, which reflects the asymmetric lane change.

Lane change can only be carried out if the acceleration of the rear vehicle in the target lane is greater than the maximum deceleration after the subject vehicle changes lanes. The discriminant condition of lane change safety is as follows:

$$a_{ta{r}_f}^{after}>-b_{safe},$$

(11)

where $b_{safe}$ represents the absolute value of maximum deceleration to ensure safe driving.

3.3. VSL Control Strategy Based on Car-Following Collision Avoidance Theory

In order to develop our VSL control strategy, two basic premises are first made here. (1) The major risks are from rear-end collisions. This assumption is reasonable since the primary objective of VSL is to proactively adjust the high speeds of vehicles and avoid longitudinal collisions for the downstream vehicles with low speeds. (2) The low market penetration rates (MPRs) of CAVs are considered for the near future and the HDVs dominate in the mixed traffic flow [38]. That is because the popularization of CAVs is a long-term process and the MPRs will not be high in the near future. With this premise, we further propose basic car-following collision avoidance theory from the IDM.

Consider that there is a pair of car-following vehicles, among which the speed of rear and preceding vehicles is $v_2$ and $v_1$, respectively. Let ${\alpha }_m$ and $\beta$ represent the desired acceleration and deceleration of driver, $v_0$ is the desired speed of subject vehicle, $T$ is the safe time gap, $L$ means the length of the vehicle, and $\Delta x$ means the net distance headway between the preceding and rear vehicles. According to IDM model, we can calculate the vehicle acceleration in the current car-following condition, and its specific expression is as follows:

$$a={\alpha }_m\left[1-{\left(\frac{v_2}{v_0}\right)}^4-{\left(\frac{2\sqrt{{\alpha }_m\beta }(v_{2}T+L)+v_2\left(v_2-v_1\right)}{2\sqrt{{\alpha }_m\beta }\Delta x}\right)}^2\right],$$

(12)

The maximum deceleration rate of the vehicle is assumed as $a_{dec}^{max}$, which is a negative value. If the acceleration of the rear vehicle calculated by the IDM model $a$ is greater than $a_{dec}^{max}$, its safety can be guaranteed in the current scenario, which means the current acceleration calculated based on the car-following model is within the braking performance of the vehicle; otherwise, it indicates that there is a rear-end collision risk. In order to ensure the safety of car following, the requirements are as follows:

$$a={\alpha }_m[1-{\left(\frac{v_2}{v_0}\right)}^4-{\left(\frac{2\sqrt{{\alpha }_m\beta }(v_{2}T+L)+v_2\left(v_2-v_1\right)}{2\sqrt{{\alpha }_m\beta }\Delta x}\right)}^2],$$

(13)

$${\left(\frac{v_2}{v_0}\right)}^4+{\left(\frac{2\sqrt{{\alpha }_m\beta }(v_{2}T+L)+v_2\left(v_2-v_1\right)}{2\sqrt{{\alpha }_m\beta }\Delta x}\right)}^2<1-\frac{a_{dec}^{max}}{{\alpha }_m},$$

(14)

$$4{\alpha }_m\beta \Delta x^2{v}_2{}^4+v_0{}^4\left(2\sqrt{{\alpha }_m\beta }(v_{2}T+L\right)+v_2\left(v_2-v_1\right){)}^2<4{\alpha }_m\beta \Delta x^2{v}_0{}^4\left(1-\frac{a_{dec}^{max}}{{\alpha }_m}\right),$$

(15)

$$4{\alpha }_m\beta \Delta x^2{v}_2{}^4+v_0{}^4{\left(v_2{}^2+\left(2\sqrt{{\alpha }_m\beta }T-v_1\right)v_2+2\sqrt{{\alpha }_m\beta }L\right)}^2<4{\alpha }_m\beta \Delta x^2{v}_0{}^4\left(1-\frac{a_{dec}^{max}}{{\alpha }_m}\right),$$

(16)

$$\begin{array}{cc}\left(4{\alpha }_m\beta \Delta x^2+v_0{}^4\right)v_2{}^4& +\left(4\sqrt{{\alpha }_m\beta }T-2v_1\right)v_0{}^4{v}_2{}^3+(4{\alpha }_m\beta T^2+v_1{}^2+4\sqrt{{\alpha }_m\beta }L\hfill \\ & -4\sqrt{{\alpha }_m\beta }T{v}_1)v_0{}^4{v}_2{}^2+\left(8{\alpha }_m\beta TL-4\sqrt{{\alpha }_m\beta }{v}_{1}L\right)v_0{}^4{v}_2+4{\alpha }_m\beta (L^2\hfill \\ & +\left(\frac{a_{dec}^{max}}{{\alpha }_m}-1\right)\Delta x^2)v_0{}^4<0\hfill \end{array}$$

(17)

Now, we obtain a unary quartic inequality about the driving speed of the rear vehicle $v_2$. Theoretically, only when $v_2$ satisfies this quartic inequality, the rear vehicle can avoid rear-end collision risks. Let $f{v}_2=\left(4{\alpha }_m\beta \Delta x^2+v_0{}^4\right)v_2{}^4+\left(4\sqrt{{\alpha }_m\beta }T-2v_1\right)v_0{}^4{v}_2{}^3+\left(4{\alpha }_m\beta T^2+v_1{}^2+4\sqrt{{\alpha }_m\beta }L-4\sqrt{{\alpha }_m\beta }T{v}_1\right)v_0{}^4{v}_2{}^2+\left(8{\alpha }_m\beta TL-4\sqrt{{\alpha }_m\beta }{v}_{1}L\right)v_0{}^4{v}_2+4{\alpha }_m\beta \left(L^2+\left(\frac{a_{dec}^{max}}{{\alpha }_m}-1\right)\Delta x^2\right)v_0{}^4$. For the convenience of expression, we simplify the formula coefficient: the quartic coefficient $p_4=4{\alpha }_m\beta \Delta x^2+v_0{}^4$, the cubic coefficient $p_3=\left(4\sqrt{{\alpha }_m\beta }T-2v_1\right)v_0{}^4$, the quadratic coefficient $p_2=\left(4{\alpha }_m\beta T^2+v_1{}^2+4\sqrt{{\alpha }_m\beta }L-4\sqrt{{\alpha }_m\beta }T{v}_1\right)v_0{}^4$, the primary term coefficient $p_1=\left(8{\alpha }_m\beta TL-4\sqrt{{\alpha }_m\beta }{v}_{1}L\right)v_0{}^4$, and constant coefficient $p_0=4{\alpha }_m\beta \left(L^2+\left(\frac{a_{dec}^{max}}{{\alpha }_m}-1\right)\Delta x^2\right)v_0{}^4$. The $\Delta x$ denotes the net distance headway between the preceding and rear vehicles and is greater than the vehicle length $L$. Meanwhile, $\frac{a_{dec}^{max}}{{\alpha }_m}-1<-1$ (${\alpha }_m>0$, $a_{dec}^{max}<0$); thus, we can obtain that $L^2+\left(\frac{a_{dec}^{max}}{{\alpha }_m}-1\right)\Delta x^2<0$. Obviously, we can obtain: $p_4>0$ and $p_0<0$. When $v_2\to +\infty$, $f{v}_2>0$. When $v_2=0$, $f{v}_2<0$. According to the zero-existence theorem, there must be at least one zero in the range from 0 to $+\infty$.

The zero-point classification is discussed below, as shown in Figure 1:

(1)

There is only one zero in [0, +∞).

It is known that when $v_2\to +\infty$, $f{v}_2>0$; when $v_2=0$, $f{v}_2<0$. In addition, there is only one zero in [0,+∞). There must be a zero $x_0$, so that when $v_2$ ∈ [0, $x_0$), $f{v}_2<0$. That is, there will be no rear-end collision risk when $v_2<x_0$.

(2)

There are multiple zeros in [0, +∞)

If there are multiple zeros in [0,+∞), there may appear more than one range, which meets $f{v}_2<0$. According to the principle of vehicle dynamics, when $v_2=0$, $f{v}_2<0$, which means when the rear vehicle is at standstill, it must be safe. Therefore, $v_2=0$ must be in the feasible region. Then, there exists a minimum zero $x_0$, when $v_2$ ∈ [0, $x_0$), safety can be guaranteed. In the case of multiple zeros, there may be multiple feasible regions where they meet $f{v}_2<0$, as shown in Figure 1c. Nevertheless, when $v_2<x_0$, $f{v}_2<0$ (no rear-end collision risks); as $v_2$ increases, $f{v}_2>0$ (exist rear-end collision risks); as $v_2$ increases further, $f{v}_2<0$ (no rear-end collision risks), which is contrary to common sense. This means that other satisfying regions are theoretical solutions instead of real feasible solutions.

To sum up, there must be a minimum zero $x_0$ at [0, +∞), so that when $v_2$ ∈ [0,$x_0$), there is no rear-end collision risk between the preceding and rear vehicles. This minimum zero $x_0$ corresponds to the maximum collision avoidance speed of the rear vehicle $v_2^{*}$.

The above maximum collision avoidance speed $v_2^{*}$ (equal to $x_0$) of the rear vehicle is evaluated based on microscopic trajectory data including $v_1$ and $\Delta x$. In actual situations, however, microscopic trajectory information of human-driven vehicles cannot be obtained timely; thus, only aggregated traffic flow data can be collected from loop detectors. Next, how to use traffic flow data collected from loop detector to replace microscopic trajectory data will be introduced to develop our VSL control strategy as follows:

$${\widehat{v}}_1=\frac{1}{N}{{\displaystyle \sum }}_{n=1}^N{v}_1={\overline{V}}_D\left[t,t+\Delta T\right],$$

(18)

$$\begin{gathered} \Delta \widehat{x}=\frac{1}{N}{{\displaystyle \sum }}_{n=1}^N\Delta x=\frac{1}{N}{{\displaystyle \sum }}_{n=1}^N\left(H_i-L_i\right)=\frac{1}{N}\left({{\displaystyle \sum }}_{n=1}^N{H}_i-{{\displaystyle \sum }}_{n=1}^N{L}_i\right)=\frac{1}{N}\left({{\displaystyle \sum }}_{n=1}^N\left(\frac{1}{{\overline{K}}_U\left[t,t+\Delta T\right]}\right)-\mathrm{N}\overline{L}\right)=\frac{1}{N}\left({{\displaystyle \sum }}_{n=1}^N\left(\frac{\overline{L}}{{\overline{O}}_U\left[t,t+\Delta T\right]}\right)-\mathrm{N}\overline{L}\right) \\ =\frac{\overline{L}}{{\overline{O}}_U\left[t,t+\Delta T\right]}-\overline{L}=\overline{L}\left(\frac{1-{\overline{O}}_U\left[t,t+\Delta T\right]}{{\overline{O}}_U\left[t,t+\Delta T\right]}\right), \end{gathered}$$

(19)

where ${\overline{V}}_U\left[t,t+\Delta t\right]$ represents the average speed collected from loop detectors at upstream; ${\overline{V}}_D\left[t,t+\Delta t\right]$ represents the average speed collected from loop detectors at downstream; ${\overline{O}}_U\left[t,t+\Delta t\right]$ denotes the average occupancy collected from loop detectors at upstream; $\overline{L}$ represents the average length of the vehicles; $\mathsf{\Delta }T$ refers to the data aggregation interval of loop detectors.

The theoretical speed limit of the upstream under the current traffic condition can be obtained by substituting $v_1$ and $\Delta x$ with the traffic flow information, respectively (substitute Equations (18) and (19) into Equation (17)). Then, the upstream theoretical speed limit value $V_{vsl}\left(x_i,t+\Delta T\right)$, which is defined as the maximum collision avoidance speed calculated by aggregated traffic flow data, can be obtained.

The theoretical speed limit value $V_{vsl}\left(x_i,t+\Delta T\right)$ is calculated from downstream to upstream consecutively. However, the above-mentioned theoretical speed limits cannot be directly applied as a reliable VSL strategy. That is because the current speed limits have no spatial–temporal constraints to ensure the smooth shift of speed. and it is likely to result in a sharp change in speed regarding temporal dimension and spatial dimension. More specifically, considering a significant decrease in two temporally consecutive speed limit values, the vehicles arriving at the next strategy execution periods would slow down sharply. It forms a shock wave propagating back to the upstream, leading to an increase in rear-end collision risks. Conversely, safe deceleration is also crucial for vehicles following two spatially consecutive speed limits. If there is a dramatic change in speed limits posted by two consecutive VMSs, vehicles moving from the previous VMS to the next will suffer a deceleration scenario of high risk. It will also cause unexpected traffic flow oscillation. To solve the above issues and obtain a preferable speed limit value, spatial–temporal constraints are applied to avoid the possible turbulence of traffic flow. The spatial–temporal constraints can be expressed by the following two equations. Note that Equation (20) is used for the temporal constraint representation, and Equation (21) is used for the spatial constraint representation.

$$V_{vsl}\left(x_i,t+\Delta T\right)=\max \left(\min \left(V_{vsl}\left(x_i,t+\Delta T\right),V_{vsl}\left(x_i,t\right)+\Delta vsl\right),V_{vsl}\left(x_i,t\right)-\Delta vsl\right),$$

(20)

$$\begin{gathered} V_{vsl}\left(x_i,t+\Delta T\right)=\max \left(\min \left(V_{vsl}\left(x_i,t+\Delta T\right),V_{vsl}\left(x_{i+1},t+\Delta T\right)+\Delta vsl\right),V_{vsl}(x_{i+1},t+ \\ \Delta T)-\Delta vsl\right), \end{gathered}$$

(21)

where $V_{vsl}\left(x_i,t\right)$ represents the calculated speed of avoiding the occurrence of rear-end collision at location $x_i$ at time $t$. $\Delta vsl$ is the constraint value, which is set to be 15 km/h. $V_{vsl}\left(x_{i+1},t+\Delta T\right)$ represents the calculated speed of avoiding the occurrence of rear-end collision at location $x_{i+1}$ at time $t+\Delta T$.

Note that the collision avoidance theory is considered as the underlying philosophy for developing the VSL. This theory is based on the physical model of two vehicle interactions, which is rather intuitive. To prevent possible collisions, the interaction of two vehicles should avoid situations where the required speed changes of collision avoidance exceed the maximum ability of the vehicle. More specifically, if the current acceleration calculated by the car-following model is within the braking performance of the vehicle, the safety can be confirmed. Otherwise, it indicates that there is a rear-end collision risk. Most of the surrogate safety measures such as Time-to-Collision (TTC) and Deceleration Rate to Avoid Crash (DRAC) are proposed on the basis of this physical model and the corresponding collision avoidance theory [45,46].

3.4. Evaluative Measurements

To evaluate the effectiveness, especially the safety performance of the proposed VSL control strategy, appropriate surrogate safety measures capable of quantifying the rear-end collision risk should be considered in VSL studies [47]. Surrogate safety measures are used to bridge the gap between vehicle interactions and potential risky events, namely traffic conflicts. Previous studies have developed a variety of indicators to measure the safety status for induvial vehicles. In this study, two indicators time-exposed TTC (TET) and time-integrated TTC (TIT) derived from time-to-collision (TTC) are employed for the crash risk analysis [37,48,49,50]. The TTC value denotes the remaining time for the rear (following vehicle) vehicle to collide with the leading vehicle (preceding vehicle) if the two vehicles do not change their driving states (changing vehicular speeds or lanes). A TTC threshold (denoted by TTC*) is commonly used to identify the high-risk conditions in the dynamic driving process. Specifically, interactions are considered as unsafe when the TTC value is lower than the selected threshold since the driver does not have sufficient time to avoid the potential crash due to driver response limitations and braking limitations. Once a threshold is selected to define risky conditions, the TTC threshold value will not be affected by the dynamic traffic conditions. The TTC of a rear vehicle $i$ with respect to the leading vehicle $i-1$ at time step $t$ can be calculated as follows:

$$TT{C}_i\left(t\right)=\{\begin{array}{c}\frac{x_{i-1}\left(t\right)-x_i\left(t\right)-L_{i-1}}{v_i\left(t\right)-v_{i-1}\left(t\right)},if v_i\left(t\right)>v_{i-1}\left(t\right)\\ \infty ,if v_i\left(t\right)\le v_{i-1}\left(t\right)\end{array},$$

(22)

where $x_{i-1}$ and $v_{i-1}$ denote the current position and speed of the preceding vehicle, respectively; $x_i$ and $v_i$ represent the current position and speed of the rear vehicle, respectively; and $L_{i-1}$ is the length of preceding vehicle.

According to the definition of TTC, the TTC value varies at each timestamp. To measure the safety level over a certain period, the aggregated TET and TIT are utilized to represent the time-aggregated crash risk, which can be calculated as:

$$TET\left(t\right)={{\displaystyle \sum }}_{i=1}^M{\delta }_t·\Delta t,{\delta }_t=\{\begin{array}{c}1, \forall 0<TT{C}_i\left(t\right)\le TT{C}^{*}\\ 0, else\end{array},$$

(23)

$$TET={{\displaystyle \sum }}_{t=1}^{TI}TET\left(t\right),$$

(24)

$$TIT\left(t\right)={{\displaystyle \sum }}_{i=1}^M\left[TT{C}^{*}-TT{C}_i\left(t\right)\right]·\Delta t,\forall 0<TT{C}_i\left(t\right)\le TT{C}^{*},$$

(25)

$$TIT={{\displaystyle \sum }}_{t=1}^{TI}TIT\left(t\right),$$

(26)

where ${\delta }_t$ represents the switching variable at time $t$; $\Delta t$ is the time step; $M$ denotes the number of involved vehicles; $TI$ is time interval; $TT{C}^{*}$ denotes the threshold of TTC to identify risky car-following situations from safe ones, which is set as 2 s following the previous studies [51,52,53].

It is possible that VSL control may increase the travel time and therefore deteriorate the efficiency, since relatively lower traffic flow speed would be obtained when implementing speed limits. In this study, the average total travel time (TTT) is also applied to quantify the travel efficiency for the proposed VSL strategy, which can be calculated as follows:

$$TTT=\frac{{{\displaystyle \sum }}_{i=1}^M{T}_i}{M},$$

(27)

where $T_i$ is the travel time of vehicle $i$.

4. Simulation Experiment Design

The simulation experiments are conducted based on Python since it is flexible to incorporate the various microscopic driving models and complex simulation parameter settings considered. Furthermore, using Python can save much time in rendering and animation compared with some simulation software, especially considering the heavy simulation workload for this study. As shown in Figure 2, a 9 km three-lane freeway section is established, and there is an on-ramp entrance at 6.5 km, forming a typical freeway bottleneck scenario [54]. The main lane is divided into nine basic sections by loop detectors spaced one kilometer apart. A total of 24 VMSs are deployed at the corresponding positions of 24 (8 × 3) loop detectors in the upstream, while loop detectors are only used to collect traffic flow data. A low-speed driving zone is set up after the 8.5 km section. The established roadway would provide a generalized testing background for VSL strategy evaluation. Conversely, the proposed VSL method can be easily adapted to similar real-world roadway sections if relevant high-resolution data such as roadway geometry are available.

The simulation experiments are then conducted to examine the safety performance and efficiency performance of the proposed VSL control strategy. It is also assumed that HDVs and CAVs will comply with the posted speed limits. The VSL strategy is tested with the assumed situation to demonstrate the optimal performance and greatest potential for safety improvements. The average safe time gap is set to be 1.1, 1.6 and 2.2 s. The same average safety gap is set for HDVs and CAVs. There are two main reasons why the same gaps are set for HDVs and CAVs. First, the average safety gap may have a significant impact on the safety performance of VSL. Hence, this parameter should be controlled when evaluating VSL strategies and different CAVs market penetration rates. Otherwise, it is hard to identify whether the safety improvements are because of the VSL or the increment of CAV MPR. Second, CAVs platoon with smaller safety gaps in the mainstream will prevent the ramp vehicles from merging into the mainstream, leading to a queue on the ramp. The traffic may be re-organized for some critical areas, such as the typical freeway bottlenecks. The CAVs may simulate human driver and follows the same driving behavior as HDVs to ensure the normal operation of critical road sections. The initial speed of individual vehicles is set to be 30 m/s. Vehicles are expected to slow down their operating speed to 5 m/s when reaching the low-speed area at the freeway bottleneck. The leading vehicle brakes to the preset bottleneck speed and hence forms a shock wave propagating back upstream. Six market penetration rates are tested, i.e., 0%, 10%, 20%, 30%, 40%, and 50%, which ensure that HDVs still dominate in the mixed traffic flow. Each single simulation run ends up when the last car passes through the low-speed area, with the first 5 minutes taken as the warm-up period. Excluding the warm-up period, the average simulation length for an individual simulation run is about 1.5 hours in this study. Other parameter settings are presented in

Table 1. Parameter settings of simulation experiments.

Parameter	Meaning	Value
		HDV	CAV
$d$ (m)	Sight distance	100	100
$\beta$ (m/s2)	Desire deceleration	2	2
$t_a$ (s)	Perception–reaction time	1	0
$\overline{L}$ (m)	Average vehicle length	5	5
${\alpha }_m$ (m/s2)	Max acceleration	1	1
$v_0$ (m/s)	Desire speed	30	30
$s_0$ (m)	Minimum gap at standstill	0	0
$T$ (s)	Safe time gap	1.1, 1.6, 2.2	1.1, 1.6, 2.2
$\mathsf{\Delta }T$ (s)	Data aggregation interval	30	30
$\Delta t$ (s)	Simulation step	0.1	0.1
$p_{alt}$	Altruistic factor	0	1
$\Delta a$	Lane changing threshold	1	1
$a_{bias}$	Asymmetric lane changing parameter	0	0

, which are selected based on previous studies [39,42,51,52]. Note that a more specific scenario is defined by three factors, including the three VSL implementations, three different average safety gaps and six CAV market penetration rates. For each specific scenario, ten individual simulation runs are repeated with different random seeds to obtain an average performance of VSL implementation. Therefore, the total time of simulation for each VSL scenario is equal to 180 times (3 average safety gaps × 6 CAV MPR × 10 repeated runs = 180).

5. Simulation Results and Discussions

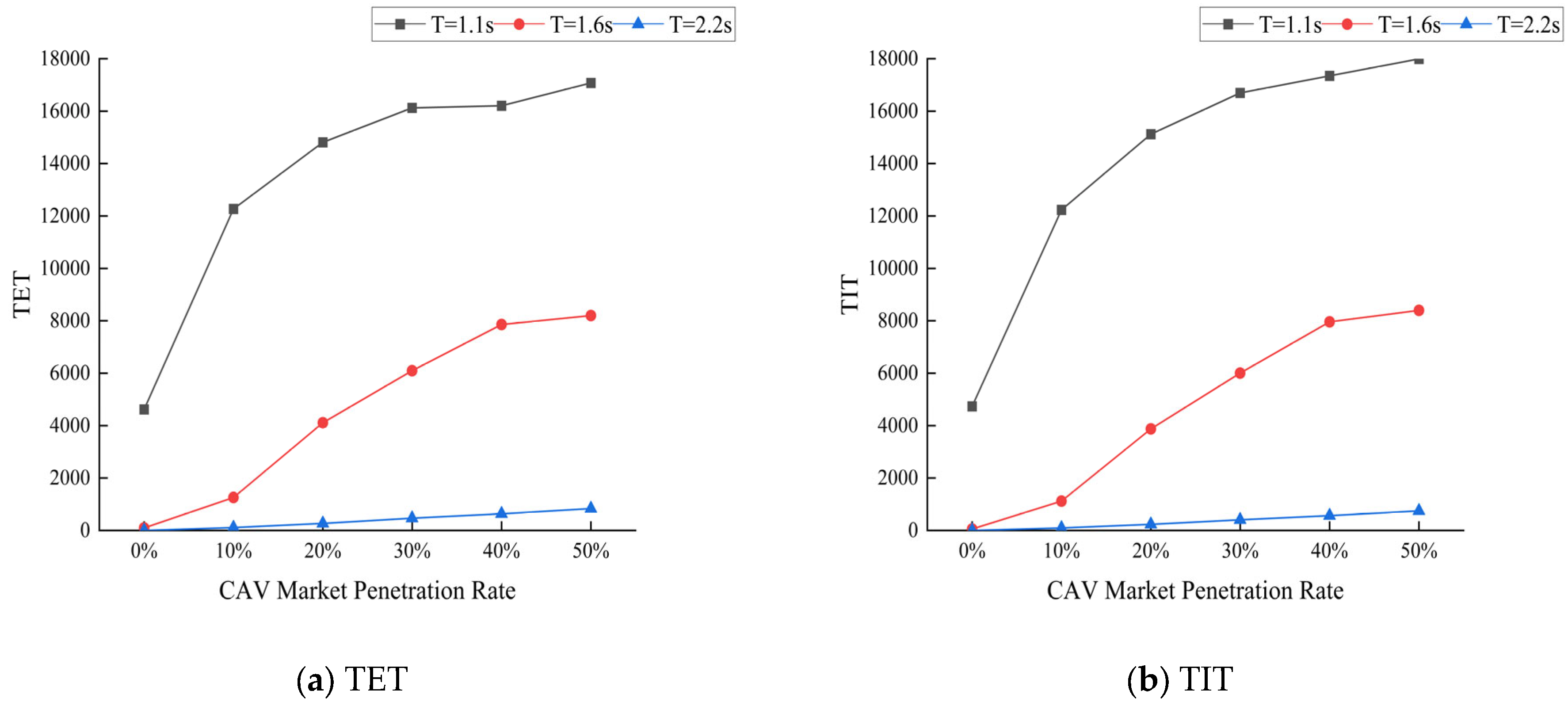
5.1. The Influence of Safe Time Gap

In this section, the impacts of different safe time gaps under the VSL control are investigated. Three types of safe time gap commonly used by commercial ACC are selected, which are 1.1, 1.6 and 2.2 s. In each set of experiments, the time gap of HDV and CAV is set to be equal to avoid the influence of the time gap difference on the experimental results. Simulation experiments are conducted under different CAV market penetration rates, and the results are shown in Figure 3. The TET and TIT values decrease significantly with the increase in safe time gap under different CAV market penetration rates, indicating that the increasing time gap can effectively reduce the rear-end collision risks. The TET and TIT values increase with the increase in CAVs MPR. The underlying causes of this phenomenon can be explained from two aspects:

(1)

Most of the CAVs will be downgraded to ACC ones in the situation of low CAV market penetration rates. Assuming that the market penetration rate of CAV is $\rho$, the market penetration rate of human-driven vehicles is (1 − $\rho$ ). Then, the theoretical probability of CAV operating in CACC mode is $\rho \ast \rho$ and that in ACC mode is $\rho \ast \left(1-\rho \right)$. When $\rho <50\%$, the theoretical probability of CAV vehicles operating in ACC mode increases with the rise of CAV MPR. Meanwhile, it has been proven that the ACC vehicles are unstable, amplifying the speed variations of preceding vehicles [42];

(2)

The initial equilibrium formulas of CAVs and HDVs are shown as follows:

$$h_{HDV}=\frac{v_0{}^{2}vT}{\sqrt{v_0{}^4-v^4}}+L,$$

(28)

$$h_{CAV}=vT+L,$$

(29)

where $h_{HDV}$ represents the headway that should be maintained between the car-following pair when the following vehicle is manually driven; $h_{CAV}$ represents the headway that should be maintained between the car-following pair in steady-state when the following vehicle is CAV.

As for $\frac{v_0{}^2}{\sqrt{v_0{}^4-v^4}}$>1, which means $h_{HDV}>h_{CAV}$, the larger the distance between the car-following pair in steady state, the smaller the disturbance to the main-lane vehicles will be when the on-ramp vehicle merges. When the on-ramp vehicle merges between two consecutive CAVs, there will form a drastic shocking wave, which has a negative impact on the safety level of the main-lane vehicles. If the on-ramp vehicle is HDV, it will further cause degradation of CAV and the formation of a more intense shocking wave. Therefore, with the increase in CAV MPR, the value of surrogate safety measures rises.

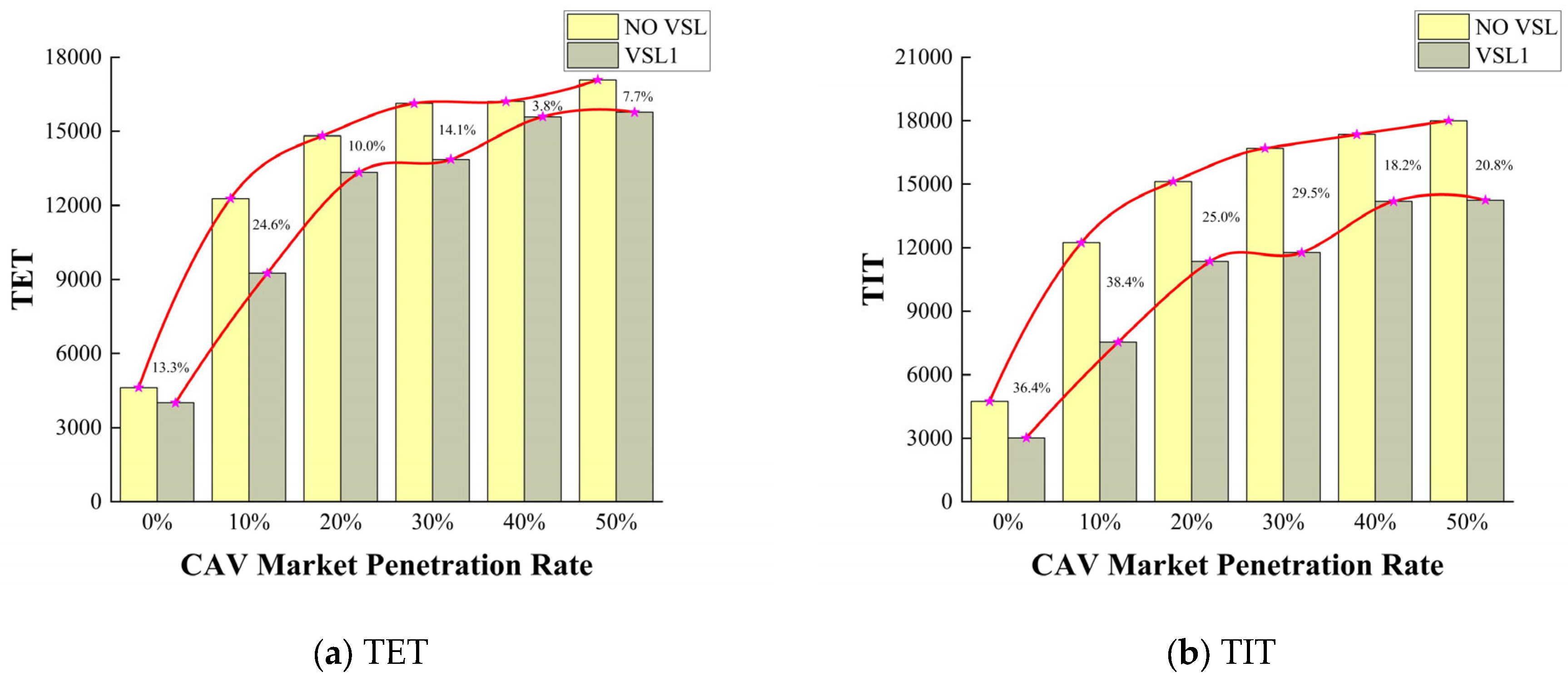
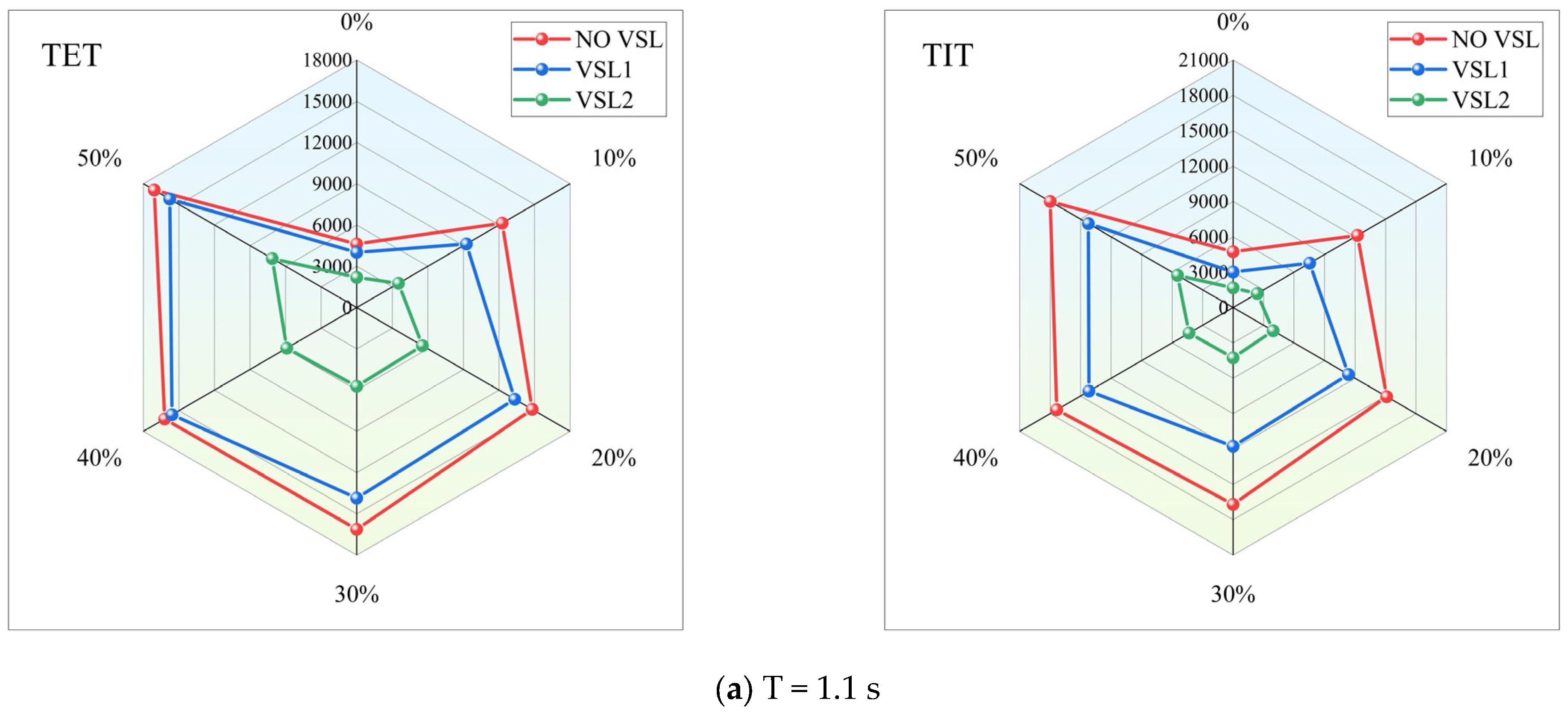
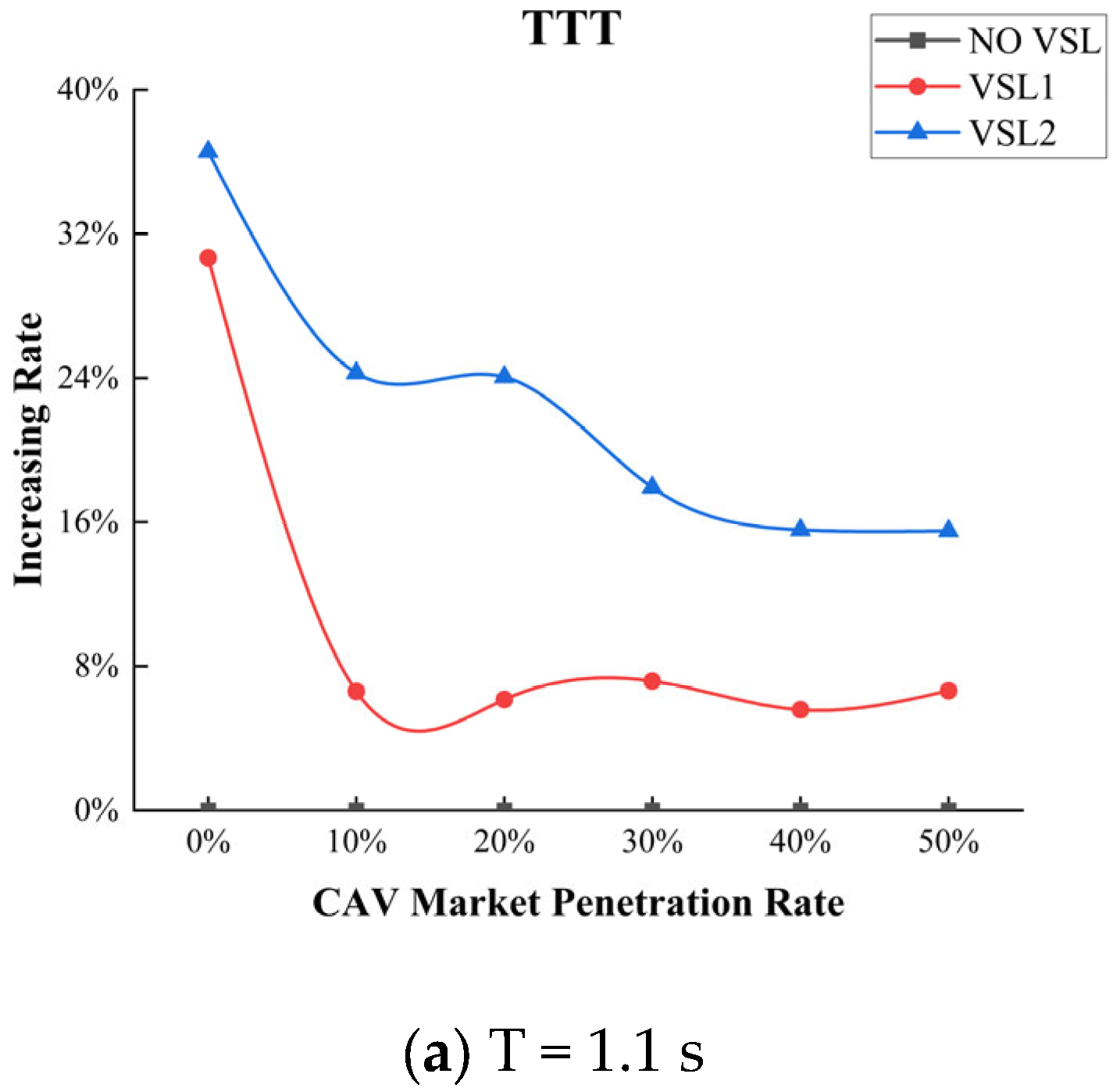
5.2. The Performance of VSL Control Strategy Derived from Secondary Collision Risks Reduction Strategy

In this section, the safety improvement performance of the VSL control strategy (VSL1) derived from secondary collision risks reduction [14] was tested for comparison. The safe time gaps of HDVs and CAVs are both set as 1.1 s. First, the simulations are conducted in scenarios without VSL control and with 0% CAV MPR. The results are used as the benchmark. Then, the safety performances with and without VSL control are further tested at different CAV MPRs. The simulation results are shown in Figure 4. Six different CAV MPRs are tested in the simulation, ranging from 0% to 50%, with an interval of 10%. The safety performance of VSL1 control is improved to a certain extent in the scenario of all HDVs when compared with that of no VSL control, and the TET and TIT values are decreased by 13.3% and 36.4%, respectively. When the CAV MPR is 50%, the values of TET and TIT are reduced by 7.7% and 20.8%, respectively. Furthermore, with the VSL1 control, the values of TET and TIT are decreased by 12.2% and 28.0% on average, respectively, with the CAV MPRs ranging from 0% to 50%. The aforementioned results indicate that the safety improvement performance of VSL1 is quite limited.

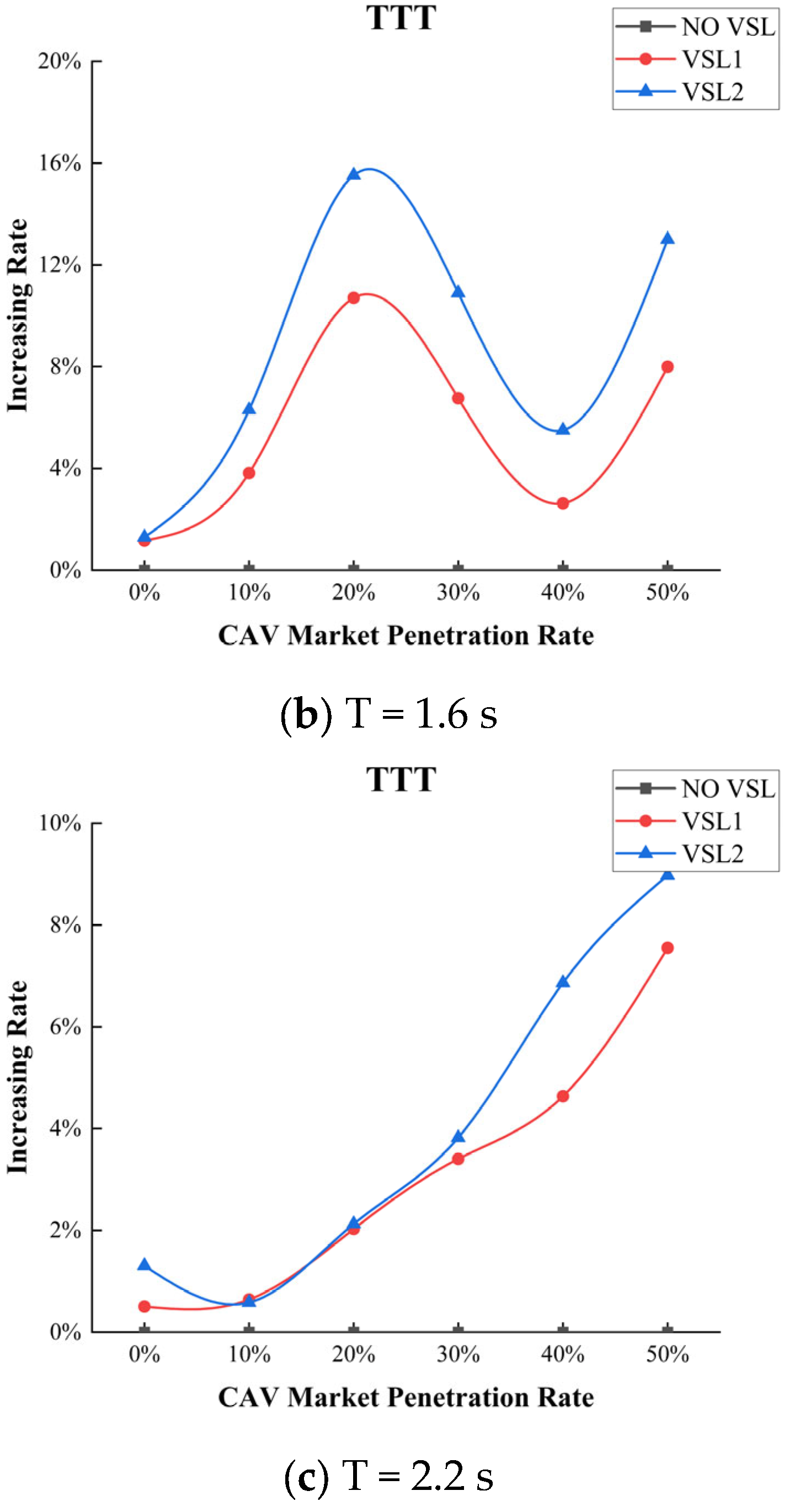
5.3. The Performance of VSL Control Strategy Derived from Collision Avoidance Theory

This section compares the performance of the VSL1 control strategy derived from secondary collision risks reducing in the previous study [15] and the proposed VSL control strategy based on collision avoidance theory in this study (VSL2). Figure 5 shows results of two sets of VSL control strategies. When T = 1.1 s, the average decreasing rates of TET and TIT under different CAV market penetration rates are 12.2% and 28.0% for VSL1, and the average decreasing rates of TET and TIT are 62.1% and 73.1% for VSL2. Similarly, when T = 1.6 s, the average decreasing rates of TET and TIT for VSL1 are 58.3%, 69.7%, respectively, and 64.8% (TET), 73.3% (TIT) for VSL2. When T = 2.2 s, the average decreasing rates of TET and TIT for VSL1 are 56.4%, 68.9% and 64.0% (TET), 73.1% (TIT) for VSL2. It can be found that under different safe time gaps, the two control strategies can improve freeway safety, and the VSL2 control strategy has a better safety improvement effect than the VSL1 control strategy. It can also be observed that the safe time gap will affect the TIT and TET value and the safety improvement magnitude of the VSL control strategy. With the increase in safe time gap, the safety improvement of the VSL2 control strategy weakens since the larger gap provides a safer traffic environment.

Figure 6 shows the comparison results of efficiency evaluation indexes of two sets of VSL control strategies with different CAV market penetration rates. NO-VSL serves as a benchmark for evaluating the impacts of the proposed VSL strategies on travel efficiency. The vertical axes represent the increment rate of TTT compared to NO-VSL for better observing the efficiency changes. The curves of NO-VSL are overlapped with the x-axis. When T = 1.1 s, the average increasing proportion of total travel time (TTT) with VSL1 and VSL2 control strategies is about 10.5% and 22.3%, respectively. When T = 1.6 s, the average increasing rate of TTT is about 5.5% and 8.8%, respectively. When T = 2.2 s, the average increasing rate of TTT is about 3.1% and 4.0% for the two sets of VSL control strategies under different CAV market penetration rates. The VSL2 control strategy significantly improves the level of road safety compared with the VSL1 control strategy, but it also increases the total travel time. However, in terms of its safety improvements, the increase in travel times is still within an acceptable level. In general, the VSL2 control strategy proposed in this study has better comprehensive performance and can effectively reduce the risk of rear-end collisions near freeway bottlenecks.

6. Conclusions

Admittedly, there is still a long way to go before full automation and a high market penetration rate of CAVs. In the current stage, CAVs have a considerable number of technical and safety issues to be resolved, for example, robust perception and prediction, data security and network security. These issues will also exist in the foreseeable future. Consequently, it is believed that the mixed flow of CAVs and HDVs will occur in the near future and will last for the long term instead of a fast transition to the transportation system with a high CAVs market penetration rate. Considering the traffic management system in the foreseeable future, there is an urgent need to investigate the proactive traffic control strategy under different CAV MPRs. This study developed a control strategy of VSL to reduce the rear-end collision risk near freeway bottlenecks considering a mixed traffic flow. Four microscopic car-following models, one lane-changing model and VSL based on the microscopic collision avoidance theory are considered to try to provide a dynamic driving process close to real traffic conditions. The simulation experiments including scenarios and parameter settings are carefully designed following previous studies. More specifically, the occurrence condition of rear-end collision based on the classical car-following model IDM was first analyzed. Then, a reliable VSL control strategy was proposed to dynamically adjust the speed limits based on collision avoidance theory, and it was further compared with the previous one based on secondary collision risk reduction. Surrogate safety measures including TTC, TET, TIT, and efficiency evaluation index TTT were used to evaluate the safety performance and efficiency performance of VSL control strategy. Scenarios with different safe time gaps and CAVs MPR were considered in the simulation experiments. Meanwhile, the two VSL control strategies are also compared in the above scenarios.

According to the experimental results, the VSL control strategy proposed in this study can effectively improve the safety performance near freeway bottlenecks at an acceptable efficiency level. The proposed VSL control strategy based on the theory of car-following collision avoidance shows good performance in the dynamic driving scenarios considering car following and lane changing. However, there are still many issues that need to be addressed. First, the rear-end collision risk caused by the small steady-state car-following gap of CAV in the on-ramp scenario should be avoided by applying reasonable control strategies. Second, modeling compliance to speed limit is an interesting and important topic for VSL studies. Future works can consider heterogeneous compliance of drivers for VSL strategy evaluation at the initial stage of CAV popularization when the compliance distribution can be obtained. It is also believed that developing VSL strategies that consider the heterogeneous behaviors regarding car following and lane changing specific to the freeway section will be a promising research direction. One viable way to consider this might be to first obtain the high-resolution trajectory data specific to a road section by drones and then calibrate the car-following models and lane-changing models based on the real-world trajectory data. Furthermore, the degradation of CAVs in mixed flow is also worth further study. The authors recommend these issues as future directions for follow-up studies.