Unbiased Identification of Fractional Order System with Unknown Time-Delay Using Bias Compensation Method
Abstract
:1. Introduction
2. Preliminaries
2.1. Fractional Order Differentiation
2.2. Fractional Order System with Time-Delay Description
2.3. Problem Formulation
3. Fractional Order System Identification
3.1. Compensation for Measurement Noises Existing in the Output Signal
Convergence Analysis
3.2. Output Error Method for Fractional Order System with Unknown Time-Delay (FOSTD-OE)
| Algorithm 1 algorithm |
Data, Maximum number of iteration.
|
4. Numerical Example
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cois, O.; Oustaloup, A.; Poinot, T.; Battaglia, J. Fractional state variable filter for system identification by fractional model. In Proceedings of the European Control Conference (ECC), Porto, Portugal, 4–7 September 2001; pp. 2481–2486. [Google Scholar]
- Peng, C.; Li, W.; Wang, Y. Frequency domain identification of fractional order time delay systems. In Proceedings of the 2010 Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010; pp. 2635–2638. [Google Scholar]
- Valério, D.; Sá da Costa, J. Identifying digital and fractional transfer functions from a frequency response. Int. J. Control 2011, 84, 445–457. [Google Scholar] [CrossRef]
- Raïssi, T.; Aoun, M. On robust pseudo state estimation of fractional order systems. In Proceedings of the International Symposium on Positive Systems, Rome, Italy, 14–16 September 2016; pp. 97–111. [Google Scholar]
- Yakoub, Z.; Naifar, O.; Amairi, M.; Chetoui, M.; Aoun, M.; Makhlouf, A.B. A Bias-Corrected Method for Fractional Linear Parameter Varying Systems. Math. Probl. Eng. 2022, 2022, 7278157. [Google Scholar] [CrossRef]
- Naifar, O.; Ben Makhlouf, A. On the stabilization and observer design of polytopic perturbed linear fractional-order systems. Math. Probl. Eng. 2021, 2021, 6699756. [Google Scholar] [CrossRef]
- Oustaloup, A.; Sabatier, J.; Lanusse, P.; Malti, R.; Melchior, P.; Moreau, X.; Moze, M. An overview of the CRONE approach in system analysis, modeling and identification, observation and control. IFAC Proc. Vol. 2008, 41, 14254–14265. [Google Scholar] [CrossRef] [Green Version]
- Reyes-Melo, M.; Martinez-Vega, J.; Guerrero-Salazar, C.; Ortiz-Mendez, U. Modelling of relaxation phenomena in organic dielectric materials. Application of differential and integral operators of fractional order. J. Optoelectron. Adv. Mater. 2004, 6, 1037–1044. [Google Scholar]
- Jallouli-Khlif, R.; Jelassi, K.; Melchior, P.; Trigeassou, J.C. Fractional modeling of rotor skin effect in induction machines. In Proceedings of the 4th IFAC Workshops on Fractional Differentiation and its Applications (IFAC FDA’10), Badajoz, Spain, 18–20 October 2010. [Google Scholar]
- Jin, B.; Kian, Y. Recovery of the order of derivation for fractional diffusion equations in an unknown medium. SIAM J. Appl. Math. 2022, 82, 1045–1067. [Google Scholar] [CrossRef]
- Krasnoschok, M.; Pereverzyev, S.; Siryk, S.V.; Vasylyeva, N. Regularized reconstruction of the order in semilinear subdiffusion with memory. In Proceedings of the International Conference on Inverse Problems, Shanghai, China, 12–14 October 2018; Springer: Singapore, 2018; pp. 205–236. [Google Scholar]
- Krasnoschok, M.; Pereverzyev, S.; Siryk, S.V.; Vasylyeva, N. Determination of the fractional order in semilinear subdiffusion equations. Fract. Calc. Appl. Anal. 2020, 23, 694–722. [Google Scholar] [CrossRef]
- Gu, W.; Wei, F.; Li, M. Parameter estimation for a type of fractional diffusion equation based on compact difference scheme. Symmetry 2022, 14, 560. [Google Scholar] [CrossRef]
- Zaborovsky, V.; Meylanov, R. Informational network traffic model based on fractional calculus. In Proceedings of the 2001 International Conferences on Info-Tech and Info-Net. Proceedings (Cat. No. 01EX479), Beijing, China, 29 October–1 November 2001; Volume 1, pp. 58–63. [Google Scholar]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J.H. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Dalir, M.; Bashour, M. Applications of fractional calculus. Appl. Math. Sci. 2010, 4, 1021–1032. [Google Scholar]
- Sabatier, J.; Aoun, M.; Oustaloup, A.; Gregoire, G.; Ragot, F.; Roy, P. Fractional system identification for lead acid battery state of charge estimation. Signal Process. 2006, 86, 2645–2657. [Google Scholar] [CrossRef]
- Victor, S.; Malti, R.; Garnier, H.; Oustaloup, A. Parameter and differentiation order estimation in fractional models. Automatica 2013, 49, 926–935. [Google Scholar] [CrossRef]
- Battaglia, J.L.; Le Lay, L.; Batsale, J.C.; Oustaloup, A.; Cois, O. Utilisation de modèles d’identification non entiers pour la résolution de problèmes inverses en conduction. Int. J. Therm. Sci. 2000, 39, 374–389. [Google Scholar] [CrossRef]
- Malti, R.; Victor, S.; Oustaloup, A.; Garnier, H. An optimal instrumental variable method for continuous-time fractional model identification. IFAC Proc. Vol. 2008, 41, 14379–14384. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Yuan, S.; Yin, C. A lithium-ion battery fractional order state space model and its time domain system identification. In Proceedings of the FISITA 2012 World Automotive Congress; Springer: Berlin/Heidelberg, Germany, 2013; pp. 795–805. [Google Scholar]
- Yakoub, Z.; Amairi, M.; Chetoui, M.; Aoun, M. On the Closed-Loop System Identification with Fractional Models. Circuits Syst. Signal Process. 2015, 34, 3833–3860. [Google Scholar] [CrossRef]
- Mani, A.K.; Narayanan, M.; Sen, M. Parametric identification of fractional-order nonlinear systems. Nonlinear Dyn. 2018, 93, 945–960. [Google Scholar] [CrossRef]
- Zhang, B.; Tang, Y.; Zhang, J.; Lu, Y. Coefficients and Orders Identification of Fractional Order Systems Based on Block Pulse Functions Through Two-Stage Algorithm. J. Dyn. Syst. Meas. Control 2022, 144, 071001. [Google Scholar] [CrossRef]
- Narang, A.; Shah, S.L.; Chen, T. Continuous-time model identification of fractional-order models with time delays. IET Control Theory Appl. 2011, 5, 900–912. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Cheng, P.; Wang, Y. Frequency domain subspace identification of commensurate fractional order input time delay systems. Int. J. Control Autom. Syst. 2011, 9, 310–316. [Google Scholar] [CrossRef]
- Liao, Z.; Peng, C.; Wang, Y. A frequency-domain identification algorithm for MIMO fractional order systems with time-delay in state. In Advanced Materials Research; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2012; Volume 383, pp. 4397–4404. [Google Scholar]
- Zhuting, Z.; Zeng, L.; Shu, L.; Cheng, P.; Yong, W. Subspace-based identification for fractional order time delay systems. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 2019–2023. [Google Scholar]
- Ahmed, S. Parameter and delay estimation of fractional order models from step response. IFAC-PapersOnLine 2015, 48, 942–947. [Google Scholar] [CrossRef]
- Tang, Y.; Li, N.; Liu, M.; Lu, Y.; Wang, W. Identification of fractional-order systems with time delays using block pulse functions. Mech. Syst. Signal Process. 2017, 91, 382–394. [Google Scholar] [CrossRef]
- Gao, Z.; Lin, X.; Zheng, Y. System identification with measurement noise compensation based on polynomial modulating function for fractional-order systems with a known time-delay. ISA Trans. 2018, 79, 62–72. [Google Scholar] [CrossRef] [PubMed]
- Moghaddam, M.J.; Mojallali, H.; Teshnehlab, M. Recursive identification of multiple-input single-output fractional-order Hammerstein model with time delay. Appl. Soft Comput. 2018, 70, 486–500. [Google Scholar] [CrossRef]
- Kothari, K.; Mehta, U.; Vanualailai, J. A novel approach of fractional-order time delay system modeling based on Haar wavelet. ISA Trans. 2018, 80, 371–380. [Google Scholar] [CrossRef]
- Alagoz, B.B.; Tepljakov, A.; Ates, A.; Petlenkov, E.; Yeroglu, C. Time-domain identification of one noninteger order plus time delay models from step response measurements. Int. J. Model. Simul. Sci. Comput. 2019, 10, 1941011. [Google Scholar] [CrossRef]
- Hashemniya, F.; Tavakoli-Kakhki, M.; Azarmi, R. Coefficients and Delay Estimation of the General Form of Fractional Order Systems Using Non-Ideal Step Inputs. IFAC-PapersOnLine 2020, 53, 590–597. [Google Scholar] [CrossRef]
- Sin, M.H.; Sin, C.; Ji, S.; Kim, S.Y.; Kang, Y.H. Identification of fractional-order systems with both nonzero initial conditions and unknown time delays based on block pulse functions. Mech. Syst. Signal Process. 2022, 169, 108646. [Google Scholar] [CrossRef]
- Yakoub, Z.; Chetoui, M.; Amairi, M.; Aoun, M. A bias correction method for fractional closed-loop system identification. J. Process Control 2015, 33, 25–36. [Google Scholar] [CrossRef]
- Lu, Y.; Tang, Y.; Zhang, X.; Wang, S. Parameter identification of fractional order systems with nonzero initial conditions based on block pulse functions. Measurement 2020, 158, 107684. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and Caputo derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef] [Green Version]
- Malti, R.; Aoun, M.; Sabatier, J.; Oustaloup, A. Tutorial on system identification using fractional differentiation models. In Proceedings of the 14th IFAC Symposium on System Identification, Newcastle, Australia, 29–31 March 2006; pp. 606–611. [Google Scholar]
- Ivanov, D.V.; Sandler, I.L.; Kozlov, E.V. Identification of fractional linear dynamical systems with autocorrelated errors in variables by generalized instrumental variables. IFAC-PapersOnLine 2018, 51, 580–584. [Google Scholar] [CrossRef]
- Ljung, L. System Identification—Theory for the User, 2nd ed.; PrenticeHall: Upper Saddle River, NJ, USA, 1999; Volume 101. [Google Scholar]
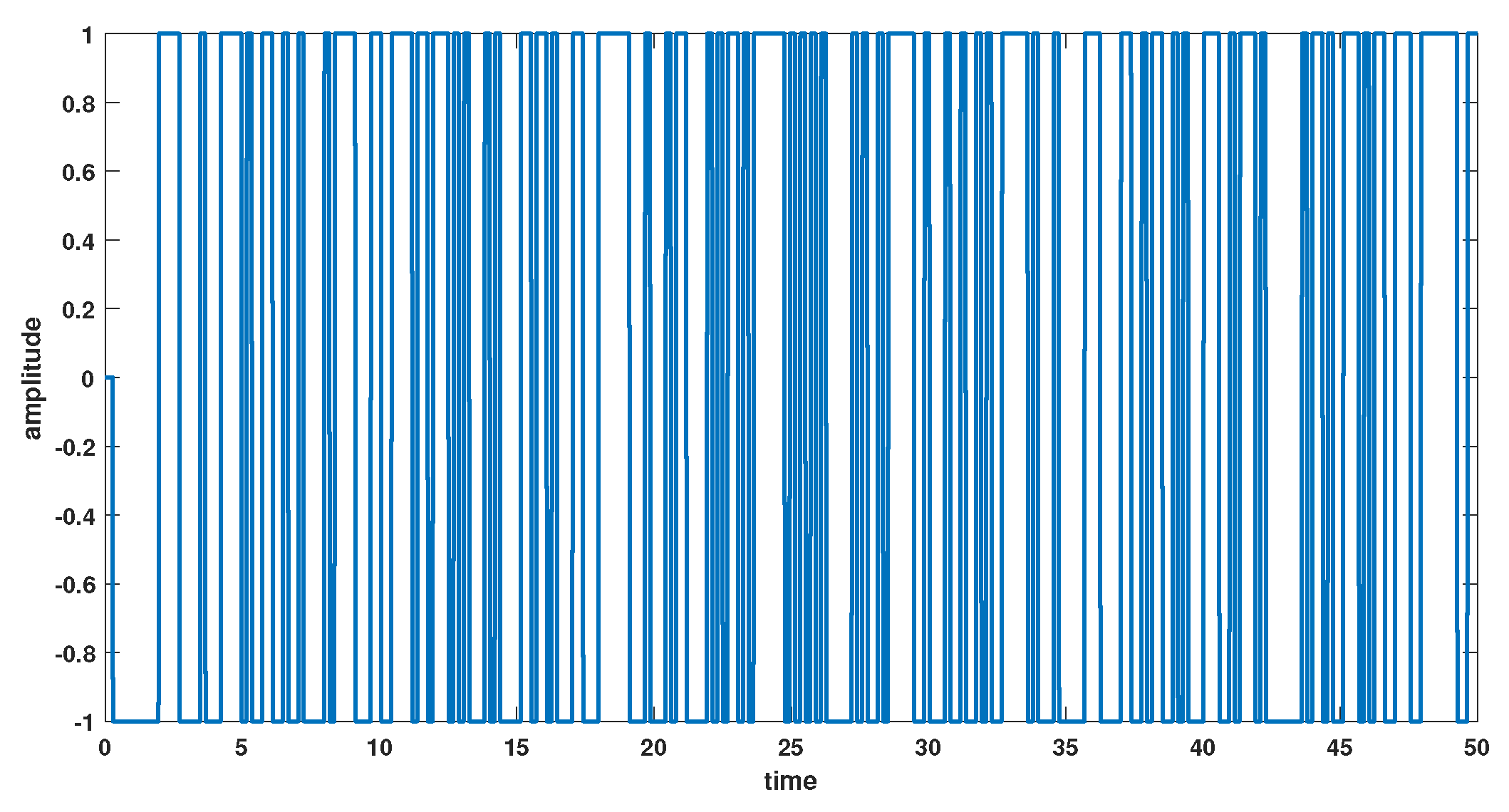
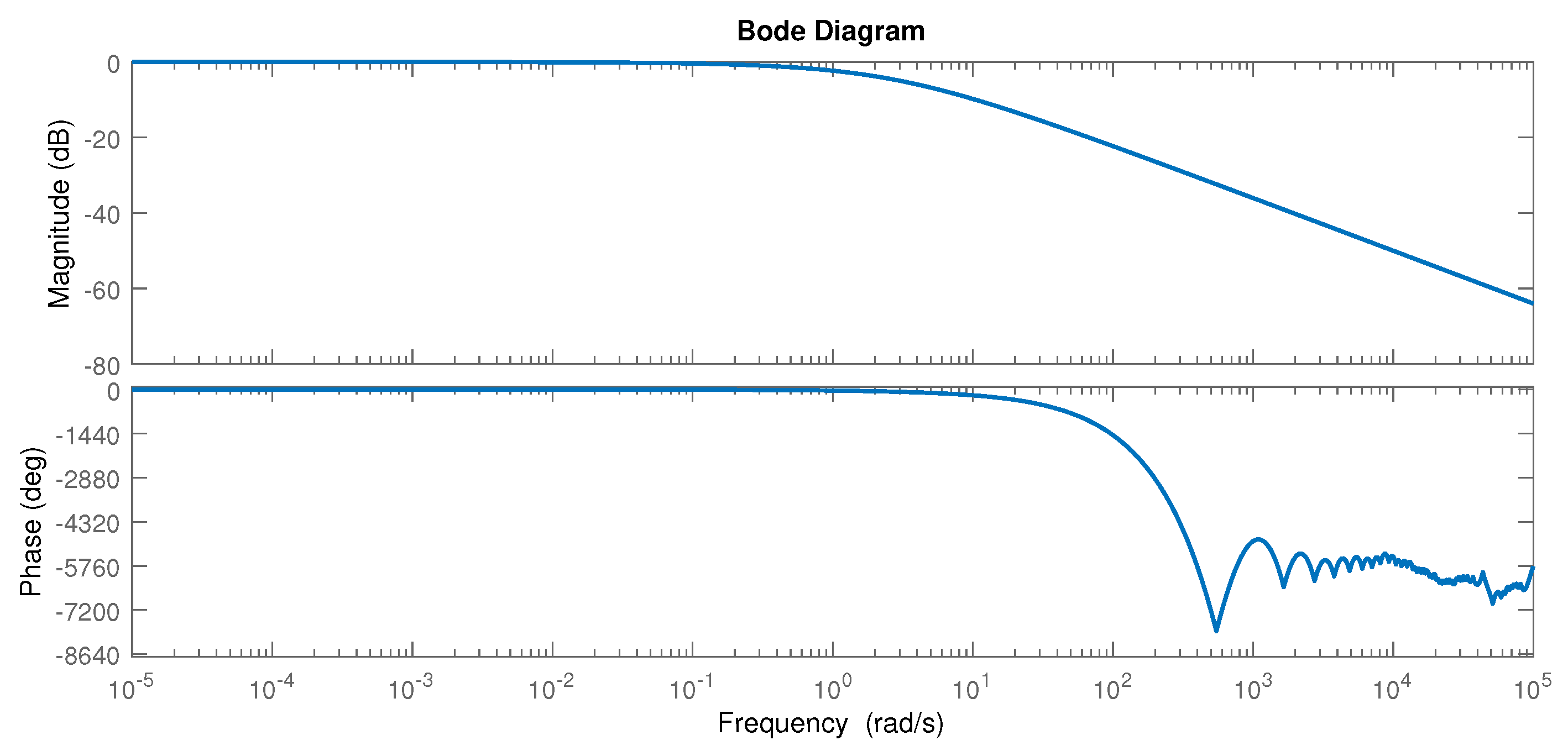
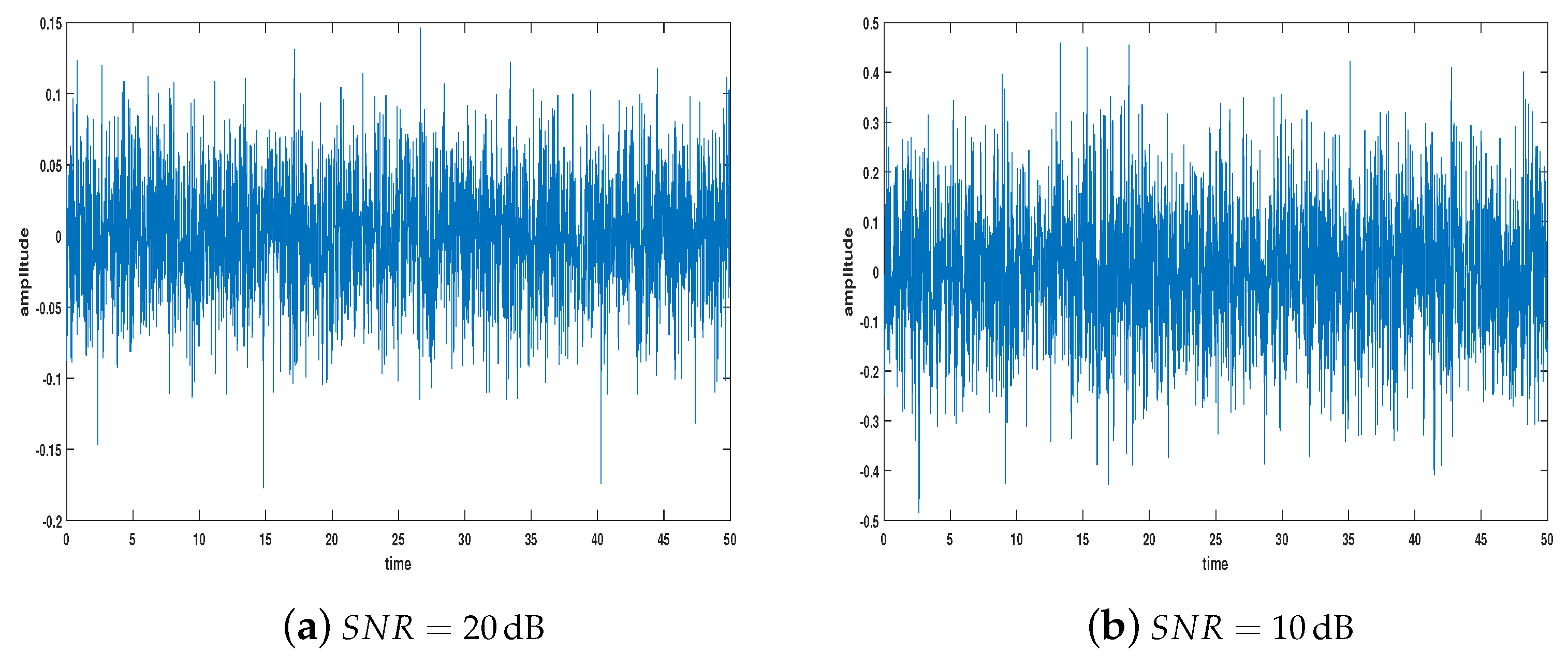
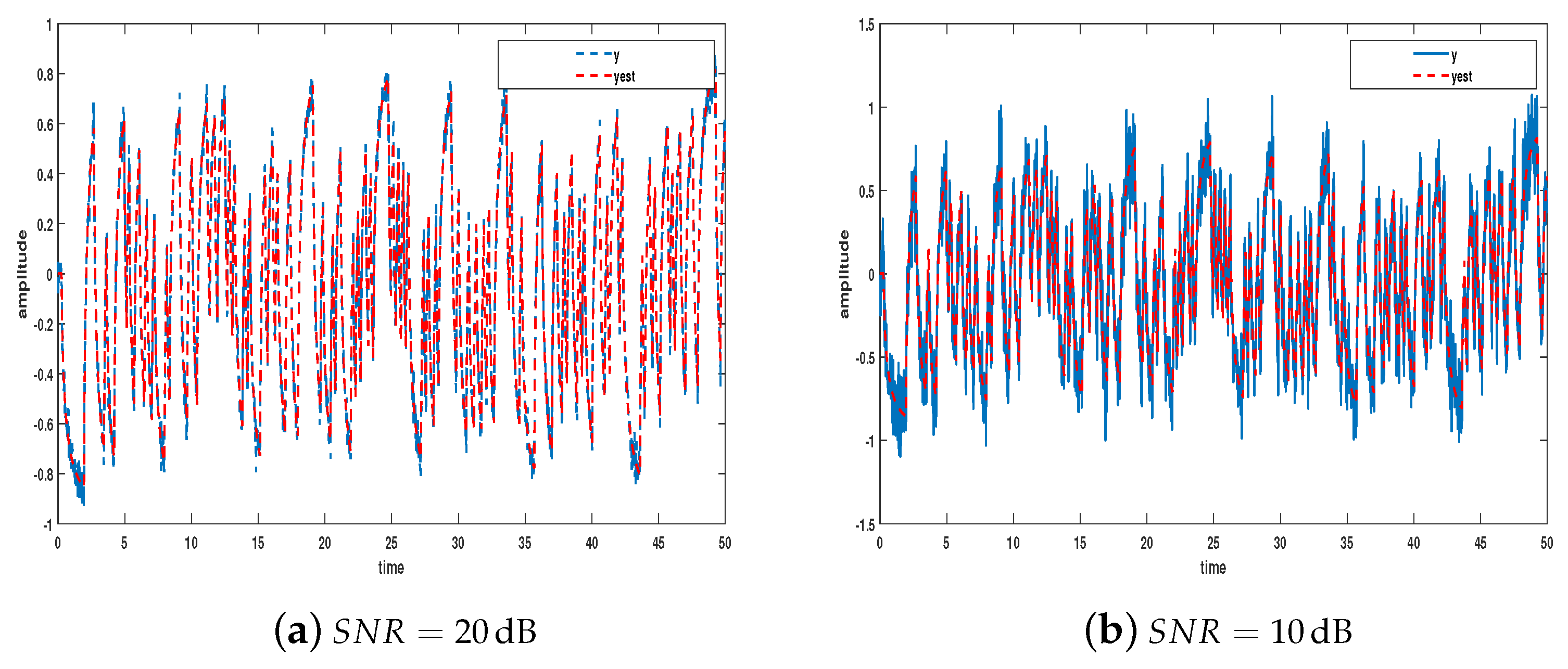
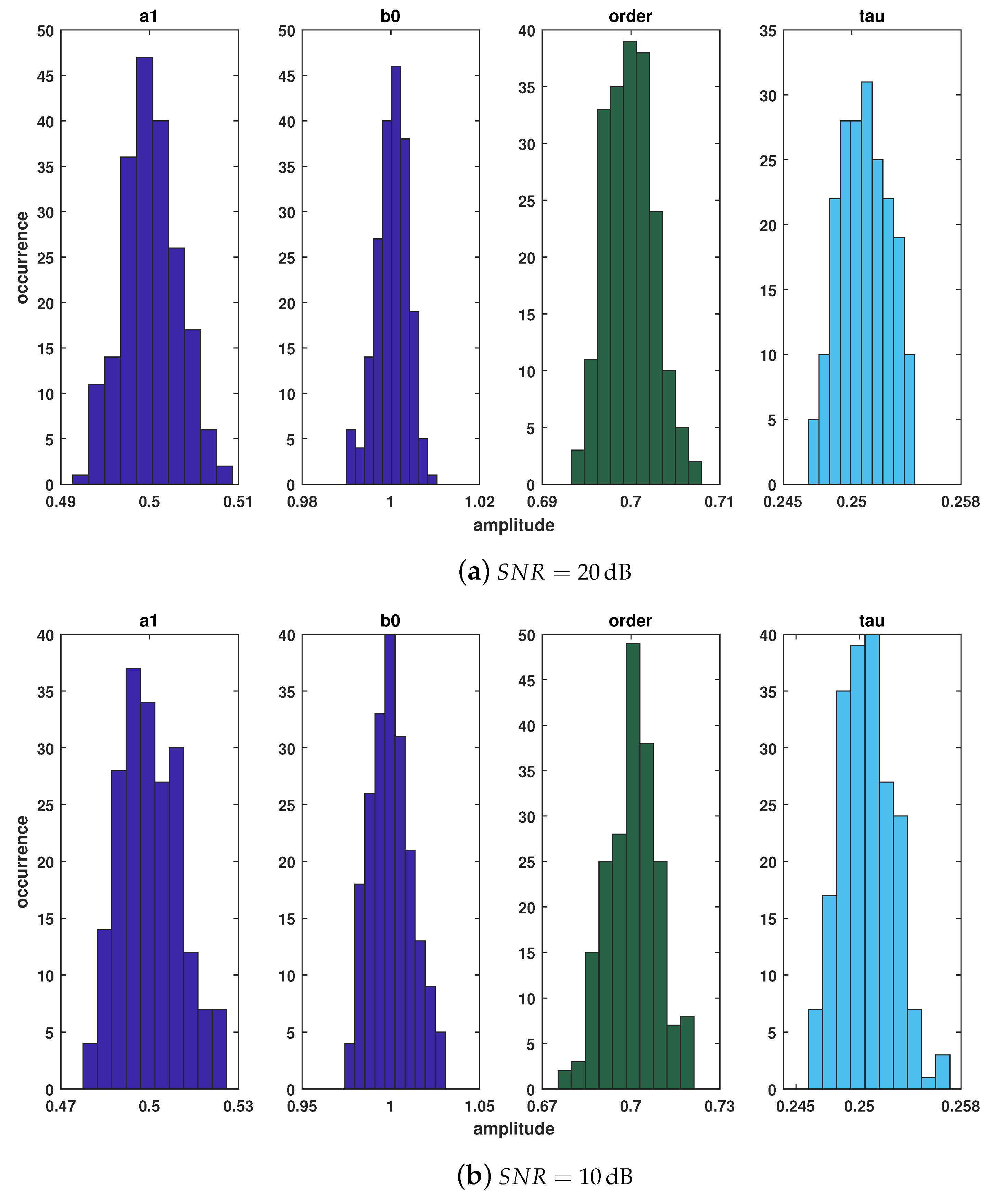


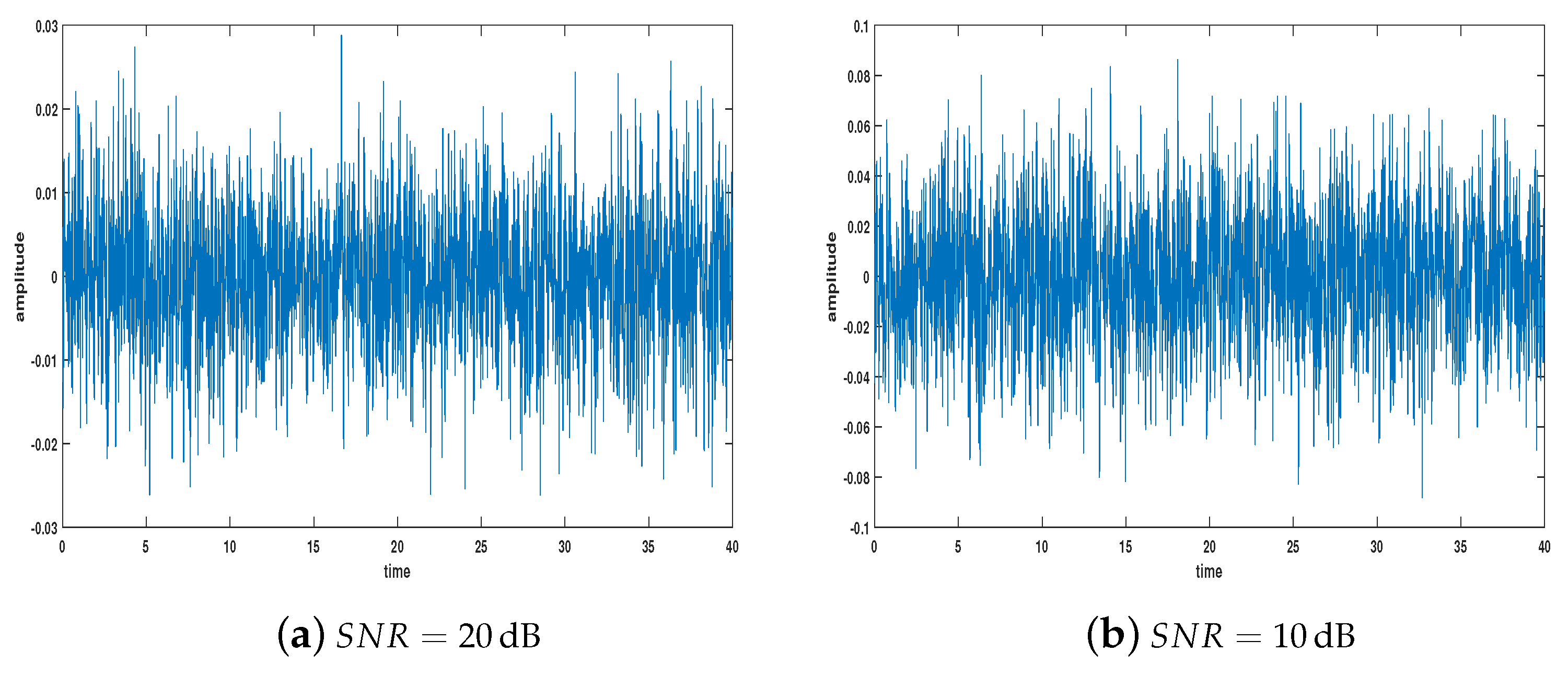
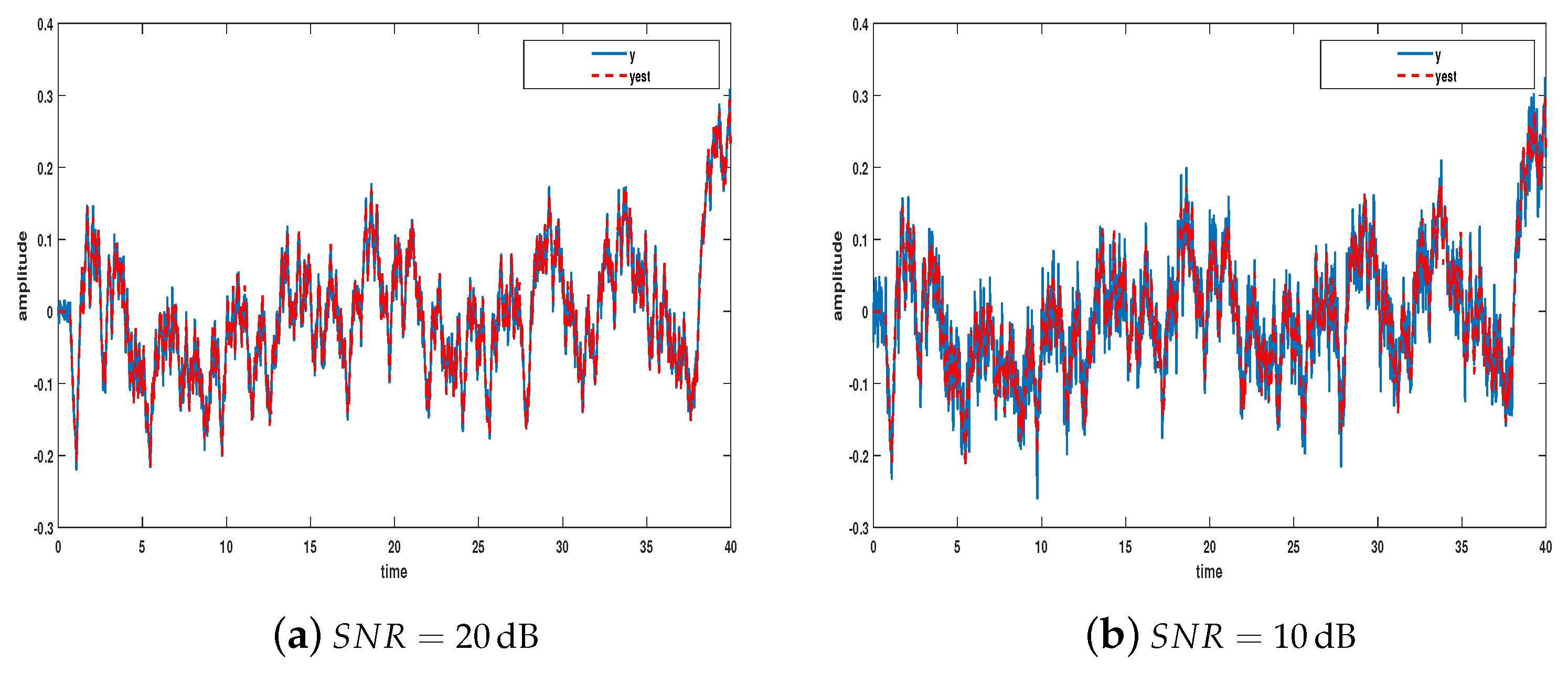
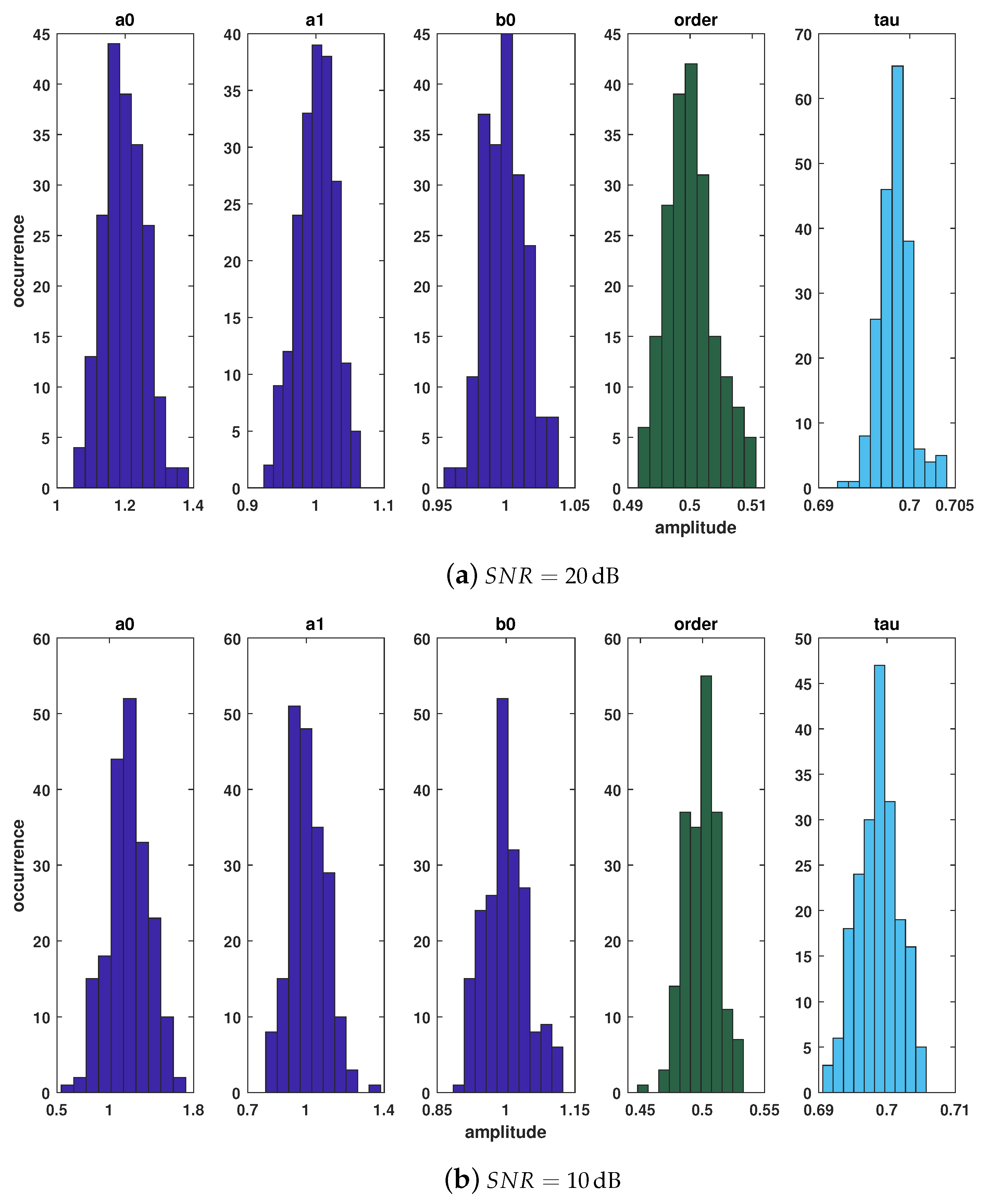
| [dB] | [dB] | ||
|---|---|---|---|
| [dB] | [dB] | |||
|---|---|---|---|---|
| Method | (%) | (%) | (%) | (%) |
| 0.0429 | 99.00 | 0.16 | 98.85 | |
| [dB] | [dB] | |
|---|---|---|
| [dB] | [dB] | |||
|---|---|---|---|---|
| Method | (%) | (%) | (%) | (%) |
| 0.340 | 98.92 | 0.540 | 96.02 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakoub , Z.; Naifar, O.; Ivanov, D. Unbiased Identification of Fractional Order System with Unknown Time-Delay Using Bias Compensation Method. Mathematics 2022, 10, 3028. https://doi.org/10.3390/math10163028
Yakoub Z, Naifar O, Ivanov D. Unbiased Identification of Fractional Order System with Unknown Time-Delay Using Bias Compensation Method. Mathematics. 2022; 10(16):3028. https://doi.org/10.3390/math10163028
Chicago/Turabian StyleYakoub , Zaineb, Omar Naifar, and Dmitriy Ivanov. 2022. "Unbiased Identification of Fractional Order System with Unknown Time-Delay Using Bias Compensation Method" Mathematics 10, no. 16: 3028. https://doi.org/10.3390/math10163028






