A Refined Closed-Form Solution for Laterally Loaded Circular Membranes in Frictionless Contact with Rigid Flat Plates: Simultaneous Improvement of Out-of-Plane Equilibrium Equation and Geometric Equation
Abstract
:1. Introduction
2. Membrane Equations and Its Solution
3. Results and Discussion
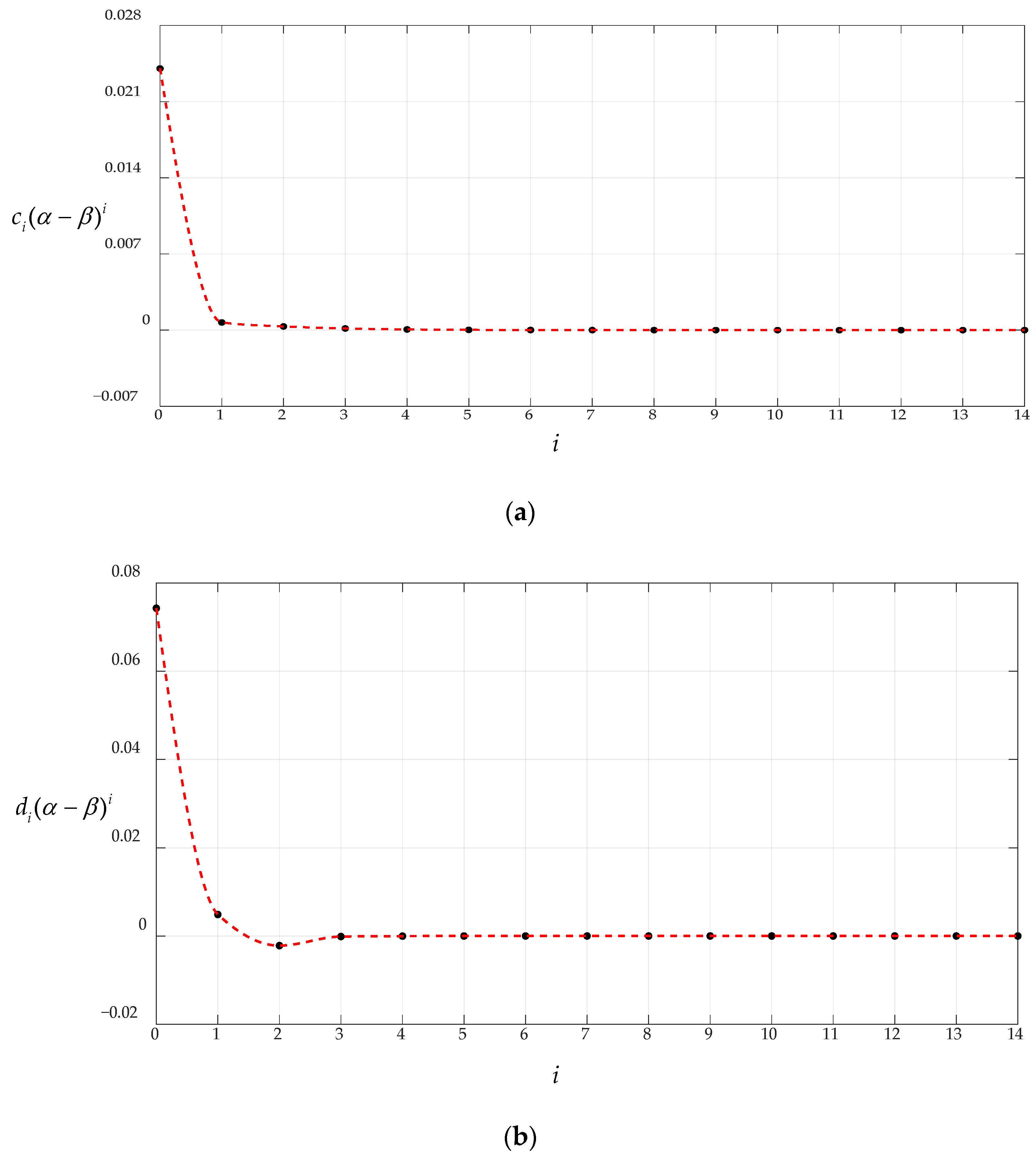
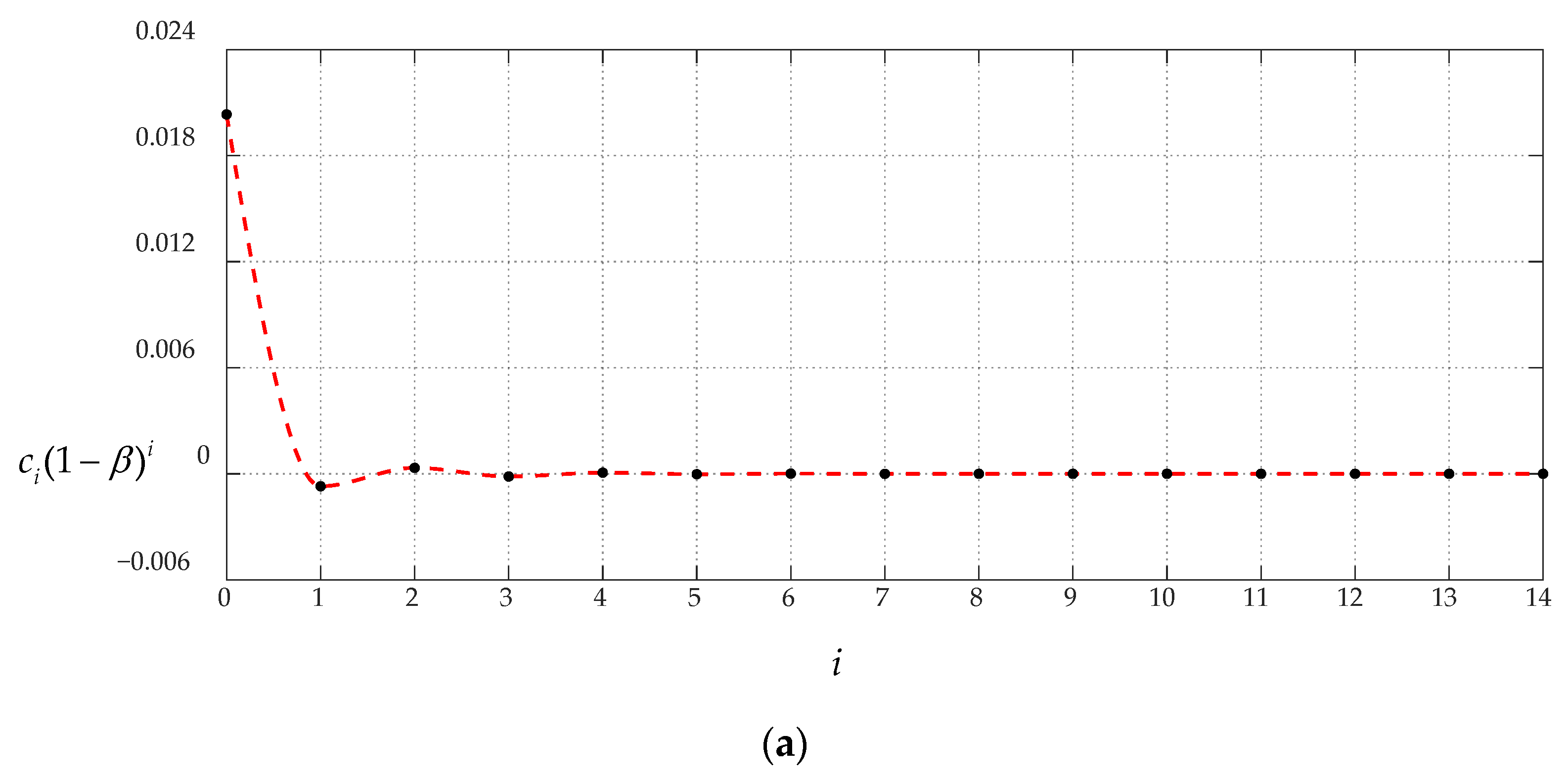
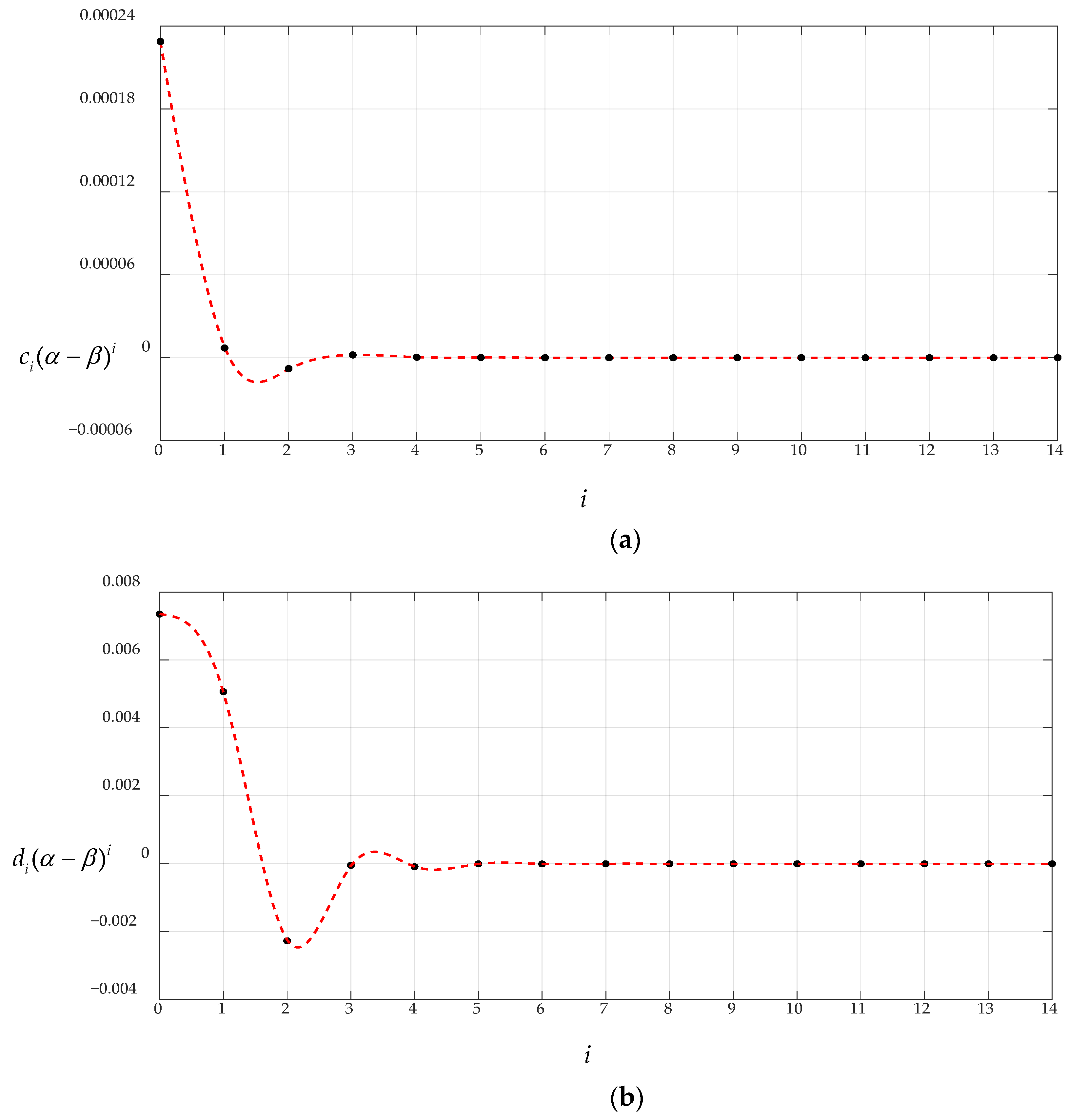
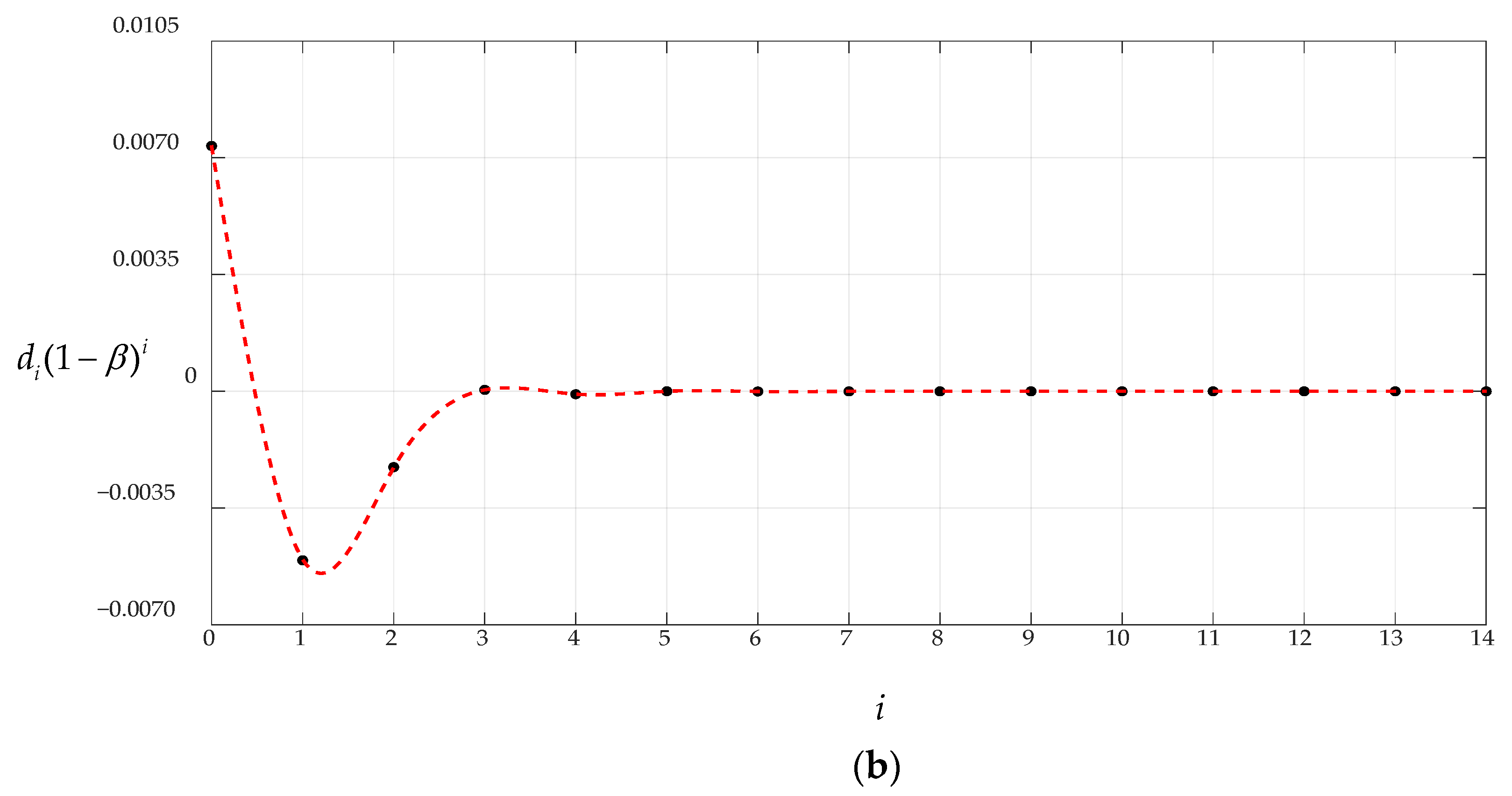
3.1. Convergence of the Closed-Form Solution Obtained in Section 2
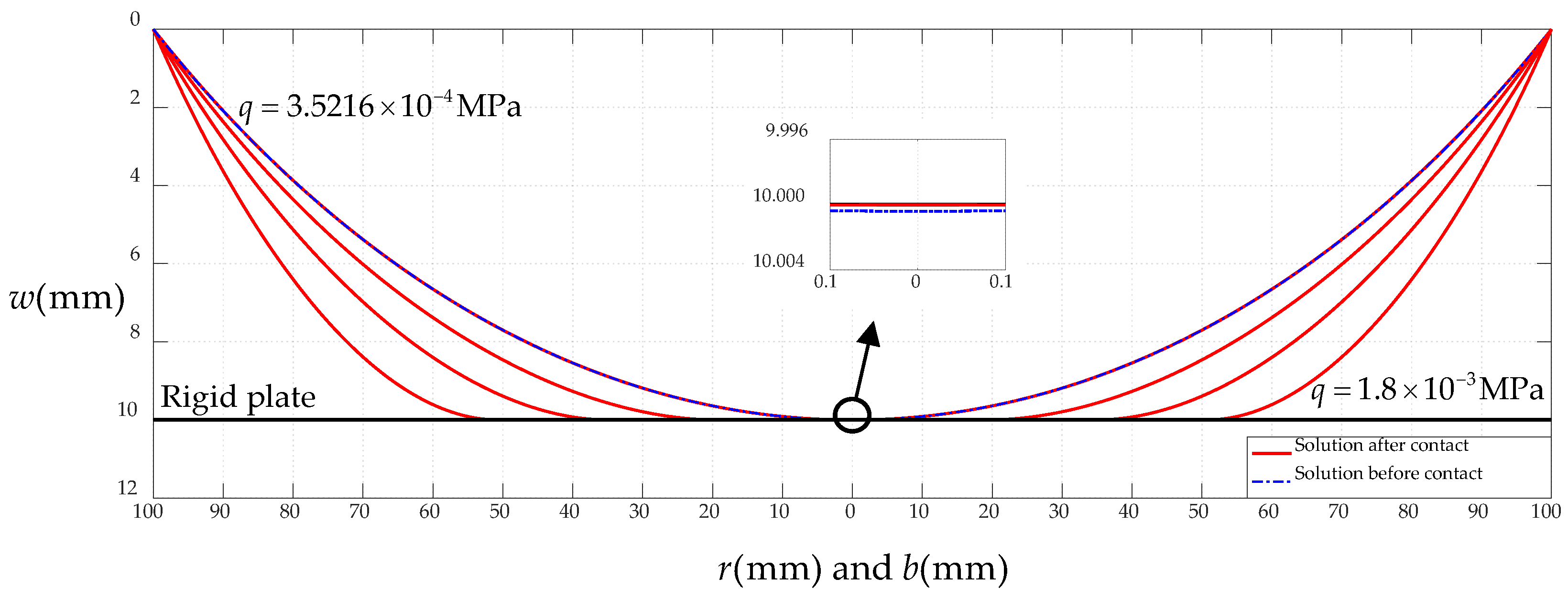
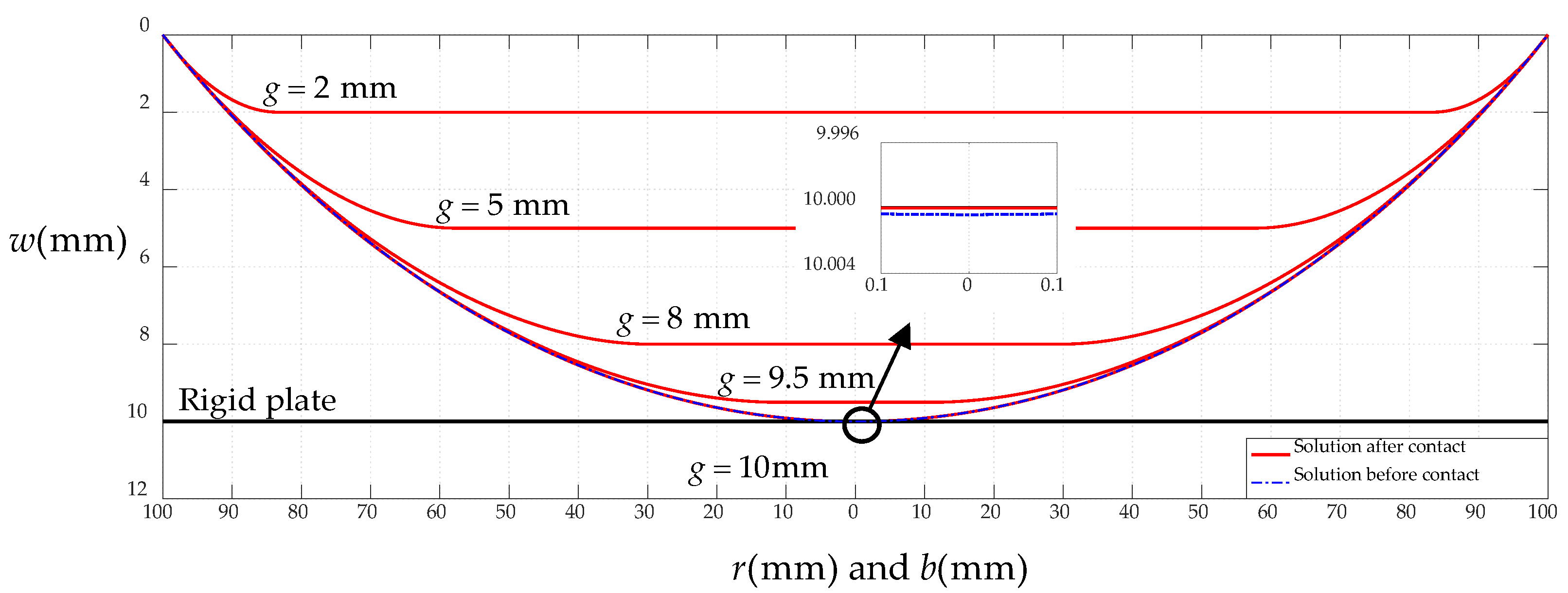
3.2. Regression of the Solution after Contact to the Solution before Contact
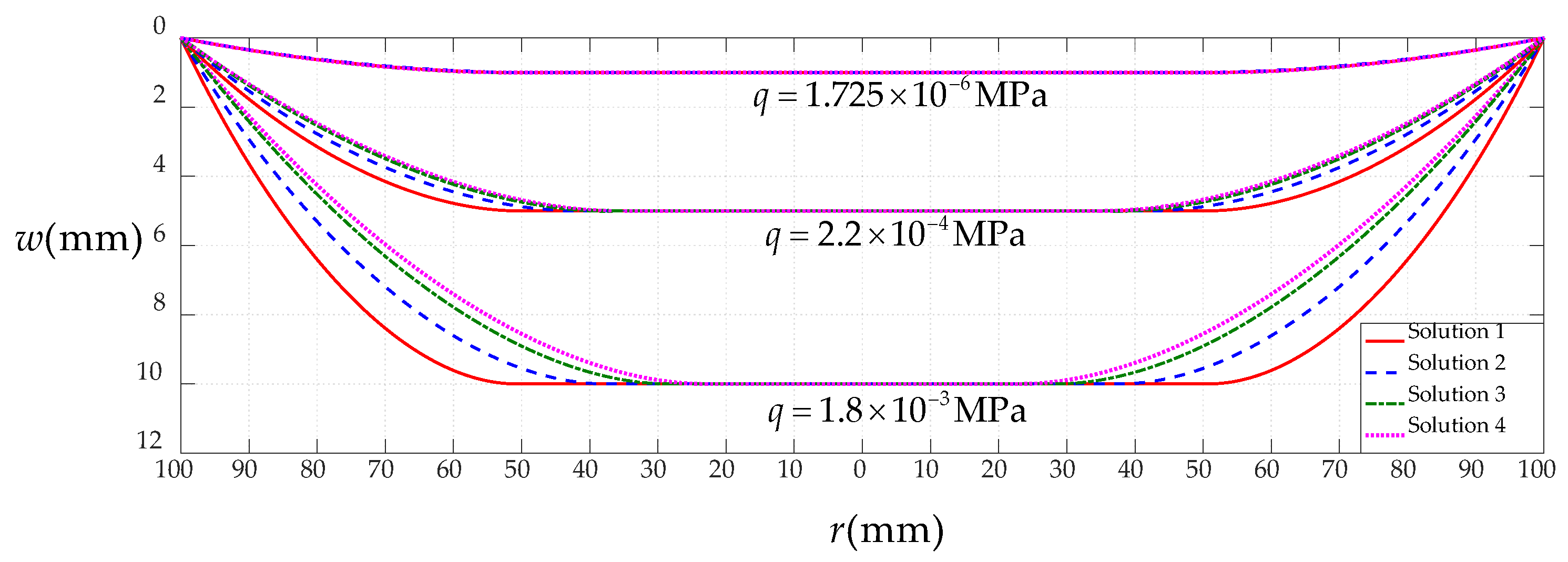
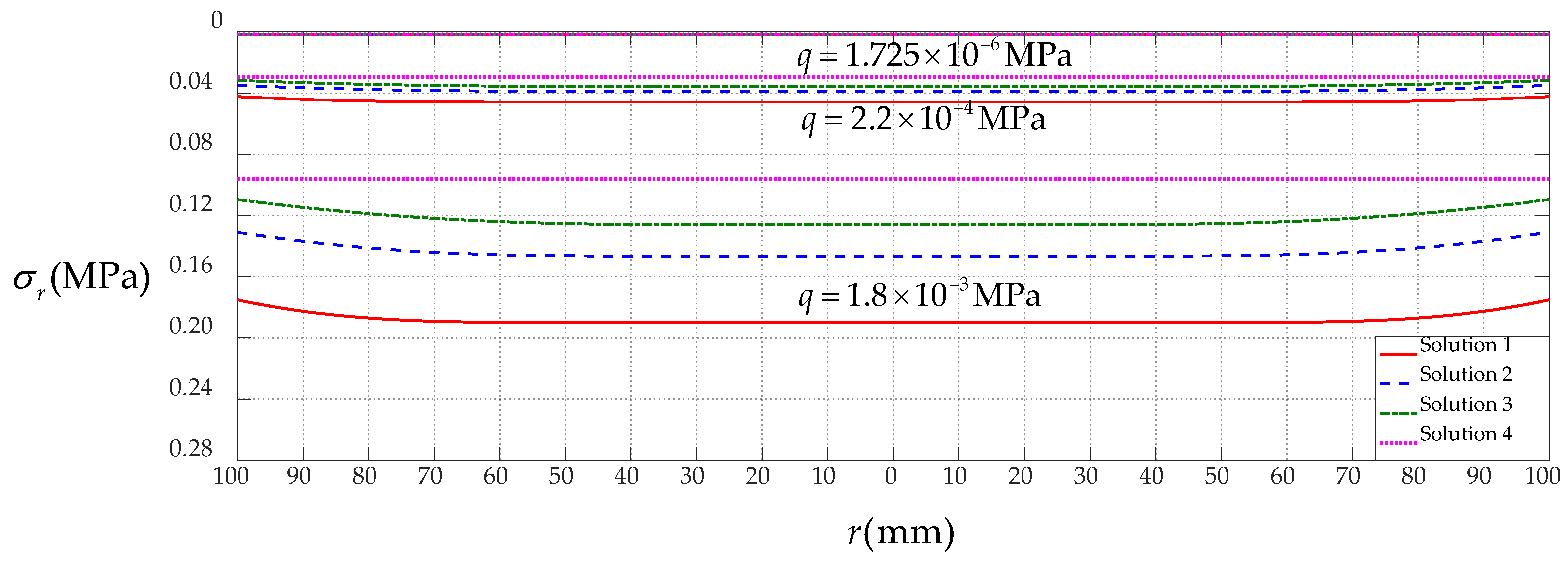
3.3. Comparison between Present Solution and Previous Solution
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
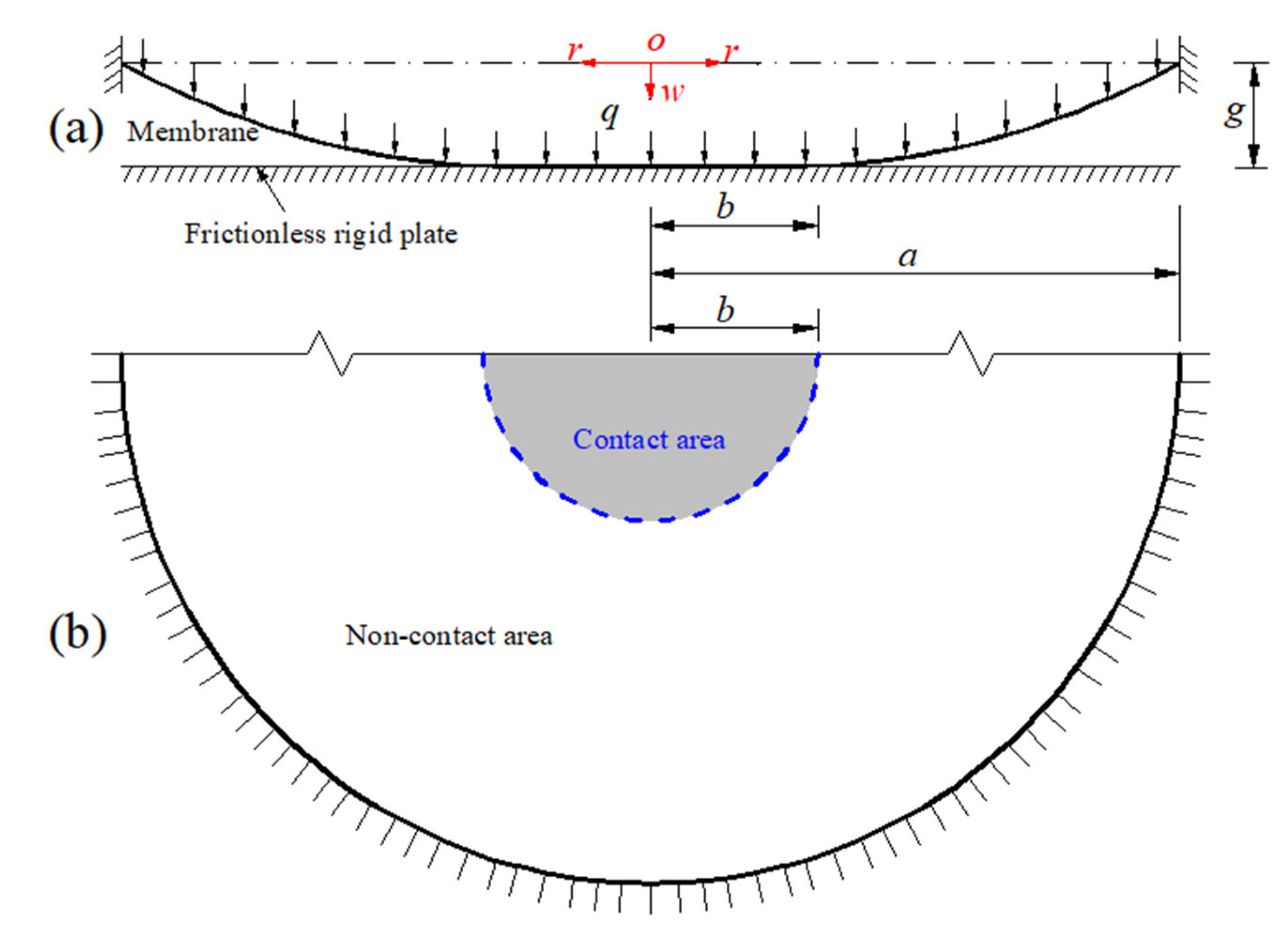
| Radius of the circular membrane | |
| Radius of the circular contact area | |
| Thickness of the circular membrane | |
| Poisson’s ratio | |
| Young’s modulus | |
| Uniformly distributed transverse loads | |
| g | Certain parallel gap between rigid flat plate and circular membrane |
| Radial coordinate | |
| Circumferential coordinate | |
| Transverse coordinate or displacement of the deflected membrane | |
| Coordinate origin | |
| Pi (ratio of circumference to diameter) | |
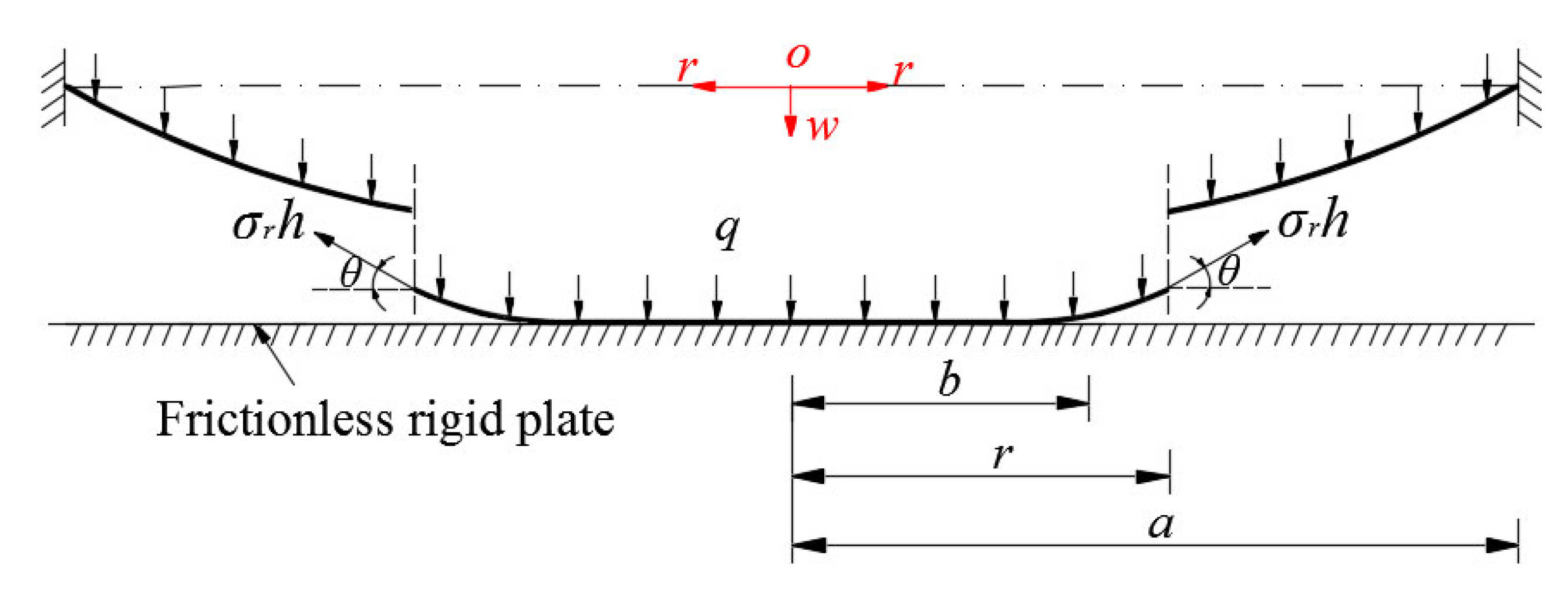
| Radial stress | |
| Rotation angle of the deflected membrane | |
| Circumferential stress | |
| Radial strain | |
| Circumferential strain | |
| Radial displacement of the deflected membrane | |
| Dimensionless loads | |
| Dimensionless transverse displacement | |
| Dimensionless radial stress | |
| Dimensionless circumferential stress | |
| Dimensionless variable () | |
| Dimensionless radial coordinate | |
| Dimensionless variable () | |
| Coefficients of the power series for | |
| Coefficients of the power series for |
Appendix A
Appendix B
References
- Delfani, M.R. Nonlinear elasticity of monolayer hexagonal crystals: Theory and application to circular bulge test. Eur. J. Mech. A-Solid. 2018, 68, 117–132. [Google Scholar] [CrossRef]
- Dai, Z.; Lu, N. Poking and bulging of suspended thin sheets: Slippage, instabilities, and metrology. J. Mech. Phys. Solids 2021, 149, 104320. [Google Scholar] [CrossRef]
- Gutscher, G.; Wu, H.C.; Ngaile, G.; Altan, T. Determination of flow stress for sheet metal forming using the viscous pressure bulge (VPB) test. J. Mater. Process. Tech. 2004, 146, 1–7. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, G.R.; Chen, Y.L.; Long, D.; Guan, Y.C.; Liu, L.Q.; Zhang, Z. Extended Hencky solution for the blister test of nanomembrane. Extreme Mech. Lett. 2018, 22, 69–78. [Google Scholar] [CrossRef]
- Sun, J.Y.; Qian, S.H.; Li, Y.M.; He, X.T.; Zheng, Z.L. Theoretical study of adhesion energy measurement for film/substrate interface using pressurized blister test: Energy release rate. Measurement 2013, 46, 2278–2287. [Google Scholar] [CrossRef]
- Cao, Z.; Tao, L.; Akinwande, D.; Huang, R.; Liechti, K.M. Mixed-mode traction-separation relations between graphene and copper by blister tests. Int. J. Solids Struct. 2016, 84, 147–159. [Google Scholar] [CrossRef]
- Napolitanno, M.J.; Chudnovsky, A.; Moet, A. The constrained blister test for the energy of interfacial adhesion. J. Adhes. Sci. Technol. 1988, 2, 311–323. [Google Scholar] [CrossRef]
- Pervier, M.L.A.; Hammond, D.W. Measurement of the fracture energy in mode I of atmospheric ice accreted on different materials using a blister test. Eng. Fract. Mech. 2019, 214, 223–232. [Google Scholar] [CrossRef]
- Zhu, T.T.; Li, G.X.; Müftü, S. Revisiting the constrained blister test to measure thin film adhesion. J. Appl. Mech.-T ASME 2017, 84, 071005. [Google Scholar] [CrossRef]
- Zhu, T.T.; Müftü, S.; Wan, K.T. One-dimensional constrained blister test to measure thin film adhesion. J. Appl. Mech.-T ASME 2018, 85, 054501. [Google Scholar] [CrossRef]
- Molla-Alipour, M.; Ganji, B.A. Analytical analysis of mems capacitive pressure sensor with circular diaphragm under dynamic load using differential transformation method (DTM). Acta Mech. Solida Sin. 2015, 28, 400–408. [Google Scholar] [CrossRef]
- Lee, H.Y.; Choi, B. Theoretical and experimental investigation of the trapped air effect on air-sealed capacitive pressure sensor. Sens. Actuat. A 2015, 221, 104–114. [Google Scholar] [CrossRef]
- Mishra, R.B.; Khan, S.M.; Shaikh, S.F. Low-cost foil/paper based touch mode pressure sensing element as artificial skin module for prosthetic hand. In Proceedings of the 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 15 May–15 July 2020; pp. 194–200. [Google Scholar]
- Meng, G.Q.; Ko, W.H. Modeling of circular diaphragm and spreadsheet solution programming for touch mode capacitive sensors. Sens. Actuat. A 1999, 75, 45–52. [Google Scholar] [CrossRef]
- Chien, W.Z.; Wang, Z.Z.; Xu, Y.G.; Chen, S.L. The symmetrical deformation of circular membrane under the action of uniformly distributed loads in its portion. Appl. Math. Mech. Engl. Ed. 1981, 2, 653–668. [Google Scholar]
- Arthurs, A.M.; Clegg, J. On the solution of a boundary value problem for the nonlinear Föppl-Hencky equation. Z. Angew. Math. Mech. 1994, 74, 281–284. [Google Scholar] [CrossRef]
- Plaut, R.H. Linearly elastic annular and circular membranes under radial, transverse, and torsional loading. Part I: Large unwrinkled axisymmetric deformations. Acta Mech. 2009, 202, 79–99. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Zhao, Z.H.; He, X.T.; Zheng, Z.L. A revisit of the boundary value problem for Föppl–Hencky membranes: Improvement of geometric equations. Mathematics 2020, 8, 631. [Google Scholar] [CrossRef]
- Rao, Y.; Qiao, S.; Dai, Z.; Lu, N. Elastic wetting: Substrate-supported droplets confined by soft elastic membranes. J. Mech. Phys. Solids 2021, 151, 104399. [Google Scholar] [CrossRef]
- Alekseev, S.A. Elastic annular membranes with a stiff centre under the concentrated force. Eng. Cor. 1951, 10, 71–80. [Google Scholar]
- Sun, J.Y.; Hu, J.L.; He, X.T.; Zheng, Z.L. A theoretical study of a clamped punch-loaded blister configuration: The quantitative relation of load and deflection. Int. J. Mech. Sci. 2010, 52, 928–936. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Ge, X.M.; Yang, Z.X.; He, X.T.; Zheng, Z.L. A theoretical study of an improved capacitive pressure sensor: Closed-form solution of uniformly loaded annular membranes. Measurement 2017, 111, 84–92. [Google Scholar] [CrossRef]
- Sun, J.Y.; Zhang, Q.; Li, X.; He, X. T. Axisymmetric large deflection elastic analysis of hollow annular membranes under transverse uniform loading. Symmetry 2021, 13, 1770. [Google Scholar] [CrossRef]
- Fichter, W.B. Some Solutions for the Large Deflections of Uniformly Loaded Circular Membranes; NASA: Washington, DC, USA, 1997; TP-3658. [Google Scholar]
- He, X.T.; Li, X.; Shi, B.B.; Sun, J.Y. A closed-form solution without small-rotation-angle assumption for circular membranes under gas pressure loading. Mathematics 2021, 9, 2269. [Google Scholar] [CrossRef]
- Hencky, H. On the stress state in circular plates with vanishing bending stiffness. Z. Angew. Math. Phys. 1915, 63, 311–317. [Google Scholar]
- Chien, W.Z. Asymptotic behavior of a thin clamped circular plate under uniform normal pressure at very large deflection. Sci. Rep. Natl. Tsinghua Univ. 1948, 5, 193–208. [Google Scholar]
- Alekseev, S.A. Elastic circular membranes under the uniformly distributed loads. Eng. Corpus. 1953, 14, 196–198. [Google Scholar]
- Lim, T.C. Large deflection of circular auxetic membranes under uniform load. J. Mater. Technol. 2016, 138, 041011. [Google Scholar] [CrossRef]
- Yang, X.Y.; Yu, L.X.; Long, R. Contact mechanics of inflated circular membrane under large deformation: Analytical solutions. Int. J. Solids Struct. 2021, 233, 111222. [Google Scholar] [CrossRef]
- Plaut, R.H. Effect of pressure on pull-off of flat cylindrical punch adhered to circular membrane. J. Adhesion 2022, 98, 1438–1460. [Google Scholar] [CrossRef]
- Sun, J.Y.; Lian, Y.S.; Li, Y.M.; He, X.T.; Zheng, Z.L. Closed-form solution of elastic circular membrane with initial stress under uniformly-distributed loads: Extended Hencky solution. Z. Angew. Math. Mech. 2015, 95, 1335–1341. [Google Scholar] [CrossRef]
- Xu, D.W.; Liechti, K.M. Analytical and experimental study of a circular membrane in Hertzian contact with a rigid substrate. Int. J. Solids Struct. 2010, 47, 969–977. [Google Scholar] [CrossRef]
- Wang, T.F.; He, X.T.; Li, Y.H. Closed-form solution of a peripherally fixed circular membrane under uniformly-distributed transverse loads and deflection restrictions. Math. Probl. Eng. 2018, 2018, 5989010. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Dong, J.; Zheng, Z.L.; Yang, Z.X. Closed-form solution of axisymmetric deformation of prestressed Föppl-Hencky membrane under constrained deflecting. Stuct. Eng. Mech. 2019, 69, 693–698. [Google Scholar]
- Varma, M.A.; Jindal, S.K. Novel design for performance enhancement of a touch-mode capacitive pressure sensor: Theoretical modeling and numerical simulation. J. Comput. Electron. 2018, 17, 1324–1333. [Google Scholar] [CrossRef]
- Li, K. Investigation of ring touch mode capacitive pressure sensor with an electrothermomechanical coupling contact model. IEEE Sens. J. 2019, 19, 9641–9652. [Google Scholar] [CrossRef]
- Jindal, S.K.; Varma, M.A.; Thukral, D. Study of MEMS touch-mode capacitive pressure sensor utilizing flexible SiC circular diaphragm: Robust design, theoretical modeling, numerical simulation and performance comparison. J. Circuits Syst. Comput. 2019, 28, 1950206. [Google Scholar] [CrossRef]
- Mishra, R.B.; Babatain, W.; El-Atab, N.; Hussain, M.M. Polymer/paper-based double touch mode capacitive pressure sensing element for wireless control of robotic arm. In Proceedings of the 2020 IEEE 15th International Conference on Nano/Micro Engineered and Molecular System (NEMS), San Diego, CA, USA, 27–30 September 2020; pp. 95–99. [Google Scholar]
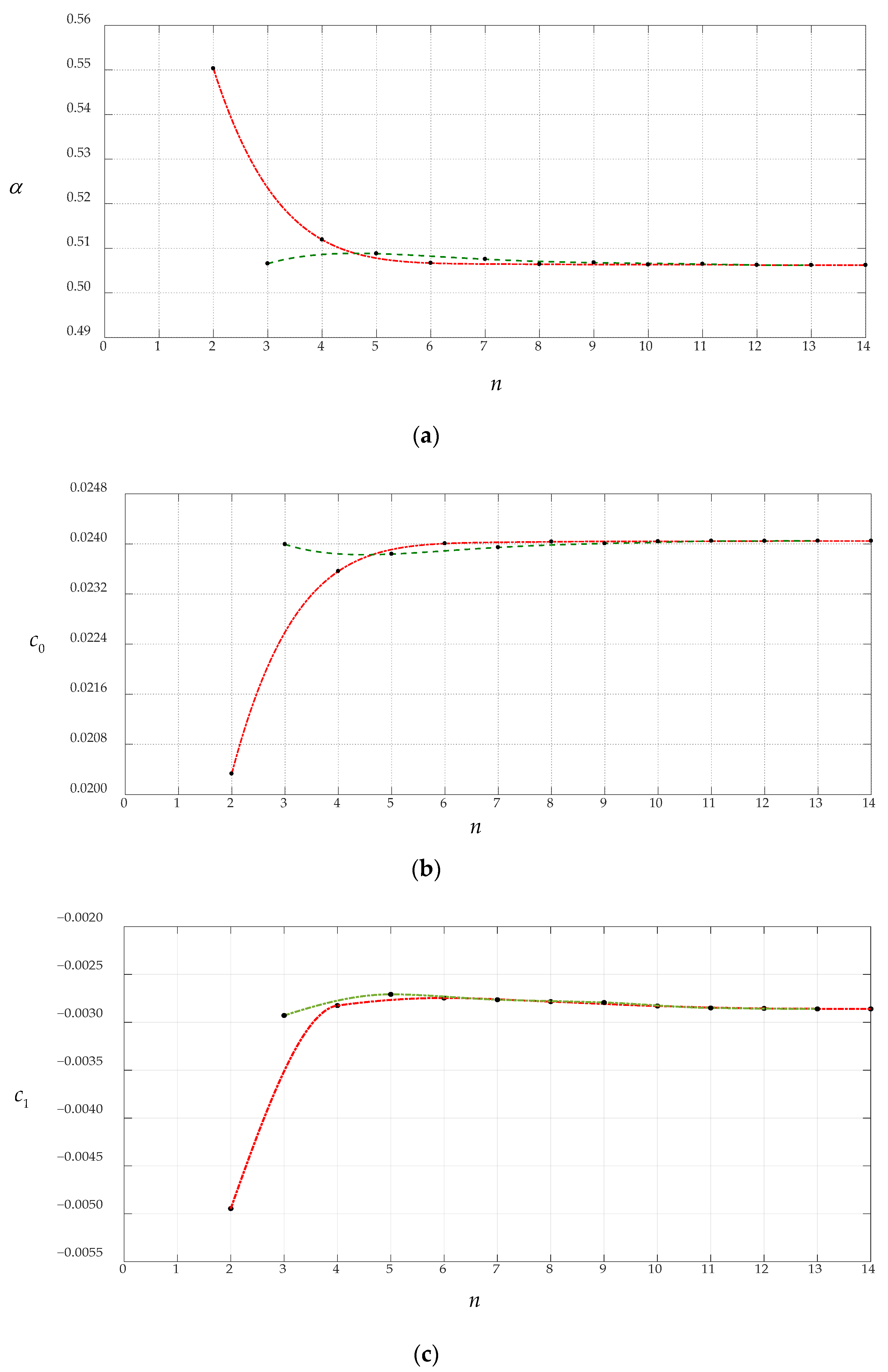
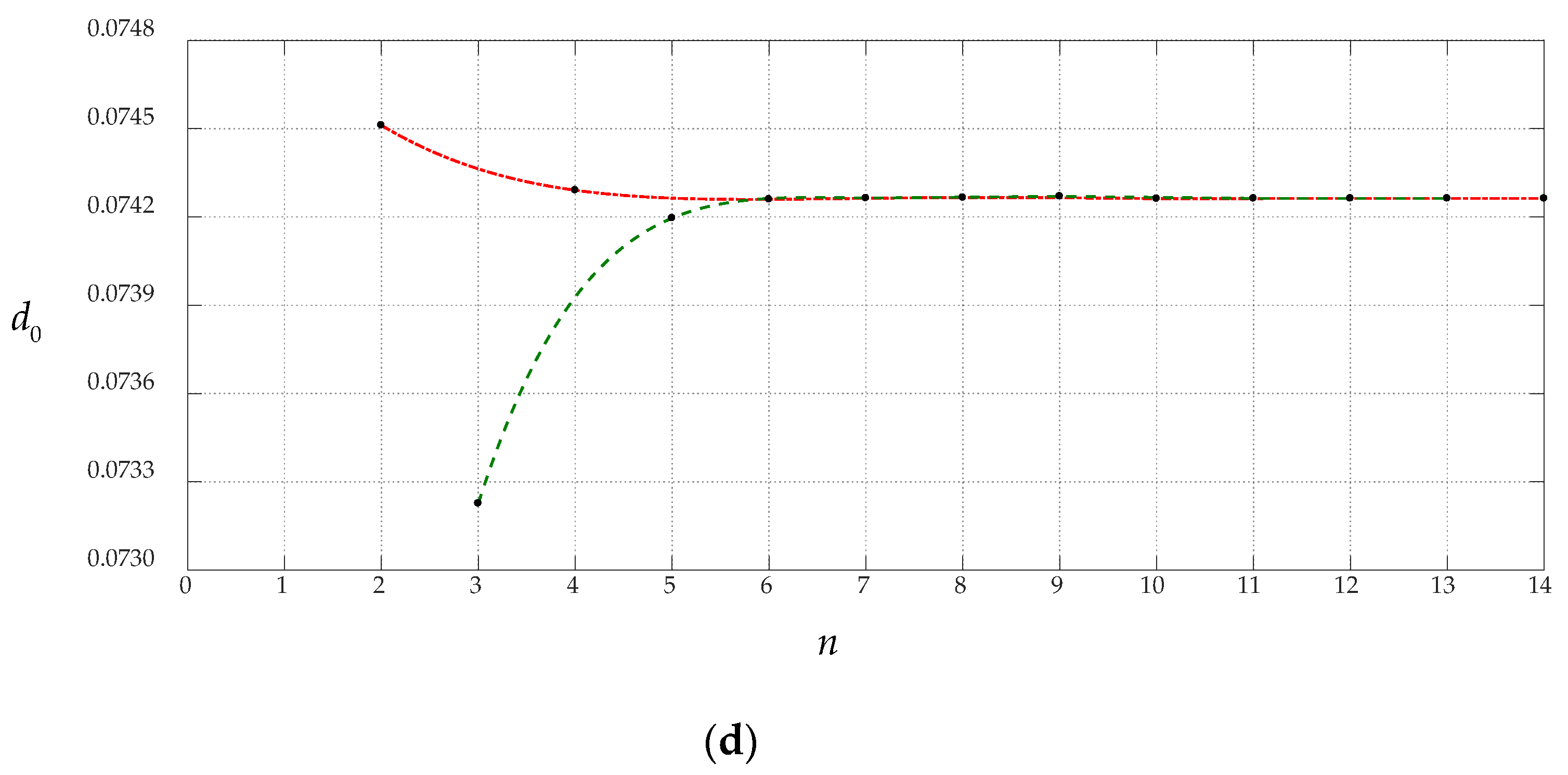

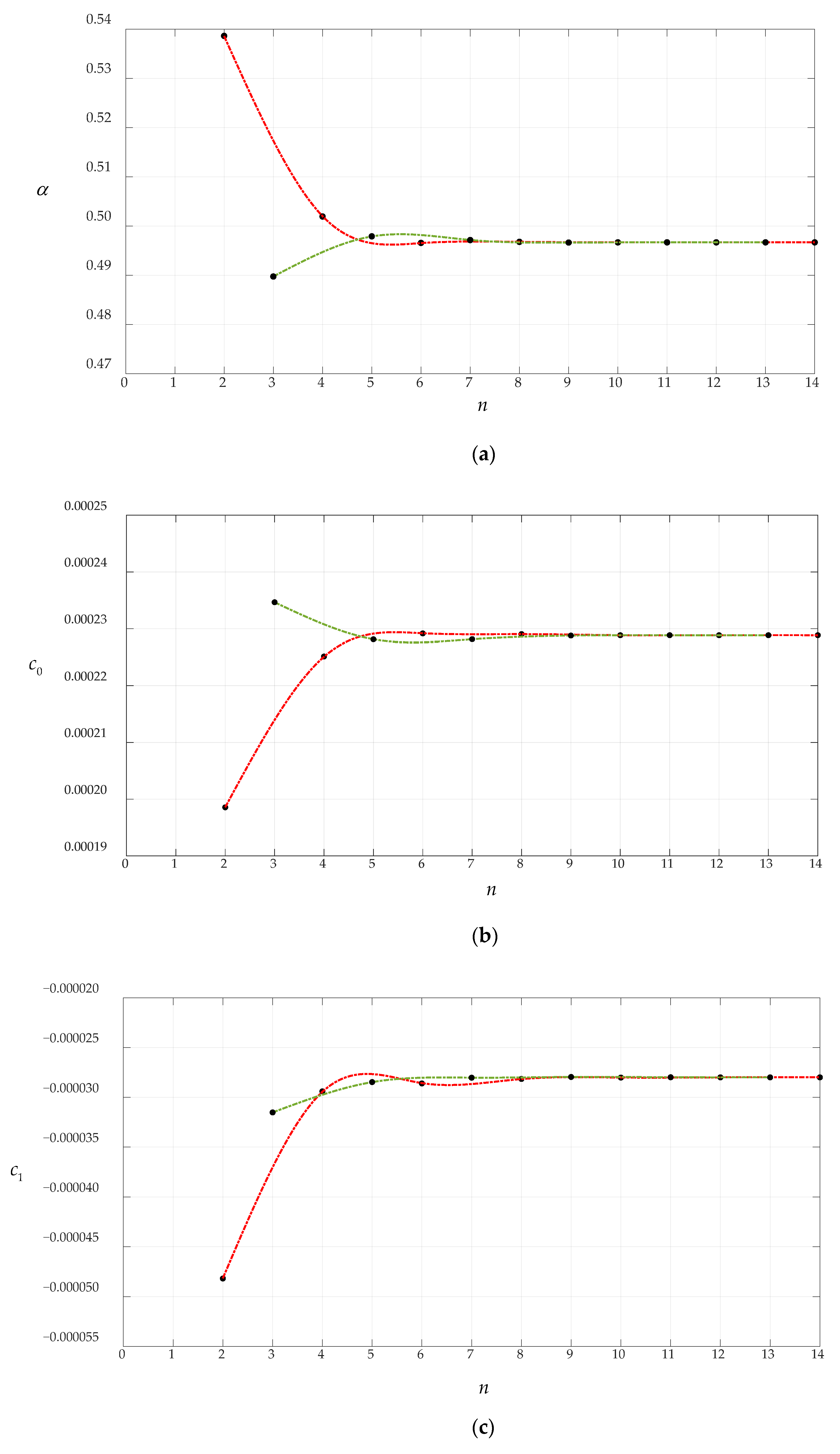
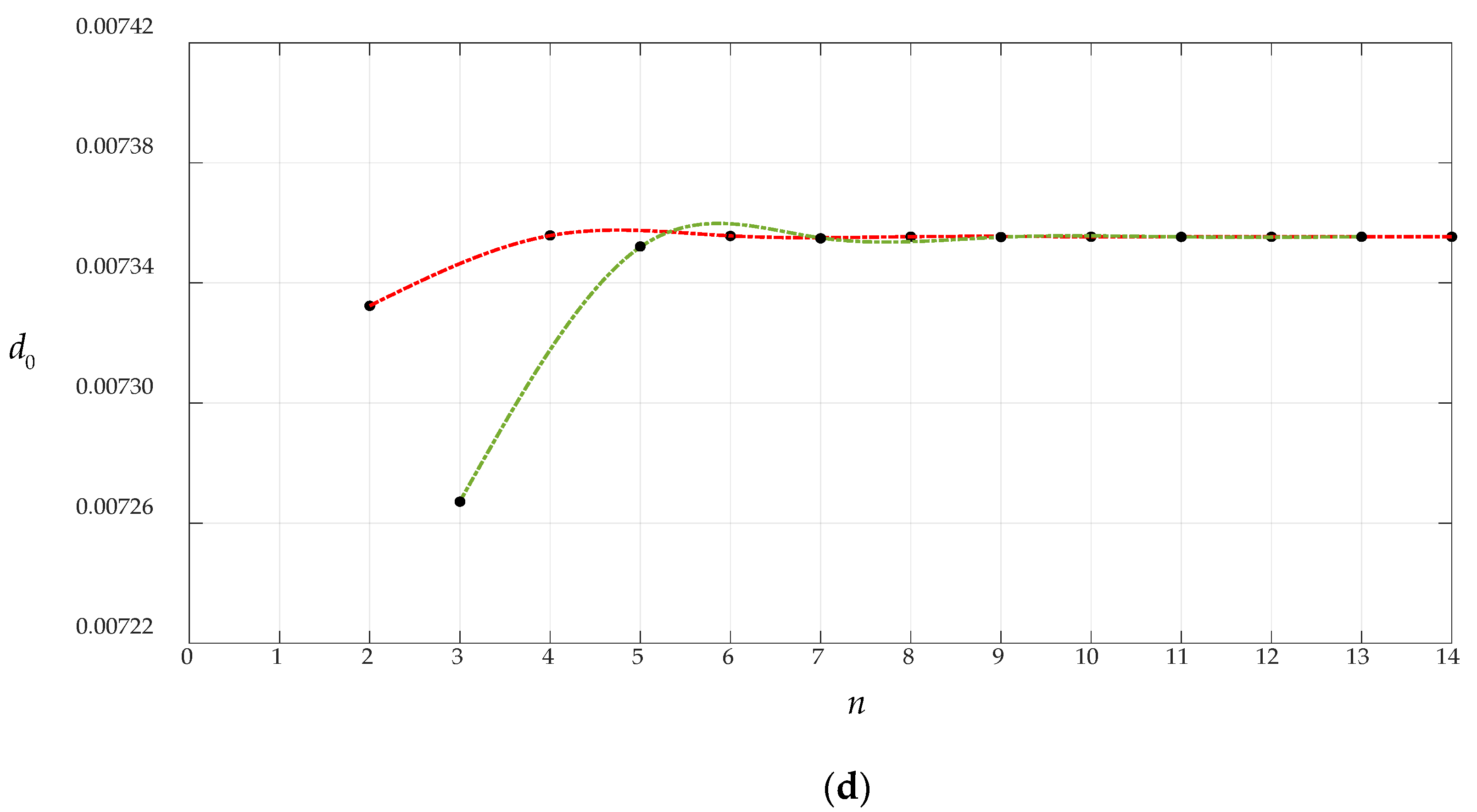

| n | α | c0 | c1 | d0 |
|---|---|---|---|---|
| 2 | 0.550304 | 0.020333 | −0.004946 | 0.074512 |
| 3 | 0.506556 | 0.023992 | −0.002929 | 0.073227 |
| 4 | 0.511924 | 0.023563 | −0.002825 | 0.074291 |
| 5 | 0.508790 | 0.023837 | −0.002708 | 0.074196 |
| 6 | 0.506674 | 0.024005 | −0.002746 | 0.074260 |
| 7 | 0.507546 | 0.023943 | −0.002764 | 0.074264 |
| 8 | 0.506410 | 0.024033 | −0.002784 | 0.074266 |
| 9 | 0.506772 | 0.024006 | −0.002793 | 0.074270 |
| 10 | 0.506318 | 0.024039 | −0.002830 | 0.074262 |
| 11 | 0.506448 | 0.024046 | −0.002850 | 0.074265 |
| 12 | 0.506230 | 0.024045 | −0.002855 | 0.074264 |
| 13 | 0.506210 | 0.024047 | −0.002860 | 0.074263 |
| 14 | 0.506210 | 0.024047 | −0.002860 | 0.074263 |
| i | ci(α − β)i | di(α − β)i | ci(1 − β)i | di(1 − β)i |
|---|---|---|---|---|
| 0 | 0.024047 | 0.074263 | 0.024047 | 0.074263 |
| 1 | 7.0612 × 10−4 | 4.8669 × 10−3 | −7.0612 × 10−4 | −4.8669 × 10−3 |
| 2 | 3.3694 × 10−4 | −2.1851 × 10−3 | 3.3694 × 10−4 | −2.1851 × 10−3 |
| 3 | 1.5232 × 10−4 | −1.2296 × 10−4 | −1.5232 × 10−4 | 1.2296 × 10−4 |
| 4 | 6.2122 × 10−5 | −2.5098 × 10−5 | 6.2122 × 10−5 | −2.5098 × 10−5 |
| 5 | 2.4282 × 10−5 | −4.6319 × 10−6 | −2.4282 × 10−5 | 4.6319 × 10−6 |
| 6 | 9.2305 × 10−6 | −7.3651 × 10−7 | 9.2305 × 10−6 | −7.3651 × 10−7 |
| 7 | 3.4402 × 10−6 | −5.7636 × 10−8 | −3.4402 × 10−6 | 5.7636 × 10−8 |
| 8 | 1.2634 × 10−6 | 2.4572 × 10−8 | 1.2634 × 10−6 | 2.4572 × 10−8 |
| 9 | 4.5869 × 10−7 | 1.8160 × 10−8 | −4.5869 × 10−7 | −1.8160 × 10−8 |
| 10 | 1.6500 × 10−7 | 8.1933 × 10−9 | 1.6500 × 10−7 | 8.1933 × 10−9 |
| 11 | 5.8903 × 10−8 | 3.1359 × 10−9 | −5.8903 × 10−8 | −3.1359 × 10−9 |
| 12 | 2.0894 × 10−8 | 1.0994 × 10−9 | 2.0894 × 10−8 | 1.0994 × 10−9 |
| 13 | 7.3714 × 10−9 | 3.6352 × 10−10 | −7.3714 × 10−9 | −3.6352 × 10−10 |
| 14 | 2.5883 × 10−9 | 1.1475 × 10−10 | 2.5883 × 10−9 | 1.1475 × 10−10 |
| n | α | c0 | c1 | d0 |
|---|---|---|---|---|
| 2 | 0.538654 | 1.9856 × 10−4 | −4.8200 × 10−5 | 7.3324 × 10−3 |
| 3 | 0.489766 | 2.3466 × 10−4 | −3.1514 × 10−5 | 7.2671 × 10−3 |
| 4 | 0.501960 | 2.2515 × 10−4 | −2.9399 × 10−5 | 7.3553 × 10−3 |
| 5 | 0.497930 | 2.2814 × 10−4 | −2.8463 × 10−5 | 7.3522 × 10−3 |
| 6 | 0.496600 | 2.2917 × 10−4 | −2.8560 × 10−5 | 7.3556 × 10−3 |
| 7 | 0.497174 | 2.2817 × 10−4 | −2.8024 × 10−5 | 7.3549 × 10−3 |
| 8 | 0.496810 | 2.2905 × 10−4 | −2.8150 × 10−5 | 7.3554 × 10−3 |
| 9 | 0.496670 | 2.2880 × 10−4 | −2.7950 × 10−5 | 7.3553 × 10−3 |
| 10 | 0.496704 | 2.2885 × 10−4 | −2.8010 × 10−5 | 7.3554 × 10−3 |
| 11 | 0.496710 | 2.2886 × 10−4 | −2.7980 × 10−5 | 7.3553 × 10−3 |
| 12 | 0.496708 | 2.2885 × 10−4 | −2.7990 × 10−5 | 7.3554 × 10−3 |
| 13 | 0.496708 | 2.2886 × 10−4 | −2.7980 × 10−5 | 7.3553 × 10−3 |
| 14 | 0.496708 | 2.2885 × 10−4 | −2.7990 × 10−5 | 7.3554 × 10−3 |
| i | ci(α − β)i | di(α − β)i | ci(1 − β)i | di(1 − β)i |
|---|---|---|---|---|
| 0 | 2.2885 × 10−4 | 7.3554 × 10−3 | 2.2885 × 10−4 | 7.3554 × 10−3 |
| 1 | 7.0436 × 10−6 | 5.0657 × 10−3 | −7.0436 × 10−6 | −5.0657 × 10−3 |
| 2 | −7.9021 × 10−6 | −2.2719 × 10−3 | −7.9021 × 10−6 | −2.2720 × 10−3 |
| 3 | 2.0236 × 10−6 | −4.4641 × 10−5 | −2.0236 × 10−6 | 4.4641 × 10−5 |
| 4 | 3.5072 × 10−7 | −8.7459 × 10−5 | 3.5072 × 10−7 | −8.7459 × 10−5 |
| 5 | 1.4484 × 10−7 | −2.4508 × 10−6 | −1.4484 × 10−7 | 2.4508 × 10−6 |
| 6 | −3.3957 × 10−8 | −4.0025 × 10−6 | −3.3958 × 10−8 | −4.0025 × 10−6 |
| 7 | −3.4012 × 10−8 | 2.1156 × 10−7 | 3.4012 × 10−8 | −2.1156 × 10−7 |
| 8 | −2.3883 × 10−8 | −2.5281 × 10−7 | −2.3883 × 10−8 | −2.5281 × 10−7 |
| 9 | −1.1568 × 10−8 | −2.8124 × 10−8 | 1.1568 × 10−8 | 2.8124 × 10−8 |
| 10 | −5.3121 × 10−9 | −5.4178 × 10−8 | −5.3121 × 10−9 | −5.4178 × 10−8 |
| 11 | −2.2077 × 10−9 | −1.9538 × 10−8 | 2.2077 × 10−9 | 1.9538 × 10−8 |
| 12 | −9.0917 × 10−10 | −1.1500 × 10−8 | −9.0917 × 10−10 | −1.1499 × 10−8 |
| 13 | −3.6399 × 10−10 | −4.1701 × 10−9 | 3.6399 × 10−10 | 4.1702 × 10−9 |
| 14 | −1.4728 × 10−10 | −1.8333 × 10−9 | −1.4728 × 10−10 | 1.8333 × 10−9 |
| q (MPa) | g (mm) | b (mm) | σm (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Solution 1 | Solution 2 | Solution 3 | Solution 4 | Solution 1 | Solution 2 | Solution 3 | Solution 4 | ||
| 1.725 × 10−6 | 1 | 49.66 | 47.97 | 47.01 | 46.66 | 1.82 × 10−3 | 1.75 × 10−3 | 1.67 × 10−3 | 1.66 × 10−3 |
| 2.2 × 10−4 | 5 | 50.12 | 41.47 | 36.72 | 34.87 | 4.60 × 10−2 | 3.88 × 10−2 | 3.57 × 10−2 | 2.96 × 10−2 |
| 1.8 × 10−3 | 10 | 50.72 | 37.55 | 28.34 | 23.04 | 1.90 × 10−1 | 1.46 × 10−1 | 1.26 × 10−1 | 9.61 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.-Y.; Li, X.; Zhang, Q.; He, X.-T.; Sun, J.-Y. A Refined Closed-Form Solution for Laterally Loaded Circular Membranes in Frictionless Contact with Rigid Flat Plates: Simultaneous Improvement of Out-of-Plane Equilibrium Equation and Geometric Equation. Mathematics 2022, 10, 3025. https://doi.org/10.3390/math10163025
Li F-Y, Li X, Zhang Q, He X-T, Sun J-Y. A Refined Closed-Form Solution for Laterally Loaded Circular Membranes in Frictionless Contact with Rigid Flat Plates: Simultaneous Improvement of Out-of-Plane Equilibrium Equation and Geometric Equation. Mathematics. 2022; 10(16):3025. https://doi.org/10.3390/math10163025
Chicago/Turabian StyleLi, Fei-Yan, Xue Li, Qi Zhang, Xiao-Ting He, and Jun-Yi Sun. 2022. "A Refined Closed-Form Solution for Laterally Loaded Circular Membranes in Frictionless Contact with Rigid Flat Plates: Simultaneous Improvement of Out-of-Plane Equilibrium Equation and Geometric Equation" Mathematics 10, no. 16: 3025. https://doi.org/10.3390/math10163025
APA StyleLi, F.-Y., Li, X., Zhang, Q., He, X.-T., & Sun, J.-Y. (2022). A Refined Closed-Form Solution for Laterally Loaded Circular Membranes in Frictionless Contact with Rigid Flat Plates: Simultaneous Improvement of Out-of-Plane Equilibrium Equation and Geometric Equation. Mathematics, 10(16), 3025. https://doi.org/10.3390/math10163025






