The Existence and Uniqueness of Riccati Fractional Differential Equation Solution and Its Approximation Applied to an Economic Growth Model
Abstract
:1. Introduction
2. Preliminaries
2.1. Banach Fixed Point Theorem
2.2. Adomian Decomposition Method
3. Results and Discussion
3.1. The Existence and the Uniqueness in the Riccati Fractional Differential Equation
3.2. ADM-Kamal Combined Theorem
- Transform Equation (17) using Kamal’s Integral Transform Theorem, we obtain:with order of the Caputo fractional derivative, where is a positive integer, we obtain:for , so that k = 0, thus we obtained:
- Furthermore, by using the inverse Kamal Integral Transform (9), so that Equation (18) becomes:
- The Adomian Decomposition Method assumes that the function w can be decomposed into an infinite series as follows:where can be determined recursively. This method also assumes that the nonlinear operator can be decomposed into an infinite polynomial series, so that from Equation (20) we obtain:where An is an Adomian polynomial, defined as:where is a parameter. Adomian polynomial An can be described as follows:
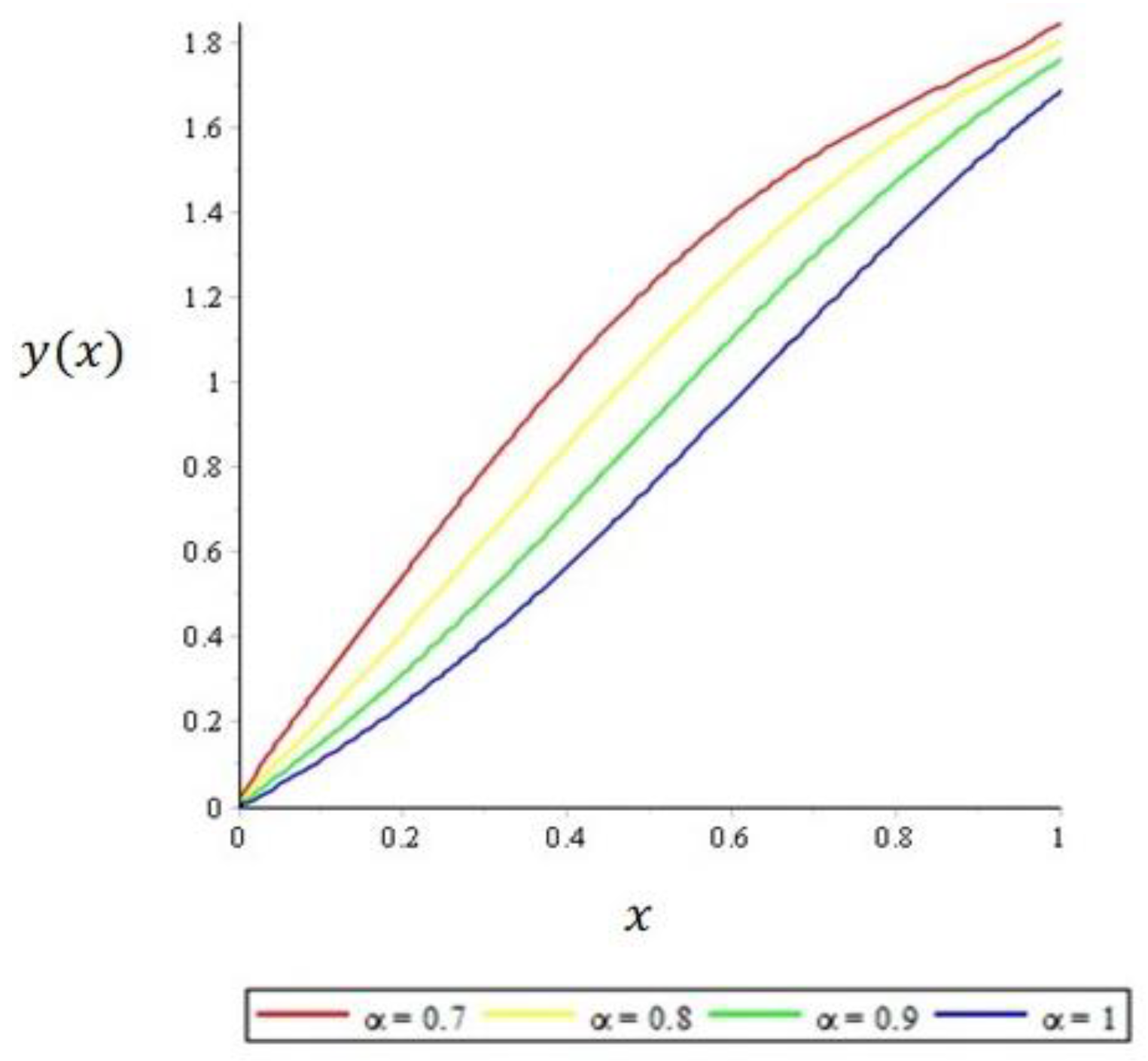
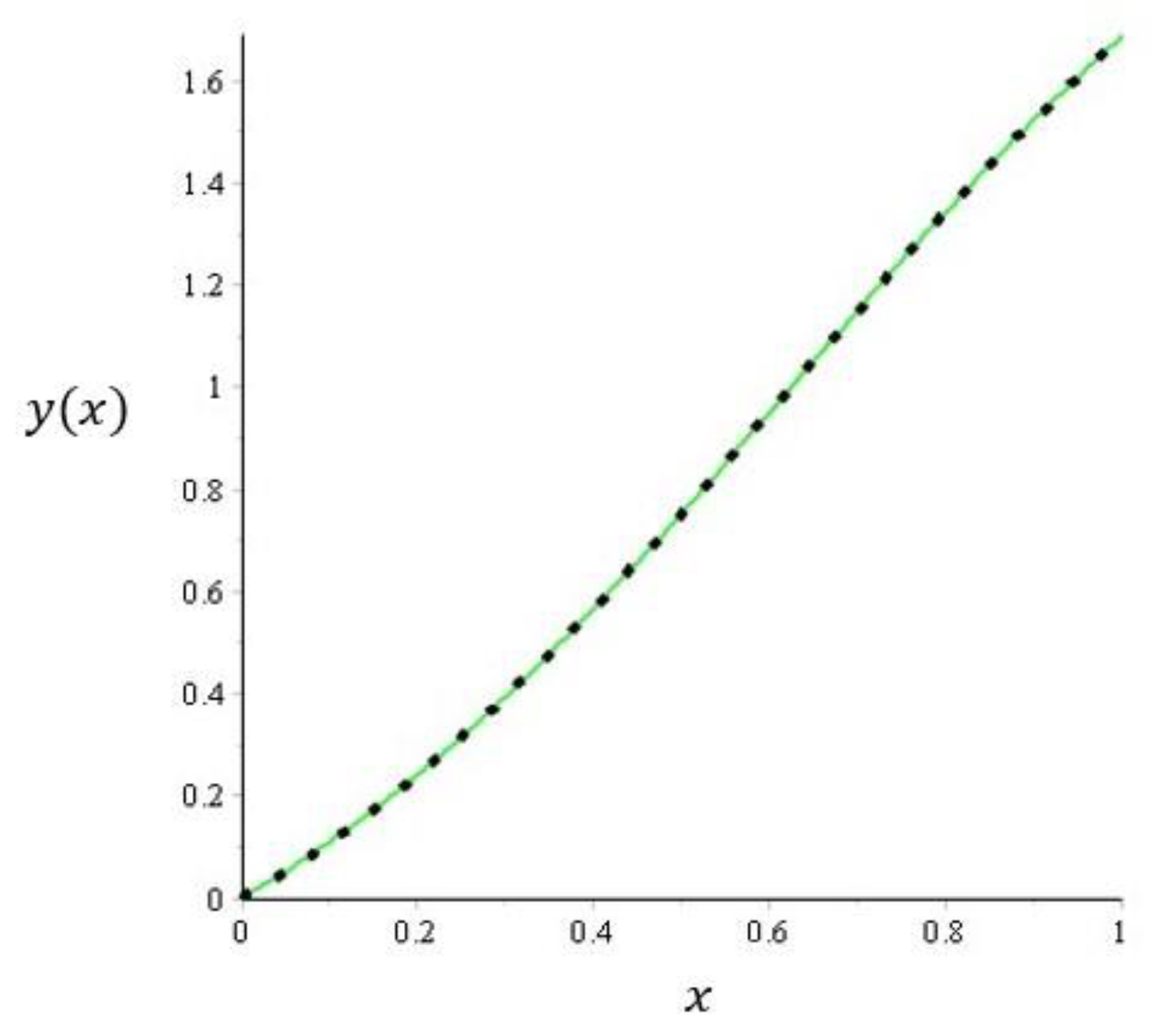
3.3. The Comparison of the Exact Solution of the Odetunde and Taiwo with ADM-Kamal Combined Theorem
3.4. Numerical Simulation of Economic Growth Model Using ADM-Kamal Combined Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johansyah, M.D.; Supriatna, A.K.; Rusyaman, E.; Saputra, J. Application of fractional differential equation in economic growth model: A systematic review approach. AIMS Math. 2021, 6, 10266–10280. [Google Scholar] [CrossRef]
- Johansyah, M.D.; Supriatna, A.K.; Rusyaman, E.; Saputra, J. Solving the Economic Growth Acceleration Model with Memory Effects: An Application of Combined Theorem of Adomian Decomposition Methods and Kashuri–Fundo Transformation Methods. Symmetry 2022, 14, 192. [Google Scholar] [CrossRef]
- Sukono; Sambas, A.; He, S.; Liu, H.; Vaidyanathan, S.; Hidayat, Y.; Saputra, J. Dynamical analysis and adaptive fuzzy control for the fractional-order financial risk chaotic system. Adv. Differ. Equ. 2020, 2020, 674. [Google Scholar] [CrossRef]
- Subartini, B.; Vaidyanathan, S.; Sambas, A.; Zhang, S. Multistability in the Finance Chaotic System, Its Bifurcation Analysis and Global Chaos Synchronization via Integral Sliding Mode Control. IAENG Int. J. Appl. Math. 2021, 51, 995–1002. [Google Scholar]
- Xin, B.; Zhang, J. Finite-time stabilizing a fractional-order chaotic financial system with market confidence. Nonlinear Dyn. 2015, 79, 1399–1409. [Google Scholar] [CrossRef]
- Jia, H.; Pu, Y. Fractional calculus method for enhancing digital image of bank slip. Congr. Image Signal Process. 2008, 3, 326–330. [Google Scholar]
- Chen, T.; Wang, D. Combined application of blockchain technology in fractional calculus model of supply chain financial system. Chaos Solitons Fractals 2020, 131, 109461. [Google Scholar] [CrossRef]
- Wang, W.; Khan, M.A.; Kumam, P.; Thounthong, P. A comparison study of bank data in fractional calculus. Chaos Solitons Fractals 2019, 126, 369–384. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A.; Lopes, A.M. Relative fractional dynamics of stock markets. Nonlinear Dyn. 2016, 86, 1613–1619. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Zhang, X.; Koyuncu, I.; Bonny, T.; Tuna, M.; Alcin, M.; Zhang, S.; Sulaiman, I.M.; Awwal, A.M.; et al. A Novel 3D Chaotic System with Line Equilibrium: Multistability, Integral Sliding Mode Control, Electronic Circuit, FPGA and its Image Encryption. IEEE Access 2022, 10, 68057–68074. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Tlelo-Cuautle, E.; Abd-El-Atty, B.; Abd El-Latif, A.A.; Guillen-Fernandez, O.; Sukono; Hidayat, Y.; Gundara, G. A 3-D multi-stable system with a peanut-shaped equilibrium curve: Circuit design, FPGA realization, and an application to image encryption. IEEE Access 2020, 8, 137116–137132. [Google Scholar]
- Vaidyanathan, S.; Sambas, A.; Mamat, M.; Sanjaya, W.S.M. A new three-dimensional chaotic system with a hidden attractor, circuit design and application in wireless mobile robot. Arch. Control. Sci. 2017, 27, 541–554. [Google Scholar]
- Silva-Juárez, A.; Tlelo-Cuautle, E.; De La Fraga, L.G.; Li, R. FPAA-based implementation of fractional-order chaotic oscillators using first-order active filter blocks. J. Adv. Res. 2020, 25, 77–85. [Google Scholar]
- Sambas, A.; Vaidyanathan, S.; Bonny, T.; Zhang, S.; Hidayat, Y.; Gundara, G.; Mamat, M. Mathematical model and FPGA realization of a multi-stable chaotic dynamical system with a closed butterfly-like curve of equilibrium points. Appl. Sci. 2021, 11, 788. [Google Scholar] [CrossRef]
- Karakaya, B.; Gülten, A.; Frasca, M. A true random bit generator based on a memristive chaotic circuit: Analysis, design and FPGA implementation. Chaos Solitons Fractals 2019, 119, 143–149. [Google Scholar]
- Wazwaz, A.M. The combined Laplace transform–Adomian decomposition method for handling nonlinear Volterra integro–differential equations. Appl. Math. Comput. 2010, 216, 1304–1309. [Google Scholar]
- Babolian, E.; Vahidi, A.R.; Shoja, A. An efficient method for nonlinear fractional differential equations: Combination of the Adomian decomposition method and spectral method. Indian J. Pure Appl. Math. 2014, 45, 1017–1028. [Google Scholar]
- Varsoliwala, A.C.; Singh, T.R. An approximate analytical solution of non linear partial differential equation for water infiltration in unsaturated soils by combined Elzaki Transform and Adomian Decomposition Method. J. Phys. Conf. Ser. 2020, 1473, 012009. [Google Scholar]
- Ahmed, S.; Elzaki, T. The solution of nonlinear Volterra integro-differential equations of second kind by combine Sumudu transforms and Adomian decomposition method. Int. J. Adv. Innov. Res. 2013, 2, 90–93. [Google Scholar]
- Chindhe, A.D.; Kiwne, S.B. Application of Combine Natural Transform and Adomian Decomposition Method in Volterra Integro-Differential Equations. Math. J. Interdiscip. Sci. 2016, 5, 1–14. [Google Scholar]
- Johansyah, M.D.; Supriatna, A.K.; Rusyaman, E.; Saputra, J. Solving Differential Equations of Fractional Order Using Combined Adomian Decomposition Method with Kamal Integral Transformation. Math. Stat. 2022, 10, 187–194. [Google Scholar] [CrossRef]
- Ramezani, M.; Nourazar, S.S.; Dehghanpour, H. Combination of Adomian decomposition method with Fourier transform for solving the squeezing flow influenced by a magnetic field. AUT J. Model. Simul. 2021, 53, 1–25. [Google Scholar]
- Liaqat, M.I.; Khan, A.; Alam, M.; Pandit, M.K.; Etemad, S.; Rezapour, S. Approximate and closed-form solutions of Newell-Whitehead-Segel equations via modified conformable Shehu transform decomposition method. Math. Probl. Eng. 2022, 2022, 6752455. [Google Scholar]
- Khandelwal, R.; Khandelwal, Y. Solution of Blasius Equation Concerning with Mohand Transform. Int. J. Appl. Comput. Math. 2020, 6, 128. [Google Scholar]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Vatsala, A.S. Basic theory of fractional differential equations. Nonlinear Anal. Theory Methods Appl. 2008, 69, 2677–2682. [Google Scholar] [CrossRef]
- Benlabbes, A.; Benbachir, M.; Lakrib, M. Existence solutions of a nonlinear fractional differential equations. J. Adv. Res. Dyn. Control. Syst. 2014, 6, 10266–10280. [Google Scholar]
- Elsaid, A.; Latif, M.A.; Kamal, F.M. Series solution for fractional Riccati differential equation and its convergence. J. Fract. Calc. Appl. 2015, 6, 186–196. [Google Scholar]
- Asaduzzaman, M.; Ali, M.Z. Existence of Multiple Positive Solutions to the Caputo-Type Nonlinear Fractional Differential Equation With Integral Boundary Value Conditions. Fixed Point Theory 2022, 23, 127–129. [Google Scholar]
- Asaduzzaman, M.; Ali, M.Z. Existence of positive solution to the boundary value problems for coupled system of nonlinear fractional differential equations. AIMS Math. 2019, 4, 880–895. [Google Scholar]
- Asaduzzaman, M.; Ali, M.Z. Existence of Triple Positive Solutions for Nonlinear Second Order Arbitrary Two-point Boundary Value Problems. Malays. J. Math. Sci. 2020, 14, 335–349. [Google Scholar]
- Asaduzzaman, M.; Kilicman, A.; Ali, M.Z.; Sapar, S.H. Fixed point theorem based solvability of 2-Dimensional dissipative cubic nonlinear Klein-Gordon equation. Mathematics 2020, 8, 1103. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; El-Mesiry, A.E.M.; El-Saka, H.A.A. On the fractional-order logistic equation. Appl. Math. Lett. 2007, 20, 817–823. [Google Scholar]
- Bartle, R.G.; Sherbert, D.R. Introduction to Real Analysis, 4th ed.; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. An Introduction to Fractional Calculus; Nova Science Publishers: New York, NY, USA, 2017. [Google Scholar]
- Kamal, A.; Sedeeg, H. The new integral transform Kamal transform. Adv. Theor. Appl. Math. 2016, 11, 451–458. [Google Scholar]
- Wazwaz, A.M.; El-Sayed, S.M. A new modification of the Adomian decomposition method for linear and nonlinear operators. Appl. Math. Comput. 2001, 122, 393–405. [Google Scholar]
- Odetunde, O.S.; Taiwo, O.A. A decomposition algorithm for the solution of fractional quadratic Riccati differential equations with Caputo derivatives. Am. J. Comput. Appl. Math. 2014, 4, 83–91. [Google Scholar]
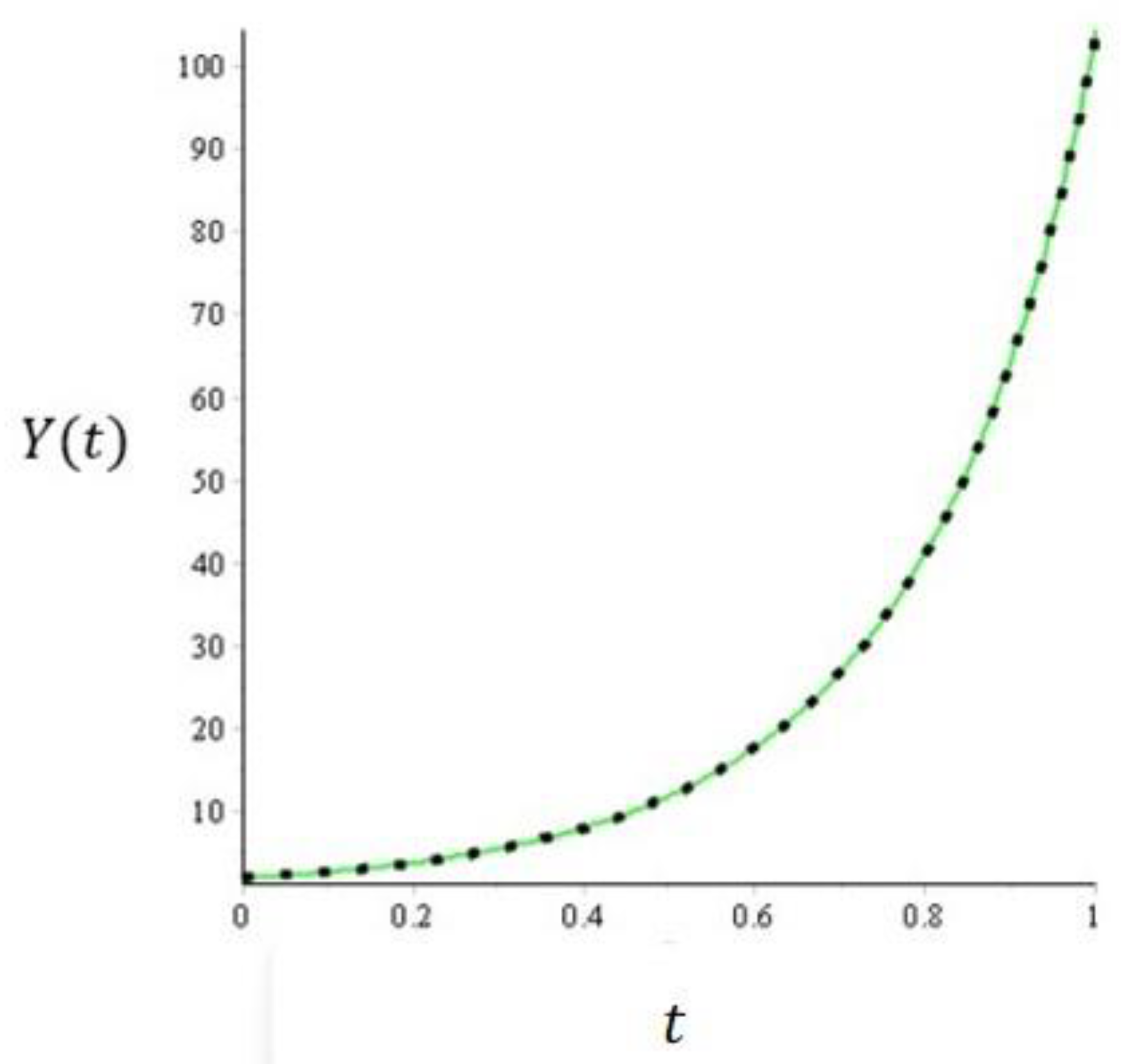
| Approximate Solution | ||||
|---|---|---|---|---|
| 0 | 2 | 2 | 2 | 2 |
| 0.2 | 9.687973998 | 6.260302407 | 4.710244008 | 3.861227413 |
| 0.4 | 46.21972094 | 19.56419792 | 11.57216925 | 8.074385875 |
| 0.6 | 328.0381130 | 69.24841234 | 30.29195286 | 17.79339967 |
| 0.8 | 3635.669747 | 331.8435757 | 87.92003272 | 41.22290131 |
| 1 | 38,049.84591 | 2366.054814 | 321.7714120 | 103.9547603 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johansyah, M.D.; Supriatna, A.K.; Rusyaman, E.; Saputra, J. The Existence and Uniqueness of Riccati Fractional Differential Equation Solution and Its Approximation Applied to an Economic Growth Model. Mathematics 2022, 10, 3029. https://doi.org/10.3390/math10173029
Johansyah MD, Supriatna AK, Rusyaman E, Saputra J. The Existence and Uniqueness of Riccati Fractional Differential Equation Solution and Its Approximation Applied to an Economic Growth Model. Mathematics. 2022; 10(17):3029. https://doi.org/10.3390/math10173029
Chicago/Turabian StyleJohansyah, Muhamad Deni, Asep Kuswandi Supriatna, Endang Rusyaman, and Jumadil Saputra. 2022. "The Existence and Uniqueness of Riccati Fractional Differential Equation Solution and Its Approximation Applied to an Economic Growth Model" Mathematics 10, no. 17: 3029. https://doi.org/10.3390/math10173029
APA StyleJohansyah, M. D., Supriatna, A. K., Rusyaman, E., & Saputra, J. (2022). The Existence and Uniqueness of Riccati Fractional Differential Equation Solution and Its Approximation Applied to an Economic Growth Model. Mathematics, 10(17), 3029. https://doi.org/10.3390/math10173029







