Abstract
In order to overcome the problem of the low fitting accuracy of the expected improvement point infill criteria (EI) and the improved expected improvement point infill criteria (IEI), a high-precision surrogate modeling method based on the parallel multipoint expected improvement point infill criteria (PMEI) is presented in this paper for solving large-scale complex simulation problems. The PMEI criterion takes full advantage of the strong global search ability of the EI criterion and the local search ability of the IEI criterion to improve the overall accuracy of the fitting function. In the paper, the detailed steps of the PMEI method are introduced firstly, which can add multiple sample points in a single iteration. At the same time, in the process of constructing the surrogate model, it is effective to avoid the problem of the low fitting accuracy caused by adding only one new sample point in each iteration of the EI and IEI criteria. The numerical examples of the classical one-dimensional function and two-dimensional function clearly demonstrate the accuracy of the fitting function of the proposed method. Moreover, the accuracy of the multi-objective optimization surrogate model of a truck cab constructed by the PMEI method is tested, which proves the feasibility and effectiveness of the proposed method in solving high-dimensional modeling problems. All these results confirm that the Kriging model developed by the PMEI method has high accuracy for low-dimensional problems or high-dimensional complex problems.
MSC:
65Y05
1. Introduction
The surrogate model optimization method is considered as the most important and efficient analysis method, which has become one of the hot research topics in the engineering fields [,,,]. Bacigalupo applied the surrogate model optimization method to the field of architected materials and proposed an efficient algorithm strategy based on machine learning technology, which effectively solved the computational efficiency problem related to seeking the optimal solution of strong nonlinear and unilateral constraint problems in the large-scale multidimensional space of design parameters []. Tian proposed an enhanced variable-fidelity surrogate model optimization method to improve the global optimizing ability of surrogate-based optimizations []. At present, the widely used surrogate model construction techniques mainly include the Response Surface Methodology (RSM) [], Radial Basis Functions (RBF) [], Kriging interpolation method and Support Vector Machine (SVM) []. Among these methods, the Kriging model not only has high accuracy in fitting linear and high-order nonlinear functions but can also obtain the response value and predict the variance, which has attracted more and more attention.
As an important surrogate model construction method, the Kriging method has been widely applied to the automotive engineering, computer engineering, electromagnetics and aerospace fields [,,,,,]. Designing reasonable point infill criteria is the core technology of the Kriging method, which is very important to improve the efficiency and accuracy of the surrogate model. Therefore, in recent years, the Kriging model has been studied by many scholars and a series of improved methods have been put forward. Fuhg [] reviewed and summarized the different types of Kriging adaptive schemes proposed in the literature and introduced the main principles of different adaptive technologies in detail. Kaps [] proposed an optimization scheme based on a hierarchical Kriging for large-scale and highly nonlinear crashworthiness problems. In order to minimize the global Kriging variance, Xiao put forward a novel sampling algorithm to adaptively sample landmarks that was associated with a high information capacity []. To effectively analyze the interval-valued data, Bean developed an interval-valued Kriging based on the modification of the random sets theory []. Maia [] combined an adaptive Kriging framework with a hybrid particle swarm optimization (PSO) algorithm to improve the computational efficiency of the optimization process. Koziel and Pietrenko-Dabrowska conducted a series of in-depth studies on the agent model of antenna electromagnetic simulation and proposed some effective agent model modeling methods, including nested Kriging, gradient enhanced Kriging, etc., in order to effectively reduce the modeling time cost [,,,]. Moreover, the EI is the most widely used point infill criterion in the Kriging model, so as to improve the accuracy and efficiency of the surrogate model. The research on the improvement of the EI point infill criterion has become a hotspot. Jones proposed an improved expectation improvement (EI) method, which can search for points with large model prediction errors in the entire region, balance global accuracy and local accuracy and achieve the purpose of optimizing the overall accuracy of the surrogate model []. In order to improve modeling efficiency, Kleijnen proposed an improved estimator of the Kriging predictor variance []. For the efficient estimation of small failure probabilities, Cadini put forward an algorithm, which combined FORM to an adaptive Kriging-based importance sampling strategy []. Marzat considered an algorithm strategy in which expected improvement was computed in the minimax optimization context, which allowed to further reduce the number of costly evaluations of the performance index [].
With the increasing complexity of computational models in engineering, parallel computing and optimization have become an important way to improve the computational efficiency and accuracy of large-scale models [,]. As can be seen from the above, most of the existing research mainly focuses on the single-point infill criteria and less on the parallel-point infill criteria. Single-point infill criteria can only generate one sample point in each iteration, which is low in optimization efficiency and the accuracy of the surrogate model. Therefore, based on the introduction of the Kriging model EI and IEI point infill criterion, this paper proposes a parallel multipoint infill criterion, named the PMEI method. Firstly, the detailed steps of constructing the Kriging model based on the PMEI point infill criteria are introduced, which realize the effect of adding multiple points in an iterative process. Then, the classical one-dimensional function and two-dimensional function are used to test the accuracy of the PMEI method. Finally, taking the truck cab as the research object, the PMEI method is used to create the Kriging surrogate model for multi-objective optimization of the truck cab and test the accuracy of the model. The results show that the PMEI point infill criterion can improve the accuracy of the complex surrogate model, which demonstrates the capability and potential of this method in solving the high-dimensional model of engineering practice.
2. Kriging Model of Point Infill Criterion
When constructing the surrogate model, the design variables and their response values of the samples are usually obtained by the experimental design. Then, the prediction point data are obtained by fitting or interpolating the obtained sample point set. In the process of constructing a surrogate model, the randomness of sampling leads to some differences between the surrogate model and the real target value in some regions. Therefore, the point infill criterion is very important to improve the accuracy of the surrogate model.
2.1. Kriging Model
The Kriging method is mainly based on the known position and correlation of known samples to obtain the linear unbiased variable with the smallest estimation error in the unknown region []. Kriging equation [] is composed of global approximation model and local model deviation:
where V(x) is a polynomial function of variable x, β is the regression coefficient, V(x)·β is used to express the overall trend of the function of G(x), Z(x) is the realization of a normally distributed Gaussian random process with mean zero, and variance σ2, which is used to represent the global local deviation. For n sample points, the covariance is given by the following expression:
where RN represents N × N correlation matrix and is the correlation equation between two points xi and xj, and its expression is shown in formula:
where and represent the s-th component at points xi and xj, and θs is the undetermined parameter, which can be calculated by maximum likelihood estimation:
It can be seen from the above formula that the coefficient θs in the correlation function must be calculated to obtain the surrogate model.
For the known sample point x and response G(x), the regression coefficient and random process are estimated as:
where l is the N-dimensional unit column vector and Y is the N-dimensional column vector.
Using Kriging model, the response value [] and estimated variance can be expressed as follows:
where u(x0) = lTR−1r(x0) − l, r represents the correlation vector between the unknown point x0 and the sample point, and its expression is given by:
2.2. Expected Improvement Point Infill Criteria (EI)
Jones [] proposed the improved expected improvement (EI) method, which is one of the most widely used point infill criteria at present. When designing the experiment, there may be a point xt where the estimated value is smaller than the known best (usually minimum) value Gmin. Adding this point to the existing sample set can improve the predicted value of Kriging surrogate model in the optimal value region. The improvement at point xt is defined as . For Kriging model, it is assumed that variable Y obeys normal distribution , where is the predicted response value of Kriging surrogate model and is the predicted variance. Then, the expected expression [] is expressed as:
where Φ(*) denotes the distribution function and φ(*) denotes the density function of the standard normal distribution. Meanwhile, if , it means that the estimated value can not be improved at this point, and I = 0.
As can be seen from Equation (10), the essence of EI criteria of Kriging model is to search for the point with the smallest predicted value or the point with the largest variance in the design space. Consequently, this method ignores the search for the maximum region of the prediction target.
2.3. Improved Expected Improvement Point Infill Criteria (IEI)
In view of the shortcomings of EI criteria, Henkenjohann and Kunert [] proposed IEI criteria to enhance the search ability of the global maximum area, and its expression is as follows:
where Gmax represents the current best. Therefore, the new improved expectation expression is defined by:
Although IEI criteria can improve the global accuracy of the surrogate model, it often needs to add more sample points to improve the local accuracy. This will lead to low iterative efficiency of surrogate model. In other words, with the same number of samples, the accuracy of the surrogate model constructed by IEI criterion is relatively low, especially in the complex high-dimensional computing model.
2.4. Parallel Multipoint Expected Improvement Point Infill Criteria (PMEI)
From the above analysis, it can see that the single EI and IEI criteria both have their own limitations. In order to complement the advantages of the two criteria, a PMEI criterion based on EI and IEI criteria is proposed. Using the EI and IEI point infill criteria can achieve the effect of adding two points simultaneously. In the process of surrogate model construction, adding multiple sample points can not only accelerate the fitting efficiency of surrogate model but also improve the fitting accuracy.
The flowchart of the PMEI criteria can be shown in Figure 1. The detailed optimization modeling processes of the PMEI criteria are described as follows. Step1, initial experiment design. For the objective function, N initial sample points of design variables are generated by optimal Latin hypercube design. Step2, sample response. According to the numerical simulation analysis, the response of the sample is calculated. Step3, construct Kriging model. The Kriging surrogate model is constructed by using the design variables and responses of the initial sample set. Step4, accuracy test of Kriging surrogate model. The accuracy of the new model is calculated according to the accuracy evaluation criteria to judge whether it meets the optimization requirements. Step5, if the accuracy evaluation criteria are not met, calculate EI criteria and IEI criteria to obtain multiple new sample points. In particular, duplicate sample points are generated between these new sample points or between the new sample point and the initial sample point. Step6, repeat step4 and step5 until the accuracy of the surrogate model meets the accuracy evaluation standard. Then, the final optimized Kriging surrogate model is obtained.
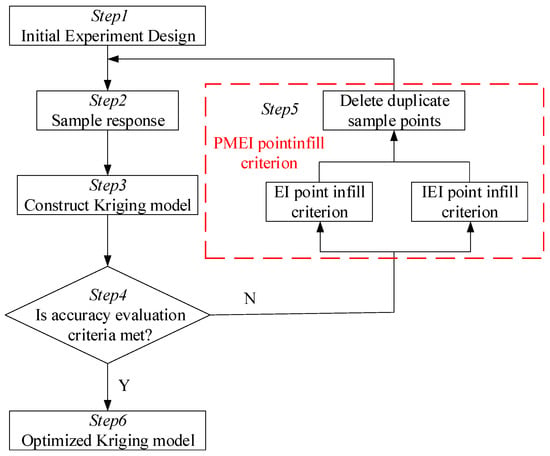
Figure 1.
The flowchart of the PMEI method.
3. Numerical Tests for The PMEI Method
In order to verify the effectiveness of the PMEI point infill criteria, the Kriging models of the classical one-dimensional function and two-dimensional function are constructed by the EI, IEI and PMEI methods, respectively. The fitting accuracy and the efficiency of different methods are compared and analyzed.
3.1. One-Dimensional Function Example
The expression of one-dimensional function is: f(x) = x2*cos(3x) + (0.1x + 2)*sin(x) + (x − 1)2, x ∈ [0, 9].
Six initial sample points are extracted by optimal Latin hypercube design (Opt LHD), and the one-dimensional function is optimized by EI, IEI and PMEI methods, with 10, 10 and 5 iterations, respectively. In addition, in order to be more intuitive, the accuracy of the Kriging models is evaluated by several evaluation criteria in this case. The Kriging model curves and the absolute error curves are shown in Figure 2 and Figure 3, respectively, and the R2 and RMAE values of different methods are shown in Figure 4.
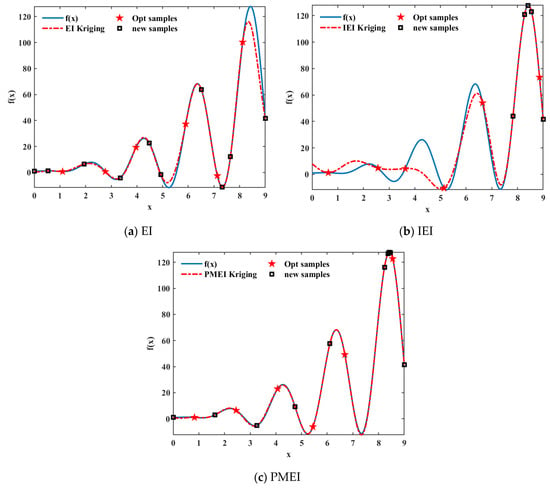
Figure 2.
The Kriging curve of one-dimensional function.
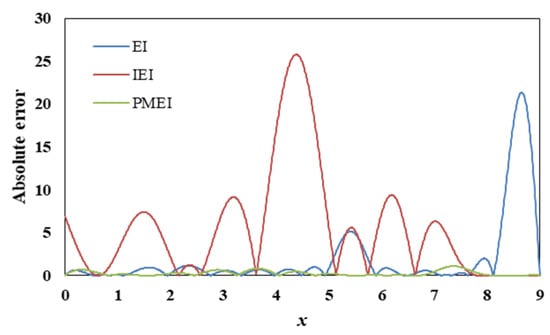
Figure 3.
The absolute error of one-dimensional function.
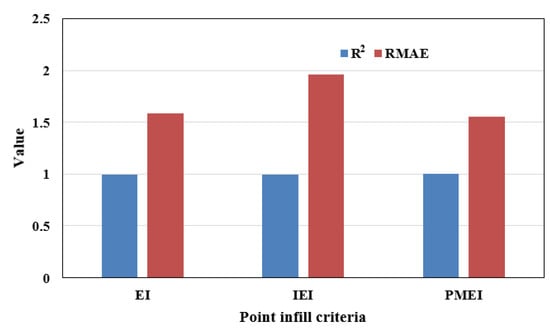
Figure 4.
The R2 and RMAE values of different methods.
In addition, the determination coefficient R2 [] and the relative maximum absolute error RMAE [] are used to evaluate the global accuracy and local accuracy of the surrogate models, respectively. The calculation expressions of R2 and RMAE are as follow:
where is the true value of sample points, is the predicted value of Kriging model, s(x) is the sample standard deviation and μ(x) is the sample mean. Obviously, if RMAE is close to 0, it indicates that the local accuracy of the model is high. Similarly, if R2 is close to 1, it means that the surrogate model has more accurate global accuracy. Overall, the closer the value of R2 to 1 and the smaller the values of RMAE, the better the surrogate accuracy.
As can be seen from Figure 2a, the distribution of the new sample points of the EI method is relatively uniform, which has good global fitting accuracy. However, comparing the EI fitting function with the original function curve, the search ability of the EI method in the maximum region is relatively weak, and the local fitting accuracy is low. As can be seen from Figure 2b, the new sample points of the IEI method are concentrated in the maximum region and have high local fitting accuracy in this region. Nevertheless, because there are few new sample points in other places, the global fitting accuracy of the IEI method is relatively low. Obviously, the Kriging model based on the PMEI method is in good agreement with the original function, as can be seen from Figure 2c. The new sample points of the PMEI method are not only relatively uniform but also have very high fitting accuracy in both the minimum and maximum regions. Figure 3 shows the absolute error curves of the three methods. It is obvious that the absolute errors of the PMEI Kriging model are smaller than those of the EI Kriging model and the IEI Kriging model. It can be clearly seen from Figure 4 that although the R2 values of the Kriging model of the three methods are almost equal to 1, the RMAE value of the PMEI method is larger than that of the other two methods. On the whole, the PMEI complements the advantages of the EI and IEI, which not only improves the global accuracy but also improves the local accuracy of the Kriging model.
3.2. Two-Dimensional Function Example
The expression of two-dimensional function is: f(x,y) = y*sin(x) − x*sin(y), x, y ∈ [0, 5].
Five initial sample points are extracted by optimal Latin hypercube sampling method, and the two-dimensional function is optimized by EI, IEI and PMEI methods, with 6, 6 and 3 iterations, respectively. Moreover, the accuracy of the Kriging models is evaluated by four evaluation criteria in this case. The results on the predicted MSEs and absolute errors of the three criterions for two-dimensional problems are shown in Figure 5 and Figure 6, respectively, and the R2 and RMAE values of different methods are shown in Figure 7.
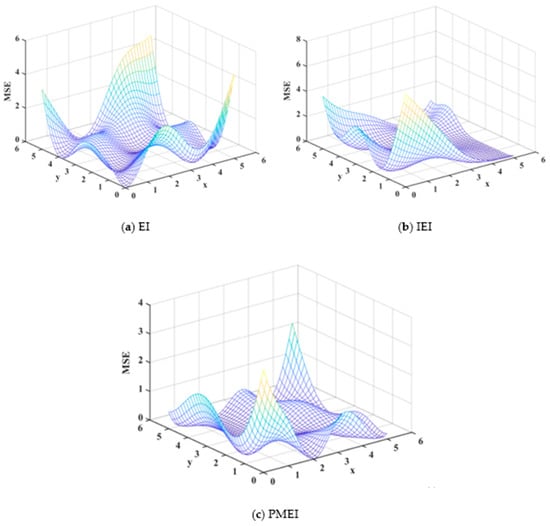
Figure 5.
Test results on the predicted MSE for the two-dimensional function.
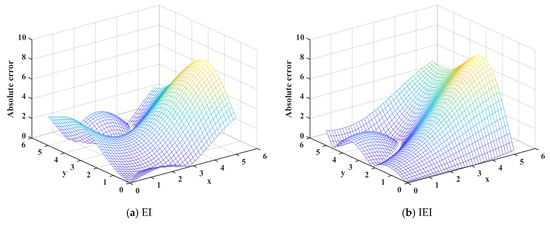
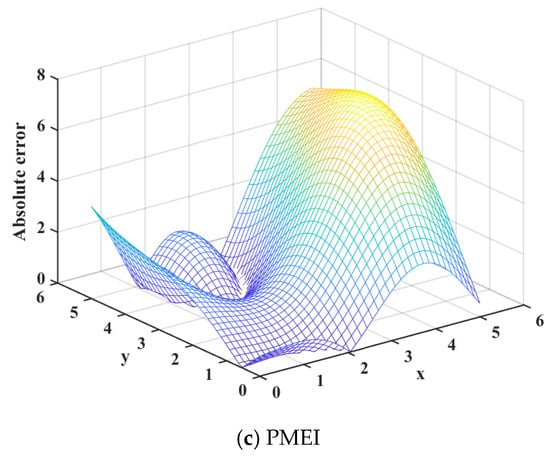
Figure 6.
The absolute error for the two-dimensional function.
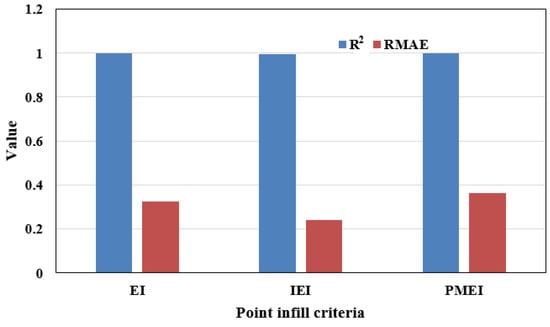
Figure 7.
The R2 and RMAE values of different methods.
It can be seen from the mean square error analysis results of the surrogate model generated by the three point adding criteria in Figure 5, the mean square error of the PMEI is less than the EI and IEI, which means that the surrogate model constructed by the PMEI criterion has better accuracy. Simultaneously, it can be seen from Figure 6 that the absolute error of the PMEI Kriging model is smaller than that of the EI Kriging and IEI Kriging models. Figure 7 shows the R2 and RMAE values of the surrogate models established by the three methods, which shows that the PMEI method has very good accuracy, despite that the RMAE value of the PMEI is worse than the EI and IEI methods when the same number of total iterations are taken into account. In addition, the shape and characteristics of the test function and surrogate model based on the PMEI criterion are shown in Figure 8 and the distribution of the sampling points is shown in Figure 9. It can be clearly seen that the surrogate model created by the PMEI has a smooth shape and good fitting compared with the original function. The PMEI method can construct an appropriate Kriging model to replace the original function. In a word, it shows that the proposed method can provide good modeling accuracy. Therefore, the PMEI method is verified to be effective for two-dimensional problems.
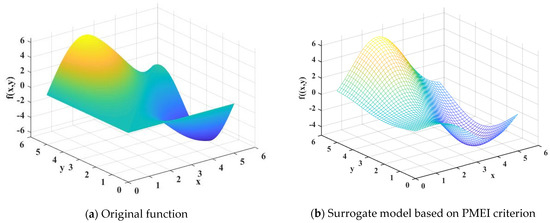
Figure 8.
Shape and characteristics of the two-dimensional functions.
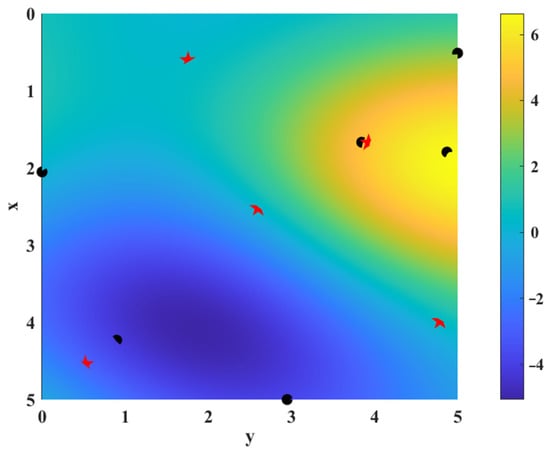
Figure 9.
Sampling points for the two-dimensional function.
4. Kriging Surrogate Model of a Truck Cab
The calculation accuracy of the PMEI has been numerically tested by the one-dimensional function and two-dimensional function, respectively, in Section 3. However, for the complex engineering calculation, the accuracy of the PMEI needs to be further verified.
The structural optimization design of truck cab crash safety is a multi-objective optimization problem, which requires a repeated finite element analysis [,,,]. In the automotive industry, A-pillar impact is usually used to design and verify the safety of vehicle structures [,]. Therefore, as an example, the surrogate model of a truck cab is constructed, and the accuracy of the model is tested in this paper. First, the finite element model of the truck cab is established in HyperMesh software according to the ECE R-29 standard, which is shown in Figure 10. Afterward, the A-pillar collision simulation is carried out by the LS-DYNA solver, and the deformation of the cab is shown in Figure 11.
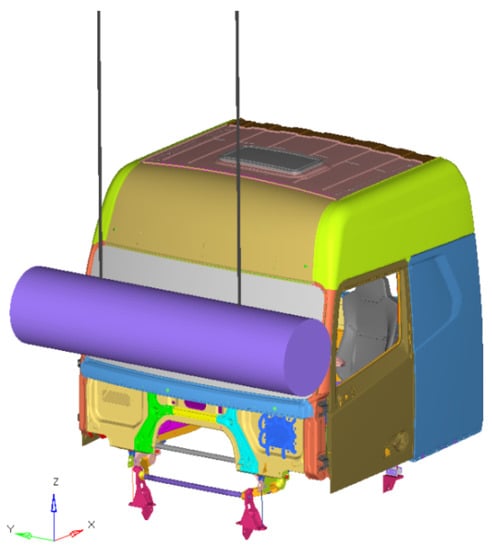
Figure 10.
Finite element model of the truck cab.
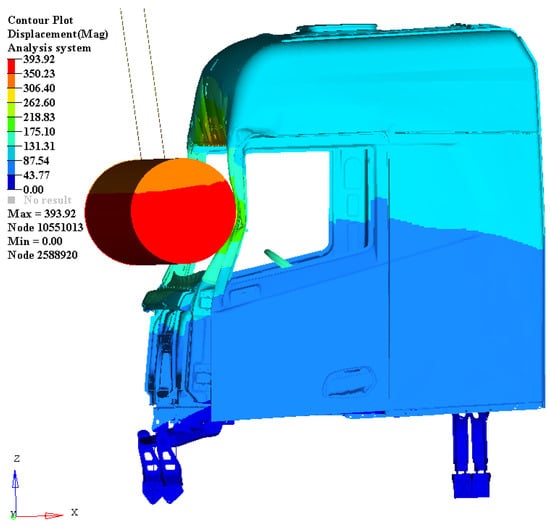
Figure 11.
Deformation of the truck cab.
4.1. Construction of Surrogate Model
According to the ECE R-29 standard, the crash safety performance of the cab is tested by measuring the living space of the fiftieth-percentile male manikin model after the crash test []. Specifically, the living space is represented by characteristic dimensions, which means the minimum distances between the manikin and any inelastic part of the cab. Therefore, the minimum distance Lmin between the steering column and the manikin knee after the A-pillar impact test simulation is extracted as the characteristic dimensions of the living space of the cab, which is shown in Figure 12. Hence, it is necessary to construct Kriging surrogate models of the cab A-pillar collision safety index Lmin.
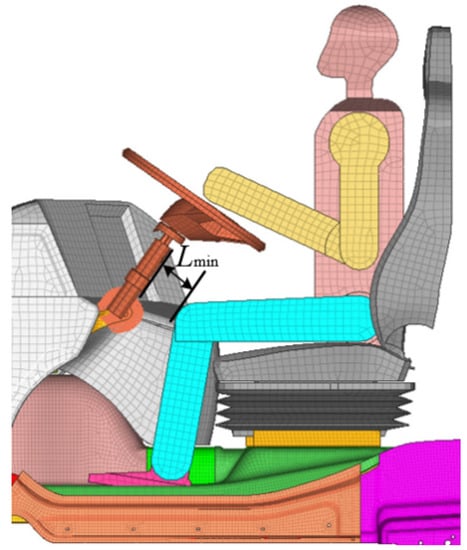
Figure 12.
Schematic diagram of the characteristic dimensions.
Considering that the thickness of the parts has a direct impact on the crash safety of the cab, the thickness of the top 8 parts (denoted by t1~t8) in the energy absorption sequence during the collision simulation process are extracted as the key design variable, as shown in Figure 13. In this study, it is assumed that the value range of the design variables is 70~120% of the initial thickness; the related data are shown in Table 1.
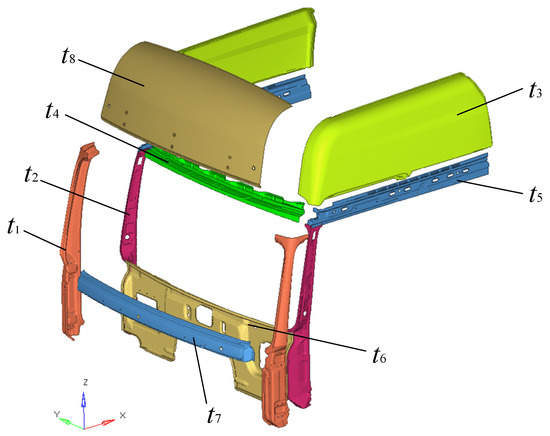
Figure 13.
Illustration of key design variables.

Table 1.
Key design variables and value range.
According to the eight selected design variables, the surrogate model is to construct an approximate function from a series of sampling points, which are typically determined using design of experiment methods. In this study, 40 groups of sample points were generated using the optimal Latin hypercube sampling method. Then, the 40 thickness design variables are substituted into the A-pillar collision finite element model of the truck cab for the simulation calculation, and the response value Lmin is obtained. For a comparative study, the surrogate models of the cab are constructed based on the EI, IEI and PMEI methods, respectively, according to the 40 sample points and response values. Then, the surrogate models are optimized with 120, 120 and 60 iterations, respectively.
4.2. Accuracy Assessment of Surrogate Model
To evaluate the accuracy of these three different surrogate schemes, 10 new validation points are also generated by using the optimal Latin cube sampling method here. According to Equations (13) and (14), respectively, the relative maximum absolute error RMAE and the determination coefficient R2 were used to measure the accuracy of these three different surrogate models; the analysis results are shown in Figure 14.
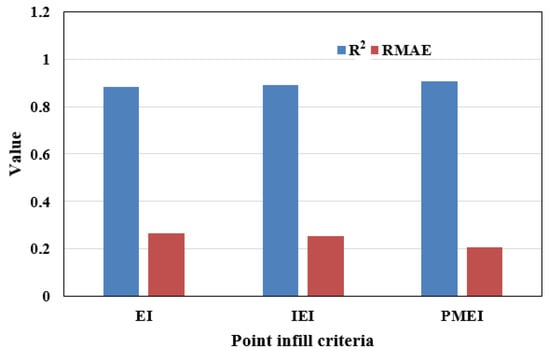
Figure 14.
The R2 and RMAE values of different methods.
The assessment results are compared in Figure 14. Apparently, the RMAE values of the surrogate model based on the PMEI criteria are less than that of the EI criteria and IEI criteria. Meanwhile, the R2 values of the surrogate model based on the PMEI criteria are greater than that of the EI criteria and IEI criteria. By comparative analysis, the surrogate models constructed by the PMEI criterion have large R2 values and small RMAE values, which means that they have not only good global accuracy but also better local accuracy. In conclusion, the truck cab surrogate model based on the PMEI method has high accuracy and can be applied to replace the original complex model in engineering practice. Consequently, the PMEI method of constructing a high-precision surrogate model is effective and feasible for high-dimensional modeling.
5. Conclusions
This paper proposes a PMEI method of a Kriging surrogate model based on the EI criterion and IEI criterion. Moreover, numerical examples of one-dimensional function and two-dimensional function are used to verify the accuracy of the PMEI surrogate model. Compared with the EI and IEI single-point infill criteria, the PMEI method can improve the global accuracy of the surrogate model. In order to verify the effectiveness of the PMEI criterion in constructing a high-dimensional model, the surrogate model of a truck cab is constructed by the EI, IEI and PMEI criterion, respectively. Then, the accuracy evaluation indexes R2 and RMAE of different surrogate models are compared and analyzed. The research results show that the cab surrogate model created by the PMEI criterion has higher accuracy and can meet the needs for engineering practical application. Therefore, the method of constructing a high-precision surrogate model by PMEI criterion has advantages in complex engineering problems.
Author Contributions
Conceptualization, S.L. and J.W. (Jian Wen); methodology, S.L., J.W. (Jun Wang) and J.W. (Jian Wen); software, J.W. (Jun Wang) and S.Y.; validation, S.L., J.W. (Jian Wen) and W.L.; formal analysis, J.W. (Jun Wang); investigation, J.W. (Jun Wang) and S.L.; resources, W.L.; data curation, J.W. (Jian Wen); writing—original draft preparation, S.L. and J.W. (Jian Wen); writing—review and editing, S.L. and J.W. (Jian Wen); visualization, S.Y.; supervision, S.L. and W.L.; project administration, S.L. and W.L.; funding acquisition, S.L. and W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Hubei Province under Grant 2020CFB510 and the New Energy, Lightweight, Intelligent Key Core Technology Research and Development Project of Suizhou China.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Acknowledgments
The useful contributions and discussions from project partners are also acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, B.L.; Yan, L.; Duan, X.J.; Yu, T.P.; Zhang, H. An integrated surrogate model constructing method: Annealing combinable Gaussian process. Inf. Sci. 2022, 591, 176–194. [Google Scholar] [CrossRef]
- Brigham, J.C.; Aquino, W. Surrogate-Model Accelerated Random Search algorithm for global optimization with applications to inverse material identification. Comput. Methods Appl. Mech. Eng. 2007, 196, 4561–4576. [Google Scholar] [CrossRef]
- Peng, Z.; Zhou, H.; Li, Y.; Li, D.Q. Process parameters optimization of injection molding using a fast strip analysis as a surrogate model. Int. J. Adv. Manuf. Technol. 2010, 49, 949–959. [Google Scholar]
- Koziel, S.; Pietrenko-Dabrowska, A. Rapid multi-objective optimization of antennas using nested kriging surrogates and single-fidelity EM simulation models. Eng. Comput. 2020, 37, 1491–1512. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Gnecco, G.; Lepidi, M.; Gambarotta, L. Computational design of innovative mechanical metafilters via adaptive surrogate-based optimization. Comput. Methods Appl. Mech. Eng. 2021, 375, 113623. [Google Scholar] [CrossRef]
- Tian, K.; Li, Z.; Huang, L.; Du, K.; Jiang, L.; Wang, B. Enhanced variable-fidelity surrogate-based optimization framework by Gaussian process regression and fuzzy clustering. Comput. Methods Appl. Mech. Eng. 2020, 366, 113045. [Google Scholar] [CrossRef]
- Ahmadi, A.; Rezaei, M.; Sadeghieh, S.M. Interaction effects of flotation reagents for SAG mill reject of copper sulphide ore using response surface methodology. Trans. Nonferr. Met. Soc. China 2021, 31, 792–806. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Qi, H.; Jiang, D.H.; He, M.J.; Ren, Y.T.; Su, M.X.; Cai, X.S. Acoustic tomography of two dimensional velocity field by using meshless radial basis function and modified Tikhonov regularization method. Measurement 2021, 175, 109107. [Google Scholar] [CrossRef]
- Tabari, M.M.R.; Sanayei, H.R.Z. Prediction of the intermediate block displacement of the dam crest using artificial neural network and support vector regression models. Soft Comput. 2019, 23, 9629–9645. [Google Scholar] [CrossRef]
- Vasu, S.S.; Davidson, D.F.; Hanson, R.K. Jet fuel ignition delay times: Shock tube experiments over wide conditions and surrogate model predictions. Combust. Flame 2008, 152, 125–143. [Google Scholar] [CrossRef]
- Han, Z.H.; Goertz, S. Hierarchical Kriging Model for Variable-Fidelity Surrogate Modeling. AIAA J. 2012, 50, 1885–1896. [Google Scholar] [CrossRef]
- Kim, J.K.; Kim, Y.J.; Yang, W.H.; Park, Y.C.; Lee, K.H. Structural design of an outer tie rod for a passenger car. Int. J. Automot. Technol. 2011, 12, 375–381. [Google Scholar] [CrossRef]
- Song, X.; Li, M.; Li, Z.; Liu, F. Global Optimization Algorithm Based on Kriging Using Multi-Point Infill Sampling Criterion and Its Application in Transportation System. Sustainability 2021, 13, 10645. [Google Scholar] [CrossRef]
- Belyaev, M.; Burnaev, E.; Kapushev, E.; Alestra, S.; Dormieux, M.; Cavailles, A.; Chaillot, D.; Ferreira, E. Building Data Fusion Surrogate Models for Spacecraft Aerodynamic Problems with Incomplete Factorial Design of Experiments. Adv. Mater. Res. 2014, 3413, 405–412. [Google Scholar]
- Koziel, S.; Pietrenko-Dabrowska, A. Reduced-cost surrogate modelling of compact microwave components by two-level kriging interpolation. Eng. Comput. 2020, 52, 960–972. [Google Scholar] [CrossRef]
- Fuhg, J.N.; Fau, A.; Nackenhorst, U. State-of-the-Art and Comparative Review of Adaptive Sampling Methods for Kriging. Arch. Comput. Methods Eng. 2020, 28, 2689–2747. [Google Scholar] [CrossRef]
- Kaps, A.; Czech, C.; Du, D.E. A hierarchical kriging approach for multi-fidelity optimization of automotive crashworthiness problems. Struct. Multidiscip. Optim. 2022, 65, 114. [Google Scholar] [CrossRef]
- Xiao, C.X. Nonmyopic Informative Path Planning Based on Global Kriging Variance Minimization. IEEE Robot. Autom. Lett. 2022, 7, 1768–1775. [Google Scholar] [CrossRef]
- Bean, B.; Sun, Y.; Maguire, M. Interval-valued kriging for geostatistical mapping with imprecise inputs. Int. J. Approx. Reason. 2022, 140, 31–51. [Google Scholar] [CrossRef]
- Maia, M.A.; Pa, R.E.; Melo, A.D. Kriging-based optimization of functionally graded structures. Struct. Multidiscip. Optim. 2021, 64, 1887–1908. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Design-oriented computationally-efficient feature-based surrogate modelling of multi-band antennas with nested kriging. Int. J. Electron. Commun. (AEÜ) 2020, 120, 153202. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A. Low-cost performance-driven modelling of compact microwave components with two-layer surrogates and gradient kriging. Int. J. Electron. Commun. (AEÜ) 2020, 126, 153419. [Google Scholar] [CrossRef]
- Pietrenko-Dabrowska, A.; Koziel, S.; AL-HASAN, M. Cost-Efficient Bi-Layer Modeling of Antenna Input Characteristics Using Gradient Kriging Surrogates. IEEE Access 2020, 8, 140831–140839. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A.; Al-Hzsan, M. Design-Oriented Two-Stage Surrogate Modeling of Miniaturized Microstrip Circuits With Dimensionality Reduction. IEEE Access 2020, 8, 121744–121754. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Jack, P.C.; Kleijnen; Wim, B.; Inneke, N. Expected improvement in efficient global optimization through bootstrapped kriging. J. Glob. Optim. 2012, 54, 59–73. [Google Scholar]
- Cadini, F.; Santos, F.; Zio, E. An improved adaptive kriging-based importance technique for sampling multiple failure regions of low probability. Reliab. Eng. Syst. Saf. 2014, 131, 109–117. [Google Scholar] [CrossRef]
- Marzat, J.; Walter, E.; Piet-Lahanier, H. A new expected-improvement algorithm for continuous minimax optimization. J. Glob. Optim. 2016, 64, 785–802. [Google Scholar] [CrossRef]
- Li, Y.; Cao, Y.; Liu, Z.; Liu, Y.; Jiang, Q. Dynamic optimal reactive power dispatch based on parallel particle swarm optimization algorithm. Comput. Math. Appl. 2009, 57, 1835–1842. [Google Scholar] [CrossRef]
- París, J.; Colominas, I.; Navarrina, F.; Casteleiro, M. Parallel computing in topology optimization of structures with stress constraints. Comput. Struct. 2013, 125, 62–73. [Google Scholar] [CrossRef]
- Joseph, V.R.; Hung, Y.; Sudjianto, A. Blind Kriging: A New Method for Developing Metamodels. J. Mech. Des. 2008, 130, 350–353. [Google Scholar] [CrossRef]
- Dey, S.; Mukhopadhyay, T.; Adhikari, S. Stochastic free vibration analyses of composite shallow doubly curved shells—A Kriging model approach. Compos. Part B Eng. 2015, 70, 99–112. [Google Scholar] [CrossRef]
- Parr, J.M.; Keane, A.J.; Forrester, A.I.J.; Holden, C.M.E. Infill sampling criteria for surrogate-based optimization with constraint handling. Eng. Optim. 2012, 44, 1147–1166. [Google Scholar] [CrossRef]
- Henkenjohann, N.; Kunert, J. An efficient sequential optimization approach based on the multivariate expected improvement criterion. Qual. Eng. 2007, 19, 267–280. [Google Scholar] [CrossRef]
- Zahedan, N.; Ahmadi, H.; Liaghat, G.H. Experimental and numerical investigation on the multi-optimization of reinforcing the side members of the vehicle structure. Arch. Civ. Mech. Eng. 2021, 22, 25. [Google Scholar] [CrossRef]
- Liao, X.; Li, Q.; Yang, X.; Zhang, W.; Li, W. Multiobjective optimization for crash safety design of vehicles using stepwise regression model. Struct. Multidiscip. Optim. 2007, 35, 561–569. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Simpson, T.W. Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidiscip. Optim. 2001, 23, 1–13. [Google Scholar] [CrossRef]
- Cui, A.; Xu, L.J.; Zhang, X.B.; Yang, Q. Design of Lightweight Hybrid Materials for the Cab Body-In-White of a Commercial Vehicle Based on Multi-Objective Optimization. Adv. Mater. Res. 2013, 2200, 281–286. [Google Scholar]
- Yin, H.; Wen, G.; Fang, H.; Qing, Q.; Kong, X.; Xiao, J.; Liu, Z. Multiobjective crashworthiness optimization design of functionally graded foam-filled tapered tube based on dynamic ensemble metamodel. Mater. Des. 2014, 55, 747–757. [Google Scholar] [CrossRef]
- Kodiyalam, S.; Yang, R.J.; Gu, L.; Tho, C.H. Multidisciplinary design optimization of a vehicle system in a scalable, high performance computing environment. Struct. Multidiscip. Optim. 2004, 26, 256–263. [Google Scholar] [CrossRef]
- Chen, D.Y.; Wang, L.M.; Wang, C.Z.; Yuan, L.K.; Zhang, T.Y.; Zhang, Z.Z. Finite element based improvement of a light truck design to optimize crashworthiness. Int. J. Automot. Technol. 2015, 16, 39–49. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).