Stochastic Epidemic Model for COVID-19 Transmission under Intervention Strategies in China
Abstract
:1. Introduction
2. EIQJR COVID-19 Model
3. Global Positive Solution of Stochastic EIQJR Model
4. Asymptotic Behavior of the Disease-Free Equilibrium
5. Asymptotic Behavior around the Endemic Equilibrium
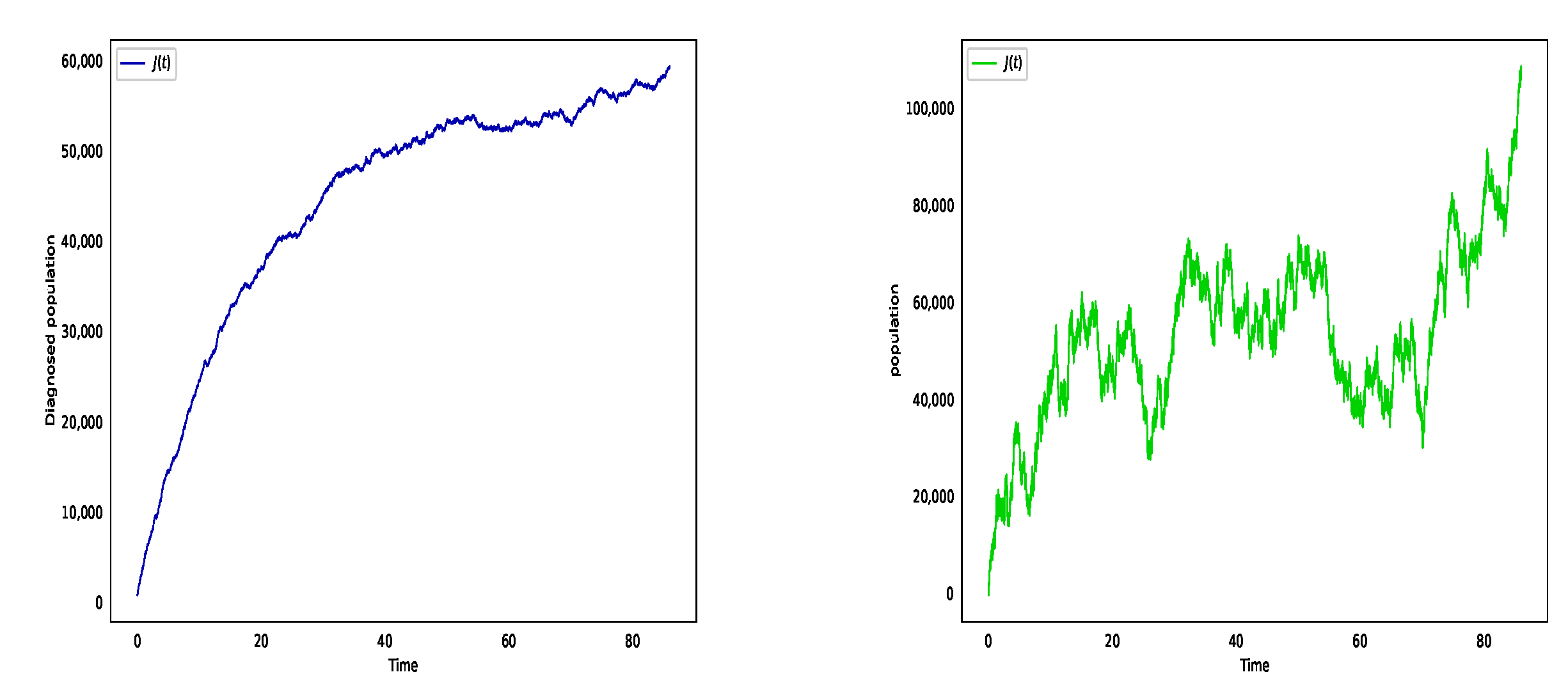
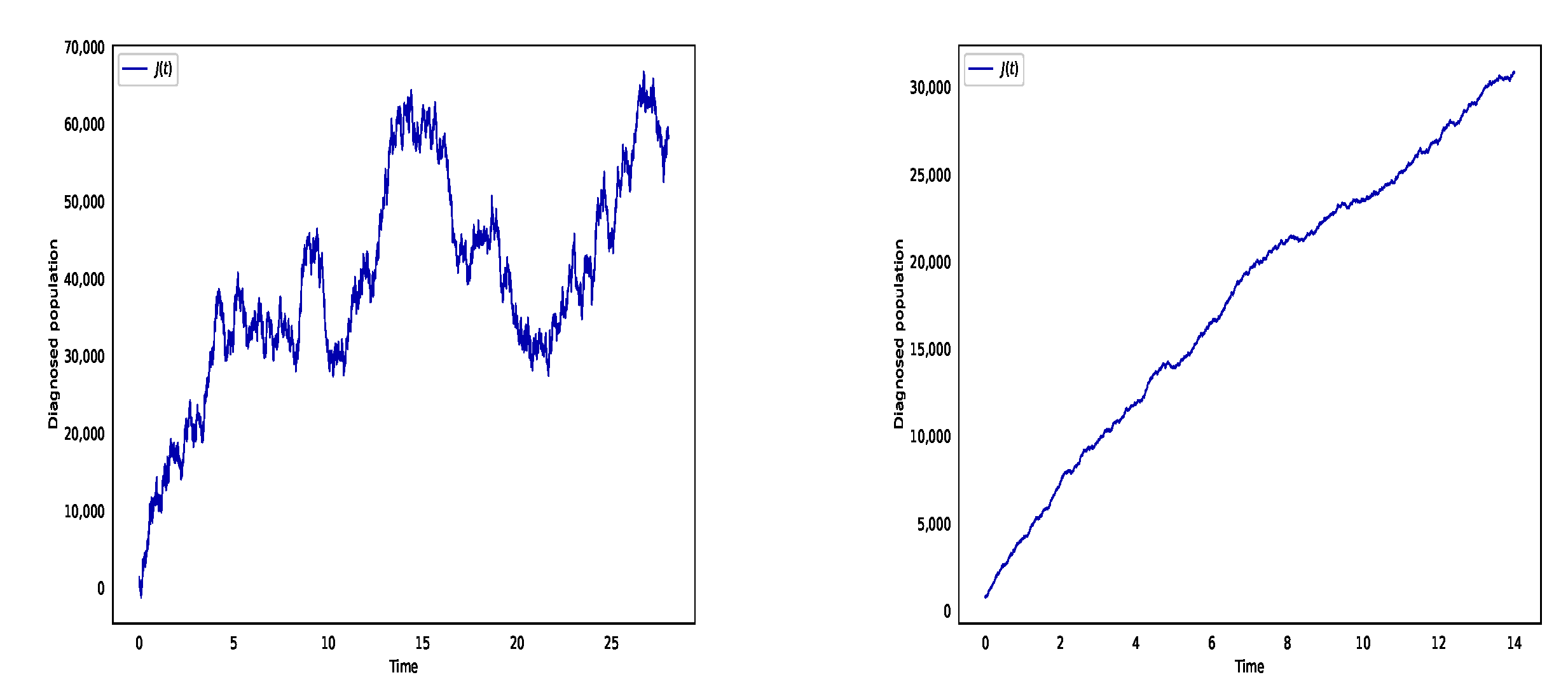
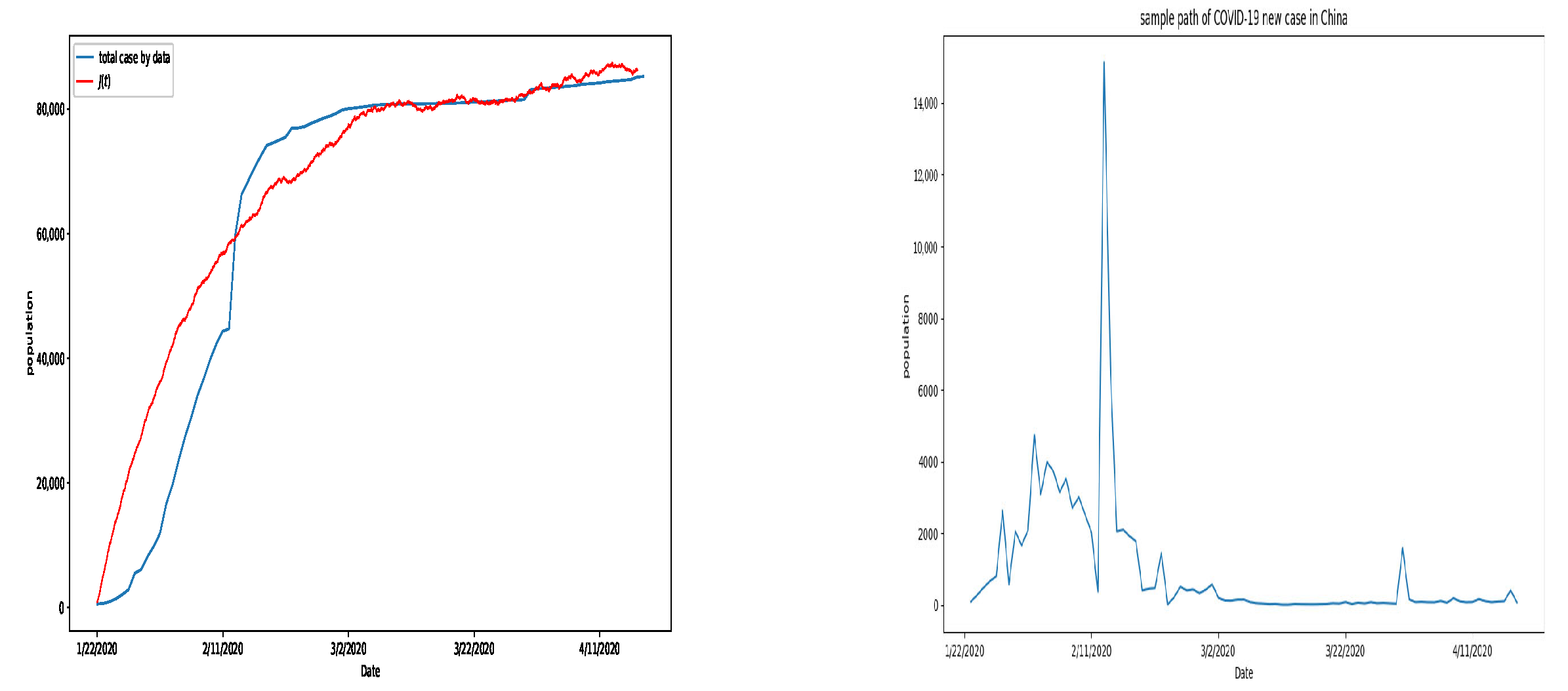
6. Numerical Simulation
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Coronavirus. Available online: https://www.who.int/health-topics/coronavirus (accessed on 19 January 2020).
- World Health Organization. Naming the Coronavirus Disease (COVID-2019) and the Virus That Causes It. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/technical-guidance/naming-the-coronavirus-disease-(covid-2019)-and-the-virus-that-causes-it#:~:text=Human (accessed on 24 February 2020).
- Gorbalenya, A.E.B. Severe acute respiratory syndrome-related coronavirus: The species and its viruses, a statement of the Coronavirus Study Group. bioRxiv 2020. [Google Scholar]
- Gao, Q.; Hu, Y.; Dai, Z.; Xiao, F.; Wang, J.; Wu, J. The epidemiological characteristics of 2019 novel coronavirus diseases (COVID-19) in Jingmen, Hubei, China. Medicine 2020, 99, e20605. [Google Scholar] [CrossRef] [PubMed]
- Thinley, P. Technical comments on the design and designation of biological corridors in Bhutan: Global to national perspectives. J. Renew. Nat. Resour. Bhutan 2010, 6, 91–106. [Google Scholar]
- World Health Organization. Coronavirus Disease 2019. 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (accessed on 18 June 2020).
- How Does Coronavirus Spread? NBC News, 29 January 2020.
- U.S. Centers for Disease Control and Prevention (CDC). How COVID-19 Spreads. Available online: https://www.cdc.gov/coronavirus/2019-ncov/about/transmission.html (accessed on 27 January 2020).
- World Health Organization. Getting Your Workplace Ready for COVID-19. Available online: https://www.who.int/docs/default-source/searo/thailand/getting-your-workplace-ready-for-covid19.pdf?sfvrsn=1a068386_0 (accessed on 3 March 2020).
- Wang, F.S.; Zhang, C. What to do next to control the 2019-nCoV epidemic? Lancet 2020, 395, 391–393. [Google Scholar] [CrossRef]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Feng, Z. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef]
- Zhou, Y.; Ma, Z. A discrete epidemic model for SARS transmission and control in china. Math. Comput. Model. 2004, 40, 1491–1506. [Google Scholar] [CrossRef]
- Lin, Q.; Zhao, S.; Gao, D.; Lou, Y.; Yang, S.; Musa, S.S.; Wang, M.H.; Cai, Y.; Wang, W.; Yang, L.; et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and government action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef]
- Chen, T.M.; Rui, J.; Wang, Q.P.; Zhao, Z.Y.; Cui, J.A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 1–8. [Google Scholar] [CrossRef]
- Tang, S.; Xiao, Y.; Yuan, L.; Cheke, R.A.; Wu, J. Campus quarantine (Fengxiao) for curbing emergent infectious diseases: Lessons from mitigating A/H1N1 in Xian, China. J. Theor. Biol. 2012, 295, 47–58. [Google Scholar] [CrossRef]
- Xiao, Y.; Tang, S.; Wu, J. Media impact switching surface during an infectious disease outbreak. Sci. Rep. 2015, 5, 1–9. [Google Scholar] [CrossRef]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Nat. Med. 2020, 395, 689–697. [Google Scholar] [CrossRef]
- Zeb, A.; Alzahrani, E.; Erturk, V.S.; Zaman, G. Mathematical model for coronavirus disease 2019 (COVID-19) containing isolation class. BioMed Res. Int. 2020, 2020, 3452402. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J. Some discrete-time SI, SIR, and SIS epidemic models. Math. Biosci. 1994, 124, 83–105. [Google Scholar] [CrossRef]
- Jamshidi, S.; Baniasad, M.; Niyogi, D. Global to USA county scale analysis of weather, urban density, mobility, homestay, and mask use on COVID-19. Int. J. Environ. Res. Public Health 2020, 17, 7847. [Google Scholar] [CrossRef]
- Keeling, M.; Rohani, P. Modeling Infectious Diseases in Human and Animals; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Ikram, R.; Khan, A.; Zahri, M.; Saeed, A.; Yavuz, M.; Kumam, P. Extinction and stationary distribution of a stochastic COVID-19 epidemic model with time-delay. Comput. Biol. Med. 2022, 141, 105115. [Google Scholar] [CrossRef]
- Mao, X.; Marion, G.; Renshaw, E. Environmental brownian noise suppresses explosions in population dynamics. Stoch. Process. Their Appl. 2002, 97, 95–110. [Google Scholar] [CrossRef]
- Britton, T. Stochastic epidemic models: A survey. Math. Biosci. 2010, 225, 24–35. [Google Scholar] [CrossRef]
- Ji, C.; Jiang, D.; Shi, N. The behavior of an SIR epidemic model with stochastic perturbation. Stoch. Anal. Appl. 2012, 30, 755–773. [Google Scholar] [CrossRef]
- Tornatore, E.; Buccellato, S.M.; Vetro, P. Stability of a stochastic SIR system. Phys. A 2005, 354, 111–126. [Google Scholar] [CrossRef]
- Tornatore, E.; Vetro, P.; Buccellato, S.M. SIVR epidemic model with stochastic perturbation. Neural Comput. Appl. 2014, 24, 309–315. [Google Scholar] [CrossRef]
- Lahrouz, A.; Omari, L.; Kiouach, D. Global analysis of a deterministic and stochastic nonlinear SIRS epidemic model. Nonlinear Anal. Model. Control 2011, 16, 59–76. [Google Scholar] [CrossRef] [Green Version]
- Hou, T.; Lan, G.; Yuan, S.; Zhang, T. Threshold dynamics of a stochastic SIHR epidemic model of COVID-19 with general population-size dependent contact rate. Math. Biosci. Eng. 2022, 19, 4217–4236. [Google Scholar] [CrossRef] [PubMed]
- Hussain, S.; Madi, E.N.; Khan, H.; Etemad, S.; Rezapour, S.; Sitthiwirattham, T.; Patanarapeelert, N. Investigation of the stochastic modeling of COVID-19 with environmental noise from the analytical and numerical point of view. Mathematics 2021, 9, 3122. [Google Scholar] [CrossRef]
- Tesfaye, A.W.; Satana, T.S. Stochastic model of the transmission dynamics of COVID-19 pandemic. Adv. Differ. Equ. 2021, 2021, 457. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zeb, A.; Hussain, S.; Alzahrani, E. Dynamics of COVID-19 mathematical model with stochastic perturbation. Adv. Differ. Equ. 2020, 2020, 451. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Fu, Y.; Kang, Y. Stochastic analysis of COVID-19 by a SEIR model with lévy noise. Chaos Interdiscip. J. Nonlonear Sci. 2021, 31, 043132. [Google Scholar] [CrossRef]
- Nino-Torres, D.; Rios-Gutierrez, A.; Arunachalam, V.; Ohajunwa, C.; Seshaiyer, P. Stochastic modelling, analysis, and simulation of the COVID-19 pandemic with explicit behavioral changes in Bogota: A case study. Infect. Dis. Model. 2022, 7, 199–211. [Google Scholar] [CrossRef]
- Tesfay, A.; Saeed, T.; Zeb, A.; Tesfay, D.; Khalaf, A.; Brannan, J. Dynamics of a stochastic COVID-19 epidemic model with jump-diffusion. Adv. Differ. Equ. 2021, 2021, 228. [Google Scholar] [CrossRef]
- Arnold, L. Stochastic Differential Equations: Theory and Applications; Wiley: Hoboken, NJ, USA, 1972. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications; Horwood: Chichester, UK, 1997. [Google Scholar]
- Kingi, H. Numerical SDE Simulation-Euler vs. Milstein Methods. Available online: https://hautahi.com/sde-simulation (accessed on 31 December 2019).
- Zhang, W.; Du, R.; Li, B.; Zheng, X.; Yang, X.; Hu, B.; Wang, Y.; Xiao, G.; Yan, B.; Shi, Z.; et al. Molecular and serological investigation of 2019-nCoV infected patients: Implication of multiple shedding routes. Emerg. Microbes Infect. 2020, 9, 386–389. [Google Scholar] [CrossRef]
- Mi, Y.; Huang, T.; Zhang, J.; Qin, Q.; Gong, Y.; Liu, S.; Xue, H.; Ning, C.; Cao, L.; Cao, Y. Estimating instant case fatality rate of COVID-19 in China. Int. J. Infect. Dis. 2020, 97, 1–6. [Google Scholar] [CrossRef]
- Zhang, X.-S.; Vynnycky, E.; Charlett, A.; Angelis, D.D.; Chen, Z.; Liu, W. Transmission dynamics and control measures of COVID-19 outbreak in China: A modelling study. Sci. Rep. 2021, 11, 2652. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Xia, F.; Tang, S.; Bragazzi, N.L.; Li, Q.; Sun, X.; Liang, J.; Xiao, Y.; Wu, J. The effectiveness of quarantine and isolation determine the trend of the COVID-19 epidemic in the final phase of the current outbreak in China. Int. J. Infect. Dis. 2020, 96, 636–647. [Google Scholar] [CrossRef] [PubMed]
- Eissa, M.A.; Zhang, H.; Xiao, Y. Mean-square stability of split-step theta milstein methods for stochastic differential equaitons. Math. Probl. Eng. 2018, 2018, 1682513. [Google Scholar] [CrossRef]
- Eissa, M.A. Mean-square stability of two classes of theta milstein methods for nonlinear stochastic differential equations. Proc. Jangjeon Math. Soc. 2019, 22, 119–128. [Google Scholar]
- Eissa, M.A.; Ye, Q. Convergence, nonnegativity and stability of a new Lobatto IIIC-Milstein method for a pricing option approach based on stochastic volatility model. Jpn. J. Ind. Appl. Math. 2021, 38, 391–424. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Win, Z.T.; Eissa, M.A.; Tian, B. Stochastic Epidemic Model for COVID-19 Transmission under Intervention Strategies in China. Mathematics 2022, 10, 3119. https://doi.org/10.3390/math10173119
Win ZT, Eissa MA, Tian B. Stochastic Epidemic Model for COVID-19 Transmission under Intervention Strategies in China. Mathematics. 2022; 10(17):3119. https://doi.org/10.3390/math10173119
Chicago/Turabian StyleWin, Zin Thu, Mahmoud A. Eissa, and Boping Tian. 2022. "Stochastic Epidemic Model for COVID-19 Transmission under Intervention Strategies in China" Mathematics 10, no. 17: 3119. https://doi.org/10.3390/math10173119
APA StyleWin, Z. T., Eissa, M. A., & Tian, B. (2022). Stochastic Epidemic Model for COVID-19 Transmission under Intervention Strategies in China. Mathematics, 10(17), 3119. https://doi.org/10.3390/math10173119





