Novel Authentication Protocols Based on Quadratic Diophantine Equations

Abstract

The Diophantine equation is a strong research domain in number theory with extensive cryptography applications. The goal of this paper is to describe certain geometric properties of positive integral solutions of the quadratic Diophantine equation $x_1^2+x_2^2=y_1^2+y_2^2(x_1,x_2,y_1,y_2>0)$, as well as their use in communication protocols. Given one pair $(x_1,y_1)$, finding another pair $(x_2,y_2)$ satisfying $x_1^2+x_2^2=y_1^2+y_2^2$ is a challenge. A novel secure authentication mechanism based on the positive integral solutions of the quadratic Diophantine which can be employed in the generation of one-time passwords or e-tokens for cryptography applications is presented. Further, the constructive cost models are applied to predict the initial effort and cost of the proposed authentication schemes.

1. Introduction

Number theory is the branch of mathematics that focuses on the appealing qualities of integers. Number theory is known as the Queen of Mathematics because of many unanswered problems it contains. With the advancement of supercomputers, number theory is now used in various engineering domains, particularly in cryptography. Everybody relies on online exchanges in the current advanced period, where security plays an enormous role. To ensure online safety, cryptographic algorithms that are developed using number theoretic ideas play a significant task. Cryptography is typically defined as the study of mathematical approaches for achieving various information security goals such as secrecy, authenticity, integrity, non-repudiation, and so on. The term refers to a subset of strategies rather than the mechanism of delivering data security. In most cryptographic algorithms, the generation of large prime numbers is required to encrypt and decrypt the messages passed through the online channel.

The reasoning of Diophantine equations and their applications is a growing field in number theory. The Diophantine equation is a multivariate polynomial equation with integer coefficients which seeks only integral solutions. Subsequently, the Diophantine problem is notable to be a difficult problem and is relied upon to be utilized in cryptography applications. In general, Diophantine equations have been solved by considering the ring of integers, Z. But, because of its arising applications, presently the specialists are begun to think about the problem over arbitrary rings. The linear Diophantine equation $ax+by=c$ is the simplest form of the Diophantine equation, where $a,b,c$ are integers and $x,y$ are unknown integers. Another important class of Diophantine equation is the Pell’s equation. The Indian mathematicians Brahmagupta and Bhaskara were the first to explore the Pell’s equation. Since ancient times, Pell’s Equation, which pertains to the cyclic group and has several solutions, has been used in the domain of number theory for a wide range of applications. Numerous disciplines are now addressing the binary quadratic Diophantine equations, both homogeneous and non-homogeneous. Since various Diophantine problems are evolving day by day, various mathematicians across the globe study these problems. Many cryptography methods have been developed based on these characteristics  [1,2,3,4,5,6,7,8]. Thirumala et al. [9] recently devised an efficient technique based on Pell’s equation that provides good reliability in opposition to side-channel exploits such as timing attacks. RSA (Rivest–Shamir–Adleman) is a widely used public key cryptographic method in security systems. Raghunandan et al. [10] used the generalized Pell’s equation for compelling the safety of RSA.

A trapdoor function is one that is computationally simple in one direction but hard to determine in the reverse directions (identifying its inverse) without particular information. In cryptography, trapdoor functions are usually applied. Mathematically, if f is a trapdoor function, then there exists a secret information t, such that given $f\left(x\right)$ and t, it is straightforward to compute x. Making trapdoors is regarded as the core of the process of developing public key cryptosystems. Bijective trapdoor functions are universally recognized as adequate for public key cryptography [11,12]. The recent developments in the theory of trapdoor functions can be seen in [13,14]. An authentication protocol is a kind of protocol that is intended to secure the exchange of authentication data between two or more clients. The factors to be taken into account in the authentication process are

• A protocol must constitute at least two clients, and everyone associated must be aware of the protocol ahead of time.
• The protocol must be followed by all the concerned clients.
• The steps involved in the protocol must be well defined.
• A protocol must be comprehensive, containing instructions for every possible scenario.

“Smart” devices and technologies have enabled substantial advancements in industry revenue and safety in recent decades. Hernández-Álvarez et al. [15] developed a new device to avail estimates of the temperature of diabetic foot where cryptographic protocols are present to ensure data security. Bullón Pérez et al. [16] performed another interesting research on Blockchain systems in the retail sector. In 2017, Rey and Dios [17] carried out a critical review on cryptographic protocols on wireless sensor networks concentrating on secret key cryptosystems. Malware has now emerged as a possible threat to the IoT, and hence to Wireless Sensor Networks. Batista et al. [18] presented an Agent-Based design for assessing trojan transmission on these networks. Recently, Martinez et al. [19] performed a critical review on the cryptographic techniques associated with block chain and bitcoin. Okumura [20] developed a new public key cryptosystem based on Diophantine equations of degree increasing type. He used those type of Diophantine equations to recover the plaintext. Murthy and Swamy [21] derived a new authentication protocol as well as a new encryption-decryption algorithm based on the Pell’s equation. Later, Alvarez et al. [22] and Youssef [23] modified the algorithm developed by [21]. Recently, Alecci and Dutto [24] studied the use of Pell hyperbolas in cryptosystems with security based on the discrete logarithm problem.

In the present work, the authors aim to develop a new authentication protocol based on the geometric properties of solutions of the second degree Diophantine equation $u_1^2+u_2^2=v_1^2+v_2^2$ and also analysed the initial cost and effort required to develop a new software for this protocol using the basic constructive cost models (COCOMO).

2. Mathematical Properties of the Equation ${\mathit{u}}_{\mathbf{1}}^{\mathbf{2}}+{\mathit{u}}_{\mathbf{2}}^{\mathbf{2}}={\mathit{v}}_{\mathbf{1}}^{\mathbf{2}}+{\mathit{v}}_{\mathbf{2}}^{\mathbf{2}}$

This section deals with the study on mathematical properties of the equation $u_1^2+u_2^2=v_1^2+v_2^2$.

Theorem 1.

The positive integral solutions of the Diophantine equation $u_1^2+u_2^2=v_1^2+v_2^2$ do not lie on a straight line with slope $m=-\left[\frac{u_1+v_1}{u_2+v_2}\right]$.

Proof. 

The Diophantine equation $u_1^2+u_2^2=v_1^2+v_2^2$ can be written as

$$\begin{array}{ccc}\hfill u_1^2-v_1^2& =& v_2^2-u_2^2\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill (u_1-v_1)(u_1+v_1)& =& (v_2-u_2)(v_2+u_2)\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \frac{v_2-u_2}{u_1-v_1}& =& \frac{u_1+v_1}{u_2+v_2}\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \frac{v_2-u_2}{v_1-u_1}& =& -\left[\frac{u_1+v_1}{u_2+v_2}\right]\hfill \end{array}$$

(4)

Let $m=\frac{v_2-u_2}{v_1-u_1}=1$ which is the slope of the straight line joining $(u_1,u_2)$ and $(v_1,v_2)$. It follows that the relationship (4) gives $u_1+u_2+v_1+v_2=0$. It is not true due to positive integral solutions of the Diophantine equation. Hence the positive integral solutions do not lie on a straight line when $m=1$. Also, (4) does not hold when $m>1$ or $m<1$.

Note 1.

In general, a slope of the straight line joining $(u_1,v_1)$ and $(u_2,v_2)$ is $m=\frac{v_2-v_1}{u_2-u_1}$. The relationship (4) does not hold when $m>1$ or $m<1$. If $m<1$, consider the case when $m=0$. Then $\left[\frac{u_1+v_1}{u_2+v_2}\right]=0$ implies that $u_1=-v_1$. Also from (4), it is clear that $u_2=v_2$ when $m=0$. Hence, we obtain the solution of $u_1^2+u_2^2=v_1^2+v_2^2$ as $\{u_1,u_2\},\{-u_1,u_2\}$ which is considered as the equivalent solution but not distinct.

Theorem 2.

Let one pair $(u_1,v_1)$ of the Diophantine equation $u_1^2+u_2^2=v_1^2+v_2^2$ be known. Then the distance δ between the constructed points $(u_1,u_2)$ and $(v_1,v_2)$ satisfies the condition $\frac{{\delta }^2}{2}>k$ where $k=u_1(u_1-v_1)$ provided $u_2>v_2$.

Proof. 

Given one pair $(u_1,v_1)$, finding out another pair $(u_2,v_2)$ satisfying $u_1^2+u_2^2=v_1^2+v_2^2$ is a challenge. Let $\delta$ be the distance between the constructed points $(u_1,u_2)$ and $(v_1,v_2)$, where $u_2$ and $v_2$ are unknown. Then $\delta =\sqrt{{(v_1-u_1)}^2+{(v_2-u_2)}^2}$. This implies ${\delta }^2={(v_1-u_1)}^2+{(v_2-u_2)}^2=v_1^2+u_1^2-2u_1{v}_1+v_2^2+u_2^2-2u_2{v}_2$. Since $u_1^2+u_2^2=v_1^2+v_2^2$, ${\delta }^2=2(u_1^2+u_2^2)-2u_1{v}_1-2u_2{v}_2$. So $\frac{{\delta }^2}{2}=u_1(u_1-v_1)+u_2(u_2-v_2)$. Given $(u_1,v_1)$, $u_1(u_1-v_1)$ becomes a constant and let it be k. Then $\frac{{\delta }^2}{2}-k=u_2(u_2-v_2)>0$, provided $u_2>v_2$. This implies that $\frac{{\delta }^2}{2}>k$.

Theorem 3.

If one pair $(u_1,v_1)$ is known, then the other point $(u_2,v_2)$ of the Diophantine equation $u_1^2+u_2^2=v_1^2+v_2^2$ satisfies $u_2<v_2$ or $u_2>v_2$.

Proof. 

Consider $u_1^2+u_2^2=v_1^2+v_2^2$. This can be written as $u_1^2-v_1^2=v_2^2-u_2^2$ which implies $(u_1-v_1)(u_1+v_1)=(v_2-u_2)(v_2+u_2)$. Since all $u_i^{\prime }$s and $v_i$’s are positive, $\frac{(u_1-v_1)}{(v_2-u_2)}>0$. Thus $(u_1-v_1)=k(v_2-u_2);k>0$. For the given $(u_1,v_1)$, $(u_1-v_1)$ is a constant. Let us assume that $(u_1-v_1)<0$. Then $(v_2-u_2)<0$ which implies $u_2>v_2$. Similarly, if $(u_1-v_1)>0$, then $(v_2-u_2)>0$ which implies $u_2<v_2$.

Theorem 4.

If $(u_1,v_1)$ is known and $u_2$ is chosen as $u_2>u_1$ and $u_2>v_1,v_2$ then the upper bound for the distance d between the points $(u_1,v_1)$ and $(u_2,v_2)$ which satisfies the relation $u_1^2+u_2^2=v_1^2+v_2^2$ is given by $d^2<2{\lambda }^2{(u_1+v_1)}^2$ where $\lambda >0.5$.

Proof. 

Let d be the distance between $(u_1,v_1)$ and $(u_2,v_2)$. Then, we have $d^2={(v_2-v_1)}^2+{(u_2-u_1)}^2$. Since $u_2>v_2$,

$$\begin{array}{ccc}\hfill d^2& <& {(u_2-v_1)}^2+{(u_2-u_1)}^2\hfill \\ & =& u_2^2+v_1^2-2u_2{v}_1+u_2^2+u_1^2-2u_1{u}_2\hfill \\ & =& u_1^2+2u_2^2+v_1^2-2u_1{u}_2-2u_2{v}_2\hfill \end{array}$$

Since $u_2>v_2$, $(v_2-v_1)<u_2$ and $(u_2-u_1)<u_2$. Thus $d^2<2u_2^2$. Since $u_2>u_1,v_1$ we have $u_2>\left(\frac{u_1+v_1}{2}\right)$ or $u_2=\lambda (u_1+v_1)$, where $\lambda >0.5$. Hence $\frac{d^2}{2}<{\lambda }^2{(u_1+v_1)}^2$ follows.

Note 2.

Let one positive integral pair $(u_1,v_1)$ of the Diophantine equation $u_1^2+u_2^2=v_1^2+v_2^2$ be known. Then we are finding out the relationship between δ and d (from Theorems 2 and 4) given as

$$\begin{array}{ccc}\hfill {\delta }^2& =& {(v_1-u_1)}^2+{(v_2-u_2)}^2=2(u_1^2+u_2^2)-2u_1{v}_1-2u_2{v}_2\hfill \\ \hfill d^2& =& {(u_2-u_1)}^2+{(v_2-v_1)}^2=2(u_1^2+u_2^2)-2u_1{u}_2-2v_1{v}_2\hfill \\ \hfill {\delta }^2-d^2& =& 2(u_1{u}_2+v_1{v}_2)-2(u_1{v}_1+u_2{v}_2)\hfill \\ \hfill \frac{{\delta }^2-d^2}{2}& =& u_1{u}_2+v_1{v}_2-t-u_2{v}_2,\mathrm{where}t=u_1{v}_1\hfill \\ & <& (u_1+v_1)u_2-u_2^2-t,\mathrm{where}{v}_2<u_2\hfill \\ & =& \alpha u_2-u_2^2-t,\mathrm{where}\alpha =u_1+u_2\hfill \end{array}$$

Example 1.

Let $u_1=1$ and $v_1=5$. Given $u_1<v_1$. Then ${\delta }^2={(5-1)}^2+{(v_2-u_2)}^2=16+{(v_2-u_2)}^2$. It follows ${\delta }^2>17$ as ${(v_2-u_2)}^2\ge 1$. Now $d^2<1+25+2u_2^2-12u_2$ which implies $d^2<26+2u_2(u_2-6)$. But $u_2=\lambda (u_1+v_1)$, where $\lambda >0.5$. Let us choose $\lambda =7/6$. Then $u_2=7$ and $d^2<26+14(7-6)=40$. Hence ${\delta }^2-d^2<4$.

Example 2.

Let $u_1=2$ and $v_1=5$. Then ${\delta }^2={(5-2)}^2+{(v_2-u_2)}^2$. Thus, ${\delta }^2>10$. Now, $d^2<25+4+2u_2^2-14u_2$. But, $u_2=\lambda (u_1+v_1)$, where $\lambda >0.5$. By taking $\lambda =11/7$, we get $u_2=11$ and $d^2<117$. Hence ${\delta }^2-d^2<24$.

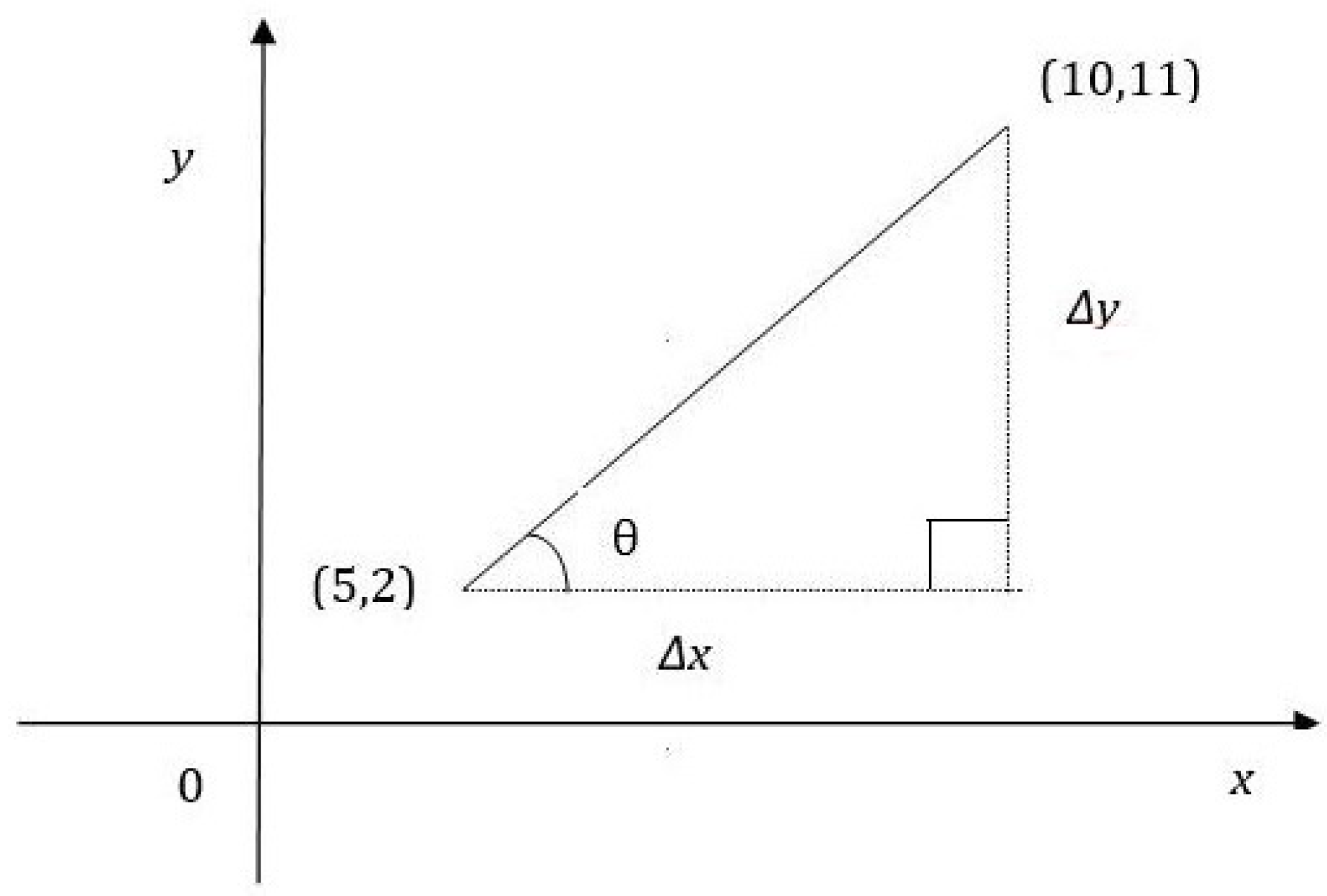
Example 3.

Let us have $(u_1,v_1)=(5,2)$ and $(u_2,v_2)=(10,11)$ satisfying the Diophantine equation $u_1^2+u_2^2=v_1^2+v_2^2$ where $u_2>u_1,v_1$ and $u_2<v_2$. The slope of the line between $(u_1,v_1)$ and $(u_2,v_2)$ is $m=\frac{\Delta y}{\Delta x}=\frac{v_2-v_1}{u_2-u_1}=\frac{9}{5}=1.8$. Let θ be the angle of inclination. Then $\theta ={tan}^{-1}\left(\frac{\Delta y}{\Delta x}\right)=60.{9454}^{\circ }$. Further, distance $d=\sqrt{{(\Delta x)}^2+{(\Delta y)}^2}=\sqrt{106}=10.29563$ units. Therefore, the equation of the line is $y=1.8x-7$. Now we can construct a right-angled triangle with vertices $(u_1,v_1)$, $(u_2,v_2)$ and $(u_1+\Delta x,y_1)$ as in Figure 1.

Example 4.

Let us have $(u_1,v_1)=(10,2)$ and $(u_2,v_2)=(5,11)$ satisfying the Diophantine equation $u_1^2+u_2^2=v_1^2+v_2^2$ where $u_1>u_2$ and $v_2>v_1$. The slope of the line between $(u_1,v_1)$ and $(u_2,v_2)$ is $m=\frac{\Delta y}{\Delta x}=\frac{v_2-v_1}{u_2-u_1}=\frac{9}{(-5)}=-1.8$. Let θ be the angle of inclination. Then $\theta ={tan}^{-1}(\frac{\Delta y}{\Delta x}+{180}^o)=119.{05460}^{\circ }$. Further, distance $d=\sqrt{{(\Delta x)}^2+{(\Delta y)}^2}=\sqrt{106}=10.29563$ units. Therefore the equation of the line is $y=-1.8x+20$. Now we can construct another right angled triangle with vertices $(u_1,v_1)$, $(u_2,v_2)$ and $(u_2,v_2-\Delta y)$ as in Figure 2.

Theorem 5.

If the two points $(u_1,v_1)$ and $(u_2,v_2)$ are the solutions of the quadratic Diophantine equation $u_1^2+u_2^2=v_1^2+v_2^2$ where $u_2>u_1$ and $v_2>v_1$, then the four points $(u_1,v_1)$, $(u_1+\Delta x,v_1)$, $(u_2,v_2)$ and $(u_1,v_1+\Delta y)$ constitute a rectangle where $\Delta x=u_2-u_1>0$ and $\Delta y=v_2-v_1>0$.

Proof. 

Given that $\Delta x=u_2-u_1>0$ and $\Delta y=v_2-v_1>0$. Let the given points $A(u_1,v_1)$, $B(u_1+\Delta x,v_1)$, $C(u_2,v_2)$ and $D(u_1,v_1+\Delta y)$ be the four vertices of a four-sided polygon. By two-dimensional geometry, either $\Delta x$ and $\Delta y$ denote the length and width of the polygon $(\Delta x>\Delta y)$ or $\Delta x$ and $\Delta y$ be the width and length $(\Delta y>\Delta x)$. The distance d between the points $(u_1,v_1)$ and $(u_2,v_2)$ acts as a diagonal of the polygon as in Figure 3.

Thus, we obtain two right-angled triangle, say $\Delta ABC$ and $\Delta ADC$ having the same hypotenuse d. Similarly, the right-angled triangles $\Delta BAD$ and $\Delta BCD$ have the hypotenuse as $d^{\prime }=\sqrt{{(\Delta y)}^2+{(\Delta x)}^2}$. Note that $d=d^{\prime }$. Thus, the two diagonals of the polygon ABCD are equal and with the choice of $u_1,u_2,v_1,v_2$ it is clear that ABCD is a rectangle.

3. Existence of Trapdoor Function in Diophantine Cryptography

Everybody depends on the secret key to guarantee the security of data. So, it must be assured that the secret key is extremely difficult to crack. Note that cryptanalysis is the field of attacking cryptosystems. One method of cryptanalysis involves the attacker possessing both the message’s plaintext and ciphertext and attempting to decipher the key that converts the plaintext to the ciphertext. Using a brute-force attack, or checking all potential keys, is one way they can achieve this. The key space, or range of potential keys, should be very large in order to protect against a brute-force attack. A secret key shared by two users is used in symmetric-key cryptography. Party A can encrypt data with the secret key and transfer the output to Party B, who can decrypt and interpret data with the same key. Key management, or the secure exchange of secret keys between users, is the secure framework for symmetric cryptography. The drawback of the symmetric key cryptography is Key distribution and management is a serious problem—for N users $O\left(N^2\right)$ keys are needed. In this section, we have invented a secure authentication communication protocol between client and server using Diophantine equation $x_1^2+x_2^2=y_1^2+y_2^2$ as in Figure 4.

In the step 1, Server sends a trapdoor information (message) $\lambda$ to Client. The server keeps a distinct pair of $128/256$-bit session key $(x_1,y_1)$ to each client. During every transaction, the server generates a trapdoor information in accordance with session key to each client. Each client receives a distinct trapdoor information $\lambda$ computed by server. In the step 2, the client computes $x_2=\lambda (x_1+y_1)$ and $y_2^2=x_1^2+x_2^2-y_1^2$. Then the client sends Hash($y_2$) to server which verifies the result. Then the authentication mechanism has been established between both parties. In this protocol, when $\lambda$ and $y_2$ are hacked by an attacker, it is computationally challenge to retrieve the values $x_1,y_1$ and $x_2$ due to Diophantine equation. It is observed that the client uses the $x_2$ as one time password (OTP)/E-token for any network transactions. Similar to the above protocol, we can send $y_2$ instead of Hash($y_2$) to server as a plaintext. It is termed as transparent (naked) Diophantine authentication protocol. Along with big data tools, the proposed protocol helps to generate, distribute, store and revoke a large volume of E-tokens and keeps an eye on cryptographic attacks.

The ElGamal cryptosystem, a subset of public key cryptography, is based on the Discrete Logarithm Problem (DLP). It is vulnerable to the man-in-the-middle attack, chosen-plaintext attacks and not useful for one way communication. The computational complexity of DLP has come around O($nlogn$) where n is the amount of resources or operations required to execute the discrete logarithm. In the present study, the authors described Diophantine cryptography that could be solved in O($n^2$). It is useful to one-way communication system. Due to high computational complexity to crack or identify an exact integral solution to a given Diophantine equation, it is a real challenge to perform rudimentary cryptographic attacks.

Given a point $(x_1,y_1)$, estimating another point $(x_2,y_2)$ satisfying $x_1^2+x_2^2=y_1^2+y_2^2$ is computationally difficult for higher integral values. But for smaller integral values this process is not so hard. For the given point $(x_1,y_1)$, an attacker can try to form a rectangle in which a right angled triangle with angles ${\theta }_1,{\theta }_2,{90}^{\circ }$ where ${\theta }_1+{\theta }_2={90}^{\circ }$. The attacker requires to vary ${\theta }_1$ and ${\theta }_2$ and verify the Diophantine relationship. It needs $O\left(n^2\right)$ computations. Subsequently, the attacker tries to make two right angled triangles comprised into a rectangle which inscribed in a circle must have its diagonal as the diameter of the circle. The attacker computes the perimeter of the rectangle and verifies whether perimeter is equal to $2(\Delta x+\Delta y)$. Gradually, the attacker increases the perimeter of the rectangle and the corresponding area of the circle in order to find a suitable point $(x_2,y_2)$. This ensures the existence of trapdoor function in Diophantine and very hard to crack this challenge. Algorithm 1 describes the pseudocode for the authentication protocol based on the equation $x_1^2+x_2^2=y_1^2+y_2^2$.

Algorithm 1 Pseudocode for the authentication protocol

Input: B, the trapdoor message in a binary form.

Input: $x_1,y_1>0$.

Output: decimal $=0$, base $=1$

while  $B\ne 0$ do

remainder = B% 10

decimal = decimal + remainder * base

B = B / 10

base = base * 2

end while

Output: n = decimal

$x_2\leftarrow n*(x_1+y_1)$;

$y_2\leftarrow sqrt\{x_1^2+x_2^2-y_1^2\}$;

$sum1\leftarrow x_1^2+x_2^2$;

$sum2\leftarrow y_1^2+y_2^2$;

if  $sum1==sum2$ then

Trapdoor is possible using Diophantine equation;

else

No solution

end if

It is to be noted that the 128/256-bit session key $(x_1,y_1)$ and the trapdoor message $\lambda$ act as the secret keys and it should be known to the server as well as clients to do the authentication. As a result, any safe key exchange mechanism should be used to exchange the keys. The symmetric cryptography is exposed in two ways: the requirement to communicate the key raises the risk of it being intercepted in transit, and quantum computers can employ Grover’s algorithm to enhance the accuracy of a brute-force attack. Since quantum algorithms do not completely break Hash-based digital signatures, the newly discovered authentication systems enable a secure digital data transmission.

In the symmetric key cryptography, a private key of a specific size is developed using a source of randomness. There is no mathematical proof (or analysis) to crack a private key because of the random creation process and the non-availability of patterns. Eventhough, brute-force attacks are included in cryptanalysis, a brute-force attack entails attempting to decipher the ciphertext and retrieve the plaintext using every feasible key. In order to find the correct key, an attacker would have to test 50% of all possible keys. As a result, a secret (or private key) with suitable entropy and length could adequately safeguard encrypted data. Grover’s approach, on the other hand, can leverage qubit superposition to expedite the brute-force attack by a quadratic factor. Also, when a cryptographic algorithm permits to use, doubling the symmetric key sizes keeps this type of encryption safe. However, doubling the key size is not a simple operation. When a cryptographic algorithm is deployed by a software under the environment of Cloud setup, it is quite simple since an update may provide for an efficient key-size change.

4. Cost and Effort Evaluation Using COCOMO Equations

One of the most widely used software prediction models is the constructive cost model (COCOMO). The two key factors that determine the integrity of any software development project are effort and schedule, both of which are consequences of COCOMO. One can choose a model of COCOMO based on the requirements on accuracy and correctness. There are three COCOMO models: Basic, Intermediate and Complex. Basic COCOMOs are developed for a rapid and fuzzy analysis of software estimation. Intermediate models consider cost drivers into account, while complex models take the influence of individual project phases. All these models can be used for various software developments under the Cloud based on the characteristics of the different system types: organic, semi-detached, and embedded.

This section explains how to create software utilising organic COCOMO equations to implement the new authentication protocol that is discussed in Section 3. For organic model software projects, the fundamental COCOMO equations are

$$\begin{array}{ccc}\hfill X& =& \alpha \times {\left(l\right)}^{\beta }\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill R& =& \gamma \times {\left(X\right)}^{\delta }\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill P& =& X/R\hfill \end{array}$$

(7)

where X is the effort applied in persons-months, R is the build-up time in chronological months, l is the calculated number of lines of code for the project (expressed in thousands) and P is the number of persons.

Table 1. Coefficients and exponent values as in [25].

Software Project	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$	$\mathit{\delta }$
Organic	2.4	1.05	2.5	0.38
Semi-detached	3.0	1.12	2.5	0.35
Embedded	3.6	1.20	2.5	0.32

represents the values of the coefficients and exponents in COCOMO equations for different project types as in [25].

The COCOMO parameter is used to quantify the workload of software and runtime after l has been evaluated. The COCOMO equation shows that as l increases, the workload and duration increase as well.

Table 2. Approximated values of COCOMO attributes.

Code Length (Lines in Thousands)	Effort	Time Period	Manpower
50	0.10	1.04	0.09
150	0.33	1.64	0.20
550	1.28	2.75	0.47
1200	2.91	3.75	0.78
1400	3.42	3.99	0.86
2000	4.96	4.59	1.08
5000	13.00	6.62	1.96

represent the estimated work, time, and labor involved in creating each line of code in the program using basic COCOMO equations.

The number of lines of code for C++ program developed for the protocol is 42. Thus for authentication protocol, the effort $X=0.086$ persons-months, time $R=0.9841$ months and the manpower $P=0.874$ persons. Hence, using the basic COCOMO equations, the initial cost, effort and manpower can be derived for developing a new software in order to implement the authentication protocol.

5. Conclusions

In the present work, some geometric properties of quadratic Diophantine equations are derived and explained their uses in the communication protocols. Also, a new secure authentication mechanism based on the positive integral solutions of the quadratic Diophantine is presented which can be employed in the generation of one-time passwords or E-tokens for cryptography applications. Further, the existence of trapdoor functions in Diophantine equation is well analysed. It is noted that the proposed authentication protocol is secure either performing Hashing method or without Hashing. Also, the initial cost and effort of a new software library under the environment of Cloud are determined for implementing the authentication protocols using basic COCOMO equations.