Multipurpose Aggregation in Risk Assessment
Abstract
:1. Introduction
- Risks are aggregated, however, only on two (error mode and functional error, effect) or on three (cause, error mode, effect) levels. This is the general approach in risk-management of production systems.
- Although there is a hierarchical (vertical) aggregation, the model is not suitable for area-based (horizontal) aggregation and the opposite.
- The model is specific to a given area, for example insurance, bankruptcy risk, and production.
- Model/framework does not establish a link between the aggregation of risks and the generation of corrective, preventive measures. For this reason, the previous aggregation methods (including FMEA) can be considered as a special case of the aggregation model presented in this paper.
- A multilevel framework known as the enterprise-level matrix (ELM), which consists of three matrices, is proposed to evaluate risk at different enterprise levels. The three matrices are the risk-level matrix (RLM), the threshold-level matrix (TLM), and the action-level matrix (ALM).
- The proposed framework aggregates not only the risk components but also the overall risk indicators of the process components at all levels of the corporate process hierarchy. Thus, appropriate corrective/preventive actions can be prescribed at each process hierarchy level, as different types of corrective/preventive actions may be needed at the process and corporate levels.
- We use data-mining methods such as seriation and biclustering techniques to simultaneously identify risk components/warnings and process components to select an appropriate set of corrective/preventive actions.
2. Preliminaries
2.1. The Set of Enterprise-Level Matrices (ELM)
2.1.1. Risk-Level Matrix
- is the weighted geometric mean of the process components.
- is the maximum value of the process risks.
- is the weighted median of the process risks.
- is the weighted radial distance of the process risks.
- 1.
- In the case of the traditional FMEA approach, thresholds are specified only in the second level. Furthermore, the same threshold is usually specified for all processes. If the risk values are between [1, 10], the critical RPN is usually defined as the product of the average risk factors, [34,35]. Formally, we have . Different corrective/preventive actions can be specified for each process component. However, in this case, the aim of these corrective/preventive actions is to mitigate the RPN, and distinct corrective/preventive actions are not specified for each risk component. Formally, we have .
- 2.
- The TREF method specifies the thresholds of the risk components in the first factor level and their aggregations in the second level; however, these thresholds are the same for all processes. This method proposes the use of six risk factors in the first level. Formally, we have . This method proposes several aggregation approaches, and, similar to the traditional FMEA technique, this method specifies the threshold of the next factor level. Formally, . A warning is generated if either a risk-component value or the aggregated value is greater than the threshold. In addition, the TREF method allows warnings to be generated manually due to a seventh factor, namely, the criticality factor, where a value of 1 indicates that the process is critical process that must be corrected regardless of the risk value.Due to the column-specific thresholds, different corrective/preventive actions can be specified to mitigate each risk component and its aggregations. Nevertheless, in this case, common corrective/preventive actions are specified to mitigate the risk components.
- 3.
- On the one hand, the new FMEA method considers three factors in the first factor level. On the other hand, the new FMEA method specifies the threshold for the first factor level; however, corrective preventive tasks are carried out if at least two factors are greater than a threshold (based on the action priority logic [36]).
- 4.
- The ELM can be used to specify cell-specific corrective/preventive actions. In general, these actions can be row-specific (process component-specific), such as in the FMEA method, or column-specific, such as in the TREF method; importantly, different corrective/preventive tasks can be specified for various cells.
- specific thresholds for all processes; and
- specific thresholds for all risk components simultaneously.
2.1.2. Specific Processes
- step 1
- The risk priorities of all corrective/preventive tasks are specified.
- step 2
- The seriation technique [37] is used to simultaneously reorder the rows (process components) and columns (risk components), yielding a set of risk and process components with high risk priorities.
- step 3
- The biclustering technique, which uses a bicluster to specify the mitigated risk and process components, is proposed. This set of corrective/preventive actions specifies the set of tasks included in the improvement process.
- step 4
- After screening, conventional process and project management methods are used to schedule the correction tasks according to time, cost, and resource constraints.
- Step 1—Specification of the task priority matrix
- Step 2—Seriation of the task priority matrix
- Step 3—Specification of risky blocks in the task priority matrix
- Step 4—Specification of corrective/preventive processes
2.2. Requirements of the Aggregation Functions
- Objectives: What are the objectives of risk management? The aggregated value is an indicator that reflects the basis underlying managerial or engineering decisions. Different aggregation functions have distinct component risk scales. As a result, a top-to-bottom approach is proposed instead of the traditional bottom-to-top approach when scale definition is an early step. This requirement can be used to classify aggregation functions, such as summation type (total risk), average type (mean or median risk), or distance (from a given value) type aggregated risk indicators. This expectation indicates that there is usually no best or worst aggregation function, and the applied aggregation function depends on the situation and the purpose of the aggregation.
- Validity: The validity is determined according to the nature of the components and processes via the aggregated risk of the components. For example, in the case of extremely high severity, such as nuclear disasters, natural disasters, or war, the severity is excluded, and the probability is used as the primary risk indicator. In more frequent cases, the ‘severity × probability’ is calculated as the expected value. In this case, the aggregation is either the most characteristic value (no aggregation) or an estimation of the expected value. The ‘expected’ value can be interpreted in broader terms that extend beyond probability theory approaches [41,42,43,44,45]. Another scenario is when the risk in multiple areas is combined. In this case, the expected total risk is the sum of the risks in the areas, as discussed above. The traditional RPN calculation (occurrence × severity × detection) can be viewed as an expected value if the occurrence and detection are independent. The introduction of additional components (such as multiplication factors) might cause difficulties in interpreting the aggregated value as an indicator. Smart weighting can be used to address this problem.Next, we formulate the mathematical requirements. The mathematical requirements guarantee a lack of distortion.
- Uniformity, linearity: When the components have a uniform distribution, the distribution of the aggregated values should also be uniform [41,44].The above requirements appear to be logical; however, the requirements are difficult to satisfy, and it is not certain that these requirements are adequate, contrary to the literature. For example, in the case of additive or multiplicative models, the values near the mean appear more frequently because these values originate from not only medium-medium risk value combinations but also small–large and large–small risk value combinations.
- Scale fit: Aggregation operations should be performed with the applied scale values [46].
- Scale end point identity: The result should be in the same interval as the components (if they are equal) or a common scale if the components have different scales. On the one hand, this requirement helps in assessing the resulting risk, which is a psychological advantage. On the other hand, successive aggregations between different hierarchal levels may distort the result if the components have different scales [47].
2.3. Characterization of Potential Aggregation Functions
3. Practical Example
3.1. Research Plan
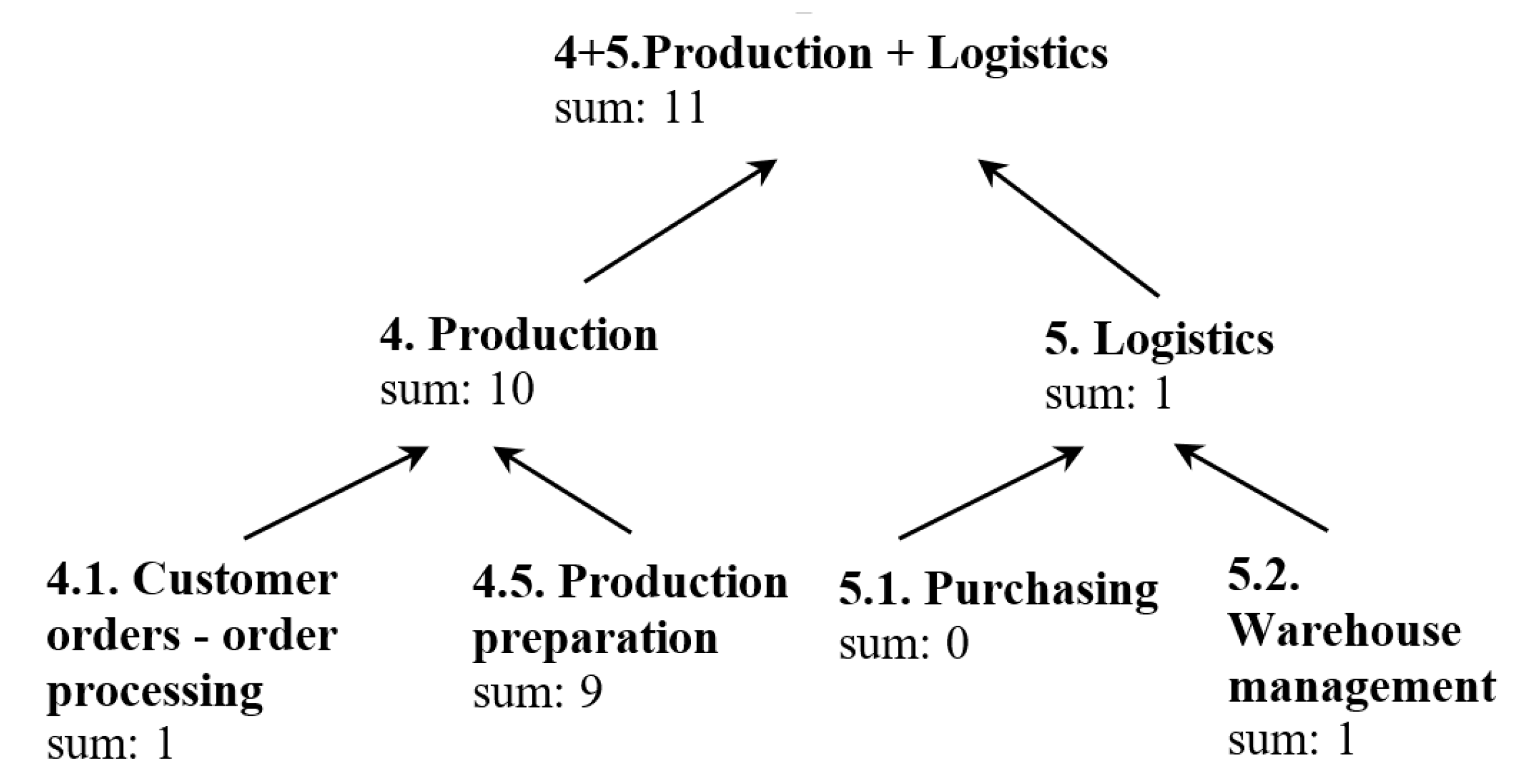
3.2. Process Hierarchy
- 4.
- Production
- 4.1
- Customer orders - order processing
- 4.1.1
- Start processing order
- 4.1.2
- Entry production control form
- 4.5
- Production preparation
- 4.5.1
- Product engineering
- 4.5.2
- Product planning
- 5.
- Logistics
- 5.1
- Purchasing
- 5.1.1
- Offer request
- 5.1.2
- Demand form
- 5.1.3
- Place order
- 5.1.4
- Receive material on time
- 5.2
- Warehouse management
- 5.2.1
- Vehicle arrival
- 5.2.2
- Unloading
- 5.2.3
- Unwrapping, inspection.
3.3. Results of the Matrix-Based Risk Assessment
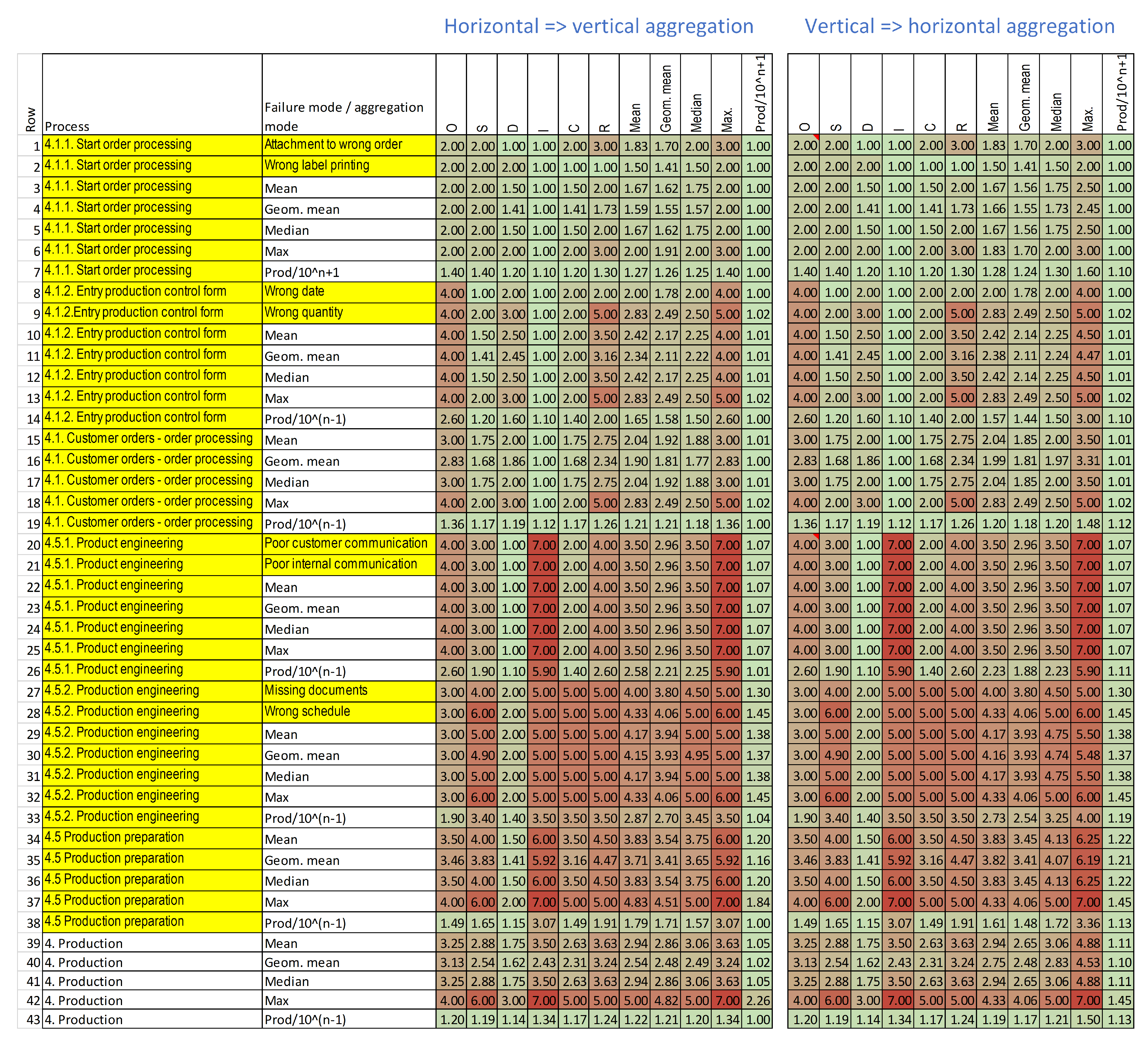
3.3.1. Bidirectional Aggregation
- Determining which functions should be used in different aggregation situations; and
- Comparing the results of the two aggregation directions.
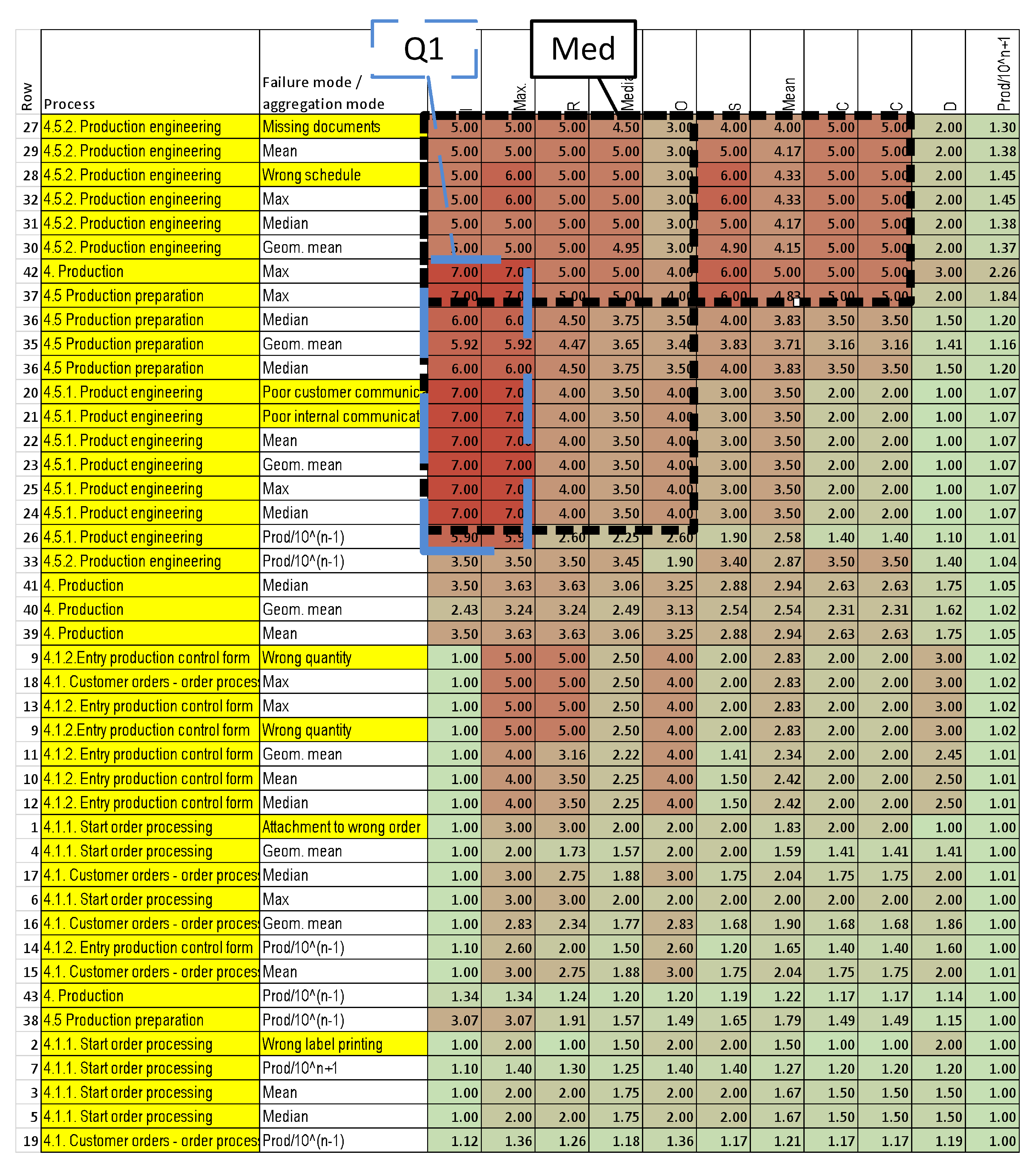
3.3.2. Aggregating Warnings
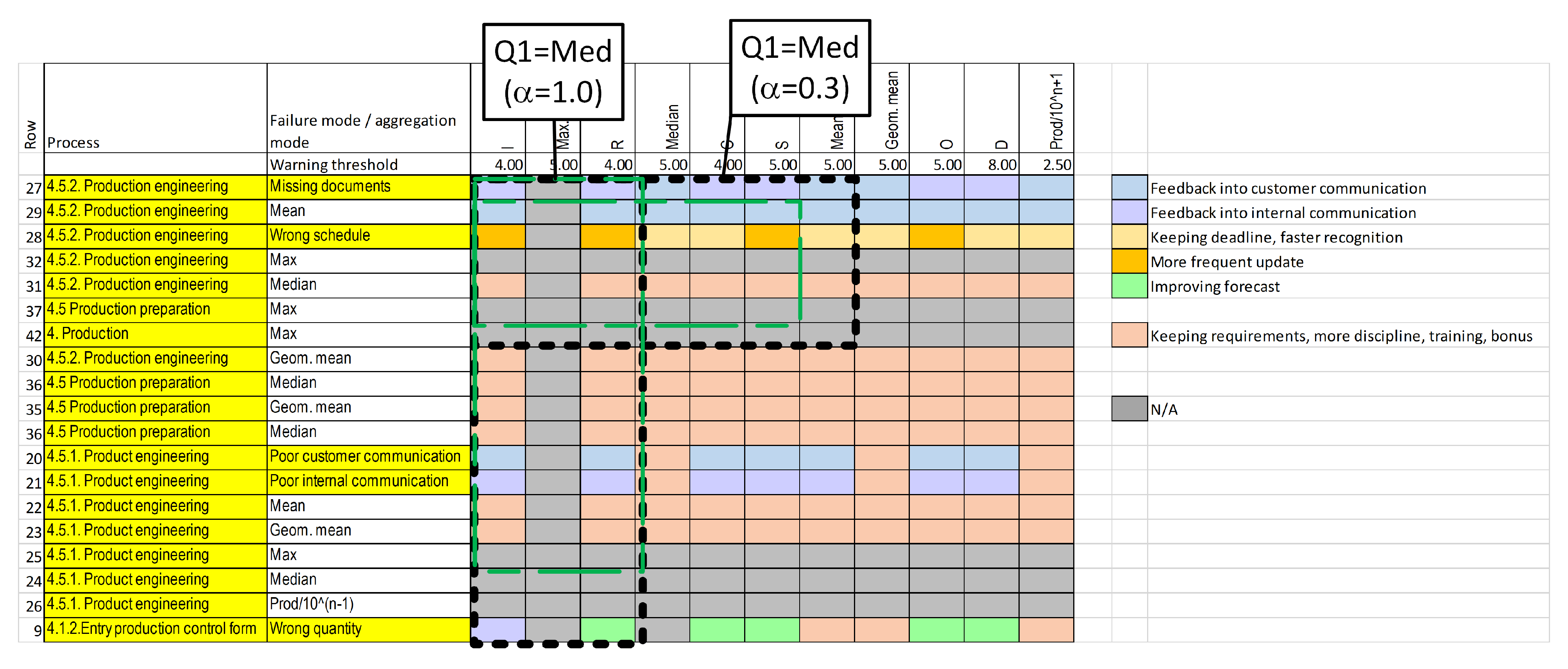
3.3.3. Generating Preventive Actions
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AHP | Analytical Hierarchy Process |
| ALM | Action-Level Matrix |
| ANP | Analytical Network Process |
| Criticality factor | |
| Consistency Index | |
| Consistency Ratio | |
| Vector of risk factors | |
| EDAS | Evaluation Based on the Distance from the Average Solution |
| ELECTRE | Elimination and Choice Expressing the Reality |
| ELM | Enterprise-Level Matrix |
| FMEA | Failure Mode and Effects Analysis |
| Fuzzy FMEA | Fuzzy Failure Mode and Effects Analysis |
| GRA | Grey Relational Analysis |
| ISO | International Standardization Organization |
| K | Invention function |
| MULTIMOORA | Multiplicative Form of the Multiobjective Optimization by Ratio Analysis |
| n | Number of risk factors |
| PROMETHEE | Preference Ranking Organization Method for Enrichment Evaluations |
| RAP | Risk Aggregation Protocol |
| Random Consistency Index | |
| RLM | Risk-Level Matrix |
| RPN | Risk Priority Number |
| SRD | Sum of Ranking Differences |
| Threshold vector | |
| TLM | Threshold-Level Matrix |
| TODIM | TOmada de Decisao Iterativa Multicriterio |
| TOPSIS | Technique for Order Preference by Similarity to the Ideal Solution |
| TREF | Total Risk Evaluation Framework |
| Risk aggregation function | |
| VIKOR | VIsekriterijumska optimizacija i KOmpromisno Resenje |
| Vector of weights | |
| Warning rules | |
| WS | Warning System |
References
- Bani-Mustafa, T.; Zeng, Z.; Zio, E.; Vasseur, D. A new framework for multi-hazards risk aggregation. Saf. Sci. 2020, 121, 283–302. [Google Scholar] [CrossRef]
- Bjørnsen, K.; Aven, T. Risk aggregation: What does it really mean? Reliab. Eng. Syst. Saf. 2019, 191, 106524. [Google Scholar] [CrossRef]
- Pedraza, T.; Rodríguez-López, J. Aggregation of L-probabilistic quasi-uniformities. Mathematics 2020, 8, 1980. [Google Scholar] [CrossRef]
- Pedraza, T.; Rodríguez-López, J. New results on the aggregation of norms. Mathematics 2021, 9, 2291. [Google Scholar] [CrossRef]
- Fattahi, R.; Khalilzadeh, M. Risk evaluation using a novel hybrid method based on FMEA, extended MULTIMOORA, and AHP methods under fuzzy environment. Saf. Sci. 2018, 102, 290–300. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Liu, N. Risk evaluation approaches in failure mode and effects analysis: A literature review. Expert Syst. Appl. 2013, 40, 828–838. [Google Scholar] [CrossRef]
- Spreafico, C.; Russo, D.; Rizzi, C. A state-of-the-art review of FMEA/FMECA including patents. Comput. Sci. Rev. 2017, 25, 19–28. [Google Scholar] [CrossRef]
- Karasan, A.; Ilbahar, E.; Cebi, S.; Kahraman, C. A new risk assessment approach: Safety and Critical Effect Analysis (SCEA) and its extension with Pythagorean fuzzy sets. Saf. Sci. 2018, 108, 173–187. [Google Scholar] [CrossRef]
- Maheswaran, K.; Loganathan, T. A novel approach for prioritization of failure modes in FMEA using MCDM. Int. J. Eng. Res. Appl. 2013, 3, 733–739. [Google Scholar]
- Ouédraogo, A.; Groso, A.; Meyer, T. Risk analysis in research environment–part II: Weighting lab criticity index using the analytic hierarchy process. Saf. Sci. 2011, 49, 785–793. [Google Scholar] [CrossRef]
- Yousefi, S.; Alizadeh, A.; Hayati, J.; Baghery, M. HSE risk prioritization using robust DEA-FMEA approach with undesirable outputs: A study of automotive parts industry in Iran. Saf. Sci. 2018, 102, 144–158. [Google Scholar] [CrossRef]
- Bognár, F.; Hegedűs, C. Analysis and Consequences on Some Aggregation Functions of PRISM (Partial Risk Map) Risk Assessment Method. Mathematics 2022, 10, 676. [Google Scholar] [CrossRef]
- Kosztyán, Z.T.; Csizmadia, T.; Kovács, Z.; Mihálcz, I. Total risk evaluation framework. Int. J. Qual. Reliab. Manag. 2020, 37, 575–608. [Google Scholar] [CrossRef]
- Wang, J.; Wei, G.; Lu, M. An extended VIKOR method for multiple criteria group decision making with triangular fuzzy neutrosophic numbers. Symmetry 2018, 10, 497. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, N. A multiple criteria hesitant fuzzy decision making with Shapley value-based VIKOR method. J. Intell. Fuzzy Syst. 2014, 26, 1065–1075. [Google Scholar] [CrossRef]
- Kutlu, A.C.; Ekmekçioğlu, M. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP. Expert Syst. Appl. 2012, 39, 61–67. [Google Scholar] [CrossRef]
- Wei, G.W. Extension of TOPSIS method for 2-tuple linguistic multiple attribute group decision making with incomplete weight information. Knowl. Inf. Syst. 2010, 25, 623–634. [Google Scholar] [CrossRef]
- Chen, N.; Xu, Z. Hesitant fuzzy ELECTRE II approach: A new way to handle multi-criteria decision making problems. Inf. Sci. 2015, 292, 175–197. [Google Scholar] [CrossRef]
- Figueira, J.R.; Greco, S.; Roy, B.; Słowiński, R. An overview of ELECTRE methods and their recent extensions. J. Multi-Criteria Decis. Anal. 2013, 20, 61–85. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Turskis, Z. Extended EDAS method for fuzzy multi-criteria decision-making: An application to supplier selection. Int. J. Comput. Commun. Control 2016, 11, 358–371. [Google Scholar] [CrossRef]
- Zindani, D.; Maity, S.R.; Bhowmik, S. Fuzzy-EDAS (evaluation based on distance from average solution) for material selection problems. In Advances in Computational Methods in Manufacturing; Springer: Berlin, Germany, 2019; pp. 755–771. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z. Multi-criteria decision making with intuitionistic fuzzy PROMETHEE. J. Intell. Fuzzy Syst. 2014, 27, 1703–1717. [Google Scholar] [CrossRef]
- Vetschera, R.; De Almeida, A.T. A PROMETHEE-based approach to portfolio selection problems. Comput. Oper. Res. 2012, 39, 1010–1020. [Google Scholar] [CrossRef]
- Li, X.; Wei, G. GRA method for multiple criteria group decision making with incomplete weight information under hesitant fuzzy setting. J. Intell. Fuzzy Syst. 2014, 27, 1095–1105. [Google Scholar] [CrossRef]
- Sun, G.; Guan, X.; Yi, X.; Zhou, Z. Grey relational analysis between hesitant fuzzy sets with applications to pattern recognition. Expert Syst. Appl. 2018, 92, 521–532. [Google Scholar] [CrossRef]
- Liu, H.C.; Fan, X.J.; Li, P.; Chen, Y.Z. Evaluating the risk of failure modes with extended MULTIMOORA method under fuzzy environment. Eng. Appl. Artif. Intell. 2014, 34, 168–177. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Lu, C.; Shan, M.M. Application of interval 2-tuple linguistic MULTIMOORA method for health-care waste treatment technology evaluation and selection. Waste Manag. 2014, 34, 2355–2364. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.H.; Wei, G.W. TODIM method for Pythagorean 2-tuple linguistic multiple attribute decision making. J. Intell. Fuzzy Syst. 2018, 35, 901–915. [Google Scholar] [CrossRef]
- Wang, J.; Wei, G.; Lu, M. TODIM method for multiple attribute group decision making under 2-tuple linguistic neutrosophic environment. Symmetry 2018, 10, 486. [Google Scholar] [CrossRef]
- Héberger, K. Sum of ranking differences compares methods or models fairly. TrAC Trends Anal. Chem. 2010, 29, 101–109. [Google Scholar] [CrossRef]
- Héberger, K.; Kollár-Hunek, K. Sum of ranking differences for method discrimination and its validation: Comparison of ranks with random numbers. J. Chemom. 2011, 25, 151–158. [Google Scholar] [CrossRef]
- Gueorguiev, T.; Kokalarov, M.; Sakakushev, B. Recent trends in FMEA methodology. In Proceedings of the 2020 7th International Conference on Energy Efficiency and Agricultural Engineering (EE&AE), Ruse, Bulgaria, 2–14 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Filipović, D. Multi-level risk aggregation. ASTIN Bull. J. IAA 2009, 39, 565–575. [Google Scholar] [CrossRef]
- Ayyub, B.M. Risk Analysis in Engineering and Economics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014; p. 640. [Google Scholar]
- Keskin, G.A.; Özkan, C. An alternative evaluation of FMEA: Fuzzy ART algorithm. Qual. Reliab. Eng. Int. 2008, 25, 647–661. [Google Scholar] [CrossRef]
- AIAG-VDA. Failure Mode and Effects Analysis—FMEA Handbook; Verband der Automobilindustrie, Southfild, Michigan Automotive Industry Action Group: Berlin, Germany, 2019; Volume 1. [Google Scholar]
- Hahsler, M.; Hornik, K.; Buchta, C. Getting Things in Order: An Introduction to the R Package seriation. J. Stat. Softw. 2008, 25, 1–34. [Google Scholar] [CrossRef]
- Bar-Joseph, Z.; Gifford, D.K.; Jaakkola, T.S. Fast optimal leaf ordering for hierarchical clustering. Bioinformatics 2001, 17, S22–S29. [Google Scholar] [CrossRef]
- Gusenleitner, D.; Howe, E.A.; Bentink, S.; Quackenbush, J.; Culhane, A.C. iBBiG: Iterative binary bi-clustering of gene sets. Bioinformatics 2012, 28, 2484–2492. [Google Scholar] [CrossRef] [PubMed]
- Kosztyán, Z.T.; Pribojszki-Németh, A.; Szalkai, I. Hybrid multimode resource-constrained maintenance project scheduling problem. Oper. Res. Perspect. 2019, 6, 100129. [Google Scholar] [CrossRef]
- Calvo, T.; Kolesárová, A.; Komorníková, M.; Mesiar, R. Aggregation Operators: Properties, Classes and Construction Methods. In Aggregation Operators; Physica-Verlag HD: Heidelberg, Germany, 2002; pp. 3–104. [Google Scholar] [CrossRef]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A Guide for Practitioners; Springer-Verlag GmbH: Berlin, Germany, 2008. [Google Scholar]
- Kolesarova, A.; Mesiar, R. On linear and quadratic constructions of aggregation functions. Fuzzy Sets Syst. 2015, 268, 1–14. [Google Scholar] [CrossRef]
- Grabisch, M.; Marichal, J.L.; Mesiar, R.; Pap, E. Aggregation Functions; Cambridge University Press: Cambridge, UK, 2009; Volume 127. [Google Scholar]
- Grabisch, M.; Marichal, J.L.; Mesiar, R.; Pap, E. Aggregation functions: Means. Inf. Sci. 2011, 181, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Marichal, J.L.; Mesiar, R. Meaningful aggregation functions mapping ordinal scales into an ordinal scale: A state of the art. Aequationes Math. 2009, 77, 207–236. [Google Scholar] [CrossRef]
- Zotteri, G.; Kalchschmidt, M.; Caniato, F. The impact of aggregation level on forecasting performance. Int. J. Prod. Econ. 2005, 93, 479–491. [Google Scholar] [CrossRef]
- Malekitabar, H.; Ardeshir, A.; Sebt, M.H.; Stouffs, R.; Teo, E.A.L. On the calculus of risk in construction projects: Contradictory theories and a rationalized approach. Saf. Sci. 2018, 101, 72–85. [Google Scholar] [CrossRef]



| Risk-Level Matrix | Aspects | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| = Quality | = Environment | ||||||||
| Risk Components | Aggr. | Risk Components | Aggr. | ||||||
| Process | Process | ||||||||
| Components | |||||||||
| Aggregated values | |||||||||
| Process | |||||||||
| Components | |||||||||
| Aggregated values | |||||||||
| Aggregation Function | Advantages | Disadvantages |
|---|---|---|
| Sum | Easy to calculate and relatively good linearity. | Fits additive components only. The resulting scale is not identical to the scale of the components ([1, 10]), which can be an advantage in determining the total risk. The result is a sum rather than an average, and the resulting value is greater than the components’ risks when there are more areas or processes. This characteristic is critical for managing the risks of several or a few areas in managerial work. |
| Arithmetic mean | Easy to calculate and relatively good linearity. The resulting scale is identical to the components’ scale ([1, 10]). | Fits additive components only. The components must be measured on the same interval scale. This function does not return the full risk; for example, it does not take into account the need to manage the risks of several or a few areas. |
| Product | Fits with multiplicative models, such as the expected values of the probability (occurrence) and severity. This is the most commonly used aggregation method | Poor linearity. Does not map to the original [1, 10] scale and instead maps to the interval [1, 10]. |
| Product/10 | Correction to the product function. The resulting scale ([1/10, 10]) is close to the original scale (e.g., [1, 10]). | Poor linearity; mapping to almost the same scale does not help. This function tends to output extremely small values. |
| Geometric mean | Normalizes values in different ranges; thus, various scale intervals can be applied. The resulting scale is identical to the components’ scale ([1, 10]). | Not easy to calculate in practice. This function fits better with multiplicative models than with other models. |
| Radial distance / | Moderately good linearity when compared to the linearity of other functions. | The calculation is not easy in practice. |
| Median | The resulting scale is the same as the components’ scale, and this function can also be used on ordinal scales. | The calculation is not easy in practice. The scale is relatively rough and can be considered correct only for homogeneous risk components. |
| Maximum | Easy to calculate. The large values focus attention on critical areas. | Poor representation of the total risk population. |
| Minimum | Easy to calculate. | Poor representation of the total risk population. |
| Number of values over threshold | Easy to calculate. This method focuses attention on critical areas. | Poor representation of the total risk population. |
| Range and standard deviation | Easy to calculate. These approaches show the range or dispersion of the risk components. | Does not output the risk level. |
| Quantile | Outputs the top occurrence values | Does not output the risk level. |
| No. | Aggregation Situation | Number of Components | Function | Remark |
|---|---|---|---|---|
| 1 | Aggregation of different risk components of the same entity (process or product component) at the lowest level. (The horizontal aggregation is shown in Table 2, 1a.). | Number of risk components: 6, namely, the occurrence, severity, detection, control, information, and range. | Arithmetic mean, corrected product, geometric mean, radial distance, median, minimum, maximum, range, number of values over warning threshold, and sum. | This is the most commonly used aggregation method for calculating the RPN of the components of a product or process. This approach shows the overall risk of a subprocess or product component. |
| 2 | Aggregation of the same risk components of different entities (process or product component) at the lowest level. (The vertical aggregation is shown in Table 2, 2a.). | Number of entities (subprocesses or product components): 1–4. | Same as in 1. | This method shows the overall risk in specific levels. |
| 3 | Further (vertical) aggregation of 1a (1b). | The aggregated values from 1, namely, the number of entities (subprocesses or product components) | Sum, arithmetic mean, and number of values over threshold. | This method shows the total risk in a certain level (within the limitations of the applied function). |
| 4 | Further (horizontal) aggregation of 2a (2b). | The aggregated values from 2; thus, there are 6 risk components, namely, the occurrence, severity, detection, control, information, and range. | Sum, arithmetic mean, and number of values over threshold. | This method shows the total risk in a certain level (within the limitations of the applied function). |
| 5 | Aggregation of all risk components at higher levels (Figure 1 and Figure 2). | Number of risk components: 6; number of entities (subprocesses or product components): 1–4.: | Arithmetic mean, geometric mean, radial distance, median, number of values over warning threshold, and sum | This method shows the total risk in a certain level (within the limitations of the applied function). |
| 5 | Aggregation of warnings (Figure 3). | Number of entities. | Sum and number of values over threshold | This method shows the total risk in a certain level (within the limitations of the applied function). |
| 6 | Generating preventive actions (Figure 4). | Number of entities. | Arithmetic mean, geometric mean, median, maximum, and corr. product | This step selects the threshold for the optimal preventive action. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovács, Z.; Csizmadia, T.; Mihálcz, I.; Kosztyán, Z.T. Multipurpose Aggregation in Risk Assessment. Mathematics 2022, 10, 3166. https://doi.org/10.3390/math10173166
Kovács Z, Csizmadia T, Mihálcz I, Kosztyán ZT. Multipurpose Aggregation in Risk Assessment. Mathematics. 2022; 10(17):3166. https://doi.org/10.3390/math10173166
Chicago/Turabian StyleKovács, Zoltán, Tibor Csizmadia, István Mihálcz, and Zsolt T. Kosztyán. 2022. "Multipurpose Aggregation in Risk Assessment" Mathematics 10, no. 17: 3166. https://doi.org/10.3390/math10173166
APA StyleKovács, Z., Csizmadia, T., Mihálcz, I., & Kosztyán, Z. T. (2022). Multipurpose Aggregation in Risk Assessment. Mathematics, 10(17), 3166. https://doi.org/10.3390/math10173166








