Analytical Investigations into Anomalous Diffusion Driven by Stress Redistribution Events: Consequences of Lévy Flights
Abstract
:1. Introduction
2. CTRW
3. Lévy Flight
3.1. Generalised Diffusion Equation
3.1.1. Probability Density Current
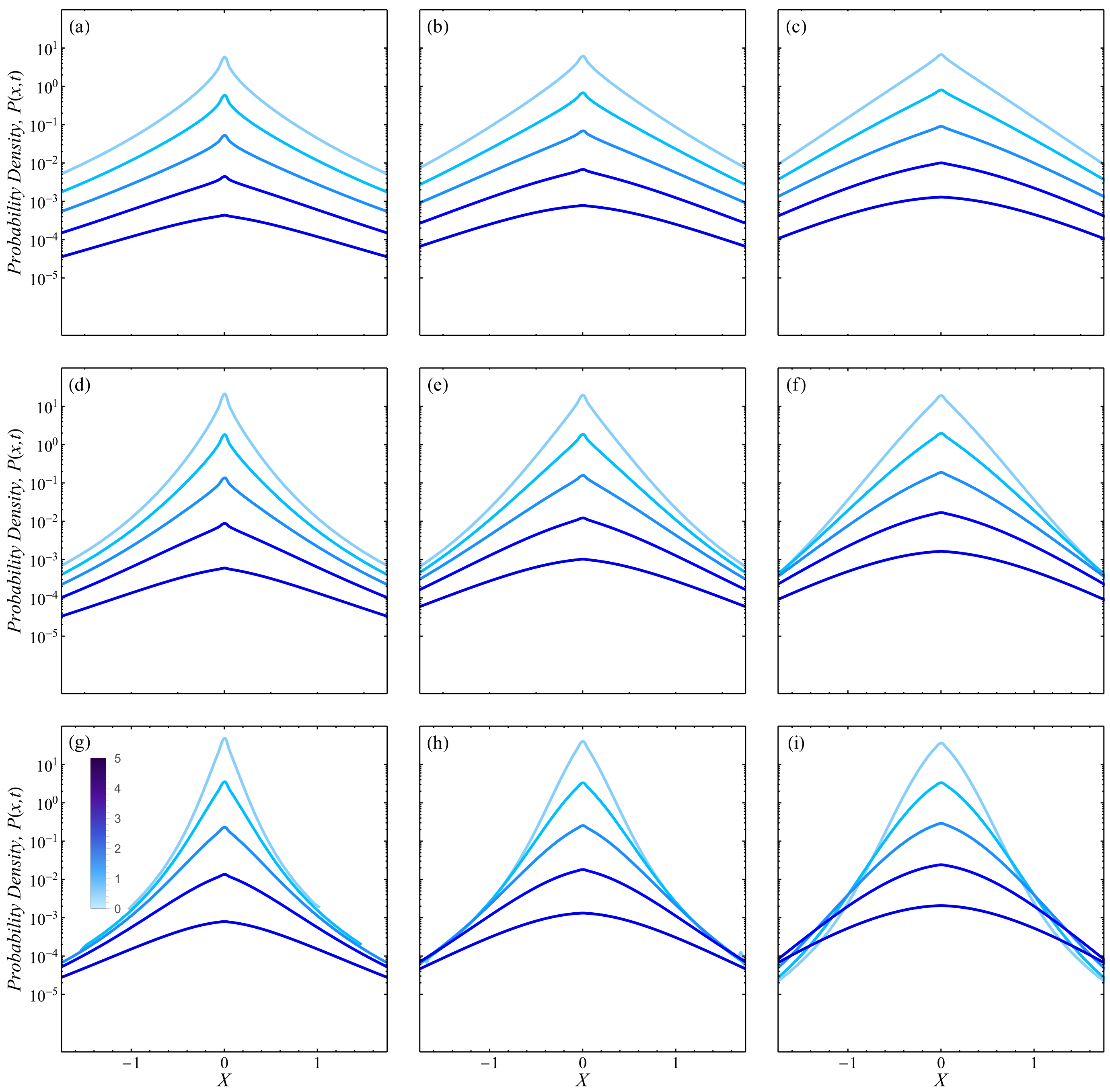
3.2. Displacement PDF
3.2.1. Subordinator Form
3.2.2. Normalisation
3.2.3. Reduction
3.2.4. Reduction
3.2.5. Short Timescale Asymptotics
3.2.6. Long Timescale Asymptotics
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Fox H-Function]
Appendix A.1. Expansion Formulae
- Formula I
- Formula II
- Formula III
- Formula IV
Appendix A.2. Transformation Properties
- Laplace Transform
- Fourier Cosine Transform
References
- Yin, Q.Q.; Li, Y.Y.; Marchesoni, F.; Nayak, S.; Ghosh, P.K. Non-Gaussian normal diffusion in low dimensional systems. Front. Phys. 2021, 16, 1–14. [Google Scholar] [CrossRef]
- Abe, S. Fokker-Planck approach to non-Gaussian normal diffusion: Hierarchical dynamics for diffusing diffusivity. Phys. Rev. E 2020, 102, 042136. [Google Scholar] [CrossRef] [PubMed]
- Gu, Q.; Schiff, E.A.; Grebner, S.; Wang, F.; Schwarz, R. Non-Gaussian transport measurements and the Einstein relation in amorphous silicon. Phys. Rev. Lett. 1996, 76, 3196–3199. [Google Scholar] [CrossRef] [PubMed]
- Scher, H.; Shlesinger, M.F.; Bendler, J.T. Time-scale invariance in transport and relaxation. Phys. Today 1991, 44, 26–34. [Google Scholar] [CrossRef]
- Klammler, F.; Kimmich, R. Geometrical restrictions of incoherent transport of water by diffusion in protein of silica fineparticle systems and by flow in a sponge—A study of anomalous properties using an nmr field-gradient technique. Croat. Chem. Acta 1992, 65, 455–470. [Google Scholar]
- Schaufler, S.; Schleich, W.P.; Yakovlev, V.P. Keyhole look at Lévy flights in subrecoil laser cooling. Phys. Rev. Lett. 1999, 83, 3162–3165. [Google Scholar] [CrossRef]
- Schaufler, S.; Schleich, W.P.; Yakovlev, V.P. Scaling and asymptotic laws in subrecoil laser cooling. Europhys. Lett. 1997, 39, 383–388. [Google Scholar] [CrossRef]
- Balescu, R. Anomalous transport in turbulent plasmas and continuous-time random-walks. Phys. Rev. E 1995, 51, 4807–4822. [Google Scholar] [CrossRef]
- Barkai, E.; Silbey, R. Diffusion of tagged particle in an exclusion process. Phys. Rev. E 2010, 81, 041129. [Google Scholar] [CrossRef]
- Fokker, A.D. The median energy of rotating electrical dipoles in radiation fields. Ann. der Phys. 1914, 43, 810–820. [Google Scholar] [CrossRef]
- Cleland, J.; Williams, M.A.K. Anomalous diffusion driven by the redistribution of internal stresses. Phys. Rev. E 2021, 104, 014123. [Google Scholar] [CrossRef]
- Montroll, E.W.; Weiss, G.H. Random walks on lattices. II. J. Math. Phys. 1965, 6, 167–181. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I. First Steps in Random Walks. From Tools to Applications; OUP Oxford: Oxford, UK, 2011. [Google Scholar]
- Shlesinger, M.F. Origins and applications of the Montroll-Weiss continuous time random walk. Eur. Phys. J. B 2017, 90, 1–5. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep.-Rev. Sect. Phys. Lett. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Vivirschi, B.N.; Boboc, P.C.; Baran, V.; Nicolin, A.I. Scale-free distributions of waiting times for earthquakes. Phys. Scr. 2020, 95, 044011. [Google Scholar] [CrossRef]
- Bialecki, M. On mechanistic explanation of the shape of the universal curve of earthquake recurrence time distributions. Acta Geophys. 2015, 63, 1205–1215. [Google Scholar] [CrossRef]
- Povstenko, Y. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional integrals and derivatives: Theory and applications. Teor. Mater. Fiz 1993, 3, 397–414. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications Of Fractinal Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar] [CrossRef]
- Podlubny, I. (Ed.) Chapter 2—Fractional derivatives and integrals. In Fractional Differential Equations; Mathematics in Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1999; Volume 198, pp. 41–119. [Google Scholar] [CrossRef]
- Pica Ciamarra, M.; Lippiello, E.; De Arcangelis, L.; Godano, C. Statistics of slipping event sizes in granular seismic fault models. EPL (Europhys. Lett.) 2011, 95, 54002. [Google Scholar] [CrossRef]
- Fox, C. The g and h functions as symmetrical fourier kernels. Trans. Am. Math. Soc. 1961, 98, 395–429. [Google Scholar]
- Chechkin, A.V.; Sokolov, I.M. Relation between generalized diffusion equations and subordination schemes. Phys. Rev. E 2021, 103, 032133. [Google Scholar] [CrossRef]
- Sokolov, I.M. Solutions of a class of non-Markovian fokker-Planck equations. Phys. Rev. E 2002, 66 Pt 1, 041101. [Google Scholar] [CrossRef] [PubMed]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef]
- Mathai, A.M.; Saxena, R.K. The H-Function with Applications in Statistics and Other Disciplines; John Wiley & Sons: Hoboken, NJ, USA, 1978. [Google Scholar]
- Sandev, T.; Chechkin, A.V.; Korabel, N.; Kantz, H.; Sokolov, I.M.; Metzler, R. Distributed-order diffusion equations and multifractality: Models and solutions. Phys. Rev. E 2015, 92, 042117. [Google Scholar] [CrossRef]
- Skibiński, P. Some expansion theorems for the H-function. Ann. Pol. Math. 1970, 23, 125–138. [Google Scholar] [CrossRef]
- Mathai, A.; Saxena, R.; Haubold, H. The H-Function: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Tomovski, Z. Fractional diffusion equation with a generalized Riemann-Liouville time fractional derivative. J. Phys. A Math. Theor. 2011, 44, 255203. [Google Scholar] [CrossRef]
- Wright, E.M. The asymptotic expansion of the generalized hypergeometric function. Proc. Lond. Math. Soc. 1940, s2-46, 389–408. [Google Scholar] [CrossRef]
- Langlands, T. Solution of a modified fractional diffusion equation. Appl. Anal. Acta. Phys. Pol. B 2003, 630, 259–279. [Google Scholar] [CrossRef]
- Awad, E.; Metzler, R. Crossover dynamics from superdiffusion to subdiffusion: Models and solutions. Fract. Calc. Appl. Anal. 2020, 23, 55–102. [Google Scholar] [CrossRef] [Green Version]
- Soury, H.; Alouini, M.S. On the symmetric alpha-stable distribution with application to symbol error rate calculations. In Proceedings of the 2016 IEEE 27th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (Pimrc), Valencia, Spain, 4–8 September 2016; pp. 990–995. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cleland, J.D.; Williams, M.A.K. Analytical Investigations into Anomalous Diffusion Driven by Stress Redistribution Events: Consequences of Lévy Flights. Mathematics 2022, 10, 3235. https://doi.org/10.3390/math10183235
Cleland JD, Williams MAK. Analytical Investigations into Anomalous Diffusion Driven by Stress Redistribution Events: Consequences of Lévy Flights. Mathematics. 2022; 10(18):3235. https://doi.org/10.3390/math10183235
Chicago/Turabian StyleCleland, Josiah D., and Martin A. K. Williams. 2022. "Analytical Investigations into Anomalous Diffusion Driven by Stress Redistribution Events: Consequences of Lévy Flights" Mathematics 10, no. 18: 3235. https://doi.org/10.3390/math10183235
APA StyleCleland, J. D., & Williams, M. A. K. (2022). Analytical Investigations into Anomalous Diffusion Driven by Stress Redistribution Events: Consequences of Lévy Flights. Mathematics, 10(18), 3235. https://doi.org/10.3390/math10183235







