Memristor-Based Lozi Map with Hidden Hyperchaos
Abstract
:1. Introduction
2. Modeling of Memristor-Based Lozi Map
2.1. Brief Review of the Lozi Map
2.2. Discrete-Time Modeling of Memristor
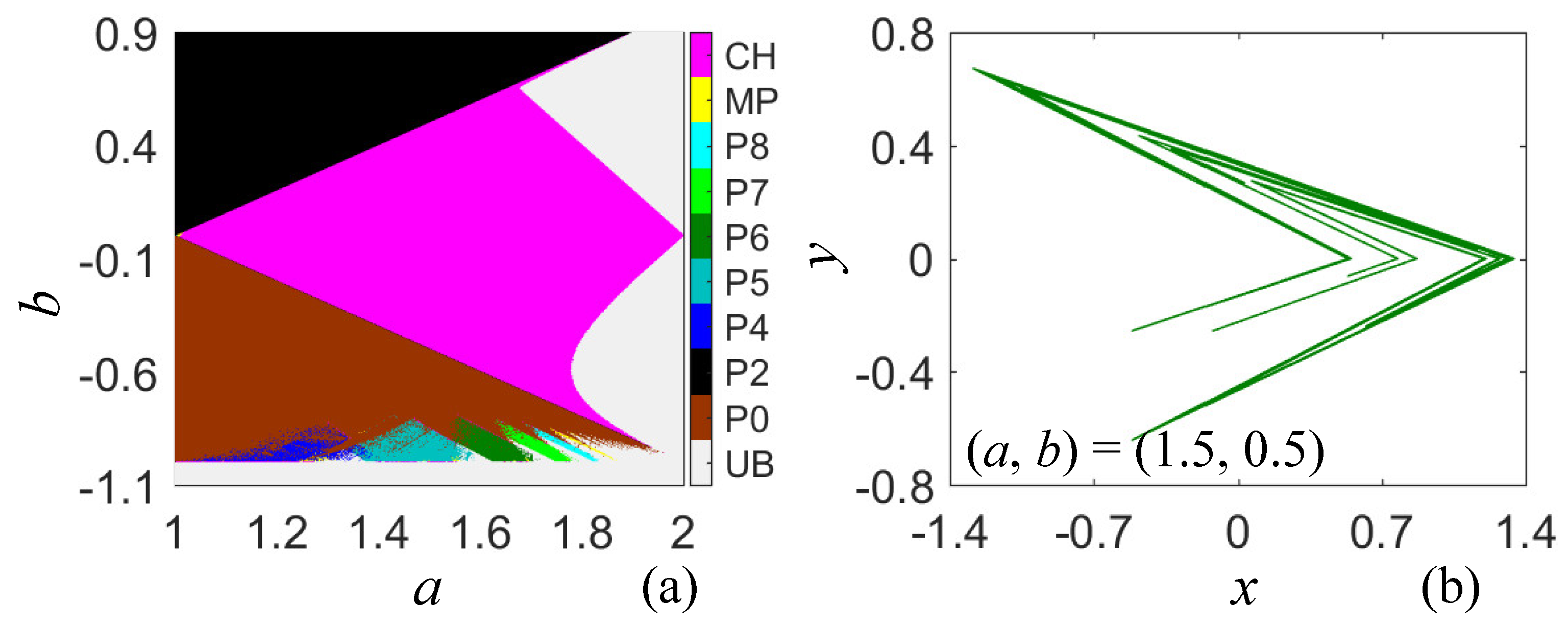
2.3. Memristor-Based Lozi Map with no Fixed Points
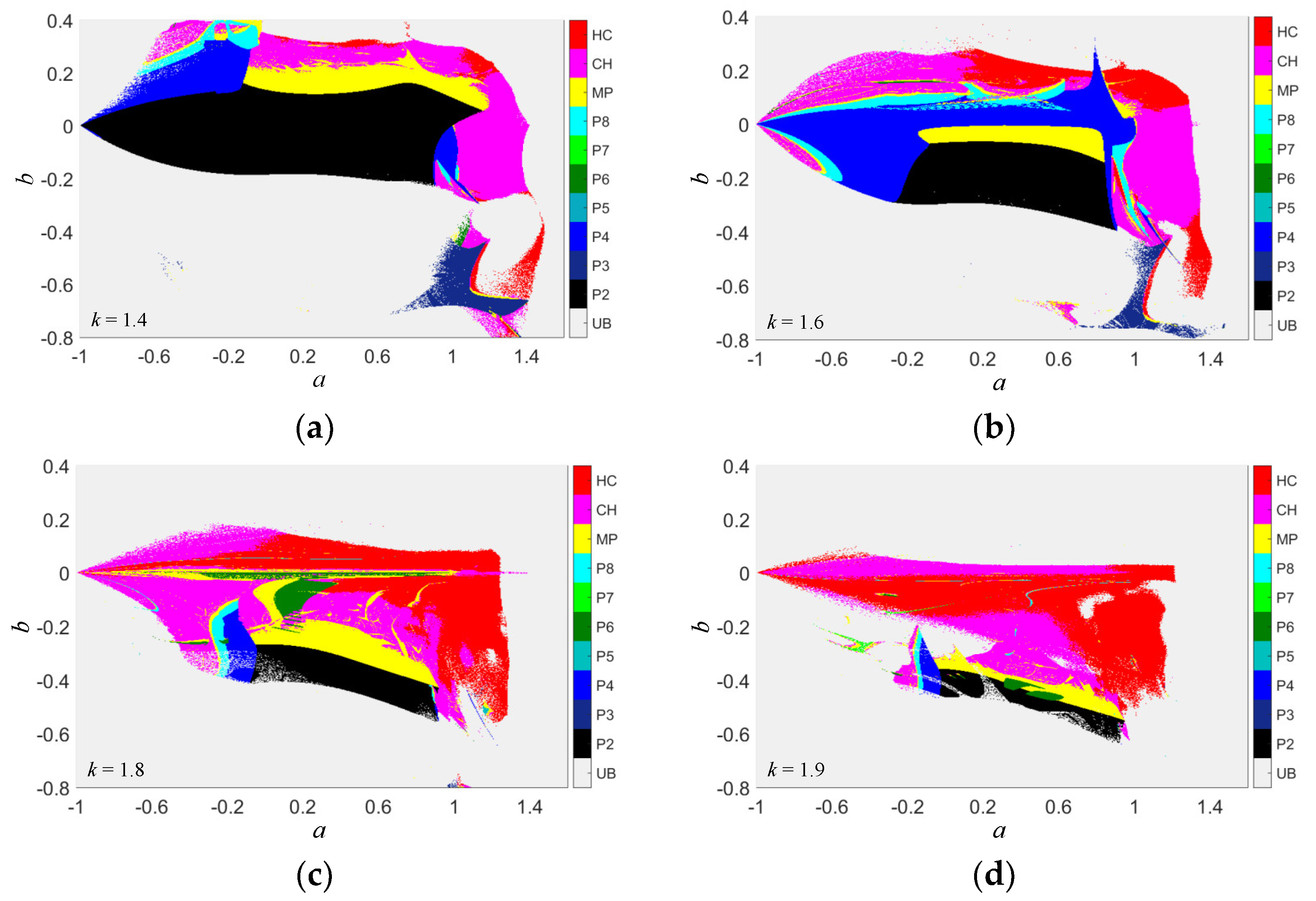
3. Dynamical Effect Induced by Discrete Memristor
3.1. 2-D Hybrid Bifurcation Plots
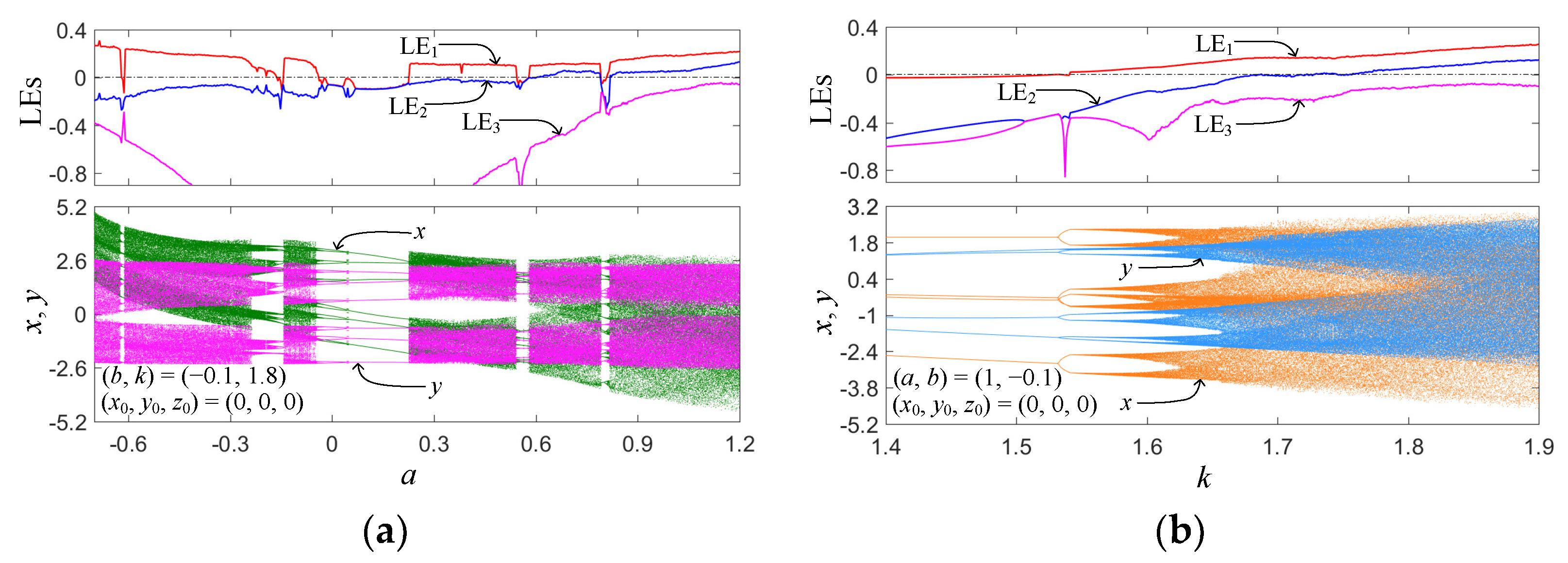
3.2. 1-D Bifurcation Plots and Hidden Hyperchaos
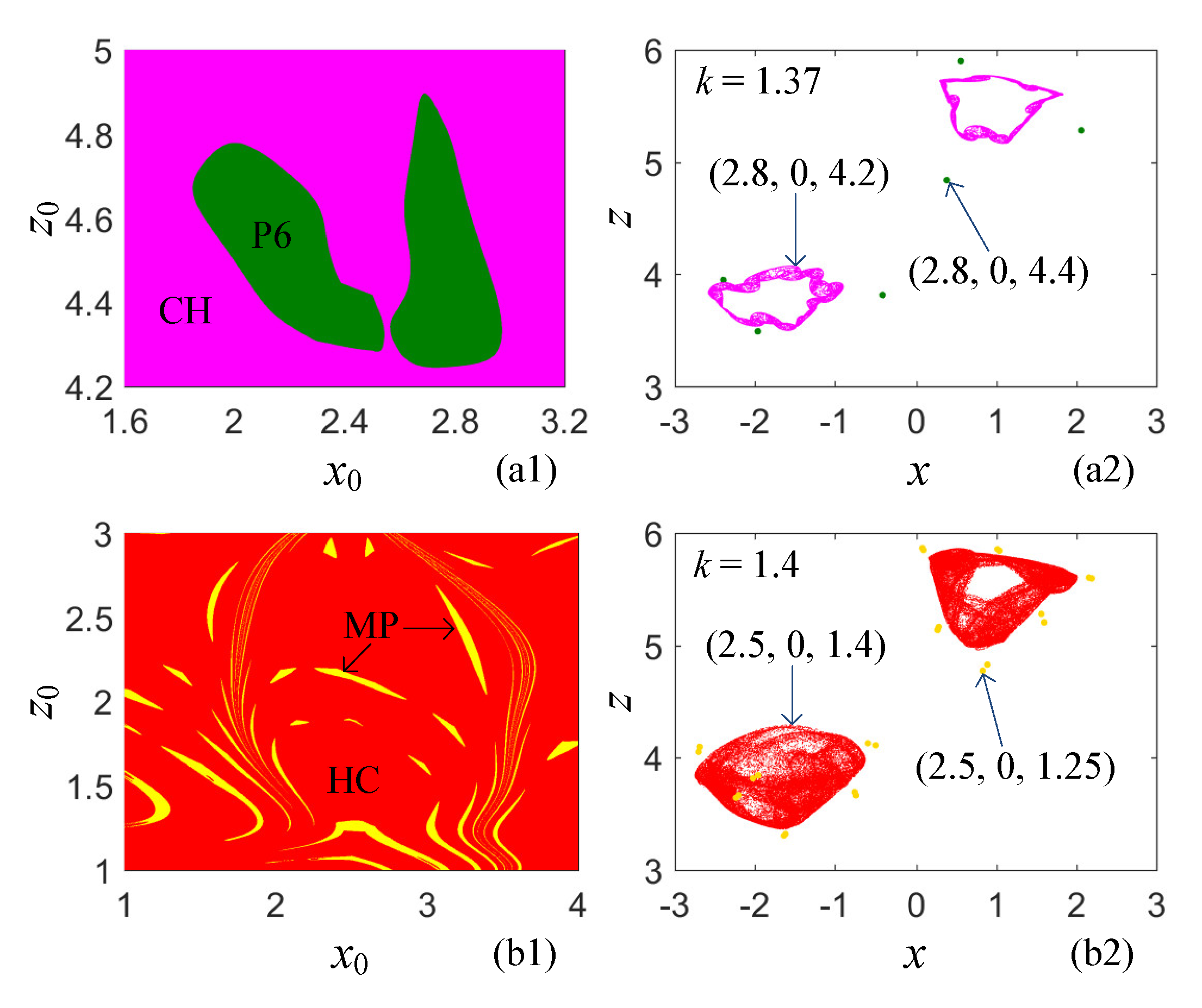
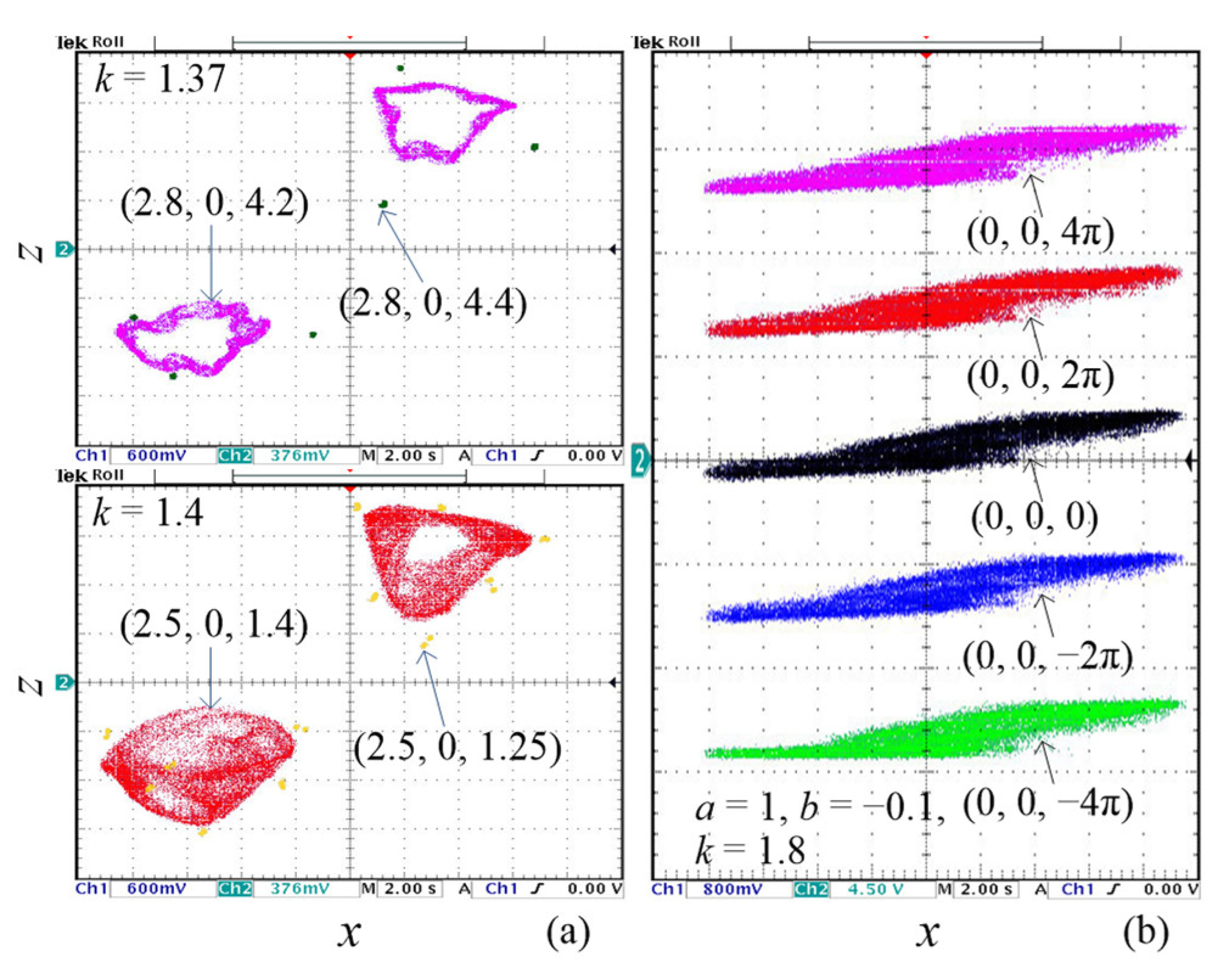
4. Heterogeneous and Homogeneous Hidden Multistability
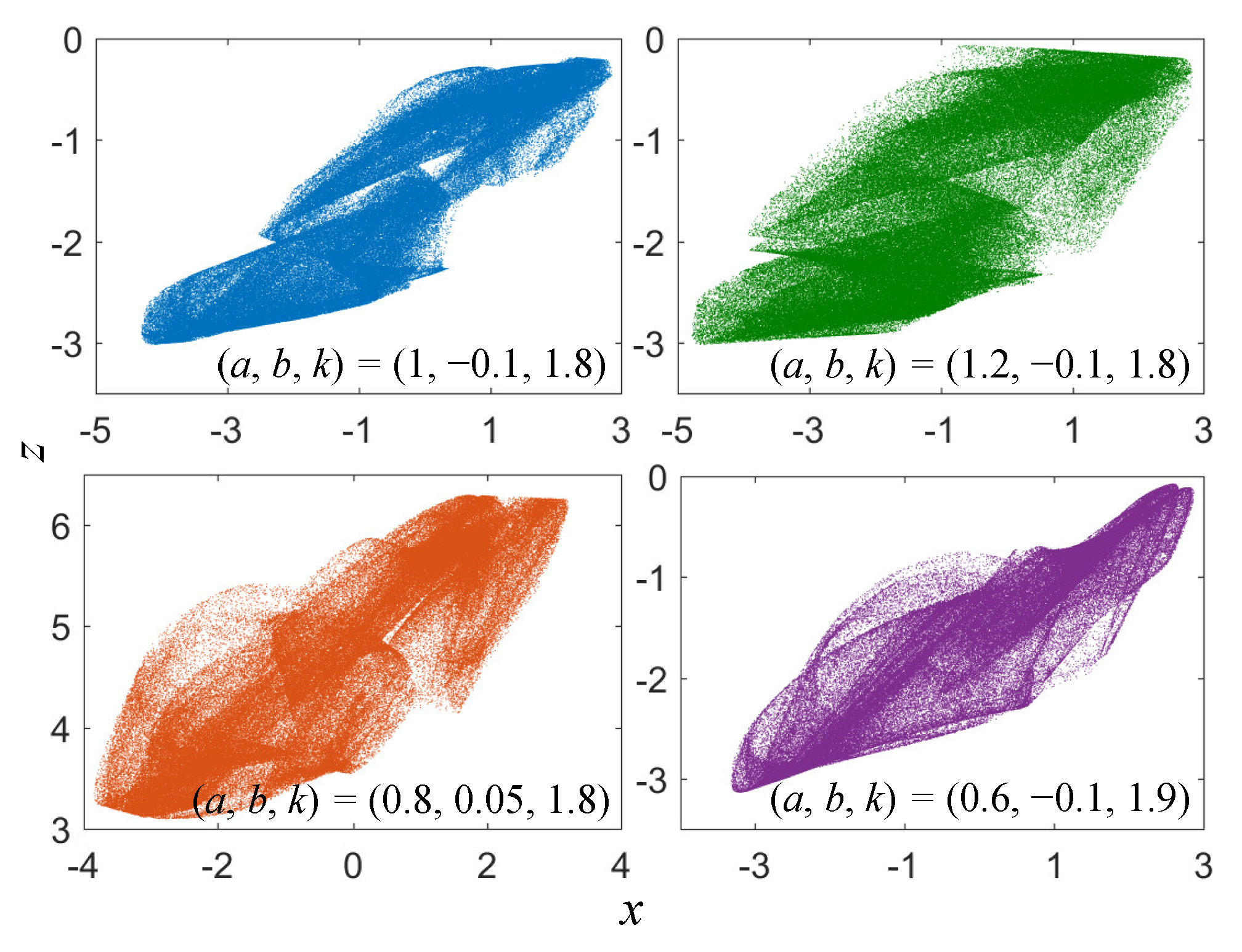
4.1. Coexistence of Heterogeneous Hidden Attractors
4.2. Coexistence of Homogeneous Hidden Hyperchaotic Attractors
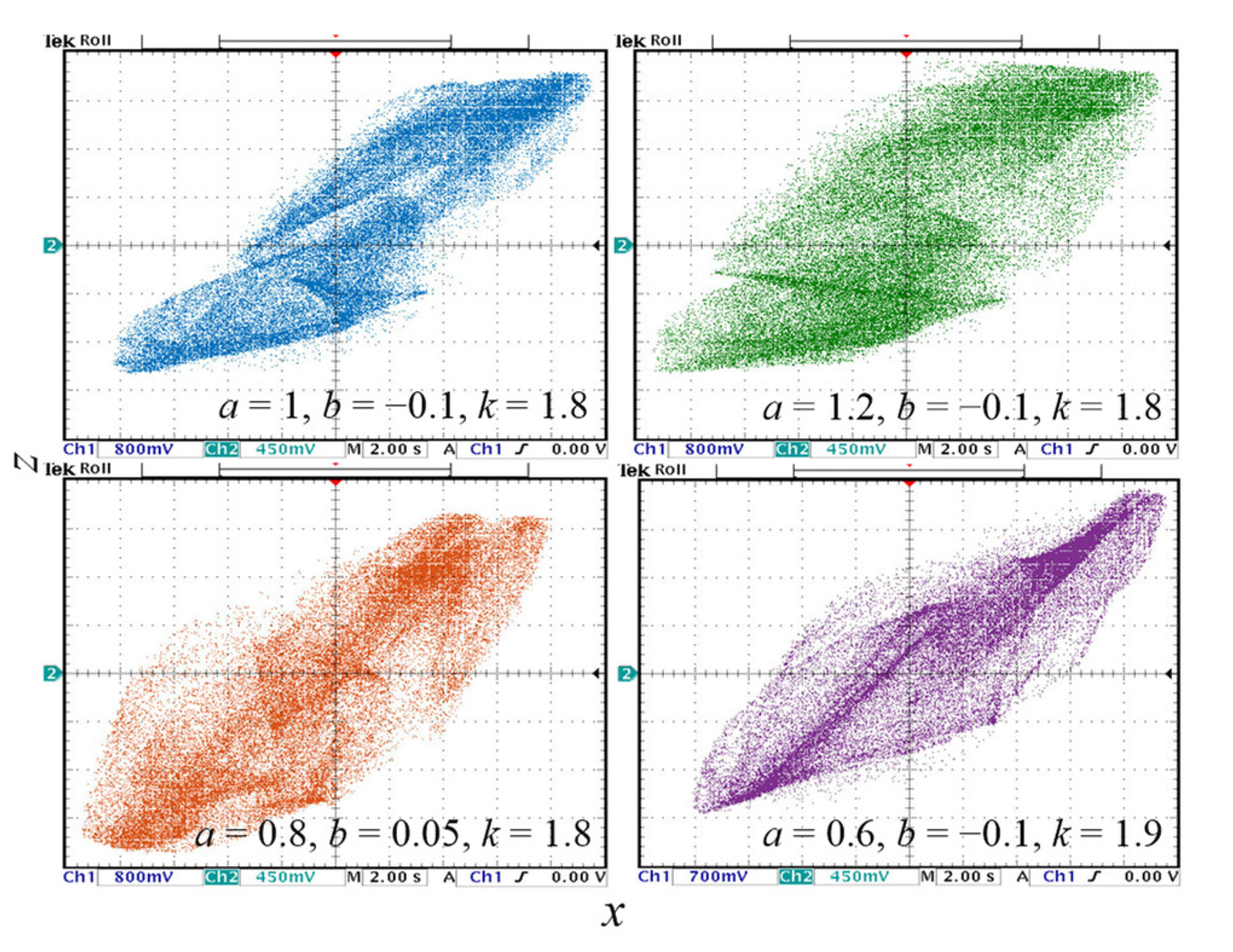
5. Microcontroller-Based Hardware Experiments
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chua, L.O. The fourth element. Proc. IEEE 2012, 100, 1920–1927. [Google Scholar] [CrossRef]
- Zhang, G.; Ma, J.; Alsaedi, A.; Ahmad, B.; Alzahrani, F. Dynamical behavior and application in Josephson Junction coupled by memristor. Appl. Math. Comput. 2018, 321, 290–299. [Google Scholar] [CrossRef]
- Chen, M.; Sun, M.X.; Bao, H.; Hu, Y.H.; Bao, B.C. Flux-charge analysis of two-memristor-based Chua’s circuit: Dimensionality decreasing model for detecting extreme multistability. IEEE Trans. Ind. Electron. 2020, 67, 2197–2206. [Google Scholar] [CrossRef]
- Fonzin, T.F.; Srinivasan, K.; Kengne, J.; Pelap, F.B. Coexisting bifurcations in a memristive hyperchaotic oscillator. AEÜ Int. J. Electron. Commun. 2018, 90, 110–122. [Google Scholar] [CrossRef]
- Min, F.H.; Li, C.; Zhang, L.; Li, C.B. Initial value-related dynamical analysis of the memristor-based system with reduced dimensions and its chaotic synchronization via adaptive sliding mode control method. Chin. J. Phys. 2019, 58, 117–131. [Google Scholar] [CrossRef]
- Volos, C.K.; Akgul, A.; Pham, V.T.; Baptista, M.S. Antimonotonicity, crisis and multiple attractors in a simple memristive circuit. Circuits Syst. J. Comput. 2018, 27, 1850026. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Kengne, J.; Tapche, R.W.; Pelap, F.B. Uncertain destination dynamics of a novel memristive 4D autonomous system. Chaos Solitions Fractals 2018, 107, 177–185. [Google Scholar] [CrossRef]
- Chen, C.J.; Bao, H.; Chen, M.; Xu, Q.; Bao, B.C. Non-ideal memristor synapse-coupled bi-neuron Hopfield neural network: Numerical simulations and breadboard experiments. AEÜ Int. J. Electron. Commun. 2019, 94, 26–35. [Google Scholar] [CrossRef]
- Ramamoorthy, R.; Rajagopal, K.; Leutcho, G.D.; Krejcar, O.; Namazi, H.; Hussain, I. Multistable dynamics and control of a new 4D memristive chaotic Sprott B system. Chaos Solitions Fractals 2022, 156, 111834. [Google Scholar] [CrossRef]
- Bao, H.; Ding, R.Y.; Hua, M.J.; Bao, B.C.; Chen, B. Incremental integral reconstitution for detecting initial condition effects. AEÜ Int. J. Electron. Commun. 2022, 149, 154178. [Google Scholar] [CrossRef]
- Mezatio, B.A.; Motchongom, M.T.; Tekam, B.R.W.; Kengne, R.; Tchitnga, R.; Fomethe, A. A novel memristive 6D hyperchaotic autonomous system with hidden extreme multistability. Chaos Solitions Fractals 2019, 120, 100–115. [Google Scholar] [CrossRef]
- Li, H.Z.; Hua, Z.Y.; Bao, H.; Zhu, L.; Chen, M.; Bao, B.C. Two-dimensional memristive hyperchaotic maps and application in secure communication. IEEE Trans. Ind. Electron. 2021, 68, 9931–9940. [Google Scholar] [CrossRef]
- Li, K.X.; Bao, H.; Li, H.Z.; Ma, J.; Hua, Z.Y.; Bao, B.C. Memristive Rulkov neuron model with magnetic induction effects. IEEE Trans. Ind. Inform. 2022, 18, 1726–1736. [Google Scholar] [CrossRef]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.S.; Kuznetsov, N.V.; Bao, H. Hidden attractors and multistability in a modified Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105494. [Google Scholar] [CrossRef]
- Doubla, I.S.; Ramakrishnan, B.; Njitacke, Z.T.; Kengne, J.; Rajagopal, K. Hidden extreme multistability and its control with selection of a desired attractor in a non-autonomous Hopfield neuron. AEÜ Int. J. Electron. Commun. 2022, 144, 154059. [Google Scholar] [CrossRef]
- Rajagopal, K.; Bayani, A.; Khalaf, A.J.M.; Namazi, H.; Jafari, S.; Pham, V.T. A no-equilibrium memristive system with four-wing hyperchaotic attractor. AEÜ Int. J. Electron. Commun. 2018, 95, 207–215. [Google Scholar] [CrossRef]
- Bao, H.; Hu, A.H.; Liu, W.B.; Bao, B.C. Hidden bursting firings and bifurcation mechanisms in memristive neuron model with threshold electromagnetic induction. IEEE Trans. Neural. Netw. Learn. Syst. 2020, 31, 502–511. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.C.; Li, Z.J.; Zhou, C.Y. Hidden extreme multistability, antimonotonicity and offset boosting control in a novel fractional-order hyperchaotic system without equilibrium. Int. J. Bifurc. Chaos 2018, 28, 1850167. [Google Scholar] [CrossRef]
- Marius, F.D.; Michal, F. Hidden chaotic attractors and chaos suppression in an impulsive discrete economical supply and demand dynamical system. Commun. Nonlinear Sci. Numer. Simul. 2019, 74, 1–13. [Google Scholar]
- Pham, V.-T.; Jafari, S.; Volos, C.; Kapitaniak, T. Different families of hidden attractors in a new chaotic system with variable equilibrium. Int. J. Bifurc. Chaos 2017, 27, 1750138. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Nazarimehr, F. Recent new examples of hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1469–1476. [Google Scholar] [CrossRef]
- Jafari, S.; Pham, V.-T.; Golpayegani, S.M.R.H.; Moghtadaei, M.; Kingni, S.T. The relationship between chaotic maps and some chaotic systems with hidden attractors. Int. J. Bifurc. Chaos 2016, 26, 1650211. [Google Scholar] [CrossRef]
- Bao, B.C.; Li, H.Z.; Zhu, L.; Zhang, X.; Chen, M. Initial-switched boosting bifurcations in 2D hyperchaotic map. Chaos 2020, 30, 033107. [Google Scholar] [CrossRef]
- Panahi, S.; Sprott, J.C.; Jafari, S. Two simplest quadratic chaotic maps without equilibrium. Int. J. Bifurc. Chaos 2018, 28, 1850144. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Boulaaras, S.; Pham, V.-T.; Azar, A.T. A fractional map with hidden attractors: Chaos and control. Eur. Phys. J. Spec. Top. 2020, 229, 1083–1093. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, G.R. Polynomial maps with hidden complex dynamics. Discret. Contin. Dyn. Syst. Ser. B 2019, 24, 2941–2954. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Bekiros, S.; Platas-Garza, M.A.; Posadas-Castillo, C.; Agarwal, P.; Jahanshahi, H.; Aly, A.A. On chaos and projective synchronization of a fractional difference map with no equilibria using a fuzzy-based state feedback control. Phys. A 2021, 578, 126100. [Google Scholar] [CrossRef]
- Liu, X.J.; Tang, D.F.; Hong, L. A fractional-order sinusoidal discrete map. Entropy 2022, 24, 320. [Google Scholar] [CrossRef]
- Peng, Y.X.; Sun, K.H.; He, S.B. A discrete memristor model and its application in Hénon map. Chaos Solitions Fractals 2020, 137, 109873. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.Y.; Li, H.Z.; Chen, M.; Bao, B.C. Discrete memristor hyperchaotic maps. IEEE Trans. Circuits Syst. I 2021, 68, 4534–4544. [Google Scholar] [CrossRef]
- Deng, Y.; Li, Y.X. Nonparametric bifurcation mechanism in 2-D hyperchaotic discrete memristor-based map. Nonlinear Dyn. 2021, 104, 4601–4614. [Google Scholar] [CrossRef]
- Ma, M.L.; Yang, Y.; Qiu, Z.C.; Peng, Y.X.; Sun, Y.C.; Li, Z.J.; Wang, M.J. A locally active discrete memristor model and its application in a hyperchaotic map. Nonlinear Dyn. 2022, 107, 2935–2949. [Google Scholar] [CrossRef]
- Lai, Q.; Lai, C. Design and implementation of a new hyperchaotic memristive map. IEEE Trans. Circuits Syst. II 2022, 69, 2331–2335. [Google Scholar] [CrossRef]
- Fiori, S.; Di Filippo, R. An improved chaotic optimization algorithm applied to a DC electrical motor modeling. Entropy 2017, 19, 665. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, T.S.; Bao, H.; Hu, Y.H.; Bao, B.C. Stability effect of load converter on source converter in a cascaded buck converter. IEEE Trans. Power Electron. 2022. [Google Scholar] [CrossRef]
- Botella-Soler, V.; Castelo, J.M.; Oteo, J.A.; Ros, J. Bifurcations in the Lozi map. J. Phys. A: Math. Theor. 2011, 44, 305101. [Google Scholar] [CrossRef]
- Bao, B.C.; Zhou, G.H.; Xu, J.P.; Liu, Z. Unified classification of operation-state regions for switching converters with ramp compensation. IEEE Trans. Power Electron. 2011, 26, 1968–1975. [Google Scholar] [CrossRef]
- Pisarchik, A.N.; Feudel, U. Control of multistability. Phys. Rep. 2014, 540, 167–218. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.Y.; Li, H.Z.; Chen, M.; Bao, B.C. Memristor-based hyperchaotic maps and application in auxiliary classifier generative adversarial nets. IEEE Trans. Ind. Inform. 2022, 18, 5297–5306. [Google Scholar] [CrossRef]

| a, b, k | (LE1, LE2) | PermEn | Cordim | DKY |
|---|---|---|---|---|
| 1, –1, 1.8 | 0.1811, 0.0522 | 4.0498 | 1.9578 | 3.0000 |
| 1.2, –0.1, 1.8 | 0.2174, 0.1286 | 4.2544 | 1.9900 | 3.0000 |
| 0.8, 0.05, 1.8 | 0.2232, 0.1159 | 4.1908 | 2.0036 | 3.0000 |
| 0.6, –0.1, 1.9 | 0.2531, 0.0342 | 3.8748 | 1.8348 | 2.5450 |
| z0 = 2mπ | (LE1, LE2) | PermEn | Cordim | DKY |
|---|---|---|---|---|
| z0 = 4π | 0.1800, 0.0508 | 4.0513 | 1.9495 | 3.0000 |
| z0 = 2π | 0.1805, 0.0493 | 4.0467 | 1.9629 | 3.0000 |
| z0 = 0 | 0.1811, 0.0522 | 4.0498 | 1.9578 | 3.0000 |
| z0 = −2π | 0.1803, 0.0521 | 4.0431 | 1.9501 | 3.0000 |
| z0 = −4π | 0.1813, 0.0498 | 4.0543 | 1.9791 | 3.0000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Gu, Y.; Rong, K.; Xu, Q.; Zhang, X. Memristor-Based Lozi Map with Hidden Hyperchaos. Mathematics 2022, 10, 3426. https://doi.org/10.3390/math10193426
Wang J, Gu Y, Rong K, Xu Q, Zhang X. Memristor-Based Lozi Map with Hidden Hyperchaos. Mathematics. 2022; 10(19):3426. https://doi.org/10.3390/math10193426
Chicago/Turabian StyleWang, Jiang, Yang Gu, Kang Rong, Quan Xu, and Xi Zhang. 2022. "Memristor-Based Lozi Map with Hidden Hyperchaos" Mathematics 10, no. 19: 3426. https://doi.org/10.3390/math10193426
APA StyleWang, J., Gu, Y., Rong, K., Xu, Q., & Zhang, X. (2022). Memristor-Based Lozi Map with Hidden Hyperchaos. Mathematics, 10(19), 3426. https://doi.org/10.3390/math10193426






