Comparative Analysis of a Cone, Wedge, and Plate Packed with Microbes in Non-Fourier Heat Flux
Abstract
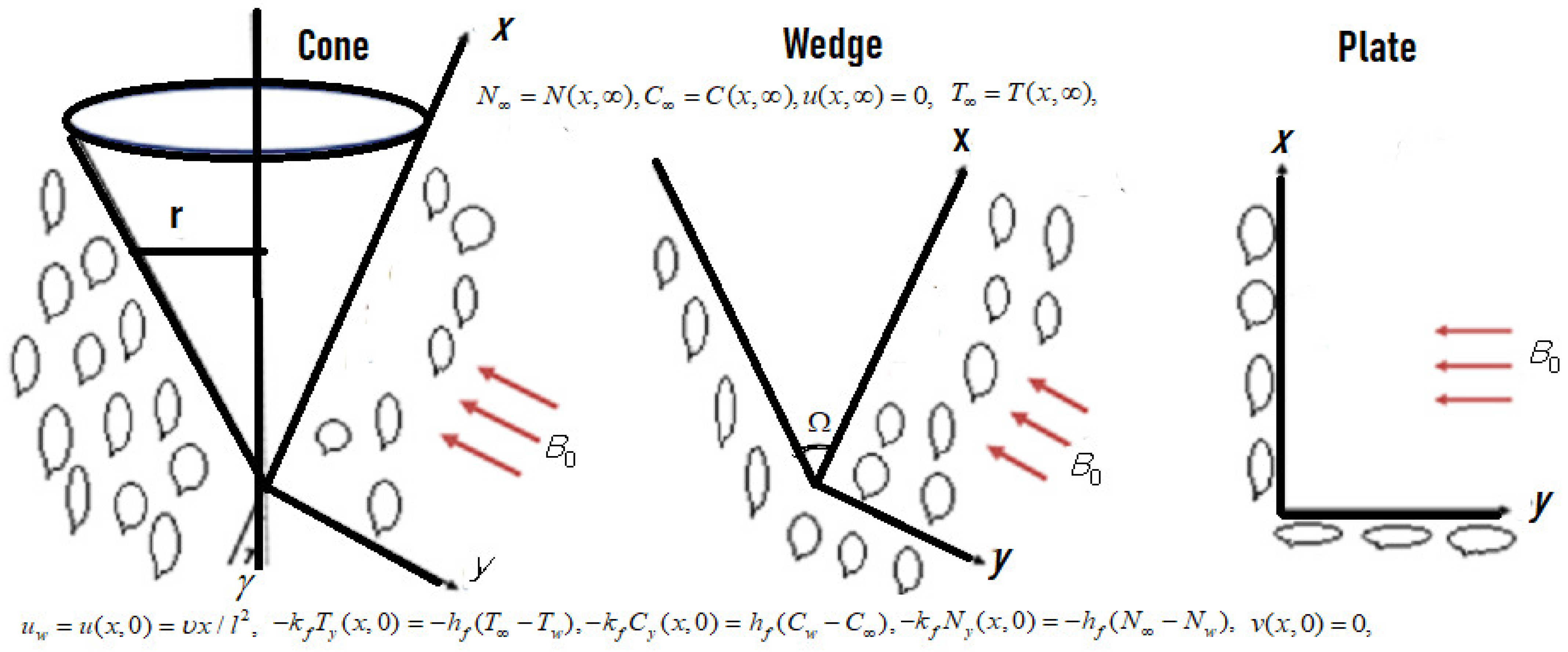
:1. Introduction
2. Mathematical Formulation
- (i)
- —relates flow across a vertical wedge.
- (ii)
- —relates flow across a vertical cone.
- (iii)
- —relates flow across a vertical plate.
3. Numerical Solutions
4. Results and Discussion



















5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| and | Components of velocities in the direction of the and axis, respectively. |
| kinematic viscosity (sq. m/s). | |
| Electrical conductivity (ohm meter). | |
| Density of fluid (kg/m3). | |
| Acceleration due to gravity (m/s2). | |
| Coefficient of concentration and volumetric thermal expansion, respectively. | |
| Relaxation time of heat flux (s). | |
| Thermal conductivity (watt). | |
| Specific heat at constant pressure (J/kg·K). | |
| Coefficient of Brownian motion. | |
| Coefficient of thermophoresis. | |
| Chemical reaction parameter. | |
| Physical parameters: | |
| Magnetic field parameter. | |
| Thermal Grashof number. | |
| Mass Grashof number. | |
| Prandtl number. | |
| Thermal relaxation parameter. | |
| Brownian motion parameter. | |
| Thermophoresis parameter |
References
- Wilkinson, W.L. Non-Newtonian Fluids; Pergamon: New York, NY, USA, 1960. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Wiley: New York, NY, USA, 1960; pp. 94–95. [Google Scholar]
- Walawender, W.P.; Chen, T.Y.; Cala, D.F. An approximate Casson fluid model for tube flow of blood. Biorheology 1975, 12, 111–119. [Google Scholar] [CrossRef] [PubMed]
- Hill, N.A.; Pedley, T.J. Bioconvection. Fluid Dyn. Res. 2005, 37, 1–20. [Google Scholar] [CrossRef]
- Kuznetsov, A. Bio-thermal convection induced by two different species of microorganisms. Int. Commun. Heat Mass Transf. 2011, 38, 548–553. [Google Scholar] [CrossRef]
- Tham, L.; Nazar, R.; Pop, I. Steady mixed convection flow on a horizontal circular cylinder embedded in a porous medium filled by a nanofluid containing gyro tactic micro-organisms. J. Heat Transf. 2013, 135, 102601. [Google Scholar] [CrossRef]
- Shah, N.A.; Wakif, A.; El-Zahar, E.R.; Ahmad, S.; Yook, S.-J. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng. 2022, 35, 102046. [Google Scholar] [CrossRef]
- Raees, A.; Xu, H.; Liao, S. Unsteady mixed nano-bio convection flow in a horizontal channel with is upper plate expanding or contracting. Int. J. Heat Mass Transf. 2015, 86, 174–182. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Jayachandrababu, M.; Sandeep, N. Chemically reacting raidiative MHD Jeffery nanofluid flow over a cone in porous medium. Int. J. Eng. Res. Afr. 2016, 19, 75–90. [Google Scholar] [CrossRef]
- Raju, C.; Sandeep, N. Heat and mass transfer in MHD non-Newtonian bio-convection flow over a rotating cone/plate with cross diffusion. J. Mol. Liq. 2016, 215, 115–126. [Google Scholar] [CrossRef]
- Khan, S.U.; Al-Khaled, K.; Aldabesh, A.; Awais, M.; Tlili, I. Bioconvection flow in accelerated couple stress nanoparticles with activation energy: Bio-fuel applications. Sci. Rep. 2021, 11, 3331. [Google Scholar] [CrossRef]
- Sajjan, K.; Shah, N.A.; Ahammad, N.A.; Raju, C.S.K.; Kumar, M.D.; Weera, W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math. 2022, 7, 18416–18449. [Google Scholar] [CrossRef]
- Cattaneo, C. Sullaconduzionedelcalore. AttidelS Eminario Mat. Dell Univ. Modenae ReggioEmilia 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame in different formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Straughan, B. Thermal convection with the Cattaneo–Christov model. Int. J. Heat Mass Transf. 2010, 53, 95–98. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A.; Almezal, S. On Cattaneo–Christov heat flux in MHD flow of Oldroyd-B fluid with homogeneous–heterogeneous reactions. J. Magn. Magn. Mater. 2016, 401, 296–303. [Google Scholar] [CrossRef]
- Rubab, K.; Mustafa, M. Cattaneo-Christov Heat Flux Model for MHD Three-Dimensional Flow of Maxwell Fluid over a Stretching Sheet. PLoS ONE 2016, 11, e0153481. [Google Scholar] [CrossRef] [PubMed]
- Salahuddin, T.; Malik, M.; Hussain, A.; Bilal, S.; Awais, M. MHD flow of Cattanneo–Christov heat flux model for Williamson fluid over a stretching sheet with variable thickness: Using numerical approach. J. Magn. Magn. Mater. 2016, 401, 991–997. [Google Scholar] [CrossRef]
- Hayat, T.; Farooq, M.; Alsaedi, A.; Al-Solamy, F. Impact of Cattaneo-Christov heat flux in the flow over a stretching sheet with variable thickness Impact of Cattaneo-Christov heat flux in the flow over a stretching sheet with variable thickness. Aip Adv. 2016, 5, 087159. [Google Scholar] [CrossRef]
- Kumar, B.R.; Sivaraj, R. Heat and mass transfer in MHD viscoelastic fluid flow over a vertical cone and flat plate with variable viscosity. Int. J. Heat Mass Transf. 2013, 56, 370–379. [Google Scholar] [CrossRef]
- Sivaraj, R.; Kumar, B.R. Viscoelastic fluid flow over a moving vertical cone and flat plate with variable electric conductivity. Int. J. Heat Mass Transf. 2013, 61, 119–128. [Google Scholar] [CrossRef]
- Vajravelu, K.; Nayfeh, J. Hydromagnetic convection at a cone and a wedge. Int. Commun. Heat Mass Transf. 1992, 19, 701–710. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Rehman, S.U.; Habib, D.; Abdal, S.; Shah, N.A.; Chung, J.D. Micropolar Dusty Fluid: Coriolis Force Effects on Dynamics of MHD Rotating Fluid When Lorentz Force Is Significant. Mathematics 2022, 10, 2630. [Google Scholar] [CrossRef]
- Ashraf, M.Z.; Rehman, S.U.; Farid, S.; Hussein, A.K.; Ali, B.; Shah, N.A.; Weera, W. Insight into Significance of Bioconvection on MHD Tangent Hyperbolic Nanofluid Flow of Irregular Thickness across a Slender Elastic Surface. Mathematics 2022, 10, 2592. [Google Scholar] [CrossRef]
- Elnaqeeb, T.; Shah, N.A.; Mirza, I.A. Natural convection flows of carbon nanotubes nanofluids with Prabhakar-like thermal transport. Math. Methods Appl. Sci. 2020, 1–14. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N.; Lorenzini, G.; Ahmadi, M.H. Chemically reacting Carreau fluid in a suspension of convective conditions over three geometries with Cattaneo-Christov heat flux model Chemically reacting Carreau fluid in a suspension of convective conditions over three geometries with Cattaneo-Christov heat flux model. Math. Model. Eng. Probl. 2018, 5, 293–302. [Google Scholar] [CrossRef]
- Kumar, R.A.; Vasu, B.; Bég, O.A.; Gorla, R.S.R.; Murthy, P.V.S.N. Homotopy semi-numerical modeling of non-Newtonian nanofluid transport external to multiple geometries using a revised Buongiorno Model. Inventions 2019, 4, 54. [Google Scholar]
- Parmar, A.; Jain, S. Influence of Non-Linear Chemical Reaction on MHD Convective Flow for Maxwell Fluid Over Three Different Permeable Vertical Surfaces. J. Nanofluids 2019, 8, 671–682. [Google Scholar] [CrossRef]
- Chaurasiya, V.; Wakif, A.; Shah, N.A.; Singh, J. A study on cylindrical moving boundary problem with variable thermal conductivity and convection under the most realistic boundary conditions. Int. Commun. Heat Transf. 2022, 138, 106312. [Google Scholar] [CrossRef]
- Raju, C.; Khan, I.; Raju, S.; Upadhya, M. Micro and Nanofluid Convection with Magnetic Field Effects for Heat and Mass Transfer Applications Using MATLAB®, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2022; ISBN 9780128231418. [Google Scholar]
| 0.1 | −0.487683 | −0.495068 | −0.556183 | 0.159062 | 0.159009 | 0.168783 | ||||||||
| 0.3 | −0.479590 | −0.490979 | −0.555061 | 0.161387 | 0.161319 | 0.168960 | ||||||||
| 0.5 | −0.469112 | −0.485634 | −0.553899 | 0.164537 | 0.164476 | 0.169217 | ||||||||
| 0.5 | −0.496125 | −0.503643 | −0.562239 | 0.160298 | 0.160251 | 0.169238 | ||||||||
| 1 | −0.495968 | −0.503565 | −0.562421 | 0.159819 | 0.159769 | 0.169215 | ||||||||
| 1.5 | −0.494092 | −0.502618 | −0.562376 | 0.159713 | 0.159656 | 0.169210 | ||||||||
| 0.1 | −0.493197 | −0.502163 | −0.561736 | 0.160745 | 0.160690 | 0.169204 | ||||||||
| 0.3 | −0.495516 | −0.503337 | −0.561990 | 0.161164 | 0.161119 | 0.169334 | ||||||||
| 0.5 | −0.497066 | −0.504119 | −0.562194 | 0.161451 | 0.161412 | 0.169441 | ||||||||
| 0.1 | −0.384018 | −0.388781 | −0.428211 | 0.161762 | 0.161735 | 0.169941 | ||||||||
| 0.3 | −0.572366 | −0.583633 | −0.655850 | 0.160428 | 0.160359 | 0.168776 | ||||||||
| 0.5 | −0.678334 | −0.694246 | −0.784126 | 0.159701 | 0.159601 | 0.168068 | ||||||||
| 0.1 | −0.502091 | −0.506638 | −0.563330 | 0.088682 | 0.088673 | 0.091467 | ||||||||
| 0.2 | −0.494485 | −0.502816 | −0.561871 | 0.160976 | 0.160927 | 0.169272 | ||||||||
| 0.3 | −0.488400 | −0.499751 | −0.560598 | 0.222081 | 0.221963 | 0.236884 | ||||||||
| 0.1 | −0.498392 | −0.504777 | −0.562058 | 0.160105 | 0.160068 | 0.169198 | ||||||||
| 0.2 | −0.494485 | −0.502816 | −0.561871 | 0.160976 | 0.160927 | 0.169272 | ||||||||
| 0.3 | −0.489989 | −0.500571 | −0.561737 | 0.161893 | 0.161825 | 0.169320 | ||||||||
| 0.05 | −0.500451 | −0.505818 | −0.562223 | 0.158785 | 0.158748 | 0.168907 | ||||||||
| 0.1 | −0.499156 | −0.505168 | −0.562117 | 0.159304 | 0.159263 | 0.169018 | ||||||||
| 0.15 | −0.497328 | −0.504249 | −0.562000 | 0.159990 | 0.159945 | 0.169139 | ||||||||
| 0.5 | −0.494485 | −0.502816 | −0.561871 | 0.160976 | 0.160927 | 0.169272 | ||||||||
| 1 | −0.492971 | −0.502050 | −0.561575 | 0.160835 | 0.160780 | 0.169296 | ||||||||
| 1.5 | −0.491706 | −0.501409 | −0.561280 | 0.160721 | 0.160660 | 0.169314 | ||||||||
| 0.5 | −0.494485 | −0.502816 | −0.561871 | 0.160976 | 0.160927 | 0.169272 | ||||||||
| 1 | −0.494484 | −0.502816 | −0.561871 | 0.165917 | 0.165885 | 0.171604 | ||||||||
| 1.5 | −0.494484 | −0.502816 | −0.561871 | 0.170061 | 0.170040 | 0.173739 | ||||||||
| 0.1 | 0.232138 | 0.232084 | 0.284529 | 0.145565 | 0.145485 | 0.161635 | ||||||||
| 0.3 | 0.221100 | 0.220981 | 0.282622 | 0.111882 | 0.111574 | 0.146700 | ||||||||
| 0.5 | 0.205327 | 0.205025 | 0.280565 | 0.070846 | 0.069964 | 0.131739 | ||||||||
| 0.5 | 0.232168 | 0.232069 | 0.286678 | 0.140435 | 0.140333 | 0.159624 | ||||||||
| 1 | 0.213561 | 0.213405 | 0.282199 | 0.149395 | 0.149315 | 0.164339 | ||||||||
| 1.5 | 0.189804 | 0.189525 | 0.277136 | 0.152112 | 0.152026 | 0.165903 | ||||||||
| 0.1 | 0.237773 | 0.237670 | 0.288263 | 0.121456 | 0.121241 | 0.151256 | ||||||||
| 0.3 | 0.239099 | 0.239013 | 0.288380 | 0.133687 | 0.133574 | 0.155192 | ||||||||
| 0.5 | 0.240015 | 0.239941 | 0.288478 | 0.142013 | 0.141945 | 0.158396 | ||||||||
| 0.1 | 0.239030 | 0.239010 | 0.288933 | 0.130374 | 0.130302 | 0.154656 | ||||||||
| 0.3 | 0.237551 | 0.237373 | 0.287843 | 0.126500 | 0.126266 | 0.152344 | ||||||||
| 0.5 | 0.235536 | 0.235163 | 0.287116 | 0.123890 | 0.123492 | 0.150928 | ||||||||
| 0.1 | 0.141544 | 0.141530 | 0.155144 | 0.079212 | 0.079186 | 0.087058 | ||||||||
| 0.2 | 0.238506 | 0.238415 | 0.288324 | 0.128222 | 0.128070 | 0.153331 | ||||||||
| 0.3 | 0.302779 | 0.302537 | 0.401857 | 0.159465 | 0.159084 | 0.204679 | ||||||||
| 0.1 | 0.261229 | 0.261129 | 0.291949 | 0.133989 | 0.133888 | 0.153632 | ||||||||
| 0.2 | 0.238506 | 0.238415 | 0.288324 | 0.128222 | 0.128070 | 0.153331 | ||||||||
| 0.3 | 0.213788 | 0.213877 | 0.285953 | 0.121605 | 0.121423 | 0.153090 | ||||||||
| 0.05 | 0.267675 | 0.267658 | 0.292523 | 0.145592 | 0.145546 | 0.156996 | ||||||||
| 0.1 | 0.261245 | 0.261219 | 0.291257 | 0.141663 | 0.141600 | 0.155889 | ||||||||
| 0.15 | 0.252289 | 0.252244 | 0.289865 | 0.136290 | 0.136199 | 0.154674 | ||||||||
| 0.5 | 0.238506 | 0.238415 | 0.288324 | 0.128222 | 0.128070 | 0.153331 | ||||||||
| 1 | 0.316324 | 0.316113 | 0.393261 | 0.131375 | 0.131202 | 0.154443 | ||||||||
| 1.5 | 0.388685 | 0.388307 | 0.493974 | 0.133854 | 0.133666 | 0.155272 | ||||||||
| 0.5 | 0.238506 | 0.238415 | 0.288324 | 0.128222 | 0.128070 | 0.153331 | ||||||||
| 1 | 0.238502 | 0.238411 | 0.288324 | 0.128221 | 0.128069 | 0.153331 | ||||||||
| 1.5 | 0.238502 | 0.238411 | 0.288324 | 0.128221 | 0.128069 | 0.153331 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santhosh, H.B.; Upadhya, M.S.; Ahammad, N.A.; Raju, C.S.K.; Shah, N.A.; Weera, W. Comparative Analysis of a Cone, Wedge, and Plate Packed with Microbes in Non-Fourier Heat Flux. Mathematics 2022, 10, 3508. https://doi.org/10.3390/math10193508
Santhosh HB, Upadhya MS, Ahammad NA, Raju CSK, Shah NA, Weera W. Comparative Analysis of a Cone, Wedge, and Plate Packed with Microbes in Non-Fourier Heat Flux. Mathematics. 2022; 10(19):3508. https://doi.org/10.3390/math10193508
Chicago/Turabian StyleSanthosh, Halavudara Basavarajappa, Mamatha Sadananda Upadhya, N. Ameer Ahammad, Chakravarthula Siva Krishnam Raju, Nehad Ali Shah, and Wajaree Weera. 2022. "Comparative Analysis of a Cone, Wedge, and Plate Packed with Microbes in Non-Fourier Heat Flux" Mathematics 10, no. 19: 3508. https://doi.org/10.3390/math10193508
APA StyleSanthosh, H. B., Upadhya, M. S., Ahammad, N. A., Raju, C. S. K., Shah, N. A., & Weera, W. (2022). Comparative Analysis of a Cone, Wedge, and Plate Packed with Microbes in Non-Fourier Heat Flux. Mathematics, 10(19), 3508. https://doi.org/10.3390/math10193508










