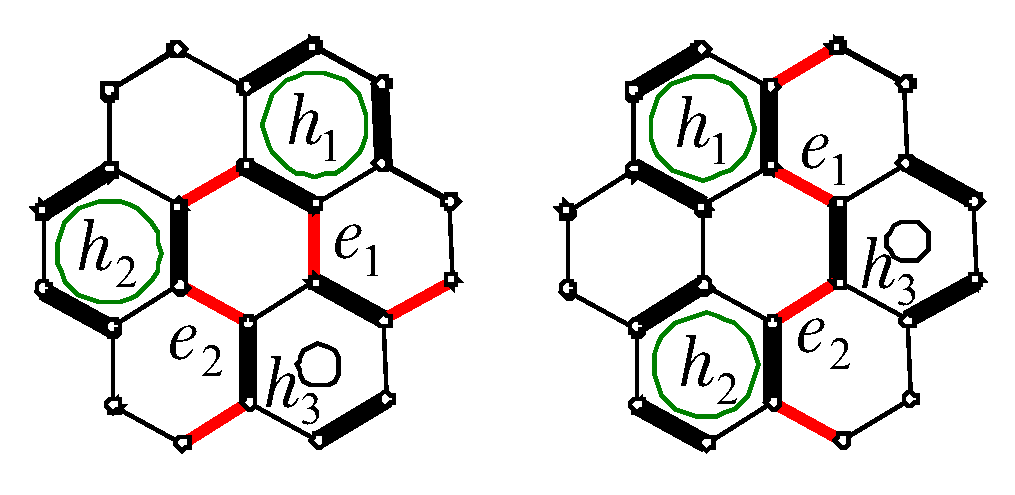Anti-Forcing Spectra of Convex Hexagonal Systems

Abstract

For any perfect matching M of a graph AG, the anti-forcing number of M $af(G,M)$ is the cardinality of a minimum edge subset $S\subseteq E\left(G\right)\backslash M$ such that the graph $G-S$ has only one perfect matching. The anti-forcing numbers of all perfect matchings of G form its anti-forcing spectrum, denoted by Spec_af$\left(G\right)$. For a convex hexagonal system $O(n_1,n_2,n_3)$ with $n_1\le n_2\le n_3$, denoted by H, it has the minimum anti-forcing number $n_1$. In this paper, we derive a formula for its maximum anti-forcing number $Af\left(H\right)$, i.e., the Fries number. Next, we prove that $[n_1,c]\cup \{c+2,c+4,\dots ,Af\left(H\right)-2,Af\left(H\right)\}\subseteq {\mathrm{Spec}}_{af}\left(H\right)$ for the specific integer c with the same parity as $Af\left(H\right)$. In particular, we obtain that if $n_1+n_2-n_3\le 1$, then $c=Af\left(H\right)$, which implies that Spec_af$\left(H\right)=[n_1,Af\left(H\right)]$ is an integer interval. Finally, we also give some non-continuous situations: Spec_af$\left(O(2,n,n)\right)=[2,4n-2]\backslash \{4n-3\}$ for $n\ge 2$; the anti-forcing spectrum of H has a gap $Af\left(H\right)-1$ for $n_1=n_2\ge 2$ and $n_3$ even, or $n_2=n_3$ and $n_1\ge 2$ even.

1. Introduction

A hexagonal system (abbreviated as HS, or polyhex or benzenoid) H is a plane 2-connected bipartite graph, whose interior faces are regular hexagons with side length 1. In chemistry, a hexagonal system containing a perfect matching can be seen as the carbon-skeleton of a benzenoid hydrocarbon. A perfect matching (or 1-factor) of a graph is a set of disjoint edges covering all vertices of the graph, which coincides with a Kekulé structure of a chemical molecule.

From 1988 to 1990, three books [1,2,3] were published on benzenoid hydrocarbons and their Kekulé structures. Randić and Klein [4] proposed the concept of “innate degree of freedom” for each Kekulé structure in a benzenoid. It means to find as few double bonds as possible to determine the entire Kekulé structure. In that paper, they also studied the sum of these innate degrees of freedom of all Kekulé structures of a zigzag hexagonal chain. Harary et al. [5] generalized the concept to the forcing number of a perfect matching of a graph. Afshani et al. [6] put these forcing numbers together to form a set called forcing spectrum. In 2015, Zhang et al. introduced the forcing polynomial of a graph, which reflects the distribution of forcing numbers of all perfect matchings of a graph, and obtained the asymptotic behavior of the average innate degrees of freedom of zigzag hexagonal systems.

Corresponding to the concept of “forcing”, Li [7] and VukiČević and Trinajstić [8] considered the anti-forcing edge and anti-forcing number of a graph, respectively. Lei et al. [9] and Klein and Rosenfeld [10] independently proposed an anti-forcing set of a perfect matching M of a graph G as a set of edges S of G not in M such that $G-S$ has a unique perfect matching M. Let $af(G,M)$ represent the anti-forcing number of M, i.e., the smallest cardinality over all anti-forcing sets of M.

The minimum and maximum values of the anti-forcing numbers over all perfect matchings of a graph G are called the minimum and maximum anti-forcing numbers of G and are denoted by $af\left(G\right)$ and $Af\left(G\right)$, respectively. Lei et al. [9] found that the maximum anti-forcing number of an HS is equal to its famous Fries number [11], which is a valuable index for understanding the structure and stability of benzenoid hydrocarbons; see also the recent article [12].

For a perfect matching M of a graph G, an even cycle (or a path) of G is called M-alternating, if its edges are alternating in or not in M. A Fries set of an HS H was first proposed as a maximum alternating hexagonal set over all perfect matchings, whose cardinality is the Fries number of H denoted by Fries(H). The Clar number [13] of H is another stable index for benzenoid hydrocarbons as the maximum cardinality of disjoint alternating hexagonal set over all perfect matchings. Xu et al. [14] showed that the maximum forcing number of an HS H is its Clar number Cl(H).

Abeledo and Atkinson [15] extended Clar and Fries numbers to 2-connected bipartite plane graphs. They proved that Clar and Fries numbers can be computed in polynomial time using linear programming methods.

The anti-forcing spectrum Spec_af$\left(G\right)$ of a graph G is the set of anti-forcing numbers of all perfect matchings of G, i.e., Spec_af$\left(G\right)=\left\{af(G,M)\right|M$ is a perfect matching of $G\}$.

Deng and Zhang [16] proved that any finite set consisting of positive integers can be the anti-forcing spectrum of a graph. For a bipartite graph with maximum degree four, they also showed that it is NP-complete to determine the anti-forcing number of a given perfect matching. They also proved that the anti-forcing spectrum of any cata-condensed hexagonal system is continuous [17], i.e., an integer interval. As for forcing spectra of graphs, Afshani et al. [6] proved that any finite set of positive integers can be the forcing spectrum of a planar bipartite graph. Based on the researches of the forcing spectra of some special fullerenes [18,19,20], Che and Chen [21] proposed a conjecture: the forcing spectrum of any fullerene graph is continuous. For other research on this direction, see [22,23,24,25,26,27,28].

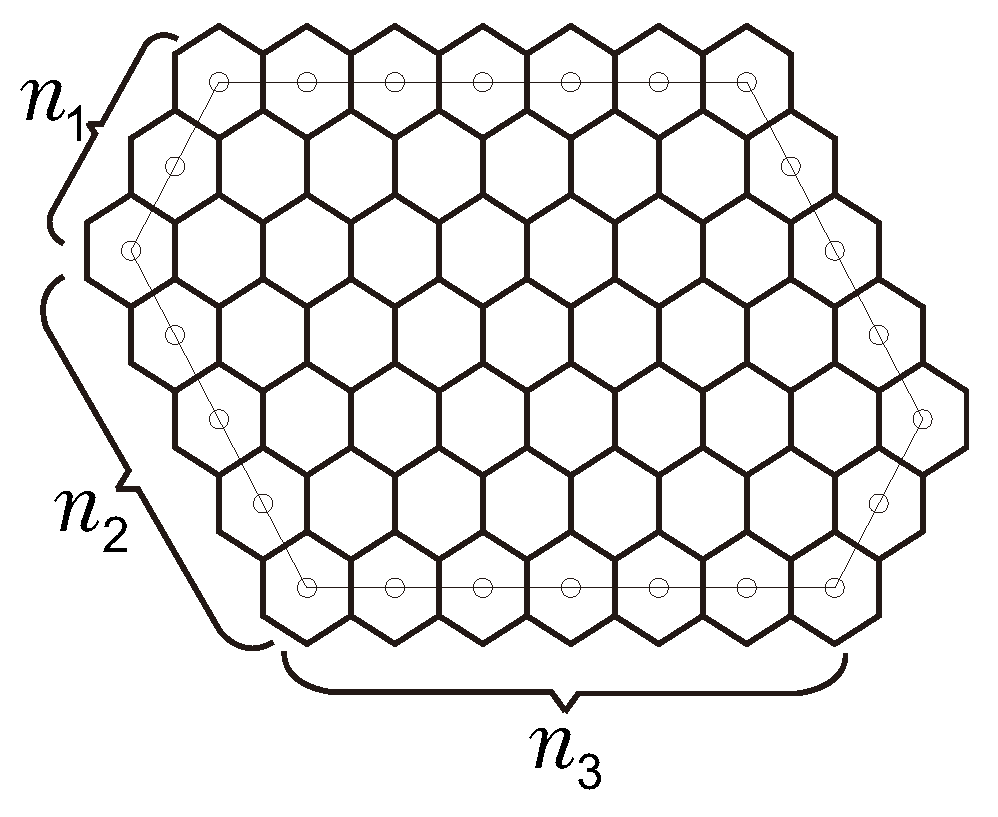
In this paper, we only consider convex HS, denoted by $O(n_1,n_2,n_3)$ with conventions $n_1\le n_2\le n_3$. For such HS, we obtained its minimum forcing number and anti-forcing number, which are both equal to $n_1$ [29], and also obtained that its forcing spectrum is an integer interval $[n_1,\mathrm{Cl}\left(O(n_1,n_2,n_3)\right)]$ by two papers: one is [30] and the other was finished by Zhang et al. So it is natural to consider whether the anti-forcing spectrum of a convex HS is an integer interval or not. First, we obtain an expression for the maximum anti-forcing number of $O(n_1,n_2,n_3)$ by constructing a Fries set. Next, we meet some gaps. That is, the anti-forcing spectra of convex HS may be not continuous, such as Spec_af$\left(O(2,2,2)\right)=\{2,3,4,6\}$ [16] and Spec_af$\left(O(3,3,3)\right)=[3,13]\backslash \left\{12\right\}$ (check by computer). So we want to know more information on the gaps.

The remainder of this paper is organized as follows. In Section 2, we exhibit some important basic HS, which can be seen as a part of a convex HS. In Section 3, we derive a formula for the maximum anti-forcing number of a convex HS, which deduces that its Fries number is equal to twice the Clar number or minus 1. Section 4 is our main body to study the anti-forcing spectra of convex HS. To make the problem easier, we restrict changes among perfect matchings of the whole graph to some subgraphs. It reduces the problem of finding a subset of the anti-forcing spectrum of the whole graph to the problem of obtaining the anti-forcing spectra of subgraphs. Section 4 is divided into two parts. The first part mainly shows the anti-forcing spectra of special constructable HS as subgraphs of convex HS. In the second part, we obtain a main subset of the anti-forcing spectra as a continuous part. In Section 5, we mainly prove a gap $Af\left(H\right)-1$ in the anti-forcing spectra of some special convex HS H, including Spec_af$\left(O(2,n,n)\right)=[2,4n-2]\backslash \{4n-3\}$ for $n\ge 2$.

2. Preliminaries

If we see the centers of all hexagons of an HS H as vertices, and two vertices are connected by one edge if and only if their corresponding hexagons have a common edge, then we obtain its inner dual graph $T\left(H\right)$. The boundary of the exterior face of a plane graph G is called the periphery of it, denoted by $\partial \left(G\right)$.

An HS H is convex if the periphery of $T\left(H\right)$ is a convex polygon. Cyvin [1] showed that a convex HS has a perfect matching if and only if the numbers of hexagons lying in the opposite sides are equal. Such convex HS is denoted by $O(n_1,n_2,n_3)$ (see Figure 1) with conventions $n_1\le n_2\le n_3$. Specially, if $n_1=1$, then such HS is called a benzenoid parallelogram.

Next, we will introduce three basic graphs, which are subgraphs of convex HS. As shown in Figure 2, the left graph is a linear hexagonal chain $H_t$ with exactly t hexagons, which satisfies that the periphery of $T\left(H_t\right)$ is a vertex or a straight line segment. The middle graph is a zigzag hexagonal chain $Z^{\prime }\left(n\right)$ with exactly n hexagons $h_1,h_2,\dots ,h_n$ such that $h_i$ is exactly adjacent to $h_{i-1}$ and $h_{i+1}$ for all $2\le i\le n-1$, and we can draw $Z^{\prime }\left(n\right)$ in the plane such that the centers of all $h_i$’s with i is odd ly on a horizontal line and the ones of others ly on another horizontal line parallel to the former. The right graph is a prolate triangle polyhex $T^{\prime }\left(p\right)$ with exactly $\frac{1}{2}p(p+1)$, which satisfies that two copies of $T^{\prime }\left(p\right)$ are joined together to form a benzenoid parallelogram with $p(p+1)$ hexagons and they happen to be joined in their maximal zigzag hexagonal chains.

In the following, we give some definitions and notations. A compatible M-alternating set of G is a set of M-alternating cycles satisfying that each pair is either disjoint or only shares the edges belonging to M. The cardinality of a maximum compatible M-alternating set of G is denoted by $c^{\prime }\left(M\right)$. If G is an HS, then any M-alternating hexagonal set of G is compatible. Next we use $\mathcal{C}\left(M\right)$ to denote the set of all M-alternating hexagons in G.

For planar bipartite graphs, Lei et al. revealed a minimax fact that connects the anti-forcing number of a perfect matching and its alternating cycles in the next theorem.

Theorem 1

([9]). For any perfect matching M of a plane bipartite graph G, $af(G,M)=c^{\prime }\left(M\right)$.

The symmetric difference of two sets $E_1$ and $E_2$ is defined by $E_1▵E_2=E_1\cup E_2-E_1\cap E_2$. For a perfect matching M and an M-alternating cycle C in a graph G, $M▵C=M▵E\left(C\right)$ is a new perfect matching of G. If $\mathcal{C}=\{C_1,C_2,\dots ,C_k\}$ is a set of disjoint M-alternating cycles in G, then $E\left(\mathcal{C}\right)=E\left(C_1\right)\cup E\left(C_2\right)\cup \dots \cup E\left(C_k\right)$ and $M▵\mathcal{C}=M▵E\left(\mathcal{C}\right)$ is also a perfect matching of G.

In Section 3, we calculate the maximum anti-forcing number of $H=O(n_1,n_2,n_3)$, i.e., Fries number, by repeatedly doing symmetric difference between M and the elements in $\mathcal{C}\left(M\right)$. According to the formula of maximum anti-forcing number of H, we also deduce the relations between Clar number and Fries number for such H.

3. Maximum Anti-Forcing Number

In order to find a Fries set of an HS, we introduce two key lemmas. First, one is a sufficient condition for a hexagon to be a member in some Fries set.

Lemma 1.

Let $\mathcal{C}\left(M\right)$ be a Fries set of an HS H for a perfect matching M. If H has a linear hexagonal chain $H_t$ such that the boundary of $H_t$ is an M-alternating cycle, then each hexagon of $H_t$ is included in a Fries set of H.

Proof. 

Since the boundary of $H_t$ is an M-alternating cycle, $H_t$ has precisely one M-alternating hexagon at one end, say $h_t$, i.e., $h_t\in \mathcal{C}\left(M\right)$ (see Figure 3). Apply induction on t. For $t=1$, it is trivial. Next we consider $t\ge 2$. Let $h_1,h_2,\dots ,h_t$ be the sequence of hexagons in $H_t$ satisfying that $h_i$ and $h_{i+1}$ share an edge for $1\le i\le t-1$. We construct a new perfect matching $M^{\prime }=M▵h_t$ of H. Then $h_{t-1}$ becomes an $M^{\prime }$-alternating hexagon. In fact, every M-alternating hexagon not adjacent to $h_t$ is also $M^{\prime }$-alternating, and H contains at most one hexagon adjacent to $h_t$. So $\mathcal{C}\left(M^{\prime }\right)$ is also a Fries set. For the linear hexagonal chain $H_t-h_t$, a hexagon obtained from $H_t$ without only the hexagon $h_t$ as its interior face, its boundary is an $M^{\prime }$-alternating cycle. Using induction hypothesis on $M^{\prime }$ and $H_t-h_t$, we know that each hexagon of $H_t-h_t$ is contained in a Fries set of H. □

In the following, we draw all hexagons with vertical edges, and we will use top, bottom, left, right freely. A cut segment of an HS H is a straight line segment l with two end points lying on $\partial \left(H\right)$ satisfying that l bisects some parallel edges of H vertically and divides H into exactly two components. The set of edges of H intersected by l is called an (elementary, orthogonal) cut of H, and denoted by L. For any edge $e\in E\left(H\right)$, $l_e$ and $L_e$ represent for the cut segment of H intersecting e and the cut containing e, respectively. We use $H\left(l\right)$ to denote the linear hexagonal chain consists of all hexagons intersecting l. If $H-L$ contains exactly two components, the top one of which is a path, then we call the path top path and $H\left(l\right)$ the top linear hexagonal chain of H without confusion.

Let $l_1$ be the highest cut segment of an HS H with a perfect matching M. Then its corresponding cut $L_1$ satisfies that $|L_1\cap M|=1$. Since the component of $H-L_1$ above $l_1$ is a path with odd order, at least one vertex of the path is covered by an edge in $L_1\cap M$. If the path has two vertices covered by $L_1\cap M$, then there is a sub-path with odd order connecting such two consecutive vertices, which implies that the vertices on the sub-path can not be absolutely covered by M, a contradiction.

Corollary 1.

Let $\mathcal{C}\left(M\right)$ be a Fries set of a convex HS H for a perfect matching M. Then for the top linear hexagonal chain $H\left(l_1\right)$ of H, the hexagons containing the only edges in $L_1\cap M$ can belong to the same Fries set of H.

Proof. 

Let $e_1=L_1\cap M$. If $H\left(l_1\right)$ contains exactly one hexagon $h_1$ using $e_1$, then H has a linear hexagonal chain including $h_1$, whose boundary is an M-alternating cycle, since H is convex. From Lemma 1, $h_1$ belongs to a Fries set of H. Otherwise, there are precisely two hexagons $h_1$ and $h_2$ using $e_1$. If both $h_1$ and $h_2$ are M-alternating, then we are done. If only one of them is M-alternating, say $h_2$, then we can consider a special linear hexagonal chain $H^1$ including $h_1$ like that above. The boundary of $H^1-h_1$ is also an M-alternating cycle, denoted by $C_1$. Let $M_1=M▵C_1$. Then $h_1$ is an $M_1$-alternating, and so is $h_2$, since $C_1$ is disjoint with $h_2$. Like Lemma 1, each M-alternating hexagon not adjacent to $C_1$ is also $M_1$-alternating, and H contains at most one hexagon adjacent to $C_1$. So $\mathcal{C}\left(M_1\right)$ is also a Fries set, and $\{h_1,h_2\}\subseteq \mathcal{C}\left(M_1\right)$. Finally, we consider that neither $h_1$ nor $h_2$ is M-alternating. Then H has two linear hexagonal chains $H^1$ and $H^2$ such that $h_i$ is a hexagon in $H^i$, but not in $H^{3-i}$ for $i=1,2$, and they only share one edge, i.e., $e_1$. Consider the boundaries of $H^1-h_1$ and $H^2-h_2$, each of which is an M-alternating cycle, denoted by $C_1$ and $C_2$ respectively. Obviously, $E\left(C_1\right)\cap E\left(C_2\right)=⌀$. Let $M^{\prime }=M▵C_1▵C_2$. Then $\mathcal{C}\left(M^{\prime }\right)$ is a Fries set of H containing $h_1$ and $h_2$ as shown in Figure 4. □

Next, we introduce two special HS. They play an important role in finding a Fries set of an HS. As shown in Figure 5, $H_1\left(p\right)$ is composed of two zigzag hexagonal chains $Z^{\prime }(2p-1)$, $Z^{\prime }\left(2p\right)$ and p independent hexagons. Let $h_1,h_2,\dots ,h_p$ be the p independent hexagons. Then each $h_i$ for $1\le i\le p-1$ is surrounded by three hexagons in $Z^{\prime }(2p-1)$ and three hexagons in $Z^{\prime }\left(2p\right)$, and $h_p$ is adjacent to exactly one hexagon in $Z^{\prime }(2p-1)$ and two hexagons in $Z^{\prime }\left(2p\right)$. $H_2\left(p\right)$ is made up of two zigzag hexagonal chains $Z^{\prime }(2p-3)$, $Z^{\prime }(2p-1)$ and p independent hexagons, where the p independent hexagons are adjacent to both $Z^{\prime }(2p-3)$ and $Z^{\prime }(2p-1)$.

If $\mathcal{C}$ is a Fries set of an HS H, then we can decide a unique perfect matching M such that $\mathcal{C}=\mathcal{C}\left(M\right)$. In this case, we call M the perfect matching corresponding to $\mathcal{C}$.

Lemma 2.

Let H be an HS with $H_1\left(n\right)$ (or $H_2\left(n\right)$) as its subgraph and the periphery of $H_1\left(n\right)$ (or $H_2\left(n\right)$) in Figure 6 is also that of H. If H has a Fries set ${\mathcal{C}}^{\prime }$ containing all $s_i$’s and H has a perfect matching M such that all $h_i$’s and $s_i$’s are M-alternating, then H has a Fries set containing all $h_i$’s and $s_i$’s.

Proof. 

Let $M^{\prime }$ be a perfect matching of H corresponding to ${\mathcal{C}}^{\prime }$.

(1). We first consider $H_1\left(n\right)$ as a subgraph of H. As the left graph shown in Figure 6, since all $s_i$’s are $M^{\prime }$-alternating hexagons, it is easy to know that $\{e_1,e_2,\dots ,e_n,a_0,a_0^{\prime }\}\subseteq M^{\prime }$, where $e_i$ is the common edge of two hexagons $s_{2i-1}$ and $h_{2i-1}$ for $1\le i\le n$, $a_0$ and $a_0^{\prime }$ are the leftmost and rightmost vertical edges in the figure, respectively.

For the hexagon $h_1$, we have $\{a_0,e_1\}\subseteq E\left(h_1\right)\cap M^{\prime }$. If $E\left(h_1\right)\cap E\left(h_2\right)=\left\{a_1\right\}\subseteq M^{\prime }$, then $h_1\in {\mathcal{C}}^{\prime }$. Otherwise, in addition to H having a perfect matching M such that all $h_i$’s and $s_i$’s are M-alternating, H contains a minimum linear hexagonal chain $H_t$ with $h_1$ as its end hexagon satisfying that for the cut segment $l_{a_1}$ of $H_t$ intersecting $a_1$, $|L_{a_1}\cap M^{\prime }|=1$, which implies that another end hexagon $h_1^{\prime }$ in $H_t$ belongs to ${\mathcal{C}}^{\prime }$. Obviously, all hexagons of $H_t$ except for $h_1$ are disjoint with $s_i$’s. By the same reason in the proof of Lemma 1, $h_1^{\prime }$ can be moved to the position of $h_1$ along the hexagons of $H_t$. Moreover, H has a Fries set containing $h_1$ and all $s_i$’s. So we can assume that $h_1\in {\mathcal{C}}^{\prime }$.

Set $t=\max \left\{i\right|h_j\in {\mathcal{C}}^{\prime }\mathrm{for}\mathrm{each}1\le j\le i\}$. We can choose one ${\mathcal{C}}^{\prime }$ such that t is as large as possible. It suffices to prove that $t=2n$. Suppose, to the contrary, that $t<2n$. Next we will deduce that $h_{t+1}\in {\mathcal{C}}^{\prime }$ to obtain a contradiction.

If t is odd (or even), then $\{a_t,a_{t+1}\}\subseteq E\left(h_{t+1}\right)\cap M^{\prime }$ (or $\{a_t,e_{\frac{t}{2}+1}\}\subseteq E\left(h_{t+1}\right)\cap M^{\prime }$), where $a_i$ is the common edge of two hexagons $h_i$ and $h_{i+1}$ for $1\le i\le 2n-1$ and $a_{2n}$ is the right vertical edge of $h_{2n}$. The same as the discussion of hexagon $h_1$, H contains a minimum linear hexagonal chain $H_t^{\prime }$ with $h_{t+1}$ and $h_{t+1}^{\prime }$ as its end hexagons, satisfying that $h_{t+1}^{\prime }$ is the unique $M^{\prime }$-alternating hexagon in $H_t^{\prime }$, and all hexagons of $H_t^{\prime }$ except for $h_{t+1}$ are disjoint with all $s_i$’s and $h_1,h_2,\dots ,h_t$. By Lemma 1, $h_{t+1}^{\prime }$ can be moved to the position of $h_{t+1}$ along the hexagons of $H_t^{\prime }$. Moreover, H has a Fries set containing $h_1,\dots ,h_{t+1}$ and all $s_i$’s, a contradiction to the choice of ${\mathcal{C}}^{\prime }$.

(2). Next, we mainly refer to the right graph shown in Figure 6, i.e., $H_2\left(n\right)$ is a subgraph of H. Since all $s_i$’s are $M^{\prime }$-alternating hexagons, $\{e_1,e_2,\dots ,e_{n-1},a_0^{\prime },a_0^{″}\}\subseteq M^{\prime }$, where $\left\{e_i\right\}=E\left(s_{2i-1}\right)\cap E\left(h_{2i}\right)$ for $1\le i\le n-1$, $a_0^{\prime }$ is the upper left edge of $p_1$ and $a_0^{″}$ is the right vertical edge of $p_n$. Let $\left\{t_i\right\}=E\left(p_i\right)\cap E\left(h_{2i-1}\right)$ for each $1\le i\le n$. If $\{t_1,t_2,\dots ,t_n\}\subseteq M^{\prime }$, then we can construct a new perfect matching $M^{\prime \prime }=M^{\prime }▵s_1▵s_3▵\dots ▵s_{2n-3}$. Further, we can find an $M^{″}$-alternating hexagonal set $({\mathcal{C}}^{\prime }-\{s_2,s_4,\dots ,s_{2n-4}\})\cup \{p_1,p_2,\dots ,p_n\}$ with size $|{\mathcal{C}}^{\prime }|+2$, a contradiction. So we can assume that $t_i\notin M^{\prime }$ for some $1\le i\le n$. Similar as above (1), H has a Fries set containing $h_{2i-1}$ and all $s_i$’s. So we can assume that $h_{2i-1}\in {\mathcal{C}}^{\prime }$.

Let $H^{\prime }$ be a new graph obtained from H by deleting all edges of $s_{2i-2}$ and $h_{2i-1}$ not covered by $M^{\prime }$. Then $H_2\left(n\right)$ is divided into two disjoint subgraphs (see the dotted lines in the right graph in Figure 6), which are isomorphic to $H_1(i-1)$ and $H_1(n-i)$, respectively. By the similar discussion as above (1), H has a Fries set containing all $s_i$’s and all $h_j$’s. □

For a subgraph $G^{\prime }$ of a graph G with a perfect matching, if $G-V\left(G^{\prime }\right)$ has a perfect matching, then $G^{\prime }$ is called a nice subgraph of G. In particular, if there is a sequence of subgraphs $G=G_1,G_2,\dots ,G_n=G^{\prime }$ obeying the rule that $G_{i+1}$ is obtained from $G_i$ by deleting a 1-degree vertex and its adjacent vertex in $G_i$ for $1\le i\le n-1$ and $G^{\prime }$ contains no 1-degree vertices, then $G^{\prime }$ is the nonsingular nice subgraph of G. Note that $G^{\prime }$ can be empty.

Theorem 2.

Let $O(n_1,n_2,n_3)$ be a convex HS with $n_1\le n_2\le n_3$. Then

$$Af\left(O(n_1,n_2,n_3)\right)=\left\{\begin{array}{cc}2n_1{n}_2-\frac{1}{2}{(n_1+n_2-n_3)}^2,\hfill & n_1+n_2-n_3\ge 2\mathit{is}\mathit{even},\hfill \\ 2n_1{n}_2-\frac{1}{2}{(n_1+n_2-n_3)}^2-\frac{1}{2},\hfill & n_1+n_2-n_3\ge 1\mathit{is}\mathit{odd},\hfill \\ 2n_1{n}_2,\hfill & n_1+n_2-n_3\le 0.\hfill \end{array}\right.$$

(1)

Proof. 

For convenience, we denote $O(n_1,n_2,n_3)$ by H.

(1). We first construct a maximal $M_r$-alternating hexagonal set $\mathcal{C}\left(r\right)$ of H which only depends on an integer r ($1\le r\le n_1+1$), where $M_r$ is a perfect matching of H. As shown in Figure 7, we can find $n_2$ zigzag hexagonal chains in H, denoted by $Z_1\left(r\right),Z_2\left(r\right),\dots ,Z_{n_2}\left(r\right)$ (they change as r changes) from the top to the bottom, and use $p_i\left(r\right)$ to represent for the length of each $Z_i\left(r\right)$. Then

$$p_i\left(r\right)=\left\{\begin{array}{cc}2i+2r-3,\hfill & 1\le i\le n_1-r+1,\hfill \\ 2n_1,\hfill & n_1-r+1<i<n_3-r+2,\hfill \\ -2i+2n_1+2n_3-2r+3,\hfill & n_3-r+2\le i\le n_2.\hfill \end{array}\right.$$

(2)

We can determine a unique perfect matching $M_r$ of H following the rule that all hexagons in each $Z_i\left(r\right)$ are $M_r$-alternating. Naturally, these hexagons form an $M_r$-alternating hexagonal set $\mathcal{C}\left(r\right)$ with size $\sum _{i=1}^{n_2}{p}_i\left(r\right)$. By Theorem 1, $af(H,M_r)\ge \left|\mathcal{C}\left(r\right)\right|$.

Let $k_1=n_1-r+1$ and $k_2=n_2-n_3+r-1$. Then $k_1+k_2=n_1+n_2-n_3$. Since $k_1\ge 0$ and $k_1+k_2\le n_2$, if $k_2\ge 0$, then $\sum _{i=1}^{n_2}{p}_i\left(r\right)=2n_1{n}_2-k_1^2-k_2^2$; otherwise, $\sum _{i=1}^{n_2}{p}_i\left(r\right)=2n_1{n}_2-k_1^2$.

We pick one vertical edge of $M_r$ from each hexagon of $Z_i\left(r\right)$ to form an edge subset $S_r$ of $M_r$. Then $M_r-S_r$ is the unique perfect matching in $H-V\left(S_r\right)$.

If such a i exists, then for $k_1<i\le n_2$, the first hexagons in all $Z_i\left(r\right)$’s form the first column of $\mathcal{C}\left(r\right)$; for $1\le i\le n_3-r+1$, the last hexagons in all $Z_i\left(r\right)$’s form the last column of $\mathcal{C}\left(r\right)$. Obviously, the left vertical edges belonging to the hexagons in the first column of $\mathcal{C}\left(r\right)$ and the right vertical edges belonging to the hexagons in the last column of $\mathcal{C}\left(r\right)$ can confirm the first and last vertical lines, respectively.

Based on $S_r$, we construct an edge subset $S_r^{\prime }$ consisting of the edges not in $M_r$ but incident with the upper end vertex (or the lower end vertex) from each edge of $S_r$ and between the above two vertical lines (see the last figure in Figure 7). Since only the hexagons in the first and last columns of $\mathcal{C}\left(r\right)$ do not share its vertical edges with other hexagons in $\mathcal{C}\left(r\right)$, we can deduce that $S_r^{\prime }$ and $\mathcal{C}\left(r\right)$ have the same cardinality. Since every perfect matching of $H-S_r^{\prime }$ must contain $S_r$, further, $M_r$ is the only perfect matching in $H-S_r^{\prime }$, and $S_r^{\prime }$ is an anti-forcing set of $M_r$ in H. So $af(H,M_r)\le |S_r^{\prime }|=|\mathcal{C}\left(r\right)|$, which implies that $af(H,M_r)=\left|\mathcal{C}\left(r\right)\right|$. If $k_2\ge 0$, i.e., $r\ge n_3-n_2+1$, then

$$\begin{array}{ccc}\hfill af(H,M_r)& =& \left|\mathcal{C}\left(r\right)\right|=2n_1{n}_2-k_1^2-k_2^2\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& =& 2n_1{n}_2-\frac{{(k_1+k_2)}^2+{(k_1-k_2)}^2}{2}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& =& 2n_1{n}_2-\frac{{(n_1+n_2-n_3)}^2}{2}-\frac{{(k_1-k_2)}^2}{2}.\hfill \end{array}$$

(5)

If $k_2\le 0$, i.e., $r\le n_3-n_2+1$, then

$$\begin{array}{ccc}\hfill af(H,M_r)& =& \left|\mathcal{C}\left(r\right)\right|=2n_1{n}_2-k_1^2=2n_1{n}_2-{(n_1-r+1)}^2.\hfill \end{array}$$

(6)

Since $1\le r\le n_1+1$, if $n_1+n_2-n_3\le 0$, then $k_2\le 0$. In this case, max $\left|\mathcal{C}\left(r\right)\right|=2n_1{n}_2$. Otherwise, for $1\le r\le n_3-n_2+1$, we have max $\left|\mathcal{C}\left(r\right)\right|=2n_1{n}_2-{(n_1+n_2-n_3)}^2$; for $n_3-n_2+1\le r\le n_1+1$, max $\left|\mathcal{C}\left(r\right)\right|=2n_1{n}_2-\frac{{(n_1+n_2-n_3)}^2}{2}-\frac{{(k_1-k_2)}^2}{2}$. If $n_1+n_2-n_3\ge 1$ is odd, then we can set $r=\frac{n_1-n_2+n_3+1}{2}$. In this case, $k_1-k_2=1$ and $\left|\mathcal{C}\left(r\right)\right|=2n_1{n}_2-\frac{1}{2}{(n_1+n_2-n_3)}^2-\frac{1}{2}$. If $n_1+n_2-n_3\ge 2$ is even, then we can set $r=\frac{n_1-n_2+n_3+2}{2}$. In this case, $k_1-k_2=0$ and $\left|\mathcal{C}\left(r\right)\right|=2n_1{n}_2-\frac{1}{2}{(n_1+n_2-n_3)}^2$. In summary, max $\left|\mathcal{C}\right(r\left)\right|=Af\left(H\right)$ shown in (1).

(2). It suffices to demonstrate that there exists a maximum M-alternating hexagonal set $\mathcal{C}$ for a perfect matching M, satisfying that it has the form such as $\mathcal{C}\left(r\right)$. First we consider the top linear hexagonal chain $H\left(l_1\right)$ of H. By Corollary 1, the only edge $e_1$ in $L_1\cap M$ belongs to exactly two hexagons $h_1$ (left) and $h_2$ (right) (one of $h_1$ and $h_2$ may not exist) and $h_1$ and $h_2$ can belong to a Fries set of H, which can be $\mathcal{C}$. Let $H_1$ be the subgraph obtained from H by deleting the end vertices of $e_1$, and $H_2$ be the nonsingular nice subgraph of $H_1$. Next we focus on the top linear hexagonal chain $H\left(l_2\right)$ of $H_2$ on the right of $e_1$ (if it exists). Once by Corollary 1, the only edge $e_2$ in $L_2\cap M$ belongs to exactly two hexagons $h_3$ (left) and $h_4$ (right), and these hexagons can also belong to $\mathcal{C}$. Since $h_2$ is M-alternating, $e_2$ is not incident with any vertex of $h_2$, and absolutely on the right of $h_2$. Let $H_3$ be the subgraph obtained from $H_2$ by deleting the end vertices of $e_2$, and $H_4$ be the nonsingular nice subgraph of $H_3$. If the top linear hexagonal chain of $H_4$ on the right of $e_2$ exists, then we denote it by $H\left(l_3\right)$. By the same reason, we will continue the above procedure until $H\left(l_r\right)$ contains two hexagons $h_{2r-1}\in \mathcal{C}$ (left) and $h_{2r}\in \mathcal{C}$ (right) sharing the only edge in $L_r\cap M$, but the top linear hexagonal chain of $H_{2r}$ on the right of $e_r$ does not exist. Thus we can set the Fries set $\mathcal{C}$ of H to include $h_i$’s for all $1\le i\le 2r$ ($h_1$ or $h_{2r}$ may not exist).

In the following, we want to move $h_i$ as far to their right hexagons as possible. If $h_{2i}$ and $h_{2i+1}$ ($1\le i\le r-1$) are not adjacent, then there are no hexagons adjacent to $h_{2i}$ to be M-alternating except for at most $h_{2i-1}$. In this case, we can obtain a new perfect matching $M▵h_{2i}$, which corresponds to a new Fries set obtained from $\mathcal{C}$ by deleting $h_{2i-1}$ and adding the hexagon on the right of $h_{2i}$. We can denote the new perfect matching and the new Fries set also by M and $\mathcal{C}$, and continue the above procedure until $h_{2i}$ and $h_{2i+1}$ ($1\le i\le r-1$) are adjacent as shown in Figure 8.

According to the above discussion, we confirm the first zigzag hexagonal chain in $\mathcal{C}$, which lies on the top right of H. We just need apply Lemma 2 $n_2-1$ times (at each step there is a new zigzag hexagonal chain in $\mathcal{C}$). Finally, we can set $\mathcal{C}$ as $\mathcal{C}\left(r\right)$. □

Remark 1.

In the proof of Theorem 2, we know that

$$\left\{\right|\mathcal{C}\left(1\right)|,|\mathcal{C}\left(2\right)|,\dots ,|\mathcal{C}(n_1+1)\left|\right\}\subseteq {\mathrm{Spec}}_{af}\left(O(n_1,n_2,n_3)\right).$$

(7)

Remark 2.

Let max $\left|\mathcal{C}\left(r\right)\right|=|\mathcal{C}\left(r_0\right)|$. Then if $n_1+n_2-n_3\ge 1$ is odd, then $r_0=\frac{n_1-n_2+n_3+1}{2}$ or $r_0=\frac{n_1-n_2+n_3+3}{2}$; if $n_1+n_2-n_3\ge 2$ is even, then $r_0=\frac{n_1-n_2+n_3+2}{2}$.

Remark 3.

From Equalities (3) and (6), we can directly obtain that $\left|\mathcal{C}\right(n_1+1\left)\right|$ is equal to $2n_1{n}_2-{(n_1+n_2-n_3)}^2$, if $n_1+n_2-n_3\ge 1$; $2n_1{n}_2$, otherwise. Moreover, if $n_1+n_2-n_3\le 1$, then $Af\left(O(n_1,n_2,n_3)\right)=\left|\mathcal{C}(n_1+1)\right|$.

Remark 4.

If $n_1+n_2-n_3\ge 1$, then for $1\le r\le n_3-n_2+1$, we have $\left|\mathcal{C}\left(r\right)\right|\le |\mathcal{C}(n_1+1)|=2n_1{n}_2-{(n_1+n_2-n_3)}^2$; for $n_3-n_2+1\le r\le n_1$, $\left|\mathcal{C}\left(r\right)\right|-\left|\mathcal{C}(r+1)\right|=2(2r-n_1+n_2-n_3-1)$, so $\left|\mathcal{C}\right(r\left)\right|$ and $\left|\mathcal{C}\right(r+1\left)\right|$ have the same parity.

Remark 5.

Since $r_0\ge n_3-n_2+1$, for $r_0\le r\le n_1$, we have $0\le \left|\mathcal{C}\left(r\right)\right|-\left|\mathcal{C}(r+1)\right|\le 2r-2=p_1\left(r\right)-1$. So $|\mathcal{C}(n_1+1)|\le |\mathcal{C}\left(n_1\right)|\le \dots \le |\mathcal{C}\left(r_0\right)|$ and they have the same parity.

A forcing set of M is an edge subset S of M not included by any other perfect matching of G. The forcing number $f(G,M)$ is equal to the cardinality of a smallest forcing set of M. The minimum (respectively, maximum) forcing number $f\left(G\right)$ (respectively $F\left(G\right)$) refers to the minimum (resp. maximum) forcing number over all perfect matchings of G. From Theorem 5 in [31], we can easily obtain the following corollary.

Corollary 2.

Let H be an $O(n_1,n_2,n_3)$ with $n_1\le n_2\le n_3$, and $n=n_1+n_2-n_3$. Then $Af\left(H\right)=2F\left(H\right)$, if $n\le 0$ or n is even; $Af\left(H\right)=2F\left(H\right)-1$, if $n\ge 1$ is odd.

4. The Anti-Forcing Spectra

Our discussion of the anti-forcing spectra relies heavily on the structure of $\mathcal{C}\left(r\right)$ for $1\le r\le n_1+1$, especially $\mathcal{C}(n_1+1)$, in the proof of Theorem 2. Since we want to find the symmetric difference between a perfect matching $M_r$ and the element in $\mathcal{C}\left(M_r\right)$ to obtain a series of new perfect matchings, we can only see the local change. It makes us to study the some special subgraphs of $O(n_1,n_2,n_3)$ in Section 4.1. In Section 4.2, we obtain a main subset of the anti-forcing spectrum of $O(n_1,n_2,n_3)$ in Lemma 8. Next we use a similar method in Lemma 8 to fill some gaps in the subset. Finally, we obtain some continuous anti-forcing spectra for special convex HS. Note that we continue to use some notations in the proof of Theorem 2.

4.1. Anti-Forcing Spectra of Special Constructable HS

According to the discussion in Theorem 2, we find that the subgraphs at the six corners of a convex HS are important, and these subgraphs are all constructable.

As shown in Figure 9, an HS H is constructable, if it can be dissected by k parallel cut segments $l_1,l_2,\dots ,l_k$ such that $H-L_1-L_2-\dots -L_k$ consists of $k+1$ disjoint paths $P_1,P_2,\dots ,P_{k+1}$, and the top path $P_1$ and the bottom path $P_{k+1}$ both are of an even length, and at the same time, the other ones are of an odd length. We call $H\left(l_i\right)$ the i-th row of H.

Proposition 1

([16]). Let M be a perfect matching of a constructable HS H. Then M contains exactly one vertical edge from each row of H.

If the end vertices of the most-left or most-right vertical edge of a row both have degree 3, then the row is called a turning row. A constructable HS is called monotonic if it contains no turning rows.

Theorem 3

([16]). The anti-forcing spectrum of a constructable HS with at most one turning is continuous.

First we consider the accurate integer intervals of the anti-forcing spectra of zigzag hexagonal chains and prolate triangle polyhexes, and these discussions are prepared for Lemmas 4–6. For a zigzag hexagonal chain, all hexagons form a Fries set, which corresponds to a unique perfect matching. In fact, such a Fries set is also unique.

For a prolate triangle polyhex $T^{\prime }\left(p\right)$, we refer to the last figure in Figure 2. For any perfect matching M of an HS H, each M-alternating hexagon of H must contain exactly one vertical edge in M, and such a vertical edge belongs to at most two M-alternating hexagons. Since the last row of $T^{\prime }\left(p\right)$ has exactly one hexagon, by Proposition 1, the maximum anti-forcing number of a prolate triangle polyhex $T^{\prime }\left(p\right)$ is at most $2p-1$. Figure 2 tells us that there is a unique perfect matching M such that $T^{\prime }\left(p\right)$ contains precisely $2p-1$ M-alternating hexagons. Then these hexagons form a Fries set of $T^{\prime }\left(p\right)$. We can also verify that such a Fries set is also unique. Combining $af\left(T^{\prime }\left(p\right)\right)=1$ in [7] with Theorem 3, we can directly obtain the anti-forcing spectra of $T^{\prime }\left(p\right)$.

Theorem 4.

$Spe{c}_{af}\left(T^{\prime }\left(p\right)\right)=[1,2p-1]$. Moreover, the Fries set of $T^{\prime }\left(p\right)$ is unique.

Based on prolate triangle polyhexes and benzenoid parallelograms, we consider other special monotonic constructable HS to prepare for the anti-forcing spectrum of convex HS. As shown in Figure 10, a benzenoid parallelogram $P(p,n)$ refers to a monotonic constructable HS with p rows satisfying that each row of it has the same length n. A monotonic constructable HS obtained from a prolate triangle polyhex $T^{\prime }\left(p\right)$ by deleting the four 2-degree vertices in exactly one hexagon is denoted by $T\left(p\right)$. Naturally, $T\left(p\right)$ includes a zigzag hexagonal chain with length $2p-2$. $T\left(p\right)+P(p,n)$ is constructed by pasting $T\left(p\right)$ and $P(p,n)$ ($P(p,n)$ can be empty) together.

We label the 2-2 edges (both end vertices have degree 2) on the 1-st row of $T\left(p\right)+P(p,n)$, which are adjacent to two 2-3 edges (one end vertex has degree 2, and the other has degree 3) by $e_1$. Also for each $2\le i\le p$, we denote the 2-2 edge on the i-th row, parallel to $e_1$, by $e_i$. Next we will consider some special perfect matchings of $T\left(p\right)+P(p,n)$ with $\{e_1,e_2,\dots ,$$e_p\}$ as their subset in the following figure.

Lemma 3

([16]). Let H be a monotonic constructable HS with a perfect matching M. Then $af(H,M)$ is equal to the number of M-alternating hexagons in H.

Lemma 4.

For any integer $2\le i\le 2p-2$, $T\left(p\right)$ has a perfect matching M containing the subset $\{e_1,e_2,\dots ,e_p\}$ and satisfying that $af\left(T\right(p),M)=i$. Moreover, Spec_af$\left(T\left(p\right)\right)=[1,2p-2]$.

Proof. 

For each perfect matching M shown in Figure 11 (except for the final graph), $\{e_1,e_2,\dots ,e_p\}\subseteq M$. Since each M-alternating hexagon contains exactly one vertical edge in M, $T\left(p\right)$ contains exactly iM-alternating hexagons for the reciprocal i-th graph, where $2\le i\le 2p-2$. By Lemma 3, we can directly get that $af\left(T\right(p),M)=i$.

According to the definition of $T\left(p\right)$, it is not difficult to know that $T\left(p\right)$ can be seen as a proper subgraph of a prolate triangle polyhex $T^{\prime }\left(p\right)$ and $T^{\prime }\left(p\right)-V\left(T\left(p\right)\right)$ has a perfect matching. By Theorem 4, $Af\left(T^{\prime }\left(p\right)\right)=2p-1$ and the Fries set of $T^{\prime }\left(p\right)$ is unique. So $Af\left(T\left(p\right)\right)\le Af\left(T^{\prime }\left(p\right)\right)-1=2p-2$. If we delete the edge $e_1$ from $T\left(p\right)$, then the result graph has a unique perfect matching, i.e., the anti-forcing number of this perfect matching is 1 in $T\left(p\right)$. In light of the above discussion, we obtain that Spec_af$=[1,2p-2]$. □

As shown in the first and second graphs of Figure 12, $Af\left(T\right(p)+P(p,1\left)\right)\ge 2p-1$ and $Af\left(T\right(p)+P(p,n\left)\right)\ge 2p$ for $n\ge 2$. Since at most two hexagons in each row belong to a Fries set of $T\left(p\right)+P(p,n)$, the above two equalities hold. Similar to Lemma 4 on $T\left(p\right)$ (it can be seen as $T\left(p\right)+P(p,0)$), we can also obtain an analogous result on $T\left(p\right)+P(p,n)$.

Lemma 5.

For any integer $2\le i\le 2p-1$, $T\left(p\right)+P(p,n)$ ($n\ge 1$) has a perfect matching M containing the subset $\{e_1,e_2,\dots ,e_p\}$ and satisfying that $af\left(T\right(p),M)=i$. Moreover, if $n=1$, then Spec_af$=[1,2p-1]$; if $n\ge 2$, then Spec_af$=[1,2p]$.

For a prolate triangle polyhex $T^{\prime }\left(p\right)$, we can also define p 2-2 edges on each row such that they lay on the same straight line (see Figure 13). Use a similar method as Lemma 4 to obtain an analogous result on $T^{\prime }\left(p\right)$.

Lemma 6.

For any odd integer $i\in [1,2p-1]$, $T^{\prime }\left(p\right)$ has a perfect matching M containing the subset $\{e_1,e_2,\dots ,e_p\}$ and satisfying that $af(T^{\prime }\left(p\right),M)=i$.

In Section 4.2, when we discuss the anti-forcing spectrum of an $O(n_1,n_2,n_3)$, we mainly use the above three lemmas.

4.2. Anti-Forcing Spectrum of $O(N_1,N_2,N_3)$

In Section 3, we obtained the maximum anti-forcing number of $O(n_1,n_2,n_3)$. Here we also need the minimum anti-forcing number.

Theorem 5

([29]). Both the minimum forcing number and the minimum anti-forcing number of an $O(n_1,n_2,n_3)$ are min $\{n_1,n_2,n_3\}$.

For the problem of anti-forcing, in order to focus on some subgraphs of an HS, we need the following lemma.

Lemma 7.

Let S be an edge subset of a graph H such that $H-S$ has a perfect matching. For any perfect matching $M^{\prime }$ of the nonsingular nice subgraph $H^{\prime }$ of $H-S$, it can be extended into a perfect matching M of $H-S$ and $af(H,M)\le af(H^{\prime },M^{\prime })+\left|S\right|$.

Proof. 

Recall the definition of a nonsingular nice subgraph; we can assume that $H^{\prime }$ is obtained from $H-S$ by deleting a 1-degree vertex u and its adjacent vertex v in $H-S$. Naturally, $M=M^{\prime }\cup \left\{uv\right\}$ is a perfect matching of H. Let $S^{\prime }$ be a minimum anti-forcing set of $M^{\prime }$. Then $S\cup S^{\prime }\subseteq E\left(H\right)-M$ is an anti-forcing set of M. Since for any other perfect matching $M_1\ne M$ of H, if $M_1\cap S=\varnothing$, then it is also a perfect matching of $H-S$ and $uv\in M_1$. According to the fact that $M_1-uv$ is a perfect matching of $H^{\prime }$ different from $M^{\prime }$, we know that $M_1\cap S^{\prime }\ne \varnothing$. So $af(H,M)\le |S\cup S^{\prime }|=|S|+af(H^{\prime },M^{\prime })$. □

In the following lemma, we will obtain our main subset of Spec_af$\left(O(n_1,n_2,n_3)\right)$.

Lemma 8.

Let H be an $O(n_1,n_2,n_3)$. Then $[n_1,|\mathcal{C}(n_1+1)\left|\right]$ is a subset of the anti-forcing spectrum of H.

Proof. 

We begin with the structure of $\mathcal{C}(n_1+1)$, which corresponds to the perfect matching $M_{n_1+1}$ and $n_2$ zigzag hexagonal chains $Z_1,Z_2,\dots ,Z_{n_2}$ ($r=n_1+1$ in this lemma, we omit it for convenience). It suffices to prove that $[n_1,k]$ and $[k,|\mathcal{C}(n_1+1)\left|\right]$ are both subsets of Spec_af$\left(H\right)$, where $k=2n_2$, if $p_{n_2}\ne 1$; otherwise, $k=2n_2-1$.

Claim 1.

$[k,|\mathcal{C}(n_1+1)\left|\right]\subseteq {\mathrm{Spec}}_{af}\left(H\right)$.

Proof. 

Theorem 2 implies that the edges, not in $M_{n_1+1}$ but incident with the lower end vertex from each vertical edge and between the first and the last vertical lines (see Figure 14 and Figure 15) form a minimum anti-forcing set S of $M_{n_1+1}$. Let $S^{\prime }$ be a subset of S on the zigzag hexagonal chain $Z_i$ for all $i\in [2,n_2]$, and $H^{\prime }=H-S^{\prime }$. Then we can obtain its nonsingular nice subgraph of $H^{\prime }$, denoted by $H^{″}$. Then $H^{″}$ is isomorphic to a monotonic constructable HS $T(n_1+1)$ (see Figure 14) or $T\left(n_1\right)+P(n_1,1)$ (see Figure 15).

By Lemmas 4 and 5, for any $2\le i\le p_1=Af\left(H^{″}\right)$, $H^{″}$ contains a perfect matching $M_i^{″}$ with $\{e_1,e_2,\dots ,e_p\}$ as its subset and $af(H^{″},M_i^{″})=i$. By Lemma 3, $H^{″}$ contains exactly i $M_i^{″}$-alternating hexagons. Since $\{e_1,e_2,\dots ,e_p\}\subseteq M_i^{″}$ (all $e_j$’s are defined in Section 2), we can extend $M_i^{″}$ to the perfect matching $M_i^{\prime }$ of H such that all hexagons in $Z_2,Z_3,\dots ,Z_{n_2}$ are $M_i^{\prime }$-alternating, which implies that $af(H,M_i^{\prime })\ge \sum _{j=2}^{n_2}{p}_j+i$. Lemma 7 tells that $af(H,M_i^{\prime })\le \left|S^{\prime }\right|+i=\sum _{j=2}^{n_2}{p}_j+i$. So $af(H,M_i^{\prime })=\sum _{j=2}^{n_2}{p}_j+i$, together with $\sum _{j=1}^{n_2}{p}_j=\left|\mathcal{C}(n_1+1)\right|$, we have

$$\left[\right|\mathcal{C}(n_1+1)|-(p_1-2),|\mathcal{C}(n_1+1)\left|\right]\subseteq {\mathrm{Spec}}_{af}\left(H\right).$$

(8)

Let $f_i$ be the upper left edge (respectively, the upper right edge) on the i-st row of $H^{″}$, where i is odd (respectively, i is even). For the perfect matching $M_2^{″}$ of $H^{″}$, neither $f_1$ nor $f_2$ is in $M_2^{″}$. However, H has two $M_2^{\prime }$-alternating hexagons $h_1$ and $h_2$ satisfying that $f_1\in E\left(h_1\right)$ and $f_2\in E\left(h_2\right)$.

Let $H_1$ be the nonsingular nice subgraph of $H-f_1-f_2$. Then $H_1$ is isomorphic to $O(n_1,n_2-1,n_3-1)$, and we can perform the process on $H_1$ as above on H. If the length of $Z_{n_2}$ is not 1, i.e., $p_{n_2}\ne 1$, then we repeat the above process $n_2$ times; otherwise, $n_2-1$ times. Finally, we can deduce that $[k,|\mathcal{C}(n_1+1)\left|\right]\subseteq {\mathrm{Spec}}_{af}\left(H\right)$. □

Claim 2.

$[n_1,k]\subseteq {\mathrm{Spec}}_{af}\left(H\right)$.

Proof. 

In Claim 1, we obtained k edges $f_1,f_2,\dots ,f_k$ such that $f_i$ lies on the i-th row of H for $1\le i\le k$. Let M be the only perfect matching of $H-f_1-f_2-\dots -f_k$. Then the i-th row of H contains exactly one M-alternating hexagon $h_i$ including the edge $f_i$.

Let $H_i^{\prime }$ be the nonsingular nice subgraph of $H-f_1-f_2-\dots -f_i$. Then $H_i^{\prime }$ is isomorphic to $O(n_1^{\prime },n_2^{\prime },n_3^{\prime })$ according to the discussion in Claim 1, where $n_1^{\prime }=n_1$, $n_2^{\prime }=n_2-\lfloor \frac{i}{2}\rfloor$ and $n_3^{\prime }=n_3-\lceil \frac{i}{2}\rceil$ (see Figure 16). By Theorem 5 and its proof in [29], $O(n_1^{\prime },n_2^{\prime },n_3^{\prime })$ has two perfect matchings such that their anti-forcing numbers are both min $\{n_1^{\prime },n_2^{\prime },n_3^{\prime }\}$, and we can pick one to extend to the perfect matching $M^i$ of H such that $h_1,h_2,\dots ,h_i$ are all $M^i$-alternating. Since $H_i^{\prime }$ contains min $\{n_1^{\prime },n_2^{\prime },n_3^{\prime }\}$ $M^i$-alternating disjoint (compatible) cycles and these cycles are compatible with $h_1,h_2,\dots ,h_i$, $af(H,M^i)\ge \min \{n_1^{\prime },n_2^{\prime },n_3^{\prime }\}+i$. In addition that Lemma 7 tells that $af(H,M^i)\le \min \{n_1^{\prime },n_2^{\prime },n_3^{\prime }\}+i$. So

$$af(H,M^i)=\min \{n_1^{\prime },n_2^{\prime },n_3^{\prime }\}+i=\min \{n_1,n_2-\lfloor \frac{i}{2}\rfloor ,n_3-\lceil \frac{i}{2}\rceil \}+i.$$

(9)

Next we mainly use Equality (9) to prove Claim 2.

Case 1.

$n_2<n_3$.

In this case, $n_2-\lfloor \frac{i}{2}\rfloor \le n_3-\lceil \frac{i}{2}\rceil$, $p_{n_2}=2n_3-2n_2+1>1$ and $0\le i\le k=2n_2$. For each $0\le i\le 2(n_2-n_1)+1$, we have $n_1\le n_2-\lfloor \frac{i}{2}\rfloor$ and $af(H,M^i)=n_1+i$. For each $2(n_2-n_1)+2\le i\le 2n_2$, we have $n_2-\lfloor \frac{i}{2}\rfloor \le n_1$ and $af(H,M^i)=n_2-\lfloor \frac{i}{2}\rfloor +i=n_2+\lceil \frac{i}{2}\rceil$. Then we can deduce that $[n_1,2n_2]\subseteq {\mathrm{Spec}}_{af}\left(H\right)$.

Case 2.

$n_2=n_3$.

Obviously, $n_3-\lceil \frac{i}{2}\rceil \le n_2-\lfloor \frac{i}{2}\rfloor$, $p_{n_2}=2n_3-2n_2+1=1$ and $0\le i\le k=2n_2-1$. If $0\le i\le 2(n_3-n_1)$, then $n_1\le n_3-\lceil \frac{i}{2}\rceil$ and $af(H,M^i)=n_1+i$. If $2(n_3-n_1)+1\le i\le 2n_2-1$, then $n_3-\lceil \frac{i}{2}\rceil \le n_1$ and $af(H,M^i)=n_3-\lceil \frac{i}{2}\rceil +i=n_3+\lfloor \frac{i}{2}\rfloor$. Once we obtain that $[n_1,2n_2-1]\subseteq {\mathrm{Spec}}_{af}\left(H\right)$.

According to the discussion of the above two cases, we directly obtain that $[n_1,k]\subseteq {\mathrm{Spec}}_{af}\left(H\right)$, and we are done. □

Combining Claims 1 and 2, we finish the proof of Lemma 8. □

Remark 3 tells that for an $O(n_1,n_2,n_3)$ with $n_1\le n_2\le n_3$, if $n_1+n_2-n_3\le 1$, then its maximum anti-forcing number is equal to the size of $\mathcal{C}(n_1+1)$ in Theorem 2. Theorem 5 also gives its minimum anti-forcing number $n_1$. Applying Lemma 8, we directly obtain the following result.

Theorem 6.

Let $O(n_1,n_2,n_3)$ be a convex HS with $n_1\le n_2\le n_3$. If $n_1+n_2-n_3\le 1$, then its anti-forcing spectrum is continuous.

Since a benzenoid parallelogram satisfies the condition of Theorem 6 and is also a monotonic constructable HS, it is a part of Theorem 3 that the anti-forcing spectra of benzenoid parallelograms are continuous.

For $O(n_1,n_2,n_3)$ with $n_1+n_2-n_3\ge 2$, Remark 5 tells us that for $r_0\le r\le n_1$, $\left|\mathcal{C}\right(r\left)\right|-\left|\mathcal{C}\right(r+1\left)\right|$ is even and at most $p_1\left(r\right)-1$ (even). Naturally, $|\mathcal{C}(n_1+1)|\equiv Af\left(O(n_1,n_2,n_3)\right)$ (mod 2). Lemma 8 mainly discuss $\mathcal{C}(n_1+1)$ based on Lemmas 4 and 5. We can also consider $\mathcal{C}\left(r\right)$ for each $r\in [r_0,n_1]$ based on Lemma 6. Applying an analogous method as the transformation of $Z_1\left(r\right)$ in Claim 1, we will get the following result.

Theorem 7.

Let H be an $O(n_1,n_2,n_3)$ with $n_1\le n_2\le n_3$. If $n_1+n_2-n_3\ge 2$, then for any odd integer $t\in [1,p_1\left(r\right)]$, $\sum _{j=2}^{n_2}{p}_j\left(r\right)+t\in {\mathrm{Spec}}_{af}\left(H\right)$. Moreover, let $c=\left|\mathcal{C}\right(n_1+1\left)\right|$, then $[n_1,c]\cup \{c+2,c+4,\dots ,Af\left(H\right)-2,Af\left(H\right)\}$ is a subset of the anti-forcing spectrum of H.

5. Non-Continuity of the Anti-Forcing Spectrum

There is a natural problem that whether all convex HS have continuous anti-forcing spectra. The answer is no. In this section, we mainly prove the existence of gaps in the anti-forcing spectra of some convex HS. Before the proof, we need some preparations.

Theorem 8

([9]). Let G be a graph with a perfect matching M. Then $f(G,M)\le af(G,M)\le \left(\Delta \right(G)-1)f(G,M)$, and thus $F\left(G\right)\le Af\left(G\right)\le \left(\Delta \right(G)-1)F\left(G\right)$, where $\Delta \left(G\right)$ is the maximum degree of G.

For a perfect matching M of a 2-connected plane graph G, a resonant set K is a set of disjoint M-alternating facial cycles of G. A maximum resonant set of G is called a Clar set (or Clar formula), and its cardinality is the Clar number (also called resonant number) of G, denoted by Cl(G).

Theorem 9

([32]). For each perfect matching M of an HS H with $f(H,M)=F\left(H\right)$, there exists a Clar set consisting of Cl(H) disjoint M-alternating hexagons of H.

Lemma 9

([16]). Let M be a perfect matching of an HS H. Then H contains a maximum compatible M-alternating set, including all M-alternating hexagons.

Theorem 10.

Let H be an $O(n_1,n_2,n_3)$ with $n_1\le n_2\le n_3$, where $n_1+n_2-n_3\ge 2$ is even. If there are two equal integers in $n_1$, $n_2$ and $n_3$, then the anti-forcing spectrum of H has a gap $Af\left(H\right)-1$.

Proof. 

By Corollary 2, we know that $Af\left(H\right)=2F\left(H\right)$. If H has a perfect matching M with $af(H,M)=Af\left(H\right)-1$, then from Theorem 8, we know that $af(H,M)=2F\left(H\right)-1\le 2f(H,M)$. Since $F\left(H\right)-\frac{1}{2}\le f(H,M)\le F\left(H\right)$, we have $f(H,M)=F\left(H\right)$.

Zhang also pointed out that such H has exactly two Clar sets ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ in [31], as shown in Figure 17, which form a Fries set of H with the form such as $C\left(r\right)$, where $r=\frac{n_1-n_2+n_3+2}{2}$. Additionally, we have that $af(H,M)=|{\mathcal{C}}_1|+|{\mathcal{C}}_2|-1$. By Theorem 9, we can find $F\left(H\right)$ disjoint M-alternating hexagons in H. Since ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ are symmetric, we can assume that these hexagons form the Clar set ${\mathcal{C}}_1$ (all white hexagons in Figure 17).

If $n_1=n_2$, then $n_1\ge 2n_1-n_3\ge 2$ and $n_3$ is even. In this case, we set $a=\frac{n_3}{2}$ and $b=n_1-a+1$. If $n_2=n_3$, then $n_1\ge 2$ and $n_1$ is even. In this case, let $a=\frac{n_1}{2}$ and $b=n_2-a+1$. Obviously, $a\ge 1$ and $b-1\ge 1$.

We label the hexagons in ${\mathcal{C}}_1$, which belong to the prolate triangle polyhexes lying on the corners of H, by $s_{1,1},s_{1,2},\dots ,s_{2,1},s_{2,2},\dots ,s_{6,1},s_{6,2},\dots$ in counterclockwise, where $s_{1,a}=s_{2,1}$, $s_{2,b}=s_{3,1}$, $s_{3,a}=s_{4,1}$, $s_{4,a+1}=s_{5,1}$, $s_{5,b-1}=s_{6,1}$ and $s_{6,a+1}=s_{1,1}$. Since H is bipartite, we can color the vertices of H by white and black such that the highest vertices in H are colored by black, in which H is drawn in the plane with vertical edges and exactly $2a$ highest vertices. The black (respectively, white) 2-degree vertex in $s_{i,1}$ is denoted by $v_i$ for i is odd (respectively, even) (see Figure 17).

An edge not belonging to any hexagon of ${\mathcal{C}}_1$ is called a join edge, if at least one end vertex of it is in some hexagon of ${\mathcal{C}}_1$. Since all hexagons in ${\mathcal{C}}_1$ are M-alternating, all join edges form an edge set J satisfying that $J\cap M=\varnothing$. We can work out that $\left|J\right|=j_1+j_2$, where $j_1=3|{\mathcal{C}}_2|=3|F\left(H\right)|$ and $j_2=(2a-2)+(2a-2)+(2b-4)=4a+2b-8$. By Lemma 9, H has a maximum compatible M-alternating set $\mathcal{F}$ containing ${\mathcal{C}}_1$, and

$$|\mathcal{F}-{\mathcal{C}}_1|=af(H,M)-|{\mathcal{C}}_1|=|{\mathcal{C}}_2|-1.$$

(10)

Claim 3.

For any$f\in \mathcal{F}-{\mathcal{C}}_1$, f must contain at least three join edges not parallel to each other.

Proof. 

Firstly, f must contain at least three edges $e_1,e_2,e_3$ in $E\left(H\right)-M-{\cup }_{h\in {\mathcal{C}}_1}E\left(h\right)\supseteq J$ not parallel to each other. If $e_i$ is not a join edge, then $e_i$ lies on one corner of H. Based on the edges saturated by M on that corner, each M-alternating path including $e_i$ must also contain a join edge parallel to $e_i$. So f must contain at least three join edges not parallel to each other. □

Next we will find M-alternating paths satrting with $v_i$ satisfying two conditions: (i) their end edges are in M and, (ii) their edges not in M are join edges. Denote the set of these paths by $\mathcal{P}$. We deduce that two end vertices of any such path are both in $\{v_1,v_2,\dots ,v_6\}$ from (ii), and have different colors by (i). So $\left|\mathcal{P}\right|=3$ and we can set $\mathcal{P}=\{P_1,P_2,P_3\}$, where $v_{2i-1}$ is an end vertex of $P_i$. We also need consider another end vertex of $P_i$.

Since $v_i$ is a 2-degree vertex in $s_{i,1}$, all join edges in these paths do not belong to any M-alternating cycle in $\mathcal{F}-{\mathcal{C}}_1$. By Claim 1, there are at least $3|\mathcal{F}-{\mathcal{C}}_1|=3(F\left(H\right)-1)=j_1-3$ edges belonging to the M-alternating cycles in $\mathcal{F}-{\mathcal{C}}_1$. So there are at most $j_2+3$ join edges in the paths of $\mathcal{P}$, i.e.,

$$j_0=|J\cap (E\left(P_1\right)\cup E\left(P_2\right)\cup E\left(P_3\right))|\le j_2+3=4a+2b-5.$$

(11)

Claim 4.

The two end vertices of$P_i$are$v_{2i-1}$and$v_{2i}$for$i=1,2,3$.

Proof. 

It suffices to show that $v_{2i}$ is an end vertex of $P_i$. $P_{i,j}$ represents for an M-alternating paths from $v_i$ to $v_j$ satisfying the above two conditions (i) and (ii), where $i\in \{1,3,5\}$ and $j\in \{2,4,6\}$. If $P_{i,j}$ does not exist, then we define its length and $|J\cap E(P_{i,j}\left)\right|$ by ∞.

We say that $P_{i,j}$ goes from k-th row to $(k+1)$-th row, which refers to that $P_{i,j}$ goes from the top vertex of a hexagon in ${\mathcal{C}}_1$ lying on the k-th row to the one of another hexagon in ${\mathcal{C}}_1$ lying on the $(k+1)$-th row with respect to a decided drawing of H. So we can deduce Fact 1 (see Figure 18).

Fact 1.

$P_{i,j}$goes through at least two join edges fromk-th row to$(k+1)$-th row, where$1\le k\le 2(a+b-1)-2=2a+2b-4$.

Let $u_i$ represents for the location of $v_i$ on the hexagon. We can first consider the length of M-alternating path $P_{i,j}^{\prime }$ from $u_i$ to $u_j$ satisfying the above two conditions (i) and (ii) and estimate the number of join edges on the path. In combination with Fact 1, it is not difficult to obtain the following initial case.

Fact 2.

If$u_i{u}_j\notin E\left(H\right)$, then$|J\cap E(P_{i,j}^{\prime }\left)\right|\ge 3$; if$u_i{u}_j\in E\left(H\right)$and$u_i{u}_j\in M$, then$|J\cap E(P_{i,j}^{\prime }\left)\right|\ge 0$; otherwise,$|J\cap E(P_{i,j}^{\prime }\left)\right|\ge 6$.

Let $r(i,j)$ be the difference of the rows of $s_{i,1}$ and $s_{j,1}$ with respect to a drawing of H such that $s_{i,1}$ lies on the first row (for $i=3,5$, we need to rotate H 120 degrees clockwise and counterclockwise). Then as $P_{i,j}$ went from $s_{i,1}$ to $s_{j,1}$, it must have gone through every row between $s_{i,1}$ and $s_{j,1}$, so it went through at least $2r(i,j)$ join edges.

Let $s_{j^{\prime },1}$ be the first hexagon when $P_{i,j}$ gets to the row of $s_{j,1}$. Then $s_{j^{\prime },1}\in {\mathcal{C}}_1$. If $s_{j^{\prime },1}$ happens to be $s_{j,1}$, then it will produce at least $|J\cap E(P_{i,j}^{\prime }\left)\right|$ more join edges. Otherwise, there are at least two hexagons between $s_{j^{\prime },1}$ and $s_{j,1}$. We consider another drawing of H such that $s_{j,1}$ lies on the first row. Then their difference of the rows is at least 3, and it will produce at least six more join edges by Fact 1. Based on these discussions, we can obtain the following inequation.

$$|J\cap E\left(P_{i,j}\right)|\ge |J\cap E\left(P_{i,j}^{\prime }\right)|+2r(i,j),$$

(12)

Based on Inequation (12), we can estimate the number of join edges on $P_{i,j}$ shown in the table of Figure 18. From Condition (ii), we can deduce that any pair of paths in $\mathcal{P}$ are disjoint. Next we consider all cases of $\mathcal{P}$ and get the lower bound of $|J\cap (E\left(P_1\right)\cup E\left(P_2\right)\cup E\left(P_3\right)\left)\right|$ based on the table in Figure 18.

Combining with Inequation (11), $j_0-(j_2+3)\le 0$. According to

Table 1. Illustration for six cases of $\mathcal{P}$.

$\mathcal{P}=$	${\mathit{j}}_0=|\mathit{J}\cap (\mathit{E}\left({\mathit{P}}_1\right)\cup \mathit{E}\left({\mathit{P}}_2\right)\cup \mathit{E}\left({\mathit{P}}_3\right))|\ge$	${\mathit{j}}_0-({\mathit{j}}_2+3)\ge$
$\{P_{1,2},P_{3,4},P_{5,6}\}$	$4a+2b-8$	$-3$
$\{P_{1,2},P_{3,6},P_{5,4}\}$	$10a+2b-5$	$6a\ge 6$
$\{P_{1,4},P_{3,2},P_{5,6}\}$	$4a+8b-11$	$6b-6\ge 6$
$\{P_{1,4},P_{3,6},P_{5,2}\}$	$16a+8b-11$	$12a+6b-6\ge 18$
$\{P_{1,6},P_{3,2},P_{5,4}\}$	$4a+2b-2$	3
$\{P_{1,6},P_{3,4},P_{5,2}\}$	$10a+2b-5$	$6a\ge 6$

, $\mathcal{P}=\{P_{1,2},P_{3,4},P_{5,6}\}$, that is, $P_1=P_{1,2}$, $P_2=P_{3,4}$ and $P_3=P_{5,6}$. □

We call an M-alternating hexagon of H is improper (respectively, proper) with respect to M, if its left (respectively, right) vertical edge belongs to M.

Table 1 tells us that there are at most three join edges can exceed the lower bound we estimate in Figure 18. First we can deduce that $s_{1,1}$ and $s_{1,a}=s_{2,1}$ are proper. Or else, from Fact 2 and the discussion above Inequation (12), we can obtain that $|J\cap E\left(P_{1,2}\right)|\ge (2a-2)+6$, which implies that $j_0\ge (4a+2b-8)+6$, i.e., $j_0-(j_2+3)\ge 3$, a contradiction to Inequation (11). Further we get that all $s_{1,j}$’s are proper. If not, we can pick the highest improper hexagon from them, denoted by $s_{1,j^{\prime }}$ ($2\le j^{\prime }\le a-1$), i.e., $s_{1,j^{\prime }-1}$ is proper. Next refer to the right graph lying on the second row in Figure 18, $P_{1,2}$ goes through exactly $2j^{\prime }$ join edges from first row to the $(j^{\prime }+1)$-th row. It happens to arrive at a hexagon in ${\mathcal{C}}_1$, denoted by $s_{1,j^{\prime }+1}^{\prime }$. The difference of rows of $s_{1,j^{\prime }+1}^{\prime }$ and $s_{1,a}$ is equal to $a-(j^{\prime }+1)+3$ with respect to a new drawing of H such that $s_{1,a}$ lies on the first row. Once $|J\cap E\left(P_{1,2}\right)|\ge (2a-2)+6$, also producing a contradiction to Inequation (11).

Thus $J^{\prime }=J-E\left(P_1\right)\cup E\left(P_2\right)\cup E\left(P_3\right)$ has cardinality $j_1+j_2-(4a+2b-8)=j_1=3\left|{\mathcal{C}}_2\right|$. Let $E=\left({\cup }_{f\in \mathcal{F}-{\mathcal{C}}_1}E\left(f\right)\right)\cap J$. Then $E\subseteq J^{\prime }\subseteq E\left(G\right)-M$, since all join edges in $E\left(P_1\right)\cup E\left(P_2\right)\cup E\left(P_3\right)$ do not belong to E. By Claim 1, $|\mathcal{F}-{\mathcal{C}}_1|\le \frac{\left|E\right|}{3}\le \frac{|J^{\prime }|}{3}=\left|{\mathcal{C}}_2\right|$.

Claim 3. 

Let $H^{\prime }$ be a subgraph of H isomorphic to $O(2,2,2)$ and including exactly three different M-alternating hexagons $h_1$, $h_2$ and $h_3$ in ${\mathcal{C}}_1$. If $h_1$ and $h_2$ are both proper, then $h_3$ is also proper.

Proof. 

Suppose to the contrary that $h_3$ is improper. Let $e_i$ be a join edge between $h_i$ and $h_3$ for $i=1,2$.

If $e_1$ or $e_2$ does not belong to any M-alternating cycle in $\mathcal{F}-{\mathcal{C}}_1$, then there are at least four join edges in $J^{\prime }-E$ (see Figure 19). We can work out that

$$|\mathcal{F}-{\mathcal{C}}_1|\le \frac{\left|E\right|}{3}\le \frac{|J^{\prime }|-4}{3}=\left|{\mathcal{C}}_2\right|-\frac{4}{3},$$

(13)

which implies that $|\mathcal{F}-{\mathcal{C}}_1|\le |{\mathcal{C}}_2|-2$, a contradiction to $|\mathcal{F}-{\mathcal{C}}_1|=|{\mathcal{C}}_2|-1$ (Equation (10)). So $e_1$ and $e_2$ are both in E; moreover, they belong to the same M-alternating cycle in $\mathcal{F}-{\mathcal{C}}_1$ containing at least nine join edges. Thus,

$$|\mathcal{F}-{\mathcal{C}}_1|\le \frac{\left|E\right|-9}{3}+1\le \frac{|J^{\prime }|-9}{3}+1=\left|{\mathcal{C}}_2\right|-2.$$

(14)

This is also a contradiction to Equation (10). We finish the proof of Claim 3. □

We can repeatedly apply Claim 3 based on the above result that every $s_{1,j}$ is proper, and infer that all M-alternating hexagons in ${\mathcal{C}}_1$ are proper. Further, as shown in Figure 17, we can find that ${\mathcal{C}}_2$ consists of M-alternating hexagons, and H contains $|{\mathcal{C}}_1|+|{\mathcal{C}}_2|$M-alternating hexagons, a contradiction to Equation (10). So the anti-forcing spectrum of H has a gap $Af\left(H\right)-1$. And we finish the proof of Theorem 10. □

Theorem 10 tells that $O(2,n,n)$ ($n\ge 2$) has a gap $Af\left(O\right(2,n,n\left)\right)-1$. For this HS, $|\mathcal{C}(n_1+1)|=2n_1{n}_2-{(n_1+n_2-n_3)}^2=4n-4=Af\left(O(2,n,n)\right)-2$. Combining with Lemma 8, we directly obtain the following result.

Theorem 11.

The anti-forcing spectrum of $O(2,n,n)$ ($n\ge 2$) has exactly one gap $Af\left(O\right(2,n,n\left)\right)-1$, i.e., Spec_af$\left(O(2,n,n)\right)=[2,4n-2]\backslash \{4n-3\}$.

By computer, we work out that Spec_af$\left(O(3,3,3)\right)=[3,13]\backslash \left\{12\right\}$ and we also obtain that Spec_af$\left(O(4,4,4)\right)=[4,24]\backslash \{23,21\}$ by excluding all perfect matchings of $O(4,4,4)$ with an anti-forcing number less than 21, which implies that the subset in Theorem 7 is not always equal to Spec_af$\left(H\right)$. So the anti-forcing spectrum of H has not been obtained and proved completely. In the case $n_1+n_2-n_3\ge 1$, we can obtain more anti-forcing numbers of H by moving each $Z_i\left(r_0\right)$ up in Section 3 in the order $i=1,2,\dots ,n_1+1-r_0$ for $r_0=\lceil \frac{n_1-n_2+n_3}{2}\rceil +1$, which deduces that $[n_1,Af\left(H\right)]\backslash \{Af\left(H\right)-1,Af\left(H\right)-3,\dots ,Af\left(H\right)-2(n_1-r_0)-1\}$ is a larger subset of Spec_af$\left(H\right)$ by a similar method, which is conjectured to be exactly the anti-forcing spectrum of an $O(n_1,n_2,n_3)$ and agrees with Spec_af$\left(O(3,3,3)\right)$ and Spec_af$\left(O(4,4,4)\right)$.

Conjecture 1.

Let$H=O(n_1,n_2,n_3)$with$n_1\le n_2\le n_3$and$n_1+n_2-n_3\ge 1$. Then Spec_af$\left(H\right)=[n_1,Af\left(H\right)]\backslash \{Af\left(H\right)-1,Af\left(H\right)-3,\dots ,Af\left(H\right)-2(n_1-r_0)-1\}$, where$r_0=\lceil \frac{n_1-n_2+n_3}{2}\rceil +1$.