Mathematical Analysis of Unsteady Stagnation Point Flow of Radiative Casson Hybrid Nanofluid Flow over a Vertical Riga Sheet
Abstract
:1. Introduction
2. Materials and Methods
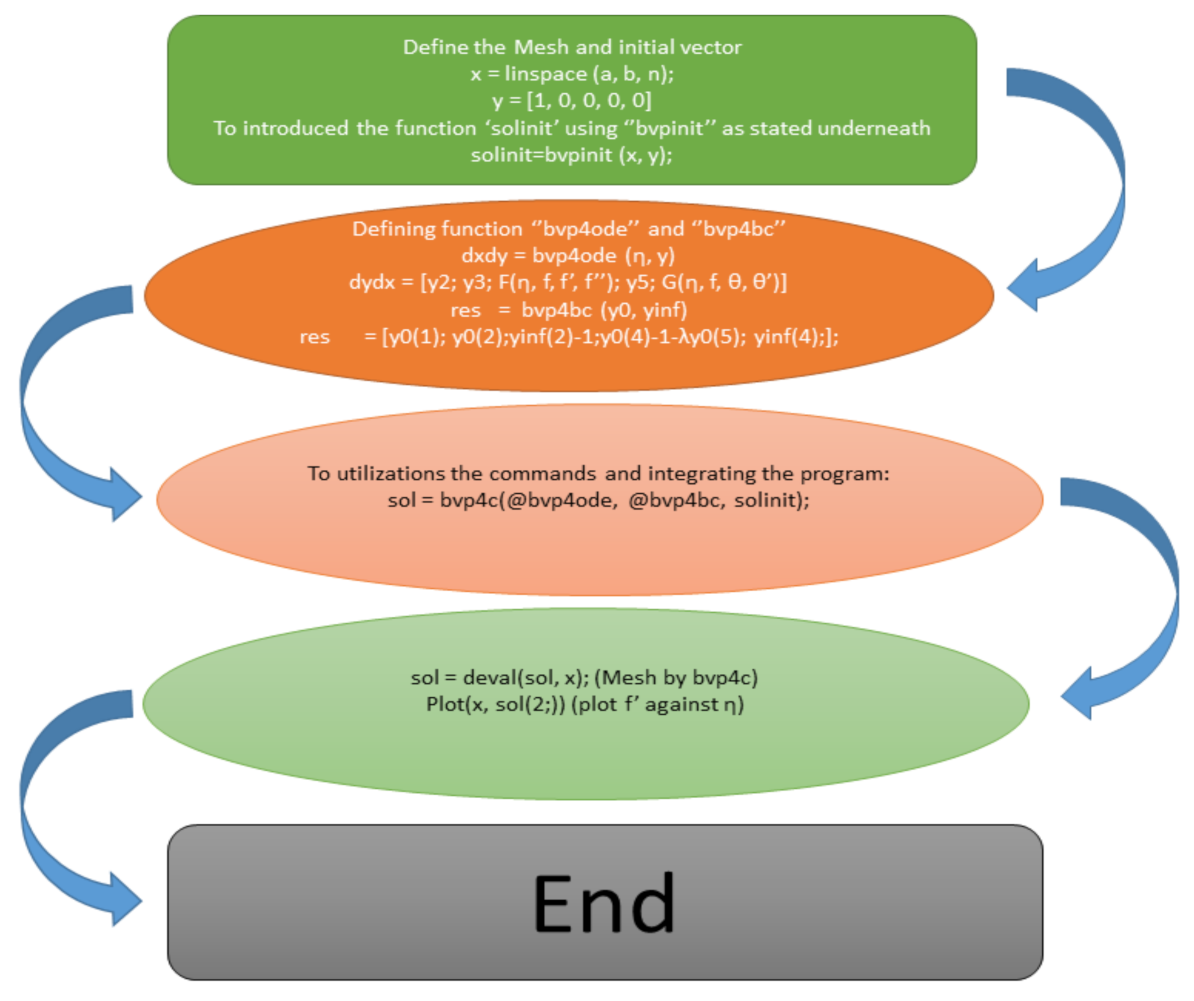
3. Numerical Procedure
4. Results and Discussion
5. Conclusions
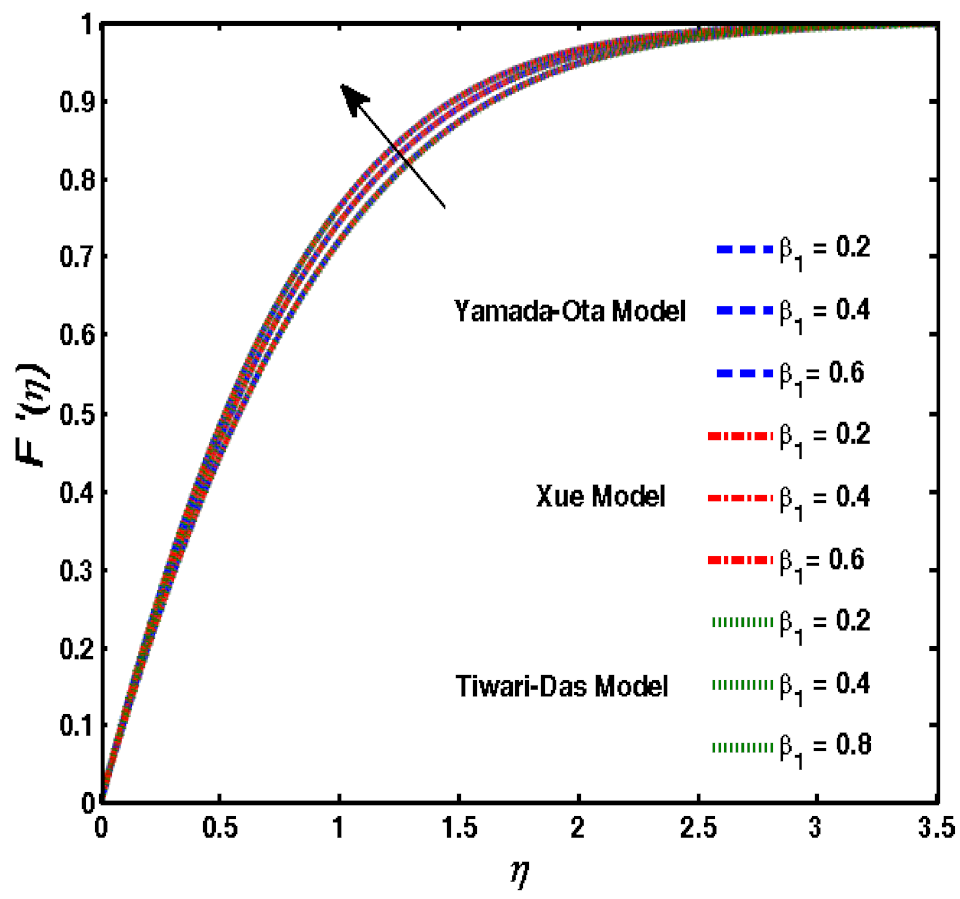
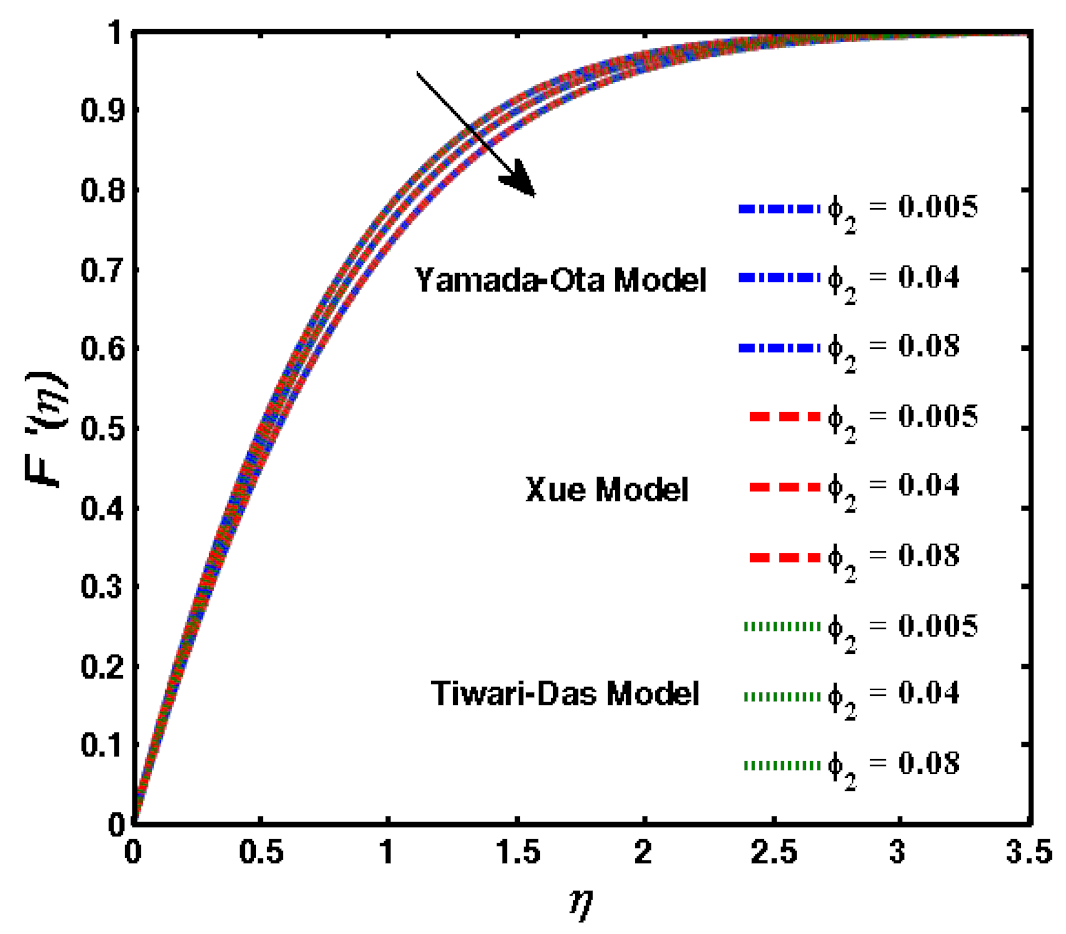
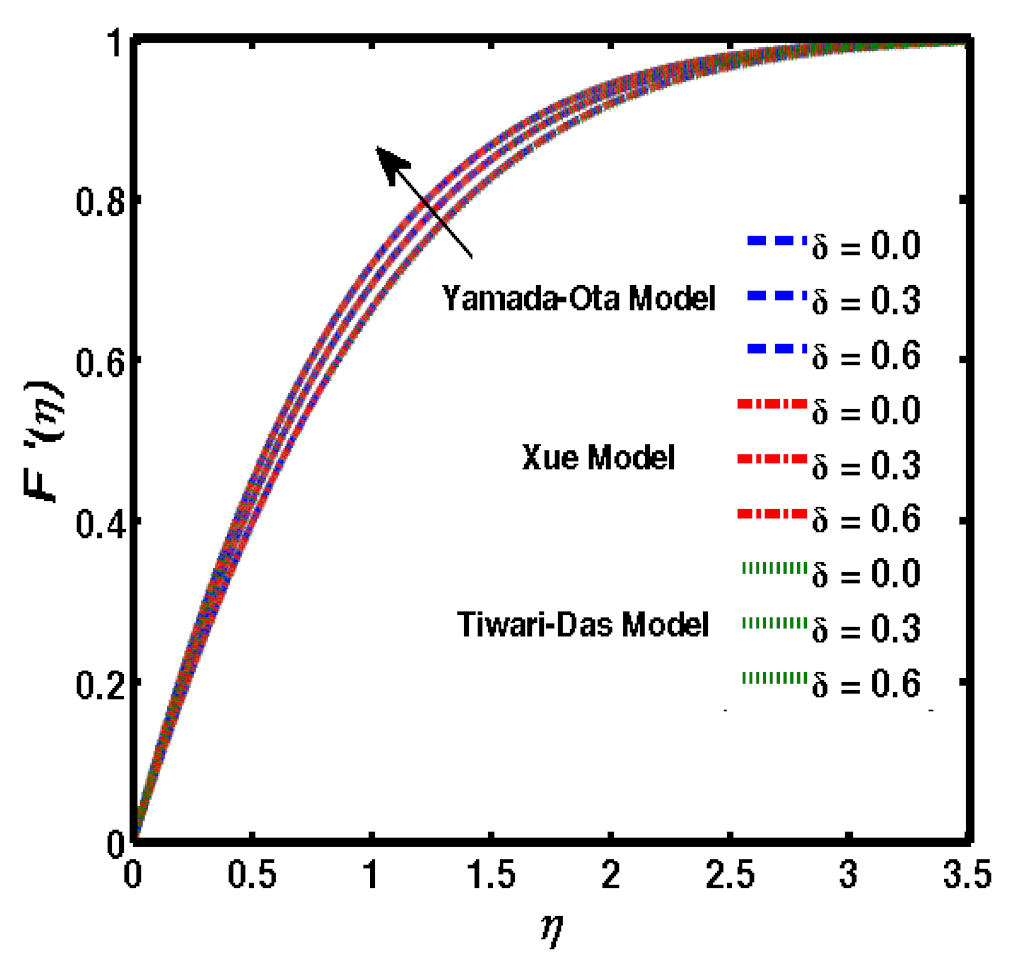
- The velocity function revealed a decline due to the incremental rise of because the quantity of solid nanoparticle increased which increased the viscosity of the fluid which, ultimately, decreases the fluid velocity.
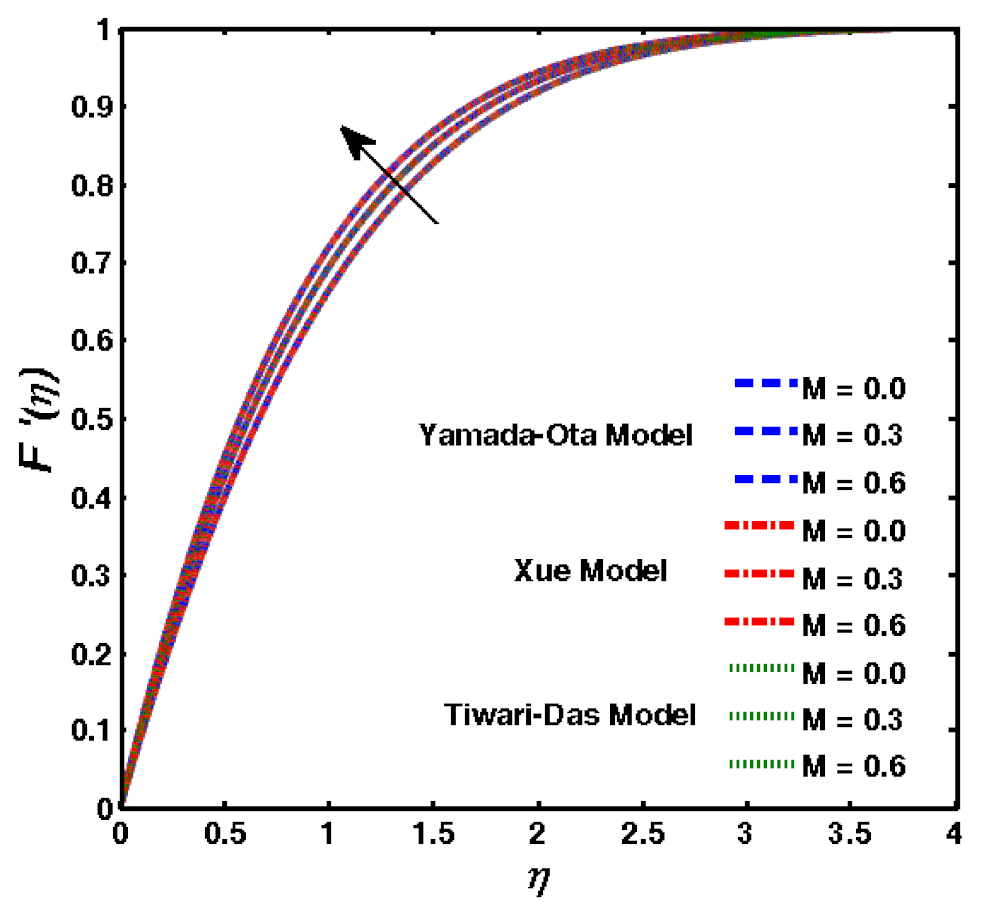
- The curves of velocity function declined due to the higher values of . The Hartmann number is the ratio of electric force to viscous force. The electric forces increased due to the higher values of the modified Hartmann number, which, ultimately, decreased the velocity function.
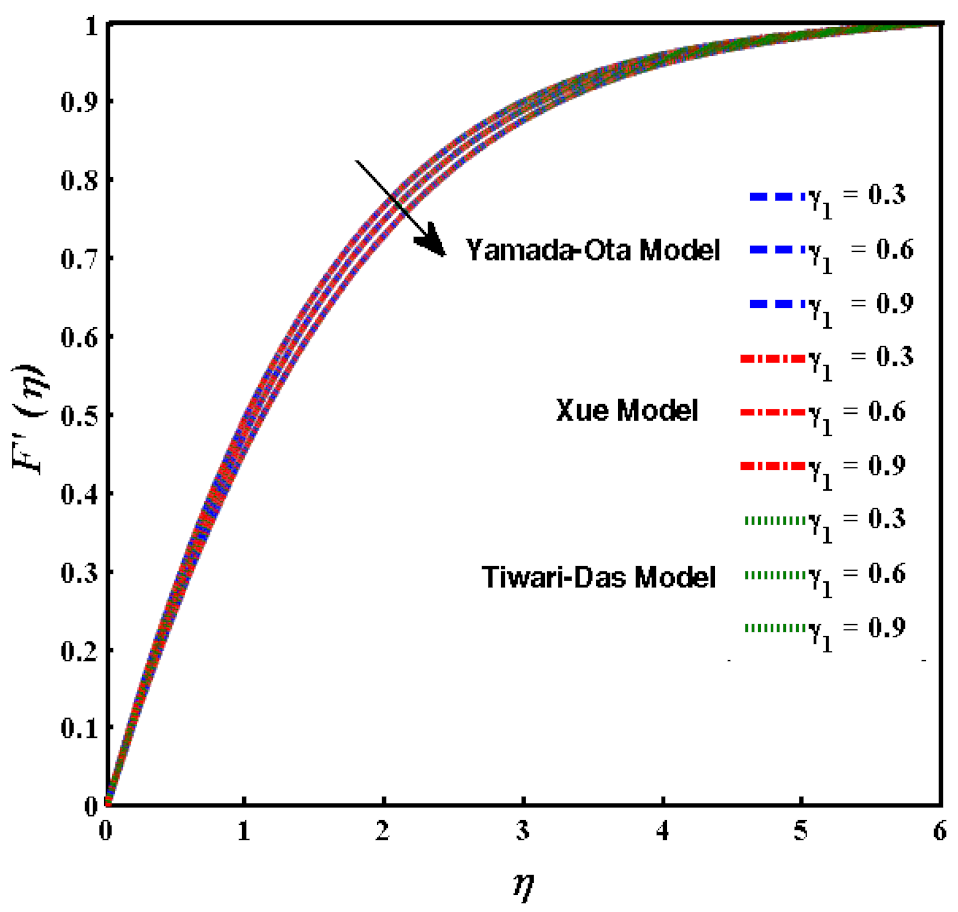
- The skin friction reduced due to the enhancement of ; physically, the shear thinning enhanced which reduced the skin friction. The Nusselt number decreased due to the enhancement of because the shear thinning enhanced which raised the heat transfer rate.
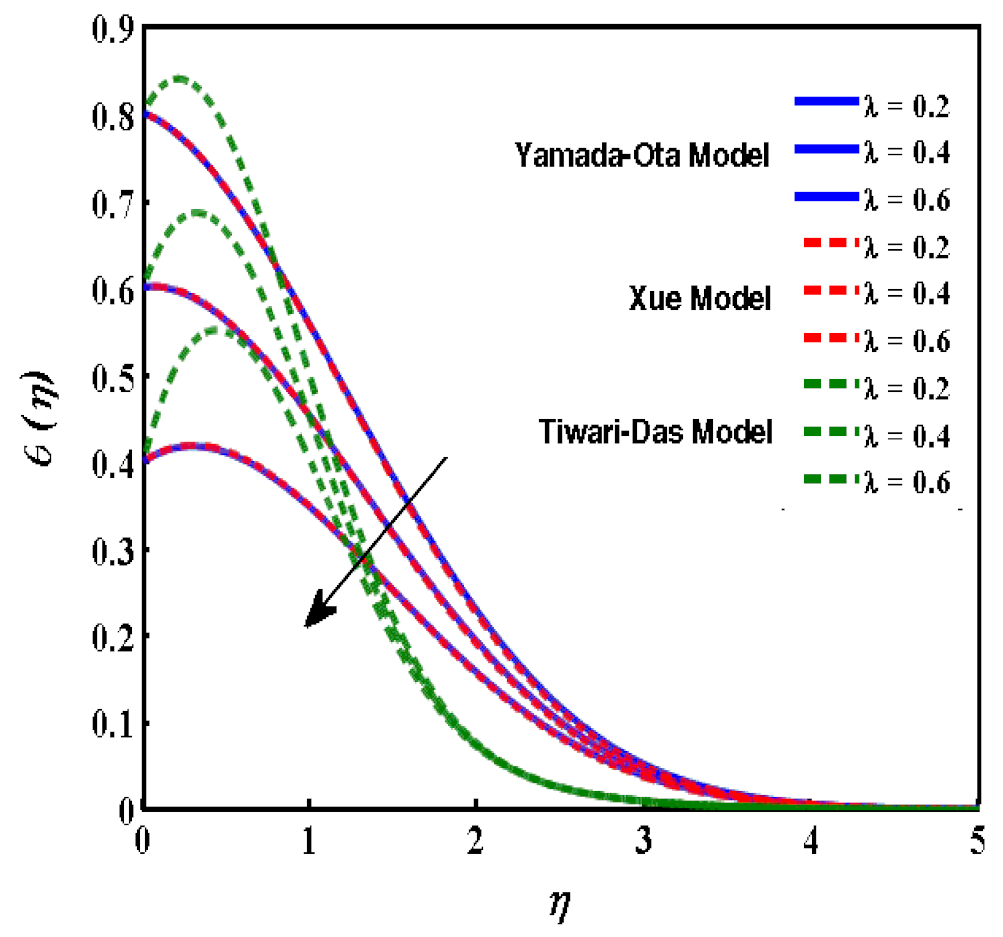
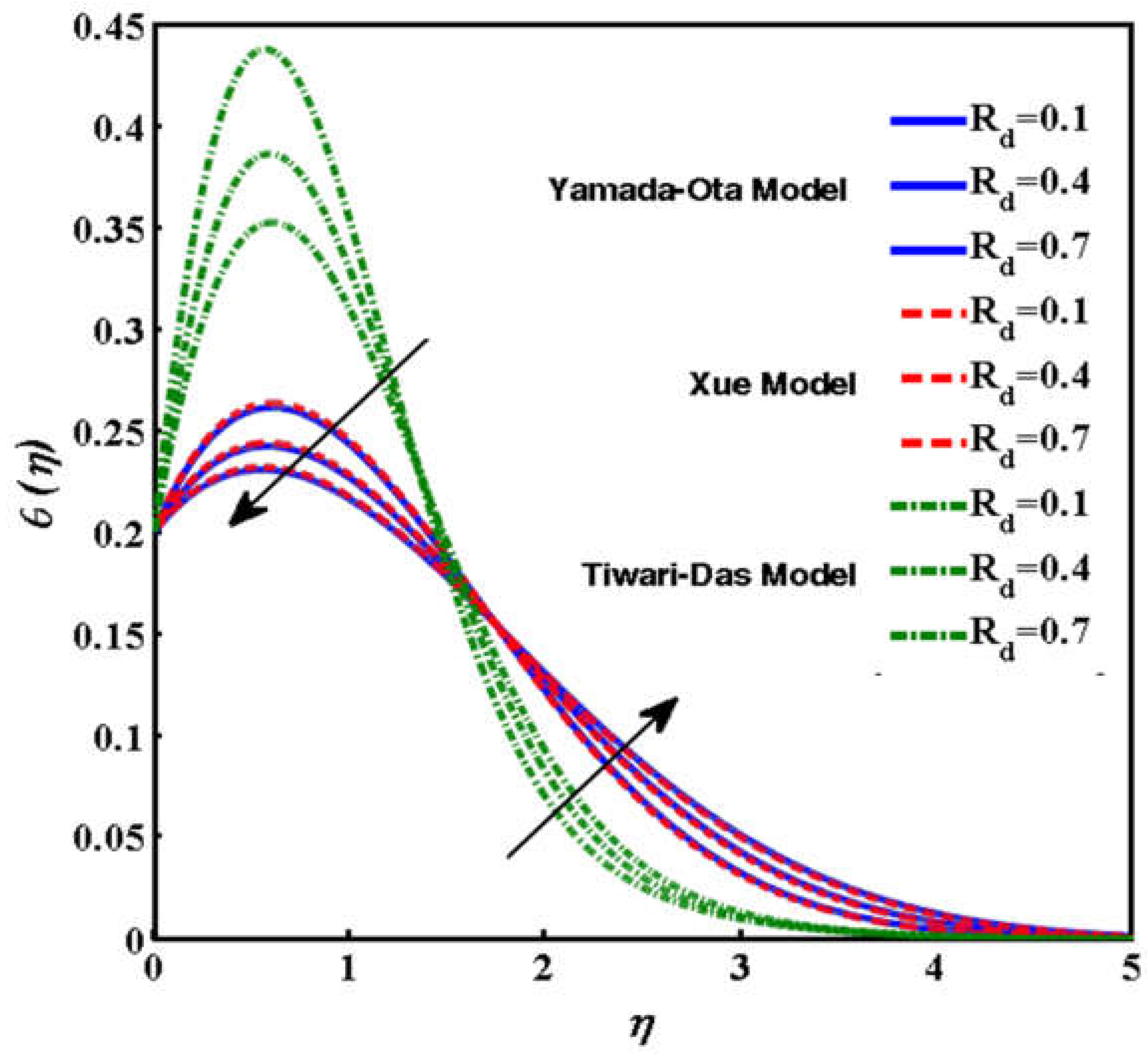
- The remained the same but enhanced due to the higher values of because the thermal slip enhanced as well as the heat transfer increasing. As the radiation increased, which, ultimately, increased the heat transfer rate, the temperature gradient increased because of the greater radiative structures characteristic of higher Nusselt numbers.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hamid, M.; Usman, M.; Khan, Z.H.; Ahmad, R.; Wang, W. Dual solutions and stability analysis of flow and heat transfer of Casson fluid over a stretching sheet. Phys. Lett. A 2019, 383, 2400–2408. [Google Scholar] [CrossRef]
- Jamshed, W.; Goodarzi, M.; Prakash, M.; Nisar, K.S.; Zakarya, M.; Abdel-Aty, A.H. Evaluating the unsteady Casson nanofluid over a stretching sheet with solar thermal radiation: An optimal case study. Case Stud. Therm. Eng. 2021, 26, 101160. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Alrashed, A.A.; Kasaeian, A. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J. Therm. Anal. Calorim. 2019, 135, 1655–1666. [Google Scholar] [CrossRef]
- Amjad, M.; Zehra, I.; Nadeem, S.; Abbas, N.; Saleem, A.; Issakhov, A. Influence of Lorentz force and induced magnetic field effects on Casson micropolar nanofluid flow over a permeable curved stretching/shrinking surface under the stagnation region. Surf. Interfaces 2020, 21, 100766. [Google Scholar] [CrossRef]
- Kasim, A.R.M.; Arifin, N.S.; Ariffin, N.A.N.; Salleh, M.Z.; Anwar, M.I. Mathematical model of simultaneous flow between Casson fluid and dust particle over a vertical stretching sheet. Int. J. Integr. Eng. 2020, 12, 253–260. [Google Scholar]
- Zehra, I.; Abbas, N.; Amjad, M.; Nadeem, S.; Saleem, S.; Issakhov, A. Casson nanoliquid flow with Cattaneo-Christov flux analysis over a curved stretching/shrinking channel. Case Stud. Therm. Eng. 2021, 27, 101146. [Google Scholar] [CrossRef]
- Khan, M.N.; Nadeem, S. A comparative study between linear and exponential stretching sheet with double stratification of a rotating Maxwell nanofluid flow. Surf. Interfaces 2021, 22, 100886. [Google Scholar] [CrossRef]
- Maleki, H.; Alsarraf, J.; Moghanizadeh, A.; Hajabdollahi, H.; Safaei, M.R. Heat transfer and nanofluid flow over a porous plate with radiation and slip boundary conditions. J. Cent. South Univ. 2019, 26, 1099–1115. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Togun, H.; Dahari, M. Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation. J. Therm. Anal. Calorim. 2019, 135, 1643–1654. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Abu-Hamdeh, N.H.; Goodarzi, M. Entropy optimization of first-grade viscoelastic nanofluid flow over a stretching sheet by using classical Keller-box scheme. Mathematics 2021, 9, 2563. [Google Scholar] [CrossRef]
- Sajid, T.; Jamshed, W.; Shahzad, F.; Eid, M.R.; Alshehri, H.M.; Goodarzi, M.; Nisar, K.S. Micropolar fluid past a convectively heated surface embedded with nth order chemical reaction and heat source/sink. Phys. Scr. 2021, 96, 104010. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Alsulami, R.A.; Rawa, M.J.; Alazwari, M.A.; Goodarzi, M.; Safaei, M.R. A Significant Solar Energy Note on Powell-Eyring Nanofluid with Thermal Jump Conditions: Implementing Cattaneo-Christov Heat Flux Model. Mathematics 2021, 9, 2669. [Google Scholar] [CrossRef]
- Aouinet, H.; Dhahri, M.; Safaei, M.R.; Sammouda, H.; Anqi, A.E. Turbulent boundary layers and hydrodynamic flow analysis of nanofluids over a plate. J. Cent. South Univ. 2021, 28, 3340–3353. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Alshehri, H.M.; Goodarzi, M. Marangoni-bioconvectional flow of Reiner–Philippoff nanofluid with melting phenomenon and nonuniform heat source/sink in the presence of a swimming microorganisms. Math. Methods Appl. Sci. 2021, in press. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Khan, S.A.; Alshehri, H.M.; Goodarzi, M. Numerical analysis of dual variable of conductivity in bioconvection flow of Carreau–Yasuda nanofluid containing gyrotactic motile microorganisms over a porous medium. J. Therm. Anal. Calorim. 2021, 145, 2033–2044. [Google Scholar] [CrossRef]
- Imran, M.; Farooq, U.; Waqas, H.; Anqi, A.E.; Safaei, M.R. Numerical performance of thermal conductivity in Bioconvection flow of cross nanofluid containing swimming microorganisms over a cylinder with melting phenomenon. Case Stud. Therm. Eng. 2021, 26, 101181. [Google Scholar] [CrossRef]
- Wang, F.; Ahmad, S.; Al Mdallal, Q.; Alammari, M.; Khan, M.N.; Rehman, A. Natural bio-convective flow of Maxwell nanofluid over an exponentially stretching surface with slip effect and convective boundary condition. Sci. Rep. 2022, 12, 2220. [Google Scholar] [CrossRef]
- Devi, S.A.; Devi, S.S.U. Numerical investigation of hydromagnetic hybrid Cu–Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Khan, A.U. Characteristics of three dimensional stagnation point flow of Hybrid nanofluid past a circular cylinder. Results Phys. 2018, 8, 829–835. [Google Scholar] [CrossRef]
- Al-Hanaya, A.M.; Sajid, F.; Abbas, N.; Nadeem, S. Effect of SWCNT and MWCNT on the flow of micropolar hybrid nanofluid over a curved stretching surface with induced magnetic field. Sci. Rep. 2020, 10, 8488. [Google Scholar] [CrossRef]
- Abbas, N.; Nadeem, S.; Saleem, A.; Malik, M.Y.; Issakhov, A.; Alharbi, F.M. Models base study of inclined MHD of hybrid nanofluid flow over nonlinear stretching cylinder. Chin. J. Phys. 2021, 69, 109–117. [Google Scholar] [CrossRef]
- Li, P.; Duraihem, F.Z.; Awan, A.U.; Al-Zubaidi, A.; Abbas, N.; Ahmad, D. Heat Transfer of Hybrid Nanomaterials Base Maxwell Micropolar Fluid Flow over an Exponentially Stretching Surface. Nanomaterials 2022, 12, 1207. [Google Scholar] [CrossRef]
- Abbas, N.; Nadeem, S.; Malik, M.Y. Theoretical study of micropolar hybrid nanofluid over Riga channel with slip conditions. Phys. A Stat. Mech. Appl. 2020, 551, 124083. [Google Scholar] [CrossRef]
- Nadeem, S.; Malik, M.Y.; Abbas, N. Heat transfer of three-dimensional micropolar fluid on a Riga plate. Can. J. Phys. 2020, 98, 32–38. [Google Scholar] [CrossRef]
- Nadeem, S.; Amin, A.; Abbas, N.; Saleem, A.; Alharbi, F.M.; Hussain, A.; Issakhov, A. Effects of heat and mass transfer on stagnation point flow of micropolar Maxwell fluid over Riga plate. Sci. Iran. 2021, 28, 3753–3766. [Google Scholar]
- Prasad, K.V.; Vaidya, H.; Mebarek-Oudina, F.; Choudhari, R.; Nisar, K.S.; Jamshed, W. Impact of surface temperature and convective boundary conditions on a Nanofluid flow over a radially stretched Riga plate. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 236, 942–952. [Google Scholar] [CrossRef]
- Tabassum, R.; Al-Zubaidi, A.; Rana, S.; Mehmood, R.; Saleem, S. Slanting transport of hybrid (MWCNTs-SWCNTs/H2O) nanofluid upon a Riga plate with temperature dependent viscosity and thermal jump condition. Int. Commun. Heat Mass Transf. 2022, 135, 106165. [Google Scholar] [CrossRef]
- Yamada, E.; Ota, T. Effective thermal conductivity of dispersed materials. Wärme Stoffübertrag. 1980, 13, 27–37. [Google Scholar] [CrossRef]
- Xue, Q.Z. Model for thermal conductivity of carbon nanotube-based composites. Phys. B 2005, 368, 302–307. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Abbas, N.; Nadeem, S.; Malik, M.Y. On extended version of Yamada–Ota and Xue models in micropolar fluid flow under the region of stagnation point. Phys. A Stat. Mech. Its Appl. 2020, 542, 123512. [Google Scholar] [CrossRef]
- Abbas, N.; Malik, M.Y.; Nadeem, S.; Alarifi, I.M. On extended version of Yamada–Ota and Xue models of hybrid nanofluid on moving needle. Eur. Phys. J. Plus 2020, 135, 1–16. [Google Scholar] [CrossRef]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non-Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Stagnation-point flow over a stretching/shrinking sheet in a nanofluid. Nanoscale Res. Lett. 2011, 6, 623. [Google Scholar] [CrossRef] [Green Version]


| Thermophysical Properties | |||
|---|---|---|---|
| 1600 | 2600 | 997.1 | |
| 3000 | 6600 | 0.613 | |
| 796 | 425 | 4179 | |
| (Yamada-Ota Model) | (Xue Model) | (Tiwari-Das Model) | |||||
|---|---|---|---|---|---|---|---|
| 0.10 | 0.0038 | 0.0962 | 1061.19 | 3653.363 | 2.788343 | 2.711645 | 0.8172003 |
| 0.33 | 0.0125 | 0.3175 | 1194.612 | 2709.356 | 9.846296 | 9.510268 | 1.482817 |
| 0.75 | 0.0285 | 0.7215 | 1477.775 | 1348.05 | 59.00918 | 56.84039 | 6.117090 |
| 1.00 | 0.0380 | 0.9620 | 1638.000 | 773.6222 | 7311.015 | 7037.057 | 3136.800 |
| (Yamada-Ota Model) | (Xue Model) | (Tiwari-Das Model) | |||
|---|---|---|---|---|---|
| 0.10 | 1157.39 | 3335.689 | 2.991149 | 2.914448 | 0.8172701 |
| 0.33 | 1526.057 | 2068.376 | 11.15951 | 10.80944 | 1.5184 |
| 0.75 | 2199.275 | 850.494 | 64.6763 | 62.49929 | 6.123857 |
| 1.00 | 2600.0 | 425.0 | 15169.65 | 14649.5 | 6600.0 |
| Physical Parameters | Yamada Ota Model | Xue Model | Tiwari Das Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.04 | 0.3 | 0.4 | 0.5 | 0.3 | 0.2 | 2.5583 | 0.0188 | 2.5583 | 0.0188 | 2.5583 | 0.3323 |
| 0.2 | - | - | - | - | - | - | 2.5307 | 0.0195 | 2.5307 | 0.0195 | 2.5307 | 0.3586 |
| 0.3 | - | - | - | - | - | - | 2.5039 | 0.0201 | 2.5039 | 0.0201 | 2.5039 | 0.3843 |
| 0.4 | - | - | - | - | - | - | 2.4778 | 0.0208 | 2.4778 | 0.0208 | 2.4778 | 0.4094 |
| 0.1 | 0.02 | - | - | - | - | - | 2.2483 | 0.0428 | 2.2559 | 0.0295 | 2.2483 | 0.3890 |
| - | 0.04 | - | - | - | - | - | 2.4000 | 0.0269 | 2.4075 | 0.0210 | 2.4000 | 0.3594 |
| - | 0.06 | - | - | - | - | - | 2.5583 | 0.0188 | 2.5653 | 0.0159 | 2.5583 | 0.3323 |
| - | 0.08 | - | - | - | - | - | 2.7237 | 0.0140 | 2.7300 | 0.0125 | 2.7237 | 0.3073 |
| - | 0.04 | 0.1 | - | - | - | - | 3.9474 | 0.0349 | 3.9069 | 0.0135 | 3.9474 | 0.2681 |
| - | - | 0.3 | - | - | - | - | 2.4843 | 0.0414 | 2.4075 | 0.0210 | 2.4843 | 0.3670 |
| - | - | 0.5 | - | - | - | - | 2.0950 | 0.0438 | 2.0165 | 0.0237 | 2.0950 | 0.4045 |
| - | - | 0.7 | - | - | - | - | 1.9057 | 0.0451 | 1.8283 | 0.0250 | 1.9057 | 0.4251 |
| - | - | 0.3 | 0.2 | - | - | - | 3.7956 | 0.0265 | 2.5902 | 0.0287 | 2.5902 | 0.2625 |
| - | - | - | 0.4 | - | - | - | 3.4900 | 0.0082 | 2.4075 | 0.0210 | 2.4075 | −0.046 |
| - | - | - | 0.6 | - | - | - | 3.1814 | −0.012 | 2.2231 | 0.0126 | 2.2231 | −0.383 |
| - | - | - | 0.8 | - | - | - | 2.8697 | −0.035 | 2.0370 | 0.0033 | 2.0370 | −0.753 |
| - | - | - | 0.4 | 0.1 | - | - | 3.7358 | 0.0541 | 3.7458 | 0.0272 | 3.7458 | 0.0541 |
| - | - | - | - | 0.3 | - | - | 3.7458 | 0.0261 | 3.8344 | 0.0279 | 3.8344 | 0.0652 |
| - | - | - | - | 0.5 | - | - | 3.8344 | 0.0267 | 3.8902 | 0.0283 | 3.8902 | 0.0717 |
| - | - | - | - | 0.7 | - | - | 3.8902 | 0.0271 | 3.9276 | 0.0286 | 3.9276 | 0.0758 |
| - | - | - | - | 0.5 | 0.0 | - | 3.9276 | 0.0144 | 3.9276 | 0.0254 | 3.9276 | 0.0488 |
| - | - | - | - | - | 0.3 | - | 3.9276 | 0.0244 | 3.9276 | 0.0346 | 3.9276 | 0.1280 |
| - | - | - | - | - | 0.6 | - | 3.9276 | 0.0331 | 3.9276 | 0.0430 | 3.9276 | 0.2025 |
| - | - | - | - | - | 0.9 | - | 3.9276 | 0.0411 | 3.9276 | 0.0509 | 3.9276 | 0.2731 |
| - | - | - | - | - | 0.3 | 0.0 | 3.9276 | 0.0648 | 3.9276 | 0.0680 | 3.9276 | 0.0680 |
| - | - | - | - | - | - | 0.2 | 3.9276 | 0.0486 | 3.9276 | 0.0509 | 3.9276 | 0.0509 |
| - | - | - | - | - | - | 0.4 | 3.9276 | 0.0324 | 3.9276 | 0.0338 | 3.9276 | 0.0338 |
| - | - | - | - | - | - | 0.6 | 3.9276 | 0.0162 | 3.9276 | 0.0167 | 3.9276 | 0.0167 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shatnawi, T.A.M.; Abbas, N.; Shatanawi, W. Mathematical Analysis of Unsteady Stagnation Point Flow of Radiative Casson Hybrid Nanofluid Flow over a Vertical Riga Sheet. Mathematics 2022, 10, 3573. https://doi.org/10.3390/math10193573
Shatnawi TAM, Abbas N, Shatanawi W. Mathematical Analysis of Unsteady Stagnation Point Flow of Radiative Casson Hybrid Nanofluid Flow over a Vertical Riga Sheet. Mathematics. 2022; 10(19):3573. https://doi.org/10.3390/math10193573
Chicago/Turabian StyleShatnawi, Taqi A. M., Nadeem Abbas, and Wasfi Shatanawi. 2022. "Mathematical Analysis of Unsteady Stagnation Point Flow of Radiative Casson Hybrid Nanofluid Flow over a Vertical Riga Sheet" Mathematics 10, no. 19: 3573. https://doi.org/10.3390/math10193573
APA StyleShatnawi, T. A. M., Abbas, N., & Shatanawi, W. (2022). Mathematical Analysis of Unsteady Stagnation Point Flow of Radiative Casson Hybrid Nanofluid Flow over a Vertical Riga Sheet. Mathematics, 10(19), 3573. https://doi.org/10.3390/math10193573







