Hybrid Particle Swarm and Whale Optimization Algorithm for Multi-Visit and Multi-Period Dynamic Workforce Scheduling and Routing Problems
Abstract
1. Introduction
2. Literature Review
3. Mathematical Formulation
| Jobs and depot indices ( J) | |
| Sub-systems; mechanical, hydraulic, and electrical sub-systems () | |
| Technician teams () | |
| Working periods () | |
| Technician team skills () |
| Set of jobs and depot | |
| Set of jobs () | |
| Set of sub-systems | |
| Set of technician teams in sub-system | |
| Set of working periods | |
| Set of skill types in sub-system | |
| Labor cost of technician team in sub-system (units) | |
| Technician transportation cost moving from jobs to (units) | |
| Penalty cost from a job ’s that was finished late (unit per minutes) | |
| Overtime cost of technician team giving service sub-system (unit per minutes) | |
| Subcontracting cost of sub-system of jobs (unit) | |
| Starting time of period | |
| Completion time of period | |
| Starting time of job | |
| Completion time of job | |
| Travel time from job to job (minutes) | |
| Service time of job in sub-system (minutes) | |
| Proficiency of technician team of skill in sub-system | |
| For job , a technician team with the attribute is required | |
| The quantity of technician teams in sub-system | |
| The quantity of technicians needed to complete job for sub-system | |
| The quantity of technician team in sub-system | |
| = 1 if job needs a team of sub-system = 0, otherwise | |
| Large number | |
| Maximum allowed delay time | |
| Maximum allowed overtime |
| Amount of service delay time of job (minutes) | |
| Overtime of team in sub-system in period (minutes) | |
| Starting time of team in sub-system for job in period | |
| = 1, if team of sub-system leaves job for job in period ; = 0, otherwise | |
| = 1, if team of sub-system services job in period ; = 0, otherwise | |
| = 1, if using technician team of sub-system in period ; = 0, otherwise | |
| = 1, if job requires a service from a subcontract for subsystem ; = 0, otherwise |
| (2) | ||
| (3) | ||
| (4) | ||
| (5) | ||
| (6) | ||
| (7) | ||
| (8) | ||
| (9) | ||
| (10) | ||
| (11) | ||
| (12) | ||
| (13) | ||
| (14) | ||
| (15) | ||
| (16) | ||
| (17) | ||
| (18) | ||
| (19) |
4. The Proposed Method
4.1. Initial Solution
4.2. Particle Swarm Optimization (PSO)
4.3. Whale Optimization Algorithm (WOA)
4.3.1. Encircling Prey
4.3.2. Bubble-Net Attacking Method
4.3.3. Searching for Prey
4.3.4. Updating Position
4.4. Self-Adaptive Control Parameter
4.5. Hybrid Particle Swarm and Whale Optimization Algorithm (HPSWOA)
4.6. Current Practice Method (CP)
| Algorithm 1. Re-schedule for multi-visit and multi-period dynamic workforce scheduling and routing problem (MMDWSRP). |
| Input: MMDWSRP data, Total cost = 0, Output: Total cost For each period Set technician teams’ position at depot Add job for each sub-system that knows the repair time at start period time to . While job in period is still in need of completion do Plan by selected method Assign the technician teams by the selected method plan If new job or harvester relocation then Update Time If job in the plan completes before updated time then Remove the job in and add to period plan Update technician teams’ position End if Add new job to or update job’s position End if End of while Calculate period plan fitness by Equation (1) Total cost += period plan fitness End for |
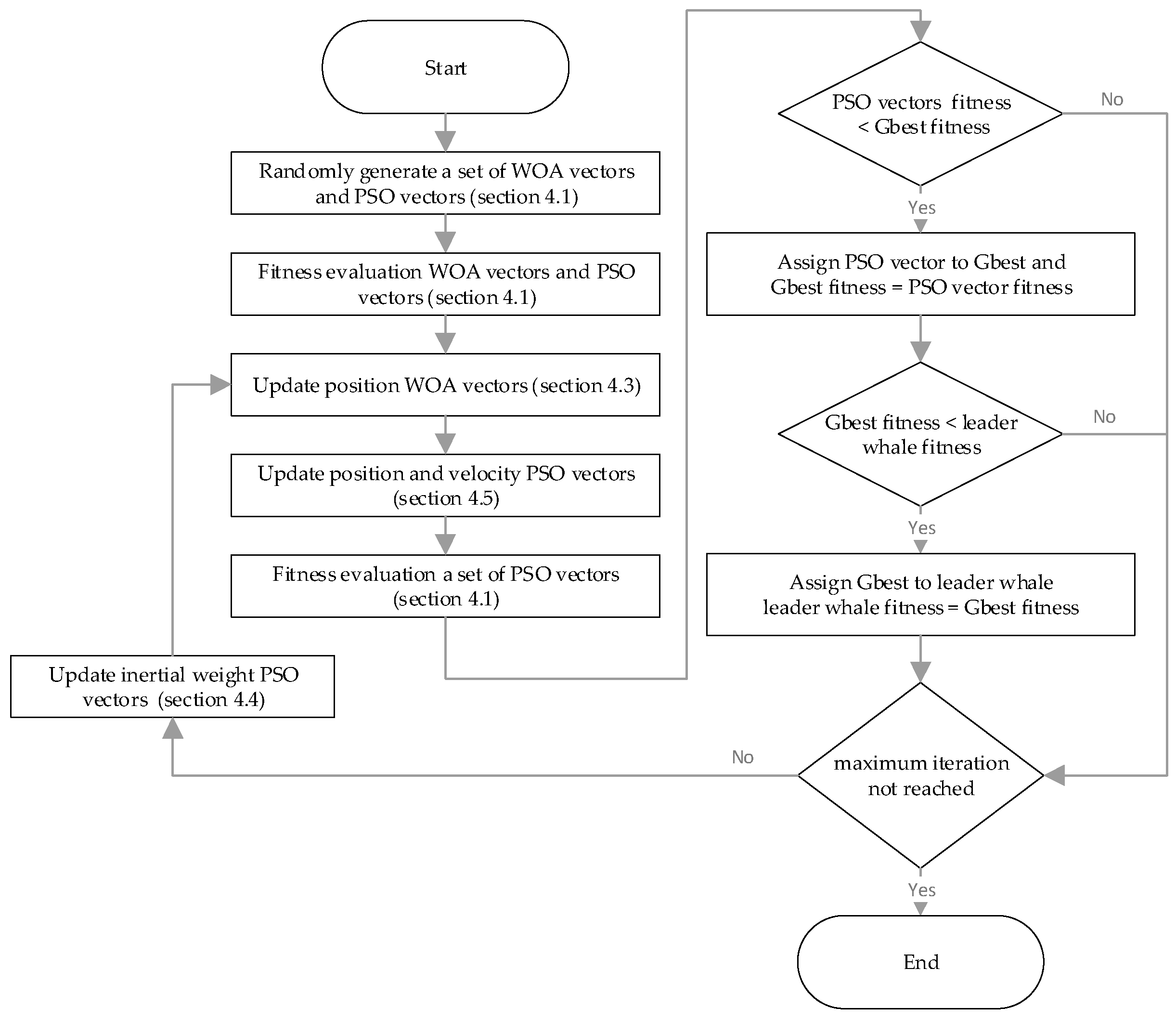
| Algorithm 2. Hybrid particle swarm and whale optimization algorithm (HPSWOA). |
| Input: MMDWSRP data, HPSWOA parameters (), maximum iteration, NP, Output: plan for technician teams Randomly generate a set of WOA vectors ( = 1…NP) (Section 4.1) Randomly generate a set of PSO vectors ( = 1…NP) (Section 4.1) While maximum iteration not reached do For = 1 to NP Update position WOA vectors (Section 4.3) Update position and velocity PSO vectors (Section 4.5) Fitness evaluation PSO vectors (Section 4.1) If PSO vectors fitness < Gbest fitness then Assign particles to Gbest Gbest fitness = PSO vectors fitness End if Update inertial weight PSO vectors (Section 4.4) End for If Gbest fitness < leader whale fitness then Assign Gbest to leader whale leader whale fitness = Gbest fitness End if End of while |
| Algorithm 3. Current practice method. |
| Input: MMDWSRP data, Output: plan for technician teams Sort jobs in with ready time in ascending order Sort technician teams with technician team cost in ascending order For sorted jobs For sorted technician teams If technician team can service then Assign the job to the technician team service Else then Assign the job to new technician team service End if End for End for |
5. Computational Results
5.1. Optimization of CEC 2017 Benchmark Functions
5.2. Static Problem
5.3. Dynamic Problem
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sugar Asia Magazine. Available online: https://Sugar-Asia.Com/the-Competitive-Capability-of-Sugar-Production-in-Thailand-in-Comparison-with-the-World-Sugar-Market (accessed on 23 August 2022).
- Pitakaso, R.; Sethanan, K. Adaptive Large Neighborhood Search for Scheduling Sugarcane Inbound Logistics Equipment and Machinery under a Sharing Infield Resource System. Comput. Electron. Agric. 2019, 158, 313–325. [Google Scholar] [CrossRef]
- Worasan, K.; Sethanan, K.; Pitakaso, R.; Moonsri, K.; Nitisiri, K. Hybrid Particle Swarm Optimization and Neighborhood Strategy Search for Scheduling Machines and Equipment and Routing of Tractors in Sugarcane Field Preparation. Comput. Electron. Agric. 2020, 178, 105733. [Google Scholar] [CrossRef]
- Junqueira, R.D.Á.R.; Morabito, R. Optimization Approaches for Sugarcane Harvest Front Programming and Scheduling. Gest. Prod. 2017, 24, 407–422. [Google Scholar] [CrossRef][Green Version]
- Najafi, P.; Asoodar, M.A.; Marzban, A.; Hormozi, M.A. Reliability Analysis of Agricultural Machinery: A Case Study of Sugarcane Chopper Harvester. Agricengint CIGR J. 2015, 17, 158–165. [Google Scholar]
- Ouertani, N.; Nouaouri, I.; Ben-Romdhane, H.; Allaoui, H.; Krichen, S. A Hypermutation Genetic Algorithm for the Dynamic Home Health-Care Routing Problem. In Proceedings of the 2019 International Conference on Industrial Engineering and Systems Management (IESM), Shanghai, China, 25–27 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- El-Amraoui, A.; Harbi, S.; Moh, A.N.S. Home Health Care Scheduling Problem Under Uncertainty: Robust Optimization Approaches. Comput. Inform. 2022, 41, 288–308. [Google Scholar] [CrossRef]
- Lesaint, D.; Voudouris, C.; Azarmi, N. Dynamic Workforce Scheduling for British Telecommunications Plc. Interfaces 2000, 30, 45–56. [Google Scholar] [CrossRef]
- Borenstein, Y.; Shah, N.; Tsang, E.; Dorne, R.; Alsheddy, A.; Voudouris, C. On the Partitioning of Dynamic Workforce Scheduling Problems. J. Sched. 2010, 13, 411–425. [Google Scholar] [CrossRef]
- Pillac, V.; Guéret, C.; Medaglia, A.-L. A Fast Reoptimization Approach for the Dynamic Technician Routing and Scheduling Problem. In Recent Developments in Metaheuristics; Springer: Cham, Switzerland, 2018; Volume 62, pp. 347–367. [Google Scholar]
- Ling, Y.; Zhou, Y.; Luo, Q. Lévy Flight Trajectory-Based Whale Optimization Algorithm for Global Optimization. IEEE Access 2017, 5, 6168–6186. [Google Scholar] [CrossRef]
- Saleh, A.A.; Mohamed, A.-A.A.; Hemeida, A.M.; Ibrahim, A.A. Multi-Objective Whale Optimization Algorithm for Optimal Allocation of Distributed Generation and Capacitor Bank. In Proceedings of the International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 459–465. [Google Scholar]
- Luan, F.; Cai, Z.; Wu, S.; Jiang, T.; Li, F.; Yang, J. Improved Whale Algorithm for Solving the Flexible Job Shop Scheduling Problem. Mathematics 2019, 7, 384. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, C.; Sun, Q.-M. Green Job Shop Scheduling Problem with Discrete Whale Optimization Algorithm. IEEE Access 2019, 7, 43153–43166. [Google Scholar] [CrossRef]
- Liu, M.; Yao, X.; Li, Y. Hybrid Whale Optimization Algorithm Enhanced with Lévy Flight and Differential Evolution for Job Shop Scheduling Problems. Appl. Soft Comput. 2020, 87, 105954. [Google Scholar] [CrossRef]
- Dewi, S.K.; Utama, D.M. A New Hybrid Whale Optimization Algorithm for Green Vehicle Routing Problem. Syst. Sci. Control Eng. 2021, 9, 61–72. [Google Scholar] [CrossRef]
- Jiang, W.; Hu, R.; Qian, B.; Yu, N.-K.; Liu, B. Hybrid Whale Optimization Algorithm for Solving Green Open Vehicle Routing Problem with Time Windows. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2021; Volume 12836, pp. 673–683. [Google Scholar]
- Petrović, M.; Miljković, Z.; Jokić, A. A Novel Methodology for Optimal Single Mobile Robot Scheduling Using Whale Optimization Algorithm. Appl. Soft Comput. 2019, 81, 105520. [Google Scholar] [CrossRef]
- Tanvir, M.H.; Hussain, A.; Rahman, M.M.; Ishraq, S.; Zishan, K.; Rahul, S.K.; Habib, M.A. Multi-Objective Optimization of Turning Operation of Stainless Steel Using a Hybrid Whale Optimization Algorithm. J. Manuf. Mater. Process. 2020, 4, 64. [Google Scholar] [CrossRef]
- Xu, J.; Chiu, S.Y. Effective Heuristic Procedures for a Field Technician Scheduling Problem. J. Heuristics 2001, 7, 495–509. [Google Scholar] [CrossRef]
- Dohn, A.; Kolind, E.; Clausen, J. The Manpower Allocation Problem with Time Windows and Job-Teaming Constraints: A Branch-and-Price Approach. Comput. Oper. Res. 2009, 36, 1145–1157. [Google Scholar] [CrossRef]
- Pillac, V.; Gueret, C.; Medaglia, A.L. A Parallel Matheuristic for the Technician Routing and Scheduling Problem. Optim. Lett. 2013, 7, 1525–1535. [Google Scholar] [CrossRef]
- Pinheiro, R.L.; Landa-Silva, D.; Atkin, J. A Variable Neighbourhood Search for the Workforce Scheduling and Routing Problem. In Advances in Nature and Biologically Inspired Computing; Springer: Berlin/Heidelberg, Germany, 2016; Volume 419, pp. 247–259. [Google Scholar] [CrossRef]
- Mathlouthi, I.; Gendreau, M.; Potvin, J.-Y. Mixed Integer Linear Programming for a Multi-Attribute Technician Routing and Scheduling Problem. INFOR Inf. Syst. Oper. Res. 2018, 56, 33–49. [Google Scholar] [CrossRef]
- Cordeau, J.-F.; Laporte, G.; Pasin, F.; Ropke, S. Scheduling Technicians and Tasks in a Telecommunications Company. J. Sched. 2010, 13, 393–409. [Google Scholar] [CrossRef]
- Kovacs, A.A.; Parragh, S.N.; Doerner, K.F.; Hartl, R.F. Adaptive Large Neighborhood Search for Service Technician Routing and Scheduling Problems. J. Sched. 2012, 15, 579–600. [Google Scholar] [CrossRef]
- Anoshkina, Y.; Meisel, F. Technician Teaming and Routing with Service-, Cost-and Fairness-Objectives. Comput. Ind. Eng. 2019, 135, 868–880. [Google Scholar] [CrossRef]
- Çakırgil, S.; Yücel, E.; Kuyzu, G. An Integrated Solution Approach for Multi-Objective, Multi-Skill Workforce Scheduling and Routing Problems. Comput. Oper. Res. 2020, 118, 104908. [Google Scholar] [CrossRef]
- Blakeley, F.; Argüello, B.; Cao, B.; Hall, W.; Knolmajer, J. Optimizing Periodic Maintenance Operations for Schindler Elevator Corporation. Interfaces 2003, 33, 67–79. [Google Scholar] [CrossRef]
- Zamorano, E.; Stolletz, R. Branch-and-Price Approaches for the Multiperiod Technician Routing and Scheduling Problem. Eur. J. Oper. Res. 2017, 257, 55–68. [Google Scholar] [CrossRef]
- Pekel, E. Solving Technician Routing and Scheduling Problem Using Improved Particle Swarm Optimization. Soft Comput. 2020, 24, 19007–19015. [Google Scholar] [CrossRef]
- Punyakum, V.; Sethanan, K.; Nitisiri, K.; Pitakaso, R.; Gen, M. Hybrid Differential Evolution and Particle Swarm Optimization for Multi-Visit and Multi-Period Workforce Scheduling and Routing Problems. Comput. Electron. Agric. 2022, 197, 106929. [Google Scholar] [CrossRef]
- Demirbilek, M.; Branke, J.; Strauss, A.K. Home Healthcare Routing and Scheduling of Multiple Nurses in a Dynamic Environment. Flex. Serv. Manuf. J. 2021, 33, 253–280. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Rana, N.; Latiff, M.S.A.; Abdulhamid, S.M.; Chiroma, H. Whale Optimization Algorithm: A Systematic Review of Contemporary Applications, Modifications and Developments. Neural Comput. Appl. 2020, 32, 16245–16277. [Google Scholar] [CrossRef]
- Sethanan, K.; Jamrus, T. Hybrid Differential Evolution Algorithm and Genetic Operator for Multi-Trip Vehicle Routing Problem with Backhauls and Heterogeneous Fleet in the Beverage Logistics Industry. Comput. Ind. Eng. 2020, 146, 106571. [Google Scholar] [CrossRef]
- Wang, P.C.; Shoup, T.E. A Poly-Hybrid PSO Optimization Method with Intelligent Parameter Adjustment. Adv. Eng. Softw. 2011, 42, 555–565. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Multi-Objective Optimisation of Retaining Walls Using Hybrid Adaptive Gravitational Search Algorithm. Civ. Eng. Environ. Syst. 2014, 31, 229–242. [Google Scholar] [CrossRef]
- Koessler, E.; Almomani, A. Hybrid Particle Swarm Optimization and Pattern Search Algorithm. Optim. Eng. 2021, 22, 1539–1555. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Keawsawasvong, S.; Sarir, P.; Khailany, D.K. Seismic Analysis of Earth Slope Using a Novel Sequential Hybrid Optimization Algorithm. Period. Polytech. Civ. Eng. 2022, 66, 355–366. [Google Scholar] [CrossRef]
- Victoire, T.A.A.; Jeyakumar, A.E. Hybrid PSO–SQP for Economic Dispatch with Valve-Point Effect. Electr. Power Syst. Res. 2004, 71, 51–59. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Damping Controller Design for Power System Oscillations Using Hybrid GA-SQP. Int. Rev. Electr. Eng. 2011, 6, 888–896. [Google Scholar]
- Abdel-Mawgoud, H.; Fathy, A.; Kamel, S. An Effective Hybrid Approach Based on Arithmetic Optimization Algorithm and Sine Cosine Algorithm for Integrating Battery Energy Storage System into Distribution Networks. J. Energy Storage 2022, 49, 104154. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Jia, L.; Gong, W.; Wu, H. An Improved Self-Adaptive Control Parameter of Differential Evolution for Global Optimization. In International Symposium on Intelligence Computation and Applications; Springer: Berlin/Heidelberg, Germany, 2009; pp. 215–224. [Google Scholar]
- Trivedi, I.N.; Jangir, P.; Kumar, A.; Jangir, N.; Totlani, R. A Novel Hybrid PSO–WOA Algorithm for Global Numerical Functions Optimization. Adv. Comput. Comput. Sci. 2018, 554, 53–60. [Google Scholar]
- Awad, N.H.; Ali, M.; Liang, J.; Qu, B.; Suganthan, P.; Definitions, P. Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization. Tech. Rep. 2016. [Google Scholar]
- Harrison, K.R.; Engelbrecht, A.P.; Ombuki-Berman, B.M. Self-Adaptive Particle Swarm Optimization: A Review and Analysis of Convergence. Swarm Intell. 2018, 12, 187–226. [Google Scholar] [CrossRef]
- Whitley, D. A Genetic Algorithm Tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm. Nat. Inspired Coop. Strateg. Optim. 2010, 284, 65–74. [Google Scholar]
- Lund, K.; Madsen, O.B.G.; Rygaard, J.M. Vehicle Routing Problems with Varying Degrees of Dynamism; Institute of Mathematical Modelling, Technical University of Denmark: Lyngby, Denmark, 1996. [Google Scholar]
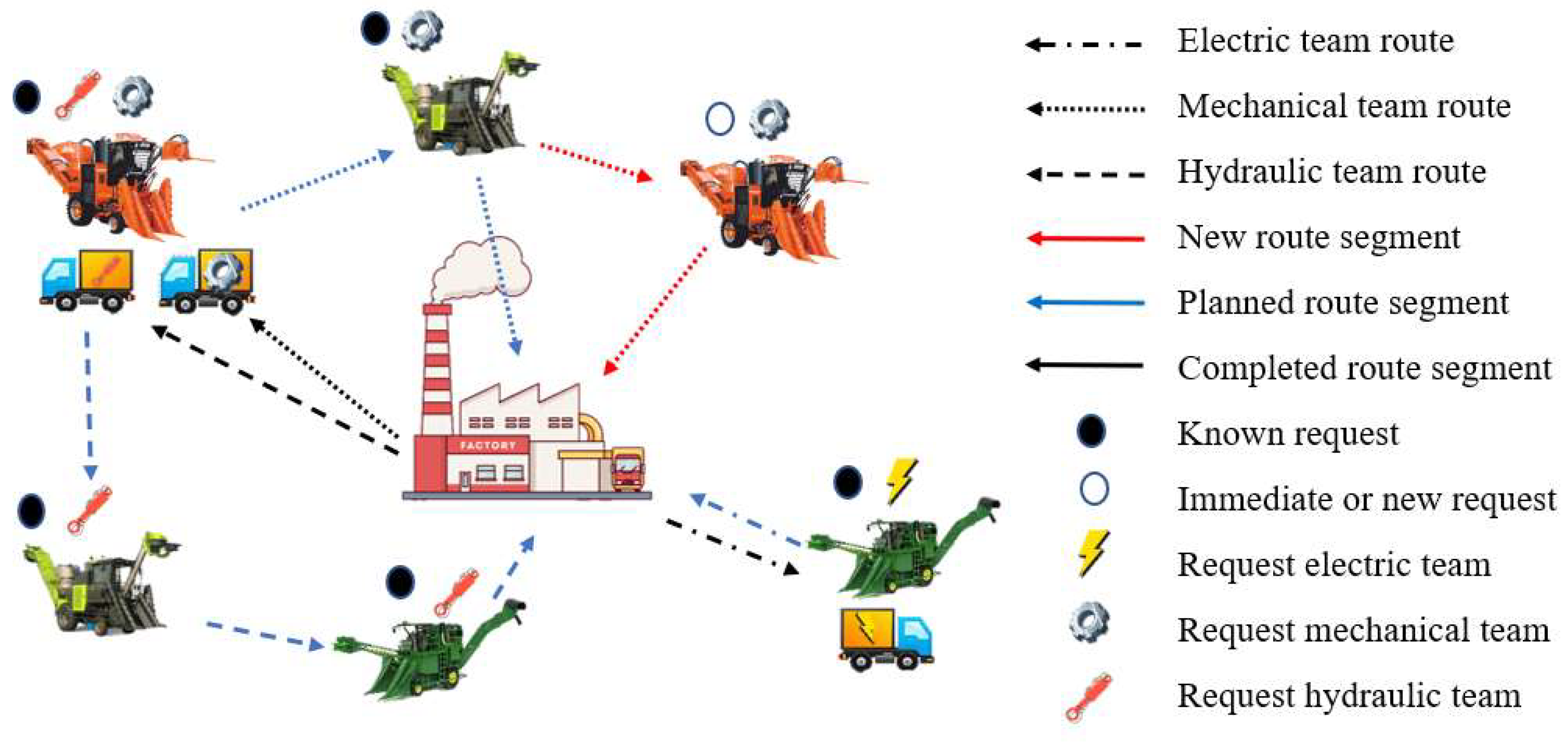

| Constraint | Description |
|---|---|
| (2) | Ensures that job in sub-system is serviced either by a team or a subcontractor. |
| (3) | Indicates that job is serviced by team in sub-system . |
| (4) | Ensures that, after service completion, the team transport vehicles had to leave the job. |
| (5) | Indicates that the start time for servicing job is equal to the sum of the completion time of job and the travel time of team . |
| (6) | Ensures that a team is able to start servicing only when the job is ready. |
| (7) | Ensures that if a team cannot finish the service in time, a delay occurs. |
| (8) | Ensures that the service delay must not exceed an allowed delay time. |
| (9) | Specifies the time when a team can start a service. |
| (10) | Indicates team overtime for late arrival at the depot. |
| (11) | Ensures that the amount of overtime used by each team in a given period must not exceed the allowed overtime. |
| (12) | Ensures that the number of teams servicing the jobs must not exceed the number of teams that are actually available. |
| (13) | Ensures that the number of technicians in team in sub-system is sufficient for servicing job . |
| (14) | Ensures that the technician teams’ skill levels and types are adequate for servicing job . |
| (15) | Determines technician team of the sub-system required during period . |
| (16)–(19) | The binary variable constraints. |
| No. | Group | Description | |
|---|---|---|---|
| F1 | Unimodal functions | Shifted and rotated bent cigar function | 100 |
| F2 | Shifted and rotated Zakharov function | 200 | |
| F3 | Simple multimodal functions | Shifted and rotated Rosenbrock’s function | 300 |
| F4 | Shifted and rotated Rastrigin’s function | 400 | |
| F5 | Shifted and rotated expanded Scaffer’s F6 function | 500 | |
| F6 | Shifted and rotated Lunacek bi-Rastrigin function | 600 | |
| F7 | Shifted and rotated non-continuous Rastrigin’s function | 700 | |
| F8 | Shifted and rotated Levy function | 800 | |
| F9 | Shifted and rotated Schwefel’s function | 900 |
| No. | GA | BA | WOA | PSO | HPSWOA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| F1 | 9.3355 × 103 | 5.2101 × 103 | 1.1542 × 1013 | 6.3627 × 1012 | 5.1413 × 103 | 3.3779 × 103 | 2.8359 × 103 | 1.8965 × 103 | 3.5739 × 103 | 2.5432 × 103 |
| F2 | 1.4435 × 103 | 9.1837 × 102 | 3.5692 × 107 | 2.9560 × 107 | 6.3598 × 10−6 | 4.1574 × 10−6 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 | 0.0000 × 100 |
| F3 | 5.6102 × 100 | 4.8250 × 10−1 | 6.8654 × 105 | 5.4167 × 105 | 1.9155 × 100 | 4.9560 × 10−1 | 9.8217 × 100 | 1.4493 × 100 | 1.1292 × 100 | 8.7680 × 10−1 |
| F4 | 9.5142 × 100 | 2.0899 × 100 | 5.9447 × 105 | 2.6542 × 104 | 2.3524 × 101 | 5.2721 × 100 | 1.2314 × 102 | 2.5796 × 101 | 1.4057 × 101 | 4.9011 × 100 |
| F5 | 2.1875 × 100 | 1.3174 × 100 | 6.2376 × 105 | 5.7474 × 104 | 1.1509 × 101 | 8.3052 × 100 | 5.2498 × 101 | 1.3300 × 101 | 1.6095 × 100 | 8.0240 × 10−1 |
| F6 | 2.6048 × 101 | 3.3328 × 100 | 7.4935 × 105 | 2.2487 × 104 | 4.9409 × 101 | 1.1489 × 101 | 1.1152 × 102 | 1.4160 × 10−1 | 2.0654 × 101 | 5.4430 × 100 |
| F7 | 6.5510 × 100 | 3.4600 × 100 | 8.4397 × 105 | 1.6496 × 104 | 2.3388 × 101 | 6.4430 × 100 | 8.3493 × 102 | 0.0000 × 100 | 2.1755 × 101 | 4.4055 × 100 |
| F8 | 4.3192 × 100 | 2.8240 × 100 | 4.7410 × 106 | 1.7545 × 105 | 1.6726 × 10−1 | 1.1135 × 10−1 | 8.7776 × 102 | 1.1230 × 101 | 1.7789 × 10−4 | 1.2279 × 10−4 |
| F9 | 3.7047 × 102 | 2.4671 × 102 | 3.6634 × 106 | 3.6975 × 105 | 6.8409 × 102 | 2.2967 × 102 | 1.8222 × 103 | 4.7987 × 102 | 2.5487 × 102 | 1.2286 × 102 |
| Ins. | No. of Job | No. of Day | Lingo | WOA | PSO | HPSWOA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | CPU Time (min) | Best | Avg | CPU Time (s) | Best | Avg | CPU Time (s) | Best | Avg | CPU Time (s) | |||
| 1 | 10 | 3 | 16,847.00 | 0.03 | 16,847.00 | 17,256.60 | 4.76 | 16,847.00 | 17,689.10 | 7.01 | 16,847.00 | 17,084.00 | 7.26 |
| 2 | 10 | 7 | 23,192.00 | 0.07 | 23,192.00 | 23,192.00 | 2.90 | 23,192.00 | 23,192.00 | 2.84 | 23,192.00 | 23,192.00 | 2.78 |
| 3 | 20 | 3 | 20,192.00 | 6.83 | 20,192.00 | 20,665.20 | 5.00 | 20,192.00 | 20,693.60 | 5.82 | 20,192.00 | 20,546.10 | 6.08 |
| 4 | 20 | 7 | 40,042.00 | 37.33 | 40,042.00 | 40,042.00 | 2.77 | 40,042.00 | 40,042.00 | 2.80 | 40,042.00 | 40,042.00 | 2.87 |
| 5 | 20 | 15 | 44,348.00 | 19.61 | 44,348.00 | 44,348.00 | 3.27 | 44,348.00 | 44,348.00 | 3.38 | 44,348.00 | 44,348.00 | 2.82 |
| 6 | 30 | 3 | 31,093.00 1 | 1440.00 | 30,697.00 | 32,056.90 | 14.68 | 30,938.00 | 32,028.00 | 23.46 | 30,068.00 | 30,938.10 | 23.29 |
| 7 | 30 | 7 | 34,853.00 1 | 1440.00 | 34,833.00 | 35,698.40 | 6.11 | 35,049.00 | 36,268.60 | 9.37 | 34,833.00 | 35,446.80 | 10.00 |
| 8 | 30 | 15 | 56,124.00 | 10.03 | 56,124.00 | 56,124.00 | 3.03 | 56,124.00 | 56,124.00 | 2.84 | 56,124.00 | 56,124.00 | 2.78 |
| WOA | PSO | HPSWOA | |
|---|---|---|---|
| Lingo | 0.757 | 0.444 | 0.492 |
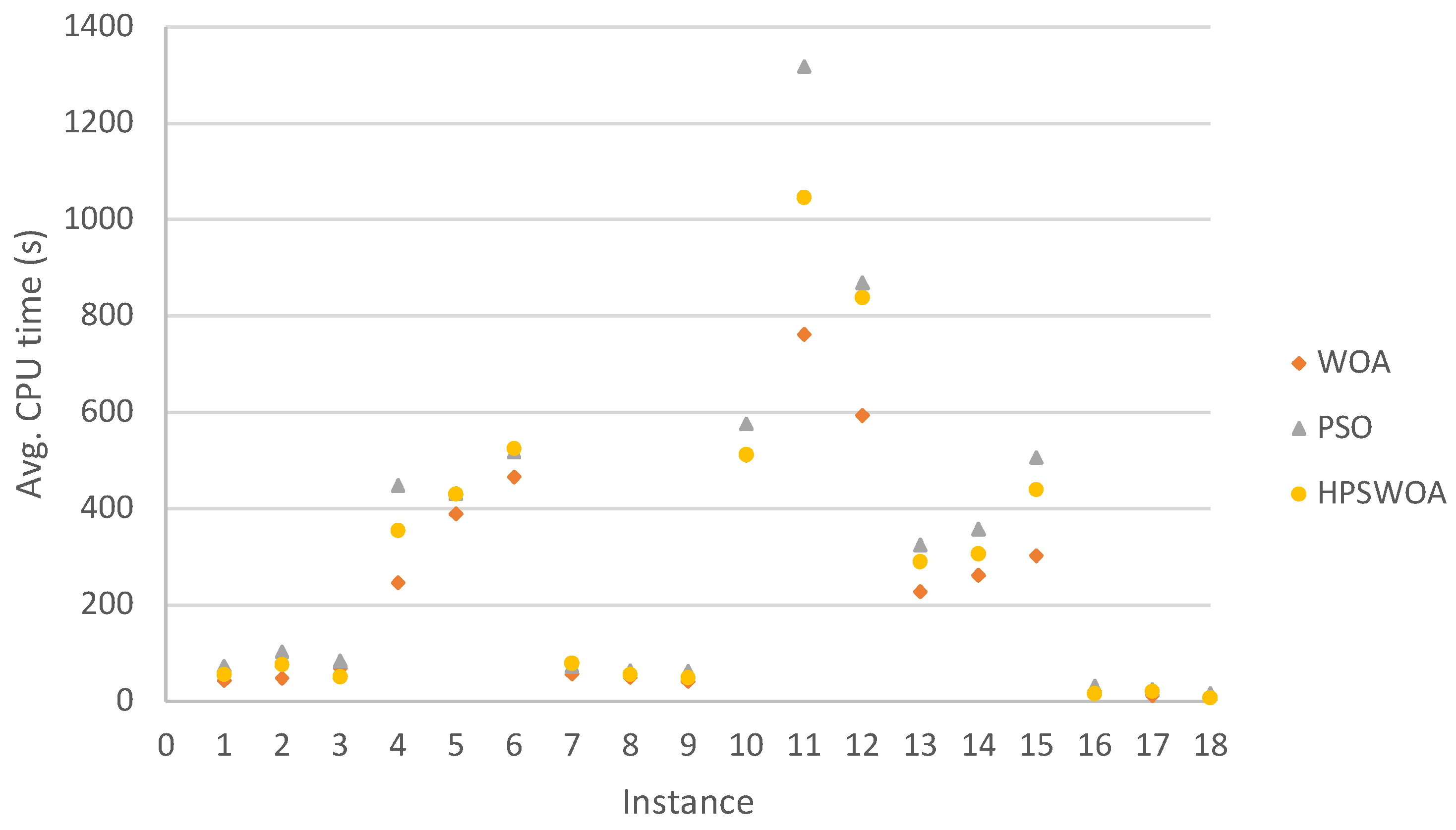
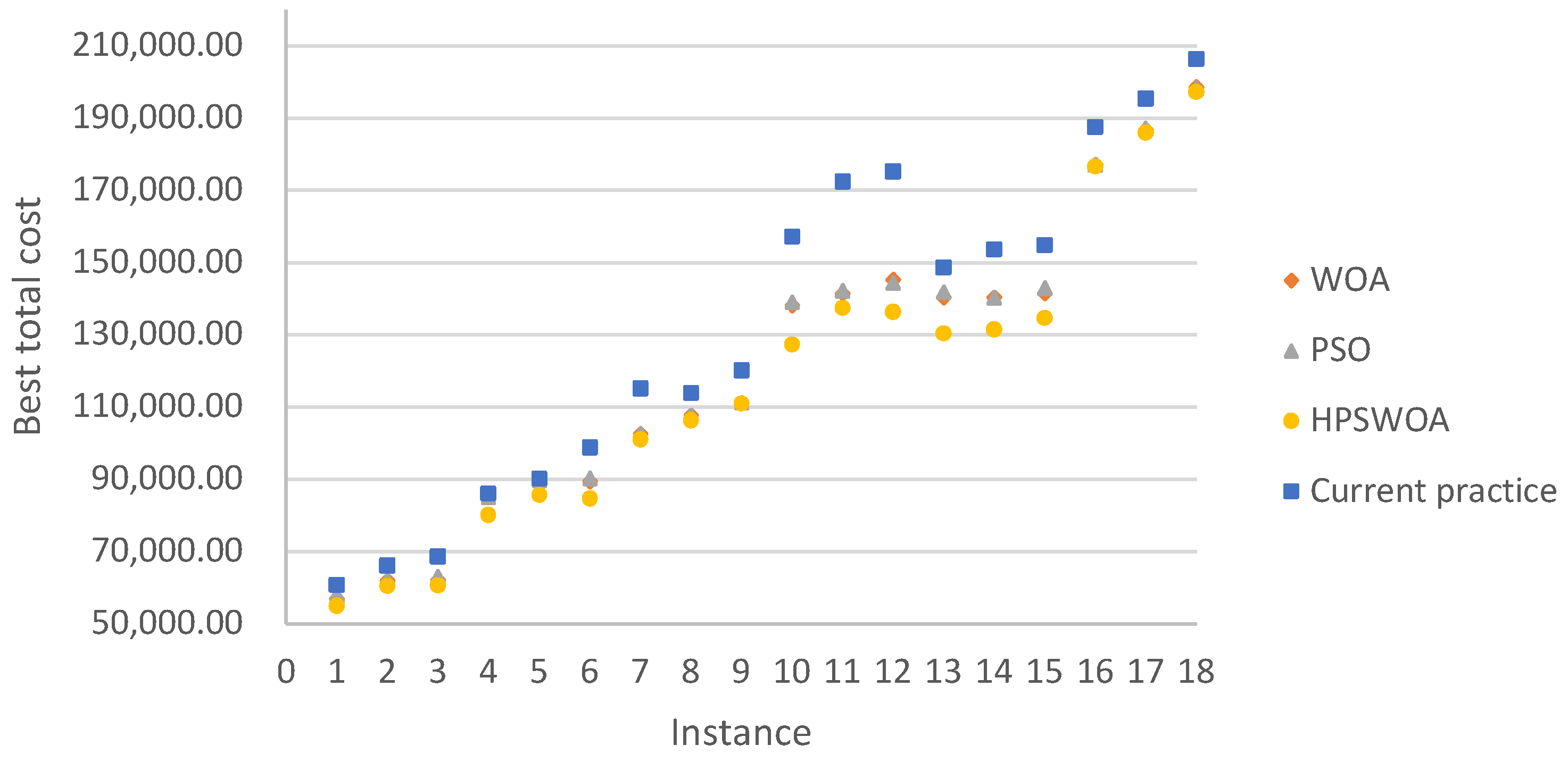
| Ins. | No. of Job | No. of Day | DoD | CP | WOA | PSO | HPSWOA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best | Best | Avg | CPU Time (s) | Best | Avg | CPU Time (s) | Best | Avg | CPU Time (s) | ||||
| 1 | 60 | 7 | 0.1 | 60,742.77 | 56,867.55 | 58,751.37 | 43.15 | 57,888.63 | 59,843.40 | 72.82 | 54,930.89 | 56,321.80 | 55.77 |
| 2 | 60 | 7 | 0.2 | 66,165.01 | 61,926.64 | 63,313.08 | 47.46 | 62,064.82 | 63,910.11 | 103.30 | 60,443.12 | 61,737.93 | 75.73 |
| 3 | 60 | 7 | 0.3 | 68,547.37 | 62,147.38 | 63,655.08 | 68.76 | 63,026.41 | 64,310.59 | 83.25 | 60,583.23 | 62,002.82 | 50.22 |
| 4 | 100 | 7 | 0.1 | 86,060.89 | 85,507.40 | 87,915.87 | 245.82 | 85,040.03 | 87,839.67 | 448.50 | 80,137.68 | 84,612.61 | 354.72 |
| 5 | 100 | 7 | 0.2 | 90,143.77 | 88,425.89 | 89,749.63 | 389.28 | 89,820.82 | 92,619.14 | 431.87 | 85,672.18 | 87,408.17 | 429.48 |
| 6 | 100 | 7 | 0.3 | 98,786.54 | 89,394.79 | 91,258.24 | 465.19 | 90,127.95 | 93,335.72 | 517.32 | 84,678.02 | 87,069.23 | 524.65 |
| 7 | 100 | 15 | 0.1 | 115,122.91 | 102,471.15 | 103,113.43 | 56.29 | 102,673.57 | 103,419.85 | 72.03 | 101,024.25 | 101,588.70 | 78.62 |
| 8 | 100 | 15 | 0.2 | 113,841.56 | 107,658.95 | 108,713.87 | 49.96 | 107,658.95 | 109,082.14 | 63.19 | 106,202.02 | 108,143.62 | 55.69 |
| 9 | 100 | 15 | 0.3 | 120,072.12 | 111,284.17 | 113,801.47 | 41.05 | 111,281.22 | 113,817.79 | 62.25 | 110,977.17 | 113,055.55 | 49.14 |
| 10 | 150 | 7 | 0.1 | 157,205.32 | 138,068.72 | 141,631.88 | 510.00 | 139,019.63 | 142,985.52 | 576.20 | 127,254.70 | 132,442.84 | 512.08 |
| 11 | 150 | 7 | 0.2 | 172,360.12 | 141,335.98 | 145,410.89 | 761.75 | 142,160.74 | 146,246.04 | 1317.51 | 137,330.67 | 141,279.73 | 1045.58 |
| 12 | 150 | 7 | 0.3 | 175,128.80 | 145,251.82 | 148,517.14 | 593.44 | 144,339.02 | 147,761.72 | 868.92 | 136,238.08 | 140,712.74 | 837.83 |
| 13 | 150 | 15 | 0.1 | 148,614.33 | 140,222.92 | 142,179.03 | 227.98 | 141,804.39 | 146,990.98 | 324.40 | 130,367.17 | 133,773.83 | 289.68 |
| 14 | 150 | 15 | 0.2 | 153,608.22 | 140,301.37 | 142,183.72 | 261.65 | 140,290.30 | 143,741.14 | 356.78 | 131,435.74 | 138,424.81 | 306.14 |
| 15 | 150 | 15 | 0.3 | 154,851.33 | 141,343.62 | 144,553.90 | 302.06 | 142,864.80 | 145,484.64 | 505.76 | 134,668.31 | 141,013.72 | 439.32 |
| 16 | 150 | 30 | 0.1 | 187,507.74 | 177,029.34 | 177,213.14 | 20.15 | 177,029.34 | 177,550.58 | 30.99 | 176,457.84 | 176,572.68 | 15.99 |
| 17 | 150 | 30 | 0.2 | 195,290.08 | 186,768.27 | 188,166.19 | 12.10 | 187,051.56 | 188,778.25 | 24.12 | 185,870.04 | 187,509.73 | 20.90 |
| 18 | 150 | 30 | 0.3 | 206,263.06 | 198,529.40 | 199,915.41 | 6.89 | 198,241.63 | 199,534.03 | 15.39 | 197,074.98 | 198,647.00 | 6.86 |
| PSO | HPSWOA | |
|---|---|---|
| WOA | 0.008 | 0.010 |
| PSO | 0.016 |
| WOA | PSO | HPSWOA | |
|---|---|---|---|
| CP | 0.001 | 0.001 | 0.001 |
| WOA | 0.018 | 0.001 | |
| PSO | 0.001 |
| CP | WOA | PSO | |
|---|---|---|---|
| HPSWOA | 11.06% | 3.47% | 3.91% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Punyakum, V.; Sethanan, K.; Nitisiri, K.; Pitakaso, R. Hybrid Particle Swarm and Whale Optimization Algorithm for Multi-Visit and Multi-Period Dynamic Workforce Scheduling and Routing Problems. Mathematics 2022, 10, 3663. https://doi.org/10.3390/math10193663
Punyakum V, Sethanan K, Nitisiri K, Pitakaso R. Hybrid Particle Swarm and Whale Optimization Algorithm for Multi-Visit and Multi-Period Dynamic Workforce Scheduling and Routing Problems. Mathematics. 2022; 10(19):3663. https://doi.org/10.3390/math10193663
Chicago/Turabian StylePunyakum, Voravee, Kanchana Sethanan, Krisanarach Nitisiri, and Rapeepan Pitakaso. 2022. "Hybrid Particle Swarm and Whale Optimization Algorithm for Multi-Visit and Multi-Period Dynamic Workforce Scheduling and Routing Problems" Mathematics 10, no. 19: 3663. https://doi.org/10.3390/math10193663
APA StylePunyakum, V., Sethanan, K., Nitisiri, K., & Pitakaso, R. (2022). Hybrid Particle Swarm and Whale Optimization Algorithm for Multi-Visit and Multi-Period Dynamic Workforce Scheduling and Routing Problems. Mathematics, 10(19), 3663. https://doi.org/10.3390/math10193663









