Diverse Multiple Lump Analytical Solutions for Ion Sound and Langmuir Waves

Abstract

In this work, we study a time-fractional ion sound and Langmuir waves system (FISLWS) with Atangana–Baleanu derivative (ABD). We use a fractional ABD operator to transform our system into an ODE. We investigate multiwaves, periodic cross-kink, rational, and interaction solutions by the combination of rational, trigonometric, and various bilinear functions. Furthermore, 3D, 2D, and relevant contour plots are presented for the natural evolution of the gained solutions under the selection of proper parameters.

1. Introduction

At the present time, various real phenomena have been formulated by integer-order nonlinear partial differential equations (NPDEs). These supermodels are studied in different domains of sciences, such as engineering, chemistry, biology, physics, optics, etc. However, it is not enough to use integer order where the nonlocal property does not appear in these forms, so different models have been systematized in fractional NPDEs to determine that kind of similarity [1]. By using numerical and computational schemes, these models give more familiar properties [2,3,4,5,6,7,8,9,10]. To use most of these schemes, one needs fractional operator to transform the fractional forms into nonlinear ODEs with integer orders such as conformable fractional derivative, Caputo, Caputo–Fabrizio definition, Riemann–Liouville derivatives, and so on [11,12,13,14,15,16,17,18,19,20,21,22,23,24]. These operators have been applied to estimate the numeric and exact solutions of fractional order NPDEs through different integration schemes, such as $({\varphi }^6)$-model expansion [25], $(\frac{G^{\prime }}{G})$-expansion [26], $tan(\frac{\Phi \left(\rho \right)}{2})$-expansion [27], Kudryashove scheme [28], $exp((-\frac{{\Psi }^{\prime }}{\Psi })\eta )$-expansion [29], extended auxiliary equation technique [30], and so many others.

Here, we consider the FISLWS as follows [17],

$$\begin{array}{cc}\hfill & i{}^{AB}{D}_t^{\alpha }m+\frac{1}{2}{m}_{xx}-nm=0,\hfill \\ \hfill & {}^{AB}{D}_t^{2\alpha }n-n_{xx}-{2(|m|}^2{)}_{xx}=0,t>0,0<\alpha \le 1.\hfill \end{array}$$

(1)

where $m{e}^{-i{\omega }_{p}t}$ and n illustrate the normalized electric-field of the Langmuir oscillation and perturbation of density, respectively. Both x and t are normalized variables and ${}^{AB}{D}_t^{\alpha }$ is the AB fractional operator in t direction.

ABD operator is well defined as

$$\begin{array}{c}\hfill {}^{ABD}{D}_{a^{+}}^{\alpha }F\left(t\right)=\frac{B\left(\alpha \right)}{1-\alpha }\frac{d}{dt}{\int }_a^{t}F\left(x\right)G_{\alpha }\left(\frac{-\alpha {(t-\alpha )}^{\alpha }}{1-\alpha }\right)dx,\end{array}$$

(2)

where $G_{\alpha }$ is Mittag-Leffler function, defined as

$$\begin{array}{c}\hfill G_{\alpha }\left(\frac{-\alpha {(t-\alpha )}^{\alpha }}{1-\alpha }\right)=\sum _{n=0}^{\infty }\frac{{\left(\frac{-\alpha }{1-\alpha }\right)}^s{(t-x)}^{\alpha s}}{\Gamma (\alpha s+1)},\end{array}$$

(3)

and $B\left(\alpha \right)$ is the normalization function that satisfies $B\left(1\right)=B\left(0\right)=1$. Thus,

$$\begin{array}{c}\hfill {}^{ABD}{D}_{a^{+}}^{\alpha }F\left(t\right)=\frac{B\left(\alpha \right)}{1-\alpha }\sum _{n=0}^{\infty }{\left(\frac{-\alpha }{1-\alpha }\right)}^s{}^{RL}{I}_a^{\alpha s}F\left(t\right).\end{array}$$

(4)

for more properties of this operator. This leads towards the following form,

$$\begin{array}{cc}\hfill & m(x,t)=u\left(\xi \right)e^{i\vartheta },n(x,t)=v\left(\xi \right),\hfill \\ \hfill & \vartheta =ax+\frac{\beta (1-\alpha )t^{-s}}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{\left(-\frac{\alpha }{1-\alpha }\right)}^s\Gamma (1-\alpha s)},\hfill \\ \hfill & \xi =bx+\frac{\gamma (1-\alpha )t^{-s}}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{\left(-\frac{\alpha }{1-\alpha }\right)}^s\Gamma (1-\alpha s)},\hfill \end{array}$$

(5)

where $\beta$ and $\gamma$ are arbitrary constants. This wave alteration converts Equation (1) into the following ODE.

$$\begin{array}{c}\hfill \frac{1}{2}{b}^2{u}^{″}+i(\gamma +ab)u^{\prime }-\frac{1}{2}(a^2+2\beta )u-uv=0,\\ \hfill ({\gamma }^2-b^2)v^{″}-4b^2({u\prime }^2+u{u}^{″})=0.\end{array}$$

(6)

Here, u and v are the functions of $\xi$. By separating the Img part from the first part of Equation (6),

$$\gamma +ab=0⟹\gamma =-ab.$$

(7)

and then by integrating the second part of Equation (6) by two times the w.r.t $\xi$, we obtain

$$v=\frac{2b^2}{-b^2+{\gamma }^2}{u}^2=\frac{2}{a^2-1}{u}^2.$$

(8)

Equations (7) and (8) transform Equation (6) into the following form:

$$\begin{array}{cc}\hfill & u^{″}-\frac{4}{b^2(a^2-1)}{u}^3-\frac{a^2+2\beta }{b^2}u=0,\hfill \\ \hfill & or\hfill \\ \hfill & u^{″}=\frac{4}{b^2(a^2-1)}{u}^3+\frac{a^2+2\beta }{b^2}u.\hfill \end{array}$$

(9)

The contents of this paper are arranged as follows: In Section 2, we present M-shaped rational solitons. In Section 3, we evaluate M-shaped interaction solutions. In Section 4, we find the multiwaves solution. In Section 5, we study homoclinic breather. In Section 6, we investigate periodic cross-kink solutions. In Section 7, we present results and discussions and Section 8 contains concluding remarks.

2. M-Shaped Rational Solitons

By using the following log transformation,

$$u=u_0+2{(ln\Phi )}_{\xi }.$$

(10)

Equation (10) transforms Equation (9) into the following bilinear form:

$$\begin{array}{c}\hfill u_0(-a^4-4u_0^2+a^2(1-2\beta )+2\beta ){\Phi }^3+4(-8+(-1+a^2)b^2){\Phi \prime }^3-6\Phi {\Phi }^{\prime }(8u_0{\Phi }^{\prime }+\\ \hfill (-1+a^2)b^2{\Phi }^{″})-2{\Phi }^2((a^4+12u_0^2-2\beta +a^2(-1+2\beta )){\Phi }^{\prime }-(-1+a^2)b^2\Phi \prime ″)=0.\end{array}$$

(11)

We choose M-shaped rational solution in bilinear form for $\Phi$, as follows [31]:

$$\Phi ={(b_2+b_1\xi )}^2+{(b_4+b_3\xi )}^2+b_5,$$

(12)

where $b_i(1\le i\le 5)$ all are real-valued parameters to be measured. Inserting $\Phi$ into Equation (11) and collecting all powers of $\xi$, we obtain proper results, as follows (See Figure 1 and Figure 2):

Set I. For $b_2=0$,

$$a=a,b=b,\beta =-\frac{a^4-a^2+4u_0^2}{2(a^2-1)},b_1=i{b}_3,b_3=b_3,b_4=b_4,b_5=b_5,u_0=u_0.$$

(13)

Using this in Equation (12), and then by using Equations (8) and (10), we obtain

$$\begin{array}{cc}& u\left(\xi \right)=u_0+\frac{2\left(-2b_3^2\xi +2b_3(b_4+b_3\xi )\right)}{b_5-b_3^2{\xi }^2+{(b_4+b_3\xi )}^2},\\ \hfill & v\left(\xi \right)=\frac{2}{a^2-1}{\left(u_0+\frac{2(-2b_3^2\xi +2b_3(b_4+b_3\xi ))}{b_5-b_3^2{\xi }^2+{(b_4+b_3\xi )}^2}\right)}^2.\end{array}$$

(14)

To obtain final results, we use Equation (5):

$$\begin{array}{cc}\hfill & m_{21}(x,t)=e^{i\left(ax-\frac{t^{-s}(a^4-a^2+4u_0^2)(1-\alpha )}{2(a^2-1)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}\left(u_0+\frac{2(2b_3(b_4+b_3\Omega )-2b_3^2\Omega )}{b_5+{(b_4+b_3\Omega )}^2-b_3{\Omega }^2}\right),\hfill \\ \hfill & n_{22}(x,t)=\frac{2}{(a^2-1)}{\left(u_0+\frac{2(2b_3(b_4+b_3\Omega )-2b_3^2\Omega )}{b_5+{(b_4+b_3\Omega )}^2-b_3{\Omega }^2}\right)}^2,\hfill \end{array}$$

(15)

where $\Omega =\left(bx-\frac{ab{t}^{-s}(1-\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

Set II. For $b_5=0$,

$$a=a,b=b,\beta =-\frac{a^4-a^2+4u_0^2}{2(a-1)(a+1)},b_1=i{b}_3,b_2=b_2,b_3=b_3,b_4=b_4,u_0=u_0.$$

(16)

Using this in Equation (12), and then by using Equations (8) and (10) in Equation (5), we obtain

$$\begin{array}{cc}\hfill & m_{23}(x,t)=e^{i\left(ax-\frac{t^{-s}(a^4-a^2+4u_0^2)(1-\alpha )}{2(a^2-1)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}\left(u_0+\frac{2(2i{b}_3(b_2+i{b}_3\Omega )+2b_3(b_4+b_3\Omega ))}{{(b_2+i{b}_3\Omega )}^2+{(b_4+b_3\Omega )}^2}\right),\hfill \\ \hfill & n_{24}(x,t)=\frac{2}{(a^2-1)}{\left(u_0+\frac{2(2i{b}_3(b_2+i{b}_3\Omega )+2b_3(b_4+b_3\Omega ))}{{(b_2+i{b}_3\Omega )}^2+{(b_4+b_3\Omega )}^2}\right)}^2,\hfill \end{array}$$

(17)

where $\Omega =\left(bx-\frac{ab{t}^{-s}(1-\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

Set III. For $u_0=0$,

$$a=a,b=b,\beta =-\frac{1}{2}{a}^2,b_1=i{b}_3,b_2=b_2,b_3=b_3,b_4=b_4,b_5=b_5.$$

(18)

Using this in Equation (12), and then by using Equations (8) and (10), we obtain

$$\begin{array}{cc}& u\left(\xi \right)=\frac{2\left(2i{b}_3(b_2+i{b}_3\xi )+2b_3(b_4+b_3\xi )\right)}{b_5+{(b_2+i{b}_3\xi )}^2+{(b_4+b_3\xi )}^2},\\ \hfill & v\left(\xi \right)=\frac{8{\left(2i{b}_3(b_2+i{b}_3\xi )+2b_3(b_4+b_3\xi )\right)}^2}{(-1+a^2){\left(b_5+{(b_2+i{b}_3\xi )}^2+{(b_4+b_3\xi )}^2\right)}^2}.\end{array}$$

(19)

To obtain final results, we use Equation (5):

$$\begin{array}{cc}\hfill & m_{25}(x,t)=\frac{2e^{i(ax-\frac{a^2{t}^{-s}(1-\alpha )}{2B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)})}\left(2i{b}_3(b_2+i{b}_3\Omega )+2b_3(b_4+b_3\Omega )\right)}{b_5+{(b_2+i{b}_3\Omega )}^2+{(b_4+b_3\Omega )}^2},\hfill \\ \\ \hfill & n_{26}(x,t)=\frac{8}{(a^2-1)}{\left(\frac{2i{b}_3(b_2+i{b}_3\Omega )+2b_3(b_4+b_3\Omega )}{b_5+{(b_2+i{b}_3\Omega )}^2+{(b_4+b_3\Omega )}^2}\right)}^2,\hfill \end{array}$$

(20)

where $\Omega =\left(bx-\frac{ab{t}^{-s}(1-\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

3. M-Shaped Rational Soliton Interactions with

In this part, we evaluate M-shaped rational interactions with periodic and kink waves by using exponential and cos function in bilinear combinations.

3.1. One-Kink Soliton

For this, the bilinear form for $\Phi$ is as follows [31]:

$$\Phi ={(b_2+b_1\xi )}^2+{(b_4+b_3\xi )}^2+c{e}^{b_6+b_5\xi }+b_7,$$

(21)

where $b_i(1\le i\le 7),$ all are real-valued parameters to be measured. Inserting $\Phi$ into Equation (11) and collecting all powers of $e^{b_5\xi +b_6}$, $e^{2(b_5\xi +b_6)}$, $e^{3(b_5\xi +b_6)}$, $\xi e^{b_5\xi +b_6}$, $\xi e^{2(b_5\xi +b_6)}$, ${\xi }^2{e}^{b_5\xi +b_6}$, ${\xi }^3{e}^{b_5\xi +b_6}$, ${\xi }^4{e}^{b_5\xi +b_6}$, and $\xi$, we obtain proper results, as follows (See Figure 3, Figure 4, Figure 5 and Figure 6):

Set I. For $b_2=b_6=0$,

$$\begin{array}{cc}& a=a,b=2\sqrt{2}\sqrt{\frac{1}{a^2-1}},\beta =-\frac{a^4-a^2+4b_5^2}{2(a-1)(a+1)},b_1=i{b}_3,b_3=b_3,b_4=b_4,b_5=b_5,\\ \hfill & b_7=b_7,u_0=-b_5.\end{array}$$

(22)

Using Equation (22) in Equation (21), and then by using Equations (8) and (10), we obtain

$$\begin{array}{c}\hfill u\left(\xi \right)=-b_5+\frac{2\left(b_{5}c{e}^{b_5\xi }-2b_3^2\xi +2b_3(b_4+b_3\xi )\right)}{b_7+c{e}^{b_5\xi }-b_3^2{\xi }^2+{(b_4+b_3\xi )}^2},\\ \hfill v\left(\xi \right)=\frac{2{\left(b_5(b_4^2+b_7-c{e}^{b_5\xi })+2b_3{b}_4(-2+b_5\xi )\right)}^2}{(-1+a^2){(b_4^2+b_7+c{e}^{b_5\xi }+2b_3{b}_4\xi )}^2}.\end{array}$$

(23)

Using Equation (5) to obtain the required solution for Equation (1),

$$\begin{array}{cc}\hfill & m_{31}(x,t)=-\frac{e^{\Delta }\left(4\sqrt{2}a\sqrt{\frac{1}{a^2-1}}{b}_3{b}_4{b}_5(\alpha -1)+t^s\left(b_5(b_4^2+b_7-c{e}^{{\Delta }_1})+4b_3{b}_4(-1+\sqrt{2}\sqrt{\frac{1}{a^2-1}}{b}_{5}x)\right)\Xi \right)}{4\sqrt{2}a\sqrt{\frac{1}{a^2-1}}{b}_3{b}_4(\alpha -1)+t^s\left(b_4^2+b_7+c{e}^{{\Delta }_1}+4\sqrt{2}\sqrt{\frac{1}{a^2-1}}{b}_3{b}_{4}x\right)\Xi },\hfill \\ \\ \hfill & n_{32}(x,t)=\frac{2}{(a^2-1)}{\left(\frac{4\sqrt{2}a\sqrt{\frac{1}{a^2-1}}{b}_3{b}_4{b}_5(\alpha -1)+t^s\left(b_5(b_4^2+b_7-c{e}^{{\Delta }_1})+4b_3{b}_4(-1+\sqrt{2}\sqrt{\frac{1}{a^2-1}}{b}_{5}x)\right)\Xi }{4\sqrt{2}a\sqrt{\frac{1}{a^2-1}}{b}_3{b}_4(\alpha -1)+t^s\left(b_4^2+b_7+c{e}^{{\Delta }_1}+4\sqrt{2}\sqrt{\frac{1}{a^2-1}}{b}_3{b}_{4}x\right)\Xi }\right)}^2,\hfill \end{array}$$

(24)

where $\Delta =\frac{1}{2}i(2ax+\frac{(-a^2+a^4+4b_5^2)t^{-s}(-1+\alpha )}{(-1+a)(1+a)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)})$,

${\Delta }_1=2\sqrt{2}\sqrt{\frac{1}{a^2-1}}{b}_5\left(x+\frac{a{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right),$ and $\Xi =B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s).$

Set II. For $b_1=0$,

$$\begin{array}{c}\hfill a=a,b=0,\beta =-\frac{1}{2}{a}^2,b_2=b_2,b_3=b_3,b_4=-\frac{2b_3}{u_0},b_5=-\frac{1}{2}{u}_0,b_6=b_6,b_7=-\frac{b_2^2{u}_0^2-4b_3^2}{u_0^2},u_0=u_0.\end{array}$$

(25)

Using Equation (25) in Equation (21), and then by using Equations (8) and (10), we obtain

$$\begin{array}{c}\hfill u\left(\xi \right)=u_0+\frac{2\left(-\frac{1}{2}c{e}^{b_6-\frac{u_0\xi }{2}}{u}_0+2b_3(-\frac{2b_3}{u_0}+b_3\xi )\right)}{b_2^2+c{e}^{b_6-\frac{u_0\xi }{2}}-\frac{b_2^2{u}_0^2-4b_3^2}{u_0^2}+{(-\frac{2b_3}{u_0}+b_3\xi )}^2},\\ \hfill v\left(\xi \right)=\frac{2b_3^4{e}^{u_0\xi }{u}_0^6{\xi }^4}{(-1+a^2){\left(c{e}^{b_6}{u}_0^2+b_3^2{e}^{\frac{u_0\xi }{2}}(8-4u_0\xi +u_0^2{\xi }^2)\right)}^2}.\end{array}$$

(26)

Using Equation (5), we obtain the required solution for Equation (1):

$$\begin{array}{cc}\hfill & m_{33}(x,t)=e^{i\left(ax-\frac{a^2{t}^{-s}(1-\alpha )}{2B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}\left(u_0+\frac{2(-\frac{4b_3^2}{u_0}-\frac{1}{2}c{e}^{b_6}{u}_0)}{b_2^2+c{e}^{b_6}+\frac{4b_3^2}{u_0^2}-\frac{b_2^2{u}_0^2-4b_3^2}{u_0^2}}\right),\hfill \\ \hfill & n_{34}(x,t)=0,(\because b=0).\hfill \end{array}$$

(27)

Set III. For $b_2=b_6=0$,

$$\begin{array}{cc}& a=a,b=\frac{2\sqrt{-\frac{6u_0{b}_5+4u_0^2}{a^2-1}}}{b_5},\beta =-\frac{4u_0^2-a^2+a^4}{2(a^2-1)},b_1=\frac{\frac{1}{3}i(b_7+b_4^2)u_0}{b_4},b_3=-\frac{(b_7+b_4^2)u_0}{3b_4},\\ \hfill & b_4=b_4,b_5=b_5,b_7=b_7,u_0=u_0.\end{array}$$

(28)

Using Equation (28) in Equation (21), and then by using Equations (8) and (10), we obtain

$$\begin{array}{c}\hfill u\left(\xi \right)=u_0+\frac{2\left(b_{5}c{e}^{b_5\xi }-\frac{2{(b_4^2+b_7)}^2{u}_0^2\xi }{9b_4^2}-\frac{2(b_4^2+b_7)u_0(b_4-\frac{(b_7+b_4^2)u_0\xi }{3b_4})}{3b_4}\right)}{b_7+c{e}^{b_5\xi }-\frac{{(b_4^2+b_7)}^2{u}_0^2{\xi }^2}{9b_4^2}+{(b_4-\frac{(b_7+b_4^2)u_0\xi }{3b_4})}^2},\\ \hfill v\left(\xi \right)=\frac{2{\left(-6b_{5}c{e}^{b_5\xi }+u_0(b_7-3c{e}^{b_5\xi }+2b_7{u}_0\xi +b_4^2(1+2u_0\xi ))\right)}^2}{(-1+a^2){\left(3c{e}^{b_5\xi }+b_4^2(3-2u_0\xi )+b_7(3-2u_0\xi )\right)}^2}.\end{array}$$

(29)

Now, using Equation (5), we obtain the required solution for Equation (1):

$$\begin{array}{cc}\hfill & m_{35}(x,t)=\frac{e^{\Delta }\left(-4\sqrt{2}a(b_4^2+b_7)u_0^2{\Delta }_1(\alpha -1)+t^s\left(6b_5^{2}c{e}^{{\Delta }_2}-b_5(b_4^2+b_7-3c{e}^{{\Delta }_2})u_0-4\sqrt{2}(b_4^2+b_7)u_0^2{\Delta }_{1}x\right)\Xi \right)}{-4\sqrt{2}a(b_4^2+b_7)u_0{\Delta }_1(\alpha -1)t^s\left(3b_5(b_7+c{e}^{{\Delta }_2})-4\sqrt{2}{b}_7{u}_0{\Delta }_{1}x+b_4^2(3b_5-4\sqrt{2}{u}_0{\Delta }_{1}x)\right)\Xi },\hfill \\ \\ \hfill & n_{36}(x,t)=\frac{2}{(a^2-1)}{\left(\frac{-4\sqrt{2}a(b_4^2+b_7)u_0^2{\Delta }_1(\alpha -1)+t^s\left(6b_5^{2}c{e}^{{\Delta }_2}-b_5(b_4^2+b_7-3c{e}^{{\Delta }_2})u_0-4\sqrt{2}(b_4^2+b_7)u_0^2{\Delta }_{1}x\right)\Xi }{-4\sqrt{2}a(b_4^2+b_7)u_0{\Delta }_1(\alpha -1)t^s\left(3b_5(b_7+c{e}^{{\Delta }_2})-4\sqrt{2}{b}_7{u}_0{\Delta }_{1}x+b_4^2(3b_5-4\sqrt{2}{u}_0{\Delta }_{1}x)\right)\Xi }\right)}^2,\hfill \end{array}$$

(30)

where $\Delta =\frac{1}{2}i\left(2ax+\frac{t^{-s}(-a^2+a^4+4u_0^2)(-1+\alpha )}{(-1+a)(1+a)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$, ${\Delta }_1=\sqrt{-\frac{u_0(3b_5+2u_0)}{-1+a^2}},$

${\Delta }_2=\frac{2\sqrt{2}{t}^{-s}\sqrt{-\frac{u_0(3b_5+2u_0)}{-1+a^2}}\left(a(-1+\alpha )+t^{s}xB\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)\right)}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)},$ and $\Xi =B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s).$

3.2. Two-Kink Soliton

For two-kink interaction, the bilinear solution for $\Phi$ is as follows (See Figure 7, Figure 8 and Figure 9):

$$\Phi ={(b_2+b_1\xi )}^2+{(b_4+b_3\xi )}^2+e^{b_6+b_5\xi }+e^{b_8+b_7\xi }+b_9,$$

(31)

where $b_i(1\le i\le 9)$ and all are real-valued parameters to be found. Inserting $\Phi$ into Equation (11) and collecting all powers of $\xi ,$ and $e^{3(b_5\xi +b_6)}$, $e^{2(b_5\xi +b_6)}$, $e^{2(b_7\xi +b_8)}$, $\xi e^{b_5\xi +b_6}$, $\xi e^{2(b_5\xi +b_6)}$, $\xi e^{b_7\xi +b_8}$, $\xi e^{2(b_7\xi +b_8)}$, ${\xi }^2{e}^{b_5\xi +b_6}$, ${\xi }^3{e}^{b_5\xi +b_6}$, ${\xi }^3{e}^{b_7\xi +b_8}$, ${\xi }^4{e}^{b_7\xi +b_8}$, ${\xi }^4{e}^{b_5\xi +b_6}$, we obtain proper results, as follows:

Set I. For $u_0=0$,

$$\begin{array}{cc}& a=a,b=2\sqrt{2}\sqrt{\frac{1}{a^2-1}},\beta =-\frac{a^4-a^2+16b_7^2}{2(a-1)(a+1)},b_1=i{b}_3,b_2=i{b}_4,b_3=b_3,b_4=b_4,\\ \hfill & b_5=-b_7,b_6=b_6,b_7=b_7,b_8=b_8,b_9=b_9.\end{array}$$

(32)

Using Equation (32) in Equation (31), and then by using Equations (8) and (10), we obtain

$$\begin{array}{c}\hfill u\left(\xi \right)=\frac{2\left(-b_7{e}^{b_6-b_7\xi }+b_7{e}^{b_8+b_7\xi }+2i{b}_3(i{b}_4+i{b}_3\xi )+2b_3(b_4+b_3\xi )\right)}{b_9+e^{b_6-b_7\xi }+e^{b_8+b_7\xi }+{(i{b}_4+i{b}_3\xi )}^2+{(b_4+b_3\xi )}^2},\\ \hfill v\left(\xi \right)=\frac{8}{-1+a^2}{\left(\frac{-b_7{e}^{b_6-b_7\xi }+b_7{e}^{b_8+b_7\xi }+2i{b}_3(i{b}_4+i{b}_3\xi )+2b_3(b_4+b_3\xi )}{b_9+e^{b_6-b_7\xi }+e^{b_8+b_7\xi }+{(i{b}_4+i{b}_3\xi )}^2+{(b_4+b_3\xi )}^2}\right)}^2.\end{array}$$

(33)

Using Equation (5), we obtain the required solution for Equation (1),

$$\begin{array}{cc}\hfill & m_{37}(x,t)=-\frac{2b_7{e}^{\frac{1}{2}i(2ax+\frac{(-a^2+a^4+16b_7^2)t^{-s}(-1+\alpha )}{(-1+a)(1+a)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)})}\left(e^{b_6}-e^{b_8+2\Omega }\right)}{e^{b_6}+e^{b_8+2\Omega }+b_9{e}^{\Omega }},\hfill \\ \\ \hfill & n_{38}(x,t)=\frac{8b_7^2}{(a^2-1)}{\left(\frac{e^{b_6}-e^{b_8+2\Omega }}{e^{b_6}+e^{b_8+2\Omega }+b_9{e}^{\Omega }}\right)}^2,\hfill \end{array}$$

(34)

where $\Omega =2\sqrt{2}\sqrt{\frac{1}{a^2-1}}{b}_7\left(x+\frac{a{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

Set II.

$$\begin{array}{cc}& a=a,b=4\sqrt{\frac{2+i\sqrt{2}}{a^2-1}},\beta =\frac{a^2-a^4-8i(-2i+\sqrt{2})b_7^2}{2(a^2-1)},b_1=i{b}_3,b_2=b_2,b_3=b_3,b_4=-i{b}_2,\\ \hfill & b_5=(1+\frac{1}{2}i\sqrt{2})b_7,b_6=b_6,b_7=b_7,b_8=b_8,b_9=0.\end{array}$$

(35)

Using Equation (35) in Equation (31), and then by using Equations (8) and (10), we obtain

$$\begin{array}{c}\hfill u\left(\xi \right)=\frac{2\left(b_7{e}^{b_8+b_7\xi }+(1+\frac{i}{\sqrt{2}})b_7{e}^{b_6+(1+\frac{i}{\sqrt{2}})b_7\xi }+2i{b}_3(b_2+i{b}_3\xi )+2b_3(-i{b}_2+b_3\xi )\right)}{e^{b_8+b_7\xi }+e^{b_6+(1+\frac{i}{\sqrt{2}})b_7\xi }+{(b_2+i{b}_3\xi )}^2+{(-i{b}_2+b_3\xi )}^2},\\ \hfill v\left(\xi \right)=\frac{8}{-1+a^2}{\left(\frac{b_7{e}^{b_8+b_7\xi }+(1+\frac{i}{\sqrt{2}})b_7{e}^{b_6+(1+\frac{i}{\sqrt{2}})b_7\xi }+2i{b}_3(b_2+i{b}_3\xi )+2b_3(-i{b}_2+b_3\xi )}{e^{b_8+b_7\xi }+e^{b_6+(1+\frac{i}{\sqrt{2}})b_7\xi }+{(b_2+i{b}_3\xi )}^2+{(-i{b}_2+b_3\xi )}^2}\right)}^2.\end{array}$$

(36)

Using Equation (5), we obtain the required solution for Equation (1):

$$\begin{array}{cc}\hfill & m_{39}(x,t)=\frac{b_7{e}^{\frac{1}{2}i(2ax+\frac{(-a^2+a^4+8(2+i\sqrt{2})b_7^2)t^{-s}(-1+\alpha )}{(-1+a^2)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)})}\left(2e^{b_8+\Omega }+(2+i\sqrt{2})e^{b_6+(1+\frac{i}{\sqrt{2}})\Omega }\right)}{e^{b_8+\Omega }+e^{b_6+(1+\frac{i}{\sqrt{2}})\Omega }},\hfill \\ \hfill & n_{40}(x,t)=\frac{2b_7^2}{(a^2-1)}{\left(\frac{2e^{b_8+\Omega }+(2+i\sqrt{2})e^{b_6+(1+\frac{i}{\sqrt{2}})\Omega }}{e^{b_8+\Omega }+e^{b_6+(1+\frac{i}{\sqrt{2}})\Omega }}\right)}^2,\hfill \end{array}$$

(37)

where $\Omega =4\sqrt{\frac{2+i\sqrt{2}}{-1+a^2}}{b}_7\left(x+\frac{a{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

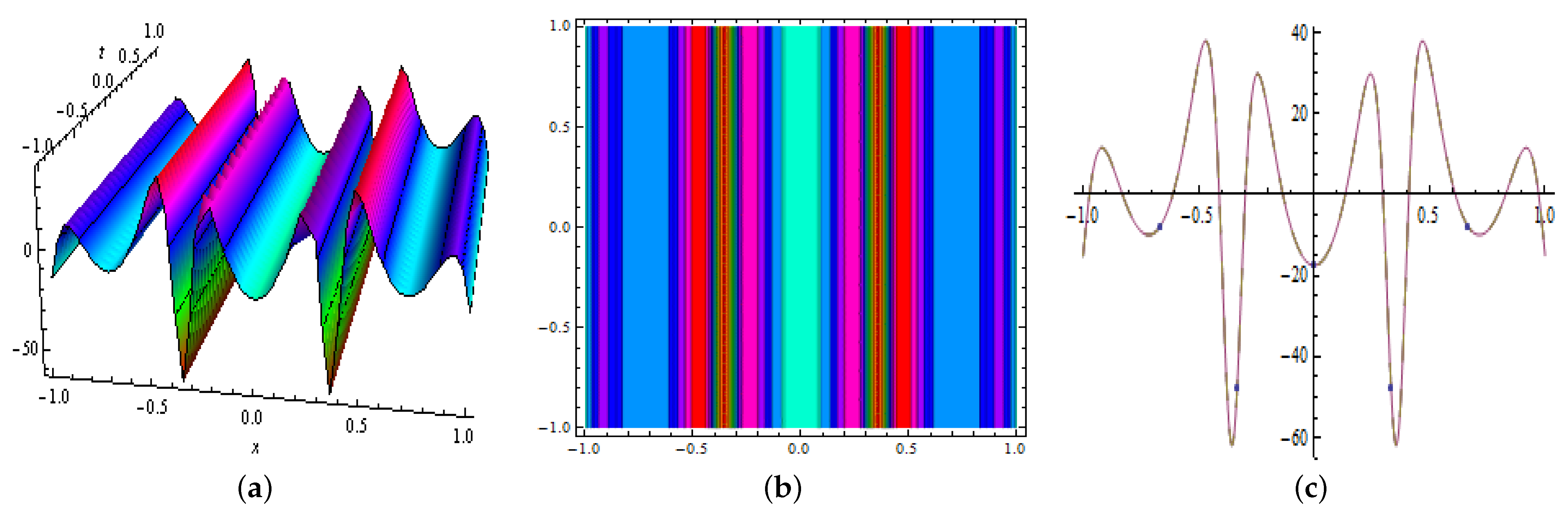
3.3. Periodic Waves

For periodic-wave interaction solutions, the bilinear form for $\Phi$ is as follows (See Figure 10 and Figure 11):

$$\Phi ={(b_2+b_1\xi )}^2+{(b_4+b_3\xi )}^2+cos(b_6+b_5\xi )+b_7,$$

(38)

where $b_i(1\le i\le 7)$ and all are real-valued parameters to be found. Inserting $\Phi$ into Equation (11) and collecting all powers of $\xi$ and $cos(b_5\xi +b_6)$, $\xi cos(b_5\xi +b_6)$, ${\xi }^{2}cos(b_5\xi +b_6)$, ${\xi }^{3}cos(b_5\xi$$+b_6)$, $\xi sin(b_5\xi +b_6)$, ${\xi }^{2}sin(b_5\xi +b_6)$, ${\xi }^{3}sin(b_5\xi +b_6)$, $\xi cos(b_5\xi +b_6)sin(b_5\xi +b_6)$, ${\xi }^{2}cos(b_5\xi +b_6)sin(b_5\xi +b_6)$, $sin{(b_5\xi +b_6)}^3$, we obtain proper results as follows:

Set I. For $u_0=0$,

$$\begin{array}{cc}& a=a,b=2\sqrt{2}\sqrt{\frac{1}{a^2-1}},\beta =-\frac{a^4-a^2+4b_5^2}{2(a-1)(a+1)},b_1=i{b}_3,b_2=b_2,b_3=b_3,b_4=b_4,b_5=b_5,\\ \hfill & b_6=b_6,b_7=-b_4^2-b_2^2.\end{array}$$

(39)

By using these parameters in Equation (38), and then by using Equations (8) and (10), we obtain

$$\begin{array}{c}\hfill u\left(\xi \right)=\frac{2\left(2i{b}_3(b_2+i{b}_3\xi )+2b_3(b_4+b_3\xi )-b_{5}sin(b_6+b_5\xi )\right)}{-b_2^2-b_4^2+{(b_2+i{b}_3\xi )}^2+{(b_4+b_3\xi )}^{2}cos(b_6+b_5\xi )},\\ \hfill v\left(\xi \right)=\frac{8}{-1+a^2}{\left(\frac{2i{b}_3(b_2+i{b}_3\xi )+2b_3(b_4+b_3\xi )-b_{5}sin(b_6+b_5\xi )}{-b_2^2-b_4^2+{(b_2+i{b}_3\xi )}^2+{(b_4+b_3\xi )}^{2}cos(b_6+b_5\xi )}\right)}^2.\end{array}$$

(40)

Now, using Equation (5), we obtain the required solution for Equation (1):

$$\begin{array}{cc}\hfill & m_1(x,t)=\frac{2e^{i\left(ax-\frac{(-a^2+a^4+4b_5^2)t^{-s}(-1+\alpha )}{2(-1+a^2)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}\left(-b_{5}sin(b_6+b_5\Omega )+2i{b}_3(b_2+i{b}_3\Omega )+2b_3(b_4+b_3\Omega )\right)}{-b_2^2-b_4^2+cos(b_6+b_5\Omega )+{(b_2+i{b}_3\Omega )}^2+{(b_4+b_3\Omega )}^2},\hfill \\ \\ \hfill & n_2(x,t)=\frac{8}{(a^2-1)}{\left(\frac{-b_{5}sin(b_6+b_5\Omega )+2i{b}_3(b_2+i{b}_3\Omega )+2b_3(b_4+b_3\Omega )}{-b_2^2-b_4^2+cos(b_6+b_5\Omega )+{(b_2+i{b}_3\Omega )}^2+{(b_4+b_3\Omega )}^2}\right)}^2,\hfill \end{array}$$

(41)

where $\Omega =2\sqrt{2}\sqrt{\frac{1}{-1+a^2}}x-\frac{2\sqrt{2}a\sqrt{\frac{1}{-1+a^2}}{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}$.

Set II. For $b_1=b_2=0$,

$$\begin{array}{cc}& a=a,b=\frac{2\sqrt{-\frac{2}{a^2-1}{u}_0}}{b_5},\beta =-\frac{a^4-a^2+4u_0^2}{2(a^2-1)},b_3=b_3,b_4=b_4,b_5=b_5,b_6=b_6,b_7=b_7,u_0=u_0.\end{array}$$

(42)

By using these parameters in Equation (38), and then by using Equations (8) and (10) in Equation (5), we obtain

$$\begin{array}{cc}\hfill & m_3(x,t)=e^{i\left(ax-\frac{t^{-s}(-a^2+a^4+4u_0^2)(-1+\alpha )}{2(-1+a^2)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}\left(u_0+\frac{2\left(-b_{5}sin(b_6+b_5\Omega )+2b_3(b_4+b_3\Omega )\right)}{b_7+cos(b_6+b_5\Omega )+{(b_4+b_3\Omega )}^2}\right),\hfill \\ \\ \hfill & n_4(x,t)=\frac{2}{-1+a^2}{\left(u_0+\frac{2\left(-b_{5}sin(b_6+b_5\Omega )+2b_3(b_4+b_3\Omega )\right)}{b_7+cos(b_6+b_5\Omega )+{(b_4+b_3\Omega )}^2}\right)}^2,\hfill \end{array}$$

(43)

where $\Omega =\frac{2\sqrt{2}\sqrt{-\frac{u_0}{-1+a^2}}x}{b_5}-\frac{2\sqrt{2}a{t}^{-s}\sqrt{-\frac{u_0}{-1+a^2}}(-1+\alpha )}{b_{5}B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}$.

4. Multiwave Solutions

For multiwave solutions, $\Phi$ in bilinear form can be assumed as [32]

$$\Phi =z_{0}cosh(b_2+b_1\xi )+z_{1}cos(b_4+b_3\xi )+z_{2}cosh(b_6+b_5\xi ),$$

(44)

where $z_i^{\prime }s$ and $b_i^{\prime }s$ all are real-valued parameters to be measured. Inserting $\Phi$ into Equation (11) and collecting all coefficients of $cosh(b_2+b_1\xi )$, $sinh(b_2+b_1\xi )$, $cos(b_4+b_3\xi )sinh(b_2+b_1\xi )$$sinh(b_6+b_5\xi )$, $cos(b_4+b_3\xi )$, $cosh(b_6+b_5\xi )$, $sin(b_4+b_3\xi )$, $cosh(b_2+b_1\xi )sinh(b_6+b_5\xi )$, $cosh(b_2+b_1\xi )cos(b_4+b_3\xi )cosh(b_6+b_5\xi ),$ and $sinh(b_2+b_1\xi )sin(b_4+b_3\xi )sinh(b_6+b_5\xi )$, we obtain proper results, as follows (See Figure 12 and Figure 13):

Case I.

$$\begin{array}{cc}& a=a,b=2\sqrt{2}\sqrt{\frac{1}{a^2-1}},\beta =-\frac{4u_0^2-a^2+a^4}{2(a^2-1)},b_1=\frac{i\sqrt{2}{u}_0}{2},b_2=b_2,b_3=\frac{\sqrt{2}{u}_0}{2},b_4=b_4,\\ \hfill & b_5=\frac{i\sqrt{2}{u}_0}{2},b_6=b_6,u_0=u_0,z_0=z_0,z_1=z_1,z_2=z_2.\end{array}$$

(45)

By using these values in Equation (44) and then by using Equations (8) and (10), we obtain

$$\begin{array}{cc}& u\left(\xi \right)=u_0-\frac{\sqrt{2}{u}_0\left(z_{1}sin(b_4+\frac{u_0\xi }{\sqrt{2}})-i{z}_{0}sinh(b_2+\frac{i{u}_0\xi }{\sqrt{2}})-i{z}_{2}sinh(b_6+\frac{i{u}_0\xi }{\sqrt{2}})\right)}{z_{1}cos(b_4+\frac{u_0\xi }{\sqrt{2}})+z_{0}cosh(b_2+\frac{i{u}_0\xi }{\sqrt{2}})+z_{2}cosh(b_6+\frac{i{u}_0\xi }{\sqrt{2}})},\\ \hfill & v\left(\xi \right)=\frac{2}{a^2-1}{\left(u_0-\frac{\sqrt{2}{u}_0\left(z_{1}sin(b_4+\frac{u_0\xi }{\sqrt{2}})-i{z}_{0}sinh(b_2+\frac{i{u}_0\xi }{\sqrt{2}})-i{z}_{2}sinh(b_6+\frac{i{u}_0\xi }{\sqrt{2}})\right)}{z_{1}cos(b_4+\frac{u_0\xi }{\sqrt{2}})+z_{0}cosh(b_2+\frac{i{u}_0\xi }{\sqrt{2}})+z_{2}cosh(b_6+\frac{i{u}_0\xi }{\sqrt{2}})}\right)}^2.\end{array}$$

(46)

Using Equation (5), we obtain the following multiwave solutions for Equation (1):

$$\begin{array}{cc}\hfill & m_{41}(x,t)=e^{i\left(ax+\frac{t^{-s}(4u_0^2-a^2+a^4)(-1+\alpha )}{2(a^2-1)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}\left(u_0-\frac{\sqrt{2}{u}_0\left(z_{1}sin(b_4+\Lambda )-i{z}_{0}sinh(b_2+i\Lambda )-i{z}_{2}sinh(b_6+i\Lambda )\right)}{z_{1}cos(b_4+\Lambda )+z_{0}cosh(b_2+i\Lambda )+z_{2}cosh(b_6+i\Lambda )}\right),\hfill \\ \\ \hfill & n_{42}(x,t)=\frac{2}{(a^2-1)}{\left(u_0-\frac{\sqrt{2}{u}_0\left(z_{1}sin(b_4+\Lambda )-i{z}_{0}sinh(b_2+i\Lambda )-i{z}_{2}sinh(b_6+i\Lambda )\right)}{z_{1}cos(b_4+\Lambda )+z_{0}cosh(b_2+i\Lambda )+z_{2}cosh(b_6+i\Lambda )}\right)}^2,\hfill \end{array}$$

(47)

where $\Lambda =2\sqrt{\frac{1}{a^2-1}}{u}_0\left(x+\frac{a{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

Case II.

$$\begin{array}{cc}& a=a,b=\frac{2\sqrt{-\frac{1}{a^2-1}}{u}_0}{b_5},\beta =-\frac{4u_0^2+a^4-a^2}{2(a-1)(a+1)},b_1=-b_5,b_2=b_2,b_3=i{b}_5,b_4=b_4,b_5=b_5,\\ \hfill & b_6=b_6,u_0=u_0,z_0=z_0,z_1=z_1,z_2=z_2.\end{array}$$

(48)

By using these values in Equation (44) and then by using Equations (8) and (10), we obtain

$$\begin{array}{cc}& u\left(\xi \right)=u_0+\frac{2b_5\left(-i{z}_{1}sin(b_4+i{b}_5\xi )-z_{0}sinh(b_2-b_5\xi )+z_{2}sinh(b_6+b_5\xi )\right)}{z_{1}cos(b_4+i{b}_5\xi )+z_{0}cosh(b_2-b_5\xi )+z_{2}cosh(b_6+b_5\xi )},\\ \hfill & v\left(\xi \right)=\frac{2}{-1+a^2}{\left(u_0+\frac{2b_5\left(-i{z}_{1}sin(b_4+i{b}_5\xi )-z_{0}sinh(b_2-b_5\xi )+z_{2}sinh(b_6+b_5\xi )\right)}{z_{1}cos(b_4+i{b}_5\xi )+z_{0}cosh(b_2-b_5\xi )+z_{2}cosh(b_6+b_5\xi )}\right)}^2.\end{array}$$

(49)

Using Equation (5), we obtain the following multiwave solutions for Equation (1):

$$\begin{array}{cc}\hfill & m_{43}(x,t)=e^{i\left(ax+\frac{t^{-s}(4u_0^2-a^2+a^4)(-1+\alpha )}{2(a^2-1)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}\left(u_0+\frac{2b_5\left(-i{z}_{1}sin(b_4+i\Lambda )-z_{0}sinh(b_2-\Lambda )+z_{2}sinh(b_6+\Lambda )\right)}{z_{1}cos(b_4+i\Lambda )+z_{0}cosh(b_2-\Lambda )+z_{2}cosh(b_6+\Lambda )}\right),\hfill \\ \\ \hfill & n_{44}(x,t)=\frac{2}{(a^2-1)}{\left(u_0+\frac{2b_5\left(-i{z}_{1}sin(b_4+i\Lambda )-z_{0}sinh(b_2-\Lambda )+z_{2}sinh(b_6+\Lambda )\right)}{z_{1}cos(b_4+i\Lambda )+z_{0}cosh(b_2-\Lambda )+z_{2}cosh(b_6+\Lambda )}\right)}^2,\hfill \end{array}$$

(50)

where $\Lambda =2\sqrt{\frac{1}{1-a^2}}{u}_0\left(x+\frac{a{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

5. Homoclinic Breather Approach

To obtain breather solutions, $\Phi$ in bilinear form can be assumed as [32]

$$\Phi =e^{-p\left(b_1\xi +b_2\right)}+z_1{e}^{p\left(b_3\xi +b_4\right)}+z_{2}cos\left(q\left(b_5\xi +b_6\right)\right),$$

(51)

where p, q, $z_1$, $z_2$, and $b_i^{\prime }s$ all are real-valued parameters to be found. Inserting $\Phi$ into Equation (11) and collecting all coefficients of $e^{p(b_4+b_3\xi )},$$sin\left(q(b_6+b_5\xi )\right),$$cos\left(q(b_6+b_5\xi )\right),$$e^{p(b_4+b_3\xi )}sin\left(q(b_6+b_5\xi )\right),$$e^{-p(b_2+b_1\xi )+p(b_4+b_3\xi )}cos\left(q(b_6+b_5\xi )\right),$ and $cos\left(q(b_6+b_5\xi )\right)$$sin\left(q(b_6+b_5\xi )\right)$, we obtain an algebraic system of equations, then, after solving them, we obtain proper results, as follows (See Figure 14 and Figure 15):

Case I.

$$\begin{array}{cc}& a=a,b=2\sqrt{2}\sqrt{\frac{1}{a^2-1}},\beta =-\frac{a^4-16b_5^2{q}^2-a^2}{2(a^2-1)},b_1=\frac{iq{b}_5}{p},b_2=b_2,b_3=\frac{iq{b}_5}{p},b_4=b_4,b_5=b_5,\\ \hfill & b_6=b_6,u_0=0,p=p,q=q,z_1=z_1,z_2=z_2.\end{array}$$

(52)

By using these parameters in Equation (51) and then by using Equations (8) and (10), we obtain

$$\begin{array}{cc}& u\left(\xi \right)=\frac{2i{b}_{5}q\left(-1+e^{b_{2}p+b_{4}p+2i{b}_{5}q\xi }{z}_1+i{e}^{b_{2}p+i{b}_{5}q\xi }{z}_{2}sin\left(q(b_6+b_5\xi )\right)\right)}{1+e^{b_{2}p+b_{4}p+2i{b}_{5}q\xi }{z}_1+e^{b_{2}p+i{b}_{5}q\xi }{z}_{2}cos\left(q(b_6+b_5\xi )\right)},\\ \hfill & v\left(\xi \right)=-\frac{8b_5^2{q}^2}{a^2-1}{\left(\frac{-1+e^{b_{2}p+b_{4}p+2i{b}_{5}q\xi }{z}_1+i{e}^{b_{2}p+i{b}_{5}q\xi }{z}_{2}sin\left(q(b_6+b_5\xi )\right)}{1+e^{b_{2}p+b_{4}p+2i{b}_{5}q\xi }{z}_1+e^{b_{2}p+i{b}_{5}q\xi }{z}_{2}cos\left(q(b_6+b_5\xi )\right)}\right)}^2.\end{array}$$

(53)

Using Equation (5), we obtain the following breather solutions for Equation (1):

$$\begin{array}{cc}\hfill & m_{51}(x,t)=\frac{2i{b}_5{e}^{\Delta }q\left(-1+e^{b_{2}p+b_{4}p+4i\Omega }{z}_1+i{e}^{b_{2}p+2i\Omega }{z}_{2}sin(q(b_6+\frac{2}{q}\Omega ))\right)}{1+e^{b_{2}p+b_{4}p+4i\Omega }{z}_1+e^{b_{2}p+2i\Omega }{z}_{2}cos(q(b_6+\frac{2}{q}\Omega ))},\hfill \\ \\ \hfill & n_{52}(x,t)=-\frac{8b_5^2{q}^2}{(-1+a^2)}{\left(\frac{-1+e^{b_{2}p+b_{4}p+4i\Omega }{z}_1+i{e}^{b_{2}p+2i\Omega }{z}_{2}sin(q(b_6+\frac{2}{q}\Omega ))}{1+e^{b_{2}p+b_{4}p+4i\Omega }{z}_1+e^{b_{2}p+2i\Omega }{z}_{2}cos(q(b_6+\frac{2}{q}\Omega ))}\right)}^2,\hfill \end{array}$$

(54)

where $\Delta =\frac{1}{2}i\left(2ax+\frac{(-16b_5^2{q}^2-a^2+a^4)t^{-s}(\alpha -1)}{(-1+a)(1+a)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right),$

$\Omega =\sqrt{2}\sqrt{\frac{1}{-1+a^2}}{b}_{5}q\left(x+\frac{a{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

Case II.

$$\begin{array}{cc}& a=a,b=2\sqrt{2}\sqrt{\frac{1}{a^2-1}},\beta =-\frac{a^4+4u_0^2-a^2}{2(a^2-1)},b_1=\frac{u_0}{p},b_2=b_2,b_3=-\frac{u_0}{p},b_4=b_4,b_5=0,\\ \hfill & b_6=b_6,u_0=u_0,p=p,q=q,z_1=z_1,z_2=z_2.\end{array}$$

(55)

By using these parameters in Equation (51), and then by using Equations (8) and (10) in Equation (5), we obtain the following solutions for Equation (1):

$$\begin{array}{cc}\hfill & m_{53}(x,t)=-\frac{e^{\frac{1}{2}i\left(2ax+\frac{t^{-s}(4u_0^2-a^2+a^4)(\alpha -1)}{(-1+a)(1+a)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}{u}_0\left(1+e^{b_{2}p+b_{4}p}{z}_1-e^{p(\Omega )}{z}_{2}cos\left(b_{6}q\right)\right)}{1+e^{b_{2}p+b_{4}p}{z}_1+e^{p(\Omega )}{z}_{2}cos\left(b_{6}q\right)},\hfill \\ \\ \hfill & n_{54}(x,t)=\frac{2u_0^2}{(-1+a^2)}{\left(\frac{1+e^{b_{2}p+b_{4}p}{z}_1-e^{p(\Omega )}{z}_{2}cos\left(b_{6}q\right)}{1+e^{b_{2}p+b_{4}p}{z}_1+e^{p(\Omega )}{z}_{2}cos\left(b_{6}q\right)}\right)}^2,\hfill \end{array}$$

(56)

where $\Omega =b_2+\frac{2\sqrt{2}\sqrt{\frac{1}{-1+a^2}}{u}_0\left(x+\frac{a{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}{p}$.

6. The Periodic Cross-Kink Wave Solutions

For this, $\Phi$ in bilinear form can be assumed as [33]

$$\Phi =e^{-(b_1\xi +b_2)}+z_1{e}^{b_1\xi +b_2}+z_{2}cos(b_3\xi +b_4)+z_{3}cosh(b_5\xi +b_6)+b_7,$$

(57)

where $z_i^{\prime }s$ and $b_i^{\prime }s$ all are real-valued parameters to be measured. Inserting $\Phi$ into Equation (11) and collecting all coefficients of $e^{b_1\xi +b_2},$$e^{-b_1\xi -b_2},$$e^{b_2+b_1\xi +2(b_2+b_1\xi )}$, $e^{-(b_1\xi +b_2)+2(b_1\xi +b_2)},$$cos(b_4+b_3\xi ),$$cos(b_4+b_3\xi )cosh(b_6+b_5\xi ),$$e^{-(b_1\xi +b_2)+2(b_1\xi +b_2)}cos(b_4+b_3\xi ),$$e^{-(b_1\xi +b_2)+2(b_1\xi +b_2)}$$sin(b_4+b_3\xi ),$$cos(b_4+b_3\xi )cosh(b_6+b_5\xi )sinh(b_6+b_5\xi )$, $e^{-(b_1\xi +b_2)+2(b_1\xi +b_2)}cos(b_4+b_3\xi )cosh(b_6+b_5\xi ),$ and $e^{-(b_1\xi +b_2)+2b_1\xi +2b_2)}sin(b_4+b_3\xi )$$sinh(b_6+b_5\xi )$, after solving them, we attain the following parameters (See Figure 16 and Figure 17):

Case I. For $b_4=0,$

$$\begin{array}{cc}& a=a,b=8\sqrt{2}\sqrt{\frac{1}{a^2-1}},\beta =-\frac{64b_1^2-a^2+a^4}{2(a^2-1)},b_1=b_1,b_2=b_2,b_3=b_3,b_5=0,b_6=b_6,\\ \hfill & b_7=0,u_0=-2b_1,z_1=z_1,z_2=0,z_3=z_3.\end{array}$$

(58)

By using these values in Equation (57), and then by using Equations (8) and (10), we obtain

$$\begin{array}{cc}& u\left(\xi \right)=-2b_1+\frac{2\left(-b_1{e}^{-b_2-b_1\xi }+b_1{e}^{b_2+b_1\xi }{z}_1\right)}{e^{-b_2-b_1\xi }+e^{b_2+b_1\xi }{z}_1+z_{3}cosh\left(b_6\right)},\\ \hfill & v\left(\xi \right)=\frac{2}{a^2-1}{\left(-2b_1+\frac{2\left(-b_1{e}^{-b_2-b_1\xi }+b_1{e}^{b_2+b_1\xi }{z}_1\right)}{e^{-b_2-b_1\xi }+e^{b_2+b_1\xi }{z}_1+z_{3}cosh\left(b_6\right)}\right)}^2.\end{array}$$

(59)

Now, using Equation (5), we obtain the following solutions for Equation (1):

$$\begin{array}{cc}\hfill & m_{61}(x,t)=-\frac{2b_1{e}^{\frac{i}{2}\left(2ax+\frac{(64b_1^2-a^2+a^4)t^{-s}(\alpha -1)}{(a^2-1)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)}\left(2+e^{\Omega }{z}_{3}cosh\left(b_6\right)\right)}{1+e^{2\Omega }{z}_1+e^{\Omega }{z}_{3}cosh\left(b_6\right)},\hfill \\ \\ \hfill & n_{62}(x,t)=\frac{8b_1^2}{(a^2-1)}{\left(\frac{2+e^{\Omega }{z}_{3}cosh\left(b_6\right)}{1+e^{2\Omega }{z}_1+e^{\Omega }{z}_{3}cosh\left(b_6\right)}\right)}^2,\hfill \end{array}$$

(60)

where $\Omega =b_2+8\sqrt{2}\sqrt{\frac{1}{a^2-1}}{b}_1\left(x+\frac{a{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

Case II.

$$\begin{array}{cc}& a=a,b=2\sqrt{2}\sqrt{\frac{1}{a^2-1}},\beta =-\frac{a^4-a^2-16b_3^2}{2(a^2-1)},b_1=i{b}_3,b_2=b_2,b_3=b_3,b_5=-i{b}_3,b_6=b_6,\\ \hfill & b_7=0,z_1=z_1,z_2=z_2,z_3=z_3.\end{array}$$

(61)

Now, by using these values in Equation (57), and then by using Equations (8) and (10) in Equation (5), we obtain the following solutions for Equation (1):

$$\begin{array}{cc}\hfill & m_{63}(x,t)=\frac{2i{b}_3{e}^{\Lambda }\left(-2+2e^{2b_2+\Omega }{z}_1-e^{b_2}{z}_2+e^{b_2+\Omega }{z}_2+e^{b_2}(-1+e^{\Omega })z_{3}cosh\left(b_6\right)-e^{b_2}(1+e^{\Omega })z_{3}sinh\left(b_6\right)\right)}{2+2e^{2b_2+\Omega }{z}_1+e^{b_2}{z}_2+e^{b_2+\Omega }{z}_2+e^{b_2}(1+e^{\Omega })z_{3}cosh\left(b_6\right)-e^{b_2}(-1+e^{\Omega })z_{3}sinh\left(b_6\right)},\hfill \\ \\ \hfill & n_{64}(x,t)=-\frac{8b_3^2}{(a^2-1)}{\left(\frac{2-2e^{2b_2+\Omega }{z}_1+e^{b_2}{z}_2-e^{b_2+\Omega }{z}_2-e^{b_2}(-1+e^{\Omega })z_{3}cosh\left(b_6\right)+e^{b_2}(1+e^{\Omega })z_{3}sinh\left(b_6\right)}{2+2e^{2b_2+\Omega }{z}_1+e^{b_2}{z}_2+e^{b_2+\Omega }{z}_2+e^{b_2}(1+e^{\Omega })z_{3}cosh\left(b_6\right)-e^{b_2}(-1+e^{\Omega })z_{3}sinh\left(b_6\right)}\right)}^2,\hfill \end{array}$$

(62)

where $\Lambda =\frac{1}{2}i\left(2ax+\frac{(-16b_3^2-a^2+a^4)t^{-s}(\alpha -1)}{(a^2-1)B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right),$ and $\Omega =4i\sqrt{2}\sqrt{\frac{1}{-1+a^2}}{b}_3\left(x+\frac{a{t}^{-s}(-1+\alpha )}{B\left(\alpha \right){\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s\Gamma (1-\alpha s)}\right)$.

7. Results and Discussion

The study of new imposed solutions for the ion sound and Langmuir waves (ISLWs) has huge importance among scientists. Much of the work has been carried out on ISLWs, for example, Mohammed et al. constructed new traveling wave solutions for ISLWs by using He’s semi-inverse and extended Jacobian elliptic function method [34]. Shakeel et al. studied new wave behaviors for ISLWs with the aid of modified exp-function approach [35]. Seadawy et al. used direct algebraic and auxiliary equation mapping to obtain the families of new exact traveling wave solutions for ISLWs [36]. Tripathy and Sahoo studied a variety of analytical solutions for ISLWs [37]. Seadawy et al. studied a variety of exact solutions with modified Kudraysov and hyperbolic-function scheme for ISLWs [38].

Here, we obtained a variety of analytical solutions with rational and trigonometric forms for ISLWs, in which some of them are represented graphically in 3D, contour, and 2D shapes. In Figure 1 and Figure 2, we present M-shaped solutions for $m_{23}$ and $m_{25}$ with contour and 2D plots, respectively. In Figure 3, Figure 4, Figure 5 and Figure 6, we see the interactional phenomena with M-shaped and one-kink for $m_{31}$, $n_{32}$, $m_{35}$, and $n_{36}$ at different values of the parameters. In these figures, we see M-shaped waves with multiple bright and dark solutions. In Figure 4, waves strongly increased their amplitude according to time. In Figure 7, Figure 8 and Figure 9, we see the interactional phenomena with M-shaped and two-kink for $n_{38}$, $m_{39}$, and $n_{40}$. In Figure 7, multiple bright, dark, and M-size solitons appear. In Figure 8 and Figure 9, large-sized dark and bright waves appear. Figure 10 and Figure 11 represent the evolution of M-shaped and periodic waves for $m_3$ and $n_4$. Figure 12 and Figure 13 represent the evolution of multiwaves solution for $m_{43}$ and $n_{44}$ at different values. In Figure 14 and Figure 15, two solutions, $m_{51}$ and $n_{54}$, of homoclinic breather are presented graphically, and we also see the changes in graphs by varying the value of a. In Figure 16 and Figure 17, we present periodic cross-kink solutions $m_{63}$ and $n_{44}$ graphically, and we also see the change in waves into bright and dark solutions by varying the value of a. As $\alpha \in (0,1]$, in all these solutions, we can see that when $\alpha =1$, ${\sum }_{s=0}^{\infty }{(-\frac{\alpha }{1-\alpha })}^s$ does not converge.

8. Conclusions

In this work, we successfully derived some new analytic solutions for FISLWS with Atangana–Baleanu derivative. These exact solutions are derived in the form of bilinear, trigonometric, and exponential functions. As a result, new traveling wave solutions are gained in the form of rational, periodic, multiwaves, multi-kink, solitary waves, bright and dark solitons that are shown graphically in 3D, 2D, and contour structures. These solutions play an important role in different areas of physics, engineering, and other branches of sciences.