Dynamical Analysis of Discrete-Time Two-Predators One-Prey Lotka–Volterra Model
Abstract
1. Introduction
2. Linearization and Stability
3. Main Results
4. Global Stability
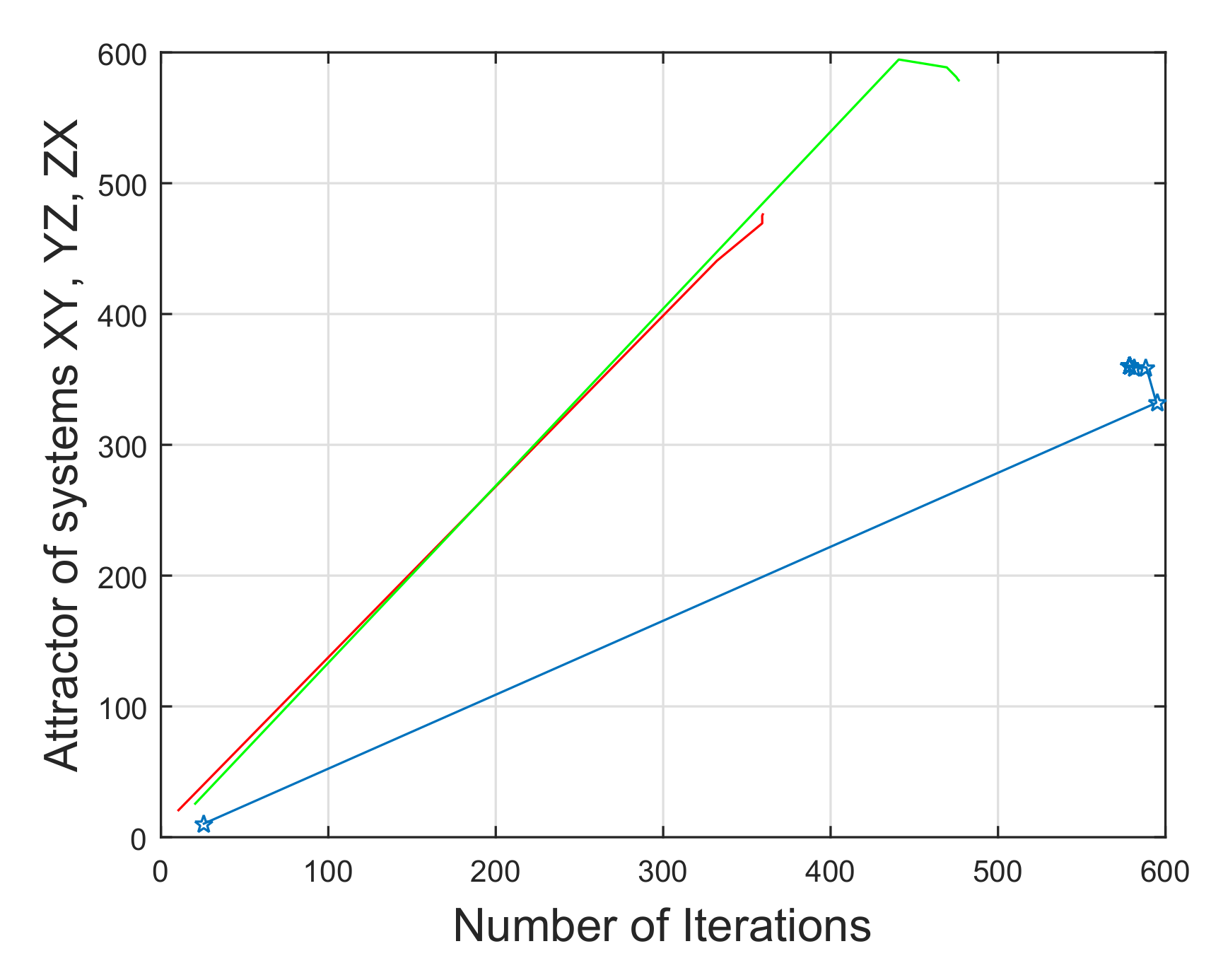
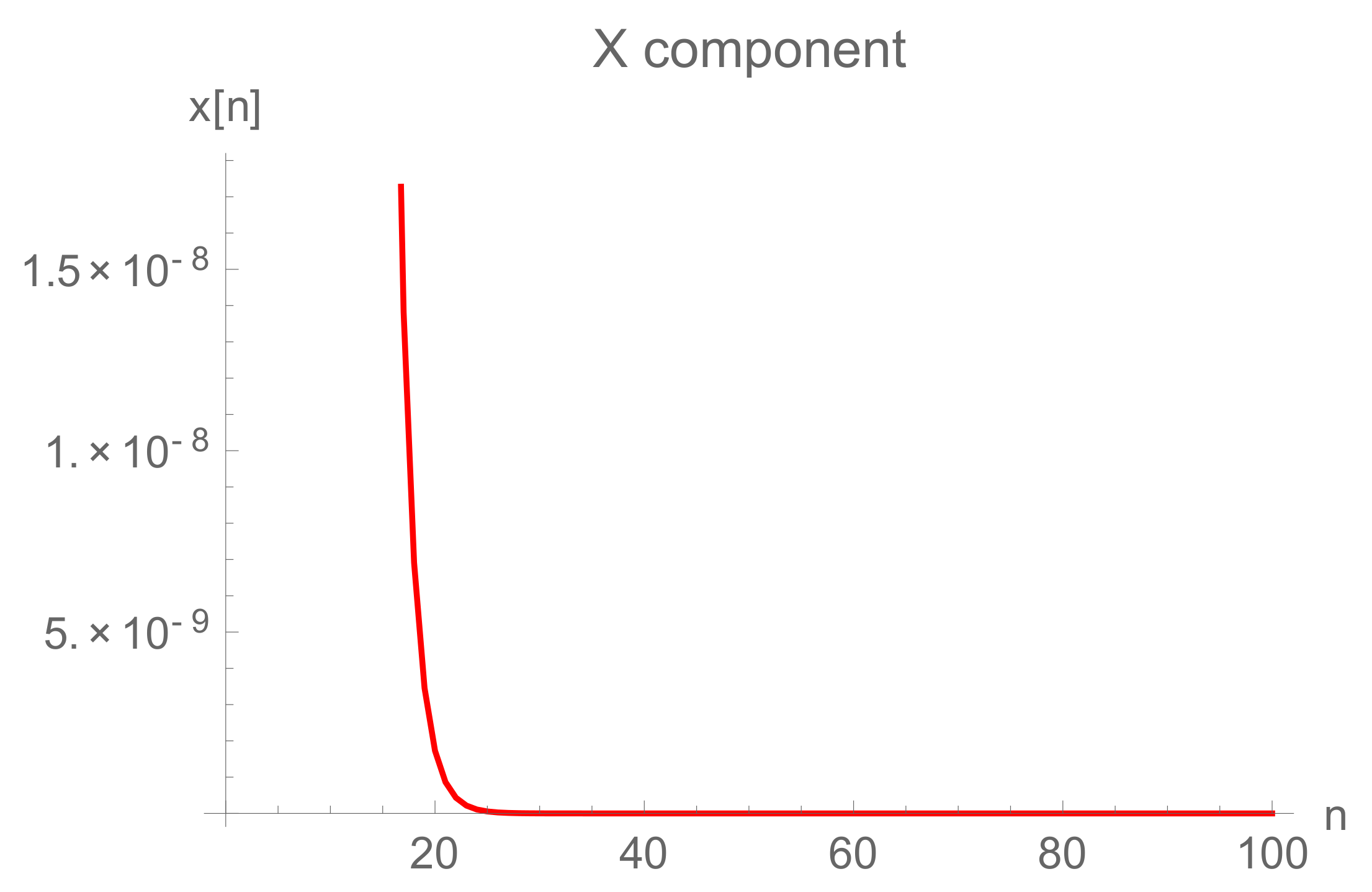
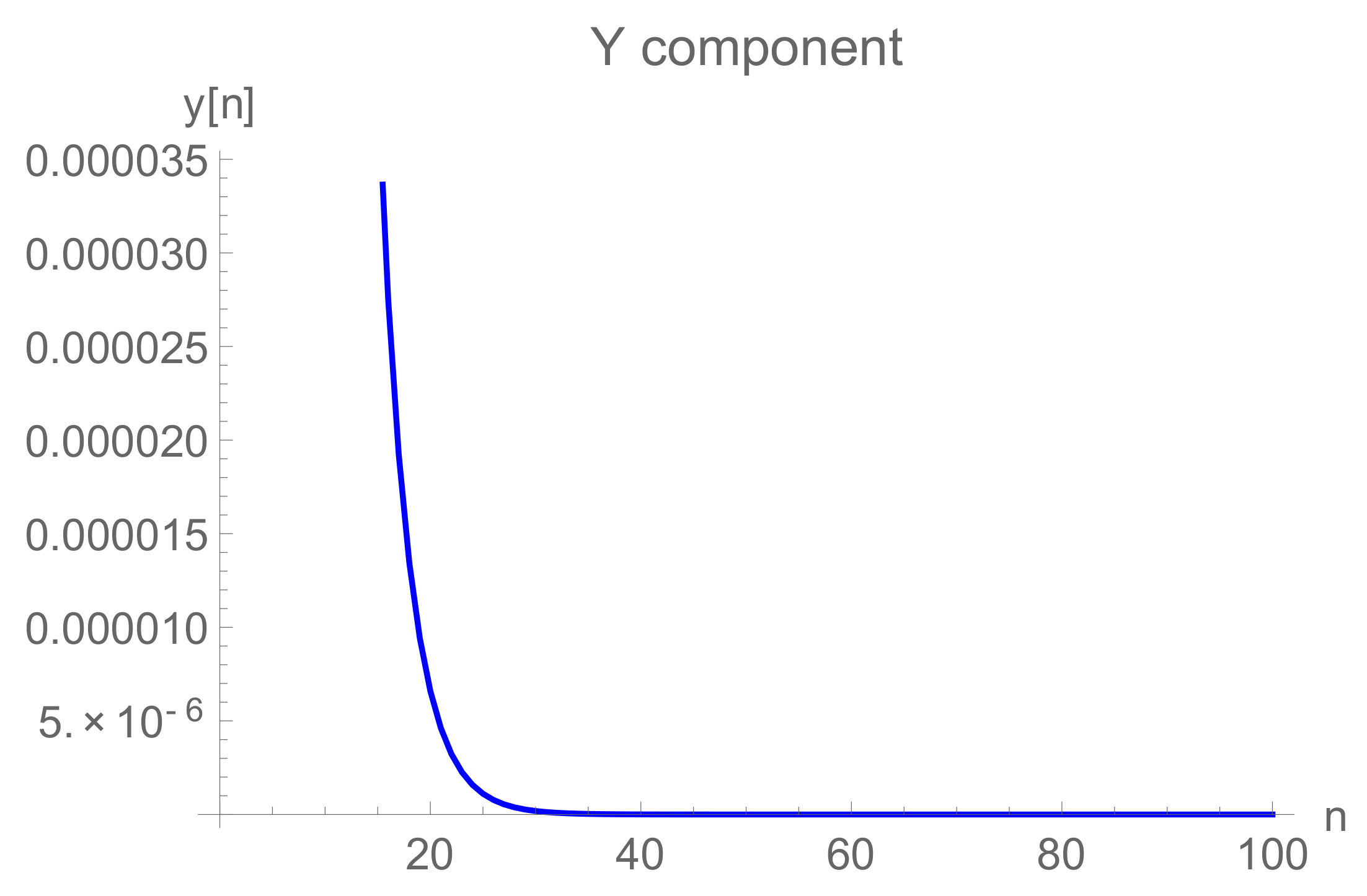
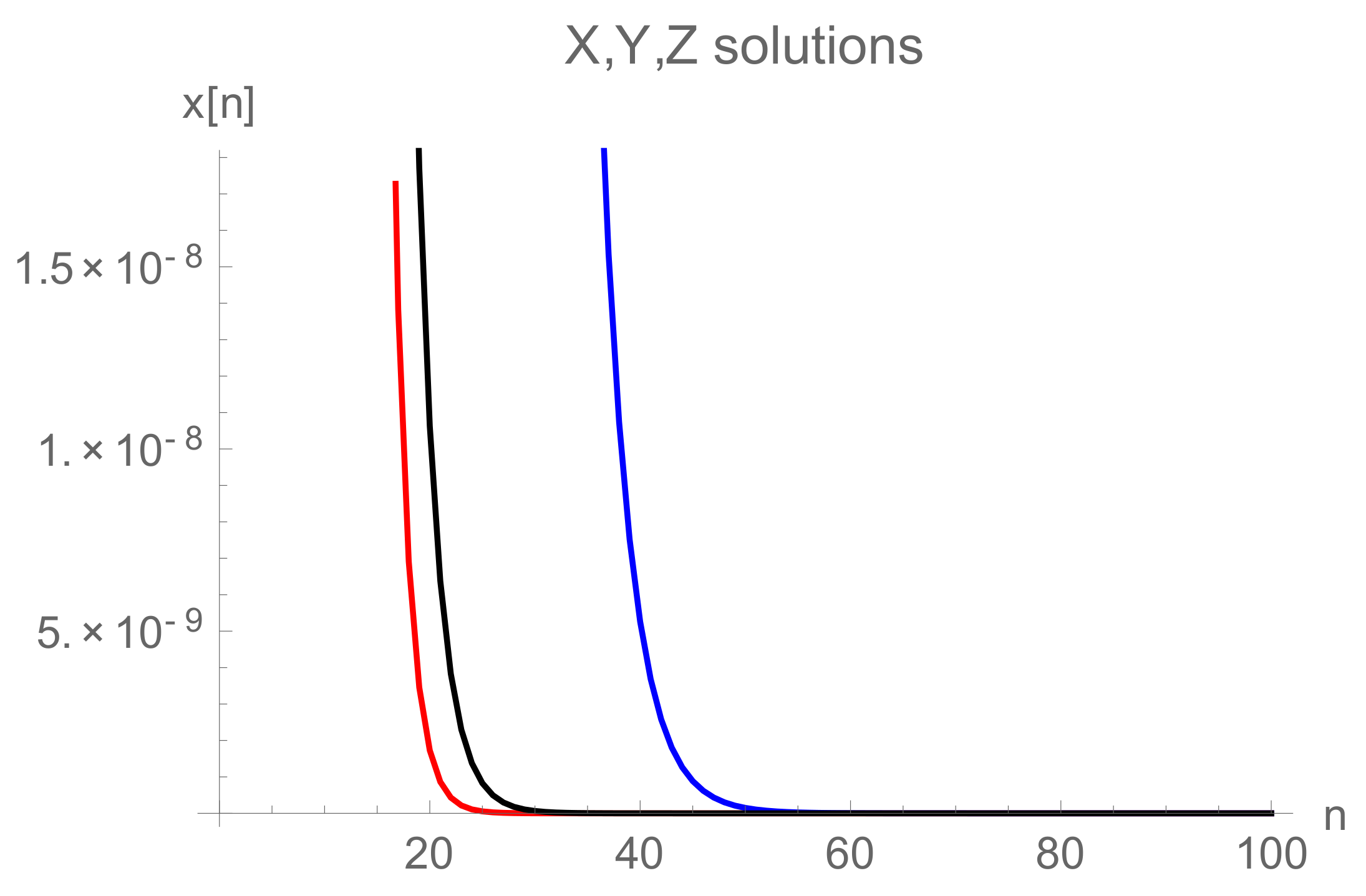
5. Rate of Convergence
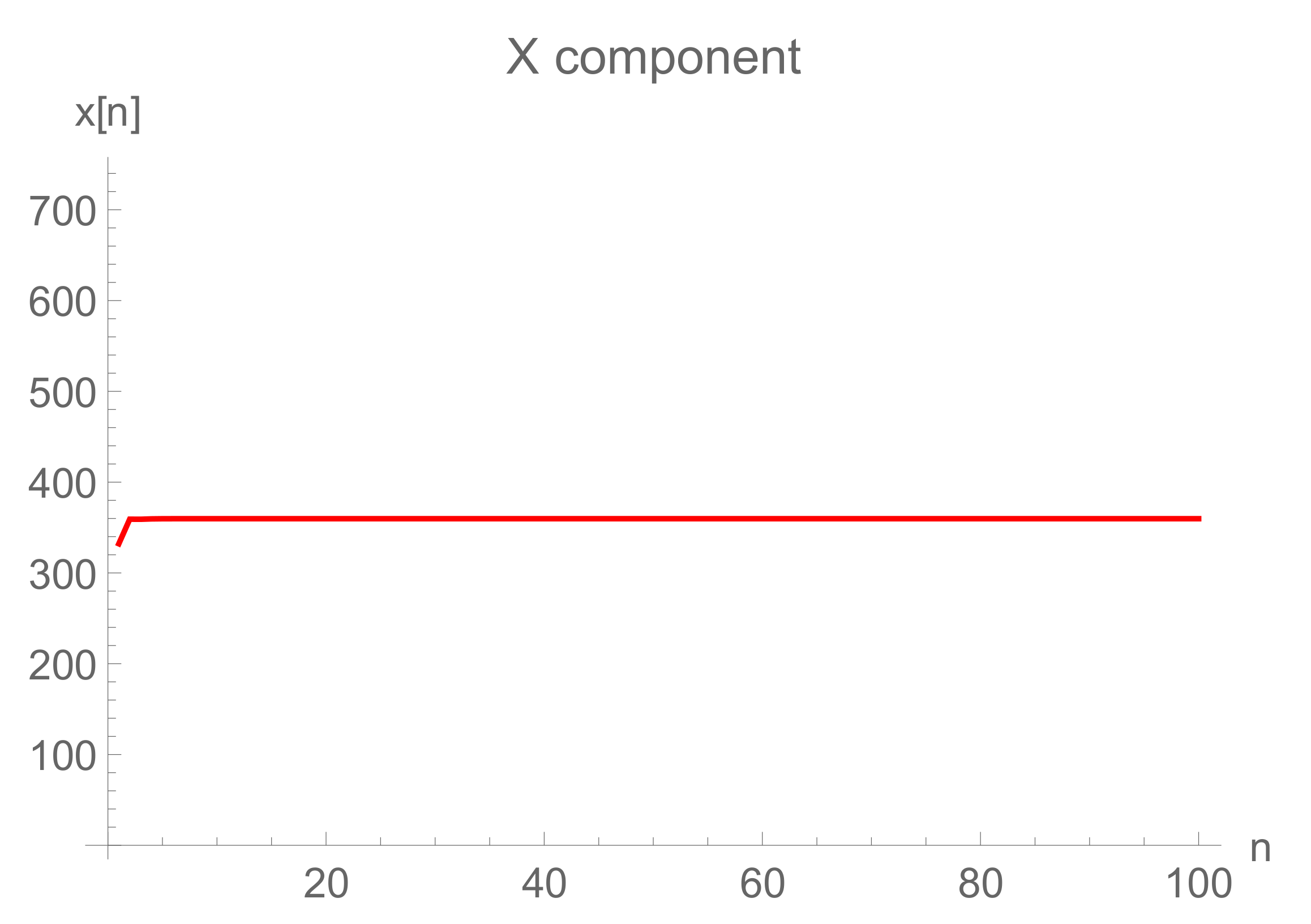
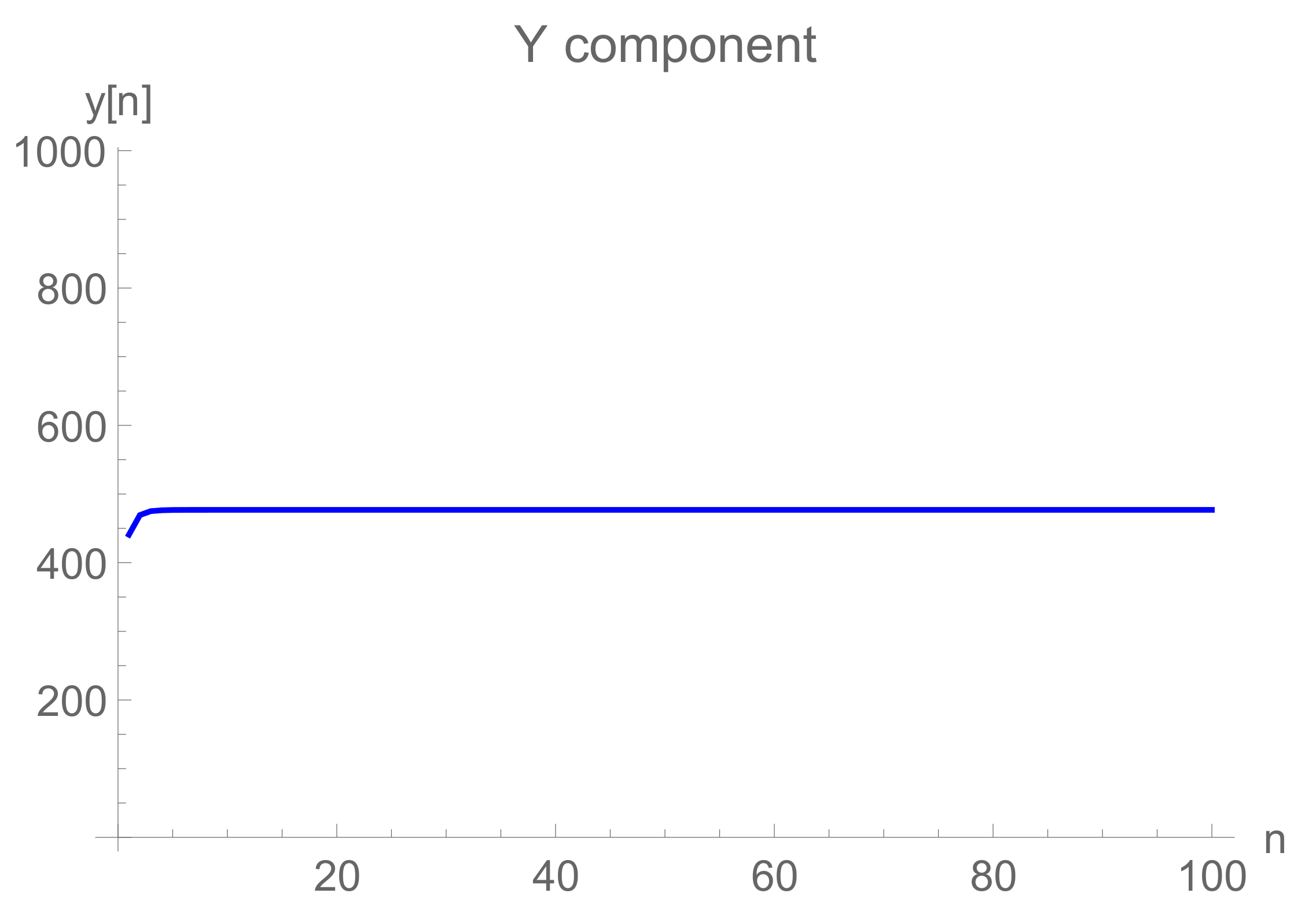
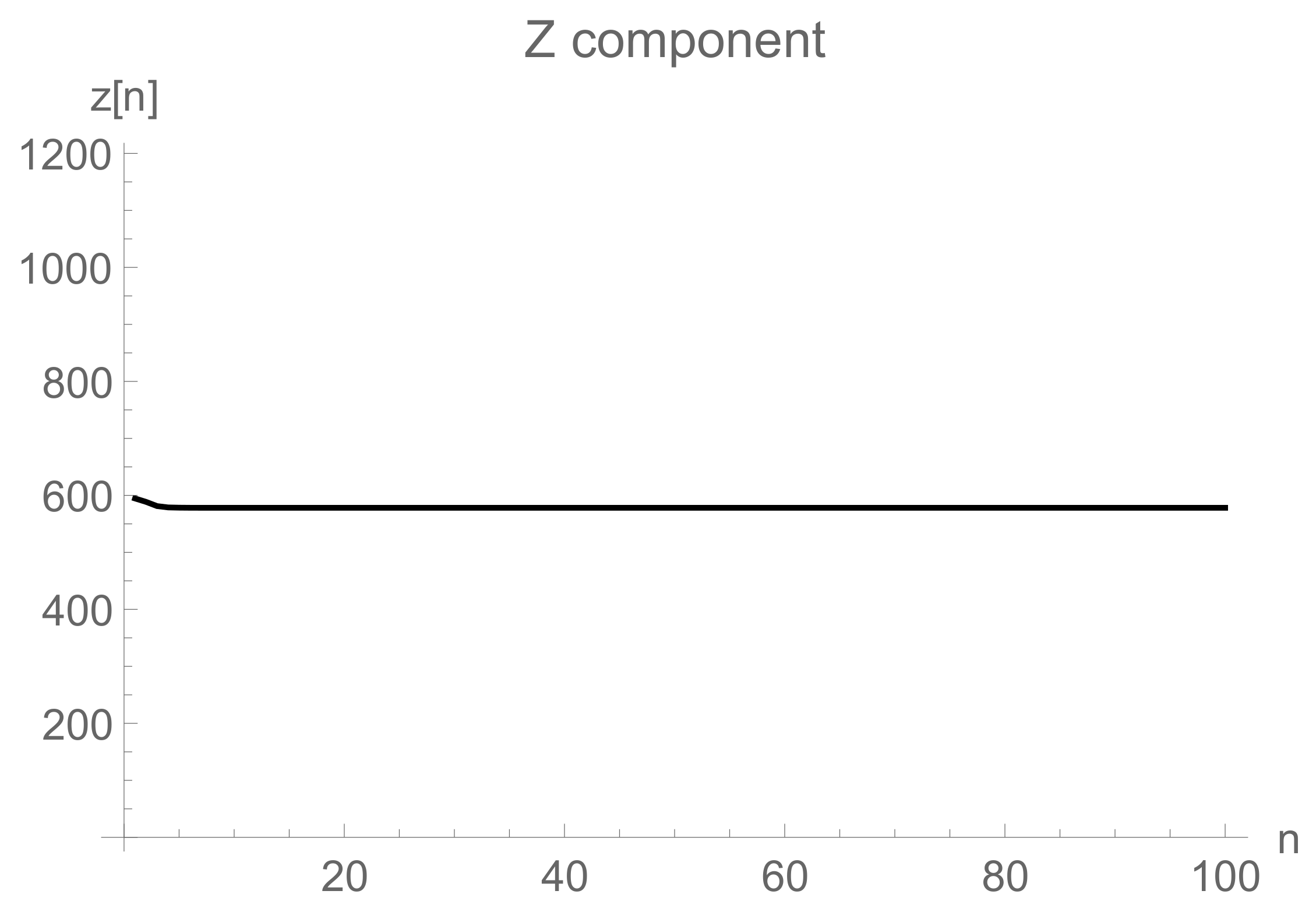
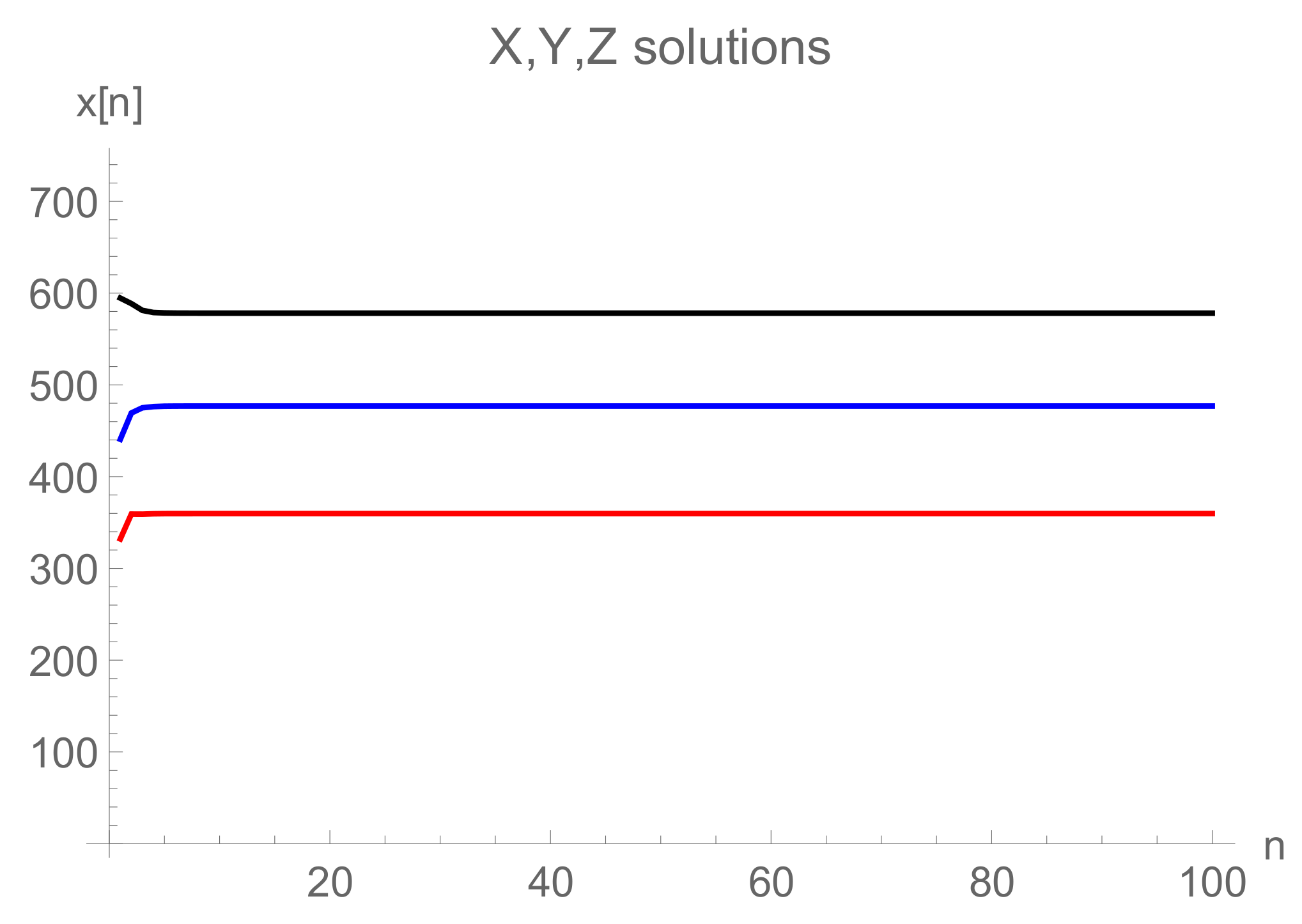
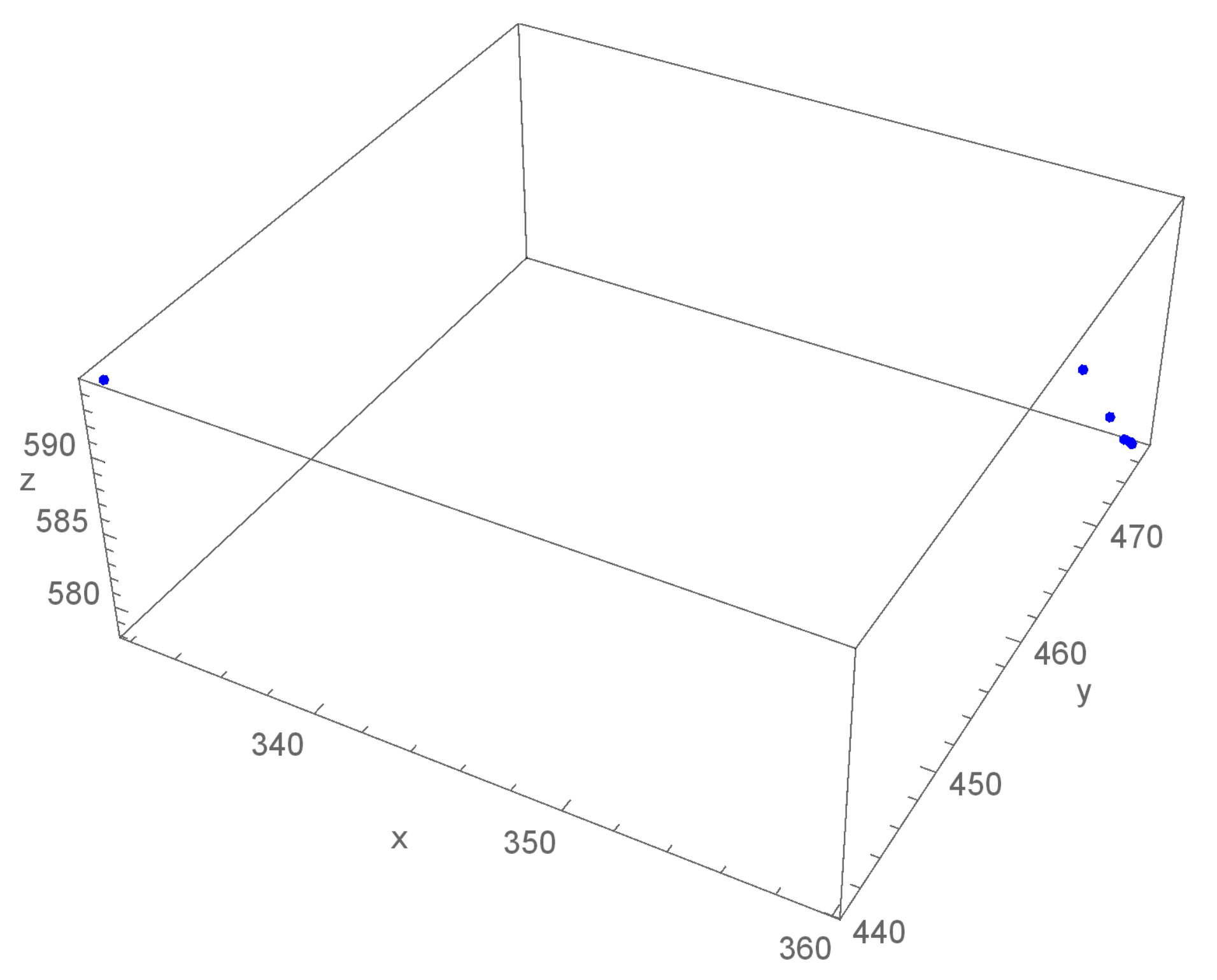
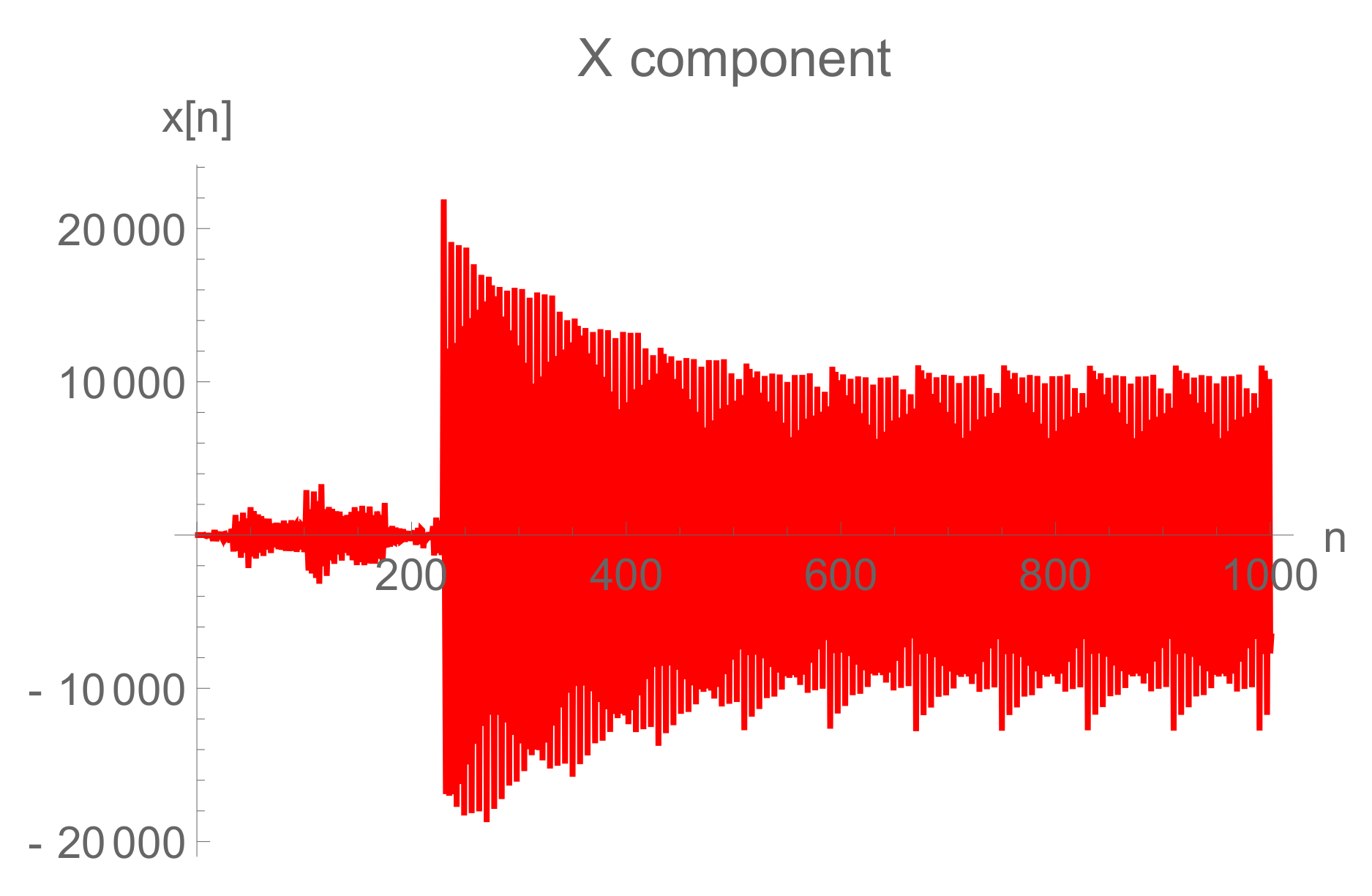
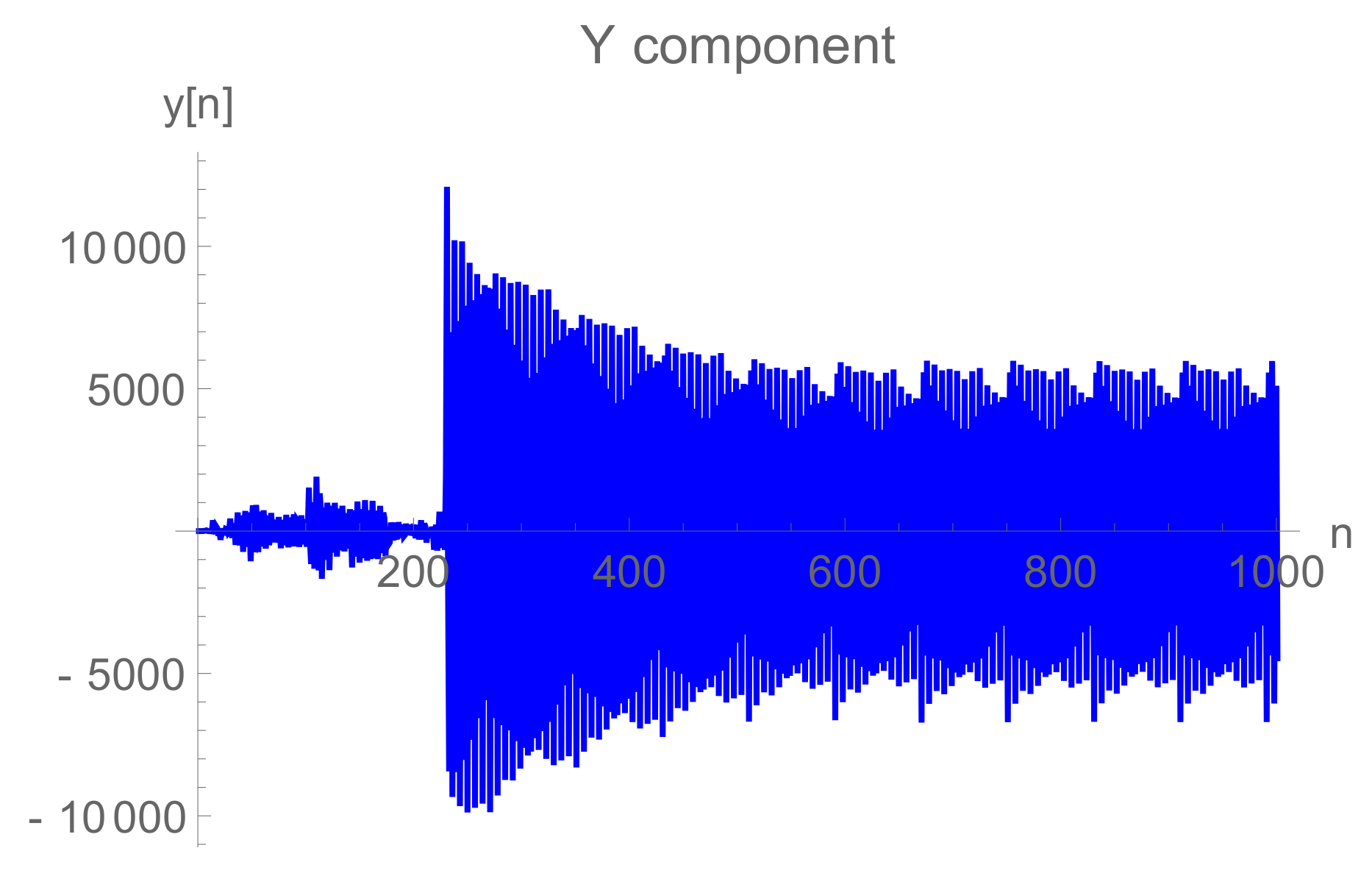
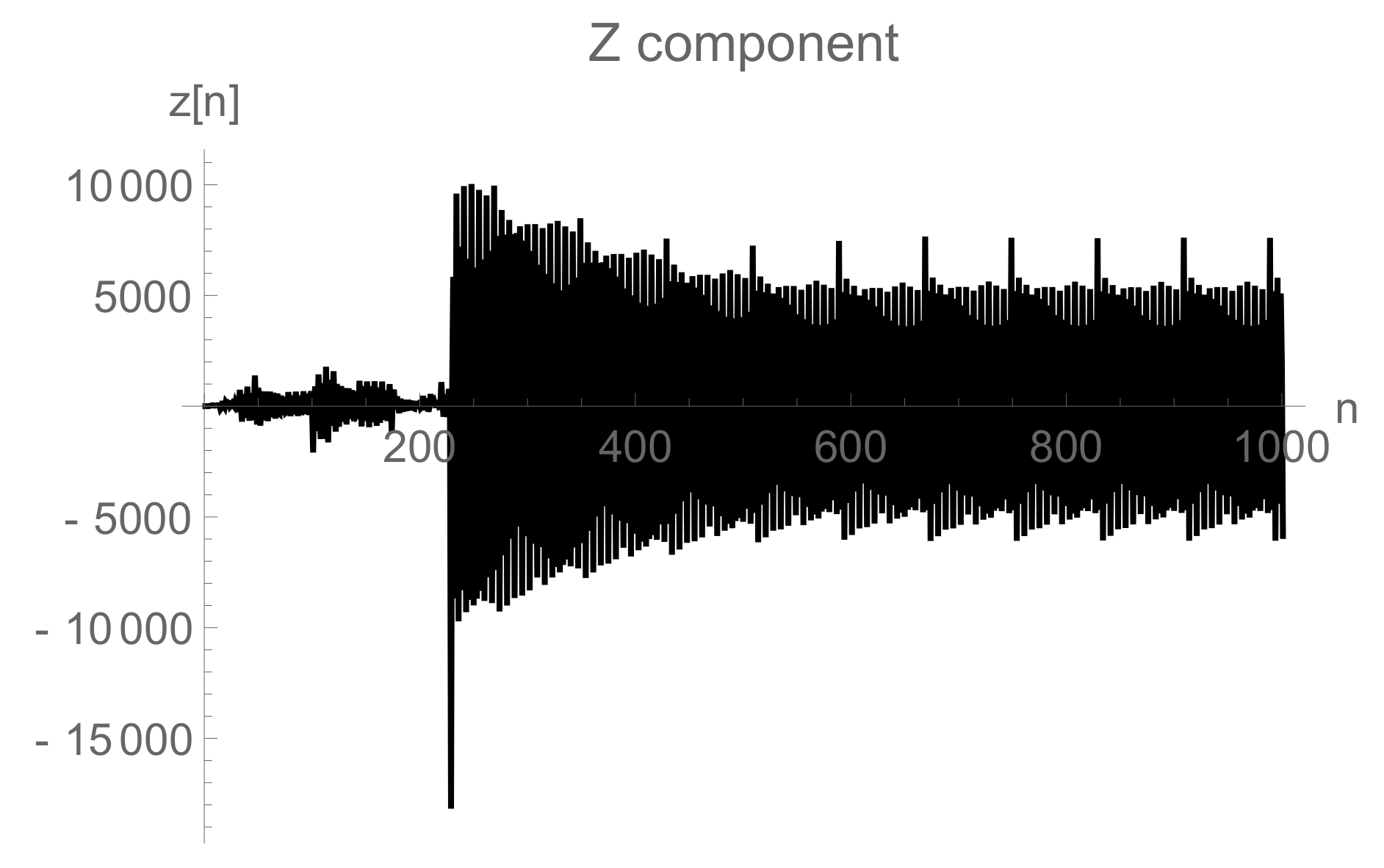
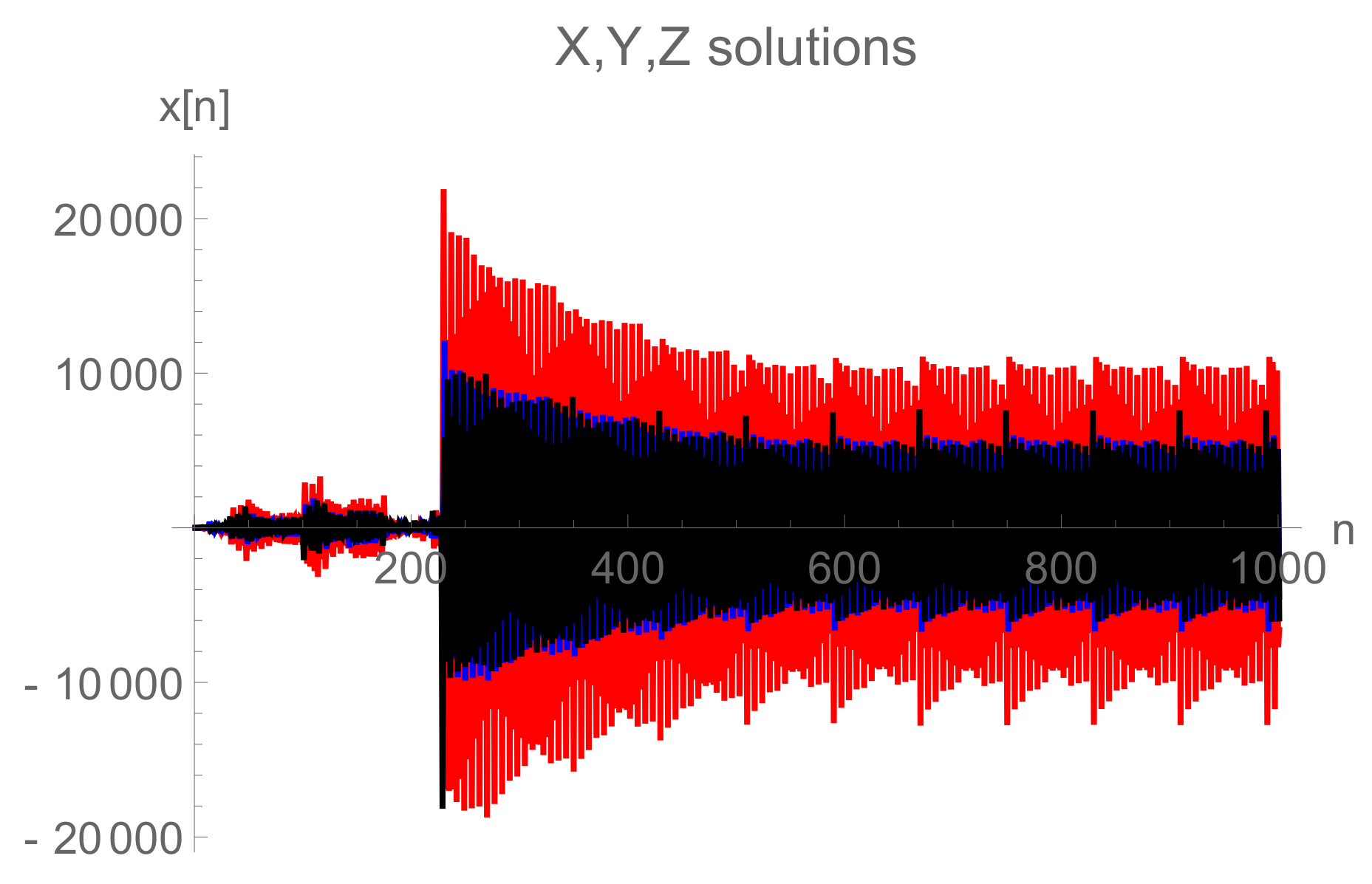
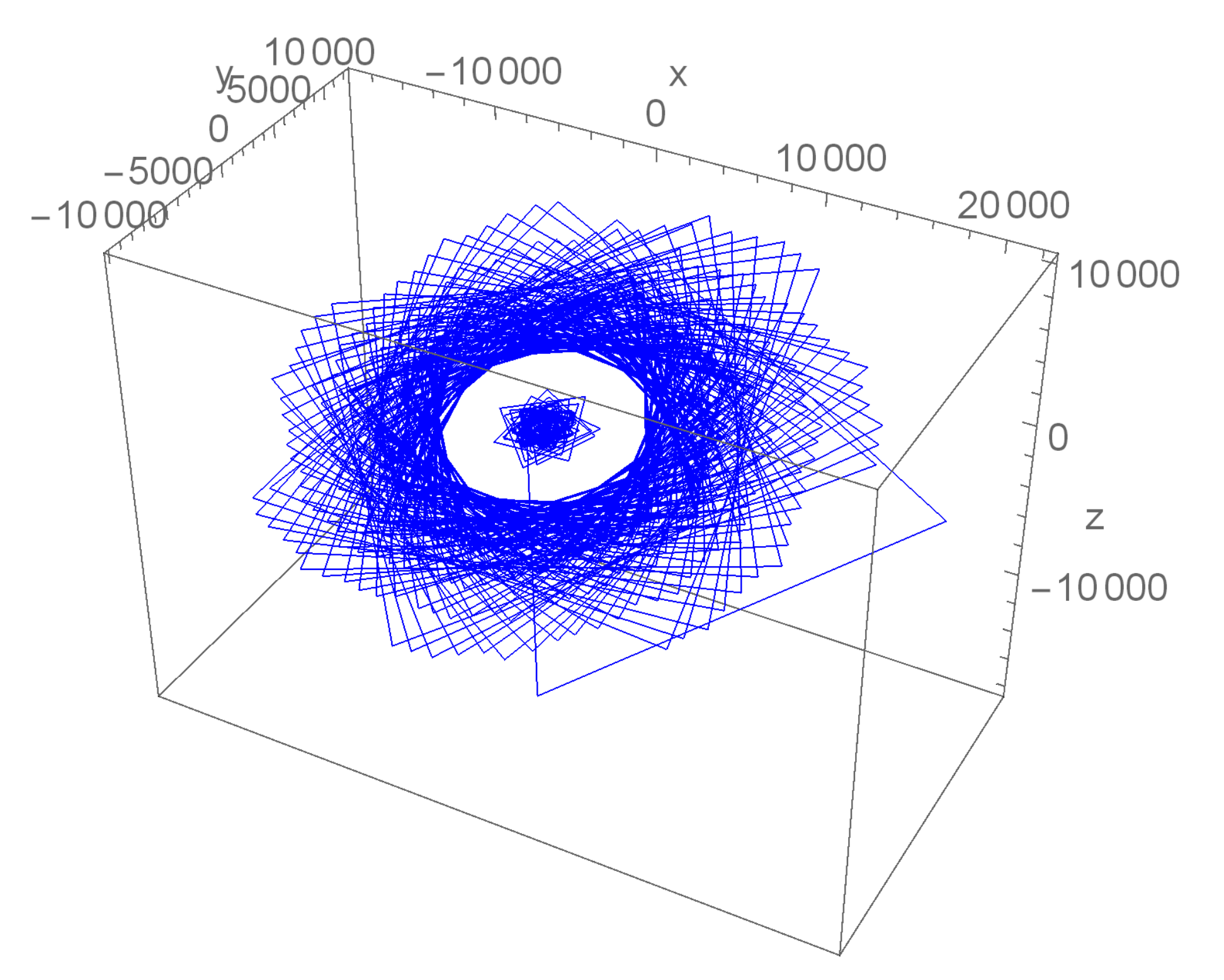
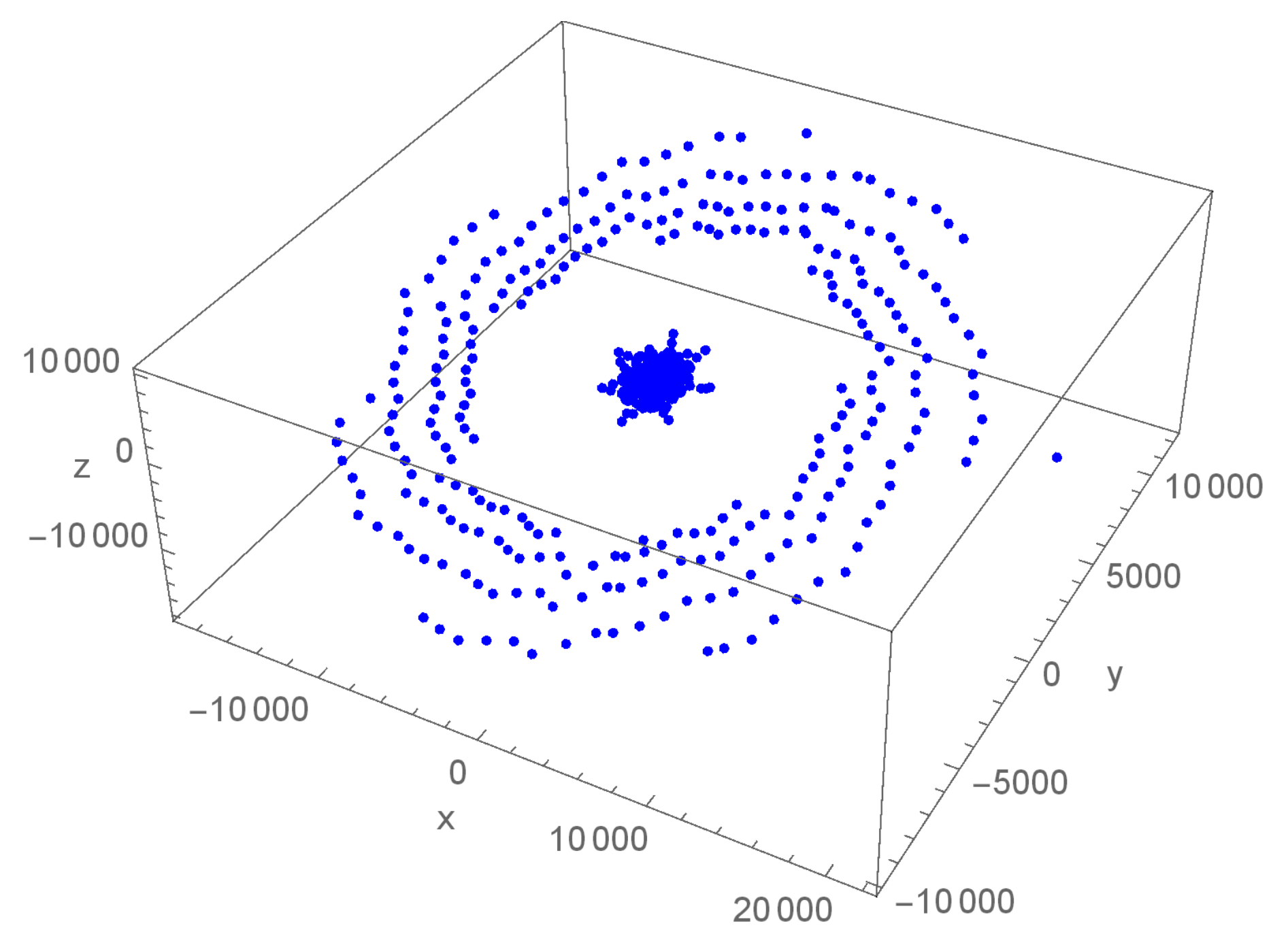
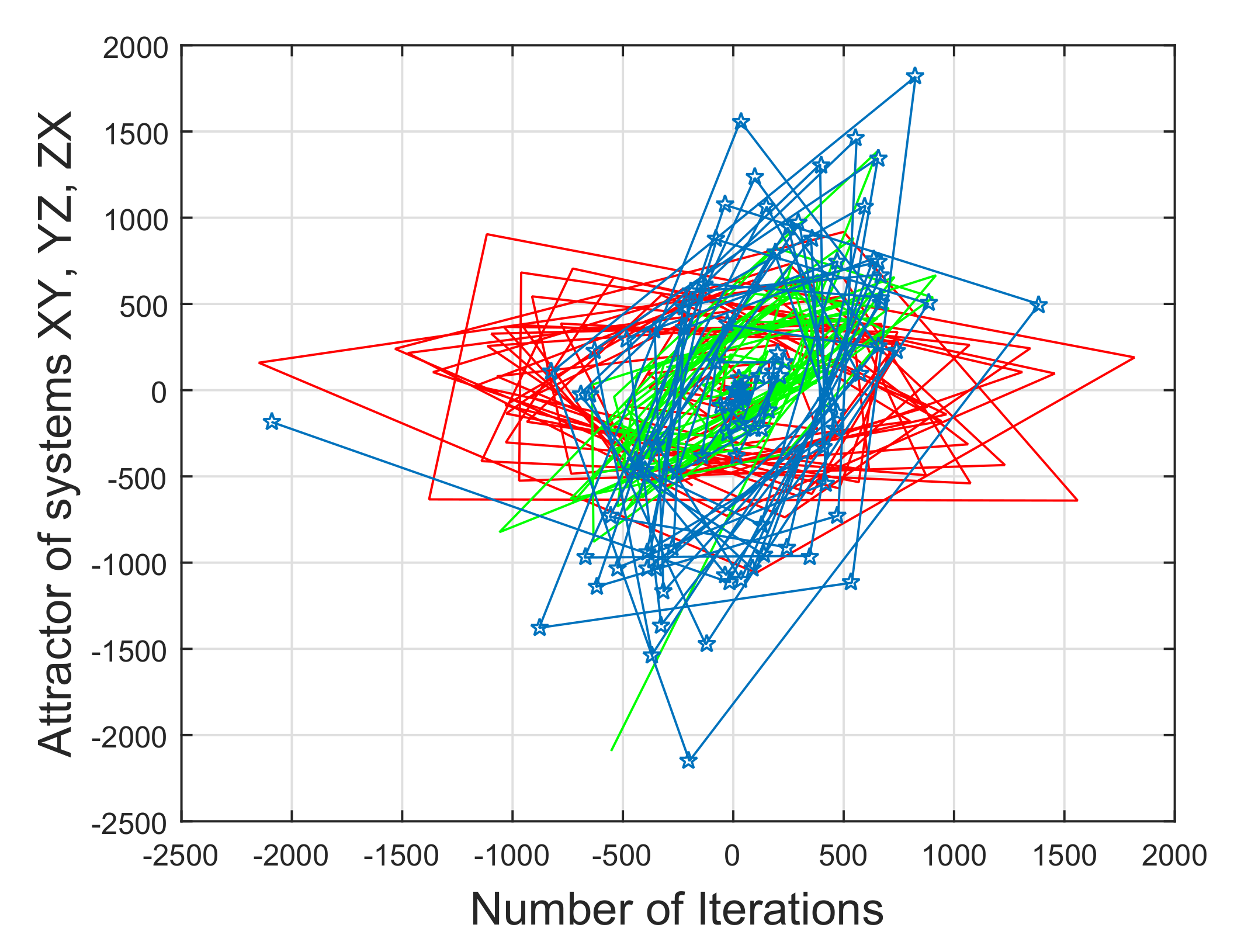
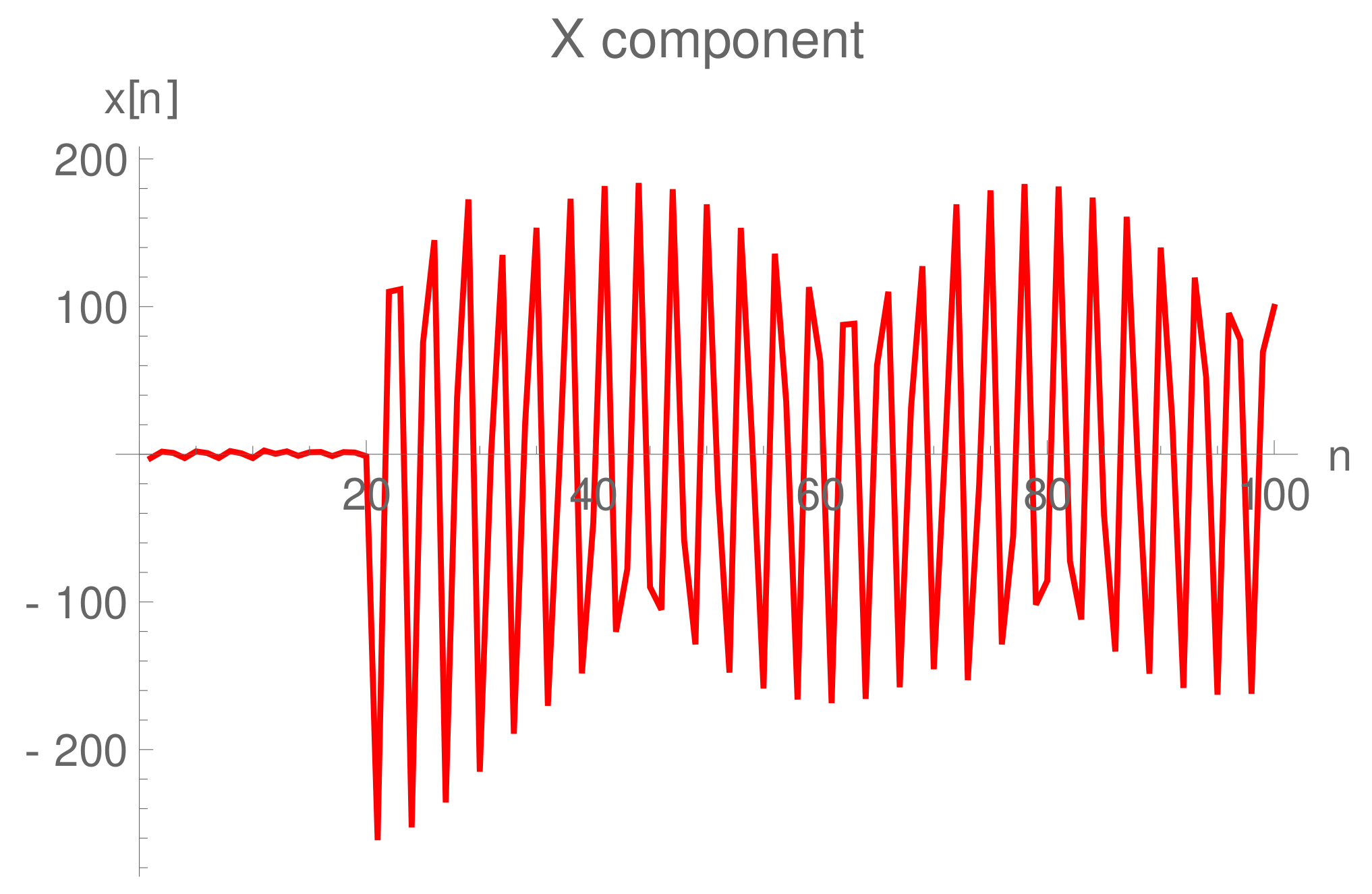
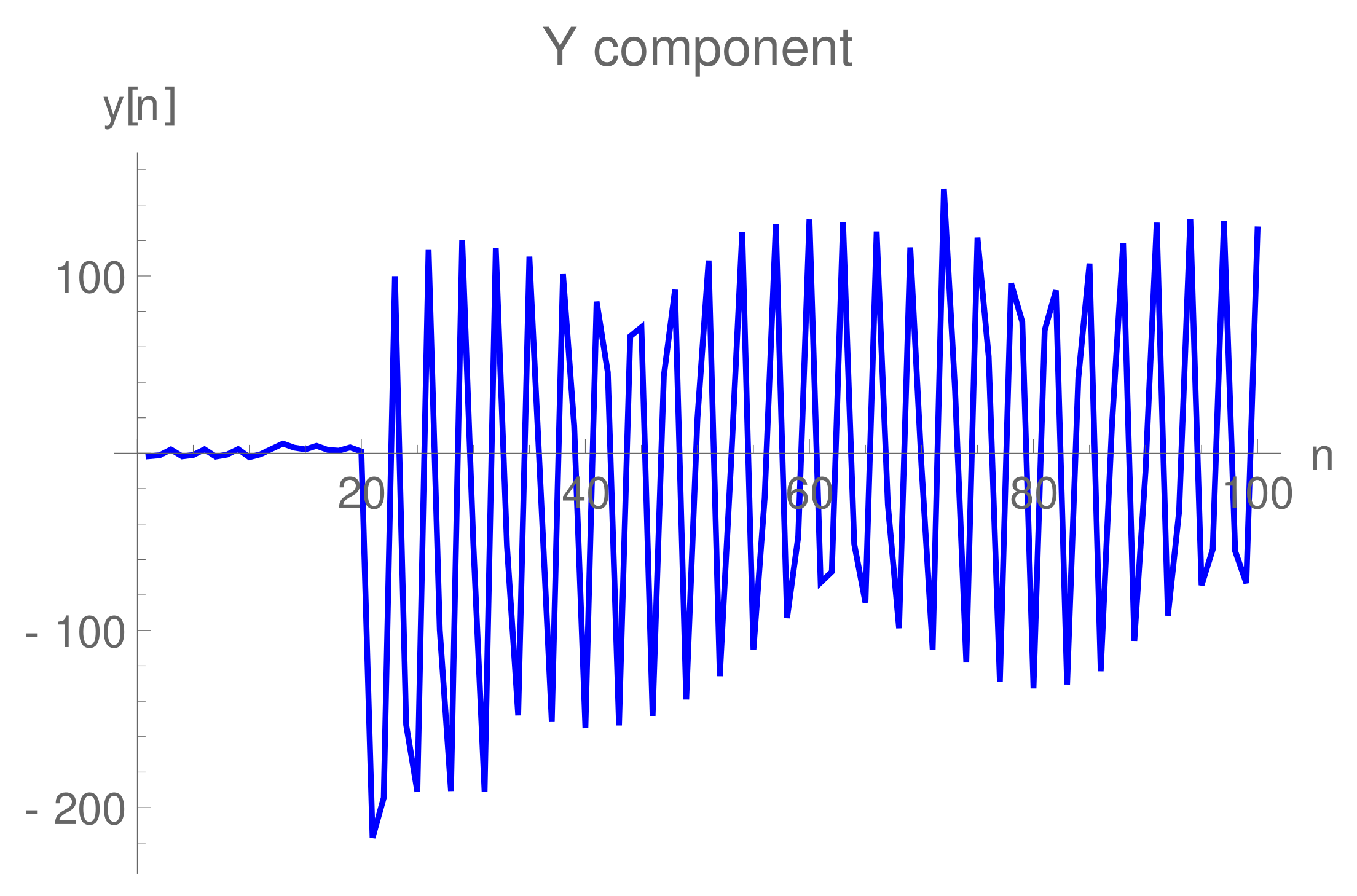
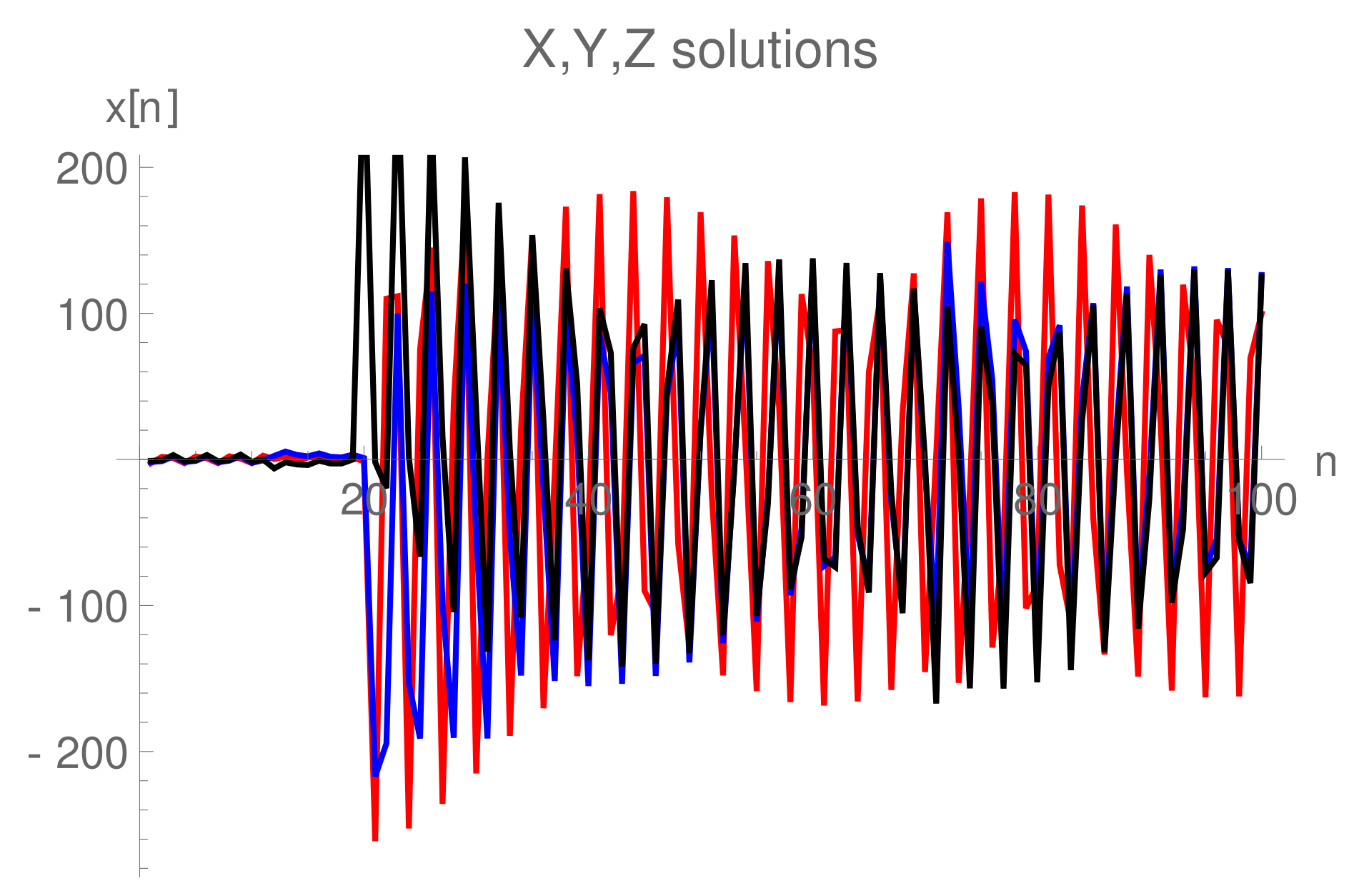
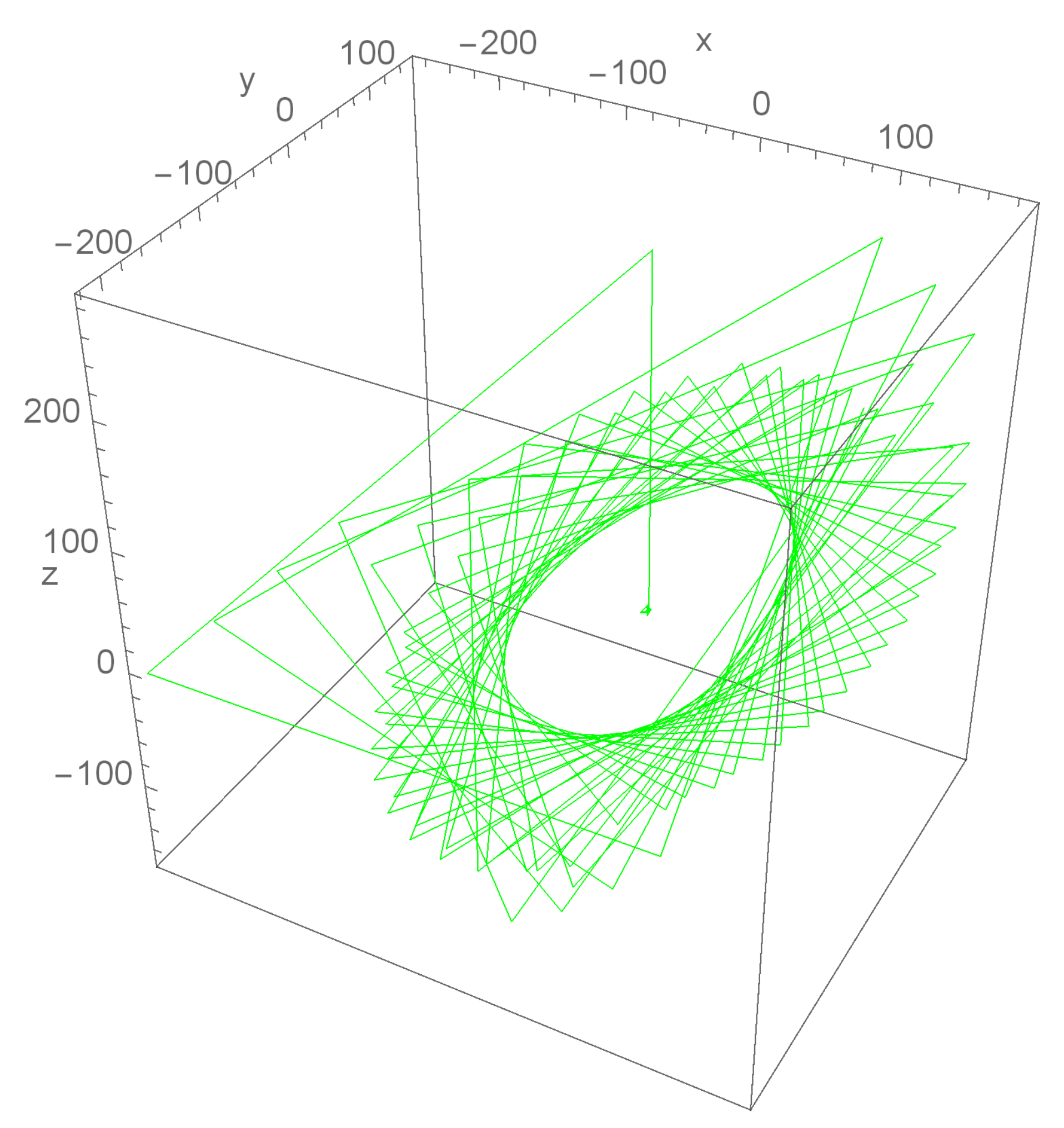
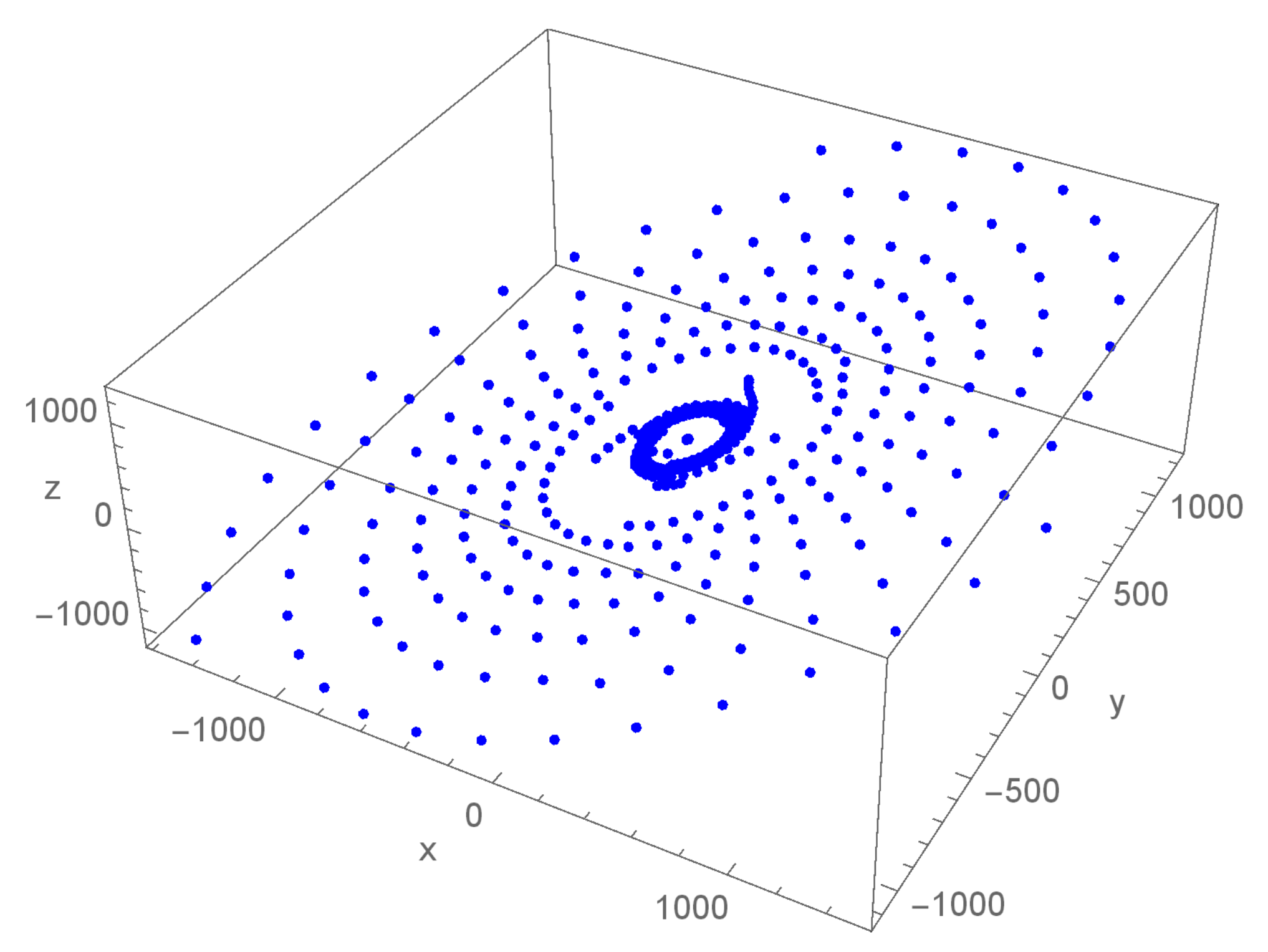
6. Numerical Debate
7. Conclusions
8. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Freedman, H.I. Deterministic Mathematical Models in Population Ecology; Marcel Dekker, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Allen, L.J.S. An Introduction to Mathematical Biology; Pearson Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Krebs, W. A General Predator-Prey Model. Math. Comp. Model. Dyn. Syst. 2003, 9, 387–401. [Google Scholar] [CrossRef]
- Edelstein-Keshet, L. Mathematical Models in Biology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Akgül, A.; Sarbaz, H.; Khoshnaw, A. Application of fractional derivative on non-linear biochemical reaction models. Int. J. Intell. Netw. 2020, 1, 52–58. [Google Scholar] [CrossRef]
- Sintunavarat, W.; Turab, A. A unified fixed point approach to study the existence of solutions for a class of fractional boundary value problems arising in a chemical graph theory. PLoS ONE 2022, 17, e0270148. [Google Scholar] [CrossRef]
- Kang, H.; Pesin, Y. Dynamics of a discrete Brusselator model: Escape to infinity and Julia set. Milan J. Math. 2005, 73, 1–17. [Google Scholar] [CrossRef]
- Wikan, A.; Mjølhus, E. Over-compensatory recruitment and generation delay in discrete age-structured population models. J. Math. Biol. 1996, 35, 195–239. [Google Scholar]
- Din, Q.; Elsayed, E.M. Stability analysis of a discrete ecological model. Comput. Ecol. Softw. 2014, 4, 89–103. [Google Scholar]
- Levin, S.A.; Goodyear, C.P. Analysis of an age-structured fishery model. J. Math. Biol. 1980, 9, 245–274. [Google Scholar] [CrossRef]
- Kulenovic, M.R.S.; Ladas, G. Dynamics of Second Order Rational Difference Equations; Chapman and Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Elsayed, E.M.; Khaliq, A. The Dynamics and Global Attractivity of a Rational Difference Equation. Adv. Stud. Contemp. Math. 2016, 26, 183–202. [Google Scholar]
- Gakkhar, S.; Singh, B.; Naji, R.K. Dynamical behavior of two predators competing over a single prey. BioSystems 2007, 90, 808–817. [Google Scholar] [CrossRef]
- Khan, A.Q.; Qureshi, M.N. Global Dynamics and Bifurcation Analysis of a Two-Dimensional Discrete-Time Lotka-Volterra Model. Complexity 2018, 2018, 7101505. [Google Scholar] [CrossRef]
- Tang, X.; Zou, X. On positive periodic solutions of Lotka-Volterra competition systems with deviating arguments. Pro. Am. Math. Soc. 2006, 134, 29672–29974. [Google Scholar] [CrossRef]
- Alebraheem, J.; Abu-Hasan, Y. Persistence of Predators in a Two Predators- One Prey Model with Non-Periodic Solution. Appl. Math. Sci. 2012, 6, 943–956. [Google Scholar]
- Huo, H.F.; Ma, Z.P.; Liu, C.Y. Persistence and Stability for a Generalized Leslie-Gower Model with Stage Structure and Dispersal. Abstr. Appl. Anal. 2009, 135843. [Google Scholar] [CrossRef]
- Belhannache, F.; Touafek, N.; Abo-Zeid, R. Dynamics of a third-order rational difference equation. Bull. Math. Soc. Sci. Math. Roum. Tome 2016, 59, 13–22. [Google Scholar]
- Dubey, B.; Upadhyay, R.K. Persistence and Extinction of One-Prey and Two-Predators System. Nonlinear Anal. Model. Control 2004, 9, 307–329. [Google Scholar] [CrossRef]
- Ahmad, S. On the nonautonomous Lotka-Volterra competition equation. Proc. Am. Math. Soc. 1993, 117, 199–204. [Google Scholar] [CrossRef]
- Kocic, V.L.; Ladas, G. Global Behavior of Nonlinear Difference Equations of Higher Order with Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Zhang, Q.; Yang, L.; Liu, J. Dynamics of a system of rational third order difference equation. Adv. Differ. Equ. 2012, 2012, 136. [Google Scholar] [CrossRef][Green Version]
- Grove, E.A.; Ladas, G. Periodicities in Nonlinear Difference Equations; Chapman and Hall/CRC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Sedaghat, H. Nonlinear Difference Equations: Theory with Applications to Social Science Models; Kluwer Academic Publishers: Dordreacht, The Netherlands, 2003. [Google Scholar]
- Thai, T.H.; Khuong, V.V. Stability analysis of a system of second-order difference equations. Math. Methods Appl. Sci. 2016, 39, 3691–3700. [Google Scholar] [CrossRef]
- Elaydi, S. An Introduction to Difference Equations, 2nd ed.; Springer Science+Business Media, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Tanaka, Y. Brouwer’s fixed point theorem with isolated fixed points and his Fan theorem. Int. Sch. Res. Netw. 2012, 2012, 843256. [Google Scholar] [CrossRef]
- Elsayed, E.M. Solutions of Rational Difference System of Order Two. Math. Comput. Model. 2012, 55, 378–384. [Google Scholar] [CrossRef]
- Elsayed, E.M. Behavior and expression of the solutions of some rational difference equations. J. Comput. Anal. Appl. 2013, 15, 73–81. [Google Scholar]
- Khaliq, A.; Alayachi, H.S.; Zubair, M.; Rohail, M.; Khan, A.Q. On stability analysis of a class of three dimensional system of exponential difference equations. 2022. to be appeared. [Google Scholar]
- Elsayed, E.M. Dynamics and Behavior of a Higher Order Rational Difference Equation. J. Nonlinear Sci. Appl. 2016, 9, 1463–1474. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Ahmed, A.M. Dynamics of a three-dimensional systems of rational difference equations. Math. Methods Appl. Sci. 2016, 39, 1026–1038. [Google Scholar] [CrossRef]
- Elsayed, E.M.; Alghamdi, A. Dynamics and Global Stability of Higher Order Nonlinear Difference Equation. J. Comput. Appl. 2016, 21, 493–503. [Google Scholar]
- Din, Q. Dynamics of a discrete Lotka-Volterra model. Adv. Differ. Equ. 2013, 2013, 95. [Google Scholar] [CrossRef]
- Pituk, M. More on Poincare’s and Perron’s Theorems for Difference Equations. J. Differ. Equ. Appl. 2002, 8, 201–216. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khaliq, A.; Ibrahim, T.F.; Alotaibi, A.M.; Shoaib, M.; El-Moneam, M.A. Dynamical Analysis of Discrete-Time Two-Predators One-Prey Lotka–Volterra Model. Mathematics 2022, 10, 4015. https://doi.org/10.3390/math10214015
Khaliq A, Ibrahim TF, Alotaibi AM, Shoaib M, El-Moneam MA. Dynamical Analysis of Discrete-Time Two-Predators One-Prey Lotka–Volterra Model. Mathematics. 2022; 10(21):4015. https://doi.org/10.3390/math10214015
Chicago/Turabian StyleKhaliq, Abdul, Tarek F. Ibrahim, Abeer M. Alotaibi, Muhammad Shoaib, and Mohammed Abd El-Moneam. 2022. "Dynamical Analysis of Discrete-Time Two-Predators One-Prey Lotka–Volterra Model" Mathematics 10, no. 21: 4015. https://doi.org/10.3390/math10214015
APA StyleKhaliq, A., Ibrahim, T. F., Alotaibi, A. M., Shoaib, M., & El-Moneam, M. A. (2022). Dynamical Analysis of Discrete-Time Two-Predators One-Prey Lotka–Volterra Model. Mathematics, 10(21), 4015. https://doi.org/10.3390/math10214015






