Adaptive Finite-Time Control of Stochastic Genetic Regulatory Networks with Time-Varying Delays

Abstract

This article discusses the finite-time stability problem for stochastic genetic regulatory networks (SGRNs) with time-varying delays. By designing suitable adaptive controllers and skillfully choosing appropriate Lyapunov and multi-Lyapunov functions, respectively, the above non-switched and switched SGRNs can achieve finite time stability in probability. Superior to some existing controllers for GRNs, the above adaptive design procedures can reduce the dependence of the system parameters. Finally, two numerical simulation examples illustrate the effectiveness of the theoretical results.

1. Introduction

Gene regulatory networks (GRNs) have received considerable attention for their potential applications [1,2]. The GRNs actually act as a complex dynamical system and describe the regulatory mechanism of interactions among DNA, mRNA, and proteins of biological systems at a molecular level. The analysis of a gene regulatory network is not only an important way to understand and master the operating mechanism of cell life activities [1,3,4,5,6], but it also has broad application prospects in disease gene prediction, drug target screening, and other fields [7,8,9,10]. To this end, it is necessary and useful to present appropriate mathematical models to represent expression mechanisms and signal transduction ways. At present, the modeling approaches of GRNs generally include Boolean models, Bayesian models, differential equation models, etc. [11,12]. Among them, the two most widely used models are the Boolean models and differential equation models [13,14]. In particular, differential equations describe the concentration changes in proteins and mRNAs. This model is more accurate and can accurately describe the nonlinear dynamic behavior of biological systems, so it has attracted more attention [15,16,17,18].

On the one hand, gene expression is often affected by internal and external noise interference and environmental fluctuations, so the process of gene expression is a random process [19]. Moreover, this noise will inevitably affect the dynamic analysis of the network. Therefore, stochastic noise should be considered in the modeling of gene regulatory networks [20]. On the other hand, since the processes of the transcription and translation of proteins are slow in organisms, time delay is inevitable in modeling GRNs. Time delay plays a very important role in the dynamic behavior of gene regulatory networks, and some models without time delay may lead to the wrong results [21,22,23]. Recently, there have been many good results in the research into delayed gene regulatory networks [24,25,26,27,28,29,30,31]. Therefore, in this paper, we consider the stochastic genetic regulatory networks (SGRNs) with time-varying delays.

Furthermore, as a dynamic system, the stability analysis and regulation of GRNs are very important. The instability of protein and mRNA molecular concentrations can lead to fatal consequences [32,33]. So it is necessary to adjust the molecular concentration through external input to make the system reach a stable state. Recently, people have paid more attention to GRNs [34]. For the general network, not only is the study of the finite-time stability significant [35,36,37], but the finite-time control also has the advantages of high precision, strong robustness, and anti-interference ability [35,38]. When we consider the SGRNs, how do we define the stability of a system in finite time? In 2008, Mao et al. first proposed the finite-time stability theorems for stochastic differential equations [39]. Then, Yin et al. introduced a new definition of finite time stability for stochastic nonlinear systems (that is, finite time stability in probability) and presented a stochastic finite time theorem [40]. Compared with the stability in probability and asymptotic stability in probability, finite-time stability in probability has shown its advantage in control design because of the faster convergence, higher accuracy, and better disturbance rejection ability. Khoo ea al. obtained some sufficient conditions to ensure the finite-time stability in probability [41]. Then, Wang et al. dealt with the problem of finite time stabilization in probability for a class of high-order stochastic nonlinear systems in strict feedback form in 2015 [42]. Based on the above definitions and sufficient conditions in a stochastic nonlinear system, we study the finite time stability of SGRNs. With the help of the analyses of the stochastic nonlinear systems, the control and analysis of SGRNs have achieved remarkable developments in recent years [43,44,45,46,47]. These studies not only promote the development of finite-time stability in gene regulatory networks but also provide some research basis and ideas for our research on adaptive controller design. In 2018, Li et al. studied the problem of input-to-state stability for a class of switched neural networks with stochastic disturbance [45]. In 2019, Wang et al. considered the stability problem of uncertain GRN with time-varying delay and reaction–diffusion terms [46]. In 2021, Saravanan et al. discussed the finite-time stability of switched GRNs using Wirtinger’s integral inequality, a reciprocally convex combination technique [48]. The above literature has studied the stability of gene regulatory networks from the aspects of input-state stability, finite-time stability, etc., under the conditions of time delay, randomness, and switching. However, in the above discussion, we need to obtain the parameter information of the gene network, which may be obtained based on large numbers of experiments. This leads to a strong dependence on the precision of the experiments and instruments. In this paper, we consider the lowest amount of parameter information to design an appropriate controller, which can make the stochastic GRNs achieve finite-time stability.

Based on the above considerations, we design adaptive controllers under non-switched and switched SGRNs (which we denote as NSGRNs and SSGRNs, respectively) with time-varying delays, respectively, and give sufficient conditions of the finite-time stability in probability using the method of the Razumikhin theorem. The rest of the paper is organized as follows. The problem formulation and some preliminaries are given in Section 2. Section 3 presents the finite-time stability analysis for non-switched GRNs by designing adaptive controllers. In addition, the above adaptive design methods are extended to the case of switched GRNs, which is shown in Section 4. Then, two examples are provided to demonstrate the effectiveness of the obtained results; finally, Section 6 concludes the paper.

$Notations$: $R_{+}$ denotes the set of all nonnegative real numbers, and $R^n$ denotes the real n-dimensional space. For a given vector or matrix X, $X^T$ denotes its transpose, $Tr\left\{X\right\}$ denotes its trace when X is square, and $\parallel X\parallel$ is the Euclidean norm of a vector X. ${\mathcal{C}}^i$ denotes the set of all functions with continuous $ith$ partial derivatives; ${\mathcal{C}}^{2,1}(R^n\times [-d,\infty );R_{+})$ denotes the family of all nonnegative functions $V(x,t)$ on $R^n\times [-d,\infty )$, which are ${\mathcal{C}}^2$ in x and ${\mathcal{C}}^1$ in t; K denotes the set of all functions, $R_{+}\to R_{+}$, which are continuous, strictly increasing, and vanishing at zero; $K_{\infty }$ denotes the set of all functions, which are of K class and unbounded. $E(x)$ denotes the expectation of the stochastic variable x, $a\wedge b$ means the minimum of a and b, and $a\vee b$ means the maximum.

2. Problem Formulation and Some Preliminaries

Consider the following n-molecular species uncertain switched GRNs [46,47,48]:

$$\left\{\begin{array}{cc}\hfill & \dot{m}(t)=-A_{\sigma (t)}m(t)+f_{\sigma (t)}(p(t-{\tau }_2(t)))),\hfill \\ \hfill & \dot{p}(t)=-C_{\sigma (t)}p(t)+D_{\sigma (t)}m(t-{\tau }_1(t))),\hfill \\ \hfill & m(t_0+\theta )=m_0(\theta ),p(t_0+\theta )=p_0(\theta ),\theta \in [-\tau ,0]\hfill \end{array}\right.,$$

(1)

where $m(t)={[m_1(t),\dots m_n(t)]}^T\in R^n$ and $p(t)={[p_1(t),\dots p_n(t)]}^T\in R^n$ are the state vectors and represent the concentration of mRNA and protein at time t.

$$A_{\sigma (t)}=diag[a_{1_{\sigma (t)}},a_{2_{\sigma (t)}},\dots a_{n_{\sigma (t)}}],C_{\sigma (t)}=diag[c_{1_{\sigma (t)}},c_{2_{\sigma (t)}},\dots c_{n_{\sigma (t)}}],$$

$$D_{\sigma (t)}=diag[d_{1_{\sigma (t)}},d_{2_{\sigma (t)}},\dots d_{n_{\sigma (t)}}]$$

$A_{\sigma (t)}$, $C_{\sigma (t)}$ are the degradation rates of mRNA and protein, and $D_{\sigma (t)}$ is the translation rate, where $\sigma (t):[0,+\infty )\to \mathcal{N}=\{1,2,\dots ,N\}$, is a piecewise constant function depending on time t, which represents the switched signal. Specifying the index of the active subsystem, i.e., $\sigma (t)\in \mathcal{N}$ for $t\in [t_k,t_{k+1})$, $t_k$ is the kth switched instant. ${\tau }_1(t),{\tau }_2(t)$ are the time-varying delays with

$$0\le {\tau }_1(t)\le {\widehat{\tau }}_1,0\le {\tau }_2(t)\le {\widehat{\tau }}_2,0\le {\dot{\tau }}_1(t)\le {\tilde{\tau }}_1,0\le {\dot{\tau }}_1(t)\le {\tilde{\tau }}_1,$$

where $\tau =max\{{\widehat{\tau }}_1,{\widehat{\tau }}_2\}$, and $\mu =max\{{\tilde{\tau }}_1,{\tilde{\tau }}_2\}$.

$f_{\sigma (t)}(p(t))=[f_{1_{\sigma (t)}}(p(t)),f_{2_{\sigma (t)}}(p(t)),\dots ,f_{n_{\sigma (t)}}(p(t))]\in R^n$ denotes the feedback regulation of proteins on the transcription of mRNAs, which is called SUM logic [1].

$$f_{i_{\sigma (t)}}(p(t))=\sum _{j=1}^n{f}_{i{j}_{\sigma (t)}}(p_j(t)),$$

where

$$f_{i{j}_{\sigma (t)}}(p_j(t))=\left\{\begin{array}{cc}{r}_{i{j}_{\sigma (t)}}\frac{{(p_j(t)/{\beta }_j)}^{H_j}}{1+{(p_j(t)/{\beta }_j)}^{H_j}},\hfill & \mathrm{if}jisaregressorofgenei,\hfill \\ 0,\hfill & \mathrm{if}jdoesnotregulategenei,\hfill \\ r_{i{j}_{\sigma (t)}}\frac{1}{1+{(p_j(t)/{\beta }_j)}^{H_j}},\hfill & \mathrm{if}jisanactivatorofgenei.\hfill \end{array}\right.$$

$H_j$ is the Hill coefficient, ${\beta }_j$ is a positive constant, and $r_{i{j}_{\sigma (t)}}>0$ is the transcriptional rate of the factor j to i. Proceeding as in paper [47], $f_{\sigma (t)}(p(t)$ can be rewritten as

$$f_{\sigma (t)}(p(t))=B_{\sigma (t)}F(p(t))+L,$$

where $F(p(t))={[F_1(p(t)),\dots ,F_n(p(t))]}^T$ with the function $F_j(\mu )=\frac{{(\mu /{\beta }_j)}^{H_j}}{1+\mu /{\beta }_j{)}^{H_j}}$. $B_{\sigma (t)}$ is an $n\times n$ matrix with

$$b_{ij}=\left\{\begin{array}{cc}-r_{ij},\hfill & \mathrm{if}jisaregressorofgenei,\hfill \\ 0,\hfill & \mathrm{if}jdoesnotregulategenei,\hfill \\ r_{ij},\hfill & \mathrm{if}jisanactivatorofgenei.\hfill \end{array}\right.$$

$L={[l_1,l_2\dots ,l_n]}^T$ with $l_i={\sum }_{j\in R_e}{r}_{ij}$, and $R_e$ is the set of all repressers of gene i.

Let $m*$, $p*$ be an unique equilibrium point of system (1). In the following, we shift the point $m*$, $p*$ to the origin by letting $x(t)=m(t)-m*,y(t)=p(t)-p*$. Therefore, the following system is established

$$\left\{\begin{array}{cc}\hfill & \dot{x}(t)=-A_{\sigma (t)}x(t)+B_{\sigma (t)}F(y(t-{\tau }_2(t))),\hfill \\ \hfill & \dot{y}(t)=-C_{\sigma (t)}y(t)+D_{\sigma (t)}x(t-{\tau }_1(t))),\hfill \\ \hfill & x_0(\theta )=m_0(\theta )-m*,y_0(\theta )=p_0(\theta )-p*,\theta \in [-\tau ,0]\hfill \end{array},\right.$$

(2)

where $F(y(t-{\tau }_2(t)))=f(p(t-{\tau }_2(t)))-f(p*)$. Then, letting $\mathcal{X}(t)={[x^T(t),y^T(t)]}^T$, the system (2) can be changed to

$$\left\{\begin{array}{cc}\hfill & \dot{\mathcal{X}}(t)=-{\mathcal{A}}_{\sigma (t)}\mathcal{X}(t)+{\mathcal{B}}_{\sigma (t)}F(\mathcal{X}(t-{\tau }_2(t)))+\mathcal{D}\mathcal{X}(t-{\tau }_1(t)),\hfill \\ \hfill & \mathcal{X}(t_0+\theta )={\mathcal{X}}_0(\theta ),\theta \in [-\tau ,0],\hfill \end{array}\right.$$

(3)

where

$$f(\mathcal{X}(t-{\tau }_2))=f(y(t-{\tau }_2)),\mathcal{A}=\left[\begin{array}{cc}A& 0\\ 0& C\end{array}\right],\mathcal{D}=\left[\begin{array}{cc}0& 0\\ D& 0\end{array}\right],\mathcal{B}=\left[\begin{array}{c}B\\ 0\end{array}\right].$$

In this paper, we take extracellular noises and control items into account; then, the GRNs model (3) can be expressed as follows:

$$\left\{\begin{array}{cc}\hfill \mathrm{d}\mathcal{X}(t)& =[-{\mathcal{A}}_{\sigma }\mathcal{X}(t)+{\mathcal{B}}_{\sigma }f(\mathcal{X}(t-{\tau }_2(t)))+{\mathcal{D}}_{\sigma }\mathcal{X}(t-{\tau }_1(t))\hfill \\ \hfill & +u(t)]\mathrm{d}t+g_{\sigma }(\mathcal{X}(t),\mathcal{X}(t-{\tau }_1(t)),\mathcal{X}(t-{\tau }_2(t)))\mathrm{d}\omega (t),\hfill \\ \hfill \mathcal{X}(t_0+\theta )& ={\mathcal{X}}_0(\theta ),\theta \in [-\tau ,0],\hfill \end{array}\right.$$

(4)

where $g_j(:,:,:,)\in R^{n\times r}$, $\omega (t)\in R^r$ is a stand Wiener process defined in the complete probability space $(\mathsf{\Omega },\mathcal{F},{\mathcal{F}}_t,\mathcal{P})$.

In order to conduct the stability analysis for systems (4), it is necessary to make the following assumptions and definitions.

Assumption 1.

For the system (4), the noise intensity matrices $g_i({\omega }_1,{\omega }_2,{\omega }_3)$ satisfy the following condition

$$Tr\left\{g_i^T({\omega }_1,{\omega }_2,{\omega }_3)g_i({\omega }_1,{\omega }_2,{\omega }_3)\right\}\le {\xi }_1{\omega }_1^T{\omega }_1+{\xi }_2{\omega }_2^T{\omega }_2+{\xi }_3{\omega }_3^T{\omega }_3,$$

where $i\in \mathcal{N},$${\xi }_1,{\xi }_2,{\xi }_3$ are positive constant and ${\omega }_1,{\omega }_2,{\omega }_3\in R^{2n}$.

Definition 1

([39]). Consider the following stochastic system with time delays

$$\mathrm{d}x(t)=f(x(t),x(t-d(t)),t)\mathrm{d}t+g(x(t),x(t-d(t)),t)\mathrm{d}w,\forall t\ge 0.$$

For any given $V(x(t),t)\in {\mathcal{C}}^{2,1}$ associated with above system, the differential operator $\mathcal{L}$ is defined as

$$\mathcal{L}V=\frac{\partial V}{\partial x}f+\frac{1}{2}Tr\left\{g^T\frac{{\partial }^{2}V}{\partial x^2}g\right\},$$

which is called as the Hassian term of $\mathcal{L}$.

In the following, we will design adaptive controllers for above system to achieve finite-time stability in probability. The exact definition of the finite-time stability in probability is as follows.

Definition 2

([39]). The trivial solution of system (4) is said to be finite-time stable in probability, if the equation admits a unique solution for any initial value $\{\mathcal{X}(\theta ):-\tau \le \theta \le 0\}={\mathcal{X}}_0\in R^{2n}$, the following statements hold:

(i) Finite-time attractiveness in probability: For every initial value ${\mathcal{X}}_0\in R^{2n}\backslash \left\{0\right\}$, the first time ${\tau }_{{\mathcal{X}}_0}=inf\{t;\mathcal{X}(t;{\mathcal{X}}_0)=0\}$, which is called the stochastic settling time, is finite almost surely, that is, $P\{{\tau }_{{\mathcal{X}}_0}<\infty \}=1$;

(ii) Stability in probability: For every pair of $\epsilon \in (0,1)$ and $r>0$, there exists a $\delta =\delta (\epsilon ,r)>0$ such that

$$P\left\{\right|\mathcal{X}(t;{\mathcal{X}}_0)|<r,forallt\ge 0)\ge 1-\epsilon ,$$

whenever $\parallel {\mathcal{X}}_0\parallel <\delta$.

3. Finite-Time Stability in Probability of Non-Switched SGRNs with Time-Varying Delay

In this section, our first goal is to design an adaptive controller that can make the system achieve finite-time stability in probability in non-switched cases, which can be seen as:

$$\left\{\begin{array}{cc}\hfill \mathrm{d}\mathcal{X}(t)& =[-\mathcal{A}\mathcal{X}(t)+\mathcal{B}f(\mathcal{X}(t-{\tau }_2(t)))+\mathcal{D}\mathcal{X}(t-{\tau }_1(t))\hfill \\ \hfill & +u(t)]\mathrm{d}t+g(\mathcal{X}(t),\mathcal{X}(t-{\tau }_1(t)),\mathcal{X}(t-{\tau }_2(t)))\mathrm{d}\omega (t),\hfill \\ \hfill \mathcal{X}(t_0+\theta )& ={\mathcal{X}}_0(\theta ),\theta \in [-\tau ,0].\hfill \end{array}\right.$$

(5)

For system (5), the controller is designed as:

$$\begin{array}{cc}\hfill u(t)& =-\widehat{k}\mathcal{X}(t)-k_2{\mathrm{sig}}^a(\mathcal{P}\mathcal{X}(t))\hfill \end{array},$$

(6)

where $k_2>0$, $0<a<1$ are constants, with positive definite matrix $\mathcal{P}$ satisfying (8), and $\widehat{k}$ is the adaptive feedback gain with

$$\dot{\widehat{k}}={\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t),$$

(7)

and the initial values $\widehat{k}(t_0)>0$.

The definitions of ${\mathrm{sig}}^a(·)$ and $\mathrm{sgn}(·)$ are given as:

$${\mathrm{sig}}^a(z)=\left[\begin{array}{c}|z_1{|}^a\mathrm{sgn}(z_1)\\ ⋮\\ |z_n{|}^a\mathrm{sgn}(z_n)\end{array}\right],\mathrm{sgn}(z_i)=\left\{\begin{array}{c}1,\mathrm{if}{z}_i>0,\hfill \\ 0,\mathrm{if}{z}_i=0,\hfill \\ -1,\mathrm{if}{z}_i<0,\hfill \end{array}\right.$$

where $z={[z_1,\dots ,z_n]}^T\in R^n$. Based on the above controller and definition, the following lemma will be given for the later use of derivations.

Lemma 1

([40]). For system (5), if there is a Lyapunov function $V(\mathcal{X}(t),t)\in {\mathcal{C}}^{2,1}(R^{2n}\times [-\tau ,\infty );R_{+})$ and $K_{\infty }$ class function ${\alpha }_1$ and ${\alpha }_2$, such that:

$$\begin{array}{cc}\hfill & (i){\alpha }_1(|\mathcal{X}(t)|)\le V(\mathcal{X}(t),t)\le {\alpha }_2(\underset{\theta \in [-\tau ,0]}{sup}\left|\mathcal{X}(t+\theta )\right|),\hfill \\ \hfill & (ii)\mathcal{L}V(\mathcal{X}(t),t)\le -\beta {(V(\mathcal{X}(t),t))}^{\gamma }\hfill \\ \hfill & wheneverV(\mathcal{X}(t+\theta ),t+\theta )\le rV(\mathcal{X}(t),t)for\theta \in [-\tau ,0],\hfill \end{array}$$

where $r>1$, $\beta >0$ and $0<\gamma <1$ are positive real numbers, then the trivial solution of system (5) is finite-time stable in probability.

Lemma 2

([40]). Let $0<\gamma <1$ and $\lambda >0$. Assume that there exists a continuous function $h:[0,\infty )\to [0,\infty )$ with $h(0)>0$ such that, for any $0\le u\le t$,

$$h(t)-h(u)\le -\lambda {\int }_u^t{h}^{\gamma }(s)ds.$$

Then, there exists a positive real constant T, such that

$$h(t)\le {[h^{1-\gamma }(0)-\lambda (1-\gamma )t]}^{\frac{1}{1-\gamma }},\forall t\in [0,T],$$

where T can be chosen as

$$T=T_0\le \frac{h^{1-\gamma }(0)}{\lambda (1-\gamma )}.$$

Lemma 3

([49]). For the positive definite matrix $\mathcal{A}$ in system (5) and a positive matrix $\mathcal{Q}$, there exists a unique positive definite matrix $\mathcal{P}$ satisfying

$${\mathcal{A}}^T\mathcal{P}+\mathcal{P}\mathcal{A}=\mathcal{Q}.$$

(8)

In general, we take $\mathcal{Q}$ as the unit matrix I.

Lemma 4

([49]). For the nonlinear function $F(\mathcal{X})$ in system (5), there exists a constant $\rho >0$, such that ${\parallel F(\mathcal{X})\parallel }^2\le \rho {\parallel \mathcal{X}\parallel }^2$.

Lemma 5

([50]). Let $x,y\in R$. Given any positive real numbers c, d, and $\overline{\gamma }$, then

$${\left|x\right|}^c{\left|y\right|}^d\le \frac{c}{c+d}\overline{\gamma }{\left|x\right|}^{c+d}+\frac{d}{c+d}{\overline{\gamma }}^{-\frac{c}{d}}{\left|x\right|}^{c+d}.$$

(9)

Lemma 6

([50]). Let $x,y\in R$ are constants, for any $p>1$, then

$$(|x|+{\left|y\right|)}^{\frac{1}{p}}\le {\left|x\right|}^{\frac{1}{p}}+{\left|y\right|}^{\frac{1}{p}}\le 2^{\frac{p-1}{p}}(|x|+{\left|y\right|)}^{\frac{1}{p}}.$$

(10)

Theorem 1.

For the given controller (6) and the adaptive law (7), the non-switched SGRNs (5) are finite-time stability in probability.

Proof. 

We construct

$$V(t)=V_1(t)+V_2(t)$$

(11)

$$\begin{array}{cc}\hfill V_1(t)& ={\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t),V_2(t)={(\widehat{k}-k_1)}^2,\hfill \end{array}$$

(12)

where $k_1=\frac{1}{2}[-\frac{{\lambda }_{min}(\mathcal{Q})}{{\lambda }_{max}(\mathcal{P})}+\frac{{\lambda }_{max}({\mathcal{D}}^T\mathcal{P}\mathcal{D})}{{\lambda }_{min}(\mathcal{P})}+\frac{{\rho }^2{\lambda }_{max}({\mathcal{B}}^T{\mathcal{P}}^T\mathcal{P}\mathcal{B})}{{\lambda }_{min}(\mathcal{P})}+{\xi }_1\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}+r({\xi }_2\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}+1)+r({\xi }_3+1)\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}]$. □

To begin, we show that there exist positive constants $\beta ,\gamma$ to satisfy $\mathcal{L}V(t)\le -\beta V_1^{\gamma }(t)$. By taking the derivation of the given Lyapunov function with respect to t along the trajectory of system (5), we can obtain

$$\begin{array}{cc}\hfill & \mathcal{L}V(t)\hfill \\ \hfill & =-{\mathcal{X}}^T(t)(\mathcal{A}\mathcal{P}+\mathcal{P}\mathcal{A})\mathcal{X}(t)+2{\mathcal{X}}^T(t)\mathcal{P}\mathcal{B}F(\mathcal{X}(t-{\tau }_2(t)))+2{\mathcal{X}}^T(t)\mathcal{P}\mathcal{D}\mathcal{X}(t-{\tau }_1(t))\hfill \\ \hfill & -2\widehat{k}{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)-2k_2{\mathcal{X}}^T(t)\mathcal{P}{\mathrm{sig}}^a(\mathcal{P}\mathcal{X}(t))\hfill \\ & +Tr\left\{g^T(\mathcal{X}(t),\mathcal{X}(t-{\tau }_1),\mathcal{X}(t-{\tau }_2))\mathcal{P}g(\mathcal{X}(t),\mathcal{X}(t-{\tau }_1),\mathcal{X}(t-{\tau }_2))\right\}.\hfill \\ \hfill & \le {\rho }^2{\mathcal{X}}^T(t){\mathcal{B}}^T{\mathcal{P}}^T\mathcal{P}\mathcal{B}\mathcal{X}(t)+\frac{1}{{\rho }^2}{F}^T(\mathcal{X}(t-{\tau }_2(t)))F(\mathcal{X}(t-{\tau }_2(t)))\hfill \\ \hfill & +{\mathcal{X}}^T(t){\mathcal{D}}^T\mathcal{P}\mathcal{D}\mathcal{X}(t)+{\mathcal{X}}^T(t-{\tau }_1(t))\mathcal{P}\mathcal{X}(t-{\tau }_1(t))-{\mathcal{X}}^T(t)\mathcal{P}{\parallel \mathcal{P}\mathcal{X}(t)\parallel }^a{\mathrm{sgn}}^a(\mathcal{P}\mathcal{X}(t))\hfill \\ \hfill & +{\lambda }_{max}(\mathcal{P})\{{\xi }_1{\mathcal{X}}^T(t)\mathcal{X}(t)+{\xi }_2{\mathcal{X}}^T(t-{\tau }_1(t))\mathcal{X}(t-{\tau }_1(t))+{\xi }_3{\mathcal{X}}^T(t-{\tau }_2(t))\mathcal{X}(t-{\tau }_2(t))\}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & \le \frac{{\rho }^2{\lambda }_{max}({\mathcal{B}}^T{\mathcal{P}}^T\mathcal{P}\mathcal{B})}{{\lambda }_{min}(\mathcal{P})}{\mathcal{X}}^T(t)P\mathcal{X}(t)+{\mathcal{X}}^T(t-{\tau }_2(t))\mathcal{X}(t-{\tau }_2(t))+\frac{{\lambda }_{max}({\mathcal{D}}^T\mathcal{P}\mathcal{D})}{{\lambda }_{min}(\mathcal{P})}{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)\hfill \\ \hfill & +{\mathcal{X}}^T(t-{\tau }_1(t))\mathcal{P}\mathcal{X}(t-{\tau }_1(t))-{\left({\lambda }_{min}(\mathcal{P}){\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)\right)}^{\frac{1+a}{2}}\hfill \\ \hfill & +{\lambda }_{max}(\mathcal{P})\{{\xi }_1{\mathcal{X}}^T(t)\mathcal{X}(t)+{\xi }_2{\mathcal{X}}^T(t-{\tau }_1(t))\mathcal{X}(t-{\tau }_1(t))+{\xi }_3{\mathcal{X}}^T(t-{\tau }_2(t))\mathcal{X}(t-{\tau }_2(t))\}.\hfill \\ \hfill & \le -{\mathcal{X}}^T(t)\mathcal{Q}\mathcal{X}(t)+\frac{{\rho }^2{\lambda }_{max}({\mathcal{B}}^T{\mathcal{P}}^T\mathcal{P}\mathcal{B})}{{\lambda }_{min}(\mathcal{P})}{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)+{\mathcal{X}}^T(t-{\tau }_2(t))\mathcal{X}(t-{\tau }_2(t))\hfill \\ \hfill & +\frac{{\lambda }_{max}({\mathcal{D}}^T\mathcal{P}\mathcal{D})}{{\lambda }_{min}(\mathcal{P})}{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)+{\mathcal{X}}^T(t-{\tau }_1(t))\mathcal{P}\mathcal{X}(t-{\tau }_1(t))-2\widehat{k}{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)\hfill \\ \hfill & -2k_2{\left({\lambda }_{min}(\mathcal{P}){\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)\right)}^{\frac{1+a}{2}}-2(\widehat{k}-k_1){\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)+{\lambda }_{max}(\mathcal{P}){\xi }_1{\mathcal{X}}^T(t)\mathcal{X}(t)\hfill \\ \hfill & +{\lambda }_{max}(\mathcal{P}){\xi }_2{\mathcal{X}}^T(t-{\tau }_1(t))\mathcal{X}(t-{\tau }_1(t))+{\lambda }_{max}(\mathcal{P}){\xi }_3{\mathcal{X}}^T(t-{\tau }_2(t))\mathcal{X}(t-{\tau }_2(t))\hfill \\ \hfill & \le [-\frac{{\lambda }_{min}(\mathcal{Q})}{{\lambda }_{max}(\mathcal{P})}+{\xi }_1\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}+\frac{{\lambda }_{max}({\mathcal{D}}^T\mathcal{P}\mathcal{D})}{{\lambda }_{min}(\mathcal{P})}+\frac{{\rho }^2{\lambda }_{max}({\mathcal{B}}^T{\mathcal{P}}^T\mathcal{P}\mathcal{B})}{{\lambda }_{min}(\mathcal{P})}-2k_1]{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)\hfill \\ \hfill & -2k_2{({\lambda }_{min}(\mathcal{P}))}^{\gamma }{({\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t))}^{\gamma }+({\xi }_2\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}+1){\mathcal{X}}^T(t-{\tau }_1)\mathcal{P}\mathcal{X}(t-{\tau }_1)\hfill \\ \hfill & +({\xi }_3+1)\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}{\mathcal{X}}^T(t-{\tau }_2)\mathcal{P}\mathcal{X}(t-{\tau }_2).\hfill \end{array}$$

Whenever $\mathcal{X}(t)$ satisfies $V(\mathcal{X}(t+s),t+s)\le rV(\mathcal{X}(t),t)forall-\tau \le s\le 0,$ for some $r>1$. Then, we can conclude that

$$\begin{array}{cc}\hfill & \mathcal{L}V(t)\hfill \\ \hfill & \le [-\frac{{\lambda }_{min}(\mathcal{Q})}{{\lambda }_{max}(\mathcal{P})}+{\xi }_1\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}+\frac{{\lambda }_{max}({\mathcal{D}}^T\mathcal{P}\mathcal{D})}{{\lambda }_{min}(\mathcal{P})}+\frac{{\rho }^2{\lambda }_{max}({\mathcal{B}}^T{\mathcal{P}}^T\mathcal{P}\mathcal{B})}{{\lambda }_{min}(\mathcal{P})}-2k_1]{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)\hfill \\ \hfill & -2k_2{({\lambda }_{min}(\mathcal{P}))}^{\gamma }{({\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t))}^{\gamma }+r({\xi }_2\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}+1){\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)\hfill \\ \hfill & +r({\xi }_3+1)\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)+({\xi }_2\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}+1)[{\mathcal{X}}^T(t-{\tau }_1)\mathcal{P}\mathcal{X}(t-{\tau }_1)-r{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)]\hfill \\ \hfill & +({\xi }_3+1)\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}[{\mathcal{X}}^T(t-{\tau }_2)\mathcal{P}\mathcal{X}(t-{\tau }_2)-r{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)]\hfill \\ \hfill & \le [-\frac{{\lambda }_{min}(\mathcal{Q})}{{\lambda }_{max}(\mathcal{P})}+\frac{{\lambda }_{max}({\mathcal{D}}^T\mathcal{P}\mathcal{D})}{{\lambda }_{min}(\mathcal{P})}+\frac{{\rho }^2{\lambda }_{max}({\mathcal{B}}^T{\mathcal{P}}^T\mathcal{P}\mathcal{B})}{{\lambda }_{min}(\mathcal{P})}+{\xi }_1\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}+r({\xi }_2\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}+1)\hfill \\ \hfill & +r({\xi }_3+1)\frac{{\lambda }_{max}(\mathcal{P})}{{\lambda }_{min}(\mathcal{P})}-2k_1]{\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)-2k_2{({\lambda }_{min}(\mathcal{P}))}^{\gamma }{({\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t))}^{\gamma }\hfill \\ \hfill & \le -\beta {({\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t))}^{\gamma }\hfill \\ \hfill & \le -\beta V_1^{\gamma }(t),\hfill \end{array}$$

where $\beta =2k_2{({\lambda }_{min}(\mathcal{P}))}^{\gamma }>0$, $0<\gamma =\frac{1+a}{2}<1$. It follows that $\mathcal{L}V(t)\le 0$, and it is apparent that V is decrementing with time t in probability. Taking the expectations of both sides, we have $EV(t)-EV(t_0)\le -\beta {\int }_{t_0}^{t}E{V}_1^{\gamma }(s)\mathrm{d}s\le 0.$ Taking $V_2={(k_1-\widehat{k})}^2\le V$ into consideration, we can see that there exists a constant $C>0$ to satisfy $\widehat{k}\le C$. Therefore,

$$\begin{array}{cc}\hfill \mathcal{L}{V}_1(t)& =\mathcal{L}V(t)-\mathcal{L}{V}_2(t)\le -\beta V_1^{\gamma }(t)+2(k_1-\widehat{k}){\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)\le -\beta V_1^{\gamma }(t)+2(k_1-\widehat{k})V_1(t)\hfill \\ \hfill & \le -\beta V_1^{\gamma }(t)+2(k_1+C)V_1(t)=-\frac{\beta }{2}{V}_1^{\gamma }(t)+[(2k_1+2C)V_1^{1-\gamma }(t)-\frac{\beta }{2}]{V_1}^{\gamma }(t).\hfill \end{array}$$

In the following, we give a constant $M={\left(\frac{\beta }{4(k_1+C)}\right)}^{\frac{1}{1-\gamma }},$ then we can assume that there exist $t_1$, so that $E{V}_1(t_1)\le M$. If not, we have

$$EV(t_0)\ge EV(t_0)-EV(t)\ge \beta {\int }_{t_0}^{t}E{V}_1^{\gamma }(s)\mathrm{d}s\ge \beta M^{\gamma }(t-t_0).$$

However, $V(t_0)$ is bounded, which is a contradiction. Then, we obtain $E{V}_1(t_1)\le M$, when $t>t_1$; that is, $E(\mathcal{L}{V}_1(t))\le -\frac{\beta }{2}E{V}_1^{\gamma }(t)$. Then, we have

$$E{V}_1(t)-E{V}_1(s)={\int }_s^{t}E(\mathcal{L}{V}_1(\tau ))\mathrm{d}\tau \le -\frac{\beta }{2}{\int }_s^{t}E{V}_1^{\gamma }(\tau )\mathrm{d}\tau \le 0,$$

(13)

whenever $t>s>t_1$.

Next, we will illustrate that the trivial solution of system (5) is finite-time stable in probability, which is similar to the proof method of Theorem 3.1 in reference [40]. Let $0<\epsilon <1$ and $r>0$. Let ${\delta }_r=inf\{t:|\mathcal{X}(t,{\mathcal{X}}_0)|>r\}$. Applying $It{\widehat{o}}^{’}\mathrm{s}$ formula and (13), we have $E{V}_1(\mathcal{X}(t\wedge {\delta }_r))\le V_1({\mathcal{X}}_0).$ Then,

$$\begin{array}{cc}\hfill P_{({\delta }_r\le t)}{V}_1(r)& \le E\left(I_{\{{\delta }_r\le t\}}{V}_1(\mathcal{X}({\delta }_r))\right)\le E\left(V_1(\mathcal{X}(t\wedge {\delta }_r))\right)\le E\left(V_1({\mathcal{X}}_0)\right)\le V_1({\mathcal{X}}_0).\hfill \end{array}$$

Taking $\delta =V_1^{-1}\left(V_1(r)\epsilon \right)$, we obtain that $P({\delta }_r<t)\le \epsilon$ whenever $|{\mathcal{X}}_0|<\delta$. Letting $t\to \infty$, we derive $P({\delta }_r<\infty )\le \epsilon$, which is $P({sup}_{t\ge 0}|\mathcal{X}(t,{\mathcal{X}}_0)|\le r)\ge 1-\epsilon ,$ which completes the proof of (i) in Definition 2.

Without loss of generality, we only need to prove the required result when ${\mathcal{X}}_0\in R^{2n}\backslash \left\{0\right\}.$ We define ${\tau }_n=inf\{t>t_0,\mathcal{X}(t,{\mathcal{X}}_0)\notin (\frac{1}{n},n)\},$ where $n\in \{1,2,3,\dots \}$. We set ${\tau }_{\infty }={lim}_{n\to \infty }{\tau }_n$. For arbitrary $0\le s\le t$, we have

$$\begin{array}{cc}\hfill E{V}_1(\mathcal{X}(t\wedge {\tau }_n))& =E{V}_1(\mathcal{X}(s\wedge {\tau }_n))+E{\int }_{s\wedge {\tau }_n}^{t\wedge {\tau }_n}\mathcal{L}{V}_1(\mathcal{X}(\tau ))\mathrm{d}\tau \hfill \\ \hfill & =E{V}_1(\mathcal{X}(s\wedge {\tau }_n))+{\int }_s^{t}E[I_{\{\tau \le {\tau }_n\}}{V}_1(\mathcal{X}(\tau ))]\mathrm{d}\tau .\hfill \end{array}$$

(14)

On one hand, it is easily seen that

$$\begin{array}{cc}\hfill & E{V}_1(\mathcal{X}(t\wedge {\tau }_n))-E{V}_1(\mathcal{X}(s\wedge {\tau }_n))\hfill \\ \hfill & =E[I_{\{t\le {\tau }_n\}}{V}_1(\mathcal{X}(t))]-E[I_{\{s\le {\tau }_n\}}{V}_1(\mathcal{X}(s))]+E[(I_{\{t>{\tau }_n\}}-I_{\{s>{\tau }_n\}})V_1(\mathcal{X}({\tau }_n))]\hfill \\ \hfill & \ge E[I_{\{t\le {\tau }_n\}}{V}_1(\mathcal{X}(t))]-E[I_{\{s\le {\tau }_n\}}{V}_1(\mathcal{X}(s))].\hfill \end{array}$$

(15)

On the other hand, for any $s\in [0,+\infty \}$, we can derive that

$$\begin{array}{c}\hfill I_{\{s\le {\tau }_n\}}{V}_1(\frac{1}{n})\le I_{\{s\le {\tau }_n\}}{V}_1(\mathcal{X}(s))\le I_{\{s\le {\tau }_n\}}{V}_1(n).\end{array}$$

(16)

Combining (15) and (16), we have

$$\begin{array}{cc}\hfill E[I_{\{s\le {\tau }_n\}}\mathcal{L}{V}_1(\mathcal{X}(s))]& \le -\frac{\beta }{2}E[I_{\{s\le {\tau }_n\}}{V}_1^{\gamma }(\mathcal{X}(s))]=-\frac{\beta }{2}E{[I_{\{s\le {\tau }_n\}}{V}_1(\mathcal{X}(s))]}^{\gamma }\hfill \\ \hfill & \le -\frac{\beta }{2}\frac{V{\gamma }_1(\frac{1}{n})}{V_1^{\gamma }(n)}{[E{I}_{\{s\le {\tau }_n\}}{V}_1(\mathcal{X}(s))]}^{\gamma }.\hfill \end{array}$$

(17)

Let $C_n=-\frac{\beta }{2}\frac{V_1^{\gamma }(\frac{1}{n})}{V_1^{\gamma }(n)}$. It is obvious that $C_n$ is strictly decreasing and converges to zero as $n\to \infty$. Combining (15)–(17), we obtain

$$\begin{array}{cc}\hfill & E[I_{\{t\le {\tau }_n\}}{V}_1(\mathcal{X}(t))]-E[I_{\{s\le {\tau }_n\}}{V}_1(\mathcal{X}(s))]\le C_n{\int }_s^t{[E{I}_{\{\tau \le {\tau }_n\}}{V}_1(\mathcal{X}(\tau ))]}^{\gamma }\mathrm{d}\tau .\hfill \end{array}$$

(18)

Defining $h(t)=E[I_{\{t\le {\tau }_n\}}{V}_1(\mathcal{X}(t))]$, we obtain from (17) that $h(t)-h(s)\le -C_n{\int }_s^t{[h(\tau )]}^{\gamma }\mathrm{d}\tau .$ According to Lemma 2, we have

$$h(t)\le {[h^{1-\gamma }(t_1)-C_n(1-\gamma )(t-t_1)]}^{\frac{1}{1-\gamma }},\forall t\in [t_1,T].$$

Then, we choose $T_n=t_1+\frac{V_1^{1-\gamma }({\mathcal{X}}_0)}{C_n(1-\gamma )}.$ We can obtain a sequence $T_n$, such that

$$h(T_n)=E[I_{\{T_n\le {\tau }_n\}}{V}_1(\mathcal{X}(T_n))]=0.$$

From the definition of ${\tau }_n$ and $V_1$ as positive definite, we have $P(T_n\le {\tau }_n)=0$. Let $n\to \infty$, and we obtain $P({\tau }_{\infty }=\infty )=P(|\mathcal{X}(t,{\mathcal{X}}_0)|>0,forallt\ge 0)=0$, which implies that $P({\tau }_{{\mathcal{X}}_0}<\infty )=1$, when ${\tau }_{{\mathcal{X}}_0}=inf\{t;\mathcal{X}(t,{\mathcal{X}}_0)=0\}$. Then, we complete the proof of (ii) in Definition 2. The proof is complete.

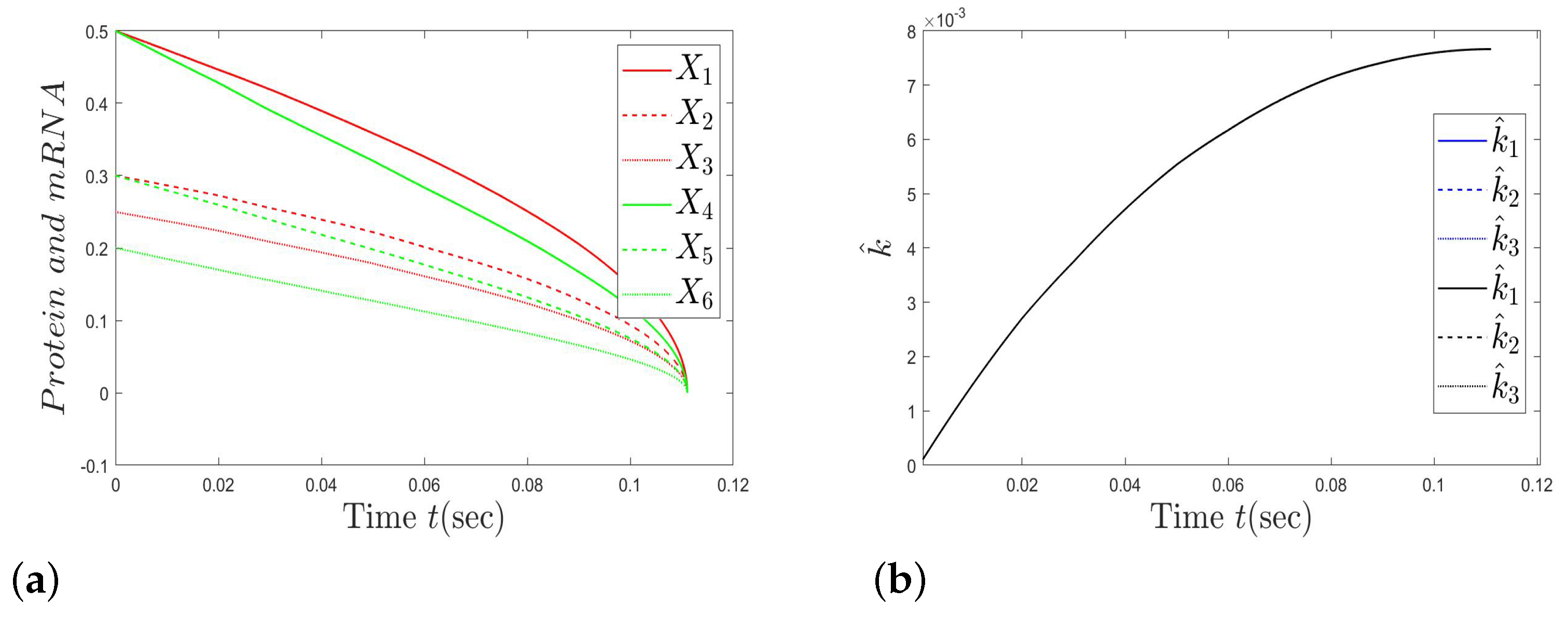
Remark 1.

For SGRNs (5), we utilize a novel adaptive controller (6) to automatically adjust the feedback gains under the condition that some information in gene regulation cannot be obtained. Here, we do not need to know some of the parameter information in gene regulation, such as the value of the upper bound of ρ in the nonlinear part. Furthermore, when designing the controller, the controller gain is relatively large in the general method to ensure that the system can reach a stable state. However, in the adaptive case, the gain can automatically adjust over time and does not need to take all cases; so, the value is relativity small.

4. Finite-Time Stability in Probability of Switched SGRNs with Time-Varying Delays

In this section, we consider the switched situation, which can be seen as Formula (4). The controller for switched SGRNs is designed as

$$\begin{array}{cc}\hfill u(t)& =-\widehat{k}\mathcal{X}(t)-k_2{\mathrm{sig}}^a(P_{\sigma }\mathcal{X}(t)),\hfill \end{array}$$

(19)

where $\gamma =\frac{1+a}{2}$, $k_2>0$, $0<a<1$ are constants, and positive definite matrix $P_{\sigma }$ satisfies Equation (8). $\widehat{k}$ is the adaptive feedback gain with

$$\dot{\widehat{k}}={\mathcal{X}}^T(t)P_{\sigma }\mathcal{X}(t)$$

(20)

and the initial values $\widehat{k}(t_0)>0$.

Definition 3

([51]). For any $T>t>0$, let $N_{\sigma }(t,T)$ represent the switch times on interval $(t,T)$. If

$$N_{\sigma }(T,t)\le N_0+\frac{T-t}{{\tau }_a}$$

holds for any given $N_0\ge 0,{\tau }_a>0$, then the constant ${\tau }_a$ is called the average dwell time, and $N_0$ is the chatter bound. As commonly used in the literature, we choose $N_0=0$.

Lemma 7

([50]). For arbitrary real numbers $x_i,i=1,2,\dots ,n$, $0<b<1$, we have

$$(|x_1|+|x_2|+\dots |x_n{|)}^b\le (|x_1{|}^b+|x_2{|}^b+...+|x_n{|}^b).$$

(21)

Theorem 2.

For system (4), if there exist multiple Lyapunov functions $V_{\sigma (t)}(\mathcal{X}(t),t)\in {\mathcal{C}}^{2,1}(R^{2n}\times [-\tau ,\infty );R_{+})$, $K_{\infty }$ class function ${\alpha }_{1\sigma (t)}$ and ${\alpha }_{2\sigma (t)}$, where $\sigma (t):[0,+\infty )\to \mathcal{N}=\{1,2,\dots ,N\}$, such that:

$$\begin{array}{cc}\hfill & (i){\alpha }_{1\sigma (t)}(|\mathcal{X}(t)|)\le V_{\sigma (t)}(\mathcal{X}(t),t)\le {\alpha }_{2\sigma (t)}(\underset{s\in [-\tau ,0]}{sup}\left|\mathcal{X}(t+s)\right|),\hfill \\ \hfill & (ii)\mathcal{L}{V}_{\sigma (t)}(\mathcal{X}(t),t)\le -\beta {(V_{\sigma (t)}(\mathcal{X}(t),t))}^{\gamma },\hfill \\ \hfill & (iii)V_{\sigma (t_k)}\le \overline{\lambda }{V}_{\sigma (t_k^{-})},\hfill \\ \hfill & (iv)q\beta (1-\gamma ){\tau }_a\ge ({\overline{\lambda }}^{1-\gamma }-1)V^{1-\gamma }(0),\hfill \end{array}$$

where $\beta >0$, $0<\gamma <1$, $0<q<1$ and $\overline{\lambda }>1$ are real constants, $t_k$ is the switched time, and $V(0)=V_{\sigma (t_0)}({\mathcal{X}}_0)$ is the initial value, then the trivial solution of system (4) is finite-time stable in probability.

Proof. 

Consider $V_{\sigma (t)}(\mathcal{X}(t),t)$, $\sigma (t):[0,+\infty )\to \mathcal{N}=\{1,2,\dots ,N\}$, which, in this paper, we shorten to $V_{\sigma }(t)$. Let $0<\epsilon <1$ and $r>0$. We define ${\delta }_r=inf\{t;|\mathcal{X}(t;{\mathcal{X}}_0)|>r\}$. For $\forall k\in N$, we consider $t\in [t_k,t_{k+1})$. By $It{\widehat{o}}^{’}\mathrm{s}$ Formulas (15) and (16), for arbitrary $t_k\le s<t$, we have

$$\begin{array}{cc}\hfill E[I_{\{t\le {\delta }_r\}}{V}_{\sigma }(t)]& \le E[I_{\{s\le {\delta }_r\}}{V}_{\sigma }(s)]+{\int }_s^{t}E[I_{\{\tau \le {\delta }_r\}}\mathcal{L}{V}_{\sigma }(\tau )]\mathrm{d}\tau \hfill \\ \hfill & \le E[I_{\{s\le {\delta }_r\}}{V}_{\sigma }(s)]-\beta {\int }_s^{t}E[I_{\{\tau \le {\delta }_r\}}{V}_{1\sigma }^{1-\gamma }(\tau )]\mathrm{d}\tau \hfill \\ \hfill & =E[I_{\{s\le {\delta }_r\}}{V}_{\sigma }(s)]-\beta {\int }_s^{t}E[{(I_{\{\tau \le {\delta }_r\}}{V}_{\sigma }(\tau ))}^{1-\gamma }]\mathrm{d}\tau \hfill \\ \hfill & \le E[I_{\{s\le {\delta }_r\}}{V}_{\sigma }(s)]-\beta {\int }_s^t{(E[I_{\{\tau \le {\delta }_r\}}{V}_{\sigma }(\tau )])}^{1-\gamma }\mathrm{d}\tau .\hfill \end{array}$$

(22)

□

Let $\varphi (t)=E[I_{\{t\le {\delta }_r\}}{V}_{\sigma }(t)]$, from (22), we have

$$\varphi (t)\le \varphi (s)-\beta {\int }_s^t{\varphi }^{1-\gamma }(\tau )\mathrm{d}\tau ,t_k\le s<t<t_{k+1};$$

(23)

then, by Lemma 2, we have

$${\varphi }^{1-\gamma }(t)\le {\varphi }^{1-\gamma }(s)-\beta (1-\gamma )(t-s),t_k\le s<t<t_{k+1}.$$

(24)

Next we will use mathematical induction to prove that $\varphi (t)\le \varphi (t_0),\forall t\ge t_0$. Since $V_{\sigma (t_k)}(t_k)\le \overline{\lambda }{V}_{\sigma (t_k^{-})}(t_k^{-})$, which is $\varphi (t_k)\le \overline{\lambda }\varphi (t_k^{-})$, and from (24), we have

$$\begin{array}{cc}\hfill {\varphi }^{1-\gamma }(t_1)& \le {\overline{\lambda }}^{1-\gamma }\varphi (t_1^{-})\le {\overline{\lambda }}^{1-\gamma }({\varphi }^{1-\gamma }(t_0)-\beta (1-\gamma )(t_1-t_0))\hfill \\ \hfill & \le {\overline{\lambda }}^{1-\gamma }{\varphi }^{1-\gamma }(t_0)-\beta (1-\gamma ){\tau }_a={\overline{\lambda }}^{1-\gamma }{\varphi }^{1-\gamma }(t_0)-\beta (1-\gamma )\frac{({\overline{\lambda }}^{1-\gamma }-1){\varphi }^{1-\gamma }(t_0)}{q\beta (1-\gamma )}\hfill \\ \hfill & \le {\varphi }^{1-\gamma }(t_0).\hfill \end{array}$$

We assume that ${\varphi }^{1-\gamma }(t)\le {\varphi }^{1-\gamma }(t_0)$, whenever $t_{k-1}\le t<t_k$. Considering an arbitrary $t\le t_k$, we obtain

$$\begin{array}{cc}\hfill {\varphi }^{1-\gamma }(t)& \le {\varphi }^{1-\gamma }(t_k)-\beta (1-\gamma )(t-t_k)\le {\overline{\lambda }}^{1-\gamma }\varphi (t_k^{-})-\beta (1-\gamma )(t-t_k)\hfill \\ \hfill & \le {\overline{\lambda }}^{1-\gamma }({\varphi }^{1-\gamma }(t_{k-1})-\beta (1-\gamma )(t_k-t_{k-1}))-\beta (1-\gamma )(t-t_k)\hfill \\ \hfill & \le {\varphi }^{1-\gamma }(t_{k-1})+({\overline{\lambda }}^{1-\gamma }-1){\varphi }^{1-\gamma }(t_{k-1})-\beta {\overline{\lambda }}^{1-\gamma }(1-\gamma )(t_k-t_{k-1})-\beta (1-\gamma )(t-t_k)\hfill \\ \hfill & \le {\varphi }^{1-\gamma }(t_{k-1})+q\beta (1-\gamma ){\tau }_a-\beta {\overline{\lambda }}^{1-\gamma }(1-\gamma )(t_k-t_{k-1})-\beta (1-\gamma )(t-t_k)\hfill \\ \hfill & \le {\varphi }^{1-\gamma }(t_{k-1})-({\overline{\lambda }}^{1-\gamma }-q)\beta (1-\gamma )(t_k-t_{k-1})-\beta (1-\gamma )(t-t_k)\hfill \\ \hfill & \le {\varphi }^{1-\gamma }(t_{k-1})\hfill \\ \hfill & \le {\varphi }^{1-\gamma }(t_0).\hfill \end{array}$$

(25)

The next proofs are almost identical to Theorem 1, the major change being the substitution of $V_{\sigma }(t)$ for $V(t)$. Next, we prove it in simple steps. Since $E{V}_{\sigma }(t\wedge {\sigma }_r))\le V(t_0)$, together with the condition (i), we have

$$\begin{array}{cc}\hfill P_{({\delta }_r\le t)}{\alpha }_{1\sigma }(r)& \le E(I_{\{{\delta }_r\le t\}}{V}_{\sigma }({\delta }_r))\le E(V_{\sigma }(t\wedge {\delta }_r))\le E(V_{\sigma }(t_0))\le {\alpha }_{2\sigma }(t_0).\hfill \end{array}$$

Taking $\delta ={\alpha }_{2\sigma }^{-1}({\alpha }_{1\sigma }(r)\epsilon )$, we obtain $P({\sigma }_r<t)\le \epsilon$ whenever $|{\mathcal{X}}_0|<\delta$. Letting $t\to \infty$, we derive $P({\sigma }_r<\infty )\le \epsilon$, which implies that $P({sup}_{t\ge 0}|\mathcal{X}(t,{\mathcal{X}}_0)|\le r)\ge 1-\epsilon ,$ and we can obtain the stability in probability.

In the same way as Theorem 1, we define ${\tau }_n=inf\{t>t_0,\mathcal{X}(t,{\mathcal{X}}_0)\notin (\frac{1}{n},n)\},$ where $n\in \{1,2,3,\dots \}$. We set ${\tau }_{\infty }={lim}_{n\to \infty }{\tau }_n$. The same as in (17),

$$E[I_{\{t\le {\tau }_n\}}V(t)]-E[I_{\{s\le {\tau }_n\}}V(s)]\le {\overline{C}}_n{\int }_s^t{[E{I}_{\{\tau \le {\tau }_n\}}V(\tau )]}^{\gamma }\mathrm{d}\tau ,$$

whenever $t_k\le s<t<t_{k+1}$ and ${\overline{C}}_n=-c\frac{{\alpha }_{1\sigma }^{\gamma }(\frac{1}{n})}{{\alpha }_{2\sigma }^{\gamma }(n)}$. Letting $l(t)=E[I_{\{t\le {\tau }_n\}}{V}_{\sigma }(t)]$, with Lemma 2, we obtain

$$l^{1-\gamma }(t)\le l^{1-\gamma }(s)-{\overline{C}}_n(1-\gamma )(t-s),t_k\le s<t<t_{k+1}.$$

As with (25), we also have

$$\begin{array}{cc}\hfill l^{1-\gamma }(t)& \le l^{1-\gamma }(t_k)-{\overline{C}}_n(1-\gamma )(t-t_k)\hfill \\ \hfill & \le l^{1-\gamma }(t_{k-1})-({\overline{\lambda }}^{1-\gamma }-q){\overline{C}}_n(1-\gamma )(t_k-t_{k-1})-{\overline{C}}_n(1-\gamma )(t-t_k)\hfill \\ \hfill & \le l^{1-\gamma }(t_{k-1})-{\overline{C}}_n(1-\gamma )\overline{a}(t-t_{k-1})\le l^{1-\gamma }(t_{k-2})-{\overline{C}}_n(1-\gamma )\overline{a}(t-t_{k-2})\hfill \\ \hfill & \le \dots \hfill \\ \hfill & \le l^{1-\gamma }(t_0)-{\overline{C}}_n(1-\gamma )\overline{a}(t-t_0),\hfill \end{array}$$

(26)

where $\overline{a}=min\{{\overline{\lambda }}^{1-\gamma }-q,1\}$. That is, $l^{1-\gamma }(t)\le l^{1-\gamma }(t_0)-{\overline{C}}_n(1-\gamma )(t-t_0),t\ge t_0.$ Then, we see that the system can achieve finite-time attractiveness in probability. The proof is complete.

Theorem 3.

For a given controller (19) and the adaptive law (20), the switched SGRNs (4) are finite-time stable in probability, if the dwell time satisfies

$${\tau }_a\ge \frac{2({\overline{\lambda }}^{1-\gamma }-1)V_1^{1-\gamma }(0)}{q\beta (1-\gamma )}$$

where $V_1(0)=V_{1\sigma (t_0)}({\mathcal{X}}_0)$ is the initial value of system (4), and $\overline{\lambda }={\overline{\lambda }}_{max}/{\underline{\lambda }}_{min}$, ${\overline{\lambda }}_{max}={max}_{1\le i\le N}({\lambda }_{max}(P_i))$, ${\underline{\lambda }}_{min}={min}_{1\le i\le N}({\lambda }_{min}(P_i))$. ${\lambda }_{max}(P_i)$ and ${\lambda }_{min}(P_i)$ denote the maximum and minimum eigenvalues of the positive definite matrix $P_i$, respectively. $\beta =2k_2{\underline{\lambda }}_{min}^{\gamma }>0$, $0<\gamma =\frac{1+a}{2}<1$, and $0<q<1$ is a constant.

Proof. 

We define

$$V_{\sigma }(t)=V_{1\sigma }(t)+V_2(t),$$

(27)

$$\begin{array}{cc}\hfill V_{1\sigma }(t)& ={\mathcal{X}}^T(t)P_{\sigma }\mathcal{X}(t),V_2(t)={(\widehat{k}-k_1)}^2.\hfill \end{array}$$

(28)

Let $k_1=\frac{1}{2}[-\frac{{\lambda }_{min}({\mathcal{Q}}_{\sigma })}{{\lambda }_{max}({\mathcal{P}}_{\sigma })}+\frac{{\lambda }_{max}({\mathcal{D}}_{\sigma }^T{\mathcal{P}}_{\sigma }{\mathcal{D}}_{\sigma })}{{\lambda }_{min}({\mathcal{P}}_{\sigma })}+\frac{{\rho }^2{\lambda }_{max}({\mathcal{B}}_{\sigma }^T{\mathcal{P}}_{\sigma }^T{\mathcal{P}}_{\sigma }{\mathcal{B}}_{\sigma })}{{\lambda }_{min}({\mathcal{P}}_{\sigma })}+{\xi }_1\frac{{\lambda }_{max}({\mathcal{P}}_{\sigma })}{{\lambda }_{min}({\mathcal{P}}_{\sigma })}+r({\xi }_2\frac{{\lambda }_{max}({\mathcal{P}}_{\sigma })}{{\lambda }_{min}({\mathcal{P}}_{\sigma })}+1)+r({\xi }_3+1)\frac{{\lambda }_{max}({\mathcal{P}}_{\sigma })}{{\lambda }_{min}({\mathcal{P}}_{\sigma })}]$, where $P_{\sigma }$ and $Q_{\sigma }$ satisfy Equation (8). □

It is easy to show that $\frac{V_{1\sigma (t_i)}}{V_{1\sigma (t_j)}}=\frac{{\mathcal{X}}^T{P}_{\sigma (t_i)}\mathcal{X}}{{\mathcal{X}}^T{P}_{\sigma (t_j)}\mathcal{X}}\le \overline{\lambda }.$ It follows that $V_{1\sigma (t_k)}\le \overline{\lambda }{V}_{1\sigma (t_k^{-})},$ for each switching time $t_k$. An argument similar to the analysis of Theorem 1 shows that $\mathcal{L}{V}_{\sigma }(t)\le -\beta V_{1\sigma }^{\gamma }(t),$ and

$$\begin{array}{cc}\hfill \mathcal{L}{V}_{1\sigma }=& \mathcal{L}{V}_{\sigma }-\mathcal{L}{V}_2\le -\frac{\beta }{2}{V}_{1\sigma }^{\gamma }+(2\parallel \tilde{k}\parallel V_{1\sigma }^{1-\gamma }-\frac{\beta }{2})V_{1\sigma }^{\gamma },\hfill \end{array}$$

where $\beta =2k_2{\underline{\lambda }}_{min}^{\gamma }>0$, and $0<\gamma =\frac{1+a}{2}<1$. In the formula, we note $V_{\sigma (t_0)}(t_0)=V_{\sigma }(0)$, $V_{1\sigma (t_0)}(t_0)=V_{1\sigma }(0)$, and define $h(t)=E{V}_{1\sigma (t)}(t)$. Let $C={\left(V_{\sigma }^{1-\gamma }(0)+\frac{V_{1\sigma }^{1-\gamma }(0)}{1-q}\right)}^{\frac{1}{1-\gamma }},M={\left(\frac{\beta }{4C^{\frac{1}{2}}}\right)}^{\frac{1}{1-\gamma }}.$ Next, we discuss the stability of system (4) in two situations.

In the first case, $h(t_0)\le M$, we can assume that $\parallel \tilde{k}{\parallel }^2\le C$ is uniformly bounded in this case, which will be proved by mathematical induction.

For each $t\in [t_k,t_{k+1})$, ${\dot{V}}_{\sigma (t)}(t)\le -\beta V_{1\sigma (t)}^{\gamma }(t)\le 0$, we have $\parallel \tilde{k}{\parallel }^2\le V_{\sigma (t_k)}(t_k).$ First when $t\in [t_0,t_1)$, we prove the conclusion is right; that is $\parallel \tilde{k}(t_0){\parallel }^2\le C$, and $h(t_1)\le M$. Using equation $\parallel \tilde{k}(t_0){\parallel }^2\le V_{\sigma (t_0)}(t_0)\le C$, we have

$$2\parallel \tilde{k}{\parallel }_2{h}^{1-\gamma }(t)-\frac{\beta }{2}\le 2C^{\frac{1}{2}}{h}^{1-\gamma }(t)-\frac{\beta }{2}\le 2C^{\frac{1}{2}}{M}^{1-\gamma }-\frac{\beta }{2}\le 0.$$

It follows that $h(t)-h(t_0)\le -\frac{\beta }{2}{\int }_{t_0}^t{h}^{\gamma }(\tau )\mathrm{d}\tau ,t\in [t_0,t_1).$ On account of Lemma 2, we have,

$$h^{1-\gamma }(t_1^{-})\le h^{1-\gamma }(t_0)-\frac{\beta }{2}(1-\gamma )(t_1-t_0).$$

Since $V_{1\sigma (t_1)}(t_1)\le \overline{\lambda }{V}_{1\sigma (t_1^{-})}(t_1^{-})$; that is, $h(t_1)\le \overline{\lambda }h(t_1^{-})$, we obtain

$$\begin{array}{c}\hfill h^{1-\gamma }(t_1)\le {\overline{\lambda }}^{1-\gamma }{h}^{1-\gamma }(t_1^{-})\le {\overline{\lambda }}^{1-\gamma }(h^{1-\gamma }(t_0)-\frac{\beta }{2}(1-\gamma )(t_1-t_0)).\end{array}$$

With the condition $t_1-t_0\ge {\tau }_a$, we obtain

$$\begin{array}{cc}\hfill & h^{1-\gamma }(t_1)\le {\overline{\lambda }}^{1-\gamma }(h^{1-\gamma }(t_0)-\frac{\beta }{2}(1-\gamma )(t_1-t_0))\le {\overline{\lambda }}^{1-\gamma }(h^{1-\gamma }(t_0)-\frac{\beta }{2}(1-\gamma ){\tau }_a)\hfill \\ \hfill & \le {\overline{\lambda }}^{1-\gamma }(h^{1-\gamma }(t_0)-\frac{\beta }{2}(1-\gamma )\frac{2({\overline{\lambda }}^{1-\gamma }-1)h^{1-\gamma }(0)}{q\beta (1-\gamma )})\le {\overline{\lambda }}^{1-\gamma }(1-\frac{{\overline{\lambda }}^{1-\gamma }-1}{q})h^{1-\gamma }(t_0)\hfill \\ \hfill & \le {\overline{\lambda }}^{1-\gamma }(1-\frac{{\overline{\lambda }}^{1-\gamma }-q}{{\overline{\lambda }}^{1-\gamma }})h^{1-\gamma }(t_0)\le q{h}^{1-\gamma }(t_0),\hfill \end{array}$$

and it follows that $h(t_1)\le h(t_0)\le M$.

Second, we prove $\parallel \tilde{k}{\parallel }^2\le C$, and $h(t_{k+1})\le M$ in section $[t_k,t_{k+1})$, when $h(t)\le M$, and $\parallel \tilde{k}{\parallel }^2\le C,[t_0,t_k)$ holds.

Based on the above assumptions, we have $h(t)\le M$ and $\parallel \tilde{k}{\parallel }^2\le C$ in section $[t_0,t_k)$. Then,

$$h(t)-h(t_0)\le -\frac{\beta }{2}{\int }_{t_0}^t{h}^{\gamma }(\tau )\mathrm{d}\tau ,t\in [t_0,t_k).$$

(29)

When $t\in [t_k,t_{k+1})$, we have

$$\begin{array}{cc}\hfill & h^{1-\gamma }(t_{k+1})\le {\overline{\lambda }}^{1-\gamma }{h}^{1-\gamma }(t_{k+1}^{-})\le {\overline{\lambda }}^{1-\gamma }(h^{1-\gamma }(t_k)-\frac{\beta }{2}(1-\gamma )(t_{k+1}-t_k))\hfill \\ \hfill & \le {\overline{\lambda }}^{1-\gamma }(h^{1-\gamma }(t_k)-\frac{\beta }{2}(1-\gamma ){\tau }_a)\le {\overline{\lambda }}^{1-\gamma }(h^{1-\gamma }(t_k)-\frac{\beta }{2}(1-\gamma )\frac{2({\overline{\lambda }}^{1-\gamma }-1)h^{1-\gamma }(0)}{q\beta (1-\gamma )})\hfill \\ \hfill & \le {\overline{\lambda }}^{1-\gamma }(h^{1-\gamma }(t_k)-\frac{\beta }{2}(1-\gamma )\frac{2({\overline{\lambda }}^{1-\gamma }-1)h^{1-\gamma }(t_k)}{q\beta (1-\gamma )})\le {\overline{\lambda }}^{1-\gamma }(1-\frac{{\overline{\lambda }}^{1-\gamma }-1}{q})h^{1-\gamma }(t_k)\hfill \\ \hfill & \le {\overline{\lambda }}^{1-\gamma }(1-\frac{{\overline{\lambda }}^{1-\gamma }-q}{{\overline{\lambda }}^{1-\gamma }})h^{1-\gamma }(t_k)\le q{h}^{1-\gamma }(t_k)\le q^2{h}^{1-\gamma }(t_{k-1})\hfill \\ \hfill & \le \dots \hfill \\ \hfill & \le q^k{h}^{1-\gamma }(t_0).\hfill \end{array}$$

It follows that $h(t_k)\le M$.

$$\begin{array}{cc}\hfill \parallel \tilde{k}{(t)\parallel }^{2(1-\gamma )}& \le {(h(t))}^{1-\gamma }\le {(h(t_k))}^{1-\gamma }=(h(t_k)+\parallel \tilde{k}(t_k){{\parallel }^2)}^{1-\gamma }\hfill \\ \hfill & \le h^{1-\gamma }(t_k)+\parallel \tilde{k}(t_k){\parallel }^{2(1-\gamma )}\le q^k{h}^{1-\gamma }(t_0)+{\parallel \tilde{k}(t_k)\parallel }^{2(1-\gamma )}\hfill \\ \hfill & \le \parallel \tilde{k}(t_0){\parallel }^{2(1-\gamma )}+\sum _{i=1}^k{q}^i{h}^{1-\gamma }(t_0)\le {\parallel \tilde{k}(t_0)\parallel }^{2(1-\gamma )}+\frac{1-q^k}{1-q}{h}^{1-\gamma }(t_0)\hfill \\ \hfill & \le V_{\sigma }^{1-\gamma }(t_0)+\frac{1}{1-q}{V}_{1\sigma }^{1-\gamma }(t_0).\hfill \end{array}$$

It can be obtained by opening the power on both sides that $\parallel \tilde{k}(t_k){\parallel }^2\le {\left(V_{\sigma (t_0)}^{1-\gamma }(t_0)+\frac{V_{1\sigma (t_0)}^{1-\gamma }(t_0)}{1-q}\right)}^{\frac{1}{1-\gamma }}.$ That is, $\parallel \tilde{k}{(t)\parallel }^2\le C,t\in [t_k,t_{k+1}).$

In the second case, $h(t_0)\ge M$. If there exists a constant $T_2$, such that $\widehat{k}(t)>k_1$, then

$$\begin{array}{cc}\hfill \mathcal{L}{V}_{1\sigma }=& \mathcal{L}{V}_{\sigma }-\mathcal{L}{V}_2\le -\beta V_{1\sigma }^{\gamma }+2(k_1-\widehat{k})V_{1\sigma }\le -\beta V_{1\sigma }^{\gamma },\hfill \end{array}$$

whenever $t>T_2$. We take $T_2$ as the starting time, and the conclusion can be proved as above.

If not, $\widehat{k}(t)\le k_1$ for $\forall t$. With the adaptive law of $\dot{\widehat{k}}(t)={\mathcal{X}}^T(t)P\mathcal{X}(t)>0$, we know that $\widehat{k}(t)$ is monotonically increasing and bounded with $k_1$. Then, there exists a constant $T_3$, such that $\parallel \widehat{k}(T_3)-k_1\parallel \le \frac{\beta }{4V_{\sigma }^{1-\gamma }(t_0)}$. By the above analysis, we obtain

$$\begin{array}{c}\hfill V_{1\sigma }^{1-\gamma }(T_3)\le V_{\sigma }^{1-\gamma }(T_3)\le V_{\sigma }^{1-\gamma }(t_0)\le \frac{\beta }{4\parallel \tilde{k}\parallel }.\end{array}$$

We take $T_3$ as the starting time, and in this case,

$$\begin{array}{cc}\hfill \mathcal{L}{V}_{1\sigma }=& \mathcal{L}{V}_{\sigma }-\mathcal{L}{V}_2\le -\frac{\beta }{2}{V}_{1\sigma }^{\gamma }+(2\parallel \tilde{k}\parallel V_{1\sigma }^{1-\gamma }-\frac{\beta }{2})V_{1\sigma }^{\gamma }\le -\frac{\beta }{2}{V}_{1\sigma }^{\gamma },\hfill \end{array}$$

whenever $t>T_3$, and the conclusion can be proved as above. Hence, the statements in Section 4 are proved in two cases. Then, we can obtain $\parallel \tilde{k}{(t)\parallel }^2\le C,t\ge 0$, when $h(t_0)\le M$. This means that equation (29) always holds. Proceeding as in the proof of the non-switched GRNs (5), we have the finite-time stability in probability of the switched SGRNs (4).

5. Numerical Examples

In this section, two examples are provided to verify the effectiveness of the results obtained in the previous section.

Example 1.

First, we consider a non-switched SGRN, and the relevant parameters are given as follows [43].

$$A=\left[\begin{array}{ccc}2.81& 0& 0\\ 0& 2.32& 0\\ 0& 0& 2.53\end{array}\right],B=\left[\begin{array}{ccc}0& 0.6& -0.6\\ -1.2& 0& 1.2\\ 0& -0.85& 0\end{array}\right],C=\left[\begin{array}{ccc}2.41& 0& 0\\ 0& 2.57& 0\\ 0& 0& 2.35\end{array}\right],$$

and $D=diag(0.92,1.02,0.98)$. We take the regulatory function as $f_i(p_i)=\frac{p_i^2}{1+p_i^2},(i=lacl,tetR,cl),$ and the time-varying delay is ${\tau }_1(t)=0.15+0.1cos(0.5t),{\tau }_2(t)=0.1+0.1sin(0.5t).$ Then, from Equation (8), it can be concluded that the adaptive matrix

$$\mathcal{P}=diag(0.1779,0.2155,0.1976,0.2075,0.1946,0.2128)$$

if we select $\mathcal{Q}=I$. Then, the controller can be designed as $u(t)=-\widehat{k}\mathcal{X}(t)-{\mathrm{sig}}^{\frac{1}{2}}(\mathcal{P}\mathcal{X}(t))$ with $\dot{\widehat{k}}={\mathcal{X}}^T(t)\mathcal{P}\mathcal{X}(t)$. The following state responses of the system (5) with adaptive controller (4) are shown in Figure 1, with the initial condition $m(0)={[0.2,0.3,0.2]}^T$, $p(0)={[0.6,0.4,0.45]}^T$.

Example 2.

We consider a switched time-varying delay SGRN with two subsystems.

$$A_1=\left[\begin{array}{ccc}2.1& 0& 0\\ 0& 1.2& 0\\ 0& 0& 2.5\end{array}\right],B_1=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right],C_1=\left[\begin{array}{ccc}4.6& 0& 0\\ 0& 4& 0\\ 0& 0& 5.2\end{array}\right]$$

$$A_2=\left[\begin{array}{ccc}1.8& 0& 0\\ 0& 2& 0\\ 0& 0& 3.1\end{array}\right],B_2=\left[\begin{array}{ccc}0& 0.7& 0\\ 0& 0& 0.7\\ 0.7& 0& 0\end{array}\right],C_2=\left[\begin{array}{ccc}5& 0& 0\\ 0& 4& 0\\ 0& 0& 5\end{array}\right]$$

$D_1=diag(0.5,0.4,0.6)$, $D_2=diag(0.3,0.3,0.4)$, and $f_i(p_i)=\frac{p_i^2}{1+p_i^2}.$ We assume that

$${\tau }_1(t)=0.15+0.1cos(0.5t),{\tau }_2(t)=0.1+0.1sin(0.5t),$$

$${\overline{\tau }}_1(t)=0.1+0.2sin(0.3t),{\overline{\tau }}_2(t)=0.15+0.2cos(0.3t).$$

Then, from Equation (8), it can be concluded that the adaptive matrix

$$P_1=diag(0.2381,0.4167,0.200,0.1087,0.1256,0.0962),$$

$$P_2=(0.2778,0.2500,0.1613,0.1000,0.1250,0.1000)$$

if we select $\mathcal{Q}=I$. In the above system, we assume that the first subsystem switches to the second subsystem after 0.3 s, while the second subsystem switches to the first subsystem after 0.4 s. For the first subsystem, we select the corresponding controller $u(t)=-\widehat{k}\mathcal{X}(t)-{\mathrm{sig}}^{\frac{1}{2}}({\mathcal{P}}_1\mathcal{X}(t))$ with $\dot{\widehat{k}}={\mathcal{X}}^T(t){\mathcal{P}}_1\mathcal{X}(t)$. For the second subsystem, the controller is $u(t)=-\widehat{k}\mathcal{X}(t)-{\mathrm{sig}}^{\frac{1}{2}}({\mathcal{P}}_2\mathcal{X}(t))$ with that $\dot{\widehat{k}}={\mathcal{X}}^T(t){\mathcal{P}}_2\mathcal{X}(t)$.

The simulation results of the mRNA and protein concentrations are shown in Figure 2, with the initial condition $m(0)={[0.5,0.3,0.25]}^T$, $p(0)={[0.5,0.3,0.2]}^T$. So, the system of switched GRNs with an adaptive controller (19) can achieve finite-time stability.

6. Conclusions

In this paper, the problem of finite-time stability was investigated for a class of switched SGRNs with uncertainties and time-varying delay. In particular, adaptive controllers in non-switched and switched SGRNs were designed, and the sufficient conditions for the systems to achieve finite-time stability in probability were given by a nonlinear matrix inequality, the Razumikhin theorem, and several stochastic analytical techniques. It should be pointed out that the proposed controllers require only partial system information and can shorten the time required for the system to achieve stability. Finally, two simulation examples were given in support of the proposed control scheme.