A New Process Performance Index for the Weibull Distribution with a Type-I Hybrid Censoring Scheme
Abstract
:1. Introduction
2. Proposed Life Performance Index
- (a)
- If , then .
- (b)
- If , then .
- (c)
- If , then .
3. Parameter Estimation Methods Based on Hybrid Censored Data
3.1. Maximum Likelihood Estimation
- Step 1:
- Step 2:
- Generate a new Type-I hybrid censored data from the Weibull distribution with parameter, , where is MLE of from Step 1.
- Step 3:
- Compute MLEs of and based on Type-I hybrid censored data and denote the obtained MLEs by and , respectively.
- Step 4:
- Repeat Step 2 to Step 3 times to obtain the bootstrap sample . Denote the empirical distribution based on the obtained bootstrap sample, by .
- Step 5:
- Given a significance level , find the th and th empirical quantiles of as the lower and upper limits of the confidence interval of , respectively.
3.2. Bayesian Estimation
- Step 1:
- Give initial values and propose the transition probability distributions, and , where and are the updates of and for the next step.
- Step 2:
- Implement Step 3 for , where B is a huge number.
- Step 3:
- (a)
- Generate and , where is the uniform distribution over the interval . Update according to the condition,
- (b)
- Generate and . Update according to the condition:
- (c)
- Step 4:
- Remove the first Markov chains for the burn-in operation. Re-coding the Markov chains of , , and . Considering the squared loss function for Bayesian estimation, the Bayes estimates , and can be, respectively, obtained by the sample means of the Markov chains of and , .
- Step 1:
- Sorting to obtain an ordered sequence of by , where for . The ordered sequence of is used to construct the empirical distribution of the Bayes estimator .
- Step 2:
- Find all intervals of that are labeled by , , where is the largest integer smaller or equal to y.
- Step 3:
- Find the interval that has the shortest length among all intervals in Step 2. The obtained interval is the HPDI.
4. Simulation Study
5. Examples
6. Conclusions and Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Proof of Theorem 1
- (a)
- Based on the condition ofwe can obtain the inequality ofMinus at the two sides of Inequality (A2), we obtainInequality (A3) can be represented byDividing at the two sides of Inequality (A4), we can show thatThen we can obtain the condition ofThus,
- (b)
- Based on similar inference procedures as (a), it is easy to show thatThus,Using (A8) for Equation (A9), we can show that .(c) Based on similar inference procedures as (a), it is easy to show thatThus,Using (A10) for Equation (A11), we can show that .
References
- Juran, J.M. Juran’s Quality Control Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Kane, V.E. Process capability indices. J. Qual. Technol. 1986, 18, 41–52. [Google Scholar] [CrossRef]
- Hsiang, T.C.; Taguchi, G. A tutorial on quality control and assurance-the Taguchi mthods. In Joint Meetings of the American Statistical Association; InASA Annual Meeting LA: Las Vegas, NV, USA, 1985; p. 188. [Google Scholar]
- Pearn, W.L.; Kotz, S.; Johnson, N.L. Distributional and inferential properties of process capability indices. J. Qual. Technol. 1992, 24, 216–231. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control, 6th ed.; John Wiley and Sons: New York, NY, USA, 2013; pp. 374–375. [Google Scholar]
- Clements, J.A. Process capability calculations for non-normal distributions. Qual. Prog. 1989, 22, 95–100. [Google Scholar]
- Epstein, B. Truncated life tests in the exponential case. Ann. Math. Stat. 1954, 25, 555–564. [Google Scholar] [CrossRef]
- Childs, A.; Chandrasekar, B.; Balakrishnan, N.; Kundu, D. Exact likelihood inference based on Type-I and Type-II hybrid censored samples from the exponential distribution. Ann. Inst. Stat. Math. 2003, 55, 319–330. [Google Scholar] [CrossRef]
- Lee, W.C. Statistical testing for assessing lifetime performance index of the Rayleigh lifetime products. J. Chin. Inst. Ind. Eng. 2008, 25, 433–445. [Google Scholar] [CrossRef]
- Hong, C.W.; Wu, J.W.; Cheng, C.H. Computational procedure of performance assessment of lifetime index of businesses for the Pareto lifetime model with the right type II censored sample. Appl. Math. Comput. 2007, 184, 336–350. [Google Scholar] [CrossRef]
- Lee, W.C.; Wu, J.W.; Hong, C.W. Assessing the lifetime performance index of products with the exponential distribution under progressively type II right censored samples. J. Comput. Appl. Math. 2009, 231, 648–656. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.F.; Lin, M.J. Computational testing algorithmic procedure of assessment for lifetime performance index of products with Weibull distribution under progressive type I interval censoring. J. Comput. Appl. Math. 2017, 311, 364–374. [Google Scholar] [CrossRef]
- Wang, Y.; He, S. Fisher information in censored data. Stat. Probab. Lett. 2005, 73, 199–206. [Google Scholar] [CrossRef]
- Kundu, D.; Pradhan, B. Estimating the parameters of the generalized exponential distribution in presence of hybrid censoring. Commun. Stat. Theory Methods 2009, 38, 2030–2041. [Google Scholar] [CrossRef]
- Lin, C.T.; Chou, C.C.; Huang, Y.L. Inference for the Weibull distribution with progressive hybrid censoring. Comput. Stat. Data Anal. 2012, 56, 451–467. [Google Scholar] [CrossRef]
- Cho, Y.; Sun, H.; Lee, K. Estimating the entropy of a Weibull distribution under generalized progressive hybrid censoring. Entropy 2015, 17, 102–122. [Google Scholar] [CrossRef] [Green Version]
- Okasha, H.; Mustafa, A. E-Bayesian estimation for the Weibull distribution under adaptive type-I progressive hybrid censored competing risks data. Entropy 2020, 22, 903. [Google Scholar] [CrossRef]
- Kundu, D. Bayesian inference and life testing plan for the Weibull distribution in presence of progressive censoring. Technometrics 2008, 50, 144–154. [Google Scholar] [CrossRef]
- Kundu, D. On hybrid censored Weibull distribution. J. Stat. Plan. Inference 2007, 137, 2127–2142. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar]
- Bain, L.J.; Engelhardt, M. Statistical Analysis of Reliability and Life-Testing Models; Marcel Dekker: New York, NY, USA, 1991. [Google Scholar]
- Joarder, A.; Krishna, H.; Kundu, D. Infrences on Weibull parameters with conventional type-I censoring. Comput. Stat. Data Anal. 2011, 55, 1–11. [Google Scholar] [CrossRef]
- Dodson, B. The Weibull Analysis Handbook, 2nd ed.; ASQ Quality Press: Milwaukee, WI, USA, 2006. [Google Scholar]
- Balakrishnan, N.; Kateri, M. On the maximum likelihood estimation of parameters of Weibull distribution based on complete and censored data. Stat. Probab. Lett. 2008, 55, 2971–2975. [Google Scholar] [CrossRef]
- Lieblein, J.; Zelen, M. Statistical investigation of the fatigue life of deep-groove ball bearings. J. Res. Natl. Bur. Stand. 1956, 57, 273–316. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Atieh, B.; Nadarajah, S. Lindley distribution and its application. Math. Comput. Simul. 2008, 78, 493–506. [Google Scholar] [CrossRef]
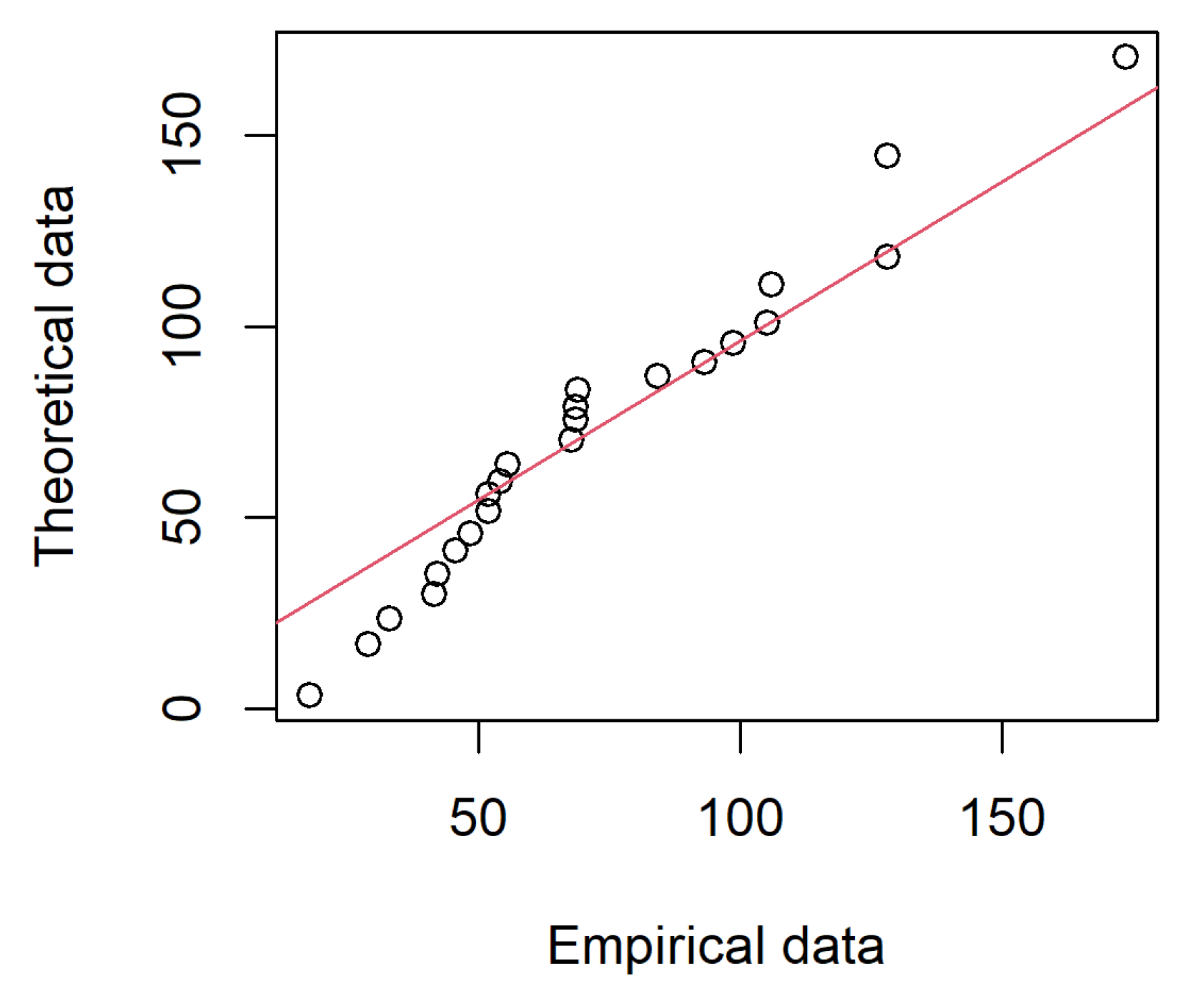
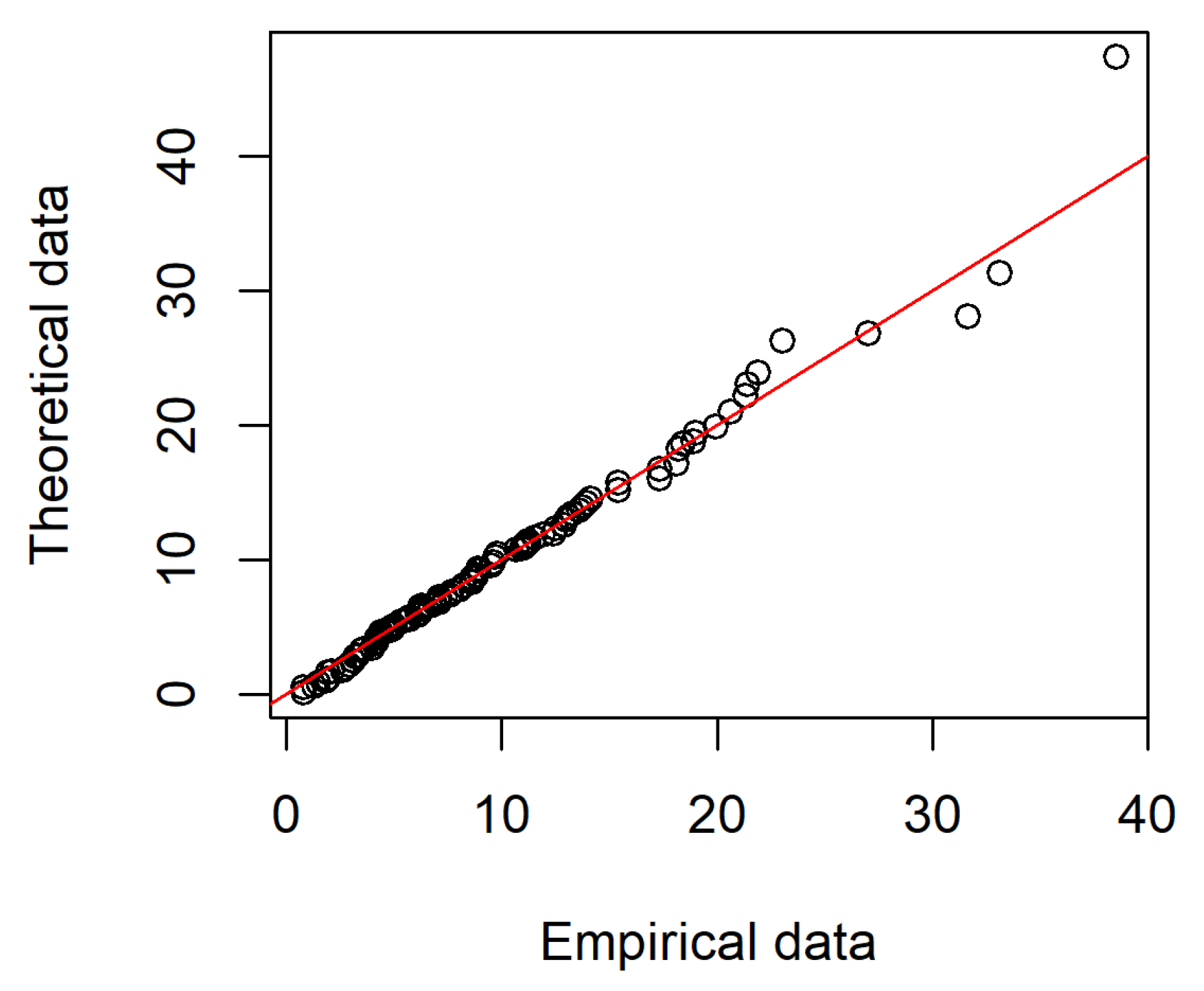
| r | Estimation | Coverage | ||||
|---|---|---|---|---|---|---|
| (30, 1) | 20 | MLE | 0.117 (0.013) | −0.022 (0.001) | 0.118 (0.014) | 0.864 |
| Non-info. | 0.063 (0.004) | 0.025 (0.001) | 0.051 (0.002) | 0.945 | ||
| Info. | 0.074 (0.005) | <0.001 (<0.001) | 0.062 (0.003) | 0.945 | ||
| 25 | MLE | 0.108 (0.011) | −0.023 (0.001) | 0.108 (0.011) | 0.862 | |
| Non-info. | 0.056 (0.003) | 0.022 (0.001) | 0.043 (0.001) | 0.948 | ||
| Info. | 0.066 (0.004) | −0.002 (<0.001) | 0.054 (0.002) | 0.949 | ||
| (30, 1.5) | 20 | MLE | 0.084 (0.007) | −0.011 (<0.001) | 0.084 (0.007) | 0.895 |
| Non-info. | 0.037 (0.001) | 0.022 (0.001) | 0.025 (0.002) | 0.950 | ||
| Info. | 0.043 (0.001) | 0.004 (<0.001) | 0.031 (0.001) | 0.950 | ||
| 25 | MLE | 0.070 (0.005) | −0.010 (<0.001) | 0.072 (0.005) | 0.899 | |
| Non-info. | 0.035 (0.001) | 0.006 (<0.001) | 0.027 (<0.001) | 0.948 | ||
| Info. | 0.034 (0.001) | −0.005 (<0.001) | 0.025 (0.001) | 0.944 | ||
| (50, 1) | 35 | MLE | 0.065(0.004) | −0.015 (<0.001) | 0.066 (0.004) | 0.893 |
| Non-info. | 0.035 (0.001) | 0.008 (<0.001) | 0.028 (0.001) | 0.949 | ||
| Info. | 0.040 (0.001) | −0.002 (<0.001) | 0.033 (0.001) | 0.949 | ||
| 40 | MLE | 0.064 (0.004) | −0.013 (<0.001) | 0.065 (0.004) | 0.892 | |
| Non-info. | 0.035 (0.001) | 0.010 (<0.001) | 0.028 (0.001) | 0.948 | ||
| Info. | 0.040 (0.002) | <−0.001 (<0.001) | 0.033 (0.001) | 0.950 | ||
| (50, 1.5) | 35 | MLE | 0.047 (0.002) | −0.006 (<0.001) | 0.048 (0.002) | 0.905 |
| Non-info. | 0.022 (0.001) | 0.009 (<0.001) | 0.015 (<0.001) | 0.947 | ||
| Info. | 0.024 (0.001) | 0.001 (<0.001) | 0.017 (<0.001) | 0.948 | ||
| 40 | MLE | 0.041 (0.001) | −0.003 (<0.001) | 0.042 (0.001) | 0.913 | |
| Non-info. | 0.020 (<0.001) | 0.007 (<0.001) | 0.015 (<0.001) | 0.949 | ||
| Info. | 0.020 (<0.001) | <0.001 (<0.001) | 0.014 (<0.001) | 0.945 |
| r | Estimation | Coverage | ||||
|---|---|---|---|---|---|---|
| (30, 1) | 20 | MLE | 0.113 (0.012) | −0.012 (<0.001) | 0.097 (0.009) | 0.874 |
| Non-info. | 0.059 (0.003) | 0.002 (<0.001) | 0.047 (0.002) | 0.951 | ||
| Info. | 0.057 (0.003) | 0.005 (<0.001) | 0.046 (0.002) | 0.953 | ||
| 25 | MLE | 0.113 (0.012) | −0.011 (<0.001) | 0.097 (0.009) | 0.864 | |
| Non-info. | 0.060 (0.003) | 0.003 (<0.001) | 0.049 (0.002) | 0.953 | ||
| Info. | 0.058 (0.003) | 0.006 (<0.001) | 0.048 (0.002) | 0.953 | ||
| (30, 1.15) | 20 | MLE | 0.090 (0.008) | −0.006 (<0.001) | 0.078 (0.006) | 0.883 |
| Non-info. | 0.043 (0.001) | 0.004 (<0.001) | 0.035 (0.001) | 0.946 | ||
| Info. | 0.041 (0.001) | 0.007 (<0.001) | 0.034 (0.001) | 0.943 | ||
| 25 | MLE | 0.073 (0.005) | −0.004 (<0.001) | 0.065 (0.004) | 0.896 | |
| Non-info. | 0.037 (0.001) | 0.001 (<0.001) | 0.031 (0.001) | 0.947 | ||
| Info. | 0.038 (0.001) | 0.002 (<0.001) | 0.033 (0.001) | 0.950 | ||
| (50, 1) | 35 | MLE | 0.066 (0.004) | −0.005 (<0.001) | 0.057 (0.003) | 0.900 |
| Non-info. | 0.036 (0.001) | 0.002 (<0.001) | 0.030 (0.001) | 0.951 | ||
| Bayes2 | 0.035 (0.001) | 0.003 (<0.001) | 0.029 (0.001) | 0.949 | ||
| 40 | MLE | 0.064 (0.004) | −0.006 (<0.001) | 0.055 (0.003) | 0.896 | |
| Non-info. | 0.035 (0.001) | 0.001 (<0.001) | 0.028 (0.001) | 0.946 | ||
| Info. | 0.034 (0.001) | 0.002 (<0.001) | 0.027 (0.001) | 0.947 | ||
| (50, 1.15) | 35 | MLE | 0.050 (0.003) | −0.003 (<0.001) | 0.044 (0.002) | 0.910 |
| Non-info. | 0.025 (0.001) | 0.003 (<0.001) | 0.020 (<0.001) | 0.946 | ||
| Info. | 0.024 (0.001) | 0.003 (<0.001) | 0.020 (<0.001) | 0.948 | ||
| 40 | MLE | 0.039 (0.002) | −0.003 (<0.001) | 0.034 (0.001) | 0.919 | |
| Non-info. | 0.017 (<0.001) | 0.001 (<0.001) | 0.014 (<0.001) | 0.948 | ||
| Info. | 0.017 (<0.001) | 0.002 (<0.001) | 0.014 (<0.001) | 0.951 |
| 17.88 | 28.92 | 33.00 | 41.52 | 42.12 | 45.60 |
| 48.48 | 51.84 | 51.96 | 54.12 | 55.56 | 67.80 |
| 68.64 | 68.64 | 68.88 | 84.12 | 93.12 | 98.64 |
| 105.12 | 105.84 | 127.92 | 128.04 | 173.40 |
| r | Estimation | Confidence Interval or HPDI | |||
|---|---|---|---|---|---|
| MLE (Complete data) | 2.1015 | 81.8743 | 1.7771 | (1.1403, 3.2407) | |
| 10 | MLE | 3.6093 | 63.7012 | 3.0302 | (1.9612, 6.5553) |
| Non-Info. | 3.2989 | 66.8305 | 2.7601 | (1.0169, 4.8253) | |
| Info. | 3.2638 | 68.3120 | 2.7290 | (1.1303, 4.4750) | |
| 16 | MLE | 2.4692 | 76.7007 | 2.1059 | (1.4421, 3.6492) |
| Non-Info. | 2.3351 | 79.3218 | 1.9704 | (0.8488, 3.1089) | |
| Info. | 2.3948 | 77.1740 | 2.0229 | (0.9891, 3.0498) | |
| 23 | MLE | 2.1059 | 76.7007 | 2.4692 | (1.4518, 3.7428) |
| Non-Info. | 2.3638 | 77.6118 | 1.9954 | (0.9942, 2.9651) | |
| Info. | 2.2771 | 79.1921 | 1.9138 | (0.9167, 2.9240) | |
| 0.8 | 0.8 | 1.3 | 1.5 | 1.8 | 1.9 | 1.9 | 2.1 | 2.6 | 2.7 |
| 2.9 | 3.1 | 3.2 | 3.3 | 3.5 | 3.6 | 4.0 | 4.1 | 4.2 | 4.2 |
| 4.3 | 4.3 | 4.4 | 4.4 | 4.6 | 4.7 | 4.7 | 4.8 | 4.9 | 4.9 |
| 5.0 | 5.3 | 5.5 | 5.7 | 5.7 | 6.1 | 6.2 | 6.2 | 6.2 | 6.3 |
| 6.7 | 6.9 | 7.1 | 7.1 | 7.1 | 7.1 | 7.4 | 7.6 | 7.7 | 8.0 |
| 8.2 | 8.6 | 8.6 | 8.6 | 8.8 | 8.8 | 8.9 | 8.9 | 9.5 | 9.6 |
| 9.7 | 9.8 | 10.7 | 10.9 | 11.0 | 11.0 | 11.1 | 11.2 | 11.2 | 11.5 |
| 11.9 | 12.4 | 12.5 | 12.9 | 13.0 | 13.1 | 13.3 | 13.6 | 13.7 | 13.9 |
| 14.1 | 15.4 | 15.4 | 17.3 | 17.3 | 18.1 | 18.2 | 18.4 | 18.9 | 19.0 |
| 19.9 | 20.6 | 21.3 | 21.4 | 21.9 | 23.0 | 27.0 | 31.6 | 33.1 | 38.5 |
| r | Estimation | Confidence Interval or HPDI | |||
|---|---|---|---|---|---|
| MLE (Complete data) | 1.4618 | 10.9768 | 1.1403 | (0.8396, 1.5746) | |
| 35 | MLE | 1.9736 | 8.7390 | 1.6373 | (1.2207, 2.3970) |
| Non-Info. | 1.9363 | 9.0463 | 1.5946 | (1.0437, 2.1372) | |
| Info. | 1.9062 | 9.1863 | 1.5673 | (1.0496, 2.1682) | |
| 70 | MLE | 1.6717 | 10.2163 | 1.3551 | (0.9573, 2.0706) |
| Non-Info. | 1.6539 | 10.3201 | 1.3338 | (0.9873, 1.6867) | |
| Info. | 1.6632 | 10.2737 | 1.3432 | (1.0167, 1.6850) | |
| 100 | MLE | 1.6426 | 10.3574 | 1.3263 | (1.0244, 1.7854) |
| Non-Info. | 1.6274 | 10.4279 | 1.3081 | (1.0028, 1.6236) | |
| Info. | 1.6232 | 10.3746 | 1.3031 | (0.9690, 1.6093) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, T.-R.; Lio, Y.; Chiang, J.-Y.; Huang, Y.-J. A New Process Performance Index for the Weibull Distribution with a Type-I Hybrid Censoring Scheme. Mathematics 2022, 10, 4090. https://doi.org/10.3390/math10214090
Tsai T-R, Lio Y, Chiang J-Y, Huang Y-J. A New Process Performance Index for the Weibull Distribution with a Type-I Hybrid Censoring Scheme. Mathematics. 2022; 10(21):4090. https://doi.org/10.3390/math10214090
Chicago/Turabian StyleTsai, Tzong-Ru, Yuhlong Lio, Jyun-You Chiang, and Yi-Jia Huang. 2022. "A New Process Performance Index for the Weibull Distribution with a Type-I Hybrid Censoring Scheme" Mathematics 10, no. 21: 4090. https://doi.org/10.3390/math10214090
APA StyleTsai, T.-R., Lio, Y., Chiang, J.-Y., & Huang, Y.-J. (2022). A New Process Performance Index for the Weibull Distribution with a Type-I Hybrid Censoring Scheme. Mathematics, 10(21), 4090. https://doi.org/10.3390/math10214090







