Convergence Behavior of Optimal Cut-Off Points Derived from Receiver Operating Characteristics Curve Analysis: A Simulation Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation Set-Up
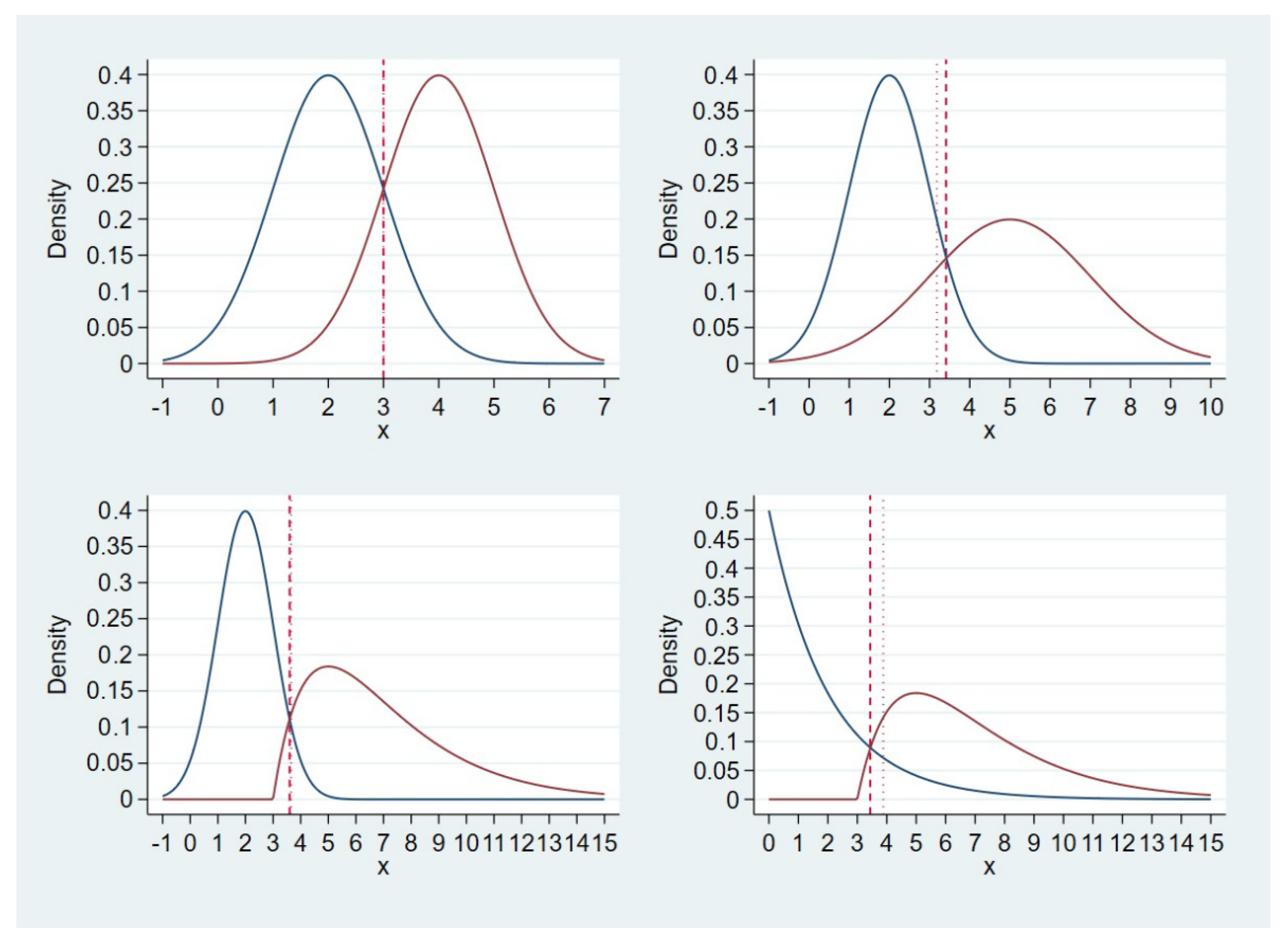
- Scenario 1: normal (mean = 2, variance = 1) and normal (mean = 4, variance = 1) for D0 and D1, respectively; top left corner of Figure 1;
- Scenario 2: normal (mean = 2, variance = 1) and normal (mean = 5, variance = 2) for D0 and D1, respectively; top right corner of Figure 1;
- Scenario 3: normal (mean = 2, variance = 1) and gamma (shape = 2, scale = 2, location = 3) for D0 and D1, respectively; bottom left corner of Figure 1;
- Scenario 4: exponential (scale = 2) and gamma (shape = 2, scale = 2, location = 3) for D0 and D1, respectively; bottom right corner of Figure 1.
2.2. Criterion for Optimality of a Cut-Off Point
2.3. True Optimal Cut-Off Points
- Closest-to-(0,1) criterion:;
- Liu’s method:;
- Youden index:.
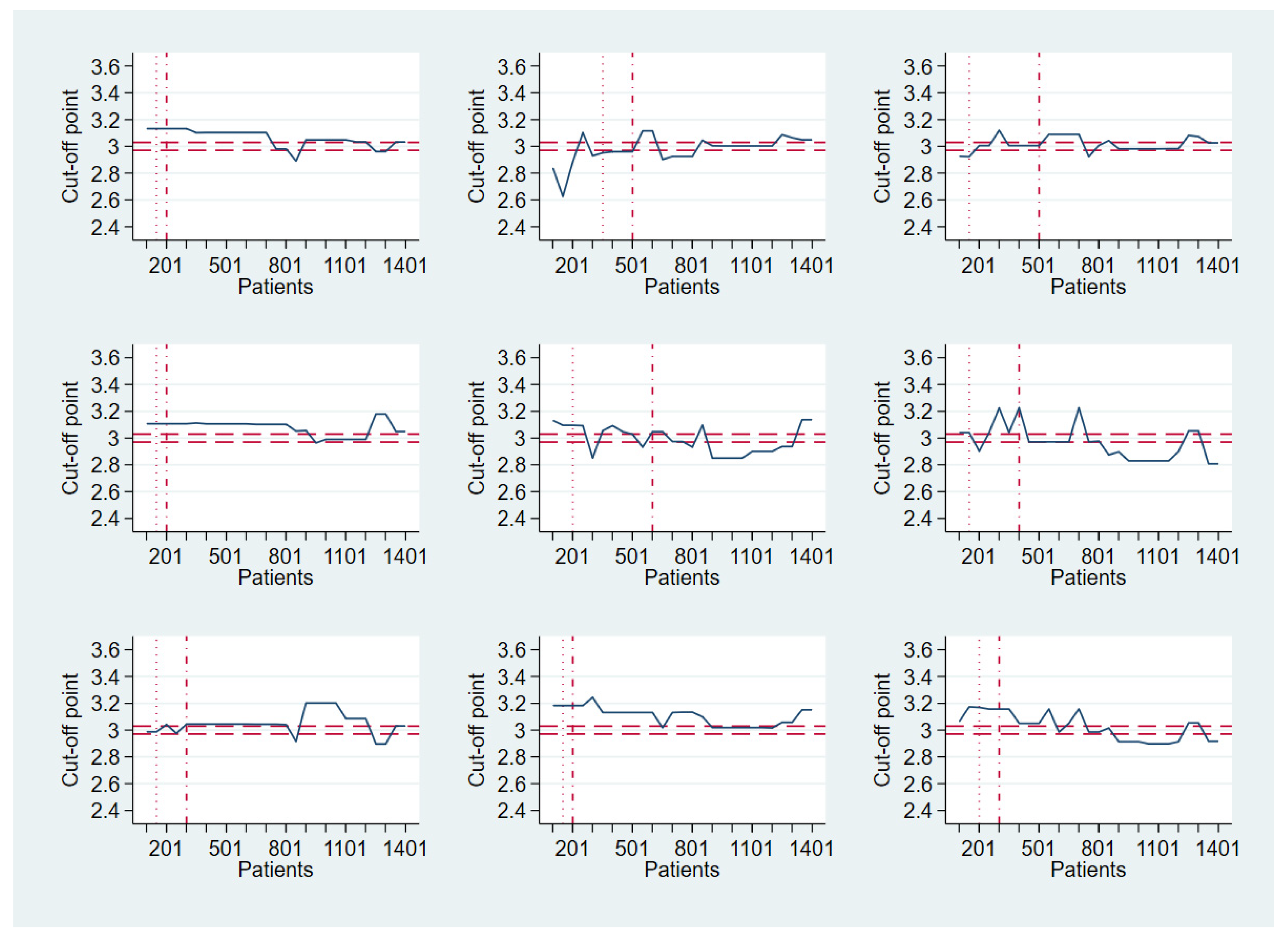
2.4. Convergence Behavior of Optimal Cut-off Points with Increasing Sample Size
2.5. A Heuristic and Path-Based Algorithm for Cut-Off Point Determination
2.6. Real-Life Example Data
3. Results
3.1. Fixed Sample Size
3.2. Heuristic and Path-Based Algorithm for Cut-Off Point Determination
4. Real-Life Example
5. Discussion
5.1. Main Findings
5.2. “Optimality” of a Cut-Off Point
5.3. Transferability of a Path-Based Design from Early Phase Cancer Research
5.4. Limitations of the Study
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Cook, N.R. Quantifying the added value of new biomarkers: How and how not. Diagn. Progn. Res. 2018, 2, 14. [Google Scholar] [CrossRef] [PubMed]
- Kuss, O. The danger of dichotomizing continuous variables: A visualization. Teach. Stat. 2013, 35, 78–79. [Google Scholar] [CrossRef]
- Altman, D.G.; Royston, P. The cost of dichotomising continuous variables. BMJ 2006, 332, 1080. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, S.S.; Levy, D.; Vasan, R.S.; Wang, T.J. The Framingham Heart Study and the epidemiology of cardiovascular disease: A historical perspective. Lancet 2014, 383, 999–1008. [Google Scholar] [CrossRef]
- D’Agostino, R.B., Sr.; Vasan, R.S.; Pencina, M.J.; Wolf, P.A.; Cobain, M.; Massaro, J.M.; Kannel, W.B. General cardiovascular risk profile for use in primary care: The Framingham Heart Study. Circulation 2008, 117, 743–753. [Google Scholar] [CrossRef] [PubMed]
- Framingham Heart Study. Available online: https://www.framinghamheartstudy.org/fhs-risk-functions/cardiovascular-disease-10-year-risk/ (accessed on 5 October 2022).
- Agatston, A.S.; Janowitz, W.R.; Hildner, F.J.; Zusmer, N.R.; Viamonte, M.; Detrano, R. Quantification of coronary artery calcium using ultrafast computed tomography. J. Am. Coll. Cardiol. 1990, 15, 827–832. [Google Scholar] [CrossRef]
- Diederichsen, A.C.; Mahabadi, A.A.; Gerke, O.; Lehmann, N.; Sand, N.P.; Moebus, S.; Lambrechtsen, J.; Kälsch, H.; Jensen, J.M.; Jöckel, K.H.; et al. Increased discordance between HeartScore and coronary artery calcification score after introduction of the new ESC prevention guidelines. Atherosclerosis 2015, 239, 143–149. [Google Scholar] [CrossRef]
- McClelland, R.L.; Jorgensen, N.W.; Budoff, M.; Blaha, M.J.; Post, W.S.; Kronmal, R.A.; Bild, D.E.; Shea, S.; Liu, K.; Watson, K.E.; et al. 10-Year Coronary Heart Disease Risk Prediction Using Coronary Artery Calcium and Traditional Risk Factors: Derivation in the MESA (Multi-Ethnic Study of Atherosclerosis) With Validation in the HNR (Heinz Nixdorf Recall) Study and the DHS (Dallas Heart Study). J. Am. Coll. Cardiol. 2015, 66, 1643–1653. [Google Scholar] [CrossRef]
- McClelland, R.L.; Chung, H.; Detrano, R.; Post, W.; Kronmal, R.A. Distribution of coronary artery calcium by race, gender, and age: Results from the Multi-Ethnic Study of Atherosclerosis (MESA). Circulation 2006, 113, 30–37. [Google Scholar] [CrossRef]
- MESA Homepage 10+. Available online: https://www.mesa-nhlbi.org/MESACHDRisk/MesaRiskScore/RiskScore.aspx (accessed on 5 October 2022).
- Zhou, X.H.; Obuchowski, N.A.; McClish, D.K. Statistical Methods in Diagnostic Medicine, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zou, K.H.; Liu, A.; Bandos, A.I.; Ohno-Machado, L.; Rockette, H.E. Statistical Evaluation of Diagnostic Performance: Topics in ROC Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Coffin, M.; Sukhatme, S. Receiver operating characteristic studies and measurement errors. Biometrics 1997, 53, 823–837. [Google Scholar] [CrossRef]
- Youden, W.J. Index for rating diagnostic tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Perkins, N.J.; Schisterman, E.F. The inconsistency of “optimal” cutpoints obtained using two criteria based on the receiver operating characteristic curve. Am. J. Epidemiol. 2006, 163, 670–675. [Google Scholar] [CrossRef] [PubMed]
- Liu, X. Classification accuracy and cut point selection. Stat. Med. 2012, 31, 2676–2686. [Google Scholar] [CrossRef]
- López-Ratón, M.; Rodríguez-Álvarez, M.X.; Cadarso-Suárez, C.; Gude-Sampedro, F. Optimalcutpoints: An R package for selecting optimal cutpoints in diagnostic tests. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Araujo, D.V.; Oliva, M.; Li, K.; Fazelzad, R.; Liu, Z.A.; Siu, L.L. Contemporary dose-escalation methods for early phase studies in the immunotherapeutics era. Eur. J. Cancer 2021, 158, 85–98. [Google Scholar] [CrossRef]
- Cook, N.; Hansen, A.R.; Siu, L.L.; Abdul Razak, A.R. Early phase clinical trials to identify optimal dosing and safety. Mol. Oncol. 2015, 9, 997–1007. [Google Scholar] [CrossRef] [PubMed]
- Le Tourneau, C.; Lee, J.J.; Siu, L.L. Dose escalation methods in phase I cancer clinical trials. J. Natl. Cancer Inst. 2009, 101, 708–720. [Google Scholar] [CrossRef] [PubMed]
- Obuchowski, N.A.; Bullen, J.A. Receiver operating characteristic (ROC) curves: Review of methods with applications in diagnostic medicine. Phys. Med. Biol. 2018, 63, 07TR01. [Google Scholar] [CrossRef]
- Leeflang, M.M.; Moons, K.G.; Reitsma, J.B.; Zwinderman, A.H. Bias in sensitivity and specificity caused by data-driven selection of optimal cutoff values: Mechanisms, magnitude, and solutions. Clin. Chem. 2008, 54, 729–737. [Google Scholar] [CrossRef]
- Gerke, O.; Lindholt, J.S.; Abdo, B.H.; Lambrechtsen, J.; Frost, L.; Steffensen, F.H.; Karon, M.; Egstrup, K.; Urbonaviciene, G.; Busk, M.; et al. Prevalence and extent of coronary artery calcification in the middle-aged and elderly population. Eur. J. Prev. Cardiol. 2021, 28, 2048–2055. [Google Scholar] [CrossRef]
- Schmermund, A. The Agatston calcium score: A milestone in the history of cardiac CT. J. Cardiovasc. Comput. Tomogr. 2014, 8, 414–417. [Google Scholar] [CrossRef] [PubMed]
- Diederichsen, A.C.; Sand, N.P.; Nørgaard, B.; Lambrechtsen, J.; Jensen, J.M.; Munkholm, H.; Aziz, A.; Gerke, O.; Egstrup, K.; Larsen, M.L.; et al. Discrepancy between coronary artery calcium score and HeartScore in middle-aged Danes: The DanRisk study. Eur. J. Prev. Cardiol. 2012, 19, 558–564. [Google Scholar] [CrossRef] [PubMed]
- Diederichsen, A.C.; Rasmussen, L.M.; Søgaard, R.; Lambrechtsen, J.; Steffensen, F.H.; Frost, L.; Egstrup, K.; Urbonaviciene, G.; Busk, M.; Olsen, M.H.; et al. The Danish Cardiovascular Screening Trial (DANCAVAS): Study protocol for a randomized controlled trial. Trials 2015, 16, 554. [Google Scholar] [CrossRef]
- Lindholt, J.S.; Rasmussen, L.M.; Søgaard, R.; Lambrechtsen, J.; Steffensen, F.H.; Frost, L.; Egstrup, K.; Urbonaviciene, G.; Busk, M.; Olsen, M.H.; et al. Baseline findings of the population-based, randomized, multifaceted Danish cardiovascular screening trial (DANCAVAS) of men aged 65-74 years. Br. J. Surg. 2019, 106, 862–871. [Google Scholar] [CrossRef] [PubMed]
- López-Ratón, M.; Cadarso-Suárez, C.; Molanes-López, E.M.; Letón, E. Confidence intervals for the symmetry point: An optimal cutpoint in continuous diagnostic tests. Pharm. Stat. 2016, 15, 178–192. [Google Scholar] [CrossRef]
- López-Ratón, M.; Molanes-López, E.M.; Letón, E.; Cadarso-Suárez, C. GsymPoint: An R package to estimate the generalized symmetry point, an optimal cut-off point for binary classification in continuous diagnostic tests. R J. 2017, 9, 262–283. [Google Scholar] [CrossRef]
- Schisterman, E.F.; Faraggi, D.; Reiser, B.; Hu, J. Youden Index and the optimal threshold for markers with mass at zero. Stat. Med. 2008, 27, 297–315. [Google Scholar] [CrossRef]
- Laking, G.; Lord, J.; Fischer, A. The economics of diagnosis. Health. Econ. 2006, 15, 1109–1120. [Google Scholar] [CrossRef]
- Greiner, M.; Pfeiffer, D.; Smith, R.D. Principles and practical application of the receiver-operating characteristic analysis for diagnostic tests. Prev. Vet. Med. 2000, 45, 23–41. [Google Scholar] [CrossRef]
- Pepe, M.S.; Janes, H.; Li, C.I.; Bossuyt, P.M.; Feng, Z.; Hilden, J. Early-Phase Studies of Biomarkers: What Target Sensitivity and Specificity Values Might Confer Clinical Utility? Clin. Chem. 2016, 62, 737–742. [Google Scholar] [CrossRef]
- Peng, L.; Manatunga, A.; Wang, M.; Guo, Y.; Rahman, A.F. A general approach to categorizing a continuous scale according to an ordinal outcome. J. Stat. Plan. Inference 2016, 172, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Mallett, S.; Halligan, S.; Thompson, M.; Collins, G.S.; Altman, D.G. Interpreting diagnostic accuracy studies for patient care. B.M.J. 2012, 345, e3999. [Google Scholar] [CrossRef] [PubMed]
- Royston, P.; Altman, D.G.; Sauerbrei, W. Dichotomizing continuous predictors in multiple regression: A bad idea. Stat. Med. 2006, 25, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Altman, D.G. Problems in dichotomizing continuous variables. Am. J. Epidemiol. 1994, 139, 442–455. [Google Scholar] [CrossRef]
- Landsheer, J.A. The Clinical Relevance of Methods for Handling Inconclusive Medical Test Results: Quantification of Uncertainty in Medical Decision-Making and Screening. Diagnostics 2018, 8, 32. [Google Scholar] [CrossRef] [PubMed]
- Landsheer, J.A. Interval of Uncertainty: An Alternative Approach for the Determination of Decision Thresholds, with an Illustrative Application for the Prediction of Prostate Cancer. PLoS ONE 2016, 11, e0166007. [Google Scholar] [CrossRef]
- Coste, J.; Jourdain, P.; Pouchot, J. A gray zone assigned to inconclusive results of quantitative diagnostic tests: Application to the use of brain natriuretic peptide for diagnosis of heart failure in acute dyspneic patients. Clin. Chem. 2006, 52, 2229–2235. [Google Scholar] [CrossRef] [PubMed]
- Coste, J.; Pouchot, J. A grey zone for quantitative diagnostic and screening tests. Int. J. Epidemiol. 2003, 32, 304–313. [Google Scholar] [CrossRef]
- Greiner, M. Two-graph receiver operating characteristic (TG-ROC): Update version supports optimisation of cut-off values that minimise overall misclassification costs. J. Immunol. Methods 1996, 191, 93–94. [Google Scholar] [CrossRef]
- Greiner, M.; Sohr, D.; Göbel, P. A modified ROC analysis for the selection of cut-off values and the definition of intermediate results of serodiagnostic tests. J. Immunol. Methods 1995, 185, 123–132. [Google Scholar] [CrossRef]
- Briggs, W.M.; Zaretzki, R. The Skill Plot: A graphical technique for evaluating continuous diagnostic tests. Biometrics 2008, 64, 250–256. [Google Scholar] [CrossRef] [PubMed]
- Altman, D.G.; Vergouwe, Y.; Royston, P.; Moons, K.G. Prognosis and prognostic research: Validating a prognostic model. B.M.J. 2009, 338, b605. [Google Scholar] [CrossRef] [PubMed]
- Ciocan, A.; Al Hajjar, N.; Graur, F.; Oprea, V.C.; Ciocan, R.A.; Bolboaca, S.D. Receiver operating characteristic prediction for classification: Performances in cross-validation by example. Mathematics 2020, 8, 1741. [Google Scholar] [CrossRef]
- Krzanowski, W.J.; Hand, D.J. ROC Curves for Continuous Data; Chapman & Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Pepe, M.; Longton, G.; Janes, H. Estimation and Comparison of Receiver Operating Characteristic Curves. Stata J. 2009, 9, 1–16. [Google Scholar] [CrossRef]
- Hajian-Tilaki, K.O.; Hanley, J.A.; Joseph, L.; Collet, J.P. A comparison of parametric and nonparametric approaches to ROC analysis of quantitative diagnostic tests. Med. Decis. Making 1997, 17, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, F.; Turnbull, B.W. Nonparametric methods for evaluating diagnostic tests. Stat. Sin. 1996, 6, 47–62. [Google Scholar]
- Hsieh, F.; Turnbull, B.W. Nonparametric and semiparametric estimation of the receiver operating characteristic curve. Ann. Stat. 1996, 24, 25–40. [Google Scholar] [CrossRef]

| Scenario | Closest-to-(0,1) Criterion | Liu’s Method | Youden Index |
|---|---|---|---|
| 1 | 3 | 3 | 3 |
| 2 | 3.18 | 3.34 | 3.42 |
| 3 | 3.65 | 3.61 | 3.6 |
| 4 | 3.88 | 3.52 | 3.45 |
| Prevalence | Patients | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Bias, % | MSE | Bias, % | MSE | Bias, % | MSE | Bias, % | MSE | ||
| 0.1 | 101 | 5.1 | 0.128 | 9.2 | 0.360 | 7.5 | 0.293 | 8.4 | 0.504 |
| 201 | 3.4 | 0.068 | 4.7 | 0.154 | 4.5 | 0.130 | 5.8 | 0.242 | |
| 301 | 2.5 | 0.047 | 3.0 | 0.093 | 3.4 | 0.089 | 4.8 | 0.168 | |
| 401 | 1.9 | 0.034 | 2.7 | 0.074 | 2.9 | 0.065 | 3.8 | 0.122 | |
| 501 | 1.6 | 0.028 | 1.9 | 0.057 | 2.5 | 0.049 | 3.3 | 0.105 | |
| 601 | 1.4 | 0.023 | 1.5 | 0.044 | 2.1 | 0.038 | 2.8 | 0.085 | |
| 701 | 1.4 | 0.021 | 1.4 | 0.037 | 1.9 | 0.032 | 2.6 | 0.073 | |
| 801 | 1.3 | 0.018 | 1.5 | 0.033 | 1.7 | 0.028 | 2.2 | 0.061 | |
| 0.3 | 101 | 1.5 | 0.045 | 1.7 | 0.098 | 1.8 | 0.069 | 2.7 | 0.169 |
| 201 | 0.76 | 0.026 | 1.1 | 0.052 | 1.1 | 0.037 | 1.7 | 0.084 | |
| 301 | 0.63 | 0.019 | 0.90 | 0.035 | 0.98 | 0.026 | 1.2 | 0.064 | |
| 401 | 0.62 | 0.016 | 0.73 | 0.028 | 0.89 | 0.021 | 1.03 | 0.050 | |
| 501 | 0.50 | 0.012 | 0.60 | 0.023 | 0.81 | 0.017 | 1.01 | 0.043 | |
| 601 | 0.46 | 0.011 | 0.57 | 0.022 | 0.72 | 0.014 | 0.88 | 0.038 | |
| 701 | 0.38 | 0.010 | 0.61 | 0.019 | 0.62 | 0.013 | 0.82 | 0.033 | |
| 801 | 0.38 | 0.009 | 0.48 | 0.016 | 0.62 | 0.012 | 0.66 | 0.029 | |
| 0.5 | 101 | −0.06 | 0.039 | 0.34 | 0.074 | −0.11 | 0.053 | 0.25 | 0.125 |
| 201 | 0.26 | 0.022 | −0.07 | 0.045 | 0.10 | 0.029 | 0.23 | 0.071 | |
| 301 | 0.12 | 0.016 | −0.05 | 0.032 | 0.15 | 0.020 | 0.36 | 0.051 | |
| 401 | 0.13 | 0.012 | −0.15 | 0.025 | 0.18 | 0.015 | 0.27 | 0.039 | |
| 501 | 0.13 | 0.010 | −0.01 | 0.022 | 0.11 | 0.013 | 0.07 | 0.033 | |
| 601 | 0.04 | 0.009 | −0.24 | 0.019 | 0.08 | 0.011 | 0.09 | 0.029 | |
| 701 | 0.09 | 0.008 | −0.26 | 0.016 | 0.14 | 0.010 | 0.19 | 0.026 | |
| 801 | 0.07 | 0.007 | −0.24 | 0.015 | 0.18 | 0.008 | 0.06 | 0.023 | |
| 0.7 | 101 | −1.1 | 0.046 | −1.7 | 0.075 | −1.7 | 0.067 | −1.6 | 0.174 |
| 201 | −0.54 | 0.026 | −1.1 | 0.044 | −0.74 | 0.033 | −0.74 | 0.993 | |
| 301 | −0.59 | 0.019 | −0.90 | 0.033 | −0.64 | 0.025 | −0.61 | 0.065 | |
| 401 | −0.63 | 0.014 | −0.81 | 0.026 | −0.35 | 0.019 | −0.35 | 0.051 | |
| 501 | −0.56 | 0.012 | −0.75 | 0.021 | −0.56 | 0.016 | −0.17 | 0.043 | |
| 601 | −0.38 | 0.010 | −0.64 | 0.019 | −0.51 | 0.014 | −0.17 | 0.035 | |
| 701 | −0.25 | 0.008 | −0.70 | 0.016 | −0.48 | 0.012 | −0.18 | 0.031 | |
| 801 | −0.28 | 0.008 | −0.58 | 0.015 | −0.43 | 0.011 | −0.05 | 0.026 | |
| Prevalence | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Bias, % (MSE) | Mean No. of Patients, 95% CI | Bias, % (MSE) | Mean No. of Patients, 95% CI | Bias, % (MSE) | Mean No. of Patients, 95% CI | Bias, % (MSE) | Mean No. of Patients, 95% CI | |
| 0.1 | 3.7 (0.071) | 192 [189–196] | 4.8 (0.169) | 192 [188–195] | 4.7 (0.153) | 189 [186–192] | 5.4 (0.241) | 200 [196–204] |
| 0.3 | 0.94 (0.028) | 194 [190–198] | 1.3 (0.056) | 198 [194–201] | 1.4 (0.043) | 195 [191–198] | 2.0 (0.096) | 197 [193–201] |
| 0.5 | 0.10 (0.024) | 199 [195–204] | 0.02 (0.047) | 196 [192–200] | −0.04 (0.032) | 193 [189–197] | 0.17 (0.078) | 199 [195–202] |
| 0.7 | −0.66 (0.026) | 197 [193–201] | −1.2 (0.047) | 203 [199–207] | −0.98 (0.038) | 190 [187–194] | −0.81 (0.100) | 197 [193–201] |
| Prevalence | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Bias, % (MSE) | Mean No. of Patients, 95% CI | Bias, % (MSE) | Mean No. of Patients, 95% CI | Bias, % (MSE) | Mean No. of Patients, 95% CI | Bias, % (MSE) | Mean No. of Patients, 95% CI | |
| 0.1 | 2.7 (0.048) | 312 [305–319] | 3.2 (0.103) | 312 [304–319] | 3.2 (0.082) | 319 [312–326] | 4.4 (0.158) | 343 [335–352] |
| 0.3 | 0.71 (0.021) | 310 [302–318] | 0.99 (0.036) | 327 [319–336] | 0.98 (0.027) | 312 [304–319] | 1.3 (0.065) | 335 [327–343] |
| 0.5 | 0.15 (0.017) | 319 [311–328] | −0.02 (0.033) | 323 [315–331] | 0.15 (0.022) | 315 [307–323] | 0.28 (0.049) | 330 [322–338] |
| 0.7 | −0.57 (0.020) | 321 [313–330] | −0.92 (0.034) | 336 [328–345] | −0.62 (0.025) | 316 [308–324] | −0.49 (0.068) | 322 [314–330] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerke, O.; Zapf, A. Convergence Behavior of Optimal Cut-Off Points Derived from Receiver Operating Characteristics Curve Analysis: A Simulation Study. Mathematics 2022, 10, 4206. https://doi.org/10.3390/math10224206
Gerke O, Zapf A. Convergence Behavior of Optimal Cut-Off Points Derived from Receiver Operating Characteristics Curve Analysis: A Simulation Study. Mathematics. 2022; 10(22):4206. https://doi.org/10.3390/math10224206
Chicago/Turabian StyleGerke, Oke, and Antonia Zapf. 2022. "Convergence Behavior of Optimal Cut-Off Points Derived from Receiver Operating Characteristics Curve Analysis: A Simulation Study" Mathematics 10, no. 22: 4206. https://doi.org/10.3390/math10224206
APA StyleGerke, O., & Zapf, A. (2022). Convergence Behavior of Optimal Cut-Off Points Derived from Receiver Operating Characteristics Curve Analysis: A Simulation Study. Mathematics, 10(22), 4206. https://doi.org/10.3390/math10224206