Optimal Estimation of Large Functional and Longitudinal Data by Using Functional Linear Mixed Model
Abstract
:1. Introduction
2. Preliminary
2.1. Settings
2.2. Functional Data Model
2.3. Methodologies of FPCA and FLMM
2.4. Comparison between FPCA and FLMM
3. Optimal Estimation for Large Balanced Longitudinal Data
3.1. Novel Estimating Procedure
3.2. Regularity Assumptions
3.3. Large Sample Property
3.4. Tuning Parameter Selection
4. Simulation Study
4.1. Simulation Settings
4.2. Simulation Results
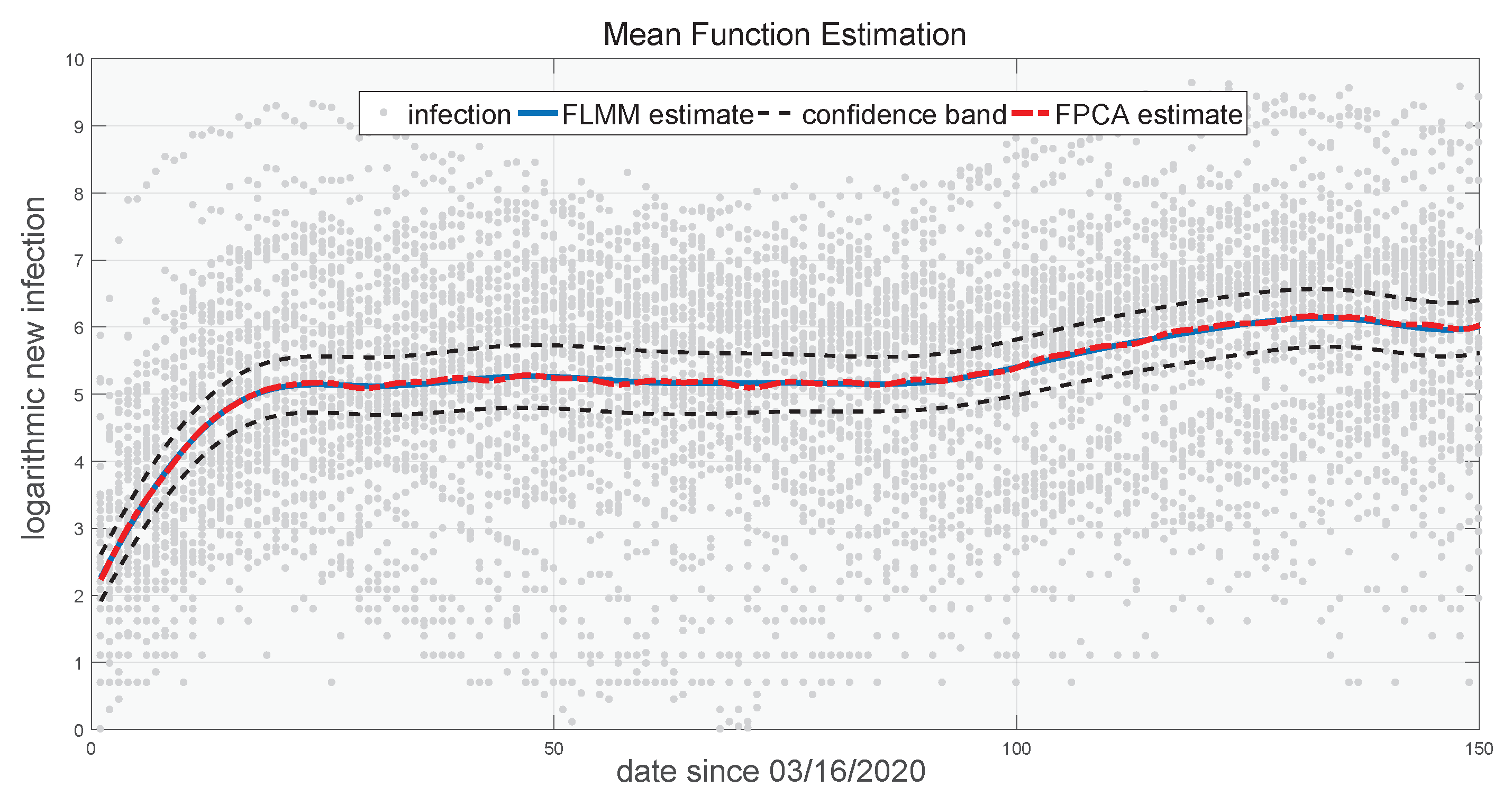
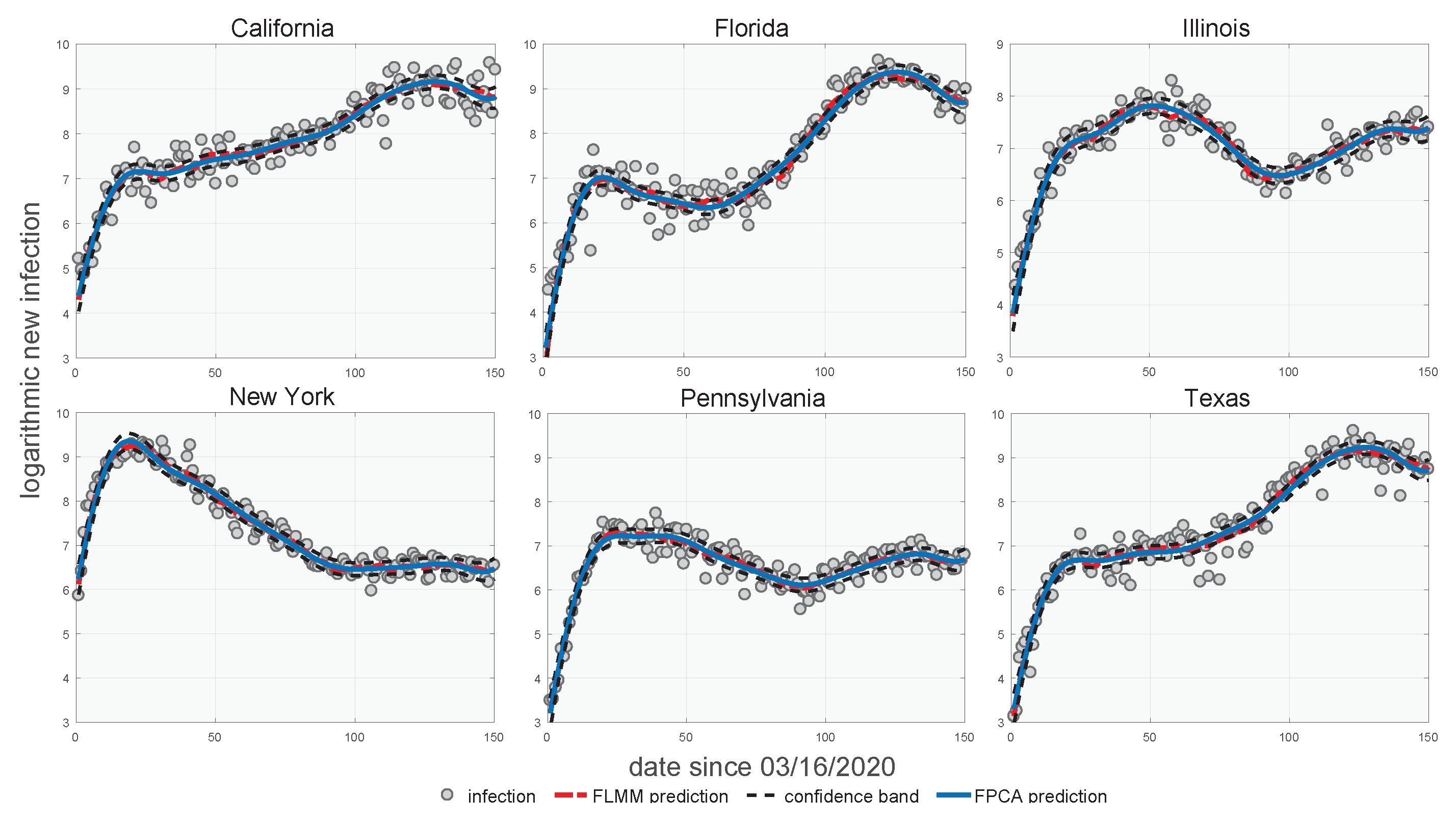
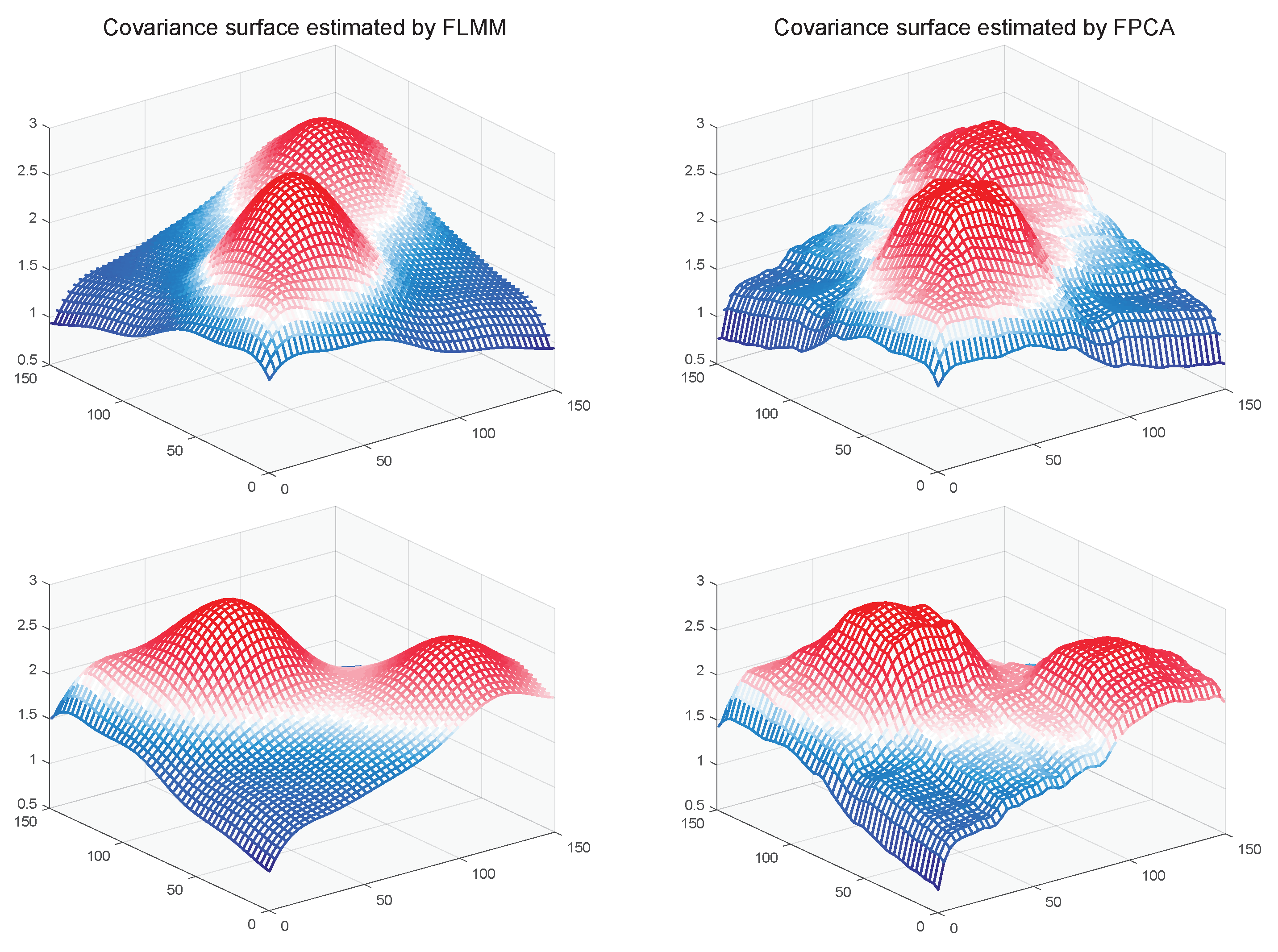
5. Real Data Analysis
6. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of Theorems
Appendix A.1. Lemmas
- Weyl’s lemma: Let be two Hermitian matrices. Then, for each ,
- Ostrowski’s lemma: Let be a Hermitian matrix, and be an matrix. Then, for each , there exists an nonnegative real with such thatwhere means the ith eigenvalues of .
Appendix A.2. Proofs
Appendix B. Estimators of FPCA and FLMM
Appendix B.1. Estimator of FPCA
Appendix B.2. Estimator of FLMM
References
- Ramsay, J.; Silverman, B. Functional Data Analysis; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Králík, M.; Klíma, O.; Ŏuta, M.; Malina, R.M.; Kozieł, S.; Polcerová, L.; Škultétyová, A.; Španěl, M.; Kukla, L.; Zemčík, P. Estimating Growth in Height from Limited Longitudinal Growth Data Using Full-Curves Training Dataset: A Comparison of Two Procedures of Curve Optimization—Functional Principal Component Analysis and SITAR. Children 2021, 8, 934. [Google Scholar] [CrossRef] [PubMed]
- Ullah, S.; Finch, C. Applications of functional data analysis: A systematic review. BMC Med Res. Methodol. 2013, 13, 43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, T.; Yuan, M. Nonparametric Covariance Function Estimation for Functional and Longitudinal Data; University of Pennsylvania and Georgia Inistitute of Technology: Philadelphia, PA, USA, 2010. [Google Scholar]
- Diggle, P.; Diggle, P.; Heagerty, P.; Liang, K.; Zeger, S. Analysis of Longitudinal Data; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Wood, S.; Wood, M. Package ‘mgcv’. R Package Version 2015, 1, 729. [Google Scholar]
- Patterson, H.; Thompson, R. Recovery of inter-block information when block sizes are unequal. Biometrika 1971, 58, 545–554. [Google Scholar] [CrossRef]
- Laird, N.; Ware, J. Random-effects models for longitudinal data. Biometrics 1982, 1, 963–974. [Google Scholar] [CrossRef]
- Hall, P.; Müller, H.; Wang, J. Properties of principal component methods for functional and longitudinal data analysis. Ann. Stat. 2006, 34, 1493–1517. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Hsing, T. Uniform convergence rates for nonparametric regression and principal component analysis in functional/longitudinal data. Ann. Stat. 2010, 38, 3321–3351. [Google Scholar] [CrossRef]
- Yao, F.; Müller, H.; Wang, J. Functional data analysis for sparse longitudinal data. J. Am. Stat. Assoc. 2005, 100, 577–590. [Google Scholar] [CrossRef]
- Paul, D.; Peng, J. Consistency of restricted maximum likelihood estimators of principal components. Ann. Stat. 2009, 37, 1229–1271. [Google Scholar] [CrossRef]
- Peng, J.; Paul, D. A geometric approach to maximum likelihood estimation of the functional principal components from sparse longitudinal data. J. Comput. Graph. Stat. 2009, 18, 995–1015. [Google Scholar] [CrossRef] [Green Version]
- Bunea, F.; Ivanescu, A.; Wegkamp, M. Adaptive inference for the mean of a Gaussian process in functional data. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2011, 73, 531–558. [Google Scholar] [CrossRef]
- Rice, J.; Silverman, B. Estimating the mean and covariance structure nonparametrically when the data are curves. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1991, 53, 233–243. [Google Scholar] [CrossRef]
- Yu, F.; Liu, L.; Yu, N.; Ji, L.; Qiu, D. A method of L1-norm principal component analysis for functional data. Symmetry 2020, 12, 182. [Google Scholar] [CrossRef] [Green Version]
- James, G.; Hastie, T.; Sugar, C. Principal component models for sparse functional data. Biometrika 2000, 87, 587–602. [Google Scholar] [CrossRef] [Green Version]
- James, G.; Sugar, C. Clustering for sparsely sampled functional data. J. Am. Stat. Assoc. 2003, 98, 397–408. [Google Scholar] [CrossRef]
- Rice, J.; Wu, C. Nonparametric mixed effects models for unequally sampled noisy curves. Biometrics 2001, 57, 253–259. [Google Scholar] [CrossRef] [Green Version]
- Shi, M.; Weiss, R.; Taylor, J. An analysis of paediatric CD4 counts for acquired immune deficiency syndrome using flexible random curves. J. R. Stat. Soc. Ser. C Appl. Stat. 1996, 45, 151–163. [Google Scholar] [CrossRef]
- Antoniadis, A.; Sapatinas, T. Estimation and inference in functional mixed-effects models. Comput. Stat. Data Anal. 2007, 51, 4793–4813. [Google Scholar] [CrossRef]
- Morris, J.; Carroll, R. Wavelet-based functional mixed models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2006, 68, 179–199. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Brown, P.; Morris, J. Robust, adaptive functional regression in functional mixed model framework. J. Am. Stat. Assoc. 2011, 106, 1167–1179. [Google Scholar] [CrossRef] [Green Version]
- Qiu, P.; Zou, C.; Wang, Z. Nonparametric profile monitoring by mixed effects modeling. Technometrics 2010, 52, 265–277. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, J. Local polynomial mixed-effects models for longitudinal data. J. Am. Stat. Assoc. 2002, 97, 883–897. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, J. Nonparametric Regression Methods for Longitudinal Data Analysis: Mixed-Effects Modeling Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Rice, J. Functional and longitudinal data analysis: Perspectives on smoothing. Stat. Sinica 2004, 1, 631–647. [Google Scholar]
- Wang, J.; Chiou, J.; Müller, H. Functional data analysis. Annu. Rev. Stat. Appl. 2016, 3, 257–295. [Google Scholar] [CrossRef] [Green Version]
- Cai, T.; Yuan, M. Optimal estimation of the mean function based on discretely sampled functional data: Phase transition. Ann. Stat. 2011, 39, 2330–2355. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Gijbels, I. Local Polynomial Modelling and Its Applications; Routledge: London, UK, 2018. [Google Scholar]
- Eilers, P.; Marx, B. Flexible smoothing with B-splines and penalties. Stat. Sci. 1996, 11, 89–102. [Google Scholar] [CrossRef]
- Acal, C.; Aguilera, A.; Escabias, M. New modeling approaches based on varimax rotation of functional principal components. Mathematics 2020, 8, 2085. [Google Scholar] [CrossRef]
- Breslow, N.; Clayton, D. Approximate inference in generalized linear mixed models. J. Am. Stat. Assoc. 1993, 88, 9–25. [Google Scholar]
- Vonesh, E.; Wang, H.; Nie, L.; Majumdar, D. Conditional second-order generalized estimating equations for generalized linear and nonlinear mixed-effects models. J. Am. Stat. Assoc. 2002, 97, 271–283. [Google Scholar] [CrossRef]
- Breslow, N.; Lin, X. Bias correction in generalised linear mixed models with a single component of dispersion. Biometrika 1995, 82, 81–91. [Google Scholar] [CrossRef]
- Lee, Y.; Nelder, J. Hierarchical generalized linear models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1996, 58, 619–656. [Google Scholar] [CrossRef]
- Lin, X.; Breslow, N. Bias correction in generalized linear mixed models with multiple components of dispersion. J. Am. Stat. Assoc. 1996, 91, 1007–1016. [Google Scholar] [CrossRef]
- Ruppert, D.; Wand, M.; Carroll, R. Semiparametric Regression; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wood, S.; Pya, N.; Säfken, B. Smoothing parameter and model selection for general smooth models. J. Am. Stat. Assoc. 2016, 111, 1548–1563. [Google Scholar] [CrossRef]
- Vershynin, R. High-Dimensional Probability: An Introduction with Applications in Data Science; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Bickel, P.; Levina, E. Regularized estimation of large covariance matrices. Ann. Stat. 2008, 36, 199–227. [Google Scholar] [CrossRef]
- Wainwright, M. High-Dimensional Statistics: A Non-asymptotic Viewpoint; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Tsybakov, A.B. Introduction to Nonparametric Estimation; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Wood, S. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2011, 73, 3–36. [Google Scholar] [CrossRef] [Green Version]
- Nelder, J.; Wedderburn, R. Generalized linear models. J. R. Stat. Soc. Ser. A (Gen.) 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Hall, P.; Müller, H.; Yao, F. Modelling sparse generalized longitudinal observations with latent Gaussian processes. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2008, 70, 703–723. [Google Scholar] [CrossRef]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 1, 461–464. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, M.; Yang, Y. Optimal Estimation of Large Functional and Longitudinal Data by Using Functional Linear Mixed Model. Mathematics 2022, 10, 4322. https://doi.org/10.3390/math10224322
Ran M, Yang Y. Optimal Estimation of Large Functional and Longitudinal Data by Using Functional Linear Mixed Model. Mathematics. 2022; 10(22):4322. https://doi.org/10.3390/math10224322
Chicago/Turabian StyleRan, Mengfei, and Yihe Yang. 2022. "Optimal Estimation of Large Functional and Longitudinal Data by Using Functional Linear Mixed Model" Mathematics 10, no. 22: 4322. https://doi.org/10.3390/math10224322




