A Bayesian Causal Model to Support Decisions on Treating of a Vineyard
Abstract
:1. Introduction
2. Methods
- : decision variable for row j set at the end of Day 4 from the start of current time interval i; the value 2 refers to the new treatment, 1 to the conventional treatment, and 0 otherwise;
- : the degree of exposition of row j to oospores in the air during the first 4 days of a time interval i, with 0 the best class and 3 the worst;
- : the average amount of oospores on leaves in the current row j during the first 4 days of time interval i; the null value refers to the best class, while 5 to the worst;
- : the average amount of oospores on leaves in the considered row j during the 3 days after treatment at time i, with 0 the best class and 5 the worst;
- : the average local humidity at row j in the first 4 days of time interval i, before making the decision; it regulates the diffusion of infection;
- : the average local temperature at row j during the first 4 days of time interval i, before making the decision; it regulates the diffusion of infection;
- : the climatological score for row j at time i based on the predicted temperature and humidity for the 3 days following treatment (unknown at the decision time); it represents climatological limitations or enhancements both on oospores and on incidence;
- : the fraction of leaves already infected in row j after the first 4 days of time interval i (prevalence);
- : the fraction of newly infected leaves in row j (incidence) at the end of the time interval i, that is after 3 days from the decision on treating.
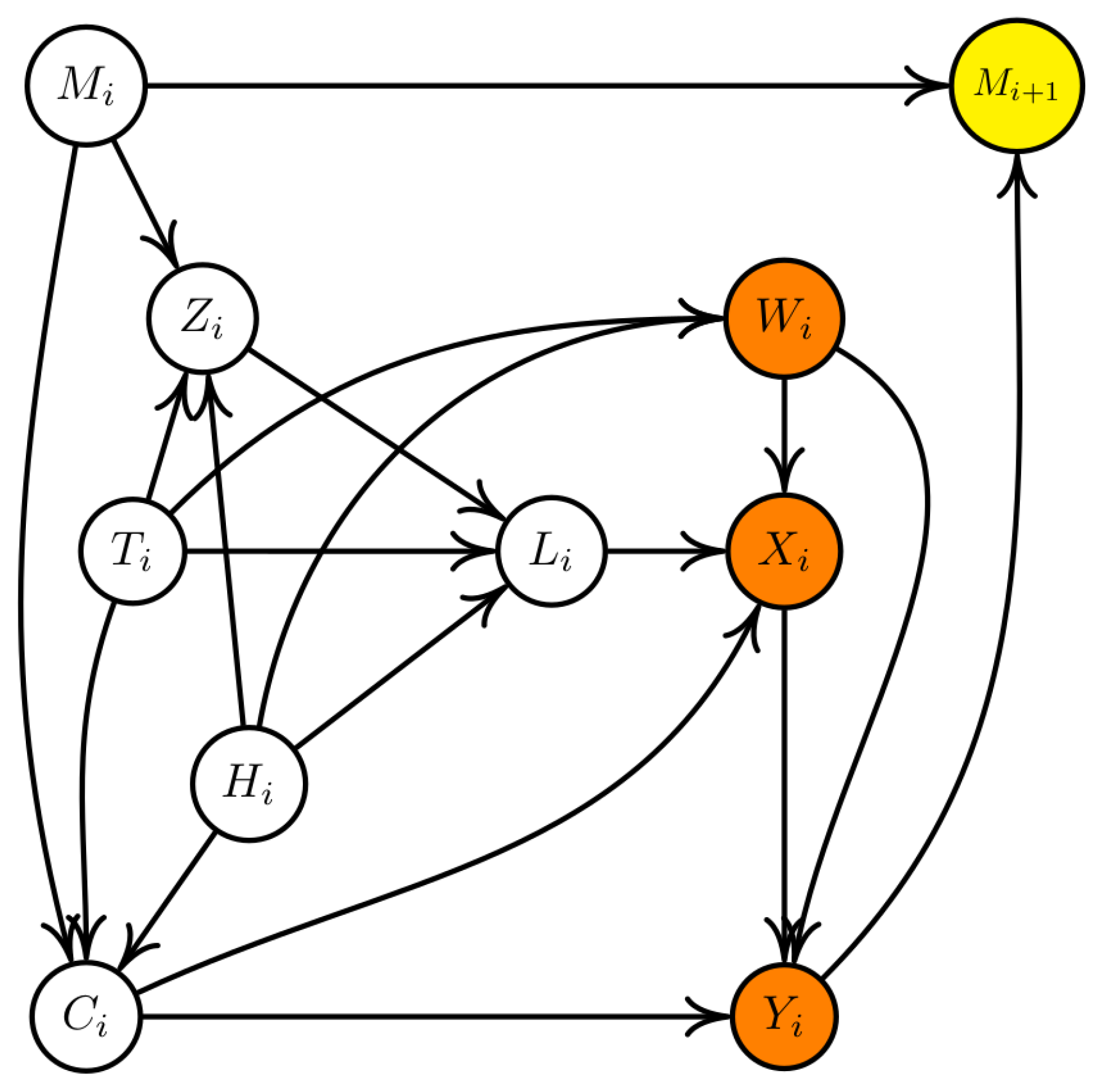
2.1. A Causal DAG
2.2. Does the Vineyard Row Need to Be Treated at Time Interval i?
2.3. Mediation Analysis
3. Results
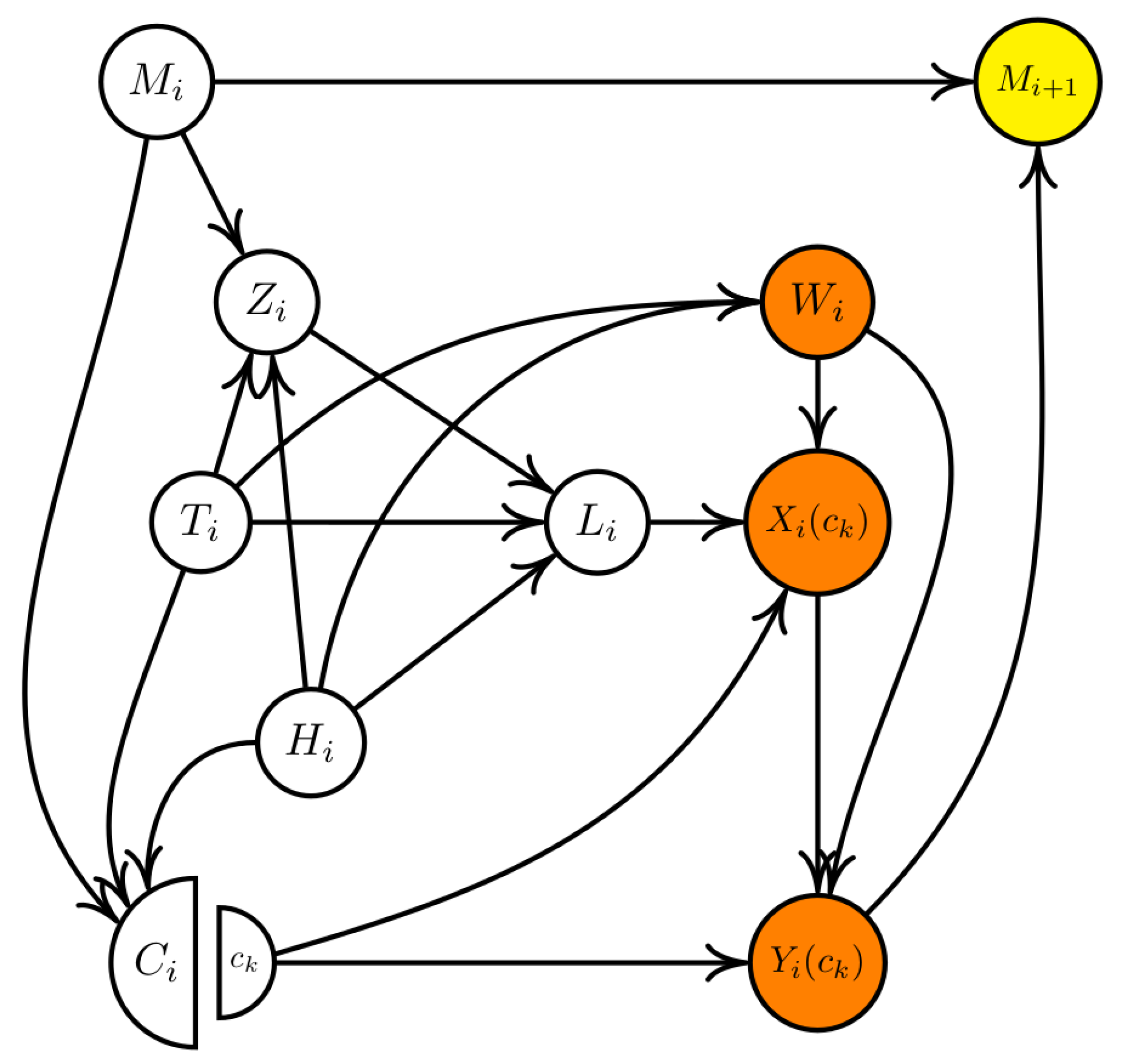
3.1. Potential Outcomes and SWIGs
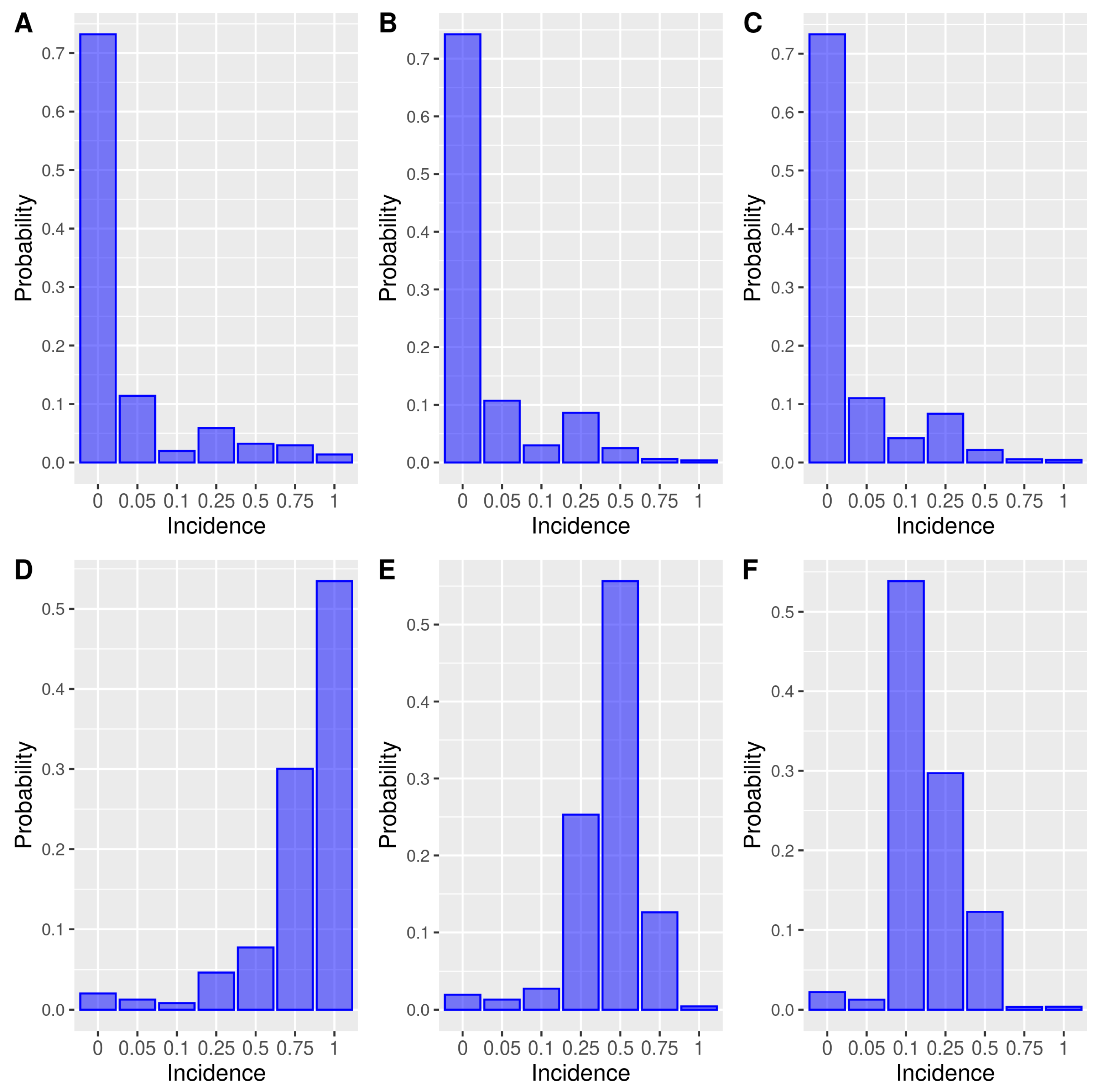
3.2. Uncertainty about Model Parameters: A Prior Predictive Approach
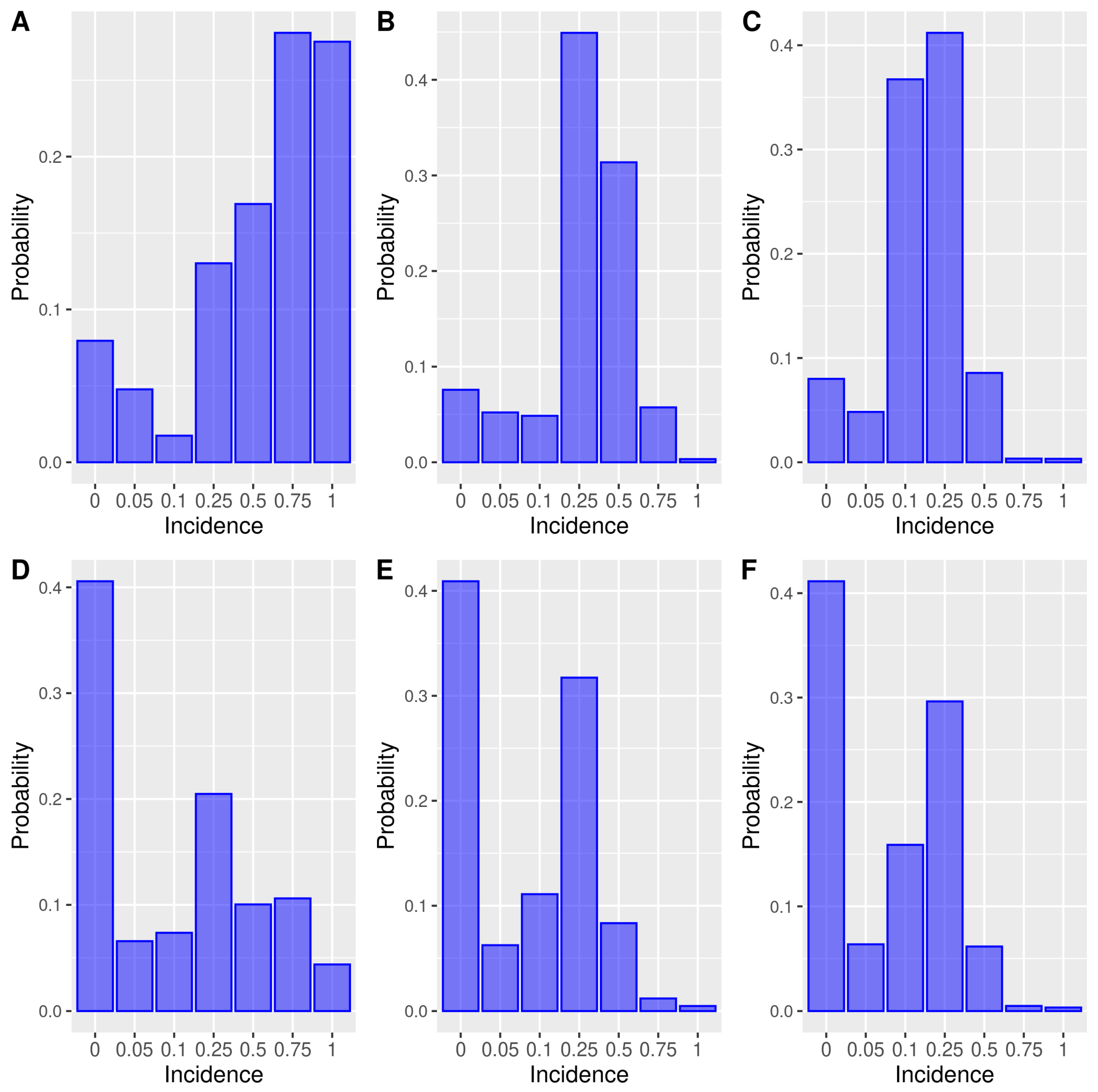
3.3. Monte Carlo Estimate of Future Incidence
| Algorithm 1: Monte Carlo estimate of incidence given information from the current time interval at the end of 3 days after treatment. |
| Data: Conditioning values for different configurations; number of iterations . Result: Estimated probability distribution of Y given each configuration . 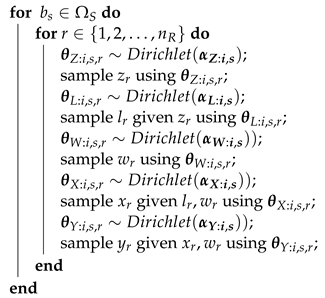 |
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BN | Bayesian Network |
| DAG | Directed Acyclic Graph |
| SCM | Structural Causal Model |
| ACE | Average Causal Effect |
References
- Koledenkova, K.; Esmaeel, Q.; Jacquard, C.; Nowak, J.; Clément, C.; Ait Barka, E. Plasmopara Viticola the Causal Agent of Downy Mildew of Grapevine: From Its Taxonomy to Disease Management. Front. Microbiol. 2022, 13, 889472. [Google Scholar] [CrossRef] [PubMed]
- Wong, F.P.; Burr, H.N.; Wilcox, W.F. Heterothallism in Plasmopara Viticola. Plant Pathol. 2001, 50, 427–432. [Google Scholar] [CrossRef]
- Kab, S.; Spinosi, J.; Chaperon, L.; Dugravot, A.; Singh-Manoux, A.; Moisan, F.; Elbaz, A. Agricultural Activities and the Incidence of Parkinson’s Disease in the General French Population. Eur. J. Epidemiol. 2017, 32, 203–216. [Google Scholar] [CrossRef] [PubMed]
- Francesca, S.; Simona, G.; Francesco Nicola, T.; Andrea, R.; Vittorio, R.; Federico, S.; Cynthia, R.; Maria Lodovica, G. Downy Mildew (Plasmopara Viticola) Epidemics on Grapevine under Climate Change. Glob. Chang. Biol. 2006, 12, 1299–1307. [Google Scholar] [CrossRef]
- Leoni, S.; Basso, T.; Tran, M.; Schnée, S.; Fabre, A.L.; Kasparian, J.; Wolf, J.P.; Dubuis, P.H. Highly Sensitive Spore Detection to Follow Real-Time Epidemiology of Downy and Powdery Mildew. BIO Web Conf. 2022, 50, 04003. [Google Scholar] [CrossRef]
- Orlandini, S.; Massetti, L.; Marta, A.D. An Agrometeorological Approach for the Simulation of Plasmopara Viticola. Comput. Electron. Agric. 2008, 64, 149–161. [Google Scholar] [CrossRef]
- Orlandini, S.; Gozzini, B.; Rosa, M.; Egger, E.; Storchi, P.; Maracchi, G.; Miglietta, F. PLASMO: A Simulation Model for Control of Plasmopara Viticola on Grapevine1. EPPO Bull. 1993, 23, 619–626. [Google Scholar] [CrossRef]
- Brischetto, C.; Bove, F.; Fedele, G.; Rossi, V. A Weather-Driven Model for Predicting Infections of Grapevines by Sporangia of Plasmopara Viticola. Front. Plant Sci. 2021, 12, 636607. [Google Scholar] [CrossRef]
- Caffi, T.; Rossi, V.; Cossu, A.; Fronteddu, F. Empirical vs. Mechanistic Models for Primary Infections of Plasmopara Viticola*. EPPO Bull. 2007, 37, 261–271. [Google Scholar] [CrossRef]
- Vercesi, A.; Toffolatti, S.L.; Zocchi, G.; Guglielmann, R.; Ironi, L. A New Approach to Modelling the Dynamics of Oospore Germination in Plasmopara Viticola. Eur. J. Plant. Pathol. 2010, 128, 113–126. [Google Scholar] [CrossRef]
- Lalancette, N. A Quantitative Model for Describing the Sporulation of Plasmopara Viticola on Grape Leaves. Phytopathology 1988, 78, 1316. [Google Scholar] [CrossRef]
- Tran Manh Sung, C.; Strizyk, S.; Clerjeau, M. Simulation of the Date of Maturity of Plasmopara Viticola Oospores to Predict the Severity of Primary Infections in Grapevine. Plant Dis. 1990, 74, 120–124. [Google Scholar] [CrossRef]
- Dubuis, P.H.; Viret, O.; Bloesch, B.; Fabre, A.L.; Naef, A.; Bleyer, G.; Kassemeyer, H.H.; Krause, R. Using VitiMeteo-Plasmopara to better control downy mildew in grape. Rev. Suisse Vitic. Arboric. Hortic. 2012, 44, 192–198. [Google Scholar]
- Bove, F.; Savary, S.; Willocquet, L.; Rossi, V. Designing a Modelling Structure for the Grapevine Downy Mildew Pathosystem. Eur. J. Plant Pathol. 2020, 157, 251–268. [Google Scholar] [CrossRef]
- Chen, M.; Brun, F.; Raynal, M.; Makowski, D. Forecasting Severe Grape Downy Mildew Attacks Using Machine Learning. PLoS ONE 2020, 15, e0230254. [Google Scholar] [CrossRef]
- Brischetto, C.; Bove, F.; Languasco, L.; Rossi, V. Can Spore Sampler Data Be Used to Predict Plasmopara Viticola Infection in Vineyards? Front. Plant Sci. 2020, 11, 1187. [Google Scholar] [CrossRef]
- Bareinboim, E.; Pearl, J. A General Algorithm for Deciding Transportability of Experimental Results. J. Causal Inference 2013, 1, 107–134. [Google Scholar] [CrossRef] [Green Version]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Pearl, J. CAUSALITY: Models, Reasoning, and Inference, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009; p. 487. [Google Scholar]
- Michaud, A.M.; Chappellaz, C.; Hinsinger, P. Copper Phytotoxicity Affects Root Elongation and Iron Nutrition in Durum Wheat (Triticum Turgidum Durum L.). Plant Soil 2008, 310, 151–165. [Google Scholar] [CrossRef]
- Perria, R.; Ciofini, A.; Petrucci, W.A.; D’Arcangelo, M.E.M.; Valentini, P.; Storchi, P.; Carella, G.; Pacetti, A.; Mugnai, L. A Study on the Efficiency of Sustainable Wine Grape Vineyard Management Strategies. Agronomy 2022, 12, 392. [Google Scholar] [CrossRef]
- Valleggi, L.; Carella, G.; Perria, R.; Mugnai, L.; Stefanini, F. A Bayesian approach for treatment selection against Plasmopara viticola infections. 2022; manuscript in preparation. [Google Scholar]
- Rubin, D.B. Causal Inference Using Potential Outcomes. J. Am. Stat. Assoc. 2005, 100, 322–331. [Google Scholar] [CrossRef]
- Pearl, J. The Mediation Formula: A Guide to the Assessment of Causal Pathways in Nonlinear Models. In Causality: Statistical Perspectives and Applications; Technical Report; John Wiley and Sons: Chichester, UK, 2011; pp. 151–179. [Google Scholar]
- Richardson, T.S.; Robins, J.M. Single World Intervention Graphs (SWIGs): A Unification of the Counterfactual and Graphical Approaches to Causality; Working Paper; Center for Statistics and the Social Sciences, University of Washington: Seattle, WA, USA, 2013; Volume 128, Available online: https://csss.uw.edu/files/working-papers/2013/wp128.pdf (accessed on 1 October 2022).
- Lavik Ming, S.; Hardaker, J.B.; Lien, G.; Berge, T.W. A multi-attribute decision analysis of pest management strategies for Norwegian crop farmers. Agric. Syst. 2020, 178, 102741. [Google Scholar] [CrossRef]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Trade-Offs, 1st ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefanini, F.M.; Valleggi, L. A Bayesian Causal Model to Support Decisions on Treating of a Vineyard. Mathematics 2022, 10, 4326. https://doi.org/10.3390/math10224326
Stefanini FM, Valleggi L. A Bayesian Causal Model to Support Decisions on Treating of a Vineyard. Mathematics. 2022; 10(22):4326. https://doi.org/10.3390/math10224326
Chicago/Turabian StyleStefanini, Federico Mattia, and Lorenzo Valleggi. 2022. "A Bayesian Causal Model to Support Decisions on Treating of a Vineyard" Mathematics 10, no. 22: 4326. https://doi.org/10.3390/math10224326
APA StyleStefanini, F. M., & Valleggi, L. (2022). A Bayesian Causal Model to Support Decisions on Treating of a Vineyard. Mathematics, 10(22), 4326. https://doi.org/10.3390/math10224326






